1 Introduction

Certain rare human cells can reveal information relevant to disease. For example, nucleated erythrocytes carry genetic information about embryos (Purwosunu et al. 2006). Circulating tumor cells provide a potential source of information about the metastatic sites from which they originated. Collecting and investigating these specific cells might provide new solutions for various ongoing tasks in the field of bio-microfluidics. However, such isolation or separation of rare cells is technically challenging because of the low cellular frequency (Stott et al. 2010).

Efforts to successfully separate these specific cells from the blood have resulted in the development of lab-on-chip technologies. Among the various ways to separate the target cells, the method of cell transportation by microfluidic systems has several advantages (Stott et al. 2010; Park and Jung 2009; Bhagat et al. 2011; Hou et al. 2010; Yamada et al. 2007; Gossett et al. 2010; McFaul et al. 2012; Tanaka et al. 2012), including low cost, small sample and reagent requirements, and device portability (Tsutsui and Ho 2009). However, because of the complex microfluidics of cell movement inside channels, high-yield or high-selectivity fluidic conditions for cell separation systems have not yet been achieved.

To understand the microfluidic system, various studies have focused on the effects of bifurcations and loops in the flow channel. Jousse et al. (2006) observed the behavior of a droplet in a loop channel with a T junction. Vanapalli et al. (2009) used a rectangular microchannel to analyze the hydrodynamic resistance of a droplet. Others tried to manipulate the flows by exerting external forces such as pressure gradients, electric fields, and magnetic fields (Ismagilov et al. 2001). There were even efforts to control the aspect of the droplet itself (Vladisavljević et al. 2012).

In addition to microfluidic issues with cells, fluid and vesicle interactions have long been a challenge (Kondaraju et al. 2012; Guido and Tomaiuolo 2009; Farhat et al. 2011). Microfluidic networks with moving vesicles are complex and nonlinear systems because of the deformation of vesicles and interactions with the surrounding fluid. A full description of the path selection of a vesicle requires a complete understanding of the interactions between individual vesicle objects, the vesicle and the surrounding carrier fluid, the fluid and the channel wall, and the vesicle and the channel wall.

In this study, we investigate the path selection of vesicle with three different capillary numbers at a tertiary junction. We use the resultant velocity hypothesis to explain the result which cannot be explained by higher flow rate hypothesis. In addition, we investigate the residence time as the time spent at a junction.

1.1 Abstraction of microfluidic systems

Link et al. (2004) considered microfluidic channels as electrical circuits, using Eq. (1) to determine the pressure difference between the inlet and outlet conditions of a system and applying the product of the flow rate and dimensions to each channel (Fox et al. 2006). The factor Δp/q in Eq. (1) is the fluidic resistance in Eqs. (2) and (3):

$$\varDelta p = q\ln \left( \frac{3}{4} \right)\frac{1}{{wh^{3} }}\left[ {1 - \frac{192h}{{w\pi^{5} }}} \right]^{ - 1}$$
(1)

where q is the volume flow rate, Δp is the pressure decrease between inlet and outlet, η is fluid viscosity, and w, h, and l are the width, height, and length of the channel, respectively. Δp can be replaced with the gradient of voltage ΔV in an electrical circuit, and q can be replaced with the electrical current I. This comparison allows the fluid resistance to be defined in terms of electrical resistance.

$$\varDelta p = qR$$
(2)
$$R = \ln \left( \frac{3}{4} \right)\frac{1}{{wh^{3} }}\left[ {1 - \frac{192h}{{w\pi^{5} }}} \right]^{ - 1}$$
(3)

This concept is useful because the fluid resistance in a complex microfluidic channel can be calculated using Kirchoff’s law for electrical systems.

1.2 High flow rate hypothesis

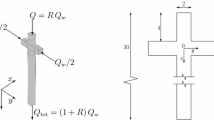
Choi et al. (2011) investigated the path selection of a bubble in a microfluidic network. They focused on networks based on T-shaped junctions where the bubble had only two choices (one of two downstream channels). Their study indicates that the bubble chooses the channel with the higher flow rate. However, this study is phenomenological and explains only circumstances in which the two downstream channels have equal width. For instance, for the channel in Fig. 1a, the path selection of the bubble can be explained using the higher flow rate hypothesis. However, for the channel in Fig. 1b, which has a point-symmetric network (about point C), the flow rate is equal in both channels, but the bubble will always choose the channel with the smaller width (path B). The difficulty of predicting the path selection of a bubble in complex microfluidic systems necessitates further analysis of microfluidic systems and bubble dynamics.

Fig. 1
figure 1

Schematic diagram of experimental bubble path selection (Choi et al. 2011): a the bubble follows the higher flow rate hypothesis; b the channel has a point-symmetric network about point C. The flow rate is equal in both channels, but the bubble always chooses the channel with the smaller width (path B)

Full size image

To understand the path selection of soft matter such as bubbles and vesicles in a complex channel system, we focused on the dynamics of a vesicle in a microfluidic system with a junction of three downstream channels. Our investigation involved downstream channels of different lengths, which allowed for passive control of the flow rate. We demonstrated that, in a microfluidic system with tertiary junctions, the path selection of the vesicle depends on the resultant velocity at the junction in each direction rather than on the flow rate of each downstream channel.

The dynamics of the microfluidic system in this study were investigated by numerical simulations. We used a lattice Boltzmann method (LBM) to simulate the incompressible low Reynolds number flow inside a microchannel. The dynamics of a vesicle inside a channel were determined using an immersed boundary method (IBM). The details of the numerical method are discussed in the numerical methods section.

2 Numerical methods

2.1 Lattice Boltzmann method (LBM)

The LBM for the single time Bhatnagar–Gross–Krook (BGK) model was used in this study (Chen and Doolen 1998; Kim et al. 2010). The main collision BGK equation with the forcing term proposed by Guo et al. (2002) can be written as

$$f_{i} \left( {{\mathbf{x}} + {\mathbf{e}}_{i} \Delta t,t + \Delta t} \right) - f_{i} \left( {{\mathbf{x}},t} \right) = - \frac{1}{\tau }\left( {f_{i} \left( {{\mathbf{x}},t} \right) - f_{i}^{eq} \left( {{\mathbf{x}},t} \right)} \right) + \Delta t\left( {1 - \frac{1}{2\tau }} \right)\omega_{i} \left[ {\frac{{{\mathbf{e}}_{i} - {\mathbf{u}}}}{{c_{\text{s}}^{2} }} + \frac{{\left( {{\mathbf{e}}_{i} \cdot {\mathbf{u}}} \right)}}{{c_{\text{s}}^{4} }}{\mathbf{e}}_{i} } \right] \cdot {\mathbf{f}},$$
(4)

with the local equilibrium distribution function

$$f_{i}^{{\text{eq}}} = \rho \omega_{i} \left[ {1 + \frac{1}{{c_{s}^{2} }}{\mathbf{e}}_{i} \cdot {\mathbf{u}} + \frac{1}{{2c_{s}^{4} }}\left( {{\mathbf{e}}_{i} \cdot {\mathbf{u}}} \right)^{2} - \frac{1}{{2c_{s}^{2} }}{\mathbf{u}} \cdot {\mathbf{u}}} \right],$$
(5)

where

$$\omega_{i} \left\{ \begin{gathered} \frac{4}{9},\quad \quad \quad i = 0 \hfill \\ \frac{1}{9},\quad \quad \quad i = 1,2,3,4 \hfill \\ \frac{1}{36},\quad \quad \;\,i = 5,6,7,8 \hfill \\ \end{gathered} \right.$$
(6)
$$e_{i} \left\{ \begin{gathered} \left( {0,0} \right)\,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,i = 0 \hfill \\ \left( {\cos \theta_{i} ,\sin \theta_{i} } \right),\quad \theta_{i} = \left( {i - 1} \right)\frac{\pi }{2}\quad \quad \quad \quad \;\;i = 1,2,3,4 \hfill \\ \sqrt 2 \left( {\cos \theta_{i} ,\sin \theta_{i} } \right),\quad \theta_{i} = \left( {i - 5} \right)\frac{\pi }{2} + \frac{\pi }{4}\quad \;\,i = 5,6,7,8 \hfill \\ \end{gathered} \right.$$
(7)

In the above equation, the density distribution function f i (x,t) indicates the portion of particles moving with the ith lattice velocity at lattice site x and time t, Δt is the time step, τ is the particle relaxation time, e i is the discrete microscopic velocity, f eq i is the local equilibrium distribution function, and \(c_{\text{s}} \left( { = c/\sqrt 3 } \right)\) is the speed of sound (c = Δx/Δt). The fluid density ρ and velocity u can be calculated using

$$\rho = \sum\limits_{i} {f_{i} } \quad \rho u = \sum\limits_{i} {f_{i} {\mathbf{e}}_{i} } .$$
(8)

The kinematic viscosity is given by

$$\nu = \left( {\tau - \frac{1}{2}} \right)c_{\text{s}}^{2} \varDelta t$$
(9)

2.2 Vesicle mechanics

Few models have been developed to simulate vesicle interactions with fluid. Deen et al. (2009) used direct numerical simulation (a combination of a front tracking model and an immersed boundary model) to elucidate drop interactions. A front tracking model was used to calculate the curvature of a membrane, and an immersed boundary model was used to calculate particle–fluid interactions. Washino et al. (2011) applied a continuous surface force (CSF) model to the interaction between fluid phases and solid particle phases, converting surface force into body force using a Dirac delta function. Zhang et al. (2008) treated the membrane of the vesicle as a neo-Hookean viscoelastic material. Similar to these approaches, we directly calculated surface tensile force to investigate vesicle membranes (Bagchi et al. 2005). The tension acting on two neighboring Lagrangian grid points on the membrane can be expressed as

$$T_{\text{e}} = \frac{{E_{\text{s}} }}{{\varepsilon^{3/2} }}\left( {\varepsilon^{3} - 1} \right),$$
(10)

where E s is the membrane shear modulus, and ε is the stretch ratio (original length by deformed length) (Zhang et al. 2008). Bending stress is calculated by the membrane curvature change as

$$T_{\text{b}} = \frac{\text{d}}{{{\text{d}}l}}\left[ {E_{\text{b}} \left( {\kappa - \kappa_{0} } \right)} \right],$$
(11)

where E b is the bending modulus, κ is the instantaneous curvature, and κ 0 is the initial stress-free curvature (Zhang et al. 2008; Bagchi et al. 2005; Pozrikidis 2001). Therefore, the total membrane stress T is calculated as

$${\mathbf{T}} = T_{\text{e}} \varvec{t} + T_{\text{b}} {\mathbf{n}}$$
(12)

2.3 Lattice Boltzmann-immersed boundary method

The IBM for the interaction between fluid and vesicle is as follows (Pozrikidis 2001; Peskin 2002; Feng and Michaelides 2004):

$${\mathbf{f}}\left( {{\mathbf{x}},t} \right) = \int {D\left( {{\mathbf{x}} - {\mathbf{X}}\left( {{\mathbf{s}},t} \right)} \right)} F\left( {{\mathbf{s}},t} \right)d{\mathbf{s}}$$
(13)
$$\frac{{\partial {\mathbf{X}}\left( {{\mathbf{s}},t} \right)}}{\partial t} = u\left( {{\mathbf{X}}\left( {{\mathbf{s}},t} \right),t} \right) = \int {u\left( {{\mathbf{x}},t} \right)} D\left( {{\mathbf{x}} - {\mathbf{X}}\left( {{\mathbf{s}},t} \right)} \right)d{\mathbf{x}}$$
(14)
$${\mathbf{F}}\left( {{\mathbf{s}},t} \right) = {\mathbf{T}}\left( {{\mathbf{X}}\left( {{\mathbf{s}},t} \right),t} \right)$$
(15)
$$D\left( {{\mathbf{x}} - {\mathbf{X}}({\mathbf{s}},t)} \right) = \frac{1}{{16h^{2} }}\left( {1 + \cos \left( {\frac{\pi x}{2h}} \right)} \right)\left( {1 + \cos \left( {\frac{\pi y}{2h}} \right)} \right),$$
(16)

when |x and y| ≤ 2h, otherwise D(x) = 0. f, x, and u are the force density acting on the fluid node, Eulerian coordinates, and fluid velocity, respectively. X and F are the Lagrangian coordinates and restoring force density of the vesicle, respectively. D is the Dirac delta function for interpolation. Equation (12) is the immersed boundary equation calculated by the Lagrangian form. Unknown factors are the force per unit area, f(x,t), applied by the immersed boundary to the fluid and the velocity of each Lagrangian node u(X(s,t),t). Equation (13) describes the force density of fluid, f(x,t), calculated from Lagrangian restoration of the vesicle force density, F(s,t), via interpolation over the immersed boundary. Equation (14) assumes that no-slip boundary conditions are applied at the membrane since the Lagrangian nodes move at the same velocity as the surrounding fluid. Equations (13) and (14) use the two-dimensional Dirac delta function, D(x − X(s,t)), which relates interactions between Eulerian coordinates (fluid nodes) and Lagrangian coordinates (vesicle boundary nodes). We used the first-order accurate IBM scheme for this study.

3 Results

3.1 Vesicle properties

To visualize the capillary number of a vesicle, three cases were simulated with Ca = 0.10, 0.05, and 0.025. The capillary number Ca represents the relative effect of viscous and elastic forces and is defined as follows:

$$Ca = \mu \dot{\gamma }R/k .$$
(17)

The capillary number varies with viscous strength (μγ), vesicle size (R), and membrane elasticity (k).

Also, we used a deformation index (DI) computed by the following formula:

$${\text{DI}} = \frac{a - b}{a + b},$$
(18)

where a and b are the major and minor axes of the vesicle, respectively. Figure 2a shows a schematic diagram of the simulation with vesicle shape. For each case, the capillary number of the vesicle varied with Ca = 0.025, 0.05, and 0.10, as shown in Fig. 2b–d, respectively. All cases had a velocity inlet boundary condition, a constant pressure outlet boundary condition, no-slip boundary conditions, and a low Reynolds number of Re = ρUd/μ = 0.11, where ρ, U, d, and μ are the density, mean velocity of the inlet channel, channel diameter, and viscosity, respectively. Figure 2b–d shows the shape change in the vesicle due to the decrease in membrane modulus. These deformations were digitized by measuring the DI using Eq. (18). Figure 2e shows the change in DI of the vesicle, which was associated with an increase in the capillary number of the vesicle. In this simulation, the DI was 0.35 for Ca = 0.10, 0.21 for Ca = 0.05, and 0.1 for Ca = 0.025. The case with the lowest capillary number (Ca = 0.025) shows that the vesicle maintained its original shape against the viscous force. However, the membrane of the vesicle did not withstand the hydrodynamic forces from the surrounding fluid at the highest capillary number of the vesicle, resulting in a high DI. As shown in Fig. 2b, the vesicle was bullet-shaped at a higher capillary number.

Fig. 2
figure 2

a Schematic diagrams of vesicle deformation in a straight channel with three different capillary numbers: b Ca = 0.1, c Ca = 0.05, d Ca = 0.025, e DI dependence on the capillary number of vesicle

Full size image

3.2 Validation

The numerical model was validated qualitatively by comparison with the empirical results. Three different microfluidic systems, two of which were used by Choi et al. (2011), were simulated as shown in Fig. 3a, c, e. In Fig. 3a, c, the numerical results show that the vesicle chose the same path as in the experimental cases (Choi et al. 2011). Figure 3e, f shows the path selection at a tertiary junction; the simulated routing of the vesicle again matched our empirical observation. The experiment in Fig. 3f was performed following the protocol discussed in Choi et al. (2011); surfactant-stabilized bubbles of nitrogen were infused into PDMS-based microfluidic networks and then carried by water. The qualitative comparison in Fig. 3 shows that discrepancies between the numerical results and experimental results are small. The vesicle path selection is further analyzed with the concept of resultant velocity in the next section.

Fig. 3
figure 3

Simulation and experimental results of microfluidic systems for vesicle path selection. Scale bars represent 200 μm. a Vesicle in a T-shaped junction system with downstream channels of equal width chose path A, which had a higher flow rate. b Experimental result (Choi et al. 2011) of a T-shaped junction channel to validate the simulation result in a. c Simulation result of vesicle path selection in a T-shaped junction system with downstream channels of unequal width. d Experimental result (Choi et al. 2011) of a T-shaped junction channel to validate the simulation result in c. e, f Simulated and observed path selections by a vesicle and bubble at a tertiary junction, respectively. The central channel was designed to be much longer than the peripheral channels, so the flow rate along the middle channel was the lowest. Numerical simulation predicted the relative flow rates along the three channels

Full size image

3.3 Microfluidic channel networks with tertiary bifurcations at the inlet junction

To study the path selection of the vesicle at a junction with tertiary downstream channels, we simulated the microfluidic system as shown in Fig. 4. We performed simulations by varying the location of the inlet channel, as tabulated in Table 1 and shown in Fig. 4, where d is the channel diameter. As shown in Table 1, the inlet location was varied as a function of the channel diameter d. For each channel, three cases of vesicle capillary number were simulated (Ca = 0.1, Ca = 0.05, and Ca = 0.025). The inlet Reynolds number was kept sufficiently low at Re = 0.11. The same value of the flow rate of the inlet Q A was used for all simulated cases. Q B is the flow rate of the fluid in the channel below the inlet (path B), Q C is the flow rate in the channel above the inlet (path C), and Q D is the flow rate of the fluid in the central channel (path D). We found that the flow rate was higher in shorter channels and lower in longer channels, as predicted using Eq. (2).

Fig. 4
figure 4

Path chosen by the vesicle in the microfluidic systems of cases A–E when Ca = 0.025. Resultant fluid velocity in each direction in the downstream channels is indicated. a Velocity field of Stokes flow microfluidic channel with an 11.5d inlet location. b Velocity field of Stokes flow microfluidic channel with an 8.25d inlet location. c Velocity field of Stokes flow microfluidic channel with a 6.75d inlet location. d Velocity field of Stokes flow microfluidic channel with a 5.25d inlet location. e Velocity field of Stokes flow microfluidic channel with a d inlet location. f Electric circuit for representing the microfluidic channel

Full size image
Table 1 Inlet channel location in each simulation case
Full size table

To study the path selection of the vesicle in our tertiary microfluidic setup, the microfluidic systems in Fig. 4 were simulated under same fluid conditions. Table 2 shows the result of simulations shown in Fig. 4a–e. Vesicle with Ca = 0.1 and Ca = 0.05 chose the channel with the highest flow rate, but for Ca = 0.025 the vesicle in Cases B, C, and D chose the channel with flow rate Q D despite flow rate Q D being smaller than Q B and Q C (Table 2). With the higher flow rate hypothesis, the path selection of vesicle in a tertiary junction system could not be completely predicted.

Table 2 Flow rates along channels calculated by the LBM
Full size table

To understand the physics that governs the path chosen in a tertiary junction system, the average velocities of each channel and the resultant velocity at the junction were calculated. The resultant velocity at the junction was defined as a vector summation of the average velocities of the fluid in the downstream channel in each direction without a vesicle. For example, the vertical resultant velocity of the downstream channel was the difference of average velocities in channels B and C; the horizontal resultant velocity of the downstream channel was the average flow velocity in channel D due to the presence of only a single channel in the horizontal direction. For Cases A–E with Ca = 0.025, the vesicle chose the path with the highest resultant velocity (Fig. 4). Table 2 shows the differences between flow rates in the downstream channels B and C (indicated as Q B − Q C). Difference between the flow rates was proportional to the resultant velocity because the downstream channels had equal width.

The concept of resultant velocity was also applied to the microfluidic systems in Fig. 3a, c. The resultant velocity in Fig. 3a was positive into channel A; thus, the vesicle accessed into channel A. In the microfluidic system shown in Fig. 3c, despite having the same flow rates in both channels, the vesicle chose path B because the resultant velocity into channel B was higher than that into channel A. Thus, the experimental results shown in Fig. 3b, d and the numerical simulation results shown in Fig. 3a, c indicate that the vesicle tended to choose channels with a high resultant velocity.

3.4 Path selection and vesicle deformation

Path selection has previously been discussed in terms of resultant velocity. To analyze path selection based on physical evidence, we observed the deformation of the vesicle and the change in flow caused by the vesicle. Case C with three capillary numbers of the vesicle (Ca = 0.1, Ca = 0.05, and Ca = 0.25) was used for this analysis. To digitize the deformation of the vesicle, the longest distance inside the vesicle (d s) was calculated as shown in Fig. 5a. Also, the stretched angle of the vesicle (θ) is plotted in Fig. 5b.

Fig. 5
figure 5

Deformation of vesicles with three capillary numbers (Ca = 0.1, Ca = 0.05, and Ca = 0.25) in Case C. a Digitized deformation of vesicle. b Stretched angle of vesicle

Full size image

As shown in Fig. 5a, the deformation of the vesicle in channel A was the largest in the case of Ca = 0.1. This was due to the influence of shear force on the vesicle close to the wall. As the capillary number decreased, the deformation also decreased in order to maintain equilibrium between elasticity and the effect of the viscous force, resulting in film thinning. In other words, when the vesicle passes through channel A, the higher capillary number corresponds to a greater distance between the vesicle and the wall as the viscous force becomes dominant over the elasticity.

As shown in Fig. 5b, when the vesicle reached the tertiary junction, the vesicle with Ca = 0.1 greatly stretched in the vertical direction, where the shear was maximized by the high flow rate. Once deformed, the vesicle could not recover to its original shape, and the viscous force acted on the vesicle surface in the vertical direction. As a result, channel C was selected due to it maximal flow rate. However, for Ca = 0.025, the elasticity of the vesicle resisted the viscous force, resulting in movement down channel D, which had the higher resultant velocity. Our results suggest that, in the condition of low capillary numbers (Ca ≤ 0.025), instead of being affected by the viscous force from the high flow rate, the vesicle in the tertiary junction tends to follow the resultant velocity hypothesis.

3.5 Quantification of the hydrodynamic resistance and effect of capillary number

To further understand the effect of resultant velocity on the path selection of the vesicle, we investigate the hydrodynamic resistance due to the moving vesicle. Flow rates of each channel were measured to quantify the hydrodynamic resistance due to a single moving vesicle. The microfluidic channel systems of Cases A–E are expressed as an electric circuit system in Fig. 4f. In the circuit system, R A is the hydrodynamic resistance of the channel generated from the initial point of the inlet channel to the first tertiary junction. R B is the hydrodynamic resistance of the channel between the initial point of the bottom downstream channel at the first tertiary junction and the initial point of the second tertiary junction. R C is the hydrodynamic resistance of the channel between the initial point of the upper downstream channel at the first tertiary junction and the initial point of the outlet channel. R D is the hydrodynamic resistance of the channel between the initial point of the middle downstream channel at the first tertiary junction and the initial point of the second tertiary junction. R E is the hydrodynamic resistance of the channel between the second tertiary junction and the initial point of the outlet channel. The hydrodynamic resistance difference due to the presence of the moving vesicle is ΔR = R−R 0, where R and R 0 are the hydrodynamic resistances in each channel with and without a vesicle, respectively. This microfluidic system can be calculated using Ohm’s law as an electric circuit, which can be expressed as

$$\frac{{Q_{C} }}{{Q_{B} + Q_{D} }} = \left( {\frac{{R_{B} R_{D} + R_{B} R_{E} + R_{D} R_{E} }}{{R_{B} R_{C} + R_{C} R_{D} }}} \right).$$
(19)

We neglect the change in hydrodynamic resistance ΔR E at channel E due to the small magnitude. To calculate the hydrodynamic resistance at each channel, the flow rates Q B, Q C, and Q D were acquired from simulation results by integrating the fluid velocity at the point where the distance from the first junction is 2d. The normalized hydrodynamic resistance (R/R A) was adopted in the analysis procedure.

Figure 6 shows the normalized hydrodynamic resistance and flow rate for Case C with three different capillary numbers at the first junction. Circle, triangle, and square data points represent the normalized hydrodynamic resistance of R B/R A, R B/R A, and R B/R A, respectively. As shown in the result of Case C in Table 2 (which is used for the analysis), the vesicle chose path B when Ca = 0.1 and Ca = 0.05. On the other hand, when the capillary number was lowest (Ca = 0.025), the vesicle chose path D. We found that, from Ca = 0.1 to Ca = 0.025, the gradient of normalized hydrodynamic resistance decreased with Ca regardless of the path chosen by the vesicle. The change in hydrodynamic resistance by the movement of the vesicle was small when the capillary number was high. This was observed previously by Fuerstman et al. (2007). As the capillary number decreased, however, the resistance at the junction changed dramatically. If the capillary number of the vesicle was large, it could not resist the viscous force and thus deformed, which had little impact on the value of hydrodynamic resistance at the moment when the vesicle selected its path at the junction. On the contrary, the vesicle with the low capillary number (Ca ≤ 0.025) resisted the viscous force and the hydrodynamic force from the inlet and moved to path D, which increased the flow rate at channel D and consequently decreased hydrodynamic resistance.

Fig. 6
figure 6

a–c Measured normalized hydrodynamic resistance for Case C with three different capillary numbers at the first junction. Circle, triangle, and square data points represent normalized hydrodynamic resistance in channels B, C, and D, respectively. a Ca = 0.1, b Ca = 0.05, c Ca = 0.025. d–f Normalized flow rate for Case C with three different capillary numbers at the first junction. Circle, triangle, and square data points represent flow rate at channels B, C, and D, respectively. d Ca = 0.1, e Ca = 0.05, f Ca = 0.025

Full size image

3.6 Residence time

Furthermore, we observed the relationship between resultant velocity and residence time. The residence time of the vesicle was defined as the time spent at a junction before passing into a downstream channel. Figure 7a shows the residence time of the vesicle. The residence time was measured from when the front part of the vesicle entered the junction to when the back membrane of the vesicle left the junction. The inset of Fig. 7a shows the movement of the vesicle along the junction. The time at which the front part of the vesicle entered the junction was set as 0 s for all cases. The total time taken by the vesicle to travel through the junction was measured based on this value.

Fig. 7
figure 7

Residence of a vesicle during path selection with Ca = 0.025. a Velocity field of a microfluidic channel for Case C at the moment of vesicle residence after path selection. Enlarged pictures (bottom) show movement of a vesicle at the junction with time. Inlet location is 6.75d. b Moment of vesicle residence for choosing the middle channel in Case F, which took 471 ms. Inlet location is 6.0d. c Moment of vesicle residence in Case D for choosing the middle channel, which took 488 ms residence time. Inlet location is 5.25d. d Moment of vesicle residence in Case G for choosing the middle channel, which took 504 ms residence time. Inlet location is 4.5d. e Moment of vesicle residence in Case H for choosing the middle channel, which took 690 ms residence time. Inlet location is 3.75d. f Moment of vesicle residence in Case E for choosing the bottom channel, which took 186 ms residence time. Inlet location is 2.0d

Full size image

To understand the relationship between resultant velocity and residence time of the vesicle, we performed simulations on six microfluidic systems at Ca = 0.025 (which follows the resultant velocity), with inlet location gradually decreasing from the mid-point symmetry to the bottom (Cases C–E and F–H). In all cases except E, the vesicle moves into channel D (Fig. 7). Velocities, resultant velocities, and residence time for each case are tabulated in Table 3. The resultant velocity in the vertical direction increases as the inlet channel location decreases due to the increase in flow rate in the direction of channel B. This result shows that the vesicle selected the path with the higher resultant velocity for all cases. In Cases C, D, and F–H, the resultant velocity in the bottom channel increased, and the residence time of the vesicle also increased. Cases C, D, and F–H show slower resultant velocities in the bottom direction.

Table 3 Resultant velocity of microfluidic system junctions for cases C–E and F–H with path chosen by vesicle and residence time at junction
Full size table

The motion of the vesicle into channel D caused the vesicle to reside longer at the junction. However, the vesicle residence time in Case E is much less than in other cases. Case E shows that the resultant velocity was not a factor in determining the residence time of the vesicle. The average velocities of each channel (V B, V C, and V D) and V B–V C explain why Case E had a short residence time. All cases show that a higher average velocity of the selected channel corresponds to a smaller residence time. The resultant velocity was important only for the path selection of a vesicle. After the path selection, the residence time of the vesicle was influenced by the average velocity of each channel rather than the resultant velocity. These results suggest that the resultant velocity is a dominant factor in the path selection of a vesicle (Ca = 0.025) in a complex microfluidic system, and the average velocity of each channel is the dominant factor for residence time.

4 Conclusion

This study investigated the path selection of a vesicle in complex microfluidic systems. Simulations of microfluidic systems with inlet junctions with tertiary downstream channels were performed using an LB–IBM numerical model using LBM to study fluid dynamics and IBM to determine vesicle dynamics. The assumption that the vesicle selects the channel with the higher flow rate, which was observed for binary downstream channels, did not apply for all cases.

When the elasticity of the vesicle could withstand viscous forces, the resultant velocity, rather than the flow rate, was the critical factor for path selection. The resultant velocity predicted the path selection of a vesicle with a lower capillary number. This hypothesis of resultant velocity also explains the vesicle movement in microfluidic systems with binary T-shaped junctions. The residence time of a vesicle at a junction was also studied for different cases, and the relationship with the average velocity of each channel was observed. The simulation data showed that the residence time of the vesicle was influenced by the average velocity of the channel. This study therefore demonstrates a fundamental understanding of path selection of vesicle in microchannel, which is significant for the design of logic gate channel (Prakash and Gershenfeld 2007) and microdevice for sorting vesicle-like object (Cupelli et al. 2013).