Actuation of co-flowing electrolytes in a microfluidic system by microelectrode arrays

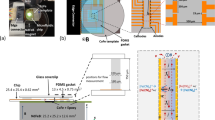
Abstract

Electric fields induce forces at the interface between liquids with different electrical properties (conductivity and/or permittivity). We explore how to use these forces for the manipulation of two coflowing streams of electrolyte in a microchannel. A microelectrode array is fabricated at the bottom of the channel and one of the two liquids is labelled with a fluorescent dye. The diffuse interface between the two liquids is deflected depending on the ac signal applied to microelectrodes and the conductivity (or permittivity) difference between the liquids. The phenomenon is found to be important over a wide frequency range and increases with conductivity ratio. An immediate application of this deflection is that electrolyte mixing time is reduced since the area of the diffusing interface is greatly increased. Remarkably, only a few volts are needed to observe the interface deflection, in contrast with other electrode configurations where hundreds of volts are applied. We present the simplest theoretical modelling capable of reproducing the experimental observations in the case of water solutions with different conductivities. Numerical computations show good agreement with the experimental observations.

1 Introduction

‘Lab-on-a-Chip’ technologies demand the development of new techniques for liquid control at the micrometer scale (Whitesides et al. 2006; Dittrich et al. 2006). Electrodes integrated within microchannels represent an opportunity for direct actuation either on the liquid or suspended particles. Therefore, electrohydrodynamics (EHD) in microsystems is of central interest in current microfluidics research (Morgan and Green 2003; Ramos 2008; Ed Ramos 2011). Electroosmosis (Pretorius 1974), electro-wetting (Beni and Tenan 1981), ion-drag pumping (Richter and Sandmaier 1990), electrohydrodynamic induction pumping (Fuhr et al. 1992) and AC electroosmosis (ACEO) (Brown et al. 2000; Studer et al. 2004) are examples of phenomena where electric fields are used for driving fluids within micrometer dimension systems.

Manipulation of coflowing electrolytes with different conductivities occur in microfluidic operations like, for example, sample stacking (Jacobson and Ramsey 1995). Electric fields can also be used to actuate on liquids with gradients in conductivity. For example, El Moctar et al. (2003) and Choi and Ahn (2000) demonstrate the use of microelectrodes to achieve mixing of liquids with different electrical properties. Santiago and co-workers have recently studied the stability of coflowing electrolytes in a microchannel with an applied electric field longitudinal to the channel (Lin et al. 2004; Chen et al. 2005) and with a transversal electric field (Posner and Santigo 2006; Oddy et al. 2001). Typical voltages in their experiments are around 100 V and electrodes are placed at the channel ends. In this work we focus on a different situation: microelectrodes are built onto the channel bottom wall and, as demonstrated in Morgan et al. (2007), the boundary between the two liquids is deflected upon application of ac signals of only a few volts of amplitude. Figure 1 shows an example for two aqueous solutions.

Fig. 1

a When no voltage is applied the two liquids flow together down the channel. The liquid with a higher conductivity bears a fluorescent dye, while the lower conductivity liquid appears dark. b Upon application of an ac signal, the whole channel is fluorescent, indicating the presence of the more conducting liquid. Microelectrodes are oblique to the channel. Brighter stripes appear because of the light reflected by the microelectrodes. The horizontal yellow lines indicate the lines along which intensity profiles were obtained (colour figure online)

The electrical force density in a liquid is given by Stratton (1941):

$${\mathbf f} _{\rm E} = \rho {\mathbf E} -\frac{1}{2}|{\mathbf E} |^2\nabla \varepsilon +\frac{1}{2}\nabla \left(\rho_{\rm m}\left(\frac{\partial \varepsilon }{\partial \rho_{\rm m}}\right)_{T}|{\mathbf E} |^2\right) $$

(1)

where ρ and ρ _m are the free electrical charge density and mass density, respectively. The last term in Eq. (1), the electrostriction, can be incorporated into the pressure for incompressible fluids. The other two terms correspond, respectively, to the Coulomb and the dielectric forces. Figure 2 shows a sketch of the origin of the electrical forces responsible for the interface deflection in the case of electrodes subjected to ac signals and for two liquids with the same permittivity ε and different conductivities σ ₁ and σ ₂, respectively. Free charges are induced at the interface between the two liquids.¹ In effect, the free surface charge density $q_{\rm s}$ is given by the jump in the normal component of the displacement vector, i.e. $q_{\rm s}=({\mathbf D}_2-{\mathbf D}_1)\cdot {\mathbf n}=\varepsilon ({\mathbf E}_2-{\mathbf E}_1)\cdot {\mathbf n },$ where n is a unit vector normal to the interface directed from medium 1 to medium 2. For an applied signal of frequency ω, the conservation of the normal component of the total electrical current (ohmic and displacement) at the sharp interface between liquids is $(\sigma _1+i\omega \varepsilon ){\mathbf E}_1\cdot {\mathbf n}=(\sigma _2+i\omega \varepsilon ){\mathbf E}_2\cdot {\mathbf n}.$ Thus, the surface charge phasor can be written as

$$q_{\rm s}=\varepsilon [(\sigma _1-\sigma _2)/(\sigma _2+i\omega \varepsilon )]{\mathbf E}_1\cdot {\mathbf n} $$

(2)

When the polarity of the electrodes is reversed, the induced charge changes sign. This gives rise to a non-zero time-averaged electrical force towards the less conducting liquid. In addition, in the case of two liquids with equal conductivities but different permittivities, polarization charges are induced and, consequently, dielectric forces are expected.

In this paper, we present a quantitative experimental study of the interface deflection as a function of frequency, voltage amplitude and conductivity ratio between the two liquid streams. We also present results using ethanol and water as working liquids of the same conductivity but different permittivity. It demonstrates that the strength of dielectric forces is also sufficient to produce an important deflection. The experimental study is completed with the measurement of the impedance of the microelectrode array. Finally, we include a theoretical analysis and discuss the necessary approximations to capture the main features of the experiments using electrolytes with different conductivities. Numerical results obtained using this theoretical analysis show good agreement with experimental results.

Fig. 2

Induced charges at the interface between liquids with different conductivities $(\sigma _1 >\sigma _2).$ A nonzero time-averaged force pulls the higher conductivity liquid into the region of more intense electric field

2 Experimental details

Figure 3 shows a picture of the actual device: platinum microelectrodes are fabricated on glass and a polymeric microfluidic T-shape channel ($100\,\upmu\text{m}$ high and $500\,\upmu\text{m}$ wide) is built on it. Each liquid is inserted on one side and they flow together down the main channel, where the electrode array is placed. The microelectrode array consists of 100 parallel coplanar electrodes oblique to the channel. A planar electrode array generates an electric field that decays exponentially with height, with typical length on the order of the electrode width. Therefore, a planar array is convenient to deflect the interface between the two streams because a vertical gradient of electric field is also necessary (if the electric field is homogeneous, the force can be compensated by pressure). Electrodes oblique to the channel are used because they allow for the arising of both tangential and normal components of the electric field along the diffuse interface between the two co-flowing liquids and, also, because they are easily aligned with the channel. Electrodes are 10 μm wide, separated by 10 μm gaps and they are energized with an ac signal of amplitude between 0 and 10 V in the frequency range 1 kHz to 1 MHz. Both fluids are driven by hydrostatic heads and the pressures are adjusted to have the same flow rate in both liquids prior to the application of the electric field. Working liquids are aqueous solutions where KCl is added to control the conductivity. In some experiments, ethanol with dissolved salts and water were used to have liquids with the same conductivity but different permittivity (e.g. water with KCl as liquid 1; and ethanol with KCl as liquid 2).

Fig. 3

a Sketch of the microfluidic device showing the inlets for the two fluids and the outlet. An array of interdigitated microelectrode is placed in the middle of the main channel. b Photograph of the device. Microelectrodes are 10 μm wide and the channel is 500 μm wide and 100 μm high. The pads are for electrical connections

The experimental procedure relies on quantitative measurements of the fluorescence intensity in a given position of the channel. The liquid with higher conductivity is labelled with a fluorescent dye (fluorescein), while the less conducting liquid appears dark. An Epifluorescence microscope was used to capture grayscale images with a camera (model HCC-1000) with the possibility of controlling the integration time. We have used FITC fluorescence (excitation and emission wavelengths are around 480 and 525 nm, respectively). From these images, we extract the light intensity profiles along a straight line transverse to the channel (yellow lines in Fig. 1 indicate the positions where the intensity profile is obtained). We show in Fig. 4 an example of the intensity profiles obtained from the images in Fig. 1. Figure 4a shows high light intensity in the half of the channel where the fluorescent liquid is present. In the other half, no fluorescence appears (because there is no deflection without applied voltage) and the intensity is zero. Figure 4b shows the intensity profile upon application of the ac signal. The fluorescence is homogeneously distributed across the channel as a consequence of the interface deflection. The intensity of each pixel is represented by an integer in a scale from 0 to 255. The time integration in the camera and the illumination were adjusted in experiments to have a maximum value of fluorescence intensity below 255, i.e. we avoid saturation of any pixel in the photosensor. This fluorescence intensity results from the light coming from all fluorescent molecules within the depth of the channel. In other words, we do not just collect the light coming from the focal plane (as in confocal microscopy) but integrate the light over the thickness of the fluid layer. We checked this by taking images while focusing at different planes and we obtained the same intensity profiles. Note that, with this measurement, we obtain how much of the fluorescent liquid moved to the region of lower conductivity and vice versa, but we do not obtain a full 3D picture of the phenomenon. Therefore, we have also used fluorescent beads (500 nm diameter, supplied by molecular probes) suspended in the more conducting liquid. Focusing the beads allows us to distinguish the region occupied by each liquid (these beads diffuse slowly for the typical time of the experiment). After application of the electric field, we observe that the more conducting liquid occupies the region near the electrode array, i.e. the region where the electric field is more intense (see Fig. 5). Because of incompressibility the upper part is, obviously, occupied by the less conducting liquid. The interface deflection occurs in less than one second. The experimental measurements below correspond to steady state.

Fig. 4

Intensity profiles along the yellow lines in Fig. 1. Fluorescence is homogeneously distributed across the channel upon application of the electric field. Note that the bumps in the plot are due to the light reflected by the microelectrodes

Fig. 5

Top voltage off: fluorescent particles remain in one half of the channel (liquid with higher conductivity). Bottom voltage on: fluorescent particles occupy the region near the electrodes, indicating that the more conducting liquid moved to the region of more intense electric field

3 Experimental measurements

In order to analyse the effect of frequency, voltage and conductivity ratio, we fix our attention on a given point in the channel. We chose a position on the right half of Fig. 1, that is, a region occupied by the less conducting liquid in the absence of applied field. Therefore, the fluorescence is zero when no voltage is applied and relative changes in the fluorescence intensity indicate the presence of the more conducting liquid. In all experiments, the total flow rate was fixed to 8 mL/h by adjusting the height of the pressure heads.

3.1 Electrolytes with different conductivities

Figure 6 shows the fluorescence intensity as a function of the signal amplitude for a frequency of 500 kHz and different conductivity ratios. Figure 7 shows the fluorescence intensity as a function of frequency for a signal amplitude $V_0=7.5\,\text{V}.$ The results are normalized, which means that fluorescence intensity equal to 0 corresponds to no fluorescence at all, while intensity 1 corresponds to maximum intensity (i.e., fluorescence intensity given by the channel filled with the more conducting liquid). The induced surface charge phasor, expression (2), vanishes for frequencies much higher than the reciprocal of the charge relaxation time $\varepsilon{/}\sigma$; here $\sigma$ is the maximum of $\sigma _1$ and $\sigma _2.$ Interestingly, Fig. 7 also shows that the phenomenon tends to vanish for low frequencies (see Sect. 3.3 for an explanation).

Fig. 6

Fluorescence intensity versus voltage at a position in the channel where, with no applied field, there would only be non-fluorescing liquid. Signal frequency is 500 kHz

Fig. 7

Fluorescence intensity versus frequency, the phenomenon disappears at both high and low frequencies. Voltage amplitude is fixed to 7.5 V

3.2 Coflowing streams of water and ethanol with the same conductivity

Figure 8 shows the relative normalized intensity versus frequency in experiments with water ($\varepsilon_{\rm r}=80$) and ethanol ($\varepsilon_{\rm r}=24$). The voltage amplitude was 7.5 V. The conductivity of both streams are adjusted to 1.5 mS/m using KCl. In this case, the phenomenon is almost independent of frequency,² as expected from expression (1). Figure 9 shows the dependence with voltage at a frequency of 500 kHz. It is found that dielectric forces are also capable of producing an important interface deflection with just a few volts.

Fig. 8

Fluorescence intensity versus frequency for water and ethanol with the same conductivities. Intensity 1 corresponds to the channel filled with water

Fig. 9

Fluorescence intensity versus voltage amplitude for water and ethanol with the same conductivities for a frequency of 500 kHz. Intensity 1 corresponds to the channel filled with water

3.3 Electrical impedance measurements

We have used an impedance analyzer (Agilent 4294A) to measure the electrical impedance of the microelectrode–liquids system. Figure 10 shows the impedance magnitude and phase of the complete array with the liquids of conductivity 0.75 and 1.5 mS/m on it. It is found that the impedance magnitude increases for frequencies below tens of kHz. This is due to polarization of the electrodes, i.e. for sufficiently low frequencies, the counterions accumulate at the electrode–electrolyte interface and screen the electric field. This is the reason that the phenomenon also disappears at low frequencies (Fig. 7).

Fig. 10

Impedance measurements of the system versus frequency. The increase of the impedance at low frequencies is due to electrode polarization

Figure 11 shows the impedance magnitude for the same conductivity combinations used in experiments. The typical frequencies for electrode polarization (between 1 and 10 kHz) correspond with those in Fig. 7 at which the interface deflection diminishes. The reduction of the absolute impedance at high frequency (>1 MHz) is related to the liquid charge relaxation frequency. We can see that this relaxation correlates with the disappearance of the interface deflection at frequencies >1 MHz.

Fig. 11

Impedance magnitude of the system versus frequency for several conductivity ratios. The increase of the impedance at low frequencies is due to electrode polarization

4 Theoretical analysis

We aim to provide a theoretical model to compare with the experiments using electrolytes with different conductivities. The formulation of the full electrohydrodynamic problem can be very complicated if we consider that the concentration of each ionic species has to satisfy a convection–diffusion equation coupled to the Navier–Stokes equation, which, in turn, is also coupled to the electrical problem via the Coulombic force term. These equations must be solved in a 3D domain with specific boundary conditions for the electric potential, fluid velocity and ionic concentrations. In this section we find the simplest model that, while tractable, captures all basic features observed in experiments.

4.1 Electrical equations

The electrical current in the bulk of a dilute electrolyte is given by (Newman and Thomas-Alyea 2004)

$${\mathbf J}=\sum _i ez_i(n_i\mu _i{\mathbf E}-D_i\nabla n_i+n_i{\mathbf v}) $$

(3)

where e is the charge of a proton, $ez_i, n_i, \mu _i, D_i$ are, respectively, the charge, ion number density, mobility and diffusivity of ionic species i, E is the electric field and v is the electrolyte velocity. Electrolytes are quasi-electroneutral (i.e. $\rho{/}e\ll \sum _i n_i,$ where $\rho =e\sum _i z_in_i$ is the electrical charge density) in the micrometer length scale. For instance, in the case of a 1:1 electrolyte (as KCl), the relative difference in ion number densities is, according to Gauss law, $(n_+-n_-)/(n_++n_-)=\nabla \cdot (\varepsilon {\mathbf E} )/e(n_++n_-)$ and is very small for saline solutions (Saville 1997). In effect, if d is a typical distance, this ratio is of order $\varepsilon E{/}de2n,$ which is much smaller than unity for $d\ge 1\,\upmu\hbox{m}$ and for typical electric fields used to deflect the interface $(10^5\,\text{V/m} ).$ This allows to neglect the convective current $\sum _i ez_in_i{\mathbf v}$ when compared with conduction current $\sum _i ez_in_i\mu _i{\mathbf E}.$ It is also found that the ratio between diffusion and electro-migration for each species ($|D_i\nabla n_i|/|n_i\mu _i{\mathbf E} |$) is much smaller than unity. This ratio is on the order of $D_i/\mu _iEd,$ with d a typical distance of the system. From Einstein’s relation for monovalent ions we obtain $D_i/\mu _i=k_BT/e=0.025\,\hbox{V}$ at room temperature (where $k_B$ is the Boltzmann’s constant and T the absolute temperature) and it is much smaller than $Ed,$ i.e. the typical voltage drop in the liquid bulk (within the range from 1 to $10\,\text{V}$ in experiments). Taking into account these approximations, the charge conservation equation reads

$$\nabla \cdot ((\sigma +i\omega \varepsilon )\nabla \Phi )=0 $$

(4)

where $\sigma =\sum _i ez_in_i\mu _i$ is the electrolyte conductivity and $\Phi$ is the phasor of the electrical potential, so that $\mathbf{E} (t)=-\mathrm{Re} [\nabla \Phi \exp (i\omega t)].$ The boundary conditions for this equation are: fixed potential at the electrodes and normal current equal to zero at the remaining boundaries. Note that we are not considering the electrode polarization and, therefore, the electric field in the electrolyte bulk will not vanish at low frequencies, in contrast to the results in Sect. 3.3.

Under the quasi-electroneutrality assumption, the conductivity of a binary symmetric electrolyte (as KCl) satisfies a convection–diffusion equation (Newman and Thomas-Alyea 2004):

$$D\nabla ^2\sigma =\partial \sigma /\partial t+(\mathbf{ v} \cdot \nabla )\sigma $$

(5)

where $D=2D_+D_-/(D_++D_-)$ is the ambipolar diffusion coefficient and $D_\pm$ are the diffusion coefficients of positive and negative species. The boundary conditions for Eq. (5) are normal flux equal to zero on all boundaries but on the channel inlet, where the conductivity is fixed to $\sigma _1$ on the left half part and to $\sigma _2$ on the right one.

4.2 Mechanical equations

Reynolds number ($\rho_\mathrm{m} v d/\eta$) in microsystems is usually much smaller than one. In our system $\rho _\mathrm{m}$ and $\eta$ are, respectively, the mass density and viscosity of water, v the typical velocity (around $1\,\text{mm/s}$), d the typical length (around $10\,\upmu\text{m}$), and we obtain $Re\sim 10^{-3}.$ Therefore, the liquid motion is governed by Stokes equations

$$\rho _{\rm m}\frac{\partial {\mathbf v}}{\partial t}=\eta \nabla ^2{\mathbf v} -\nabla P+{\mathbf f}_{\rm E};\quad \nabla \cdot {\mathbf v} =0$$

(6)

where P is the pressure and $\mathbf{f} _{\rm E}$ is the electrical body force, given by Eq. (1). For the case of electrolytes with different conductivities, $\mathbf{f}_{\rm E}$ corresponds to the Coulomb force term since dielectric forces vanish. We are interested in the steady-state solution; therefore, time derivatives are discarded in Eqs. (5) and (6) and we use the time-average Coulomb force. Although electrolytes are quasi-electroneutral, the residual charge can lead to a significant force. The free charge density in the bulk can be obtained from Eq. (4) and Poisson’s equation, leading to a charge density phasor:

$$\rho =\frac{\varepsilon }{\sigma +i\omega \varepsilon }\nabla \sigma \cdot \nabla \phi $$

(7)

The time-average Coulomb force is $\mathbf{f}_{\rm E}=1/2\text{Re}[\rho{\mathbf E} ^*],$ where $\mathbf{E} ^*$ is the complex conjugate of the electric field phasor. For a sharp liquid–liquid interface, the charge density phasor transforms into expression (2). The boundary conditions for the Stokes equations are normal and tangential velocity equal to zero for all channel walls, zero pressure at the channel outlet and fixed pressure $p_0$ at the channel inlet.

5 Numerical results

The equations for the electrical potential, conductivity and velocity are solved using the commercial software COMSOL Multiphysics. Figure 12 shows the 3D domain where Eqs. (4)–(6) are solved. The channel is 5 mm long and the cross section is $500\times 100\,\upmu\text{m},$ as in the experimental device. The electrode array is placed $1.5\,\text{mm}$ from the channel inlet and consists of 100 microelectrodes 10 μm wide and 10 μm gap. Electrodes are alternatively subjected to an ac potential of amplitude $V_0$ or grounded. For consistency, we checked the solution of Stokes equation for the fluid velocity in the absence of the body force and it corresponds to a Poiseuille flow with a flow rate equal to the one imposed at the inlet. We have also checked the solution of the convection–diffusion equation for the conductivity with a given fluid flow. For testing the computation of the electrical body force, we have used the analytical solution for a 2D problem in a semi-infinite plane where the potential at one boundary varies sinusoidally. We have also solved a diffusion equation for the conductivity with fixed values at both the left and right sides. From the numerical solution of the potential and conductivity, we compute the force and the result coincides with the analytical expression. In all simple cases that we tested, the results for the fluid velocity, conductivity and electrical force agree with the analytical expressions. For the fully coupled electrohydrodynamics problem, no analytical solution is known.

Fig. 12

Computational domain for solving governing Eqs. (4)–(6). The channel is 5 mm long and the cross section is $500\times 100\,\upmu\text{m},$ as in the experimental device. The electrode array is placed $1.5\,\hbox{mm}$ from the channel inlet and consists of 100 microelectrodes 10 μm wide and 10 μm gap. Electrodes are alternatively subjected to an ac potential of amplitude $V_0$ or grounded

Figure 13 shows the solution for the electrolyte conductivity on a horizontal plane 1 μm above the electrodes and for conductivities $\sigma _1=1.5$ mS/m and $\sigma _2=15$ mS/m. It is also shown the solution for the conductivity in several vertical slices of the 3D domain. The applied signal in this case was 4 V and 10 kHz, considerably smaller than, for example, the 10 V in experiments of Fig. 1. It was not possible to find numerical convergence for higher voltages and/or conductivity ratios. It is a convection–diffusion problem and computational difficulties are common (Chung 2002). Finding appropriate numerical methods is beyond the scope of this work. However, the solution in Fig. 13 is in agreement with experimental observations. It is shown how the electrolyte with higher conductivity tends to occupy the region above the electrodes.

Fig. 13

Numerical results of the electrolyte conductivity for two streams with $\sigma _1=1.5$ mS/m and $\sigma _2=15$ mS/m, and an applied signal of 4 V and 10 kHz. The more conducting electrolyte tends to occupy the region above the electrodes

For a more quantitative comparison, Fig. 14 shows the integral of the conductivity over the depth of the channel versus frequency for a given signal amplitude of 4 V. The integral is performed in a position in the channel where only the liquid with lower conductivity ($\sigma _1$) is present with no applied electric field. This magnitude compares directly to the measurements in Fig. 7 since, there, the fluorescence intensity was indicating the total amount of the more conducting electrolyte in a position occupied by the less conducting one (see the experimental details section). A rigorous comparison with experiments demands the inclusion of another convection–diffusion equation for the concentration of fluorescent dye. Together with the numerical convergence problems at high applied voltages, we also experienced convergence problems for the diffusion–convection equation for very low diffusivity (fluorescein molecules have a diffusion constant of $D=4\times 10^{-10}\,\hbox{m}^2/\text{s}$). Anyway, we have solved the problem in the case of small voltage (4 V) and for a higher diffusivity. Subsequently, we have smoothly diminished the diffusivity and we have found that the solution does not noticeably change for D smaller than $10^{-9}\,\hbox{m}^2/\text{s} .$ We could not compute the exact solution for the diffusion constant of fluorescein but the result is not expected to vary. This is what we expect a priori if we estimate the diffusion length for the duration of our experiment. The distance from the junction of the two streams to the measurement point is 0.5 mm and the typical velocity in the channel is 0.02 m/s. This means that the fluorescent dye is diffusing during 0.2 s and the corresponding diffusion length is around 10 μm ($L=\sqrt{D t}$), i.e. in good approximation, the fluorescent dye is a tracer for the fluid with higher conductivity. Figure 13 is the solution to the convection–diffusion equation for the diffusion constant of KCl ($D=2\times 10^{-9}\,\hbox{m}^2/\text{s}$) and the conductivity profile is not affected much when this value is further decreased. Approximately, the conductivity profile can be also considered to be a tracer of the liquid behaviour. In Fig. 14 it is found that the phenomenon vanishes for frequencies of the order or above the reciprocal of the charge relaxation time. Obviously, the numerical results do not reproduce the reduction of the phenomenon at low frequency in Fig. 7. As mentioned earlier, this is due to electrode polarization, which was not included in the model, though this could be done by including a surface impedance at the electrode–electrolyte interface.

Fig. 14

Integral of the conductivity at a given position in the channel versus frequency for a given signal amplitude of 4 V. The computations are normalized so 1 corresponds to the integral when the channel is filled with higher conductivity (compare to Fig. 7)

6 Conclusions

Using fluorescent dyes is a useful method for characterizing the behaviour of two coflowing liquids under ac fields. We found that, using arrays of microelectrodes, ac signals of a few volts are sufficient to induce the deflection of the diffuse interface between two water streams of different conductivities. The more conducting liquid occupies the region near the electrodes, where the electric field is higher. The phenomenon decreases for frequencies of the order or above the reciprocal of the charge relaxation time. The fundamental equations describing the electrohydrodynamics problem were presented and numerical computations are in accordance with experimental measurements. At low frequencies the phenomenon tends to disappear because the electric field in the bulk is strongly reduced due to electrode polarization, in accordance with impedance measurements. Experiments with water and ethanol also show that dielectric forces are capable of producing a considerable interface deflection; the liquid with higher permittivity occupies the region of more intense electric field. In this case, the phenomenon is almost independent of the frequency of the ac signal. The theoretical analysis of Sect. 3 is not applicable to this case of miscible liquids with different dielectric permittivities. In particular, the diffusion–convection equation for the conductivity is valid in the case of dilute binary electrolytes and it is not clear at present which conservation equation is satisfied by the dielectric permittivity of the ethanol–water mixture.

Combination of several deflection arrays might find application in, for example, enhancing the mixing in microchannels. A remarkable advantage is that only a few volts are required, in contrast with other electrode geometries that apply around 100 V.