1 Introduction

For vertically oscillating resonators, squeeze-film damping could be a significant dissipation source that limits the performance of these resonators. For this reason, extensive research efforts have been devoted to the development of modeling approaches and tools for the accurate prediction of squeeze-film damping. Some relevant work can be found in (Andrews et al. 1993; Pan et al. 1998; Hutcherson and Ye 2004; Gallis and Torczynski 2004; Nayfeh and Younis 2004; Veijola et al. 1995, 2005; Bao and Yang 2007; Pandey and Pratap 2008; Sujilen et al. 2009; Hong and Ye 2010; Leung et al. 2010; Bidkar et al. 2009; Guo and Alexeenko 2009; Veijola 2004; Lee et al. 2009) and references cited in a review article by Bao and Yang (2007). Depending on the ambient pressure level and the characteristic length of the resonators, gas between the resonant structure and the fixed substrate could be in a rarefied flow regime and therefore be governed by fundamentally different physics. Under the normal operation conditions such as the atmospheric pressure, if gas film thickness is larger than 6 μm or so, it is in the continuum regime and squeeze-film damping can be modeled using Navier–Stokes equations or isothermal Reynolds equation if the film thickness is much smaller than the lateral dimensions of the resonator. Otherwise it enters into the rarefied regime, and Navier–Stokes equations are no longer accurate due to the breakdown of Newton’s viscosity law.

Current modeling approaches in the rarefied regime can be classified roughly into two groups: continuum and non-continuum methods. Non-continuum methods include those based on gas kinetic theory such as the ellipsoidal statistical Bhatnagar-Gross-Krook (ES-BGK) model based method (Bidkar et al. 2009; Guo and Alexeenko 2009) and molecular approaches. The ES-BGK-model-based method numerically solves the approximated Boltzmann equation in which the real collision integral is replaced by the ES-BGK model. Molecular approaches directly model molecular transport and hence are more accurate because fewer assumptions are employed. In the free-molecule regime in which molecular collisions are negligible compared with gas-wall collisions, approaches such as a semi-molecular dynamics simulation approach (Hutcherson and Ye 2004), a Monte Carlo simulation approach (Hong and Ye 2010; Leung et al. 2010) and a relaxation time-based approach (Sujilen et al. 2009) have been developed and accurate predictions of air damping on some resonators have been demonstrated. Compared with continuum methods, non-continuum methods, although more accurate, are computationally intensive and may not be practical to be used for the design of micro-resonators. One way to circumvent this difficulty is to develop efficient compact models based on non-continuum simulations (Guo and Alexeenko 2009; Hong and Ye 2010).

Continuum methods rely on the modifications made to Navier–Stokes equations to take into account the rarefaction effect. A popular approach for the modeling of squeeze-film damping of a plate resonator is to use Reynolds equation coupled with an effective viscosity (Nayfeh and Younis 2004; Veijola et al. 1995; Pandey and Pratap 2008; Lee et al. 2009; Li and Hughes 2000; Li 1999). A fundamental assumption inherent in this approach is that rarefaction effect can be accurately accounted for via a modified viscosity model that depends only on the Knudsen number. For a slightly rarefied gas, that is, when it is in the slip regime, this approach is valid because Navier–Stokes equations are still accurate and the slip effect at the boundaries can be incorporated into an effective flow rate model. For highly rarefied cases particularly when the gas is in the free-molecule regime, such an assumption does not have any theoretical ground and has not been validated rigorously. Nevertheless, several viscosity models have been proposed in the literature and have been applied to the highly rarefied situations (Nayfeh and Younis 2004; Veijola et al. 1995; Pandey and Pratap 2008; Li and Hughes 2000; Li 1999). Most of these models were developed based on Fukui and Kaneko’s work (Fukui and Kaneko 1990) in which the effective viscosity was obtained from solving the linearized BGK model equation of a Poiseuille flow. In a recent study (Pandey and Pratap 2008), a comparison of several effective viscosity models was conducted and it was concluded that Li’s model (Li 1999) fitted the best with the numerical solutions of the BGK model equation. The application of Li’s model to the modeling of a simple torsion mirror, however, did not produce a good prediction of the quality factor when compared with the experimental data (Pandey and Pratap 2008). A modified model with a parameter extracted from experimental data was proposed. This model was then applied to the prediction of the quality factor of a double-gimballed MEMS torsion mirror, and a good agreement with the measurements was achieved. In some other cases, it was demonstrated that Veijola’s model (Veijola 2004) was able to produce good predictions of air damping of several resonators even at low pressures (Guo and Alexeenko 2009; Lee et al. 2009). However, as mentioned in (Lee et al. 2009), the underlying physics behind these results is not yet understood. Also in (Guo and Alexeenko 2009), it was pointed out that the good match may not lead to a conclusion that the Reynolds equation reflects the real physics at high Knudsen cases. In summary, the reported success of the effective viscosity approach seems to be case dependent. This could due to the fact that an accurate effective model is yet to be developed or the fundamental assumption of the approach, that rarefaction effect on squeeze-film damping can be accurately modeled via an effective viscosity model, is not valid.

Given the widespread applications of the effective viscosity approach in MEMS community and its high efficiency compared with molecular-based methods, a careful evaluation of its applicability in the highly rarefied gas regime is necessary. This paper reports the findings from a study on the validity of the effective viscosity approach for the prediction of squeeze-film damping on resonators operated in a free-molecule gas low-pressure environment. Particular emphasize will be on the free-molecule gas regime in which the intermolecular collisions are negligible compared with gas-wall collisions. An experimentally validated Monte Carlo (MC) simulation method is developed and employed together with a nonlinear Reynolds equation solver to first find the best effective viscosity models for both translation-type and rotation-type resonators based on experimental measurements. The generality of these models is then examined on resonators with different dimensions but with the same Knudsen number and oscillation mode.

Following this introduction, in Sect. 2, theoretical background of squeeze-film damping and methodologies employed in this study are briefly described. The main results, that is, the validation of the MC simulation approach, the performance of several existing effective viscosity models, the new viscosity models, and the performance of the effective viscosity approach, are presented next in Sect. 3. A brief discussion on the cause of the poor performance of the effective viscosity approach is also given in this section. Finally, conclusions are provided and possible extensions of the modified Reynolds equation approach are discussed in Sect. 4.

2 Theoretical background and methodologies

When two plates move perpendicularly to each other, the gas between them is being squeezed in and out, resulting in an energy dissipation of the moving plate through the interaction between the gas and the plates. Under the normal operation conditions, if the plates are flat and the gap between the plates is much smaller than the lateral dimensions of the plates, Navier–Stokes equations, which describe gas transport in the continuum regime, can be simplified into Reynolds equation as shown in Eq. 1.

$$ \frac{\partial }{\partial x}\left( {\frac{{\rho h^{3} }}{12\mu }\,\frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{\rho h^{3} }}{12\mu }\,\frac{\partial p}{\partial y}} \right) = \frac{\partial (\rho h)}{\partial t}, $$
(1)

where ρ, p denote the density and the pressure of the gas film, respectively, h is the film thickness and μ is the coefficient of viscosity. The solution of Eq. 1 provides a gas pressure profile from which the damping force acting on the moving plate can be obtained by integrating the pressure along the plate. For a rarefied gas film, the modified Reynolds equation is often employed in which the rarefaction effect is modeled by replacing μ with an effective viscosity, \( Q_{p}^{ - 1} \mu \) where Q p is a relative flow rate coefficient that reduces to one in the continuum regime. Various models for Q p have been proposed in the literature, for example, Veijola’s (Veijola et al. 1995) and Li’s models (Li 1999). A common feature of all the existing models is that Q p is a function of the Knudsen number and is independent of other parameters. If indeed the rarefaction effect on the damping force can be captured by a single parameter, that is, the relative flow rate coefficient, there should exist a unified viscosity model that is valid for all plate resonators with different dimensions and under different operation conditions as long as they possess the same Knudsen number. In this study, an accurate Monte Carlo simulation method combined with a nonlinear Reynolds equation solver is employed to derive such a unified model in the free-molecule regime. For a given resonator operated at a certain Knudsen number, an initial guess of Q p is first provided to the nonlinear Reynolds equation solver. Damping force acting on the moving plate is then computed and compared with the reference value that could be either the measured data or the force simulated from the MC approach. If they match, the final Q p corresponding to this particular Knudsen number is thus found. Otherwise, Q p is modified and the above steps are repeated until the damping forces match. Repeating this process for different Knudsen numbers allows the flow rate model to be derived. The derived model is then employed to simulate damping forces on different resonators and results are compared with MC simulations to examine the validity of the effective viscosity approach in the free-molecule regime.

A common approach to quantify energy dissipation in resonant structures is to measure the quality factor of the resonator defined as the ratio of total input energy, E i, and dissipated energy, E loss, within a cycle as shown in Eq. 2.

$$ Q = 2\pi \frac{{E_{\text{i}} }}{{E_{\text{loss}} }} $$
(2)

In addition to the loss due to fluid damping, other losses such as anchor loss, thermoelastic damping, internal friction, etc., also contribute to the energy dissipation. In this work, we focus mainly on fluid damping. Hence, all calculated quality factors are based on fluid damping only. The total input energy of a resonator is obtained from the maximum kinetic energy of the resonator when it oscillates at one of its resonant frequencies. Take a plate resonator as an example. The motion of the plate resonator can be described by

$$ y(x,t) = A(x)\,\sin (\omega t), $$
(3)

where A(x) and ω are the oscillation amplitude and angular frequency, respectively. The total input energy then reads

$$ E_{\text{i}} = \frac{1}{2}\rho bh\omega^{2} \int\limits_{0}^{a} {[A(x)]^{2} {\text{d}}x,} $$
(4)

where ρ is the mass density of the resonator, a, b and h are the length, the width and the thickness of the moving plate, respectively. For translation-type resonators, A is a constant and the expression of the total input energy reduces to

$$ E_{\text{i}} = \frac{1}{2}\rho abh\omega^{2} A^{2} . $$
(5)

Energy dissipation due to fluid damping is computed via the work done by the damping force. In the Reynolds equation approach, the damping force is calculated by integrating the pressure over the plate area. In the Monte Carlo simulation approach, the damping force is obtained from the momentum change of gas molecules colliding with the resonator.

The two key components of this study are the Monte Carlo simulation method and the Reynolds equation solver. The following sections provide descriptions of these two methods.

2.1 Monte Carlo simulation approach

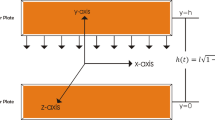
The Monte Carlo simulation approach is a three-dimensional molecular simulation method, which tracks the motion of each gas molecule and its interaction with the structure. Since the targeted flow regime in this study is the free-molecule regime, the intermolecular collisions are not modeled in this program. Denote the space sandwiched between two plates by the interaction region as illustrated in Fig. 1. The top plate represents the oscillating structure, while the bottom one represents the fixed substrate. At any time instance, there are new gas molecules entering into the interaction domain from the surrounding gas reservoir which is assumed to be at equilibrium and at ambient pressure. All molecules inside the interaction domain are tracked. After interacting with the plates, they leave the interaction region without being re-introduced on the opposite side.

Fig. 1
figure 1

Schematic of the Monte Carlo simulation domain. Gas molecules enter into the interaction region from all four sides of the open boundary. For clarity, only those entering the region from the left and right sides of the domain are illustrated

Full size image

The key steps of the MC algorithm are listed as follows.

  • Initialization: at the beginning of a cycle, gas molecules inside the interaction domain are initialized by assuming a uniformly random distribution for their positions and the Maxwellian distribution characterized by the ambient pressure and temperature for their velocities.

  • Time discretization: discretize the oscillation cycle into N small time intervals.

  • At each small time interval,

    • generate new molecules that enter the interaction domain within this time interval; A surface generation algorithm is employed for this step (Tysanner and Garcia 2005). Molecules are emitted into the interaction region from its open boundary at a rate that is determined by the gas density and temperature at the surrounding reservoir. Their initial positions are uniformly distributed along the boundary. The normal velocity of these molecules is generated based on the one-sided Maxwell–Boltzmann velocity distribution and their tangential components are generated based on the Maxwell–Boltzmann distribution (Kennard 1938).

    • move all gas molecules inside the interaction domain according to their velocities and update the moving plate position based on its oscillation frequency and mode.

    • detect collision for each gas molecule inside the interaction domain. If no collision occurs, simply update the position of the molecule. Otherwise, update the velocity of the gas molecule based on the Maxwell gas-wall interaction model (Cercignani 1988); for a collision with the moving plate, calculate the momentum change of the gas molecule and multiple it with the velocity of the plate to obtain the work done by the impact force; accumulate the work for all collisions occurring within this time interval and store it to be used in the calculation of the total energy change of the moving plate at the end of the cycle.

  • Repeat the previous steps for each time interval until one cycle is complete. Calculate the net energy loss of the moving plate based on the stored work at each time interval and obtain the quality factor.

  • Repeat the entire simulation process to perform ensemble averaging until the quality factor is converged for a given criterion.

A detailed description of the method for parallel-plate resonators can be found in (Hong and Ye 2010; Leung et al. 2010). This method is extended for the simulation of rotational resonators in this study.

2.2 Reynolds equation solver

The Alternating Direction Implicit (ADI) numerical scheme is applied to solve the modified Reynolds equation shown in Eq. 6.

$$ \frac{\partial }{\partial x}\left( {\frac{{\rho h^{3} }}{12\mu }Q_{p} \frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{\rho h^{3} }}{12\mu }Q_{p} \frac{\partial p}{\partial y}} \right) = \frac{\partial (\rho h)}{\partial t} $$
(6)

The ADI method involves breaking each time step up into two half steps, such that the first half step treats derivatives in the x-direction explicitly and in the y-direction implicitly, and the second half step treats derivatives in the x-direction implicitly and in the y-direction explicitly. Using the classic first-order central difference discretizations for both first and second derivatives, this results in an implicit, tridiagonal system of equations at each half step which can be solved much faster than fully implicit methods while possessing much better stability properties than fully explicit schemes. A more exhaustive description of the ADI method can be found in (Bradie 2006). The solution at each time step is determined with the method of lines by iterating Newton’s method along each row or column of grid points.

3 Results and discussions

In this section, validation of the developed MC simulation approach using measured quality factors of two microresonators is first presented, followed by the evaluation of the performance of two existing viscosity models. The devised new viscosity models based on the measured quality factors and the validity of the modified Reynolds equation approach are presented next. Lastly, a brief discussion on the failure mechanism of the modified Reynolds equation approach is provided.

3.1 Validation of MC simulation approach

The MC simulation approach for the modeling of air damping in the free-molecule regime was validated previously with experimental data of two resonators: a clamped–clamped beam resonator (Leung et al. 2010) and a rigidly oscillating resonator (Hong and Ye 2010). In the following section, additional validation using two test cases, a torsion mirror (Minikes et al. 2005) and a vertically oscillating plate resonator (Sumali 2007), is presented. In both cases, a diffuse collision model is assumed. Hence, the post-collision velocities of gas molecules are generated from a Maxwellian distribution characterized by the wall velocity and temperature. In all simulations, gas temperature is assumed to be at 293 K. Dry air with a molecular mass of 4.81e−26 kg is used. Since the MC simulation is a statistical method, ensemble averaging is performed until the variation of the energy loss per cycle is within 1% in all cases. The entire simulation takes about 10 days on a workstation with Intel Xeon 2.66 GHz processor for each case.

3.1.1 Case 1: Torsion mirror

Minikes et al.’s torsion mirror 1 (Minikes et al. 2005) as shown in Fig. 2 was modeled to validate the developed MC simulation approach for the modeling of air damping of torsion-type resonators. In this device, a rectangular plate, that is, the mirror, is suspended above the substrate and supported by two clamped microbeams that serve as torsional elastic springs. The spring constant of the microbeams and the mass of the mirror determine the resonant frequency which was measured and listed in Table 1. Other parameters relevant to the calculation of the quality factor of the resonator such as the dimensions of the mirror are also listed in the table and illustrated in Fig. 2.

Fig. 2
figure 2

Schematics of Minikes et al.’s torsional mirror. Left the top view; Right the side view. The vertical dash lines indicate the interaction region where the squeeze-film damping takes place. Outside this region, the pressure is assumed to be at the ambient pressure

Full size image
Table 1 Device parameters
Full size table

The simulation results together with the measured values which are extracted from Fig. 6 in (Minikes et al. 2005) are plotted in Fig. 3. The agreement between the simulated quality factors and the measurements is very good between 0.1 and 2 torr. Within this range, the mean free path of gas molecules, which is about 25 μm at 2 torr, is comparable to or larger than the 28 μm gap between the mirror and the substrate, and hence, the free-molecule assumption is valid. Outside this range, the deviation increases with the increased pressure at the high end and decreases with the increased pressure at the low end. At high pressures, the mean free path of gas molecules is much smaller than the gap and hence the intermolecular collisions become important. The simulated quality factors that are based on the free-molecule assumption are no longer accurate, resulting in a discrepancy that increases with the increased pressure due to the increased intermolecular collisions. In the ultra-low-pressure range, gas is still in the free-molecule regime; but because of the low density, air damping contributes very litter to the total energy dissipation and other damping sources particularly the anchor loss become dominate. This can be observed from the experimental curve at the low-pressure end that is nearly flat, indicating damping is independent of the pressure in this range. The MC simulation calculates only the air damping and hence the resulting quality factor is much larger than the actual quality factor that includes all energy dissipation.

Fig. 3
figure 3

Experimental and simulation results for the quality factor versus pressure: Minikes et al.’s resonator

Full size image

3.1.2 Case 2: Vertically oscillating plate resonator

Sumali’s resonator (Sumali 2007) as shown in Fig. 4 was modeled to validate the MC simulation approach for the modeling of air damping of translation-type resonators. A rectangular plate is supported by four folded beams, which are clamped at the anchor points. The plate is oscillating vertically to the substrate which is located 4.1 μm beneath the plate. The dimensions of the plate as well as its oscillation frequency and amplitude are listed in Table 1.

Fig. 4
figure 4

Schematic of Sumali’s vertical oscillating plate resonator. Left the top view; Right the side view. The vertical dash lines indicate the interaction region

Full size image

The measured quality factors are extracted from Fig. 12 in (Sumali 2007). The simulation results are plotted together with the experimental results indicated by squares in Fig. 5. Again excellent agreement between the simulated and measured quality factors has been obtained in the range of (0.03 Torr, 20 Torr). Similar to the previous example, large discrepancies between the simulation results and measurements have been observed at high pressures due to the free-molecule flow assumption used in our simulation.

Fig. 5
figure 5

Experimental and simulation results for the quality factor versus pressure: Sumali’s resonator

Full size image

The results presented above are obtained by assuming a diffuse collision model. If a specular collision model is employed, the change in the quality factor of Sumali’s device is less than 4% (Hong and Ye 2010). But the change in Minikes et al.’s device can be as large as 33%. Hence, the actual value of the tangential moment accommodation coefficient (TMAC) is important for the prediction of the quality factors of some devices. For most micromachined devices, it is commonly assumed that collisions are of diffuse type due to the relatively rough surface. This can be witnessed in most modeling work cited previously. It is also supported by some experimental work on the measurement of the TMAC based on flow rate inside a microchannel (Arkilic et al. 2001; Maurer et al. 2003).

3.2 Performance of the existing viscosity models

Minikes et al.’s torsion mirror is used to evaluate the performance of the effective viscosity approach for the prediction of squeeze-film damping in the free-molecule regime. Two effective viscosity models namely Veijola’s model (Veijola et al. 1995) and Li and Hughes’s model (Li and Hughes 2000) are considered. In both models, the relative flow rate coefficient is in the form of

$$ Q_{p} = 1 + a({\text{K}}n)^{b} $$
(7)

where Veijola uses a = 9.658, b = 1.159; and Li and Hughes uses a = 6.8636, b = 0.9906. It should be emphasized that the Knudsen number in Eq. 7 is a local Knudsen number determined by the local pressure and local characteristic length. Hence, it varies spatially. Only when both the pressure and the film thickness variations within the gas film are small, the local Knudsen number is near constant and can be replaced by a global Knudsen number determined by the ambient pressure and the mean film thickness. In this case, an analytical solution is available (Langlois 1961) and is used to validate the Reynolds equation solver.

The validated Reynolds equation solver is employed to solve Eq. 6 with Veijola and Li and Hughes’ effective viscosity models. The work done by the damping force is calculated from the computed pressure and integrated it across the entire mirror to obtain the total energy loss of the rotational mirror in one cycle. The resulting quality factor is then calculated based on the input energy and the energy loss within this cycle. In the simulation, the gas is assumed to be ideal and isothermal. Due to the small gap compared with the lateral dimensions, pressure across the gap is assumed to be uniform, that is, pressure gradients exist only in the plane of the plate. Boundaries are held at atmospheric pressure as illustrated in Figs. 2 and 4. Figure 6 presents the computed quality factors at different ambient pressures. Calculations based on both the local Knudsen number and the global Knudsen number are performed and results are shown in Fig. 6. It is evident that in this particular case, employing a local flow rate coefficient offers no significant improvement over a global one, indicating that the pressure variation within the film is small. Such a fact is a consequence of the small oscillation amplitude and frequency of the device.

Fig. 6
figure 6

Simulated quality factors of Minikes et al.’ mirror: Reynolds equation solutions versus MC simulation results and experimental data

Full size image

The experimental data together with MC simulated quality factors are also shown in Fig. 6 for comparison. Clearly, the MC approach offers a more accurate prediction in the low-pressure region where air damping is important, that is, in the range of 0.1–2 torr. The predictive capabilities of the two effective viscosity models in general within the rarefied regime are tenuous at best. In (Pandey and Pratap 2008), another model, Li’s model (Li 1999), was employed to simulate the damping force of the same device. Again, the accuracy of the prediction is unsatisfactory. Although the authors have shown that it is possible to improve the accuracy by adjusting the Knudsen number based on experimental data, the generality of such a model is unclear.

3.3 New effective viscosities and the validity of the modified Reynolds equation approach

To investigate the applicability of the modified Reynolds equation approach to rarefied squeeze-film situations, a test has been devised which considers devices with differing geometries at equivalent Knudsen numbers, all other variables held constant. Since the current modification to viscosity is only a function of the Knudsen number, it is hypothesized that if the modified Reynolds equation approach works, it should be possible to use the Reynolds equation approach to inversely find the accurate effective viscosity coefficient for a given Knudsen number from a device with a known quality factor that is obtained either from experimental measurement or from accurate Monte Carlo simulation. The derived effective viscosity coefficient could then be applied to a device of any reasonable geometry at the same Kn. To test this hypothesis, experimental results from the torsional mirror of Minikes et al. and the flat plate resonator of Sumali were used to derive the effective viscosities for each configuration at various Knudsen numbers. Figure 7 shows the flow rate coefficients obtained from Minikes et al.’s mirror and Sumali’s plate resonator via the aforementioned inverse approach. Also shown in the same figure are coefficients from various models including the asymptotic models of Robert (Huang et al. 1997) and Fukui and Kaneko (1990) in the free-molecule regime. Except Li and Hughes’s model (Li and Hughes 2000) which is close to the coefficients obtained from Minikes et al.’s device, none of the other existing models fit well with any of the experimentally derived coefficients. Such a fact further demonstrates that most existing models cannot provide accurate predictions of the damping forces of the two resonators. Also the coefficients obtained from a rotational mirror and a translational plate resonator are distinctly different indicting that a unified viscosity model that suits for all resonators is not possible. Different effective viscosity models must be employed for different types of resonator.

Fig. 7
figure 7

Relative flow rate coefficients in the rarefied gas regime

Full size image

To further examine the validity of the effective viscosity approach, the derived modified viscosities were used as input for two new hypothetical devices, a mirror and a parallel-plate resonator, respectively, and the quality factors obtained in this way were compared against MC simulations. The operational parameters of the two hypothetical devices are summarized in Table 2 and the results are shown in Figs. 8 and 9. It is evident from both figures that the modified viscosity models derived from Minikes et al.’s and Sumali’s resonators do not work for these two hypothetical devices. This indicates a deficiency in the Reynolds equation approach when investigating the highly rarefied regime and possibly suggests a need to modify or even move away from such an approach.

Table 2 Device parameters
Full size table
Fig. 8
figure 8

Comparison of the two approaches for the hypothetical mirror: Modified Reynolds equation versus Monte Carlo simulation

Full size image
Fig. 9
figure 9

Comparison of the two approaches for the hypothetical plate resonator: Modified Reynolds equation versus Monte Carlo simulation

Full size image

3.4 Discussion and analysis

As demonstrated in the previous section, the modified Reynolds equation approach in general is unable to accurately model the low-pressure squeeze-film damping. The key factor for its failure is the effective viscosity model, which by itself cannot capture the rarefaction effect on the squeeze-film damping. On the other hand, in the field of nanoscale gas lubrication, the modified Reynolds equation approach, particularly the MGL method proposed by Fukui and Kaneko, has been routinely applied and accurate predictions of the pressure profiles of gas films have been demonstrated in numerous examples. In (Huang et al. 1997), a three-dimensional direct simulation Monte Carlo method was employed to systematically validate the MGL method. It was concluded that the MGL method works very well in the entire gas regime and in fact its accuracy improves with the increasing Knudsen number when the film thickness decreases into the nanometer range. However, the reason for its success is not because the effective viscosity is able to accurately capture the rarefaction effect, but rather is due to the fact that the gas flow becomes increasingly independent of Knudsen number in this regime and hence continuum model works well (Huang et al. 1997). For squeeze-film damping in a low-pressure environment, the situation is different. Consider the normalized Reynolds equation shown in Eq. 8.

$$ \frac{\partial }{\partial X}\left( {Q_{p} PH^{3} \frac{\partial P}{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {Q_{p} PH^{3} \frac{\partial P}{\partial Y}} \right) = \sigma \frac{\partial (PH)}{\partial \tau } $$
(8)

The left-hand side of the equation describes Poiseuille flow behavior, while the right-hand side of the equation is the squeeze term characterized by the squeeze number σ. In the free-molecule regime, the relative flow rate coefficient is of the order of Kn log Kn. The squeeze number, on the other hand, is proportional to Kn/h 0, where h 0 is the nominal film thickness. As the pressure decreases, that is, Knudsen number increases, the influence of the Poiseuille flow term characterized by Q p on the overall flow behavior is much more significant than that of the squeeze term. Hence, the performance of the effective viscosity model becomes crucial in the accurate prediction of squeeze-film damping. For nanoscale gas film lubrication, the squeeze term is replaced by a Couette flow term characterized by the bearing number which is also proportional to Kn/h 0. As the film thickness decreases while the pressure remains unchanged, the bearing number is of the order of Kn2 indicating that the dominant term is the Couette term. The influence of the Poiseuille term, and thus the effective viscosity model, on the overall flow behavior diminishes. This explains the fact that the modified Reynolds equation approach works well for the modeling of nanoscale gas lubrication but fails in the prediction of squeeze-film damping in a low vacuum.

4 Conclusions

A numerical study was conducted to validate the modified Reynolds equation approach for the prediction of low-pressure squeeze-film damping. It has been found that the existing effective viscosity models are unable to model the rarefaction effect in the highly rarefied gas regime and hence the corresponding Reynolds equation approach should not be employed in this regime if accurate prediction of squeeze-film damping is demanded. The main reason for its failure is the fundamental assumption that the rarefaction effect can be captured simply by an effective viscosity that depends only on Knudsen number, which has been numerically demonstrated to be invalid in the high Knudsen regime.

The relatively simple relationship between the quality factor of a plate resonator and the ambient pressure in the high Knudsen regime, on the other hand, implies that it is possible to construct an effective viscosity model such as the modified Li’s model (Pandey and Pratap 2008) that computes an accurate damping for one particular type of resonator. However, there is no theoretical guideline for such a construction. One must rely on either experimental data or accurate molecular simulation results, for example, the results obtained from our Monte Carlo simulation approach, to extract parameters. Moreover, to make the model more general, in addition to Knudsen number, several other parameters such as the width-to-gap ratio and the oscillation mode shape must be included in the model. It should be emphasized that the oscillation mode shape plays an important role in the damping (Leung et al. 2010). An effective viscosity that works for a translational resonator in general does not work for a rotational resonator. Such a fact has been demonstrated in this study.