1 Introduction

The simplest configuration of valveless pumps consists of a pump chamber connected to two diffuser/nozzle elements (Fig. 1b). The volume displacement caused by diaphragm deformation combined with the asymmetric pressure drop across the diffuser/nozzle elements with the flow direction, result in a rectified mean flow. These pumps are usually characterised by a volume flow rate versus pressure drop relation. Broadly, both experiments and numerical calculations report a linear decrease of the pump volume flux Q with pressure drop across the pump ΔP, and so the characteristics tend to be reported in terms of the maximum volume flux Q 0 (for zero pressure drop) and the maximum pressure drop ΔP max (for zero volume flux). The major design challenge for developing compact micropumps is that the volume flow rate and pressure rise are not large enough for current applications. For instance the design envelope, at least for electronic cooling, requires typical value of 100 kPa for back pressure and 10 ml/min for the maximum flow rate. Most attention has focused on using multiply connected pumps to increase both the maximum back pressure that the pump can overcome and maximum volume flow rate. The simplest configurations, after the single pump, are the double-chamber series and parallel micropumps. The most comprehensive experimental-published data exist for double-chamber parallel pumps (Olsson et al. 1995), and currently none for the case of double-chamber series pumps and for this reason we focus in this article on double-chamber parallel pumps.

Fig. 1
figure 1

a Schematic of parallel configuration of a two-chamber valveless pump with flat-walled diffuser/nozzle elements. b One branch of the system (chamber A) in (a) is divided into three control volumes

Full size image

Various methods have been applied to understand the characteristics of parallel micropumps. Computational fluid-dynamical (CFD) codes have been previously applied to single- and double-chamber parallel micropumps (Cui et al. 2008; Azarbadegan et al. 2009). The major challenge in applying CFD to study valveless pumps in closed circuits is the consistency between the volumetric change in the pump chamber and the incompressibility of the working fluid. For open systems, which are much closer to the experimental configuration, the difficulty is that the boundary conditions which must be applied at the pipe’s inlet and outlet are unknown, because the direction of the flow changes with time. The second difficulty is that the Reynolds number based on the nozzle throat (hydraulic) diameter can typically vary from zero to 4,600 over one pumping cycle (Olsson et al. 1995). The transitional nature of the flow, coupled with the requirement to resolve in three-dimensions, means that flow must be highly resolved to capture the unsteady flow separation which is responsible for the pressure losses in the valves. An alternative approach is to use mathematical models. A number of studies (Stemme and Stemme 1993; Gerlach and Wurmus 1995; Olsson et al. 1999; Pan et al. 2003; Ullmann 1998) have applied this approach, largely employing a one-dimensional description. The complexity of many such models means that it is difficult to draw any general conclusions. The most relevant to our discussion are the models developed by Stemme and Stemme (1993) and Eames et al. (2009). In the recent study of Eames et al. (2009), a closed-form expression for the relationship between the volume flux and back pressure were derived which agreed with the numerical solution of the non-linear one-dimensional model and the published experimental results for single pumps.

The aim of this article is to analyse the characteristics of double-chamber parallel valveless pumps to understand the implications in terms of pumping volume flow rate and maximum back pressure that can be overcome. This article is structured as follows. The mathematical formulation is presented in Sect. 2. The limiting case of the pumps being exactly in and out of phase are studied analytically (in Sect. 2.3). In order to validate this approach, we compare our analytical results with the published results of Olsson et al. (1995) in Sect. 3. We discussed the implications of this study for the design of parallel valveless pumps in Sect. 4.

2 Mathematical formulation

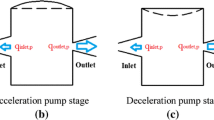
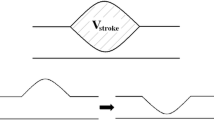
Figure 1a shows a schematic of a double-chamber parallel valveless pump. Both pump chambers are cylindrical cavities (of radius R) whose planar surfaces are forced vertically with an amplitude of maximum deflection X d and angular frequency ω. Volume of chamber A, V c(t), oscillates with an amplitude V m and is defined to be

$$ V _{\rm c}(t) = V_0 - V_{\rm m} \sin \omega t, $$
(1)

where V 0 is the chamber volume in the absence of surface deflection. Geometrically, the amplitude of the maximum volumetric displacement is related to X d and R through

$$ V_{\rm m} = \alpha \pi R^2 X_{\rm d}. $$
(2)

α is a dimensionless coefficient which characterises the shape of the deformed planar surface. The forcing for volume of chamber A lags the forcing for chamber B by an angle ϕ so that its volume is V c(t + ϕ/ω). The cross-sectional area of the throat of the diffuser/nozzle elements and channels are A 1 and A 0, respectively. The pump overcomes an exit pressure of P E and an inlet pressure of P I. The pressure before and after the diffuser/nozzle elements for chamber A are P Ai and P Ae, respectively, and the chamber pressure is defined to be P CA. Similarly, the pressure before and after the diffuser/nozzle elements for chamber B are P Bi and P Be, respectively, and the chamber pressure is defined to be P CB. In order to develop the one-dimensional model for a parallel micropump, we used the model of a single pump described by Eames et al. (2009) as the basic building block.

2.1 One-dimensional model

A one-dimensional model is developed by applying the Navier-Stokes and continuity equations for incompressible flows, and using semi-empirical closures for wall drag and pressure-drop coefficients across the diffuser/nozzle elements.

Each of the two pump chambers in Fig. 1a can be divided into three control volumes as illustrated in Fig. 1b. In going from the differential to the integral form of the momentum equation, we take integrals over a plane perpendicular to mean flow, assuming that the channels have a uniform cross-sectional area A 0, then for the inlet and the outlet channels momentum equation can be applied as follows:

$$ \rho \frac{\hbox{d} {\it u}_{\rm Ae}}{\hbox{d} {\it t}}= -\frac {(P_{\rm f}-P_{\rm Ae})} {{\beta}L} - \frac{1}{2} \rho f u_{\rm Ae}|u_{\rm Ae}| \frac{L_{\rm r}}{A_{\rm 0}}, $$
(3)
$$ \rho \frac{\hbox{d} u_{\rm Ai}}{\hbox{d} {t}} = -\frac {(P_{\rm Ai}-P_{\rm s})}{ {\beta}L} -\frac {1}{2} \rho f u_{\rm Ai}|u_{\rm Ai}|\frac{L_{\rm r}}{A_{\rm 0}}.$$
(4)

Here, the constant β (see Fig. 1) is the ratio of pipe length from the junction to the nozzles, to the external pipes in the circuit. L r is the wetted perimeter of the channel. The viscous stresses on the channel walls are parametrised as \(f \frac{1}{2} \rho u^2\) (White 2006) where f is the Darcy-Weisbach friction factor or simply the friction coefficient; which is assumed to be constant. The pressure-drops across the diffuser/nozzle elements are estimated using a semi-empirical relationship (Stemme and Stemme 1993):

$$ P_{\rm CA}-P_{\rm Ae} = \frac{1}{2} \zeta (u_{\rm Ae}) \rho u_{\rm Ae}|u_{\rm Ae}|\left(\frac{A_0}{A_1}\right)^2,$$
(5)
$$ P_{\rm Ai}-P_{\rm CA} = \frac{1}{2} \zeta (u_{\rm Ai}) \rho u_{\rm Ai} |u_{\rm Ai}| \left(\frac{A_0}{A_1}\right)^2. $$
(6)

The pressure-loss coefficient ζ changes magnitude depending on the direction of the flow through the diffuser/nozzle elements and is defined by:

$$ \zeta(u_{\rm {Ai}}) = \left\{ \begin{array}{ll} \zeta_+, & u_{\rm Ai} >0 , \\ \zeta_-, & u_{\rm Ai} < 0. \end{array} \right.$$
(7)

The pressure-loss coefficient is higher for a nozzle than a diffuser, i.e. ζ− > ζ+ (generally this applies to small wall angles (Olsson et al. 2000)). A fundamental assumption in this model is that a constant pressure-loss coefficient can be defined which corresponds to the steady flow value. In each forcing cycle, fluid moves a characteristic distance ∼V m/A 1 from the throat of the diffuser/nozzle element. When \(V_{\rm m}/A_1 \gg L_{\rm v},\) where L v is the valve length (diffuser/nozzle element length), sufficient fluid is pushed through the diffuser/nozzle elements so a constant pressure-loss coefficient is appropriate. For \(V_{\rm m}/A_1\ll L_{\rm v},\) a streaming flow develops. In this regime, the pump is very inefficient and may not even generate a rectified mean flow and the assumption of a constant pressure-loss coefficient is no longer appropriate.

The conservation of mass requires that the difference between the flux out of and into the pump chamber to be equal to the rate of decrease of the pump chamber volume

$$A_0 (u_{\rm Ae}-u_{\rm Ai} ) =- \frac{\hbox{d} V_{\rm c}}{\hbox{d} t}=V_{\rm m}\omega \cos \omega t. $$
(8)

Adding (3) and (4), and using (5) and (6), we obtain

$$ \begin{aligned} \rho \frac{ \hbox{d} (u_{\rm Ae}+u_{\rm Ai})}{\hbox{d} t} = -\frac {(P_{\rm f} -P_{\rm s})}{ {\beta}L} &-\frac{1}{2} f \rho \frac{L_{\rm r}}{A_{\rm 0}} (u_{\rm Ae}|u_{\rm Ae}|+u_{\rm Ai}|u_{\rm Ai}|)- \frac{\rho \zeta ({u_{\rm Ae}})u_{\rm Ae}|u_{\rm Ae}|}{2{\beta}L} \left(\frac{A_0}{ A_1}\right)^2 \\ &- \frac{\rho \zeta ({u_{\rm Ai}}) u_{\rm Ai}|u_{\rm Ai}|}{ 2{\beta}L} \left(\frac{A_0}{A_1}\right)^2. \end{aligned}$$
(9)

The analysis of a single pump (as expressed by 9) is the same as Eames et al. (2009). With the same approach, the following equations can be applied to chamber B and the whole system depicted in Fig. 1:

$$ \rho \frac{ \hbox{d} u_1}{\hbox{d} t}= -\frac{(P_{\rm E}-P_{\rm f})}{L} - \frac{1}{ 2} \rho f u_1|u_1| \frac{L_{\rm r}}{A_0}, $$
(10)
$$\rho \frac{ \hbox{d} u_2 }{\hbox{d} t} = -\frac{(P_{\rm s}-P_{\rm I})}{L} - \frac{1}{2} \rho f u_2|u_2|\frac{L_{\rm r}}{A_0}, $$
(11)
$$ \rho \frac{\hbox{d} u_{\rm Bi}}{\hbox{d} t}= -\frac{(P_{\rm Bi}-P_{\rm s})}{ {\beta}L} - \frac{1}{2} \rho f u_{\rm Bi}|u_{\rm Bi}| \frac{L_{\rm r}}{A_{\rm 0}}, $$
(12)
$$ \rho \frac{\hbox{d} u_{\rm Be}}{\hbox{d} t} = -\frac{(P_{\rm f}-P_{\rm Be})}{ {\beta}L} - \frac{1}{2} \rho f u_{\rm Be}|u_{\rm Be}|\frac{L_{\rm r}}{A_{\rm 0}},$$
(13)
$$ P_{\rm CB}-P_{\rm Be} = \frac{1}{2} \zeta (u_{\rm Be}) \rho u_{\rm Be}|u_{\rm Be}|\left(\frac{A_0}{A_1}\right)^2, $$
(14)
$$ P_{\rm Bi}-P_{\rm CB} = \frac{1}{2} \zeta (u_{\rm Bi}) \rho u_{\rm Bi} |u_{\rm Bi}| \left(\frac{A_0}{A_1}\right)^2, $$
(15)
$$ A_{\rm 0} (u_{\rm Be}-u_{\rm Bi} ) =V_{\rm m}\omega \cos (\omega t+\phi), $$
(16)
$$ u_{\rm Ae}+u_{\rm Be} =u_1, $$
(17)
$$ u_{\rm Ai}+u_{\rm Bi} =u_2. $$
(18)

The system of equations are non-dimensionalised using τ = ωt, \(\tilde{u}_* = A_0u_* / V_{\rm m}\omega.\) The dimensionless groups are defined as

$$ C_{\rm p} = \frac{(P_{\rm E}-P_{\rm I})A_0}{2 \rho L V_{\rm m} \omega^2}, \qquad C = \frac{V_{\rm m}}{4L A_0} \left(\frac{A_0}{A_1}\right)^2, \qquad C_{\rm d} = \frac{L_{\rm r} f V_{\rm m}}{4 A_0^2 }. $$
(19)

The dimensionless groups C p, C and C d correspond, respectively, to measures of the ratio of applied pressure to the chamber pressure, the maximum volume displaced by the pump compared to the volume of fluid in the system, and the relative strength of the frictional force to the dynamic force. Since, the flows \(\tilde{u}_{\rm Ae}\) and \(\tilde{u}_{\rm Be}\) are dominated by the contribution from volumetric change of the pump chambers, \(\frac{1}{ 2} \cos \tau,\) it is more useful to discuss the pump properties in terms of the flow asymmetry, defined by

$$ \epsilon = \tilde{u}_{\rm Ae} - \frac{1}{2} \cos \tau = \tilde{u}_{\rm Ai} + \frac{1}{2} \cos \tau,$$
(20)
$$ \epsilon = \tilde{u}_{\rm Be} - \frac{1}{2} \cos (\tau+\phi) = \tilde{u}_{\rm Bi} + \frac{1}{2} \cos (\tau+\phi). $$
(21)

From (17), (18), (20) and (21), \(\tilde{u}_1\) and \(\tilde{u}_2\) can be written as follows

$$ \tilde{u}_1=2\epsilon +\frac{1}{2} \cos \tau+ \frac{1}{2} \cos (\tau+\phi), $$
(22)
$$ \tilde{u}_2=2\epsilon -\frac{1}{2} \cos \tau- \frac{1}{2} \cos (\tau+\phi). $$
(23)

After carrying out some algebraic operations and then simplification the following equation can be obtained,

$$ \begin{aligned} \frac{\hbox{d} \epsilon}{\hbox{d} \tau} &= -\frac{C_{\rm p}}{{2+{\beta}}} - \frac{C}{{4+2{\beta}}} (\zeta(\tilde{u}_{\rm Ae})\tilde{u}_{\rm Ae}|\tilde{u}_{\rm Ae}| + \zeta(\tilde{u}_{\rm Ai})\tilde{u}_{\rm Ai}|\tilde{u}_{\rm Ai}|+\zeta(\tilde{u}_{\rm Be})\tilde{u}_{\rm Be}|\tilde{u}_{\rm Be}|+\zeta(\tilde{u}_{\rm Bi})\tilde{u}_{\rm Bi}|\tilde{u}_{\rm Bi}|)\\ &-\frac{C_{\rm d}}{{4+2{\beta}}}(2\tilde{u}_1|\tilde{u}_1|+2\tilde{u}_2|\tilde{u}_2|+a\tilde{u}_{\rm Ai}|\tilde{u}_{\rm Ai}|+a\tilde{u}_{\rm Ae}|\tilde{u}_{\rm Ae}|+a\tilde{u}_{\rm Bi}|\tilde{u}_{\rm Bi}|+a\tilde{u}_{\rm Be}|\tilde{u}_{\rm Be}|). \end{aligned} $$
(24)

In the following sections, the general trend of \(\epsilon\) is studied.

2.2 Numerical solution

Equation 24 was solved using Matlab and the solver ODE113. For the purpose of the numerical calculations, we set ζ− = 2 and β = 1. Figure 2 shows the variation of 2\(\epsilon\) with time for C p = 0, C d = 0.0387, and C = 0.1842 (these values are taken from experimental data of Stemme and Stemme (1993)), with the pressure-drop asymmetry ζ−/ζ+ varying from 1 to 2.5. As ζ−/ζ+ increases, the average value of 2\(\epsilon\) increases, but the fluctuations are a small component to this. Figure 3 shows the dependence of 2\(\epsilon\) on phase angle ϕ for C p = 0, C d = 0.0387, C = 0.1842, ζ−/ζ+ = 2, ζ+ = 1, and β = 1. It shows that by increasing ϕ from 0 to π, non-dimensionalised mean flow rate 2\(\epsilon\) increases. This implies changing the phase angle, ϕ, is a way of controlling the flow behaviour.

Fig. 2
figure 2

The variation of the flow asymmetry 2\(\epsilon\) with dimensionless time is shown for contrasting values of the pressure-drop asymmetry (ζ−/ζ+). The initial transient is created as the pump starts from rest. The chosen values are C p = 0, C d = 0.0387, C = 0.1842 and β = 1. The solid and dotted curves show the variations of the flow asymmetry when the pumps are driven exactly out of phase (ϕ = π) or in phase (ϕ = 0), respectively

Full size image
Fig. 3
figure 3

The variation of the flow asymmetry 2\(\epsilon\) with dimensionless time is plotted for contrasting values of phase angle, ϕ. The imposed pressure-drop is set to zero (C p = 0), with the other variables are fixed at C d = 0.0387, C = 0.1842, and β = 1. The pressure-drop asymmetry is ζ−/ζ+ = 2

Full size image

2.3 Analytical solution

From Fig. 3, we see that the flow asymmetry is bounded by the values obtained when ϕ = 0 and π, is either in or out of phase. There is a transient solution before \(\epsilon\) settles down to a periodic oscillation. For Fig. 3, we see that the transient mean settles down after τ∼30, which physically corresponds to t∼30/ω∼10−2 − 10−4s. A more detailed analysis demonstrates that the transient time is weakly dependent on C and C p. The flow asymmetry then settles down to a mean and periodically oscillating components. In studying the dynamics of the parallel pump, we, therefore, restrict our attention to ϕ = 0 and π and use subscripts 0 and π to refer to these two limiting cases.

After some time, the flow asymmetry settles down with a mean value and fluctuating components, \(\epsilon=\overline{\epsilon}+\tilde{\epsilon}.\) We use this assumption that \(\tilde{\epsilon}\) is periodic to solve (24). When \(\tilde{\epsilon}\) is periodic with a period of 2π, \(\epsilon\)(τ) = \(\epsilon\)(τ + 2π) for all values of τ. This requires that \(\int_{0}^{2\pi} \hbox{d} \epsilon = 0\) and by integrating (24) over the period 0 to 2π, we obtain the constraint

$$ -2\pi {C_{\rm p}}-{C}\zeta_+(2\pi(\overline{\epsilon}^2+\frac{1}{8})+4\overline{\epsilon})+{C}\zeta_-(2\pi(\overline{\epsilon}^2+\frac{1}{8})-4\overline{\epsilon})-(32+8{\beta}){C_{\rm d}}\overline{\epsilon}=0, $$
(25)

for ϕ = 0 and

$$ -2\pi {C_{\rm p}}-{C}\zeta_+(2\pi(\overline{\epsilon}^2+\frac{1}{8})+4\overline{\epsilon})+{C}\zeta_-(2\pi(\overline{\epsilon}^2+\frac{1}{8})-4\overline{\epsilon})-8{C_{\rm d}}(2\pi\overline{\epsilon}^2+{\beta}\overline{\epsilon})=0, $$
(26)

for ϕ = π.

From (23), the mean flow rate for the parallel pump is \(E_\phi=2\overline{\epsilon}.\) Therefore, for the ϕ = 0 and ϕ = π, the non-dimensionalised mean flow asymmetries are

$$ {E}_{0} \sim \frac{\pi}{8}\frac{\zeta_--\zeta_+- 8C_{\rm p}/C}{ \zeta_-+\zeta_++(8+2{\beta})C_{\rm d}/C}, $$
(27)
$$ {E}_{\pi} \sim \frac{\pi}{8}\frac{\zeta_--\zeta_+- 8C_{\rm p}/C}{ \zeta_-+\zeta_++2{\beta}C_{\rm d}/C}. $$
(28)

Figure 4 illustrates a comparison between first order solutions (27), (28) and the numerical solution to (24). The agreement is excellent except for large values of C and large pressure-drop asymmetry.

Fig. 4
figure 4

The variation of the rectified mean flow \(E(=2\overline{\epsilon}\)) with the pressure coefficient C p (C d = 0.0387, β = 1) is shown. a The pressure asymmetry is varied from ζ−/ζ+ = 1.25 to 2.5 and C = 0.0184. b The pressure asymmetry is fixed at ζ−/ζ+ = 2 and C is varied. The numerical solutions to (24) are plotted as symbols open circle and open left pointing triangle for ϕ = π and ϕ = 0, respectively, and the expressions (27) and (28) as solid and dotted lines, respectively

Full size image

From (10) to (18), the full expressions for the difference between the chamber pressures and mean static pressure are

$$ \begin{aligned} \Updelta{P}_{\rm A}&=P_{\rm CA} - \frac{1}{2} (P_{\rm I}+P_{\rm E})=\frac{\rho L V_{\rm m}\omega^2 }{2A_0}\left(({\beta}+1)\sin \omega t+\sin(\omega t +\phi)\right)\\ &-\frac{\rho LfL_{\rm r} V_{\rm m}^2\omega^2}{ 4A_0^3}\left({\beta}\tilde{u}_{\rm Ai}|\tilde{u}_{\rm Ai}|-{\beta}\tilde{u}_{\rm Ae}|\tilde{u}_{\rm Ae}|+\tilde{u}_2|\tilde{u}_2|-\tilde{u}_1|\tilde{u}_1|\right)\\ &\quad-\frac{\rho V_{\rm m}^2\omega^2}{ 4A_1^2}\left(\zeta(\tilde{u}_{\rm Ai})\tilde{u}_{\rm Ai}|\tilde{u}_{\rm Ai}|-\zeta(\tilde{u}_{\rm Ae})\tilde{u}_{\rm Ae}|\tilde{u}_{\rm Ae}|\right), \end{aligned} $$
(29)
$$ \begin{aligned} \Updelta{P}_{\rm B}&=P_{\rm CB} - \frac{1}{2} (P_{\rm I}+P_{\rm E})=\frac{\rho L V_{\rm m}\omega^2}{2A_0}\left(\sin \omega t+({\beta}+1)\sin(\omega t +\phi)\right)\\ &-\frac{\rho LfL_{\rm r} V_{\rm m}^2\omega^2}{ 4A_0^3}\left({\beta}\tilde{u}_{\rm Bi}|\tilde{u}_{\rm Bi}|-{\beta}\tilde{u}_{\rm Be}|\tilde{u}_{\rm Be}|+\tilde{u}_2|\tilde{u}_2|-\tilde{u}_1|\tilde{u}_1|\right)\\ &\quad-\frac{\rho V_{\rm m}^2\omega^2}{ 4A_1^2}\left(\zeta(\tilde{u}_{\rm Bi})\tilde{u}_{\rm Bi}|\tilde{u}_{\rm Bi}|-\zeta(\tilde{u}_{\rm Be})\tilde{u}_{\rm Be}|\tilde{u}_{\rm Be}|\right). \end{aligned} $$
(30)

The chamber pressures have four main contributions: the mean pressure between the inlet and outlet, an inertial contribution caused by the fluid acceleration, the pressure-drop associated with the frictional losses in the system (excluding the diffuser/nozzle elements) and the pressure-drop across the diffuser/nozzle elements. Since the pipe friction factor f is typically small the inertial effect dominates the unsteady pressure contribution, \(\Updelta{P}(t)=P_{\rm C}-\frac{1}{2} (P_{\rm I}+P_{\rm E}),\) because \((LA_0/V_{\rm m})/(A_0^2/A_1^2){\sim}10^2-10^4\gg 1.\) Since f ≪ 1, the unwieldy expressions (29) and (30) are given to leading order by

$$ \Updelta{P_{\rm CA}(t)} \sim -\frac{\rho L V_{\rm m}\omega^2}{ 2A_0}(({\beta}+1)\sin \omega t+\sin(\omega t +\phi)), $$
(31)
$$ \Updelta{P_{\rm CB}(t)} \sim -\frac{\rho L V_{\rm m}\omega^2}{2A_0}(\sin \omega t+({\beta}+1)\sin(\omega t +\phi)). $$
(32)

For in phase chamber forcing (ϕ = 0), (31 and 32) reduce to

$$ \Updelta{P}_{\rm A0}=\Updelta{P}_{\rm B0} \sim -\frac{({\beta}+2)\rho L V_{\rm m}\omega^2 }{2A_{\rm 0}}\sin \omega t,$$
(33)

while for out of phase forcing (ϕ = π), (31 and 32) reduce to

$$ \Updelta{P}_{{\rm A}\pi} = -\Updelta{P}_{{\rm B}\pi} \sim -\frac{{\beta}\rho L V_{\rm m}\omega^2}{2A_0}\sin \omega t. $$
(34)

For pumps driven out of phase there is no large scale oscillatory motion throughout the pipes beyond the junctions and so the unsteady pressure contribution is small. Figure 5 shows a comparison between (29 and 30) and (31 and 32) where f = 0.001 and  f = 0.1 in (a) and (b), respectively. It can be seen that the agreement is excellent in (a) as f ≪ 1, whereas the agreement is poor in (b) as f = 0.1. Additionally, the figure confirms the domination of the inertial contribution to the unsteady pressure component only when f ≪ 1.

Fig. 5
figure 5

The unsteady component of chamber pressure ΔP is plotted as a function of time t. Full blue curve is calculated numerically from (29) and taking ϕ = 0, and corresponds to ΔP A0 which is equal to ΔP B0 where ϕ = 0. The blue open circle corresponds to (33) which defines the leading order inertial contribution to the unsteady chamber pressure where ϕ = 0. Full red and black curves are calculated numerically from (29) and (30), respectively where ϕ = π, and correspond to ΔP Aπ and ΔP Bπ respectively. The red and black open circle correspond to ΔP Aπ and ΔP Bπ from (34), respectively, which define the leading order inertial contribution to the unsteady chamber pressure where ϕ = π. In a f = 0.001 and in b f = 0.1. In these cases β = 1, L = 1 m, ω = 400π (rad/s), \(V_m=14.175\;\hbox{mm}^3,\) ζ− = 2, and ζ+ = 1 (Color figure online)

Full size image

3 Comparison between the model and Olsson et al. (1995) data

In order to compare theoretical results for the maximum volume flux Q 0 (for zero pressure head) and maximum pressure difference ΔP max (for zero flow) against the experiments of Olsson et al. (1995), (27) and (28) are expressed in dimensional form as

$$ \frac{Q_0}{V_{\rm m} \omega } =\frac{\pi}{8}\frac{\zeta_--\zeta_+}{ \zeta_-+\zeta_++(8+2{\beta})C_{\rm d}/C}, \qquad \frac{\Updelta P_{\rm max} A_1^2 }{\rho V_{\rm m}^2 \omega^2} =\frac{1}{16} (\zeta_--\zeta_+), $$
(35)

where ϕ = 0. Similarly, for ϕ = π we have

$$ \frac{Q_0}{V_{\rm m} \omega } =\frac{\pi}{8}\frac{\zeta_--\zeta_+}{ \zeta_-+\zeta_++2{\beta}C_{\rm d}/C}, \qquad \frac{\Updelta P_{\rm max} A_1^2}{ \rho V_{\rm m}^2 \omega^2} = \frac{1}{16}(\zeta_--\zeta_+). $$
(36)

Olsson et al. (1995) applied the model developed by Stemme and Stemme (1993) to estimate the maximum volume flux (Q 0) and maximum pressure-drop that can be overcome (ΔP max) for two-chamber parallel pump as follows

$$ \frac{Q_0}{V_{\rm m} \omega} = \frac{2}{\pi} \frac{(\zeta_-/\zeta_+)^\frac{1}{2} - 1}{(\zeta_-/\zeta_+)^\frac{1}{ 2}+1}, \qquad \frac{\Updelta P_{\rm max} A_1^2}{ \rho V_{\rm m}^2 \omega^2} = \frac{ \zeta_-}{((\zeta_-/\zeta_+)^\frac{1}{2}+1)^2}. $$
(37)

The characteristic scales of Q 0 and ΔP max derived in (35) and (36) (V mω and ρV 2m ω2, respectively) are identical to those in (37), which is to be anticipated. The expressions for Q 0/V mω in (35) and (36) are the same order of magnitude as (37), and Q 0 = 0 (in the absence of friction) when ζ−/ζ+ = 1. However, as the phase angle, ϕ, and frictional losses have not been considered in (37), the maximum volume flux cannot be predicted neither according to the changes in the phase angle nor the magnitude of the friction coefficient, f. Comparing (35), (36) and (37), a major difference arises in the magnitude and form of ΔP max A 21 /ρV 2m ω2 where ζ−/ζ+ = 1. (35) and (36) show that when ζ−/ζ+ = 1 and in the absence of friction ΔP max = 0, whereas (37) predicts a positive value for ΔP max which is physically impossible.

Olsson et al. (1995) designed and studied a two-chamber parallel pump with flat-walled diffuser/nozzle elements. The two identical pump chambers had radii of R = 6.5 mm and depth of 0.3 mm. The flat chamber walls were driven by four piezoelectric discs of radii 5 mm. The diffuser/nozzle elements had a neck width of 0.3 mm, an outlet width of 1.0 mm and length of 4.1 mm with a slightly rounded inlet. When ϕ = 0 and ϕ = π, the excitation frequencies were 470 and 540 Hz, respectively. The diameter of the connecting tubes were about 1.0 mm. Olsson et al. (1995) measured the steady pressure-drop coefficients across the diffuser/nozzle element (ζ−, ζ+). The surface deformation can be assumed to be close to a paraboloid (α ≈ 0.5) as the cylindrical pressure chamber diaphragm is deformed by a piezoelectric actuator (slightly smaller than R). Potential sources of error in making a comparison between experimental measurements and (35) and (36) arise from α, β, pipe length L and the friction coefficient f. From (19), the ratio C d/C can be expressed as

$$ \frac{C_{\rm d}}{C} = \frac{L_{\rm r}f L}{A_0 } \left(\frac{A_1}{A_0}\right)^2. $$
(38)

The first group of terms on the right-hand side of (38), L r fL/A 0, contains the unknowns f and L. The pipe length, L, is not known, but taking a typical length of 0.1 m, the ratio C d/C is equal to 94.25f. The nominal Reynolds number \(Re= V_{\rm m} {\omega}/A_0^\frac{1}{2} \nu\) has a typical value of 0–1,400 when ϕ = 0 and 0–4,600 when ϕ = π. The Moody chart can be used to estimate the friction coefficient values, but it should be noted that the Moody chart is for a fully developed flow in circular pipes and here the flow is not fully developed. Therefore, the friction coefficient f varies approximately over the range 0.03–0.1. In order to test (35) and (36), we estimate the maximum volume displaced using (2) and plot Q 0/πR 2 X dω and ΔP max A 21 /ρ(πR 2 X d)2ω2 against the prediction by assuming f = 0.

The non-dimensional experimental data are plotted in Fig. 6 and compared with predictions based on (35), (36) and (37). A detailed analysis of the data shows when ϕ = 0, V m/A 1 L v∼0.4 − 0.9 and when ϕ = π, V m/A 1 L v ∼0.6 − 2.6. We expect the theoretical model to provide a slightly better agreement when ϕ = π than ϕ = 0 for Q 0 as V m/A 1 L v is greater for ϕ = π, which is confirmed as seen in Fig. 6a. The expression (37) also provides a good quantitative comparison with their experimental results for Q 0, but overestimates ΔP max by a factor of 27 − 64. Our expressions (35) and (36) are in average within 50% of the experiment measurements for pressure. This difference is likely to come from the α2 value which is estimated. Another source of error raises from the fact that as V m/A 1 L v is small, a streaming flow will tend to develop and the assumption of a constant pressure-loss coefficient may no longer be appropriate.

Fig. 6
figure 6

Comparison between the non-dimensionalised experimental data and analytical results for a maximum volume flux and b maximum pressure that can be overcome. The experimental data is plotted on the ordinate axis while the theoretical prediction is plotted along the abscissa. The full line corresponds to agreement between experiments and predictions. The symbols filled circle and  open circle, correspond to predictions based on (36) and (37) when ϕ = π respectively, while the symbols plus and times correspond to predictions based on (35) and (37) when ϕ = 0 respectively

Full size image

4 Implications for pump design

Cavitation is one of the main constraints in pump design as it can damage the pump and reduce its efficiency significantly. In order to prevent cavitation P CA, P CB > P v, where P v is water vapour pressure. Vapour pressure is a function of temperature, and for water in 30°C P v is about 4 kPa. From (33) and (34), we obtained the constraints

$$ \frac{1}{2} (P_{\rm E}+P_{\rm I})-P_{\rm v} > \frac{(2+{\beta})\rho V_{\rm m} L\omega^2}{2 A_0}, $$
(39)

when ϕ = 0 and

$$ \frac{1}{2} (P_{\rm E}+P_{\rm I})-P_{\rm v} > \frac{{\beta}\rho V_{\rm m} L\omega^2}{2 A_0}, $$
(40)

when ϕ = π. These estimates suggest that cavitation is less problematic when ϕ = π as the amplitude of the chamber pressure fluctuations is smaller.

Cavitation can be avoided by controlling chamber pressure. From (35 and 39) and (36 and 40) the ratio of the maximum pressure that can be overcome to the average pump chamber pressure satisfies

$$ \frac{{\Updelta}P_{\rm max}}{{\frac{1}{2}(P_{\rm E}+P_{\rm I})}-P_{\rm v}} < \frac{A_0V_{\rm m}(\zeta_--\zeta_+)}{8(2+{\beta})A_1^2L}, $$
(41)

where ϕ = 0 and

$$ \frac{{\Updelta}P_{\rm max}}{{\frac{1}{2}(P_{\rm E}+P_{\rm I})}-P_{\rm v}} < \frac{A_0V_{\rm m}(\zeta_--\zeta_+)}{8{\beta}A_1^2L}, $$
(42)

where ϕ = π. These provide a useful criterion for avoiding cavitation, which is an important parameter to design a robust micropump.

5 Conclusions

The conclusions from this detailed analysis are

  1. (a)

    An analytical model has been developed and applied to study double-chamber parallel valveless micropumps. The mean rectified flow is shown to decrease linearly with back pressure, which is consistent with published studies of both single and double chamber pumps. The predicted maximum rectified volume flux and maximum back pressure were compared with the experiments of Olsson et al. (1995). The predictions for the rectified mean flow were on average a 10–15% improvement on the Stemme and Stemme (1993) predictions. More significantly were the improvements in the prediction of the maximum back pressure which could be overcome.

  2. (b)

    The parallel pump performs the best when the chambers are driven exactly out of phase because the rectified mean flow is largest (see Fig. 3). When the chambers are driven exactly out of phase, there is no large scale oscillation of the flow in the system and consequently the minimum chamber pressure is more favourable to reducing cavitation.

  3. (c)

    One of the constraints is the presence of cavitation inside the chamber which can disrupt the flow and significantly reduce pump efficiency. This is because gas or vapour bubble are easily compressed and they can absorb the volumetric change in the pump chamber, preventing the flow through the diffuser/nozzle elements. The model is capable of predicting when cavitation may occur.

One of the major challenges in applying CFD to micropumps are the definition of the boundary conditions. The advantage of the modeling approach presented, which includes some of the detailed physics, is that it enables the boundary conditions to be defined realistically.

A major advantage of the model is that it applies to valveless pumps which are driven by any type of forcing, providing that the mean flow is driven by rectification. The difficulty in applying this approach is that values of ζ± which are currently obtained from a steady flow measurements are not readily available for different geometries. The value of α depends on how the chamber pump is deformed which depends on the fluid-structure interaction in the chamber.