1 Introduction

Over the past 10 years, the application of micro-manufacturing technologies to the production of fluidic devices has led to the rapid development of now widely accepted micro-fluidic devices. As is often the case, the early promises—emphasising cheaper, faster, and more reliable devices with smaller volumes of liquids—have only been partially fulfilled (Abrarall and Gué 2007; Receveur et al. 2007). Manufacturing and design intricacies are issues that micro-fluidics share with their more mature parent technology, micro-electromechanical systems (MEMS). Despite recent advances in terms of computer assisted design (CAD) and modelling integration (a growing number of finite volume and finite element packages commercially available), the scientific community has only made a limited use of advanced computational tools with corresponding well-controlled experiments to optimise the design and operation of micro-fluidic devices (Erickson 2005). The reasons are numerous, and the lack of quantitative comparisons and correlations between micro-fluidic experiments and simulation results is certainly an important factor. In this work, quantitative comparisons between fluorescence lifetime imaging microscopy (FLIM) and computational fluid dynamics (CFD) results are established for the basic case of mixing in a T-junction.

Mixing remains one of the most studied issues in micro-fluidic systems, owing to the physical impossibility to create turbulence in small channels, emphasised by the low Reynolds numbers of the flows at play—usually smaller than 100. Several alternatives to turbulent mixing have been developed. Two types of mixers are commonly used: passive mixers, which involve the exclusive use of non-actuated elements, and active mixers, which include moving elements such as micro-pumps or dynamically changing the surface interactions (through the electric potential for instance) (Nguyen and Wu 2005). The former have the obvious advantage of being made of one single material, hence being much cheaper and easier to manufacture and operate than their counterpart. The latter, on the other hand, have the ability to generate large pressure gradients over small distances, eddies and/or vortices thereby enhancing mixing. The present study is limited to passive mixers, which come in a large number of geometries, as described in the extensive review of Nguyen and Wu (Nguyen and Wu 2005). For additional insight into modelling of these structures, the reader is referred to Ottino’s introduction article and the ten other contributions to the theme “Transport and mixing at the microscale” published recently (Ottino and Wiggins 2004). Most accepted designs share the common goal to enhance the diffusion of one species into the other. Among them, the T-mixers, Y-mixers and other sheath laminating designs rely on diffusion alone to mix the species. Some solutions have been devised to increase the interfacial area between the two fluids: the topological mixer creates an eddy current that allows to take advantage of the usually larger width than depth of the channel (Stroock et al. 2002a; Howell et al. 2005); the herringbone mixer creates two counter rotating eddies (Stroock et al. 2002b) and therefore promotes mixing by convection; more intricate designs are based on the division and recombination of flow. Chaotic advection is another mechanism used to achieve good mixing (Wiggins and Ottino 2004), through for example 3D serpentine geometry. As can be understood from this short, non-exhaustive presentation of the most popular mixing technologies, each geometry will have its own advantages and drawbacks, and a number of modelling issues arise from both the shape of the domain and the nature of the fluids being employed.

Irrespective of the chosen geometry, in order to design correctly at the first attempt, one needs reliable input data for the fluid properties and their mixture: density, viscosity, thermal conductivity, diffusion coefficient and others as required by the physics of the fluid domain studied. These are generally difficult to gather and the source often does not warrant their traceability to standard fluids and methods. Micro-fluidics have the potential to overcome such limitations, by allowing measurement of the properties of small fluid volumes locally. They also bear the promise of visualising and controlling chemical reactions on a small scale. To do so, one needs to be able to measure both the concentration of products and reagents, as well as the temperature. The FLIM technique has both capabilities, and the potential to be fully traceable to standard fluids and conditions. To demonstrate this last point, it was decided at the beginning of this work to run a fully independent inter-comparison exercise, where experimental and modelled results were gathered by two different teams and quantitative comparisons established. Two cases were considered, namely thermal and solutal mixing. These were illustrated by the study of mixing of water at two inlet temperatures, and mixing of methanol/water–methanol in a T-junction, respectively. In this paper, the numerical approach is introduced first, together with the geometry and experimental conditions, and the real fluid properties gathered from published data. The experimental measurement is then described, emphasising the calibration of the response of fluorophores and image treatment for noise reduction in a full-field analysis. Finally, the results of both approaches are compared and discussed.

2 Modelling

The quantification of mixing is a well-known subject in classical macro-fluidic applications, and is documented in several textbooks. Tadmor and Gogos define mixing as “a process that reduces composition non-uniformity” and a mixture as “the state formed by a complex of two or more ingredients which do not bear a fixed proportion to one another and which, however commingled, are conceived as retaining a separate existence” (Tadmor and Gogos 1979). Three mixing mechanisms are to be considered:

  • molecular diffusion: occurs spontaneously, driven by the gradient of concentration of components, dominant process in gases and low viscosity liquids;

  • eddy diffusion: in turbulent mixing, molecular diffusion is superimposed on the gross random eddy motion;

  • bulk diffusion: eddy motion may also occur on a larger scale of bulk diffusion or convective flow process.

Here, we are interested in molecular diffusion and convective flow processes only, as turbulent flows are impractical in micro-fluidic systems.

Diffusion mixing in a rectangular channel may seem a simple physical problem, yet no mathematical solution exists in the case of general fluids and conditions. The use of finite elements and finite volume codes permits the lack of analytical solutions to be overcome and numerical and graphic representation of the solution of the coupled diffusion and flow velocity equations to be obtained. Most CFD packages tested by the authors enable the solving of this coupled physics problem, with various levels of success. A few words of caution are needed at this point:

  • CFD codes are unitless, and therefore prone to round-off and conversion errors. Consistency should always be checked particularly in recent software packages where units are super-imposed through a graphical user interface (GUI);

  • the dependence of the solution on the mesh, and in particular the mesh density, should always be checked together with the conditions of convergence of the problem, as is always the case with discrete numerical solutions. This step is often omitted in micro-fluidics studies, probably because of the large number of elements they give rise to and the consequent cost of computational time;

  • for diffusion problems it is not always clear whether the codes use a mass, volume or concentration ratio;

  • the over-simplification of the GUIs is rapidly increasing the acceptance of these software solutions, but is also prone to generate mistakes, as a number of control parameters are hidden, being labelled as “expert” parameters, although they were created as solver parameters a few years ago.

Nevertheless, the increase of computer speed and memory, that has made CFD available at entry levels, is a positive evolution of the field. The above-mentioned shortcomings can be overcome by proper code validation through well-established closed-form solutions. In particular, three models are relevant for this type of problem:

  • diffusion in a box or a thin section of a box. Here the two fluids are allowed to mix starting from homogeneous concentration, typically involving a step function. This model is very useful for verifying the effect of the mesh density on the results of the diffusion equation. Most solvers consider that the diffusion coefficient does not depend on the position of the finite volume cell, which is only true for very fine mesh density (in a numerical sense). This model was also used to optimise the number and parameters of the mesh adaption process. Notice also that if the step function (Heavyside) is not available in the finite volume code, a good alternative is to apply the initial concentration profile through a hyperbolic tangent function;

  • no diffusion, 2D transport of two liquids in a channel. A bi-laminar profile is obtained, one for each fluid, and the minimum length scale of interphase mesh can be obtained for a good rendering of advection;

  • a full slip boundary condition imposed at the walls of the channel allows development of a uniform velocity profile. This model can be used to verify the mesh adaption process in a steady state flow, as the downstream position can be related to the time of diffusion of the first example—advection is negligible.

We are interested in a T-mixer geometry where both inlets and the outlet are represented. This differs from the approach of Bennett and Wiggins (2003) where a mixture boundary condition is applied at the entrance of the channel. The present representation intends to be consistent with the experiment, where a fully developed laminar flow is present when the two fluids meet. The complex flow pattern at the junction and the entrance of the channel is an essential feature of the experiment, and as a result of the mixing patterns. Flow in a T-junction, or a junction of another shape, is a complex problem which has not been solved analytically to our knowledge. Even in the simple case where two fluids sharing one property (viscosity or density) are dispensed at equal flow rates, solving the incompressible Navier–Stokes equations may prove too challenging a task. Consequently, a solution to the coupled fluid flow and diffusion equations is out of reach, and only extremely simplified cases have been solved analytically, cf. Crank (1975) for examples.

2.1 Geometry and finite volume model

The problem consists of solving the momentum, continuity and diffusion equations simultaneously. The Navier–Stokes momentum equations are written:

$$\rho \frac{\partial u_i}{\partial t} +\rho u_j \frac{\partial u_i}{\partial x_j}=\frac{\partial}{\partial x_j}\sigma_{ij}(u)+\rho f_i $$
(1)

where

$$\sigma_{ij}=-p\delta_{ij}+\eta \left(\frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i} \right) $$
(2)

with i,j = 1,…,3. The continuity equation must also be satisfied:

$$\frac{\partial \rho}{\partial t}+\rho \frac{\partial u_i} {\partial x_i} = 0 $$
(3)

In the above equations, ρ is the density, t is the time, u i is the velocity component in coordinate x i , σ ij is the strain tensor, f i is the body force in x, p the hydrostatic pressure, η denotes the dynamic viscosity, and δ ij is the Kronecker delta. The last equation solved in the system is the transport equation. For thermal transport, the transport of enthalpy through the fluid domain is obtained from the thermal energy equation:

$$\frac{\partial \left(\rho e\right)}{\partial t}+ \nabla \cdot \left(\rho \overrightarrow{u} e\right) =\nabla \cdot \left( \lambda T\right)+p \nabla \cdot \overrightarrow{u} +\tau:\nabla \overrightarrow{u} $$
(4)

where e is the internal energy given by \(h=e+\frac{P}{\rho},\) h being the enthalpy. In the case of species transport, the transport equation is simply written:

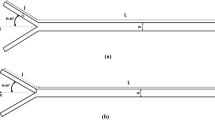
$$\nabla \cdot \left(\rho \phi \overrightarrow{u} \right) = \nabla \cdot \left( D \nabla \phi \right) $$
(5)

where ϕ is the water mass fraction in the fluid, and \(\overrightarrow{u}\) is the velocity vector. Notice that there are no additional source terms in the present problems. These equations are solved using the SIMPLE algorithm (semi-implicit pressure-linked equation) in ANSYS CFX. The convergence criterion was that the relative variation of ϕ between two successive iterations was smaller than the assigned accuracy level of 10−4, which was achieved in less than 200 iterations in all cases. The variation between two consecutive iterations of the mass and momentum were always smaller than 10−6 when convergence of ϕ was achieved. The geometry and dimensions of the T-mixer channel are shown in Fig. 1, together with the finite volume mesh used for the CFD calculations. The mesh displayed in Fig. 1 is intentionally coarse, and was imposed in the first steps of the calculation. In essence, CFD simulations in micro-fluidic channels do not pose many problems, except the large number of elements needed if one wants to obtain a full 3D rendering of the structure and accurate results. In practice, we found that for simple, i.e. non-mixing flows, tetrahedrons of edge length about 1/20th of the smallest dimension of the channel (here, the height) are sufficient for an accurate representation of the fluid flow velocity. This is not the case when thermal or solute diffusion is modelled. In this particular case, the mesh needs to be 10–25 times finer, which increases the computation time beyond reasonable limits. In order to gain accuracy in the transport simulations, a mesh adaption technique was implemented: CFX automatically re-meshes the zones were large gradients of concentration or temperature are found. A resulting mesh cross-section through cut-plane B is shown in Fig. 2. Notice that due to the mesh adaption, no obvious non-dimensional analysis is available as the re-meshing depends on the interfacial transport which is also a function of the flow rate.

Fig. 1
figure 1

Top geometry of the micro-fluidic T-mixer considered, showing the two cut plane locations: cut plane A is 10 μm below the surface, and cut plane B is the through thickness symmetry plane of the T-mixer; bottom view of the 3D mesh used for both simulations

Full size image
Fig. 2
figure 2

Top cross-section of the CFD mesh at cut plane B before (left) and after (right) refinement by the mesh adaption process; bottom effect of the mesh refinement shown when the concentration gradients are driving the mesh adaption. Notice the increased resolution and sharpening of the interphase upon mesh optimisation

Full size image

2.2 Materials

The material systems used are not considered ideal mixtures, i.e. the properties of the mixtures are not deduced from those of the constituents by direct or harmonic averaging. Furthermore, the two liquids do not have equal viscosity, as is often hypothesised to simplify calculations. Little information on the effect of accounting for real mixture viscosity, density and diffusion coefficient is available; Liu et al. (2004) presented a study of the water–glycerol system in micro-fluidic mixers, which demonstrated that mixing efficiency could be enhanced or degraded when accounting for real mixture properties depending on the flow rate. In this work, two mixtures were studied: mixing of water with the inlets at two different temperatures (thermal transport), and mixing of a methanol/water methanol solution (solutal transport).

2.2.1 Thermal properties of water

Thermal transport of water was the object of the first set of experiments in this work. The viscosity η, density ρ and heat capacity at constant pressure C p of water present a non-linear dependence on temperature, as shown in Fig. 3, and were input into the FE code through polynomials.

Fig. 3
figure 3

Viscosity (filled circles), density (opened circles) and specific heat (semi-filled circle) of water as a function of temperature, data from Lemmon et al. (2005), see text for details

Full size image

They were implemented as:

$$ \begin{aligned} \eta &= -3.7827 \times 10^{-10} \theta^5 + 1.2575\times 10^{-7} \theta^4 - 1.7087\times 10^{-5} \theta^3 \\ & \quad + 1.2653\times 10^{-3} \theta^2 - 5.8644\times 10^{-2} \theta + 1.7857 \\ \rho &= 1.3489\times 10^{-12} \theta^5 - 4.7464\times 10^{-10} \theta^4 + 7.3641\times 10^{-8} \theta^3 \\ &\quad - 8.8956\times 10^{-6} \theta^2 + 7.5204\times 10^{-5}\theta + 0.99983 \\ C_p &= -3.5877\times 10^{-11} \theta^5 + 1.2118\times 10^{-8} \theta^4 - 1.5636\times 10^{-6} \theta^3 \\ &\quad + 1.0363\times 10^{-4} \theta^2 - 3.2662\times 10^{-3} \theta + 4.2162 \\ \end{aligned} $$
(6)

where θ is the temperature in Celsius, and the units of η, ρ and C p are, respectively, mPa s, g cm−3, and J g−1.

2.2.2 Water–methanol mixture

Diffusion of water into methanol was also studied. It is well known that the properties of the mixture of these two liquids is not obtained from an average (direct or harmonic) of the liquids properties. Instead, both viscosity and density of the mixture exhibit strong non-linear relationships with the water (or methanol) content: Fig. 4. For numerical computation purposes, two options are available: either let the FV code interpolate between tabular data in a look-up table, or provide a polynomial relationship linking the viscosity and density to the water content. Such relations are obtained from a polynomial fit of the data displayed in Fig. 4:

$$ \begin{aligned} \eta^* =1.0094+2.9187 \zeta + 4.844 \zeta ^2 - 27.799 \zeta^3 \\ \quad +30.327 \zeta ^4 - 10.715 \zeta^5 \\ \end{aligned} $$
(7)
$$ \begin{aligned} \rho^* =0.9984-0.1874 \zeta +0.2577 \zeta^2 -0.6771 \zeta^3\\ \quad +0.598 \zeta^4-0.1978\zeta^5 \\ \end{aligned} $$
(8)

where ζ is the methanol mass fraction, and η* and ρ* are the mixture viscosity (in mPa s) and density (in g cm−3), respectively. The diffusion coefficient also varies with the concentration of water into methanol, as shown in Fig. 4. The data for the diffusion coefficient were converted from molar fraction in Woolf (1985) to mass fraction using molar masses of 18.052 and 32.042 g mol−1 for water and methanol, respectively. A polynomial fit was obtained:

$$ \begin{aligned} D^* =\left( 2.2741 - 5.4904\zeta + 14.4659\zeta^2 - 33.5866\zeta^3 \right.\\ \quad \left. + 60.1006\zeta^4 - 56.2985 \zeta^5 + 20.7264\zeta^6\right) \times 10^{-5}\\ \end{aligned} $$
(9)

where D * is the diffusion coefficient of water in the water–methanol mixture, given in cm2 s−1.

Fig. 4
figure 4

Viscosity (filled circles), density (opened circles) and diffusion (semi-filled circle) properties of the water–methanol mixture, data from Lide (2007) and Woolf (1985), see text for details

Full size image

3 Experimental

3.1 Fluorescence lifetime imaging microscopy

Recently, a superior approach to the imaging of micro-fluidic systems was introduced, using FLIM (Magennis et al. 2005). This technique involves spatially resolving the fluorescence lifetime of a fluorescent dye, rather than the intensity. It overcomes the usual problems of intensity-based methods—sensitivity to variations in the optical path, instability of the light source, scattering, uncertainty in the dye concentration, and photobleaching effects—because the lifetime is independent of the number of fluorescing molecules. It was demonstrated that FLIM enables spatially resolved quantitation of fluid mixing in micro-fluidic devices.

Fluorescence lifetime images were obtained by using wide-field illumination of the micro-fluidic cell with an ultra-fast pulsed laser. A gated intensified CCD camera was used to collect the resultant fluorescence within a short time window after a defined delay following the laser pulse. A series of images was acquired by varying the delay time between the detection window and the laser pulse, thereby sampling the entire fluorescence decay of the fluorescent probe; the data from each pixel was then fitted to a single exponential decay. An illustration of the experimental set-up used is shown in Fig. 5.

Fig. 5
figure 5

Principle of fluorescence lifetime imaging microscopy (I-CCD intensified charge coupled device camera, GOI gated optical intensifier), showing a single exponential lifetime decay

Full size image

3.2 Measurement of concentration

Solutions of the fluorescent dye 1,8-anilinonaphthalene sulphonate (ANS) in pure methanol and a water/methanol mixture (1:1 molar ratio, which corresponds to water at 30.8% v/v) were pumped into a micro-channel flow cell to meet head-on at a T-junction. The flow rates were varied from 10 to 75 μl min−1. These dimensions and flow rates correspond to Reynolds numbers of less than 10 so that the fluids are in the laminar flow regime. For concentration measurements, ANS was chosen as the dye because its fluorescence lifetime is extremely sensitive to the composition of water/methanol mixtures, showing a near-linear variation from 250 ps in pure water to 6 ns in pure methanol (Dougan et al. 2004). The calibration curve in Fig. 6, which correlates the fluorescence decay rate of ANS with the percentage of water in solution, was determined by time-correlated single-photon counting (TCSPC, cf. Magennis et al. 2005). ANS displays a single exponential decay at all water/methanol ratios, making it an ideal and unambiguous probe of solvent composition. In the rest of this paper, we are interested in the mixing of solutions of ANS in pure methanol and ANS in a water/methanol mixture (30:70 % v/v). The concentration of ANS in both input solutions is fixed, at 1 mM. For FLIM, the gate width was 600 ps, and 46 images were recorded at intervals of 500 ps. Every image represents the average of five separate exposures, each with an integration time of 0.1 s and a readout time of 50 ms to give a total acquisition time of about 35 s. The lifetime of ANS in pure methanol and the equimolar water/methanol solution at the input to the flow cell are the same as those measured by the TCSPC method. By using the calibration curve in Fig. 6, the composition of the fluid can be read directly from the FLIM map. To interpolate τ f values that were not determined during calibration, a stretched exponential function was chosen. The use of this function differs from the polynomial fit chosen in Magennis et al. (2005), and is justified by the physics of FLIM. It appears that the fluorescence emission of ANS decays as a single exponential with time, and that one single τ f can be determined at each concentration. However, the variation of τ f with the water concentration is non-exponential, indicating more than one single process. This can be understood as discrete steps corresponding to the various states of solvation of water into methanol, i.e. it is related to the number of methanol molecules neighbouring the water molecules. As such, there exists a distribution of relaxation times τ f,i that describes the TCSPC results for all concentrations, i.e. the fluorescence emission at one concentration is the sum of weighted processes (γ i ,τ f,i ) as:

$$\frac{I}{I_0}=\sum_{i=1}^N \gamma_i \exp \left(-\frac{t} {\tau_{{\rm f},i}}\right) $$
(10)

where I 0 and I are the intensity collected initially (at the moment of excitation) and at a time t, respectively. When N becomes large, it is generally accepted that the sum in the above equation is well represented by a simpler continuous function, the stretched exponential also known as the Kohlrauch–Williams–Watt function, given by:

$$\frac{I}{I_0}= \int\limits_0^t \gamma \exp \left[-\left(\frac{t} {\tau_{{\rm f},\beta}} \right)^\beta \right] {\rm d}t $$
(11)

and there exists a distribution of relaxation times given by:

$$\tau_{{\rm f},\beta}= \left(\beta \omega \tau_0\right)^{\frac{1}{\beta}} $$
(12)

where ω is a material parameter. In this formalism, only three parameters are therefore needed to fit the data of Fig. 6, and the function also presents the advantage of being bounded within a reasonable range, which is not always the case with polymers depending on the domain. Moreover, in the case where no coupling is present between ω and β, Eqs. 11–12 may be considered as a simpler expression also described by a stretched exponential function:

$$I=I_0 + \gamma_{\rm f} \exp -\left(\frac{\tau}{\tau_0}\right)^\beta $$
(13)

A good fit was obtained with the data displayed in Fig. 6, with the values (I 0, γ f,τ 0, β) = (0.4239, 5.549, 28.92, 1.287).

Fig. 6
figure 6

Calibration curve showing ANS fluorescence lifetime (τ f) as a function of the methanol/water ratio in the solution. Line is the best fit by the stretched exponential function, see text for details

Full size image

3.3 Measurement of temperature

An analogous approach was taken to map temperature by exploiting the temperature dependence of the fluorescence lifetime of the Rhodamine B (RhB) fluorophore. The use of FLIM of RhB to measure the temperature of methanol in micro-fluidic channels has been reported previously (Benninger et al. 2006) but the low solubility of RhB in water makes it unsuitable for measuring aqueous systems. We have found that Kiton Red (KR), a water-soluble, sulfonated derivative of RhB, shows the same temperature response as the parent fluorophore and is thus ideal for temperature measurement of aqueous solutions. The fluorescence lifetime of the RhB fluorophore decreases with increasing temperature as a result of a thermally activated change in geometry of the excited state, involving rotation of the substituent diethylamino groups, which accelerates the rate of non-radiative decay (internal conversion) (Casey and Quitevis 1988). The fluorescence decay of KR at a particular temperature is thus described by a single exponential function:

$$\frac{I}{I_0} = \kappa \exp \left(-\frac{t}{\tau_{\rm f}\left(T\right)}\right)$$
(14)

and the temperature dependence of the fluorescence lifetime obeys the Arrhenius equation, given by:

$$\frac{1}{\tau_{\rm f}(T)}= \gamma \exp \left(\frac{-E_a}{RT} \right) $$
(15)

The resulting fit, shown in Fig. 7, describes perfectly the experimental calibration data for KR in water, over the temperature range covered, in agreement with the behaviour reported previously for the parent fluorophore, RhB, in alcohols (cf. Casey and Quitevis 1988), as above.

Fig. 7
figure 7

Calibration curve showing KR fluorescence lifetime (τ f) as a function of the water temperature. Line is the best fit by the Arrhenius equation, with E a  = 24.19 kJ mol−1 and τ 0 = 9,283 ns

Full size image

3.4 Signal processing and data representation

In this section, diffusion processes are to be taken in the sense of signal processing. Unfortunately, the jargon is similar to that of materials science, but has been conserved for consistency with this field of expertise and the references cited in this section.

The noise present in the FLIM measurement results hampers direct comparison with the simulated behaviour of fluid temperature or concentration in the mixer. It needs to be removed without affecting the true value of the underlying data: the interest is mainly in the transition between temperatures or concentrations, and not in the strong local variations corresponding to measurement noise. Bi-dimensional diffusion processes were used to lower local noise while preserving the overall signal variations. This intends to maintain a constant contrast between the levels of local regions and the edges (identified as regions where transitions are comparatively large): more diffusion is applied in homogeneous regions (where level variations are low), and less in regions where transitions of large intensity are present (You et al. 1996).

Diffusion is typically used to remove such local noise from a bi-directional signal (or an image, usually) by processing it by means of a partial differential equation (PDE), as outlined below. Let us consider the continuous bi-dimensional signal I in the spatial domain (x,y), with \(I(x,y,\xi=0):{\mathbb{R}}^2 \rightarrow {\mathbb{R}}^+, \nabla I\) is its spatial image gradient, and ξ is a time-stepped diffusion parameter. In the present work, the diffusion equation first introduced by Perona and Malik (1990) was used:

$$\frac{\partial I(x,y,\xi)} {\partial \xi} = \hbox{div} \left[g\left(\|\nabla I \|\right)\nabla I\right] $$
(16)

where \(\|\nabla I\|\) is the gradient magnitude of the signal I, and g is an “edge-stopping” function, such that \(\lim_{x \to \infty}g(x) = 0:\) this function fulfils the objective to stop the diffusion along edges. Here, the Tukey’s bi-weight function first used by Black et al. (1998) was chosen:

$$g(x,\sigma) = \left\{ \begin{array}{*{20}l} {\frac{1}{2} \left[1-\left(\frac{x}{\sigma} \right)^2\right]^2,}\quad |x| \leq \sigma \\ 0,\quad \hbox{otherwise}\\ \end{array}\right.$$
(17)

where σ is set to its “robust scale” value as σ = 1.4826 MAD(∇ I), and MAD denotes the Median Absolute Deviation. The reader is referred to Black et al. (1998) for more details on the function and its properties, and on the definition of a “robust scale”. The numerical process—applied to I by means of a finite differences implicit scheme—is carried over for n steps. In practice, 10 ≤ n ≤ 30 was found sufficient for the purpose of this study.

In order to preserve values on all boundaries when the diffusion scheme is applied, a mask was implemented to explicitly constrain the “active” area where the diffusion process takes place. This mask was obtained by excluding all non-determined data, fixed to zero, and its contour was further smoothed by applying a morphological closing (see Soille 1999 for details on morphology in image processing). An example of this denoising process is shown in Fig. 8. Points in black from the mask (see Fig. 8c) are excluded from the calculation of the anisotropic diffusion process.

Fig. 8
figure 8

Noise removal procedure, where the original signal (a) yields the denoised signal (b) upon application of the mask shown in (c) to preserve boundary values, with σ = 14.5645 and n = 30. The lateral scale is the temperature in °C, and a plot of the temperature taken along the white line indicated in (b) is shown in graph (d)

Full size image

4 Results

4.1 Thermal diffusion

The first set of experiments conducted involves the determination of water temperature in the T-mixer, when water at 30 and 60°C is pumped on each side at an equal flow rate of 75 μl min−1. In this case, the FLIM response of the KR marker is followed across seven locations in the mixer, giving a composite plane view of the temperature distribution. The results are displayed in Fig. 9, with matching locations indicated on the simulation results by boxes. Given the acceptable qualitative agreement, horizontal cross-sections were also taken at the middle of each box and experimental and theoretical temperature profiles were built accordingly. The quantitative agreement, highlighted in plots of water temperature across the width of the channel, taken at seven downstream locations, is also satisfying. The general trends are comparable, and only minor discrepancies are observed between the measured and simulated data. In fact, the two largest discrepancies, observed at y = 0 mm on the hot side and at y = 2.3 mm on the cold side, are, respectively, due to the presence of a small impurity at the entrance of the T-mixer channel,Footnote 1 and a poor focus close to the edge (the same focus was maintained along the channel, for reasons explained below). Both effects are readily visible on the measurement maps after careful examination. Thus, the experiment and simulation results correlate without ambiguity. This holds for a number of reasons, and has several implications, discussed below.

Fig. 9
figure 9

Experimental versus CFD results of the temperature profiles in the x-direction at various positions z along the channel. For clarity, the curves and data points have been offset by a temperature indicated on the Figure at the right of each curve

Full size image

First, the best agreement between theory and experiment is only obtained when the correct cut-plane is considered from the CFD results. In the present case, trial and error showed that cut-plane A was the optimal match to the FLIM data. This illustrates the 3D-effects on the interplay between thermal diffusion and fluid transport. Effectively, a non-slip boundary condition was applied at the walls, and close to the upper and lower walls the thermal diffusion front is broader that at the mid-plane of the mixer. This reflects the lower fluid velocity close to the wall, where comparatively the fluid has more time to diffuse laterally than where the flow reaches its largest value, i.e. at the centre of the channel. This is illustrated in Fig. 9, in the top-right inset, where the difference between temperature maps taken at the cut-plane A (left hand cross-section view), located 10 μm below the surface, and at the cut-plane B (right hand cross-section view), located at the mid-plane of the mixer, is clearly visible. This location was determined by comparing the experimental results with the simulated temperature maps at various horizontal cross-sections. The highest gradients being found in the T-mixing zone, it was chosen as the basic measurement to determine the location precisely (within ±1 μm). This finding is important in indicating the exact nature of the measurement obtained using a FLIM set-up of the present type, which employs widefield imaging in an epifluorescence microscope. In such a microscope, the image is expected to have some contribution from (out-of-focus) fluorescence arising from excitation of the sample above and below the focal plane of the objective. However, the correlation between the experimental and simulated results here shows that the image is dominated by fluorescence intensity originating from a well-defined focal plane. Thus widefield FLIM can deliver 3D measurements, without recourse to more complex scanning confocal imaging methods cf. Benninger et al. (2006), as above.

Second, the good correlation obtained also means that all the major hypotheses of the model are valid. The most important, from a generalisation point of view, is the adiabatic conditions at the walls: because the temperature profiles correlate well along the whole channel, one easily deduces that there is no heat loss in the domain. This has numerous implications in terms of future applications of this simple technique: the determination of Soret or Dufour coefficients, a notoriously difficult measurement, should be facilitated by this type of set-up, to name only a few. The two effects have not been investigated in micro-fluidic systems yet, although they may be of practical importance in biological and fuel cell applications.

In passing, we also note that the mesh refinement procedure—exemplified in Fig. 2—is also valid, which is of great use to reduce the computation time. Close to the walls the mesh was refined initially, unfortunately the effect of this refinement cannot be investigated using these experiments. Although the experimental results permit the quantitative mapping of temperature in one plane of the channel, the noise in the data and its removal by the numerical diffusion process involve a loss of information over the first two to ten pixels on the edges of the signal depending on the strength of the filter. This corresponds to 5.44 μm to about 30 μm in the present case, that is about half to three times the thickness of the refined boundary layer modelled in the finite volume mesh. Consequently, it is not possible to draw conclusions as to the no-slip boundary condition at the walls. To do so, a narrower channel and higher microscope magnification would be needed.

4.2 Water content

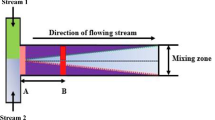
To complete the quantitative analysis of a reaction on the microscale, one needs not only to measure the thermal exchange of the system, as presented above, but also to follow the evolution of the concentration of species. In the present work, the solvation of a water–methanol mixture in methanol is followed in the T-mixer. The raw data shown in Fig. 10 was presented in Magennis et al. (2005), and is reproduced here after a more thorough signal treatment has been introduced in this work. Color maps of the water content are shown at three locations taken along the channel length, namely at the entrance (y ≈ 0 mm), at its middle (y ≈ 4.5 mm) and its end (y ≈ 9 mm). As shown in Fig. 10, pure methanol was pumped at the left inlet while the water–methanol mixture was pumped at the right inlet at the same flow rate. From the measurements taken at locations B and C, it is evident that the mixing efficiency decreases with increasing flow rates. In fact, provided there were no coupling between the diffusion and fluid velocity, one could regard these twelve results as the image of one single phenomenon—diffusion—taken at various residence times. If that were the case, the results of lines B and C could be reordered to form a composite picture of the whole channel. Yet, the first line of results (A) clearly demonstrates that this reasoning is essentially wrong. One essential feature of the high flow rate is the occurrence of a “S” shaped mixing front in the T-junction, which is found both in the experiment and numerical results, as will be shown later, and is not present at lower flow rates. This shape of the mixing front is the result of the complex pattern of fluid flow velocity that develops at the location where the two fluids meet. Because the same inlet flow rate is applied to both fluids and they have different viscosities and densities, they develop a large gradient of velocity, as shown in Fig. 11. It is apparent that the flow is non-symmetric as the low velocity region above the entrance of the junction is skewed on the left hand side. It is interesting to notice as well that the description, and calculation, of the entrance length is not straightforward. To do so, the formula introduced by Langhaar (1942) would need to be modified to account for the presence of two fluids and a finite depth. To summarise, at this point, based on the experimental results only, one first conclusion can be drawn: the interplay between diffusion and fluid velocity cannot be simplified to two separate phenomena in the T-junction. This should also apply to the rest of the channel, even provided some entrance corrections are applied.

Fig. 10
figure 10

Water content at three locations in the T-junction as obtained by FLIM, with inlet flow rates of Q = 10, 25, 50, 75 μl min−1. Scale bars are water % v/v. Location A is at the T-junction, B is centred at y = 4.5 mm, and C at y = 9 mm

Full size image
Fig. 11
figure 11

Velocity profile of methanol (injected on the left) and water/methanol (injected on the right) mixing in the T-junction; grey level lines are z-velocity isolines, numbers attached to the line is the velocity

Full size image

In the remainder of this discussion, it is chosen to concentrate on the results obtained at the high flow rate only (75 μl min−1). This choice is justified by the higher spatial gradients of concentration found in this case, which are more prone to show the limits of the model. Indeed, good correlations between experimental and numerical results could be obtained for the cases of 10 and 25 μl min−1, and the largest discrepancies were obtained at higher flow rates. Based on the knowledge gained in the previous experiment, the full 3D model is run, and only cut-plane A is analysed, i.e. the plane located 10 μm below the surface. The first modelling attempt by CFD was only successful in the sense that it confirmed the observation made on the flow front in the T-junction, that is in zone A. However, in zones B and C, 4.5 and 9 mm below the junction, respectively, it was noticed that diffusion was much more efficient in the experiment than in the model, where the effective diffusion coefficient would have to be about ten times larger than applied in the model in order to match the experimental results. The CFD results are shown in Fig. 12. To explain this discrepancy, we considered Soret diffusion, which did not lead to differences as large as observed—one order of magnitude—because the heat of solvation is small in this system. The problem was partially resolved by accounting for buoyancy effects, applying a non-zero gravitational field over the whole domain. A good match was then obtained in zone B, as shown in Figs. 12–13. The importance of buoyancy may be surprising in the field of micro-fluidics, where it is generally a good approximation to neglect it. In the peculiar case of mixing of two fluids of different properties, however, it must be accounted for as it tends to re-orient the interface between the fluids. This phenomenon has been described previously (Yoon et al. 2005; Yamaguchi et al. 2006), and Yamaguchi et al. introduced a modified non-dimensional number to described the rotation of the interface between two immiscible fluids flowing in a microchannel. To do so, the Richardson number (also equal to the square of the Froude number) is altered to account for the downstream dimension as well as the cross-dimension, and a number Z is defined as:

$$Z= Re Ri' = \frac{\Updelta \rho g w L}{2 \mu U} $$
(18)

In the case of immiscible fluids, these authors show that the tilting of the interface between the two fluids is accurately described by a second degree polynomial of Z, where the interface is rotated by 90° for Z ≈ 200 and 45° for Z ≈ 50. It is remarkable that in the present case this non-dimensional number still keeps all its sense, as we obtain Z ≈ 51 and the interface is rotated by about 45° when the mixing fluids reach zone B, as predicted by Yamaguchi et al. (2006). Thus, Z appears not to depend upon the mixing of the fluids. This is not surprising as the diffusivity of the fluid is low compared to gravitational forces. Furthermore, the rotation of the interface explains the increase of mixing compared to a model where buoyancy is neglected, as it generates an increase in interfacial area and as a result increases mixing by diffusion. It is also important to notice that buoyancy effects appear clearly in the comparison of experimental and numerical results because the measurements are taken in cut plane A (located 10 μm below the top surface of the channel) and not in a through thickness average. To summarise, with allowance for buoyancy effects, driven by the gradient of density of the two mixing fluids, the modelled and experimentally determined mixing are in good agreement in zones A and B.

Fig. 12
figure 12

Water content obtained by CFD in three planes located at 10 μm from the top and bottom surfaces and at mid-plane. The difference in mixing due to 3D and buoyancy effects is clearly visible on the limits high and low water content regions

Full size image
Fig. 13
figure 13

Experimental versus modelled water content in cut-plane A, located at 10 μm from the top surface and downstream locations indicated on the Figure. The symbols are experimentally determined values by FLIM, whereas the lines are the modelled finite volume results

Full size image

This is no longer true in zone C, where the modelled mixing is greater than the experiment, as shown in Fig. 13. Unfortunately, in this case, there is little that can be done to ameliorate the model. In fact, given the perfect match obtained in zone B, the mismatch in zone C is quite surprising: the finite volume mesh, boundary conditions together with the fluids properties render the experiment perfectly over 4.5 mm and then fails at a longer distance downstream—does this invalidate the earlier model? To understand the failure of the model at longer flow distances, it is useful to reconsider the problem. Mixing has two components: diffusion and advection. Those components cannot be split, as they are strongly coupled in the process. However, it is possible to evaluate the effect of diffusion alone, to get an insight into the extent of the effect of advection. To do so, let us consider the basic diffusion problem where a water–methanol mixture is brought in contact with methanol at a time t = 0 s, and let to diffuse for a time t. Neglecting gravitational effects and supposing that the two fluids are at rest at t = 0 s, this problem is the well-known case of diffusion along one spatial dimension. Consider also that if diffusion was independent of fluid velocity, time t would be related directly to the downstream distance y by y = QAt, where Q is the flow rate and A the cross-section area of the channel. Diffusion along the x-direction is given by Fick’s second law, i.e. is obtained from solving:

$$\frac{\partial c}{\partial t}= \frac{\partial}{\partial x} \left(D \frac{\partial c}{\partial x} \right) $$
(19)

with the boundary conditions

$$\left.\frac{\partial c}{\partial t} \right|_{x=0}=\left. \frac{\partial c}{\partial t}\right|_{x=W}=0 $$
(20)

and the initial concentration profile is given by a fit to the experimental concentration profile obtained in zone A, at y = 0 mm:

$$c\left(x,0\right)=0.175 \left(1+ \tanh \frac{x-175}{25}\right) $$
(21)

where x is expressed in micrometers. Equation 19 has a closed-form solution if the diffusion coefficient D does not depend upon x. This is not the case for the fluids chosen here, as we have seen that D strongly depends on the concentration, which has been shown to have large effects on the resulting concentration profiles (Wu et al. 2004). Accordingly, Eq. 19 is rewritten as:

$$\frac{\partial c}{\partial t}= \frac{\partial D}{\partial x} \frac{\partial c}{\partial x} + D \frac{\partial^2 c}{\partial x^2} =\frac{\partial D}{\partial c}\left(\frac{\partial c} {\partial x} \right)^2+ D \frac{\partial^2 c}{\partial x^2} $$
(22)

and Eq. 22 is solved by the finite difference method for t up to 0.3 s. Figure 14 shows the results of this approach, where the water content is plotted against the distance across channel at times corresponding to the distances downstream the fluid would travel. As such, the curves obtained at t = 0.144 and 0.288 s correspond to distances of 4.5 and 9 mm, respectively, with neglecting entrance length related effects. The results shown in Fig. 14 clearly demonstrate the effect of advection, as the diffusion model clearly underestimates mixing. In the experiment, the non-constant advective velocity effectively stretches the water content distribution, which results in sharp gradients perpendicular to the flow direction, which diffusion then irons out. Mostly, advection is due to shear in the present geometry, and its combination with diffusion leads to a more efficient mixing process than diffusion alone. As a result, advective transport is responsible for the failure of the model at longer distances, which may be due to a number of factors. First, advection is directly related to the amount of shearing of the fluid, and partial slip at the walls would reduce it. However, there is no direct experimental evidence that this phenomenon is present, and additional experiments would be needed, for instance micro-particle tracking velocimetry (PTV) to measure the fluid velocity close to the walls. Second, the FLIM measurement is taken close to the outlet, and a back pressure could develop and slow the fluid in this region. This would have two opposite effects: increase the time for diffusion, but decrease advection. Since advection is the main component of mixing in this part of the channel, this effect could explain the discrepancy although the same remark as above applies in terms of experimental validation. Third, a numerical error is present in the model, which may be relatively important at these locations: the mesh is not refined downstream of zone B, as gradients of concentration are low. The effect of the coarser mesh is to overestimate diffusion, as the solver makes use of one single interpolated value of the diffusion coefficient per finite volume element. As a result, another refinement step would be needed after zone B, to account for gradients in the derivative of fluid velocity for instance. This hypothesis could not be tested in this work due to the size of the numerical problem it generates and the computational resources available. Still, the very large effects of mesh refinement on the extent of mixing, as was shown for zone A in Fig. 2, point towards this last hypothesis as the most likely source of error in the numerical model.

Fig. 14
figure 14

Water content obtained by solving Eq. 22 at times corresponding to the average distance travelled, versus experimentally determined values by FLIM

Full size image

5 Conclusions

In this work, the quantitative response in micro-mixing experiments of FLIM was demonstrated by comparing its results to those of simulations from the finite volume method. Two cases were studied: mixing of water at two temperatures and mixing of methanol and a water–methanol mixture. The former clearly demonstrated the validity of the method for temperature measurements, and established that the FLIM measurement is not a through thickness average over the channel as previously envisaged, but instead well localised in space. Typical 3D effects highlighted by the model showed that the FLIM measurement was characteristic of only one plane section of the mixer, located at the imaging distance of the optical apparatus, where the optical microscope was focused. From these results, a wide-field 3D-FLIM technique appears possible, although intricacies similar to those found when a micro-PIV is upgraded to PTV are to be overcome. Importantly, the good comparison between experimental and simulated results demonstrated that the fluid did not exchange heat with the environment. The latter addressed the measurement of concentration profiles, and similarly showed a large influence of the plane location of the measurement. This effect was attributed to buoyancy, which is seldom accounted for in micro-fluidics. However, the difference of densities of the fluids is large enough to drive a rotation of the interface, the effect of which is non-negligible on the amount of mixing. This effect is well characterised by means of a modified Richardson number that was used previously for non-mixing flows of two fluids in a rectangular channel. Finally, the operation and accuracy of a finite volume model of the channel was considered, where it was shown that the method fully captures all the phenomena associated with thermal transport, but fails partially with solutal transport. The present study points towards issues associated with mesh refinement and the mesh density with increasing downstream distance. Where the mesh adaption was successful the numerical results appear to describe well experiments, which is no longer the case where mesh refinement is not efficient. In this study, this phenomenon could be attributed to the interplay between two mixing processes: diffusion and advection. While mesh refinement worked well for the former, following a criterion based on the gradient of concentrations, no specific mesh adaption procedure could be specified to account for the latter. This explains the failure of the model at longer mixing times.