1 Introduction

An air gap under movable structures composed of microelectromechanical (MEM) components is a widely studied problem, especially as applied to perforated plates, a common shape for various applications. Fluid interactions make damping and compressibility forces to act on movable parts, resulting in modifications of both static (e.g., switching time) and dynamic (e.g., resonance frequency, vibration amplitude) response.

Plate perforation is often necessary for sacrificial-layer removal during building processes of MEMS devices, representing a technological constraint for the designer. The resulting structures are characterized by the presence of complex fluidic phenomena influencing their behaviour. Their proper simulation is the goal of many studies. The main difficulty is the correct estimation of pressure distribution inside and below the holes and into the gap in order to evaluate the damping force acting on the movable 3D structure. Generally, the volume of fluid surrounding the plate should be considered in the analysis too. These are the reasons why reduced dimension models need to be developed. These models enable the simulation of complicated cases, as well as make the computation much faster.

Two different reduced-dimension approaches can be distinguished in modeling damping in perforated structures: analytic or compact modeling and numerical, using, e.g., a Finite Element method (FEM). The benefit of analytic models is their simplicity and ease of use in various design tools. The drawbacks are the limited accuracy and validity regime, especially the applicability to a limited number of topologies. The benefit of the numerical method is a much more general applicability to various damper topologies. These include arbitrary damper surface shapes and deflection profiles together with nonuniform perforation.

Several analytic models (Skvor 1967; Veijola and Mattila 2001; Veijola et al. 2002; Bao et al. 2002, 2003; Homentcovschi and Miles 2004; Mohite et al. 2005; Veijola 2006a, b), and dimension-reduction numerical models (Starr 1990; Veijola et al. 1995; Schrag et al. 2001; Sattler et al. 2002; Yang and Yu 2002; Mehner et al. 2003; Sattler and Wachutka 2004; Schrag and Wachutka 2004; Veijola 2007) have been published. In most of the publications, the verifications and the validity regime of applicable operation range are missing. This is explainable, since measurements of several topologies would require manufactured devices for test purposes. However, some results are available in (Kim et al. 1999). Another way to verify the models is to imitate the gas flow as realistically as possible with Navier–Stokes simulations of the 3D topology. Such results have been presented in Veijola (2006b, 2007) to verify the compact model and the reduced-dimension method presented in these papers, respectively. These results have been compared with the measured results presented in Kim et al. (1999) with good agreement. 3D flow simulation of the Navier–Stokes equations may not be applicable in solving practical damping problems in a normal design flow of the structures, but it is an excellent way to build various reference simulation topologies for the reduced-dimension models. The benefit of using 3D simulations for verification purposes is the fact that the method is very effective in solving the cases where the reduced-dimension models have problems in their accuracy.

FEM methods are used in many recent investigations of vibrating perforated plates, say, planar gas-damped accelerometers under electrostatic loading (Pursula et al. 2006); here the transient model combines electro-mechanical coupling to nonlinear squeeze-film damping effects and utilizes various reduced-order and reduced-dimension methods to significantly lower the computational cost of the simulation. A study of the application of ANSYS method for the evaluation of dynamic parameters on vibrating plates at various frequencies is presented in Somà and De Pasquale (2007, 2008).

In the present study, the force acting on a movable perforated square plate is studied with numerical simulations using two different methods that reduce the third dimension: the Perforated Profile Reynolds method (PPR) (Veijola 2007) and the simplified 2D ANSYS approach (ANSYS 2007). The results are compared with accurate 3D flow simulations (Veijola 2006b, 2007) and different simulation strategies are discussed.

2 Reduced dimension models

2.1 Operation of perforated dampers

The effective system is represented by the plate structure, the ground substrate, and the fluid surrounding the damper; when the plate moves towards the substrate, the fluid contained in the gap is compressed and generates forces acting mainly on the lower surface of the plate and on the ground surface. A complete numerical model can be realized by meshing the whole 3D volume of the fluid in the air gap, in the holes, and around the structure. This method of simulation is accurate but needs a very high number of elements and usually requires a very long computation time.

2.2 Principal flow patterns

In perforated 3D structures, several flow components must be studied in order to perform the reduction of the third dimension of the model. Figure 1 illustrates two principal flow direction patterns in perforated dampers in perpendicular motion. The arrows denote the main flow directions caused by the downward movement of the perforated body. In Fig. 1a, the flow escapes from the holes only, and the outer borders of the damper are assumed to be closed. This results in a repetitive pressure pattern (when uniform perforation is assumed), and the flow can be solved separately for each of these patterns, also called cells. In Fig. 1b, the gas flows out from the damper borders only, the holes are assumed to be closed. In this case, the resulting average pressure distribution is similar to the one for rigid surfaces without holes. In the general case, both flow directions must be considered. Under certain conditions, a closed-border flow can be assumed even if the damper borders are actually open. This is true in a situation where the air gap is very narrow compared with the diameter of the holes. If these requirements are fulfilled, the resulting model is simple to use since the geometry of the damper surface is not critical: the damping of the structure is simply the sum of the damping in all cells.

Fig. 1
figure 1

Principal flow direction patterns in perforated dampers in a closed border case and b closed holes case. The upper pictures show the perforated surface and the lower ones show their cross-sections at A–B of the air gap and holes

Full size image

Figure 1 shows several additional things that must be considered in building the reduced model. Most important are the regimes indicated with curved arrows, since the curvatures of the flow fields will introduce considerable additional damping in the system. In the region under the hole, the flow direction changes from air gap flow into capillary flow entering the hole. Also, above the hole, the capillary flow changes its form and couples to the flows from neighbouring holes. The same applies to the flow escaping from the damper borders in Fig. 1b. We call the regimes with curvature in the flow fields intermediate regimes. Fig. 1b also shows that the gas is able to flow through the regime under the holes.

The idea behind the reduced dimension model is simple: the flow in the air gap is modelled as a 2D flow and the flow in the holes is modelled as a 1D capillary flow. The 2D air gap flow is simply solved from the Reynolds equation, and the flow through the holes is introduced as additional boundary conditions or additional flow conductance terms added in the equation. In the case of uniform and dense perforations, the flow through perforations need not be considered accurately spatially; only the average flow resistance due to the perforations is considered and this flow resistance is assumed to be uniformly distributed over the surface area.

Challenges remain, e.g., in modeling the flow in intermediate regimes. Numerical methods can be used to characterize the intermediate regimes, as in Veijola (2006a, b), but rarefied gas phenomena can not be handled by usual FEM solvers in the transition flow regime. Another challenge is to calculate correctly the damping force acting on the 3D body. There are two alternatives. One is to consider the forces acting on the perforated structure only. This includes pressure forces on the upper and lower surfaces, and additionally shear forces on the sidewalls of the holes and the outer borders of the damper. The second alternative is to consider the force on the whole ground surface only.

Both analytic models and reduced-dimension FEM methods utilize the same reduction principles described above. In both methods, the flow through the perforations is modeled with compact models of flow channels. The difference is in the way how the air gap regime is treated and how the flow channel model is coupled with the air gap flow. Since reduced-dimension FEM methods also need compact models, we need to discuss them first.

2.3 Analytic models

Starting from the simplest possible model (Skvor 1967) that assumes closed borders, zero resistance for the hole, and ignores the intermediate regimes and rarefied gas effect, several improvements have been presented in the literature (Veijola and Mattila 2001; Veijola et al. 2002; Bao et al. 2002, 2003; Mohite et al. 2005; Veijola (2006a). Most of these papers lack proper verification of the models presented. A compact model for a cell in Veijola (2006b) considers all intermediate flows, rarefied gas phenomena in the slip flow regime, and contains verifications against 3D FEM simulations in a wide range of perforation ratios. All compact models presented are restricted to uniform perforation (equal pitched, equal sized holes), and constant air gap. Rectangular surface geometry is also assumed. However, if a closed-border assumption can be made, damping does not depend on the shape of the surfaces, but only on its size.

2.4 Reduced-dimension numerical methods

Here, a method is called numerical if the surface area is divided into a 2D mesh. These methods allow much wider versatility for the damper structure shape and the perforations. In principle, the holes need not be similar, nor equal pitched. Also the air gap height may vary and the surface motion can be arbitrary. However, in this comparison we discuss only uniform perforation, constant static air gap, and perpendicular motion.

In the modeling, two cases can be distinguished depending on the relative number of perforations. In the case of a large number of perforations, an efficient 2D FEM method, called homogenization method, can be applied. The flow resistance due to holes is assumed to be uniformly distributed over the surface area. The method is computationally efficient, since a sparse mesh can be used in the simulation. This is possible because the contribution of holes is included in the perforation conductance only and removed from the simulated topology. For a small number of perforations, the exact pressure distribution is needed, and the hole areas remain in the simulated topology. In the comparison in this paper, a case with a small number of holes is used.

The published numerical approaches can be divided into two categories: in the first category, the holes are considered as boundary conditions to the Reynolds equation; in the second category, an additional flow conductance term has been added in the Reynolds equation, as proposed in (Veijola and Mattila 2001). Papers belonging to the first category are the following: Starr (1990) used heat conduction equation with zero boundary conditions at the holes in modeling damping in an accelerometer. A similar approach was presented in Veijola et al. (1995), but an equivalent circuit was constructed to solve the problem with a circuit simulation tool. In Schrag et al. (2001), Sattler et al. (2002), Sattler and Wachutka (2004), and Schrag and Wachutka (2004), a tilting perforated mirror was analyzed using a finite network method. Among papers belonging to the second category, there is Yang and Yu (2002), who used an equation similar to the PPR equation to build further reduced models. Mehner et al. (2003) utilized the ANSYS approach to build further reduced models. The PPR method was presented in Veijola (2007) with comparisons against 3D simulations. A solver for the PPR equation in the multiphysical FEM software Elmer (Elmer 2007) was used in the calculations.

3 Simplified 2D ANSYS method

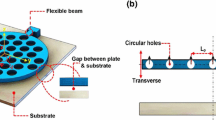
The ANSYS FEM tool gives the opportunity to realize a simple and compact model of the system that avoids the necessity to simulate the whole fluidic 3D domain as to solve Navier–Stokes equations and determine pressure distribution of the fluid contained into the gap. The FEM model is composed of two different parts: the first one reproduces the air present under the plate, while the second one models the air contained in each hole. The thin fluid layer separating the plate from the ground substrate is modeled with the Reynolds equation using fluid136 elements, which are two-dimensional and quadrilateral-shaped, defined by four corner nodes and a mid-side node. In each hole, the fluid is modeled by the one-dimensional fluid138 element having two nodes: the lower one is positioned on the air gap plane in correspondence of the middle point of the hole’s cross section, while the upper one is positioned at the middle point of the upper hole’s cross section. This element simulates fluid flow through the hole and estimates how the pressure gradient at the borders of the holes affects pressure in its lower section and consequently in the gap. The lower node of fluid138 element is pressure constrained with each of the nodes of the fluid136 elements that are present at the corresponding edges.

For both element types, the fluid environment is defined by a set of real constants that define the gap separation, the ambient pressure, the mean free path (λ), and the corresponding reference pressure.

3.1 Element description

The fluid136 element (ANSYS 2007) that is used here to model the viscous fluid flow behaviour in the gap is based on the linearized Reynolds equation familiar from lubrication technology

$$ \frac{{h^{3} }} {{12\eta _{{{\text{eff}},{\text{gap}}}} }}{\left( {\frac{{\partial ^{2} p}} {{\partial x^{2} }} + \frac{{\partial ^{2} p}} {{\partial y^{2} }}} \right)} = \frac{h} {{p_{{\text{A}}} }}\frac{{\partial p}} {{\partial t}} + v $$
(1)

where h is the gap thickness, η eff,gap is the effective viscosity coefficient for the air gap, p is the pressure, p A is the ambient pressure, and v is the vertical plate velocity that can be a function of x and y. In this study, incompressible gas is assumed, and the time derivative of the pressure becomes zero.

The element is subjected to some limitations derived from the hypothesis of application of the Reynolds equation as: lateral dimensions of structures much greater than the gap size, a small pressure gradient relative to the ambient pressure, and neglecting the heating eventually produced by viscous friction. The velocity of the moving surface is assumed to be equal to 1 m/s and is used as a body force for the static analysis.

The fluid138 element (ANSYS 2007) is used to model the fluid flow through rectangular channels defined by holes; in this case there are some assumptions too: isothermal viscous flow at low Reynolds numbers, small channel length compared with the acoustic wave length (but small lengths compared with mean free path are allowed), and small pressure drop with respect to the ambient pressure. Fringe effects at the ends of the channel are mentioned in (ANSYS 2007), but they do not figure in the equations presented.

According to continuum flow theory, the volume flow rate of the square channel is evaluated through the Hagen–Poiseuille equation

$$ Q = \frac{{8r^{2}_{{\text{h}}} }} {{\eta \chi }}\frac{{s^{2}_{0} }} {{h_{{\text{c}}} }}\Updelta p $$
(2)

where r h is the hydraulic channel radius, η is the viscosity coefficient, s 0 is the diameter of the hole, h c is the length of the hole and Δp is the pressure gradient along the channel length. The hydraulic radius is defined as

$$ r_{{\text{h}}} = \frac{{s_{0} }} {2}, $$
(3)

while the friction factor value for square holes is

$$ \chi = \frac{{24}} {{0.422}}. $$

Noting that Δp = F/A and Q = Av v (where A = s 0 2 is the cross-sectional area and v v is the velocity at the cross-sections), the mechanical resistance (R P = F/v v) of the channel becomes

$$ R_{{\text{P}}} = \frac{{\eta \chi h_{{\text{c}}} A}} {{8r^{2}_{{\text{h}}} }} \approx 28.436\eta h_{{\text{c}}} . $$
(4)

3.2 Boundary conditions

The dimensions of micromechanical components are used here. The rarefied gas properties are considered since the continuum flow conditions do not hold in such a case. Here, standard atmospheric conditions are assumed and the channel widths are not extremely small compared with the mean free path of the gas. This justifies the velocity slip conditions used here, since the maximum Knudsen number is about 0.1 (the mean free path of the gas (λ) divided by the characteristic channel width). Slip flow conditions take into account the presence of a nonzero fluid velocity component at the surface. This leads to an assumption of an effective viscosity coefficient evaluated as

$$ \eta _{{{\text{eff}},{\text{gap}}}} = \frac{\eta } {{1 + 6K_{{n,{\text{gap}}}} }} $$
(5)

and

$$ \eta _{{{\text{eff}},{\text{hole}}}} = \frac{\eta } {{1 + 7.567K_{{n,{\text{hole}}}} }} $$
(6)

for the air gap (Burgdorfer 1959) and the rectangular holes (Ebert and Sparrow 1965), respectively, where the Knudsen numbers are respectively

$$ K_{{n,{\text{gap}}}} = \frac{\lambda } {h} $$
(7)
$$ K_{{n,{\text{hole}}}} = \frac{\lambda } {{s_{0} }}; $$
(8)

accommodation factors can further be used to define the type of gas molecule reflection at the wall interface (diffuse reflection or specular reflection).

The model does not allow the simulation of a portion of air located at the sides of the damper because only the fluid situated under movable parts can be considered; boundary conditions must be imposed on the fluid borders in correspondence of plate edges. The pressure constraint is assumed to be equal to the relative ambient pressure (0 MPa), to allow a better detection of the small pressure gradient in the gap. The same pressure constraint is imposed in the upper node of each fluid138 element as shown in Fig. 2.

Fig. 2
figure 2

Fluid136 and fluid138 meshing elements in simplified ANSYS model (a = 40 μm, N = 64, s 0 = 3 μm)

Full size image

4 PPR method

The PPR method (Veijola 2007) is based on the same linearized Reynolds equation for incompressible flow as shown in Eq. 1, but augmented with an additional flow admittance Y h that considers a “leakage” flow resistance due to perforations.

$$ D_{{\text{h}}} \frac{{h^{3} }} {{12\eta _{{{\text{eff}},{\text{gap}}}} }}{\left( {\frac{{\partial ^{2} p}} {{\partial x^{2} }} + \frac{{\partial ^{2} p}} {{\partial y^{2} }}} \right)} - Y_{{\text{h}}} p = v $$
(9)

In this numerical PPR method, solving Eq. 9, the surface topology is arbitrary, and Y h and v may both depend on x and y. Equation 9 is almost identical to the equation used in Veijola and Mattila (2001), Bao et al. (2003), and Veijola (2006b), where it was solved analytically for rectangular surfaces assuming constant Y h and v. D h is an additional diffusivity coefficient that accounts for the change in the horizontal flow resistance due to the intermediate regimes under the holes. In the homogenization method, Y h is a constant, but in PPR it is made to vary spatially depending on the placement of the perforations. The conductance is also made to vary at each hole depending on the velocity profile in the channel. The value for the conductance has been calculated analytically from the flow resistance of long channels considering velocity slip boundary conditions. Since the assumption for a long channel is rarely valid in practice, additional flow resistances due to the end corrections are added in Y h. The couplings between adjacent openings of the holes are accounted for in these resistances. The values for these resistances were determined with 3D FEM simulations and simple compact parameterized equations were fitted to them. The expressions for Y h are presented in Veijola (2007). Equation 9 is then solved with a FEM solver in 2D, and the force F PPR on the ground surface is calculated from the pressure distribution solved. The influence of the diffusivity coefficient has not been studied yet. D h = 1 is assumed.

Here, the same topology and gas parameters as in Veijola (2007) is used. This allows a direct comparison of large number of topologies and dimensions. The results in Veijola (2007) have been presented only with graphs, but here the original exact numerical values are used, without any added errors due to interpretation of the graphs.

5 3D, ANSYS, and PPR simulations

5.1 Simulated test structures

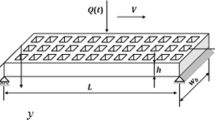
The damper structure is represented by a square movable plate with square holes oscillating out-of-plane (Fig. 3); it is separated from the ground plane by an initial gap extension h. The plate size is indicated as a, the hole size as s 0, the number of holes with N, and the plate thickness as h c. The distance between the damper border and the perforations (s 2) is assumed to be the same as the distance between the perforations (s 1). Since the dimensions s 1 and s 2 are equal, the hole interspaces are determined as

$$ s_{1} = \frac{{a - s_{0} {\sqrt N }}} {{1 + {\sqrt N }}} $$
(10)
Fig. 3
figure 3

Square damper dimensions

Full size image

Different shapes are modeled by varying the geometrical parameters, such as the number of holes, the size of the holes, air gap height, and the plate dimensions. Simulated geometries and gas parameters of air at standard atmospheric conditions are reported in Table 1.

Table 1 Geometrical dimensions of simulated dampers and physical parameters for the ambient air
Full size table

Dampers characterized by a = 20 μm and N = 16 were considered first; the force acting on the lower surface was evaluated for different hole sizes when the plate thickness h c = 1 and 5 μm and the air gap thickness h increases from 1 to 2 μm. Identical simulations were then performed for the damper where a = 40 μm and N = 64.

5.2 3D FEM simulations

To have accurate reference simulations, it is necessary to perform 3D fluid flow simulations for the whole damper with realistic boundary conditions. These conditions require that the simulated volume be extended around the damper in order to include the viscous losses due to the flow fields around the damper. Also, to extend the validity of the simulations for MEMS devices with small dimensions, the slip velocity boundary conditions should be considered at the surfaces. A requirement for accurate results is, naturally, a large number of elements due to the extended simulation volume and narrow channels. Articles by Veijola (2006b, 2007) contain such simulations for square perforated dampers with 4–64 square holes. Here, the same geometries are used so as to utilize the same results, the calculations of which required several months. Both papers utilize the same 3D reference simulations where a large number of 3D FEM analyses were made varying the air gap height and the lengths and sizes (perforation ratios) of the holes. For realistic conditions for the flow at the damper borders and at the apertures of the holes, the simulation volume was extended by 6h at the sides of the damper and by 2s 0 above the upper surface of the plate. Slip velocity boundary conditions were used to account for the slightly rarefied gas in MEMS devices.

Since a low Reynolds number and a low squeeze number were assumed, the force acting on the surfaces could be calculated assuming constant flow velocities at the boundaries. The flow velocity at the ground surface boundary was set to 1 m/s and the pressure on that surface was considered in calculating the damping force. About 450,000 elements were used to simulate a symmetric quarter of the device.

The Navier–Stokes solver in the multiphysics FEM software ELMER (Elmer 2007) was used to perform the simulations. The results shown here report the force on the whole structure. The computer used to perform the simulations was a Sun Fire 25K having 96 UltraSparc IV processors.

A subset of the numerous simulations reported in Veijola (2006b, 2007) is used here. Only the topologies with 16 and 64 holes are used and the number of hole lengths and sizes have been reduced to 2 and 4 from 4 and 9, respectively.

5.3 FEM methods comparison

A static analysis was performed, assuming a constant plate vertical velocity equal to v = 1 m/s and a rigid shape of the damper. That is, fluid compression and inertia effects were neglected. This is not generally a serious limitation, since perforations keep the compression force low. Also, isothermal conditions were assumed. Rarefied gas phenomena were included in the slip flow regime.

Tables 2 and 3 report PPR and ANSYS simulation results compared to full 3D results for a number of holes N = 16 and N = 64, respectively, and for varying geometrical parameters. Simulation values with a = 20 μm and N = 16 are plotted in Fig. 4a (h c = 1 μm) and 4b (h c = 5 μm); simulation values with a = 40 μm and N = 64 are plotted in Fig. 5a (h c = 1 μm) and 5b (h c = 5 μm).

Table 2 PPR, ANSYS, and 3D force values comparison (a = 20 μm, N = 16)
Full size table
Table 3 PPR, ANSYS, and 3D force values comparison (a = 40 μm, N = 64)
Full size table
Fig. 4
figure 4

Full 3D (open square), PPR (open diamond), and ANSYS (open triangle) force values comparison for a = 20 μm, N = 16, h = 1 μm (continuous), h = 2 μm (dashed). Gap thicknesses (h c) considered are 1 μm (a) and 5 μm (b)

Full size image
Fig. 5
figure 5

Full 3D (open square), PPR (open diamond), and ANSYS (open triangle) force values comparison for a = 40 μm, N = 64, h = 1 μm (continuous), h = 2 μm (dashed). Gap thicknesses (h c) considered are 1 μm (a) and 5 μm (b)

Full size image

Figure 6 represents fluid pressure distribution on the lower surface of the damper as extracted from ANSYS simulations. The pressure pattern in Fig. 6a with small holes represents the flow directions in Fig. 1b for closed holes, and the patterns in Fig. 6c, d with large holes represent the flow directions in Fig. 1a for closed borders. The pattern in Fig. 6b is a mixture of both flow directions.

Fig. 6
figure 6

Pressure distribution on the lower surface as extracted from ANSYS simulation; a = 40 μm, N = 64, h = 1 μm, h c = 1 μm; s 0 = 1 μm (a), s 0 = 2 μm (b), s 0 = 3 μm (c), s 0 = 4 μm (d)

Full size image

The tables and graphs show that the force given by PPR method is overall very accurate; the errors are well below 10% except for cases with a large perforation ratio and air gap (perforation ratio is the ratio between the perforated area and the original unperforated surface area, here a 2). The forces given by the ANSYS method are systematically too small. The difference is considerable for small perforations, and increases dramatically for larger perforation ratios. The poor correspondence is mainly explainable considering that only fluid pressure acting on the lower plate surface is detected, while other fluid force components are neglected. In the following, additional reasons explaining the small force in ANSYS simulations are discussed.

A reason for the low force values in the ANSYS analysis originates from the fact that only the unperforated area is assumed to move and generate fluid flow. At high perforation ratios, this causes a large error: the relative area assumed to cause the fluid motion remains very small compared to the large area under the perforations. When the perforation ratio approaches 100%, the ANSYS solution approaches 0, but in reality the force should approach a constant value that can be estimated roughly to be the NR P v , where R P is the flow resistance of a single perforation and v is the velocity of the surface.

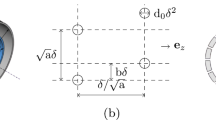
The horizontal flow is also affected in the ANSYS analysis due to the unmeshed intermediate regimes in the air gap under the holes. This causes an additional error in the ANSYS analysis for moderate and small perforation ratios in cases where the perforations are such that their flow resistance is large (e.g., long holes). In that case, the horizontal flow towards the damper borders is considerable and the flow through the perforations is small. This corresponds to the case in Fig. 1b. Whereas the PPR solution approaches the unperforated situation in this case, in the ANSYS analysis, the gas cannot flow normally in the gap under the perforation. The pressure is forced to be equal at the borders of the holes, causing an underestimation of the horizontal fluid flow resistance, leading to a force too small. The error generated can be estimated studying a simple flow resistance model in a rectangular area containing a single hole. Only the flow in the x-direction is studied here; the same analysis applies in the y-direction flow. Figure 7 shows the nominal flow resistances in four areas in the air gap. The mechanical flow resistance of the whole area is assumed to be R 0, and the resistances in the four areas scale as (length/width) × R 0. When the resistance of the hole area is assumed to be zero, the equivalent circuit gives a resistance for the studied area as

$$ R = \frac{{s_{0} /s_{1} + 1}} {{{\left( {s_{0} /s_{1} } \right)}^{2} + s_{0} /s_{1} + 1}}R_{0} = \xi R_{0} . $$
(11)
Fig. 7
figure 7

Nominal flow resistances of four different areas in the air gap. In ANSYS analysis, the resistance is effectively zero at the hole. In the figure, only flow in the x direction is considered

Full size image

According to this rough analysis, coefficient ξ scales directly the horizontal flow resistance in the ANSYS analysis.

5.4 Corrections to the ANSYS analysis

In order to verify the problems in the ANSYS analysis, simple correcting terms are derived and the resulting “corrected” results are compared with the 3D simulations. These corrections apply only to the particular case studied here: uniform perforation and perpendicular motion. The corrections include:

  • Additional border flow outside the air gap. The correction is made utilizing the surface elongation model in Veijola et al. (2005)

  • Correction for the horizontal flow resistance in the gap as presented in Eq. 11

  • Considering the neglected moving surface area under the hole.

The suggested corrected force is in the following form

$$ F_{{{\text{corr}}}} = F_{{{\text{ANSYS}}}} c_{{{\text{elo}}}} c_{{{\text{hor}}}} + F_{{{\text{RP}}}} , $$
(12)

where

$$ c_{{{\text{elo}}}} = {\left[ {1 + \frac{{1.3{\left( {1 + 3.3K_{{n,{\text{gap}}}} } \right)}h}} {a}} \right]}^{4} $$
(13)

is the correction coefficient due to surface elongation,

$$ c_{{{\text{hor}}}} = \frac{1} {\xi } $$
(14)

is the coefficient due to the modified horizontal flow resistance in Eq. 11 and

$$ F_{{{\text{RP}}}} = NR_{{\text{P}}} v $$
(15)

is an additional correcting force at large perforation ratios. It adds the contribution of the neglected area under the hole. The flow resistance of a square perforation is calculated from the flow resistance of a long square channel considering the velocity slip and the end corrections (Veijola 2006a) as

$$ R_{P} = 28.454\eta {\left( {\frac{{\eta _{{{\text{eff}},{\text{hole}}}} }} {\eta }h_{{\text{c}}} + 0.5s_{0} } \right)}; $$
(16)

a simple elongation coefficient 0.5 is used here instead of the more complicated expression in Veijola (2006a), since simple correcting equations are sufficient here.

The corrections are only approximate since the multiplying coefficients should be applied to the force components that are due to the horizontal net flow in the gap, not to the total force F ANSYS. However, the approach is justified here, since the force component due to perforations in F ANSYS is very small compared with the force component due to the horizontal flow in the air gap.

Figures 8 and 9 compare 3D simulations (F 3D), ANSYS simulations (F ANSYS) and corrected ANSYS results (F corr) for a number of holes N = 16 and N = 64, respectively, and for varying geometrical parameters.

Fig. 8
figure 8

Comparison between full 3D (open square), ANSYS (open triangle, continuous), and corrected ANSYS (open triangle, dashed) force values for a = 20 μm, N = 16, h = 1–2 μm, h c = 1–5 μm

Full size image
Fig. 9
figure 9

Comparison between full 3D (open square), ANSYS (open triangle, continuous), and corrected ANSYS (open triangle, dashed) force values for a = 40 μm, N = 64, h = 1–2 μm, h c = 1–5 μm

Full size image

6 Discussion

As the pressure distribution in Fig. 6 shows, the main consequence of the simplified ANSYS model is the absence of a fluid flow below the holes, where the air gap is not meshed effectively; this is equivalent to the presence of inner walls at borders of holes. The flow is allowed to enter into the holes at its edges, but the viscous losses taking place during its motion along the x–y plane in the hole regime are not considered. This approximation is more crucial at high plate thickness and small holes (long and narrow channels with high impedance), when only a small part of the fluid escapes through the holes. From the comparison, we notice even higher errors or large holes dimensions, when the unmeshed areas below the holes become bigger and more relevant.

For plate thickness of h c = 5 μm and a gap extension of h = 1 μm, the error between 3D force results and PPR results varies from 1 to 3% for increasing holes sizes from 1 to 4 μm; ANSYS results vary from 38 to 94% for equal conditions (from 11 to 33% after correction). For cases with smaller plate thickness h c = 1 μm, PPR results vary from 0.4 to 5% with respect to 3D results, while ANSYS results vary from 44 to 96% (from 22 to 42% after correction).

In verified cases, the perforation ratio varies from 4 to 64%. For larger ratios, the error of PPR increases since the relative contribution of the damper borders will become considerable. The simulations include all practical cases that are difficult to model with reduced-dimension models. These topologies have a small number of perforations and the contribution of intermediate flows is important; the air gap height is close to the hole diameter or the frame width between the holes.

ANSYS boundary conditions are represented by pressure constraints at the damper borders, where the ambient pressure is imposed; this represents an approximation of the real pressure gradient near the plate, where pressure waves directed outside from the gap are present.

All described assumptions included in ANSYS simplified meshing model allow a quasi-immediate computation of the result in terms of pressure distribution in the gap and force acting on the lower surface of the plate.

The computational efforts in the ANSYS and PPR approaches are quite similar. Both require only a 2D topology to be meshed. In ANSYS, each hole requires only a single additional element, while in PPR, the whole hole regime must be meshed. When the number of holes becomes large, the required element count in both methods might become intolerably large. In such cases, the PPR solver can be used effectively to apply a homogenization method, where the flow resistance of all holes is distributed equally on the surface. In the homogenized topology, the mesh can be quite dense since the holes no longer belong to the solved topology.

7 Conclusions

Numerical strategies for the evaluation of the force acting on movable perforated plates were investigated; 2D PPR and simplified ANSYS methods were compared to full 3D simulation results calculated with a Navier–Stokes solver. The accuracy of the PPR method turned out to be very good for all perforation ratios studied, but the ANSYS results contained a systematic error at small perforation ratios and were not usable for large perforation ratios. A correction equation for the ANSYS results was presented to explain the small values for the damping force. It was shown that this correction improved the results considerably.

The final conclusion is that reduced-dimension models should consider both the excitation in the intermediate regime under the hole, and also consider the losses of the flow passing this regime. This applies to both analytic models and numerical methods.

The topologies used here to compare the reduced-dimension methods had square surfaces, identical perforations with a constant pitch, and translational motion. This was done so as to re-use the existing 3D simulations that were originally performed to verify the accuracy of the compact models presented in Veijola (2006b). The reduced-dimension methods discussed here are much more general than the compact models developed for certain fixed topologies.