Streaming potential is an axial potential difference that builds up along a microchannel due to the convective transport of counter-ions in a pressure-driven flow. This potential field induces an electroosmotic backflow and thus decreases the flow rate causing the so-called electroviscous effect (Hunter 1981; Li 2004). Elton (1948a, b) conducted pioneering studies examining such effect on the flow of liquids between surfaces in close proximity. Since then a number of papers have been published addressing theoretically and experimentally the same issue in homogeneous slit pores (Burgreen and Nakache 1964; Hildreth 1970; Mala et al. 1997), cylindrical capillaries (Rice and Whitehead 1965; Bowen and Jenner 1995; Szymczyk et al. 1999) and rectangular channels (Yang and Li 1998; Ren et al. 2001; Ren and Li 2004). So far, however, very little work has been done on the streaming potential and electroviscous effect in heterogeneous channels. Surface heterogeneity on channel walls may result from solute adsorption (Zembala and Adamczyk 2000), chemical coating (Towns and Regnier 1991), etc.

The earliest interest in pressure-driven flow through heterogeneous channels involved the streaming potential (Norde and Rouwendal 1990; Elgersma et al. 1992) and streaming current (Voight et al. 1983; Werner et al. 1998) techniques for measuring the surface heterogeneity. Cohen and Radke (1991) modeled the pressure-driven flow in a non-uniformly charged slit. They found that surface heterogeneity could significantly alter the zeta potential. Erickson and Li (2001) compared numerically the streaming potential and streaming current methods for characterizing surface heterogeneity in slit channels. The same authors (2002) later performed a comprehensive study of the pressure-driven flow field through microchannels with patchwise surface heterogeneity. Their work revealed the presence of weak circulation regions perpendicular to the main flow axis. Recently, Yang et al. (2004) investigated the streaming potential in circular capillaries with non-uniform zeta potentials by considering the continuities of liquid flow and electric current.

Most of previous studies solved simultaneously the Navier–Stokes and Poisson–Nernst–Planck equations, which made available the flow behavior adjacent to surface heterogeneity. However, the true factors in streaming potential and electroviscous effect were often left behind the complicated simulations. Here, a thermodynamic analysis of this issue is presented. The streaming potential and electroviscous effect are both expressed in terms of phenomenological coefficients in individual homogeneous sections. Thus, a solution of flow field in the entire heterogeneous channel is unnecessary. Such an approach has been recently applied to the study of electrokinetic flow in microfluidic networks (Xuan and Li 2004; Berli 2007) and the optimization of electrokinetic energy conversion (Xuan and Li 2006).

One begins with the general Onsager relations for electrokinetic flow in a homogeneous channel (Brunet and Ajdari 2004, 2006)

$$ Q = G{\left({- \Delta p} \right)} + M{\left({- \Delta \phi} \right)} $$
(1)
$$ I = M{\left({- \Delta p} \right)} + S{\left({- \Delta \phi} \right)} $$
(2)

where the “fluxes” are liquid flow Q and electric current I while the two corresponding “forces” are pressure difference Δp and electric potential difference Δϕ. Among the phenomenological coefficients, G represents the hydrodynamic conductance, M characterizes the electroosmotic and streaming effects, and S indicates the electric conductance. As there is no net current in a steady-state pressure-driven flow, a streaming potential ϕsp is induced from Eq. 2

$$ \phi_{{sp}} = - \frac{M}{S}\Delta p. $$
(3)

Then, the liquid flow is easily obtained as

$$ Q_{{\rm sp}} = - G{\left({1 - Z} \right)}\Delta p $$
(4)
$$ Z = {M^{2}} \mathord{\left/{\vphantom {{M^{2}} {GS}}} \right.\kern-\nulldelimiterspace} {GS} $$
(5)

where the non-dimensional parameter Z is the previously termed “figure of merit” that gauges the performance of electrokinetic energy conversion (Morrison and Osterle 1965 Footnote 1; Xuan and Li 2006). Since Z is unconditionally positive and less than unity, Q sp is always smaller than the flow rate in a pure pressure-driven flow, Q pd = −GΔp, indicating the electroviscous retardation effect (Xuan and Sinton 2007). The apparent viscosity ratio γ as traditionally defined is thus given by

$$ \gamma = {Q_{{\rm pd}}} \mathord{\left/{\vphantom {{Q_{{\rm pd}}} {Q_{{\rm sp}}}}} \right.\kern-\nulldelimiterspace} {Q_{{sp}}} = 1 \mathord{\left/{\vphantom {1 {{\left({1 - Z} \right)}}}} \right.\kern-\nulldelimiterspace} {{\left({1 - Z} \right)}}. $$
(6)

Obviously, a higher Z leads to a stronger electroviscous effect.

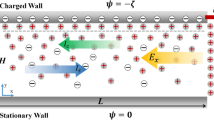
Next the phenomenological Eqs. 1 and 2 are applied to the analysis of streaming potential and electroviscous effect in heterogeneous channels. Two patterns of surface heterogeneities are considered here, i.e., q ⊥ ∇p and q ∥ ∇p where q indicates the direction of surface charge variation and ∇p is the applied pressure gradient, see the sketch in Fig. 1. Such arrangement of surface heterogeneity in microchannels has been previously considered in both pressure-driven (Cohen and Radke 1991; Erickson and Li 2001, 2002) and electroosmotic flows (Stroock et al. 2000; Herr et al. 2000; Ren and Li 2001). The immediate application of the pattern q ∥ ∇p is in a nanochannel that is connected to liquid reservoirs through microchannels (Fan et al. 2005). The surface charge density does not necessarily remain identical through the entire fluidic passage due to the dissimilar fabrication method and/or the nano-confinement effect (van der Heyden et al. 2005). The surface charge pattern q ⊥ ∇p may be present in a microchannel that is half hydrophobic and half hydrophilic, which is created artificially for the effective control of liquid–liquid surface (Zhao et al. 2001).

Fig. 1
figure 1

Scheme of heterogeneous microchannels with a q ⊥ ∇p and b q ∥ ∇p where q denotes the direction of surface charge variation and ∇p is the applied pressure gradient. Note that the channel is not drawn to scale where h indicates the half channel height

Full size image

In both types of surface patterns, the heterogeneous channel is assumed to consist of n homogeneous sections bearing discrete surface charges, see Fig. 1. The flow transition regions near the surface charge discontinuities and the end reservoirs are neglected. In other words, the liquid flow is assumed fully developed in each homogeneous section. This assumption has been demonstrated reasonable in a number of recent studies unless the length of a homogeneous section is smaller than or comparable to the characteristic dimension of its cross-section (Ren and Li 2001; Xuan and Li 2004; Berli 2007).

\({\user2{q}} \perp {\varvec{\nabla}}{\mathbf{p}}:\) in this circumstance, both liquid and electric current flow in parallel through the n sections, leading to

$$ Q_{\bot} = {\sum\limits_{i = 1}^n {G_{i}}}{\left({- \Delta p} \right)} + {\sum\limits_{i = 1}^n {M_{i}}}{\left({- \Delta \phi} \right)} $$
(7)
$$ I_{\bot} = {\sum\limits_{i = 1}^n {M_{i}}}{\left({- \Delta p} \right)} + {\sum\limits_{i = 1}^n {S_{i}}}{\left({- \Delta \phi} \right)} $$
(8)

where the subscript ⊥ represents the case with q ⊥ ∇p and the index i denotes the ith section. Hence, the zero current condition in Eq. 8 gives rise to a streaming potential

$$ \phi_{{{\rm sp}, \bot}} = - \frac{{{\sum_{i = 1}^n {M_{i}}}}}{{{\sum_{i = 1}^n {S_{i}}}}}\Delta p. $$
(9)

Accordingly, the liquid flow rate is given by

$$ Q_{{{\rm sp}, \bot}} = - {\sum\limits_{i = 1}^n {G_{i}}}{\left({1 - Z_{\bot}} \right)}\Delta p $$
(10)

where \(Z_{\bot} = {{\left({{\sum\limits_{i = 1}^n {M_{i}}}} \right)}^{2}} \mathord{\left/{\vphantom {{{\left({{\sum\limits_{i = 1}^n {M_{i}}}} \right)}^{2}} {{\sum\limits_{i = 1}^n {G_{i}}}{\sum\limits_{i = 1}^n {S_{i}}}}}} \right.\kern-\nulldelimiterspace} {{\sum\limits_{i = 1}^n {G_{i}}}{\sum\limits_{i = 1}^n {S_{i}}}}\) can be viewed as the overall “figure of merit” of the heterogeneous channel. Referring to the flow rate of a pure pressure-driven flow in the same n-section channel, Q pd = −∑ G i Δp, the apparent viscosity ratio is determined as

$$ \gamma_{\bot} = 1 \mathord{\left/{\vphantom {1 {{\left({1 - Z_{\bot}} \right)}}}} \right.\kern-\nulldelimiterspace} {{\left({1 - Z_{\bot}} \right)}} $$
(11)

which holds the same form as Eq. 6 in a homogeneous channel.

\({\user2{q}} {\varvec{\parallel}} {\varvec{\nabla}}{\mathbf{p}}:\) liquid and electric current flow in series through the n sections, and hence should be continuous through the entire heterogeneous channel,

$$ Q_{\parallel} = - G_{i} {\left({\Delta p} \right)}_{i} - M_{i} {\left({\Delta \phi} \right)}_{i} $$
(12)
$$ I_{\parallel} = - M_{i} {\left({\Delta p} \right)}_{i} - S_{i} {\left({\Delta \phi} \right)}_{i} $$
(13)

where the subscript ∥ represents the case with q ∥ p, (Δp) i and (Δϕ) i denote the pressure difference and the potential difference in the ith section, respectively. Moreover, there should be no net current through any cross-section of the heterogeneous channel (Cohen and Radke 1991; Erickson and Li 2001, 2002), i.e., I ∥ = 0. Considering the known pressure difference across the whole channel, Δp = ∑ (Δp ) i , the streaming potential, \(\phi_{{{\rm sp}, \parallel}} = {\sum {{\left({\Delta \phi} \right)}_{i}}},\) is thus obtained as

$$\phi_{{{\rm sp}, \parallel}} = - \frac{{{\sum_{i = 1}^n {\frac{{Z_{i}}}{{M_{i} {\left({1 - Z_{i}} \right)}}}}}}}{{{\sum_{i = 1}^n {\frac{1}{{G_{i} {\left({1 - Z_{i}} \right)}}}}}}}\Delta p $$
(14)

where \(Z_{i} = {M^{2}_{i}} \mathord{\left/{\vphantom {{M^{2}_{i}} {G_{i} S_{i}}}} \right.\kern-\nulldelimiterspace} {G_{i} S_{i}}\) is the “figure of merit” of the ith section. The liquid flow is then given by

$$Q_{{\rm sp}, \parallel} = - \frac{1}{\sum_{i = 1}^n {\frac{1}{{G_{i} {\left({1 - Z_{i}} \right)}}}}}\Delta p.$$
(15)

Hence, the apparent viscosity ratio is expressed as

$$ \gamma_{\parallel} = \frac{{{\sum_{i = 1}^n {{\gamma_{i}} \mathord{\left/{\vphantom {{\gamma_{i}} {G_{i}}}} \right.\kern-\nulldelimiterspace} {G_{i}}}}}}{{{\sum_{i = 1}^n {1 \mathord{\left/{\vphantom {1 {G_{i}}}} \right.\kern-\nulldelimiterspace} {G_{i}}}}}} $$
(16)

where the hydrodynamic resistance 1/G i acts as the weighting factor in the weighted average, and γ i  = 1/(1 − Z i ) denotes the apparent viscosity ratio in the ith section (see the definition in Eq. 6). If all the n sections have exactly the same structure, the hydrodynamic resistance 1/G i will be uniform so that \(\gamma_{\parallel} = {{\sum {\gamma_{i}}}} \mathord{\left/{\vphantom {{{\sum {\gamma_{i}}}} n}} \right.\kern-\nulldelimiterspace} n.\)

As for the streaming potential, dividing Eq. 14 by Eq. 15 yields

$$ \frac{\phi_{{\rm sp}, \parallel}}{Q_{{\rm sp}, \parallel}} = {\sum\limits_{i = 1}^n \frac{Z_{i}}{M_{i} {\left({1 - Z_{i}} \right)}}}. $$
(17)

Looking back at Eqs. 3 and 4, one can immediately obtain the following relationship

$$ \phi_{Q} = \frac{{\phi_{{{\rm sp}, \parallel}}}}{{Q_{{{\rm sp}, \parallel}}}} = {\sum\limits_{i = 1}^n {\phi_{{Q,\,i}}}} $$
(18)

if one defines ϕ Q as the streaming potential per unit liquid flow. Such a definition makes sense considering the requirement of constant flow rate through all sections of the heterogeneous channel.

It is now time to specify the phenomenological coefficients G, M and S in a homogeneous microchannel in order to analyze the streaming potential and the electroviscous effect in a multi-section heterogeneous channel. These coefficients can be determined through electrokinetic flow analysis, as presented below in a slit channel. It is, however, important to note that the above-developed analytical model essentially applies to microchannels of arbitrary cross-section (Xuan and Li 2004; Brunet and Ajdari 2004, 2006). The fully-developed velocity profile in a combined pressure-driven and electroosmotic flow along a slit channel is given by (Burgreen and Nakache 1964; Hildreth 1970)

$$ u = - \frac{{h^{2}}}{{2\mu}}{\left({1 - \frac{{y^{2}}}{{h^{2}}}} \right)}\frac{{\Delta p}}{l} - \frac{\varepsilon}{\mu}{\left({\psi - \zeta} \right)}\frac{{\Delta \phi}}{l} $$
(19)

where u is the axial fluid velocity, h the half channel height, μ the fluid viscosity, y the transverse coordinate originating from the channel axis, l the channel length, ɛ the fluid permittivity, Ψ the double-layer potential, and ζ the zeta potential. In a symmetric electrolyte solution, the electric current density j is given by (Burgreen and Nakache 1964; Hildreth 1970)

$$ j = - \varepsilon \frac{{d^{2} \psi}}{{dy^{2}}}u - c_{b} \Lambda \cosh {\left({\frac{{z_{v} e\psi}}{{k_{B} T}}} \right)}\frac{{\Delta \phi}}{l} $$
(20)

where c b is the ionic concentration of bulk liquid, Λ the molar conductivity, z v the valence of ions, e the unit charge, k B the Boltzmann’s constant, and T the liquid temperature.

Integrating Eqs. 19 and 20 over the channel cross-section and then comparing with Eqs. 1 and 2 yield

$$ G = \frac{{2h^{3}}}{{3\mu l}} $$
(21)
$$ M = \frac{{2\varepsilon h}}{{\mu l}}\frac{{k_{\rm B} T}}{{z_{v} e}}{\left({F_{1} - \zeta^{*}} \right)} $$
(22)
$$ S = \frac{2\varepsilon^{2}}{\mu hl}{\left(\frac{k_{\rm B} T}{z_{v} e} \right)}^{2} {\left({F_{2} + \beta K^{2} F_{3}} \right)} $$
(23)
$$ F_{1} = {\int\limits_0^1 {\Psi d\eta}}, \quad F_{2} = {\int\limits_0^1 {{\left({{d\Psi} \mathord{\left/{\vphantom {{d\Psi} {d\eta}}} \right.\kern-\nulldelimiterspace} {d\eta}} \right)}^{2} d\eta}}, \quad F_{3} = {\int\limits_0^1 {\cosh {\left(\Psi \right)}d\eta}} $$
(24)

where Ψ = z v eΨ/k B T and η = y/h are the normalized double-layer potential and y-coordinate, respectively. Note that G, M and S are defined as per unit width of the channel. Three other dimensionless parameters are involved in the phenomenological coefficients: ζ* = z v eζ/k B T is the non-dimensional zeta potential; β = Λμ/ɛRT with R the universal gas constant is the Levine number (Griffiths and Nilson 2005 Footnote 2); K = κh is the non-dimensional channel height whereFootnote 3 \(\kappa = {\sqrt {{2z^{2}_{v} e^{2} N_{A} c_{b}} \mathord{\left/{\vphantom {{2z^{2}_{v} e^{2} N_{A} c_{b}} {\varepsilon k_{B} T}}} \right.\kern-\nulldelimiterspace} {\varepsilon k_{B} T}}}\) with N A the Avogadro’s number is the inverse of Debye screening length (Hunter 1981). As such, the “figure of merit” Z is specified as

$$ Z = \frac{{3{\left({F_{1} - \zeta^{*}} \right)}^{2}}}{{F_{2} + \beta K^{2} F_{3}}} $$
(25)

The double-layer potential is solved from the Poisson–Boltzmann equation (Hunter 1981)

$$ \frac{{d^{2} \Psi}}{{d\eta^{2}}} = K^{2} \sinh {\left(\Psi \right)}. $$
(26)

As a demonstration of the proposed approach, the streaming potential and the electroviscous effect are examined below in a two-section slit channel (n = 2 in Fig. 1). The two sections are assumed symmetric except for the zeta potential. Specifically, ζ1 is maintained at −100 mV while ζ2 is varied from −100 to +100 mV mimicking the surface heterogeneity. The c b  = 10−5 M KCl aqueous solution (the Debye length is about 100 nm) is selected as the liquid. Its properties are assumed identical to pure water other than the molar conductivity, Λ = 0.015 Sm2/mol (Li 2004). The Levine number is easily calculated as β = 8.55. The double-layer potential Ψ in Eq. 26 is numerically solved in COMSOL. The functions F i (i = 1, 2, 3) defined in Eq. 24 are evaluated using the embedded function in COMSOL.

Figure 2 shows the comparison of streaming potential (normalized by ϕsp in a homogeneous channel with ζ1 = ζ2 = −100 mV) in channels with q ⊥ ∇p (filled symbols, solid lines) and q ⊥ ∇p (hollow symbols, dotted lines). Four different values of surface heterogeneity are considered, i.e., ζ2 = −50, 0, +50 and +100 mV, corresponding respectively to 〈ζ〉/ζ1 = 0.75, 0.5, 0.25 and 0 as labeled in Fig. 2. Here, 〈ζ〉 = (ζ1 + ζ2)/2 denotes the average zeta potential. The two curves at 〈ζ〉/ζ1 = 0 are not included in Fig. 2 because ϕsp,⊥ and ϕsp,∥ are both simply zero. Those at 〈ζ〉/ζ1 = 0.75 are also close to each other with a crossover at about K = 3 and differ by 8% at most throughout the range of K. At 〈ζ〉/ζ1 = 0.5 and 0.25, however, one can see a growing discrepancy in the streaming potential between the two cases when K gets smaller, which turns obvious at K < 50. This result is against the conventional understanding that streaming potential is independent of the arrangement of surface heterogeneity (Norde and Rouwendal 1990; Elgersma et al. 1992). As this discrepancy happens in small microchannels, it is probably attributed to the electroviscous effect that becomes more pronounced at a small value of K (see Fig. 3). Such a dependence has been recently justified in Erickson and Li’s (2001, 2002) numerical analyses of streaming potential in channels with either heterogeneous strips parallel to the axis (i.e., q ⊥ ∇p) or periodic heterogeneous patches (essentially a combination of q ⊥ ∇p and q ∥ ∇p).

Fig. 2
figure 2

Comparison of the streaming potential (normalized by ϕsp in a homogeneous channel) in two-section slit channels with q ⊥ ∇p (filled symbols, solid lines) and q ∥ ∇p(hollow symbols, dotted lines) at different non-dimensional channel heights K

Full size image
Fig. 3
figure 3

Comparison of the apparent viscosity ratio in two-section slit channels with q ⊥ ∇p (filled symbols, solid lines) and q ∥ ∇p (hollow symbols, dotted lines) at different non-dimensional channel heights K

Full size image

In all cases demonstrated in Fig. 2, the normalized streaming potential converges to the value of 〈ζ〉/ζ1 when K is larger than, for example, 500. This trend is consistent with the prediction of thin double layer (TDL) approximation. This approximation assumes an electroosmotic slip velocity on solid walls instead of the conventional no-slip condition, so that the solution of double-layer potential is avoided (Li 2004). Hence, the streaming potentials in the two types of heterogeneous channels become identical,

$$ \phi_{{{\rm sp}, {\rm TDL}}} = \frac{{\varepsilon {\left\langle \zeta \right\rangle}}}{{\sigma \mu}}\Delta p. $$
(27)

It is this linear relationship between ϕsp,TDL and 〈ζ〉 that underlies the streaming potential method for characterizing heterogeneous surfaces. However, Fig. 2 tells that such a method should be applied with caution to small microchannels. As for the electroviscous effect, it is straightforward to obtain γTDL = 1 because the convective transport of counter-ions within the electric double layer has been disregarded in the TDL approximation.

Figure 3 compares the apparent viscosity ratio γ in slit channels with q ⊥ ∇p (filled symbols, solid lines) and q ∥ ∇p (hollow symbols, dotted lines), respectively. One can see a reduction of electroviscous effect in both types of heterogeneous channels relative to the homogeneous one. Such a reduction is maximized at about K = 2, where nearly all γ reach their respective summits. In between the two heterogeneous channels, γ∥ is always larger than γ⊥. Moreover, a higher degree of surface heterogeneity or a larger arithmetic value of ζ2 causes a greater difference in between γ∥ and γ⊥. Particularly at ζ2 = +100 mV (or 〈ζ〉/ζ1 = 0, not illustrated in Fig. 3), γ∥ overlaps with the curve in a homogeneous channel while γ⊥ remains at unity (i.e., no electroviscous effect at all). In addition, γ⊥ depends on both the sign and the magnitude of ζ2 while γ∥ is only associated with the latter. It is also obvious in Fig. 3 that both γ∥ and γ⊥ are reduced to 1 when K gets large as predicted in the TDL approximation.

In summary, a theoretical analysis of the streaming potential and the electroviscous effect has been conducted in microchannels with two types of surface charge patterns. The phenomenological equations offer a simple and straightforward approach to deriving the streaming potential and the apparent viscosity ratio without knowledge of the complicated flow behavior adjacent to surface heterogeneity. The phenomenological coefficients are specified using electrokinetic flow analysis in a homogeneous channel. As only dimensionless parameters, including zeta potential ζ*, Levine number β and channel height K, are involved in the definition of phenomenological coefficients, the results presented in this article should apply to any combination of channel and liquid system. Such a combined thermodynamic and electro-hydrodynamic approach should also find applications in the analysis of streaming current in heterogeneous microchannels. It is, however, acknowledged that this theoretical approach is limited only to fully-developed liquid flow in each homogeneous section, the length of which should be much larger than the characteristic dimension of its cross-section.