1 Introduction

The Micro-Electro-Mechanical-Systems open a new area in the rarefied gas experiments. Indeed, since the early eighties and the beginning of the MEMS, a lot of micro devices were designed to study gas micro flows. But channel geometries involving a rectangular (or trapezoidal) cross section have been privileged until to now (Pong et al. 1994; Harley et al. 1995; Arkilic et al. 1997, 2001; Zohar et al. 2002; Maurer et al. 2003; Colin et al. 2004). In this work we present a gas micro flow study based on micro tube experiments. In this geometry the experiments are rare, only four different experiments involving rarefied gas flows in tubes or micro tubes have been undertaken in the last 50 years: using a tube with 3.64 cm of diameter in Dong (1956); with a package of ten tubes of a mean radius equal to 199.7 μm and also in a package of 100 tubes of a mean radius equal to 50 μm in Porodnov et al. (1974); then in Tison (1993), where the author did not measure directly the diameter of the tubes and finally with a package of 40 tubes with a diameter of 3.9 μm in Lalonde (2001). Thus, nobody performed experiments in a single micro tube characterized by a diameter precisely known. One of the reasons of this lack is due to the difficulty of measuring mass flow rates so weak as those flowing in a single micro tube (smaller than 10−10 kg/s): in point of fact, in a tube the mass flow rate can be from 3 to 100 times lower than that found in a rectangular channel for the same inlet/outlet pressure ratio, with the same streamwise length, and with the same small critic geometric dimension, i.e. finally for the same values of the Knudsen number. Since in micro tube the small dimension is necessary the diameter, involved in the cross sections by its square power, while in micro channel only one dimension of the rectangular section is necessary small: thus using a large width, i.e. a small height-to-with ratio it is possible to increase largely the flow rate without changing the Knudsen number. Let us add that, for the same basic geometric reasons, the dynamics of the flow in the tubes remains in any case a two-dimensional problem, contrarily to that occurs in the rectangular channels where the problem becomes three-dimensional when the height-to-width ratio is not small enough. Thus some experiments exist concerning the TMAC in MEMS but, according to our previous remarks, they occurred in rectangular channel geometries (Arkilic et al. 2001; Maurer et al. 2003; Colin et al. 2004) or using several tubes in a package (Porodnov et al. 1974). In anyway these experiments remain very few numerous compared to those carried out in the molecular beam domain (Saxena et al. 1981) which in many cases did not concern really the same accomodation coefficient. Therefore, the present determination appears of some scientific interest.

In the present study, we measure low mass flow rates in a micro tube in a 0.003–0.309 Knudsen number range, corresponding to a slip regime. We obtain satisfactory measurements with nitrogen, argon, and helium, notably implementing new powerful pressure sensors. Then we have tested, for each gas, the pertinence of a first and/or second order treatment, according to the Knudsen number, to describe our experimental results. Then using a general formulation of the slip velocity, written at the suitable order, the Navier–Stokes equations yield an analytical expression of the mass flow rate. Thus, comparing to the experimental curves, we deduce first the slip coefficients. The accommodation coefficients are calculated for each gas assuming the usual Maxwell expression of the slip coefficient and using also a slip coefficient expression deduced from the solution of the kinetic model equation (Loyalka et al. 1975). Finally the influences of various physical parameters on the TMAC are briefly discussed.

2 Experiments

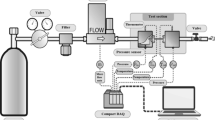
The experimental method used in the present work in order to measure the mass flow rate through a micro tube involves the use of two constant volume tanks and so may denoted “constant-volume technique”. This method requires very large tank volumes, much larger than the volume of the micro tube. Large tank sizes guarantee micro flow parameters independent of the time: although detectible (through their effects), the mass variations occurring in the tanks during the experiments do not call into question the stationary assumption. Thus, we have to put bounds for the maximal suitable pressure variations in the second tank, according to the inlet and outlet conditions. The experimental set-up shown in Fig. 1 takes into account these constraints. The gas flows through a micro tube fixed between two tanks in which the pressures remain very close to constant values P in and P out, respectively. The maximum pressure variation in the second tank due to the gas flow through the microtube is fixed at ±1% of the tank pressure, averaged over the duration of the experiment. This variation range means that the required experiment duration τ will vary from 5 min for the highest mass flow rate measured (10−9 kg/s) to about 90 min for the lowest (10−13 kg/s).

Fig. 1
figure 1

Schematic of experiment

Full size image

The experiments were performed with a fused silica cylindrical micro tube. It is of great importance to measure the diameter of the tube with a good accuracy because the analytical expression of the mass flow rate is proportional to the power four of the diameter. The surfaces of the inlet and outlet sections were scanned in environmental scanning mode (ESEM) with an electron microscope, and the following estimation of the diameter is obtained: D = 25.2 ± 0.35 μm. The roughness is estimated smaller than 0.1% of the diameter D. The diameter evaluation is also carried out indirectly, derived from the measured mass flow rate of Ar in the hydrodynamic flow regime (Kn m = 2.32 × 10−3) which yields D = 25.27 ± 0.25 μm. Moreover, the measure of the length of the tube gives L tube = 5.30 ± 0.01 cm, which is much greater than the diameter, so the entrance and exit effects can be neglected.

Here, we omit the detailed description of methodology and experimental set-up. The validity of the measurements and modus operandi were justified in Ewart et al. (2006). We will give only a brief description of the measurement technique. Let us write for the second tank the equation of state for an ideal gas under the form:

$$ P_{\rm out} V = m {\mathcal{R}} T, $$
(1)

where \({V, {\mathcal{R}}, P_{\rm out}, T}\) and m are, respectively, the volume, the specific gas constant, the pressure, the temperature and the mass of the gas in the outlet tank at any time t of the experiment time length τ. Let us define the variation dq of any thermodynamic parameter q, occurring in the tank during the experiment time length. According to the previous comments, these relative variations remain small, compared to 1. Therefore, one obtains from (1):

$$ {\frac{{\rm d} m }{\tau}}={\frac{V} {{\mathcal{R}} T }}\, {\frac{{\rm d} P_{\rm out}} {\tau}} (1-\varepsilon), \quad \varepsilon = \frac{{\rm d}T /T} {{\rm d} P_{\rm out}/ P_{\rm out}}. $$
(2)

In order to estimate ɛ we calculate firstly the temperature variation dT. In fact, when this variation is calculated directly from the standard deviation of the temperature recorded during the experiments (Ewart et al. 2006), the value of dT is overestimated by the superposition of various noises (electronic and thermal noises) to the real thermal variations occurring in the tank. Therefore, two additional statistical processes are carried out in order to eliminate the influence of these noises on the temperature variation. Taking into account these estimations of the temperature variation and the pressure rise dP out (fixed at ±1%) we can conclude that ɛ < 2 × 10−2. Since ɛ is very small compared to 1, dm/τ may be identified to the mass flow rate Q m flowing from the micro tube, and dP out allows direct measurement of Q m:

$$ Q_{\rm m} = {\frac{V} {{\mathcal{R}}T}}\, {\frac{{\rm d} P_{\rm out}}{\tau}}. $$
(3)

The pressure measurements were carried out using simultaneously two detectors chosen according to the pressure range used in each experiment. In order to measure small pressure variations (dP out < 1%), high-resolution detectors are used (from 2 × 10−2 to 2 Pa). The errors in pressure measurements in each tank depend on the characteristics of the pressure detectors. In the pressure range observed during the experiments, the errors on the measurement of the outlet pressures were estimated smaller than 0.5%.

To determine the mass flow rate we will use the registered data for the pressure at the different time instants. The flow stationary conditions physically justify the pressure rise interpolation by means of a linear fitting function of time.

The usual evaluation of the measurements errors is applied and leads to a full uncertainty smaller than ±4.5% on ΔQ m/Q m, where the non-isothermal effects are previously evaluated as ±2%; the uncertainty on the volume measure is ±2% and the error on coefficient of the linear fitting of the pressure measurements gives ±0.5%. Moreover, the leaks were estimated with two different tests as completely negligible (Ewart et al. 2006).

Finally it is to note that the capacities of the pressure sensors employed until now, have not allowed to reach the full developed transitional regime. We have determined a maximal measurement duration equal to 90 min also to be in agreement with an ambient temperature remaining quasi constant. The smallest mass flow rate which we can measure in this time period with available sensors is equal to 5.94 × 10−13 kg/s and corresponds to Argon flow with Kn m = 0.284. The corresponding values of the maximal Knudsen number for nitrogen and helium are equal to 0.291 and 0.309, respectively.

3 Background theory

For many years, pressure-driven slip flows within ducts or channels have received considerable attention. Many formulations of analytical and semi-analytical solutions have been surveyed in Karniadakis and Beskok (2002). The analytical models derived from the Navier–Stokes equations or from other continuum equation systems require the use of velocity slip boundary conditions. Several authors (Colin et al. 2004; Maurer et al. 2003) have recently proposed to use in this framework the velocity slip conditions of second order according to the Knudsen number to take better into account the rarefied effects for the moderately rarefied gas flows.

In the hydrodynamic and slip regimes the flow through the micro tube have been intensively studied theoretically. Nevertheless the questions of the choice of appropriate boundary conditions (first or second order following the Knudsen number) and the question of the limit of validity of the continuum approach (in terms of the Knudsen number range) remain open questions which are discussed below.

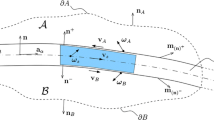
The flow analysis may be carried out in frame of the Navier–Stokes equations with slip boundary conditions. Assuming a second order boundary condition at the wall of a tube the slip velocity reads (Cercignani 1964)

$$ u_s=\pm A_1\lambda \left({\frac{\partial u}{\partial r}}\right)_w- A_2\lambda^2 \left({\frac{1} {r}}\left({\frac{\partial} {\partial r}}r {\frac{\partial u}{\partial r}} \right)\right)_w, $$
(4)

where λ is the mean free path of the molecules which could be calculated using the hard sphere (HS) model (Chapman 1970), where \({k_{\lambda} = \sqrt{\pi}/2.}\) Nevertheless, in this paper we used the variable hard sphere model (VHS) (Bird 1994) more realistic than HS model. According to this model, the coefficient k λ is equal to \({{\frac{(7 - 2 \omega )(5 - 2 \omega)}{15 \sqrt{\pi}}},}\) where ω, the viscosity index, depends only on the type of gas:

$$ \lambda = k_{\lambda} {\frac{\mu}{P}} \sqrt{2 {\mathcal{R}}T}. $$
(5)

The coefficients A 1 and A 2 in (4) may be presented in the form:

$$ A_1={\frac{\sigma_{\rm p}} {k_{\lambda}}}, \quad A_2={\frac{\sigma_{\rm 2p}} {k_{\lambda}^2}}, $$
(6)

where σp and σ2p are the first and second velocity slip coefficients.

It is to note that, according to Cercignani (1964), relation (4) involves here all the additional terms resulting from the wall curvature: these terms are represented by the Laplacian operator of the streamwise velocity (Cercignani 1964); thus, in the second term of right-hand side of Eq. (4), this operator, expressed in local cylindrical coordinates, reduces to its radial part, due to the symmetry. Furthermore, taking into account the Knudsen layer effect on the velocity profiles (Cercignani 1964) leads to modify the A 2 coefficient value, but not the form of Eq. (4).

The mass flow rate through the tube of diameter D, obtained from Navier–Stokes equations with the second order velocity slip condition (Ewart et al. 2006), reads

$$ {\dot{M}}= {\frac{\pi D^4 \Delta P P_{\rm m}}{128 \mu {\mathcal{R}} T L}} \left( 1 + 8 A_1 Kn_{\rm m}+ 32 A_2 {\frac{P_{\rm m}}{\Delta P}}\ln {\mathcal{P}} Kn_{\rm m}^2\right), $$
(7)

where \({\Delta P=P_{\rm in}-P_{\rm out}, {\mathcal{P}}=P_{\rm in}/P_{\rm out}, Kn_{\rm m}}\) is the mean Knudsen number, based on the mean pressure P m = 0.5(P in + P out). Furthermore, a non-dimensional mass flow rate S may be deduced from relation (7):

$$ S=\dot{M}\left/{\frac{\pi D^4 \Delta P P_{\rm m}}{128 \mu {\mathcal{R}} T L}} = 1+8A_1Kn_{\rm m}+16A_2 {\frac{{\mathcal{P}}+1} {{\mathcal{P}}-1}}\ln {\mathcal{P}} Kn_{\rm m}^2\right. . $$
(8)

Expression (8) may be rewritten in the more compact form:

$$ S=1+A^{\rm theor} Kn_{\rm m}+B^{\rm theor} Kn_{\rm m}^2. $$
(9)

Accordingly to the previous remarks, Eq. (4) is perfectly convenient to derive, from experiments, the complete second order slip coefficient by using Eqs. (6)–(9), supplemented with the experimental value given by expression (10). Of course, through this equation system, are also deduced “the experimental” first order coefficients and then, using various expressions proposed in the next section, the “experimental” TMAC. All these results will be given and analyzed in next section, but we can make here a preliminary remark: when comparing the various coefficients, defined here above, it appears that the slip coefficients σp, and σ2p only depend on the molecule interactions through the viscosity coefficient μ.

4 Results and discussion

We have studied the flows of argon, nitrogen and helium in a slip regime where the mean Knudsen number varies from 0.003 to 0.3. The experiments were carried out with different pressure ratios \({{\mathcal{P}} =[3,4,5] }\) between the tanks (see Table 2 for details). Figure 2 shows the experimental dimensionless mass flow rates, normalized according to left-hand side of (8), for all the gases, as a function of the mean Knudsen number.

Fig. 2
figure 2

Dimensionless mass flow rate for N2, Ar and He gases obtained according to left-hand side of (8) for \({{\mathcal{P}}_{Th} =3-5}\) and fit of first (dashed line) and second (solid line) order for \({{\mathcal{P}}=5}\)

Full size image

In order to estimate the velocity slip coefficients the measured dimensionless mass flow rate was fitted (see Fig. 2) with the first and second order polynomial form of the mean Knudsen number

$$ S^{\rm exp}_f=1+A^{\rm exp}_i Kn_{\rm m}+B^{\rm exp}_i Kn_{\rm m}^2, \quad i=1,2, $$
(10)

as it was detailed in Maurer et al. (2003) using a non-linear least square Marquard–Levenberg algorithm. The experimental fitting coefficients A exp i and B exp i , where i = 1, 2 corresponds to the order of the polynomial form (therefore B exp1  = 0), are calculated for all the gases and the uncertainty on these coefficients is calculated using the asymptotic standard error. These coefficients obtained for all the gases with a pressure ratio \({{\mathcal{P}}=5}\) are reported in Table 1. In order to analyze the respective pertinence of first or second order fitting for each gas, two additional parameters are calculated: the determination coefficient r 2 and the residual variance \({s_r = \sqrt{{\frac{1}{n-p}}\sum e^2_i},}\) where \({e_i = S^{\rm exp}_i - S^{\rm exp}_{f_i}}\) is the local difference between measured and fitting values, and so represents the local fitting error; n is the number of points and p is the number of unknown coefficients of the fitting model. Analyzing the values of these two coefficients, given in Table 1 only for \({{\mathcal{P}}=5,}\) (but the other \({{\mathcal{P}}}\) values give similar results for these coefficients) we find that the determination coefficients r 2 of Argon and Nitrogen are essentially more close to 1 for the second order fitting. For the helium flow the second order coefficient r 2 is also more close to 1 than the first order one, even if the difference between the two orders is here less important. Moreover, the values of the squared residual sum are also smaller for the second order fitting in the case of all the gases. In order to supplement this analysis, the residuals e i (fitting errors) are plotted as a function of the averaged Knudsen number for the three gases. As an example, the residual or argon are presented in Fig. 3. The analysis of the form of the distribution of the argon residuals shows that the residuals of second order fit are equi-distributed, whereas the residuals of the first order fit are largely negative from 0.003 to 0.2 on the Knudsen axis, which confirms the choice of the second order fitting as more pertinent for Argon flows. The same analysis of the form of residuals is carried out for nitrogen and helium (Fig. 3 and nitrogen). From these analyses we may conclude that the second order fitting appears clearly as the most pertinent for nitrogen and argon flows and also for the helium flow, even if, as shown in Table 1, the relative weight of the second order coefficient is smaller for helium as for the other gases. Thus, in the sequel of this paper, we will use the results of the second order fitting for all the gases.

Table 1 Fitting parameters obtained from the experiments
Full size table
Fig. 3
figure 3

He (up) and Ar (down) residuals for \({{\mathcal{P}}=5}\)

Full size image

From the comparison of the theoretical and experimental non-dimensional mass flow rate expressions (9), (10) the coefficients A 1 and A 2 from the velocity slip boundary condition (4) and respectively the slip coefficients σp and σ2p (6) may be found from the expressions:

$$ A_1={\frac{\sigma_{\rm p}} {k_\lambda}} = A^{\rm exp} / 8, \quad A_2={\frac{\sigma_{\rm 2p}} {k_{\lambda}^2}}={\frac{B^{\rm exp}} {16 \ln{\mathcal{P}}}} {\frac{{\mathcal{P}}-1} {{\mathcal{P}}+1}}. $$
(11)

The values of the coefficients σp and σ2p are given in Table 2 for the first and second order fitting. It is to note that both velocity slip coefficients depend on the molecular weight of the gases.

We also derived an experimental value of the accommodation coefficient using the Maxwell diffuse-specular scattering model. The use of Maxwell’s kernel for the gas–surface interaction gives the following value for the velocity slip coefficient, neglecting the Knudsen layer influence:

$$ \sigma_{\rm p}^{M}= {\frac{\sqrt{\pi}} {2}}\,{\frac{2-\alpha_{\rm M}} {\alpha_{\rm M}}}. $$
(12)

As well known, in the Maxwell kernel the same coefficient α may represent the energy accommodation as well as that of any momentum component. However, in isothermal slip regime it is usual and physically justified to identify α as the TMAC. In the case of a full accommodation (αM = 1) the theoretical coefficient σM p is equal to 0.886, which is different from the theoretical diffuse value given in Albertoni et al. (1963). As well known, this diffuse value equal to 1.016 is considered as a reference value. Therefore, we report also here a more accurate method to calculate the accommodation coefficient proposed by Loyalka et al. 1975. These authors (Loyalka et al. 1975) have calculated the slip coefficients from the BGK kinetic model equation with the diffuse-specular boundary conditions for the different values of the accommodation coefficient αL using the variational method. Then the calculated values of the slip coefficients have been fitted in order to obtain a simple relation connecting slip and accommodation coefficients:

$$ \sigma_{\rm p}^{\rm L}= {\frac{\sqrt{\pi}} {2}}{\frac{2-\alpha_{\rm L}} {\alpha_{\rm L}}}(1+0.1621\alpha_{\rm L}). $$
(13)

The values of α calculated from the experimental values of the velocity slip coefficient (obtained from the second order fitting σ 2ndp ) using relations (12) (αM) and (13) (αL) are given in Table 3. In this table are also given the Maxwell accommodation coefficients calculated by other authors using first order (Porodnov et al. 1974; Arkilic et al. 1997) and second order (Maurer et al. 2003; Colin et al. 2004) treatment. It is necessary to note, that the implementation of the relation (13) is more accurate from the kinetic theory point of view, but it does not change, basically, the character of the gas–wall interaction, since the Maxwellian diffuse-specular scattering is not called into question. As shown in Table 3, applying the relation coming from the kinetic theory, the surfaces under consideration (fused silica) must be described as quasi-diffuse surface.

Table 2 σ ip and σ i2p experimental coefficients obtained from a polynomial fitting of first or second degree, αM obtained from the velocity slip coefficient using Maxwell relation (12)
Full size table
Table 3 TMAC obtained from the present experiments and by other authors from various models: * is the first order fitting, ** is the second order fitting
Full size table

The previous data may be summarized as follows:

  • In the investigated Knudsen range the relative weight of the second order effect (B 2nd/A 2nd) increases with the molecular mass and does not depend significantly on the molecular internal structure (see Table 1). Furthermore, basing our comments on the investigated gases we note that both first and second order slip coefficients increase with the molecular weights. Moreover, this evaluation is preserved when changing the order of the fitting.

  • The TMAC deduced are strictly smaller than 1 excluding a complete diffuse reflection on the fused silica. The accommodation coefficient for Helium is greater than the other gas coefficients.

  • Table 1 shows a good agreement of the present values with other authors experimental results if considering that the geometry of Arkilic et al. (1997), Maurer et al. (2003), Colin et al. (2004) was not circular, that the surface materials were generally not exactly the same (generally silica and silicon are both involved for a part in the channel shape), and that finally the pressure is generally not the same; moreover, certain authors used a first order treatment.

  • In order to study the detailed influence of geometry or pressure ratio on the TMAC, more systematic experiments would be needed.

5 Conclusions

This work contributes to clarify the validity domains of slip regime modelling using first or second order boundary conditions. For the gases considered in the 0.003–0.3 Kn range, in tube geometry, the second order fitting seems the most convenient. The TMAC determination leads to conclude that the He, Ar, and N2 molecules are not reflected on silica surface following a full diffuse reflection. The helium TMAC appears significantly greater than those of two other gases. More generally the TMAC seems decreasing when the molecular weight increases and this evaluation is maintained by changing the slip coefficient model. To conclude on influence of the inlet/outlet pressure ratio (or of geometry) on the accommodation process (for a same Knudsen numbers) would need more systematic experiments.