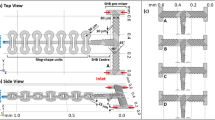
Mixing in microscale is constrained by laminar flow behavior in microchannels. One of the many techniques for improving mixing is reducing the mixing path between solvent and solute [1]. In lamination techniques, solvent and solute remain in their particular streams. Mixing path is shortened perpendicular to the axial flow direction. Time-interleaved sequential segmentation divides the solvent and solute into segments, which occupy the whole channel width. Mixing occurs through dispersion in flow direction. Sequential segmentation can be achieved by alternate switching of the inlet flows, using controlled valves for instance (Fig. 1). The mixing ratio can be adjusted by the switching ratio. Deshmukh et al. [2] described this concept numerically and observed the mixing results experimentally. The segmentation process was controlled actively by integrated micropumps. Similar concepts realized by external pumps were reported later by Fujii et al. [3] and Okamoto et al. [4]. All previous works are based on numerical simulation and experimental observation. In this communication, we report a simple analytical model of this mixing concept to present better understanding of mixing based on sequential segmentation.

Fig. 1
figure 1

Mixing concept based on time-interleaved sequential segmentation

Full size image

We start with a parallel plate model for the mixing channel. Pressure driven flow in microchannels with low aspect ratio (W ≫ H) can be reduced to this model, Fig. 2. The model assumes a flat velocity profile in the channel width direction (z-axis) and a Poiseuille velocity profile in the channel height (y-axis) [5]:

$$u(y)=6U\left(1-\frac{{y}}{{H}}\right)\frac{{y}}{{H}},$$
(1)

where U is the mean velocity in the flow direction along the x-axis. The parabolic velocity profile causes the so-called Taylor–Aris dispersion, which can be described by an effective diffusion coefficient D*. Using the Taylor–Aris approach [6] and the velocity profile Eq. 1, the effective diffusion coefficient can be determined as [7]:

$$D^*=D+\frac{{H^2U^2}}{{210D}},$$
(2)

where D is the molecular diffusion coefficient of the solute in the solvent and H is the channel height. It is to be noted that the Taylor–Aris approach considers dispersion far away from the channel inlet, which is not very accurate for our case. However, this paper will mainly focus on the transient concentration distribution along the flow direction as elaborated next.

Fig. 2
figure 2

Model of the mixing channel

Full size image

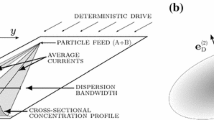
With the effective diffusion coefficient D*, the problem of time-interleaved sequential segmentation can be reduced to a simple one-dimensional macro transport model. The concentration distribution across the channel width and height is assumed to be uniform, thus, only the concentration profile along the flow direction x needs to be considered. With a mean velocity U and a switching period T, the characteristic segment length is defined as L=UT. The general transport equation can be then reduced to the transient one-dimensional form:

$$\frac{{\partial c}}{{\partial t}}+U\frac{{\partial c}}{{\partial x}}=D^*\frac{{\partial ^2 c}}{{\partial x^2}}.$$
(3)

Figure 3 depicts this one-dimensional model with the boundary condition at the inlet. Figure 4 describes the periodic boundary condition at the inlet (x=0):

$$ c(t,0) = \left\{{\begin{array}{*{20}l} {c_0} & {0 \leq t \leq \alpha T/2} \\ 0 & {\alpha T/2 < t \leq T - \alpha T/2} \\ {c_0} & {T - \alpha T/2 < t \leq T} \\ \end{array}} \right. ,$$
(4)

where c0, T, and α are the initial concentration of the solute, the period of the segmentation, and the mixing ratio, respectively.

Fig. 3
figure 3

Transient one-dimensional model for a micromixer with sequential segmentation

Full size image
Fig. 4
figure 4

The transient concentration at the inlet of the mixing channel

Full size image

Introducing the dimensionless variables \(c^*=c/c_0,\) x*=x/L, and t*=t/T, Eq. (3) has the dimensionless form:

$$\frac{{\partial c^*}}{{\partial t^*}}=\frac{{1}}{{\rm{Pe}}}\frac{{\partial ^2 c^*}}{{\partial {x^*}^2}}-\frac{{\partial c^*}}{{\partial x^*}} ,$$
(5)

where the Peclet number is defined as Pe=UL/D*. The dimensionless boundary condition of Eq. (4) is then:

$$ c^* (t^* ,0) = \left\{{\begin{array}{*{20}c} 1 & {0 \leq t^* \leq \alpha /2} \\ 0 & {\alpha /2 < t^* \leq 1/2} \\ \end{array}} \right. $$
(6)

Solving the Eq. 5 using separation of variables with Eq. 6 and (c*(∞)=α) results in the transient behavior of the concentration profile along the mixing channel:

$$c^*{\left( {x^*,t^*} \right)} = \alpha + {\sum\nolimits_{n = 1}^\infty {\frac{{2\sin {\left( {\alpha \pi n} \right)}}} {{\pi n}}} }{\Re }{\left\{ {\exp {\left[ {\frac{1} {2}{\left( {{\text{Pe - }}{\sqrt {{\text{Pe + 8}}\pi n{\text{Pe}}j} }} \right)}x^*} \right]} \times \exp {\left( {2\pi nt^*j} \right)}} \right\}}, $$
(7)

where j is the imaginary unit, ℜ indicates the real component of a complex number. The concentration distributions along the mixing channel at different Peclet numbers and at different mixing ratios are depicted in Fig. 5a and Fig. 5b, respectively. Figure 5a shows clearly that only a short mixing channel is required if the Peclet number is small, that means either a small mean velocity U or a short characteristic segment length L. A short segment length is caused by a short switching time T or a high switching frequency f=1/T. Sequential segmentation can achieve different final concentrations simply by adjusting the switching ratio α, Fig. 5b.

Fig. 5
figure 5

Concentration profile along the flow direction at t*=1: awith different Peclet numbers (α=0.5), bwith different mixing ratios (Pe=100)

Full size image

We reported a simple transient, one-dimensional model for mixing in microchannels based on time-interleaved sequential segmentation. The model describes well the concentration profile along the flow direction. If the segment length L and the switching time period T are used as the characteristic length and the characteristic time, Peclet number Pe and the mixing ratio α would be the two parameters characterizing this mixing concept. An arbitrary mixing ratio can be achieved by modulating the pulse width of the switching signal. Since this model assumes one-dimensional distribution along the flow axis, the result may suit best for the distribution on the centerline along the channel.