Evaporation in microchannels: influence of the channel diameter on heat transfer

Abstract

This paper discusses the effect of diameter on both flow boiling heat transfer and transition from macro to microchannel evaporation. A recently proposed three-zone flow boiling model based on evaporation of elongated bubbles in microchannels is briefly described and used for the present analysis. In the microscale range, the model predicts an increase in the two-phase heat transfer coefficient with a decrease of diameter for low values of vapor quality and a decrease of the heat transfer coefficient for larger values of vapor quality. This behavior is explained by the influence of the liquid film thickness, deposited periodically behind passing liquid slugs.

1 Introduction

In the domain of two-phase heat transfer in microchannels, one unsolved problem is to identify the lower limit of the diameter range where macroscale laws are still applicable. In fact, it is necessary to know this limit to distinguish the effect of the diameter due to the passage from macroscale to microscale phenomena from the effect of diameter inside the microscale domain.

On the microscale, the effect of gravity is surpassed by that of the surface tension forces, i.e., no stratified flow exists if the tube diameter is sufficiently small. The Bond number gives the ratio of these forces for a tube of diameter d:

$$ {\text{Bo}} = \frac{{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)d^2 }} {\sigma } $$

(1)

Based on experimental studies, Kew and Cornwell (1997) proposed a macro-to-microscale threshold value as the diameter obtained with Bo=4. For diameters lower than d_th the macroscopic laws are not suitable to predict the heat transfer coefficient nor the flow pattern; d_th is given by:

$$ d_{{\text{th}}} = 2\sqrt {\frac{\sigma } {{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)}}} $$

(2)

Based on the idea that no stratification exists at the microchannel scale, Jacobi and Thome (2002) chose the bubble departure diameter as their determining criterion. The macro–micro transition is reached when the diameter of the bubble reaches the diameter of the tube before detachment. Jensen and Memmel (1986) have tested different correlations available to predict bubble departure diameter in nucleate pool boiling. For example, the Fritz (1935) correlation gives this diameter d_det as:

$$ d_{{\text{det}}} = 0.0208\beta \sqrt {\frac{\sigma } {{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)}}} $$

(3)

where the contact angle β is in degrees. Nishikawa et al. (Jensen and Memmel 1986) suggested:

$$ d_{{\text{det}}} = \left[ {0.12 + 0.08\left( {\frac{{c_p T_{{\text{sat}}} }} {{\Delta h_{{\text{lv}}} }}} \right)^{2/3} } \right]\sqrt {\frac{\sigma } {{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)}}} $$

(4)

Kutateladze and Gogonin (1979) proposed:

$$ d_{{\text{det}}} = \left[ {0.25\sqrt {1 + 10^5 K_1 } } \right]\sqrt {\frac{\sigma } {{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)}}} $$

(5)

where

$$ K_1 = \left( {\frac{{\rho _{\text{l}} c_p T_{{\text{sat}}} }} {{\rho _{\text{v}} \Delta h_{{\text{lv}}} {\text{Pr}}_{\text{l}} }}} \right)^2 \frac{{\mu _{\text{l}}^2 \sqrt {g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)} }} {{\rho _{\text{l}} \sigma ^{3/2} }}\quad {\text{for}}\;k_1 < 0.06 $$

(6)

Jensen and Memmel (1986) proposed the relation:

$$ d_{{\text{det}}} = \left[ {0.19\left( {1.8 + 10^5 K_1 } \right)^{2/3} } \right]\sqrt {\frac{\sigma } {{g\left( {\rho _{\text{l}} - \rho _{\text{v}} } \right)}}} $$

(7)

It is interesting to notice the role played by the Bond number in all these relations, which are only strictly valid for pool boiling, while in a microchannel the cross flow tends to promote the detachment of the bubble before it completely spans the tube. Thus, a criterion based on bubble detachment may overestimate the threshold value of the diameter. Conversely, large boiling incipience superheats in microchannels tend to cause bubbles to rapidly grow to the size of the channel and occupy the total section of the channel and even create backflow, so that the above relation may represent the lower limit of such a threshold. The values predicted by these methods are summarized in Table 1. Only the most recent studies fall within the microscale domain according to the Kew and Cornwell (1997) criterion and only the Yen et al. (2003) study abides by all the criteria based on bubble detachment.

Table 1 Threshold diameter corresponding to studies from the literature and calculated with different criteria.

The limited number of experiments that have tested more than one diameter do not permit one to deduce a clear trend. For example, Yan and Lin (1998) concluded that evaporation heat transfer in a small diameter is more effective than in a larger diameter, when passing from macro to microscale tubes. But what happens when the diameter is decreased within the microscale range? For R-134a in multichannels for tube diameters of 0.77 mm and 2.01 mm at a mass velocity of 285 kg m⁻² s⁻¹, the data of Agostini (2002) show a higher heat transfer coefficient for their small tube but only for x<0.25. For R-142b, Palm (2003) shows a moderate increase of h when d decreases in 3.5, 2.5, 1.5 and 1 mm tubes.

Using the criteria of Kew and Cornwell, the threshold diameter for macro-to-microscale transition equals 2.14 mm for R-142b at 15°C. Thus, these results seem to be representative of the increase of the heat transfer coefficient in the passage from the macro-to-microscale. For R-134a, Owhaib and Palm (2003) at 645 kPa found that the average heat transfer coefficient increases when the diameter decreased from 1.7 to 0.8 mm. In this case, the threshold diameter is 1.68 mm and we can reasonably assume all these results correspond to the microscale. For R-123, Baird et al. (2000) tested diameters of 0.92 and 1.95 mm and affirmed that diameter had no significant effect on h. They proposed a correlation independent of the diameter to predict h. The threshold diameter for this last fluid is 1.78 mm, so once again the results correspond to the macro-to-microscale transition zone.

Yen et al. (2003) studied convective boiling of R-123 inside 0.19 and 0.51 mm tubes, for heat fluxes ranging from 5.5 to 26.9 kW m⁻². The influence of the diameter cannot be deduced because their operating conditions were different for the two tubes, particularly the heat flux. Unfortunately, it is not possible to compare this study with the result of Baird et al. (2000) because the ranges of heat flux and saturation pressure are completely different. Khodabandeh (2003) studied boiling in an advanced two-phase thermosyphon loop with isobutane as the working fluid with tube diameters ranging from 1.1 to 6 mm. He concluded that the influence of d was slight and no clear trend was seen.

2 Three-zone evaporation model

A new three-zone flow boiling heat transfer model has recently been proposed by Thome et al. (2004) and Dupont et al. (2004). A brief summary is presented below. This model was formulated to predict the local dynamic heat transfer coefficient and the local time-averaged heat transfer coefficient at a fixed location along a microchannel during flow and evaporation of an elongated bubble at a constant, uniform heat flux boundary condition. The local vapor quality, heat flux, microchannel internal diameter, mass flow rate and fluid physical properties at the local saturation pressure are the input parameters to the model.

2.1 Description of the three-zone heat transfer model

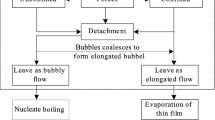
As shown in Fig. 1, bubbles are assumed to nucleate and quickly grow to the channel size upstream such that successive elongated bubbles are formed that are confined radially by the tube wall and grow in length, trapping a thin film of liquid between the bubble and the inner tube wall.

Fig. 1

Diagram illustrating a triplet comprising a liquid slug, an elongated bubble and a vapor slug.

The thickness of this film plays an important role in heat transfer. At a fixed location, the process proceeds as follows: (1) a liquid slug passes (typically without entrained vapor bubbles, contrary to macroscale flows); next, (2) an elongated bubble passes (whose liquid film is formed from liquid removed from the liquid slug); and finally, (3) a vapor slug passes if the thin evaporating film of the bubble dries out before the arrival of the next liquid slug. The cycle then repeats itself upon arrival of the next liquid slug.

Thus, either a liquid slug and elongated bubble pair or a liquid slug, elongated bubble and vapor slug triplet pass this fixed point at a frequency that is a function of the formation rate of bubbles upstream.

Figure 1 shows a representation of this process with a dry zone, i.e., a three-zone model, where L_p is the total length of the pair or triplet, L_l is the length of the liquid slug, L_v is the length of the bubble including the length of the vapor slug with a dry wall zone L_dry, and L_film is the length of the liquid film trapped by the bubble. The internal radius and diameter of the tube are R and d while δ₀ and δ_min are the thicknesses of the liquid film trapped between the elongated bubble and the channel wall at its formation and at dry out, respectively.

In brief, the heat transfer model is formulated as follows. In the absence of a void fraction model validated for two-phase elongated bubble flow in microchannels, the homogeneous model of two-phase flow is used for now to obtain the void fraction and two-phase velocity along the tube at the desired vapor quality. From the period of bubble nucleation and growth at the inlet and the local two-phase velocity, the local length of the pair or triplet passing by this point in the tube is calculated as a function of the vapor quality, which is obtained from an energy balance on the wall heat flux input. The respective lengths of the liquid slug L_l and vapor L_v in the pair or triplet are obtained directly from the void fraction at this location. Then, from the local mean velocity of the liquid slug, the initial liquid film thickness δ₀ is calculated and dry out of the wall occurs if the film thickness reaches a predetermined value of δ_min before the arrival of the next liquid slug. Mean heat transfer coefficients are determined for the liquid and vapor slug zones while the dynamic average value of the heat transfer coefficient of the evaporating film is determined for conduction across its varying thickness. The time-averaged heat transfer coefficient is then determined as a function of local vapor quality for one pair or triplet passing by this location of the tube.

The following assumptions were made in the development of the model:

• 1. The vapor and liquid travel at the same velocity (homogeneous flow).

• 2. The heat flux is uniform and constant with time along the inner wall of the microchannel.

• 3. All energy entering the fluid is used to vaporize liquid.

• 4. The local saturation pressure is used for determining the local saturation temperature and the physical properties are assumed constant.

• 5. The liquid slug initially contains all the liquid that flows past the nucleating bubble (at x=0) until it grows to the channel diameter.

• 6. The liquid film remains attached to the wall and the influence of vapor shear stress on the liquid film is assumed negligible, so that it remains smooth without ripples.

• 7. The thickness of the film is very small with respect to the inner radius of the tube: δ₀«R.

• 8. The thermal inertia of the channel wall is neglected.

2.1.1 Bubble formation and frequency

The model is based on the premise that bubble nucleation occurs at the location where the fluid reaches the saturation temperature, i.e. at x=0. Each bubble can be envisioned as a “shutter” that divides the liquid flow into successive liquid slugs. The pair frequency f is a complex function of the bubble formation process, which involves the channel diameter, surface roughness, size and distribution of nucleation sites, waiting time in the nucleation process, bubble departure dynamics and coalescence, subcooling (in many of the experimental tests), etc. Due to the complexity of the phenomenon and the indetermination of these local parameters in the different studies, f has been identified with a least-squares error method from the database—Dupont et al. (2004)—and was found empirically to be strongly dependent on the heat flux:

$$ f = \frac{1} {\tau } = \left( {\frac{q} {{3328\left( {P_{{\text{sat}}} /P_{{\text{crit}}} } \right)^{ - 0.5} }}} \right)^{1.74} $$

(8)

2.1.2 Initial conditions and basic equations

From the conservation of mass, it is possible to obtain the mean initial vapor quality x _o at the inlet during the time period τ:

$$ x_0 = \frac{1} {{1 + \left( {(3G\tau )/4\rho _{\text{v}} R} \right)}} $$

(9)

An energy balance, based on constant heat flux on the internal surface of the tube, gives a linear profile of the vapor quality along the tube:

$$ x\left( z \right) = \left( {\frac{{2q\left( {1 - x_0 } \right)}} {{GR\Delta h_{{\text{lv}}} }}} \right)z + x_0 $$

(10)

where z is the axial distance from the point of bubble nucleation at x₀.

The liquid and vapor are assumed to travel at the same velocity, such that the pair velocity U_p is:

$$ U_{\text{p}} = G\left[ {\frac{x} {{\rho _{\text{v}} }} + \frac{{1 - x}} {{\rho _{\text{l}} }}} \right] $$

(11)

The distribution of the phases in the pair (or triplet) is presented in Fig. 1. Due to the periodic condition of bubble formation at the inlet, the flow inside the tube past any fixed point is also τ-periodic. An example of the evolution of the heat transfer coefficient at a particular location z is shown in Fig. 2.

Fig. 2

Cyclic variation in h with time.

At each location during τ, a pair or triplet passes. It is possible to deduce the mean equivalent length of the pair or triplet at this given point to be:

$$ L_{\text{P}} = U_{\text{p}} \tau = \tau G\left[ {\frac{x} {{\rho _{\text{v}} }} + \frac{{1 - x}} {{\rho _{\text{l}} }}} \right] $$

(12)

This length is the “apparent length” measured by an observer at location z. To evaluate the residence time of a bubble t_v at location z, the equivalent length of the vapor is calculated using the local mean void fraction:

$$ L_{\text{v}} = \varepsilon L_{\text{p}} = \frac{{\tau G}} {{\rho _{\text{v}} }}x $$

(13)

so that:

$$ t_{\text{v}} = \frac{{L_{\text{v}} }} {{U_{\text{p}} }} = \frac{\tau } {{1 + \frac{{\rho _{\text{v}} }} {{\rho _{\text{l}} }}\frac{{1 - x}} {x}}} $$

(14)

This time t_v corresponds to the presence of vapor (dryout and film zones) passing through the cross section at location z. Similarly, to evaluate the arrival time of a bubble t_l at location z, the equivalent length of the liquid slug is calculated using the local mean void fraction:

$$ L_{\text{l}} = \left( {1 - \varepsilon } \right)L_{\text{p}} = \frac{{\tau G}} {{\rho _{\text{l}} }}\left( {1 - x} \right) $$

(15)

so that:

$$ t_{\text{l}} = \frac{{L_{\text{l}} }} {{U_{\text{p}} }} = \frac{\tau } {{1 + (\rho _{\text{l}} /\rho _{\text{v}} )(x/1 - x)}} $$

(16)

This time t_l corresponds to the presence of a liquid slug passing through the cross section at location z.

2.1.3 Liquid film thickness

The initial thickness of the liquid film δ₀ and the minimum film thickness at dryout δ_min are two other keys parameters in the model. An asymptotic method has been applied to determine δ₀ by unifying the two relations of Moriyama and Inoue (1996) that include the effect of the viscous boundary layer and the surface tension force (the Weber We number replaces the Bond number) along with a new empirical factor $C_{\delta _{\text{0}} }$ to arrive at:

$$ \frac{{\delta _0 }} {d} = C_{\delta _0 } \left( {3\sqrt {\frac{{\nu _l }} {{U_{\text{p}} d}}} } \right)^{0.84} \left[ {\left( {0.07{\text{We}}^{0.41} } \right)^{ - 8} + 0.1^{ - 8} } \right]^{ - 1/8} $$

(17)

where the Weber number based on d is:

$$ {\text{We}} = \frac{{\rho _{\text{l}} dU_{\text{p}}^2 }} {\sigma } $$

(18)

$C_{\delta _{\text{0}} } = 0.29$ was found to be the best value from comparison of the heat transfer model to the database.

The variation of liquid film thickness from its initial value of δ₀ is due only to vaporization by the heat flux q at the inner wall of the tube. For a differential length of the film Δz, all the energy transferred by conduction from the wall is used to vaporize the liquid. From assumption 7 in the model development, R-δ≈R. The time reference is defined so that time t=0 corresponds to the instant when the film is created at position z. The evolution of the thickness of the film is found by integration with the initial condition δ(z, 0)=δ₀ (z) so that:

$$ \delta \left( {z,t} \right) = \delta _0 \left( z \right) - \frac{q} {{\rho _{\text{l}} \Delta h_{{\text{lv}}} }}t $$

(19)

From this relation, one can express the maximum duration of the existence of the film t_{dry film} at position z:

$$ t_{{\text{dry film}}} \left( z \right) = \frac{{\rho _{\text{l}} \Delta h_{{\text{lv}}} }} {q}\left[ {\delta _0 \left( z \right) - \delta _{{\text{min}}} } \right] $$

(20)

The final thickness δ_end and residence time of the film t_film depend on whether or not local dryout of the film occurs. If t_{dry film}>t_v, then the next liquid slug arrives before dryout of the film occurs, so that:

$$ \delta _{{\text{end}}} \left( z \right) = \delta \left( {z,t_{\text{v}} } \right) $$

(21)

$$ t_{{\text{film}}} = t_{\text{v}} $$

(22)

If t_{dry film}<t_v, then local temporary dryout occurs, i.e. the liquid film thickness reaches the minimum feasible film thickness:

$$ \delta _{{\text{end}}} \left( z \right) = \delta _{{\text{min}}} $$

(23)

$$ t_{{\text{film}}} = t_{{\text{dry film}}} $$

(24)

Thus, the duration of the local wall dryout is:

$$ t_{{\text{dry}}} {\text{ }} = {\text{ }}t_{\text{v}} - t_{{\text{film}}} $$

(25)

2.1.4 Heat transfer model

The time-averaged local heat transfer coefficient h can be calculated for one time period τ. First, heat transfer through the thin evaporating film surrounding the elongated bubble is analyzed followed by the heat transfer in the liquid and vapor slugs. Note that a vapor slug is only present if the liquid film surrounding the elongated bubble reaches the minimum film thickness, at which point local, cyclical dryout occurs.

The local heat transfer coefficient in the evaporating liquid film h_film is:

$$ h_{{\text{film}}} {\text{ }}(z,{\text{ }}t){\text{ }} = {\text{ }}\frac{q} {{T_{\text{w}} - T_{{\text{sat}}} }} $$

(26)

The local heat transfer is assumed to be controlled by one-dimensional conduction across the film, so that:

$$ h_{{\text{film}}} \left( {\text{z}} \right) = \frac{{\text{1}}} {{t_{{\text{film}}} }}\int\limits_{\text{0}}^{t_{{\text{film}}} } {\frac{{\lambda _{\text{l}} }} {{\delta \left( {z,t} \right)}}{\text{d}}t} $$

(27)

$$ = {\text{ }}\frac{{\lambda _{\text{l}} }} {{\delta _0 - \delta _{{\text{end}}} }}\ln \left( {\frac{{\delta _0 }} {{\delta _{{\text{end}}} }}} \right) \approx {\text{ }}\frac{{2\lambda _{\text{l}} }} {{\delta _0 \left( z \right) + \delta _{{\text{end}}} \left( z \right)}} $$

(28)

When δ→ 0, then h_film → ∞ and this singularity needs to be avoided. Since the liquid film will break up before approaching this limit, a criterion is required to determine the minimum possible film thickness δ_min. In this area the liquid film interacts with the roughness to form a large number of meniscus and dry picks in direct contact with the vapor. The curvature of the liquid–vapor interfaces changes the local saturation conditions to stop the evaporation and the dry surface of the peaks allows a convective heat transfer. Due to the complexity and difficulty of predicting the break-up of this very thin layer, the minimum film thickness δ_min is the last of the three parameters to be identified from the heat transfer database in the present model. In order to reduce the sensitivity of the model to δ_min, the mean heat transfer coefficient in the film is calculated by using the average value of the film thickness during t_film in Eq. 28 instead of the logarithmic expression. With this approximation, the best value found was δ_min=0.3×10⁻⁶ m.

For the liquid and vapor slugs (the latter is for the dry wall zone), the heat transfer coefficients are calculated from their respective local Nusselt numbers and are applied to the respective “lengths” of the liquid slug L_l and dry wall zone L_dry passing by a given location z. The local Nusselt number at this location depends on the nature of the flow. The flow is assumed to be hydrodynamically and thermally developing.

For laminar developing flow, for which Re≤2300, the London and Shah correlation given by the VDI-GVC (1997) is used to obtain the local Nusselt number. For transition and turbulent developing flow, the Gnielinski correlation given by the VDI-GVC (1997) is assumed to be valid for Re>2300. To obtain a continuous expression, an asymptotic method has been applied:

$$ h = \left[ {h_{{\text{lam}}}^4 + h_{{\text{trans}}}^4 } \right]^{1/4} = \frac{\lambda } {d}\left[ {{\text{Nu}}_{{\text{lam}}}^4 + {\text{Nu}}_{{\text{trans}}}^4 } \right]^{1/4} $$

(29)

These expressions are applicable to the liquid in the slug and to the vapor in the dry zone for their respective equivalent lengths, L_l and L_dry. Fig. 2 shows the predicted variations and relative magnitudes of h_l and h_v.

Experimentally, time-averaged local heat transfer coefficients are reported in the literature. The local, time-averaged heat transfer coefficient of a pair (or triplet) passing by location z is thus:

$$ h\left( z \right) = \frac{{t_{\text{l}} }} {\tau }h_{\text{l}} \left( z \right) + \frac{{t_{{\text{film}}} }} {\tau }h_{{\text{film}}} \left( z \right) + \frac{{t_{{\text{dry}}} }} {\tau }h_{\text{v}} \left( z \right) $$

(30)

3 Results and discussion

In Fig. 3, the model with its general parameters is compared to experimental data taken from nine sources (Lazarek et al. 1982; Wambsganss et al. 1993; Tran et al. 1996; Yan and Lin 1998; Baird et al. 2000; Bao et al. 2000; Lin et al. 2001; Agostini 2002; Owhaib and Palm 2003; Yen et al. 2003) covering the following seven fluids: R-11, R-12, R-113, R-123, R-134a, R-141b and CO₂. The recent data from Owhaib and Palm (2003) and Yen et al. (2003) were not yet available to include in Dupont et al. (2004) and have been added here. The test data cover tube diameters range from 0.51 to 3.1 mm, the mass velocities are 50 to 564 kg m⁻² s, pressure covers the range from 124 to 5,766 kPa, the heat fluxes vary from 5 to 178 kW m⁻², and vapor qualities range from 0.01 to 0.99. This general model predicts 67% of the points to ±30%.

Fig. 3

Comparison between experimental heat transfer and the solution of the three-zones model.

The multichannel studies and the data from Wambsganss et al. (1993), Yen and al. (2003) and Owhaib and Palm (2003) for their 1.7 mm tube are poorly described by the model. The poor agreement with the multichannel experimental data is not surprising, especially with a rectangular cross section from Agostini (2002). The difference seems to be linked with the non-uniform distribution of the flow between the channel due to the bubble formation process. Also, reversal flow has been observed in the case of two trapezoid microchannels by Li et al. (2003). Excluding multichannel experiments from the database, the general model predicts 77% of the data to ±30%. This performance is promising considering the difficulty in accurately measuring heat transfer coefficients in microchannels, the variety of measurement methods applied, the effects of inlet subcooling used in most of the studies on the pair frequency, unknown surface roughness, the real threshold from macro-to-microscale, and so forth.

The unexpected good agreement for the CO₂ is due to the fact that intermittent and annular flows are present over a wide range of vapor quality according to Pettersen (2003). These flow regimes are similar to the elongated bubble in the current model, and an equivalent frequency and an initial film thickness can be identified.

In the model the thermal inertia of the wall is not taken into account. In reality, a thin wall and/or a wall with poor conductivity might experience strong temperature variations due to the cyclic change of the local heat transfer coefficient. These fluctuations might allow the nucleation of new bubbles inside the slugs if T_w becomes larger than the boiling incipience superheat. In this case, the assumption of constant frequency is no longer realistic. If the wall is thicker (Yan and Lin 1998; Baird et al. 2000; Bao et al. 2000), and/or if the conductivity of the tube is sufficiently large, the variation of T_w should be attenuated. From this point of view, the constant heat flux boundary condition is a simplification of reality.

3.1 Influence of d on the heat transfer coefficient

In order to illustrate the influence of tube diameter, the model has been run with R-123 at P_sat=350 kPa, G=120 kg m⁻² s⁻¹ and q=100 kW m⁻². Figure 4 shows the heat transfer coefficient versus the vapor quality for diameters ranging from 0.5 to 2 mm in increments of 0.166 mm.

Fig. 4

Heat transfer coefficient vs vapor quality for different diameters (increment of 0.166 mm).

At low vapor quality, the three-zone model predicts a strong increase of h up to its peak where local dryout occurs, i.e. when δ δ_min. After the peak, at a particular diameter, the local heat transfer decreases because of: (1) the increase of the dryout time period and the poor heat transfer from the dry wall in the heat transfer cycle, and (2) the decrease of the initial film thickness δ₀ with the increase of the two-phase flow velocity with increasing x. Indeed, for the present range of the database, δ₀ is controlled by the viscous boundary layer rather than the surface tension force.

The influence of diameter thus depends on the vapor quality: for x<0.04, h decreases with d for x>0.18, h increases with d; and in-between for 0.04<x<0.18 the heat transfer coefficient increases, reaches a peak, and afterwards decreases with d. Depending on the thermophysical properties of the fluid and the operating conditions, each zone can disappear or move as a function of x. In the model, the influence of the diameter is directly linked with Eq. 17 which gives the initial film thickness δ₀.

Figure 5 shows the comparison between the model and the data of Bao et al. (2000) and Baird et al. (2000) for R123. The vapor quality chosen corresponds to the mean value of x of their experimental points, x=0.255. The two extreme values of the range of mass flux G=167.4 and 337.6 kg m⁻² s⁻¹ are used for the 1.95 mm tube (dotted lines) and G=450 kg m⁻² s⁻¹ for the 0.92 mm tube.

Fig. 5

Heat transfer coefficient vs diameter, comparison with Baird et al. (2000).

The model predicts an increase of the heat transfer coefficient with a decrease of the diameter below a heat flux of 18 kW m⁻². Beyond this threshold value of q, decreasing the diameter should give a significant decrease in h. Unfortunately, the range of heat flux corresponding to the two diameters in these experiments does not permit this expectation to be verified, but the prediction of the model is compatible with the experimental trends.

The study of Ohwaib and Palm (2003) is the most interesting one available to observe the influence of the tube diameter. Figure 6 shows the results of the calculation.

Fig. 6

Heat transfer coefficient vs diameter, comparison with Ohwaib and Palm (2003).

Unfortunately, this study was made only for low values of the vapor quality. Other studies for R134a, in single and multi-channels (Yan and Lin 1998; Agostini 2002; Yen et al. 2003) have demonstrated a strong decrease of h beyond values of x ranging from 0.1 to 0.3. In fact, the model at this time is not able to describe the experimental trend accurately, i.e. the peak in h is shifted to very small values of x. However, a specific parameter identification on each data series permits the model to get the correct trends (Fig. 7). In conclusion, the data from Ohwaib and Palm (2003) correspond to the zone before the peak. In this case, h increases when d decreases and this trend is consistent with the results from the calculation. After the peak, no experimental data are available to confirm the negative effect of diameter reduction on the heat transfer coefficient predicted by the three-zone model. Hence, additional experimental and modelling works are called for.

Fig. 7

Heat transfer coefficient vs diameter, comparison with Agostini (2002).

4 Conclusions

• At this time, the influence of microchannel diameter on the two-phase heat transfer coefficient is poorly documented and the trends are contradictory. The majority of studies available correspond to the upper limit of the transition from the macro to microscale in respect to the transition criteria of Kew and Cornwell (1997).

• A recent model based on the periodic evaporation of the liquid film surrounding the elongated bubble is presented and compared to some new data now available. This three-zone model predicts 67% of the points to ±30% and the experimental trends are reasonably described.

• In this model the film evaporation surrounding the vapor bubbles dominates the heat transfer. Also, the influence of the diameter of the channel on the initial film thickness explains the increases of h with a decreases of d for low values of the vapor quality and a decrease of h for large values of x.