Introduction

The fast-sliding high-speed landslides are often destructive, widely spread, and difficult to prevent, easily causing serious loss of life and property in disaster areas, so they are often described as catastrophic landslides. The dynamic mechanism and motion process simulation of high-speed landslides have become the focus of engineering geologists (Hendron Jr and Patton 2015; Hungr 2007; McDougall and Hungr 2004; Sassa et al. 2010). The dynamic mechanism of high-speed landslides has long been a challenge for scholars concerned due to their high moving speed and long sliding distance, which is difficult to explain by conventional dynamic methods. Many scholars have investigated the dynamic mechanism of high-speed landslides from the perspective of friction-induced thermal pressurization in the shear band. There are two main hypotheses (Vardoulakis 2000): (i) the heat generated by friction in the sliding process vaporizes the pore water in the shear band to form a vapor cushion which is the key to the high speed movement of the landslide and (ii) even if vaporization does not happen, the pore water pressure in the shear band will increase due to thermal expansion of pore water under the condition of high temperature caused by friction, thereby reducing the frictional resistance of the sliding surface and resulting in a higher velocity and a longer distance of the slide mass.

In 1963, the world-famous Vaiont landslide occurred in northern Italy. That catastrophic landslide has a maximum sliding velocity of 25~30 m/s (Hendron Jr and Patton 2015). Habib (1975) proposed the concept of “vaporization” for the first time to reveal the dynamic mechanism of the high-speed Vaiont landslide. Habib believed that during landslide movement, the mechanical energy in the shear band was dissipated in the form of heat, and the high temperature generated might cause the pore water to vaporize, resulting in frictionless sliding. Voight and Faust (1982) argued that even without vaporization, the heat in the shear band was sufficient to generate high pore water pressure, causing the landslide to turn to catastrophic acceleration. Based on the hypothesis proposed by Voight and Faust, Vardoulakis (2002) established a one-dimensional dynamic model of friction-induced thermal pressurization regardless of vaporization, assuming a regular shape of slide mass, which was applied to the Vaiont landslide. Veveakis et al. (2007) studied the process from creep to accelerated sliding and believed that this transition was due to the localization of shear-induced heat in the shear band, causing the temperature to rise to the critical pressurization temperature. Goren and Aharonov (2009) investigated the dynamic mechanism of catastrophic landslides and creep landslides respectively based on Vardoulakis’ model and emphasized the importance of permeability. Many other studies (Cecinato 2009; Gerolymos et al. 2007; Goren and Aharonov 2007; Goren et al. 2010; Pinyol and Alonso 2010a, b; Pinyol et al. 2012) have also focused on the mechanism of thermal pressurization in the shear band of high-speed landslides based on Vardoulakis’ model. Cecinato and Zervos (2012) and Cecinato et al. (2011) introduced a thermo-mechanical model, considering the thermoplasticity and heat-induced friction softening of soil in the shear band, which further improved the thermal pressurization theory for the activation of high-speed landslides. Due to the large difference in thickness between the shear band and the overlying slide mass, the abovementioned thermal pressurization theory is limited to the generalized analysis of the one-dimensional model. Based on Vardoulakis’ model, Zhao et al. (2018) divided the irregular slide mass and shear band into a series of discrete blocks by the slice method and established a quasi two-dimensional model with thermo-hydro-mechanical coupling, which fully considers the spatial morphological characteristics of the slide mass and its influence on the thermal pressurization in the shear band.

In recent years, there has been a lot of evidence proving that heat-induced vaporizing pressurization in the shear band is an important cause of high-speed landslides. Wang et al. (2017) performed a series of ring shear tests on the sliding zone soil of Yigong high-speed landslide in Tibet, revealing the heat-induced vaporization phenomenon on the shear surface in its sliding process; they believed that it was one of the important reasons leading to the high-speed sliding of Yigong landslide. Hu et al. (2019) conducted a thermogravimetry test on dolomite samples at the sliding surface of Daguangbao landslide triggered by Wenchuan earthquake, and the results showed that the temperature generated on the sliding surface was as high as 850 °C. According to their study, the high temperature generated by friction on the sliding surface causes the dolomite to produce CO2 and the groundwater to vaporize and produce vapor, leading to a sharp increase in the pore pressure on the sliding surface, which is an important mechanism underlying the high-speed sliding of Daguangbao landslide.

Although the thermal pressurization caused by heat-induced vaporization has been gradually recognized by many scholars as an important cause of high-speed landslides, currently, this mechanism is still in the experimental research stage, and there are few relevant mathematical models available to quantify it. As mentioned above, the existing thermal pressurization model only considers the change of excess pore water pressure caused by thermal expansion, without taking into account the vaporizing pressurization induced by high temperature.

In this paper, considering the high-temperature induced vaporization of pore water in the shear band, a quasi two-dimensional dynamic model for the startup phase of high-speed landslides with thermo-hydro-vapor-mechanical (THVM) coupling is established, based on the thermal-hydro-mechanical coupling model of Vardoulakis (2002) and Zhao et al. (2018), and this model is applied to the Vaiont landslide for case study. The THVM model established in this paper can reflect the physical mechanism of thermal pressurization inside the shear band of high-speed landslides during their startup process to a certain extent, and it could also explain why some landslides quickly turn to catastrophic high-speed sliding after they start.

Simplification and assumption of the landslide model

The shear band and slide mass

The landslide model is simplified into a binary structure consisting of the overlying slide mass and the shear band at the bottom, as shown in Fig. 1. It is assumed that the shear deformation of the landslide during its movement occurs intensively in the shear band at the bottom. The shear band is usually composed of dense saturated clay (Cecinato 2009; Wen et al. 2004), the thickness of which is much smaller than the slide mass, usually only a few millimeters (Vardoulakis 2002).

Fig. 1
figure 1

Simplified landslide structure consisting of the overlying slide mass and the shear band at the bottom

Full size image

The time window considered in this paper is the initial acceleration process from the start of the slide mass to the pre-disintegration stage, which usually lasts only a few seconds. Therefore, the slide mass is assumed to be a continuum here, and only elastic deformation occurs during its movement. For the shear band, we assume that it is a three-phase porous material composed of water, gas, and clay particles. At the initial moment, it is assumed that the pores are filled with water and there is no gas. Clay in the shear band is a heat conducting material with weak water permeability. The overlying slide mass moves along the contact surface between the slide mass and the shear band. In this process, shear deformation occurs in the shear band. It is assumed that the lower boundary of the shear band is fixed, while the deformation rate of the upper boundary is consistent with the moving velocity of the overlying slide mass.

The action within the shear band is the focus of our research because it directly affects the motion of the overlying slide mass. Vardoulakis believes that the shear band undergoes a thermo-hydro-mechanical coupling process. However, this paper considers the vaporization of pore water in the shear band caused by high temperature. Therefore, it may be summarized as the thermo-hydro-vapor-mechanical (THVM) coupling process. The movement of the overlying slide mass promotes shear deformation in the shear band, and the mechanical work produced by the shear stress is converted into heat, which leads to the increase of temperature in the shear band. On the one hand, due to the thermal expansion of the pore water, the excess pore water pressure is generated. On the other hand, when the temperature reaches the boiling point, the pore water begins to vaporize and is partially converted into vapor, thereby generating pore gas pressure. The increase of pore pressure will reduce the frictional resistance, thereby promoting the acceleration of the slide mass.

Due to the great difference in thickness between the slide mass and the shear band, one-dimensional analysis is more suitable for the study of the THVM coupling process in the shear band, which assumes that the variables change only along the direction of shear band thickness. Vardoulakis (2000) simplified the slide mass into a regular shape, sliding along a plane with a fixed inclination. In this paper, we have considered the non-uniformity of geometry of the slide mass, that is, the thickness of the sliding mass and the inclination of the sliding surface are no longer constant, but change along the sliding direction. For this purpose, we use the slice method, just like what Zhao et al. (2018) have applied, to divide the slide mass and the shear band respectively into N small slide blocks and small shear bands, as shown in Fig. 1. Nonetheless, due to the limitation of the scale, one-dimensional analysis along the thickness is still used within each individual shear band.

Figure 2 depicts the interaction between adjacent slide blocks, as well as the relationship between the slide block and the corresponding shear band. The adjacent blocks interact with each other through the interslice force P, affecting their respective acceleration, velocity, and deformation. The following focuses on the relationship between the block i and the corresponding shear band i. The block i applies an initial effective normal stress \( {\left({\sigma}_n^{\prime}\right)}_{i,0} \) on the shear band at the bottom and moves along the upper boundary of the shear band at the velocity v. According to Coulomb’s law of friction, the upper boundary of the shear band is subjected to the shear stress τ. Under the action of the shear stress τ, shear strain occurs correspondingly inside the shear band, and the shear rate is assumed to be linearly distributed along the thickness. The mechanical work done by the shearing force is converted into heat, causing temperature in the shear band to rise to Ti. The saturated pore water in the shear band is thermally expanded, thereby generating excess pore water pressure. If the temperature reaches the boiling point, the pore water will gradually vaporize and a pore gas pressure will be generated in the shear band. These two pore pressures are collectively referred to as the excess pore pressure pi, which will reduce the effective normal stress between the block i and the shear band i to (\( {\left({\sigma}_n^{\prime}\right)}_{i,0} \) − pi). Although there is no direct interaction between adjacent shear bands, the above relationships will lead to indirect influence between them.

Fig. 2
figure 2

Interactions between slide blocks and shear bands

Full size image

The motion of slide mass

The shear deformation of the bottom shear band results in the movement of the overlying block; what is more, the movement of the block further promotes the shear deformation in the shear band. In order to study the complex physical processes inside the shear band during the acceleration phase of the high-speed landslide, we need to determine the motion of the overlying slide mass.

Here we simplify the sliding mass into a deformable elastomer. Therefore, in addition to the motion, each individual slide block will be elastically deformed. It is assumed that each block is deformed only in the horizontal direction, and the deformation rate is consistent in the vertical direction within each block. Based on the above assumptions, we can derive the momentum equation for each block based on the studies of Miao et al. (2001) and Zhao et al. (2018):

$$ {W}_i\sin {\alpha}_i+{P}_i\cos \left({\alpha}_{i-1}-{\alpha}_i\right)-{P}_{i+1}-\left({W}_i\cos {\alpha}_i+{P}_i\sin \left({\alpha}_{i-1}-{\alpha}_i\right)-{p}_{mi}\frac{b_i}{\cos {\alpha}_i}\right){\mu}_i={m}_i{{\dot{v}}^m}_i $$
(1)

In Eq. (1), the initial acceleration \( {{\dot{v}}^m}_i \) can be obtained as long as the initial state is determined, such as the initial interslice force Pi and the initial slip angle αi of each block. Assume that each block is uniformly accelerated during each iteration time step which is small enough. Then, the velocity and deformation of each block at the next moment can be acquired. According to Miao et al. (2001), the relationship between the elastic deformation si of each block and the horizontal interslice force Hi is expressed as

$$ {H}_{i,t+\varDelta t}={H}_{i,t}+{k}_i{s}_{i,t+\varDelta t} $$
(2)

and

$$ {P}_i=\frac{H_i}{\cos {\alpha}_{i-1}} $$
(3)

where ki is the elastic modulus of each block. Thus, the acceleration at the next moment can be acquired by Eq. (1). Following this cycle, the motion variables of each block at each moment, such as velocity, acceleration, interslice force, deformation, and displacement can be finally obtained.

Two-phase mixture model in the pore of shear band

The shear band is a clay-like porous material composed of soil skeleton and pores. The evolution of material state in pores can be divided into three stages. In the initial state, the pores are filled with water and in a saturated state, and the saturation of the pore water is s = 1. When the temperature in the shear band reaches the boiling point, the pore water begins to vaporize. At this time, water and vapor coexist in the pores, as shown in Fig. 3, and the pores are in an unsaturated state, where the water saturation is s < 1. It is assumed that the temperature in the system does not change during vaporization. When the heat in the shear band increases to a certain value, all water in the pores is converted into vapor, and the saturation of water is s = 0.

Fig. 3
figure 3

Three-phase structure of soil in the shear band

Full size image

The two-phase mixture model, which was described by Wang and Beckermann (1993), is used to describe the water-vapor coexistence state in the second stage. In the two-phase mixture model, water and vapor are treated as a whole, i.e., a water-vapor mixture. The density of the water-gas mixture is expressed as an average:

$$ {\rho}_{\mathrm{w}\mathrm{v}}=s{\rho}_{\mathrm{w}}+\left(1-s\right){\rho}_{\mathrm{v}} $$
(4)

In Eq. (4), s is the pore water saturation; ρw and ρv are the densities of pore water and vapor, respectively.

Just like density, the thermodynamic properties of the two-phase mixture are related not only to the properties of each component but also to the pore water saturation.

Heat-induced pore pressurization in the shear band

Heat generation

When the overlying block moves along the shear band, shear deformation occurs inside the shear band. The rate of shear strain work per unit volume in the shear band is given by

$$ \dot{W}=\tau \kern0.1em \dot{\gamma} $$
(5)

where τ is the shear stress acting on the shear band, and \( \dot{\gamma} \) is the rate of shear strain.

For simplification, the rate of shear strain is assumed to be linear along the thickness of the shear band (just like Vardoulakis (2002)‘s study), as shown in Fig. 2, and thus

$$ \dot{\gamma}=\frac{\partial v(z)}{\partial z}=\frac{v^m}{d} $$
(6)

where vm is the rate of shear strain on the upper boundary of the shear band or the velocity of the overlying block; d is the thickness of the shear band.

Substituting Eq. (6) into Eq. (5) gives

$$ \dot{W}=\tau \kern0.1em \frac{v^m}{d} $$
(7)

Assuming that all mechanical work is converted into heat, the heat generation rate per unit volume \( \dot{H} \) is

$$ \dot{H}=\dot{W}=\tau \kern0.1em \frac{v^m}{d} $$
(8)

In Eq. (8), the shear stress in the shear band is determined by Coulomb’s law of friction:

$$ \tau =\mu \left({\sigma}_{n,0}^{\prime }-p\right) $$
(9)

where μ is the friction coefficient of material in the shear band; \( {\sigma}_{n,0}^{\prime } \) is the initial effective normal stress in the shear band, which is derived from the overlying block; and p is the excess pore pressure generated in the shear band.

Heat balance equation

The heat balance within the shear band is related to three phases: solid phase, liquid phase, and gas phase. Heat is generated by mechanical work and is dissipated by conduction and convection to achieve heat balance. Wang and Beckermann (1993) had developed a general numerical formalism for efficient simulation of two-phase flow and heat transfer processes in porous media. In their research, a two-phase zone and single-phase regions coexisted, with irregular and moving phase interfaces in between.

In this paper, we have simplified the problem. Before the temperature reaches the boiling point, only the water phase exists in the pores; after reaching the boiling point, the water phase and the vapor phase coexist, called the two-phase mixture, whose thermodynamic properties are related to the properties of each phase and the water saturation of pores. Suppose the two phases are uniformly mixed, with no boundaries between them. In the two-phase mixed state, the heat could continue to increase, but the temperature remains unchanged until water is completely converted to vapor when the saturation s = 0. In addition, since the permeability of the dense cohesive soil in the shear band is extremely small, the heat convection is neglected, which may cause a high computational cost. Therefore, the heat balance equation in Wang’s (1997) study is simplified to the following:

$$ \varOmega \frac{\partial H}{\partial t}=\nabla \left(\varGamma \cdot \nabla H\right)+\dot{H} $$
(10)
$$ \varOmega \frac{\partial H}{\partial t}=\nabla \left(\varGamma \cdot \nabla H\right)+\mu \left({\sigma}_{n,0}^{\prime }-p\right)\frac{v^m}{d} $$
(11)

On the right-hand side of Eq. (11), the first term is heat diffusion and the second term is heat generation. The effective heat capacitance ratio Ω and effective diffusion coefficient Г in Eq. (11) are expressed as

$$ \varOmega =n+{\rho}_s{c}_s\left(1-n\right)\frac{dT}{dH} $$
(12)
$$ \varGamma ={k}_{\mathrm{eff}}\frac{dT}{dH} $$
(13)

In Eqs. (12) and (13), n is the porosity of clay in the shear band; ρs is the density of the soil skeleton; and cs is the specific heat capacity. Other variables are expressed as follows:

$$ {k}_{\mathrm{eff}}={k}_{\mathrm{s}}\left(1-n\right)+{k}_{\mathrm{w}} ns+{k}_{\mathrm{v}}n\left(1-s\right) $$
(14)

where keff is the effective heat transfer coefficient; ks, kw, and kv are the heat conduction coefficients of the solid, liquid, and gas phases, respectively; and s is the pore saturation.

$$ \frac{dT}{dH}=\left\{\begin{array}{l}\frac{1}{\rho_{\mathrm{w}}{c}_{\mathrm{w}}},\kern1em H\le -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)\kern0.3em \\ {}0\kern1.9em ,\kern1.1em -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)<H\le -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}\kern0.1em \\ {}\frac{1}{\rho_{\mathrm{v}}{c}_{\mathrm{v}}},\kern1.2em -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}<H\end{array}\right. $$
(15)

where dT/dH denotes the derivative of the temperature with respect to the volumetric heat; ρw and ρv are the densities of water and vapor, respectively; cw and cv are the specific heat capacities of water and vapor, respectively; and hwsat and hvsat are the specific enthalpies of water and vapor, respectively.

The temperature T at different states can be calculated after obtaining the heat H, and the expression is written as

$$ T=\left\{\begin{array}{l}\frac{H+2{\rho}_{\mathrm{w}}{h}_{\mathrm{v}\mathrm{sat}}}{\rho_{\mathrm{w}}{c}_{\mathrm{w}}}\kern1.9em ,\kern0.9000001em H\le -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)\kern0.3em \\ {}{T}_{\mathrm{sat}}\kern6.299996em ,\kern1em -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)<H\le -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}\\ {}{T}_{\mathrm{sat}}+\frac{H+{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}}{\rho_{\mathrm{v}}{c}_{\mathrm{v}}},\kern0.9000001em -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}<H\end{array}\right. $$
(16)

where Tsat is the saturation temperature in thermodynamics or the boiling point of water. It can be expressed as

$$ {T}_{\mathrm{sat}}=\frac{h_{\mathrm{w}\mathrm{sat}}}{c_{\mathrm{w}}} $$
(17)

The pore saturation s under different thermodynamic conditions is given by

$$ s=\left\{\begin{array}{l}1\kern10.2em ,\kern1em H\le -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)\kern0.3em \\ {}-\frac{H+{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}}{\rho_{\mathrm{w}}{h}_{\mathrm{fg}}+\left({\rho}_{\mathrm{w}}-{\rho}_{\mathrm{v}}\right){h}_{\mathrm{v}\mathrm{sat}}},\kern1.1em -{\rho}_{\mathrm{w}}\left(2{h}_{\mathrm{v}\mathrm{sat}}-{h}_{\mathrm{w}\mathrm{sat}}\right)<H\le -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}\\ {}0\kern10em ,\kern1.2em -{\rho}_{\mathrm{v}}{h}_{\mathrm{v}\mathrm{sat}}<H\end{array}\right. $$
(18)

where hfg is the latent heat of phase change, and it can be expressed as follows:

$$ {h}_{\mathrm{fg}}={h}_{\mathrm{vsat}}-{h}_{\mathrm{wsat}} $$
(19)

The specific enthalpies of water hwsat, specific enthalpies of vapor hvsat, and latent heat of evaporation hfg vary with pressure, as shown in Fig. 4.

Fig. 4
figure 4

The specific enthalpies of water hwsat, specific enthalpies of vapor hvsat, latent heat of evaporation hfg vary with pressure

Full size image

Mass balance equations

The flow of fluid within the shear band causes a change in the density of the system, thereby establishing the mass conservation equations for soil skeleton and pores, which are described by partial differential equations (Coussy 2004).

$$ \frac{D}{Dt}\left({\rho}_{\mathrm{s}}\left(1-n\right)d{\varOmega}_{\mathrm{t}}\right)=0 $$
(20)
$$ \frac{D}{Dt}\left({\rho}_{\mathrm{w}}\kern0.1em n\kern0.2em d{\varOmega}_{\mathrm{t}}\right)=0 $$
(21)

where D/Dt denotes the material derivative with respect to the time (t), D/Dt = ∂/∂t + (v∙▽); n is the porosity; ρw is the density of water; ρs is the density of solid; dΩt is the material volume.

Due to the low permeability of the medium, Darcy’s law is often used to describe the flow of fluid. Pinyol and Alonso (2010a, b) combine Eqs. (20) and (21) to obtain the following equation:

$$ \frac{n}{\rho_{\mathrm{w}}}\frac{D{\rho}_{\mathrm{w}}}{Dt}+\frac{\left(1-n\right)}{\rho_{\mathrm{s}}}\frac{D{\rho}_{\mathrm{s}}}{Dt}+{m}_{\mathrm{v}}\frac{\partial p}{\partial t}-\frac{\kappa }{\mu_{\mathrm{w}}}\frac{\partial^2p}{\partial {z}^2}=0 $$
(22)

where p is the excess pore pressure; mv is the compression coefficient of solid; κ is the permeability of porous media; μw is the dynamic viscosity of water; and z represents the direction along the thickness of the shear band.

When only the liquid phase is present in the pores, Pinyol and Alonso (2010a, b) assumes that the change in volume or density of the pore water in the above-described mass conservation equation is due to the compression caused by change in the pore pressure p and the thermal expansion caused by change in temperature T. The pore water has a compression coefficient of αw and a thermal expansion coefficient of βw, and thus,

$$ {\varepsilon}_{\mathrm{w}}=\frac{dV}{V_{\mathrm{w}}}=-\frac{d{\rho}_{\mathrm{w}}}{\rho_{\mathrm{w}}}=-{\alpha}_{\mathrm{w}} dp+{\beta}_{\mathrm{w}} dT $$
(23)
$$ {\rho}_{\mathrm{w}}={\rho}_{\mathrm{w}}^0\exp \left({\alpha}_{\mathrm{w}}\left(p-{p}^0\right)-{\beta}_{\mathrm{w}}\left(T-{T}^0\right)\right) $$
(24)

where \( {\rho}_w^0 \) is the initial density of water, and p0 and T0 are the initial pressure and the temperature, respectively.

This problem is further complicated when vaporization occurs once the temperature of pore water exceeds the boiling point. After the temperature reaches the boiling point, in addition to compression and thermal expansion, volume change of the mixture is also related to vaporization of the pore water. In addition, the fluid density and the dynamic viscosity in Eq. (22) no longer belong to water, but to the water-vapor mixture.

Define the compressibility of the water-vapor mixture as

$$ {\alpha}_{\mathrm{w}\mathrm{v}}={\alpha}_{\mathrm{w}}s+{\alpha}_{\mathrm{v}}\left(1-s\right) $$
(25)

where s is the saturation of pore water; αw is the compression coefficient of water, which is assumed as a fixed value; and αv is the compression coefficient of vapor, which is considered to vary with the pore pressure at a constant temperature. The volumetric compressibility of water vapor can be approximated by the following equation:

$$ {\alpha}_{\mathrm{v}}=\frac{v_1^{{\prime\prime} }-{v}_2^{{\prime\prime} }}{v_1^{{\prime\prime}}\cdotp \left({P}_2-{P}_1\right)} $$
(26)

where P1 and P2 are different pressure states, and \( {v}_1^{{\prime\prime} } \) and \( {v}_2^{{\prime\prime} } \) are the corresponding specific volumes of saturated vapor. According to Eq. (26), the volumetric compressibility of vapor changes with the pressure, as shown in Fig. 5.

Fig. 5
figure 5

The volumetric compressibility of vapor changes with the pressure

Full size image

Define the thermal expansion coefficient βwv of water-vapor mixture as

$$ {\beta}_{\mathrm{w}\mathrm{v}}={\beta}_{\mathrm{w}}s+{\beta}_{\mathrm{v}}\left(1-s\right) $$
(27)

where βw and βv are the thermal expansion coefficients of water and vapor, respectively.

The vaporizing expansion coefficient hw-v can be defined as the relative change in volume after absorbing 1 J of heat for a unit volume of water in a thermodynamically saturated state. It can be expressed as

$$ {h}_{\mathrm{w}-\mathrm{v}}=\frac{\left({v}^{{\prime\prime} }-{v}^{\prime}\right)}{h_{-f\mathrm{g}}} $$
(28)

where v″ is the specific volume of vapor; v′ is the specific volume of water at the same pressure; and h_fg is the latent heat of phase change.

The specific volume of water and vapor varies with the pressure, as shown in Fig. 6.

Fig. 6
figure 6

The specific volume of water and vapor varies with the pressure

Full size image

Therefore, when vaporization occurs, the excess pore pressure p in Eq. (22) is no longer merely caused by not only the thermal expansion of water but also the vapor pressure generated by vaporization.

The volumetric deformation of water-vapor mixture εwv is expressed as

$$ {\varepsilon}_{\mathrm{w}\mathrm{v}}=\frac{dV}{V_{\mathrm{w}\mathrm{v}}}=-\frac{d{\rho}_{\mathrm{w}\mathrm{v}}}{\rho_{\mathrm{w}\mathrm{v}}}=-{\alpha}_{\mathrm{w}\mathrm{v}} dp+{\beta}_{\mathrm{w}\mathrm{v}} dT+{h}_{\mathrm{w}-\mathrm{v}} dH $$
(29)

and the density of water-vapor mixture ρwv is given by

$$ {\rho}_{\mathrm{w}\mathrm{v}}={\rho}_{\mathrm{w}\mathrm{v}}^0\exp \left({\alpha}_{\mathrm{w}\mathrm{v}}\left(p-{p}^0\right)-{\beta}_{\mathrm{w}\mathrm{v}}\left(T-{T}^0\right)-{h}_{\mathrm{w}-\mathrm{v}}\left(H-{H}^0\right)\right) $$
(30)

Derivation of Eq. (30) leads to

$$ \frac{D{\rho}_{\mathrm{w}\mathrm{v}}}{Dt}={\alpha}_{\mathrm{w}\mathrm{v}}{\rho}_{\mathrm{w}\mathrm{v}}\frac{Dp}{Dt}-{\beta}_{\mathrm{w}}{\rho}_{\mathrm{w}\mathrm{v}}\frac{DT}{Dt}-{h}_{\mathrm{w}-\mathrm{v}}{\rho}_{\mathrm{w}\mathrm{v}}\frac{DH}{Dt} $$
(31)

Solid particles are assumed to be incompressible against stress changes, but not against temperature changes. The density of solid particles can be similarly expressed as

$$ {\rho}_{\mathrm{s}}={\rho}_{\mathrm{s}}^0\exp \left(-{\beta}_{\mathrm{s}}\left(T-{T}^0\right)\right) $$
(32)

where \( {\rho}_{\mathrm{s}}^0 \) and βs are the initial density and the thermal expansion coefficient of solid particles, respectively.

Derivation of Eq. (32) leads to

$$ \frac{D{\rho}_{\mathrm{s}}}{Dt}=-{\beta}_{\mathrm{s}}{\rho}_{\mathrm{s}}\frac{DT}{Dt} $$
(33)

Substituting Eq. (31) and (33) into Eq. (22), the mass conservation equation for water-vapor mixture and solid particles can be obtained:

$$ -\left(n{\beta}_{\mathrm{w}\mathrm{v}}+\left(1-n\right){\beta}_{\mathrm{s}}\right)\frac{DT}{Dt}+n{\alpha}_{\mathrm{w}\mathrm{v}}\frac{Dp}{Dt}-n{h}_{\mathrm{w}-\mathrm{v}}\frac{DH}{Dt}+{m}_{\mathrm{v}}\frac{\partial p}{\partial t}-\frac{\kappa }{\mu_{\mathrm{w}\mathrm{v}}}\frac{\partial^2p}{\partial {z}^2}=0 $$
(34)

At this point, the assumption of small strain rate along the thickness of the shear band is introduced. Thus, material derivatives are approximated replaced by Eulerian derivatives, D/Dt ≈ ∂/∂t, and Eq. (34) becomes

$$ -\left(n{\beta}_{\mathrm{w}\mathrm{v}}+\left(1-n\right){\beta}_{\mathrm{s}}\right)\frac{\partial T}{\partial t}+\left(n{\alpha}_{\mathrm{w}\mathrm{v}}+{m}_{\mathrm{v}}\right)\frac{\partial p}{\partial t}-n{h}_{\mathrm{w}-\mathrm{v}}\frac{\partial H}{\partial t}-\frac{\kappa }{\mu_{\mathrm{w}\mathrm{v}}}\frac{\partial^2p}{\partial {z}^2}=0 $$
(35)

To be more intuitive, Eq. (35) is organized as follows:

$$ \left(n{\alpha}_{\mathrm{w}\mathrm{v}}+{m}_{\mathrm{v}}\right)\frac{\partial p}{\partial t}=\frac{\kappa }{\mu_{\mathrm{w}\mathrm{v}}}\frac{\partial^2p}{\partial {z}^2}+\left(n{\beta}_{\mathrm{w}\mathrm{v}}+\left(1-n\right){\beta}_{\mathrm{s}}\right)\frac{\partial T}{\partial t}+n{h}_{\mathrm{w}-\mathrm{v}}\frac{\partial H}{\partial t} $$
(36)

In Eq. (36), the first term on the right-hand side represents the dissipation of excess pore pressure; the second term describes the change of excess pore pressure caused by thermal expansion; and the third term describes the change of excess pore pressure caused by vaporization.

The dynamic viscosity μwv of water-vapor mixture in Eq. (36) affects the dissipation of excess pore pressure, and its value is related to various factors, including density, kinematic viscosity, and relative permeability of water and vapor, as well as the saturation of water in pores. According to Chavent (1976) and Wang and Beckermann (1993), the dynamic viscosity of water-vapor mixture is expressed as follows:

$$ {\mu}_{\mathrm{w}\mathrm{v}}=\frac{\rho_{\mathrm{w}}s+{\rho}_{\mathrm{v}}\left(1-s\right)}{\left({\kappa}_{\mathrm{rw}}/{\nu}_{\mathrm{w}}\right)+\left({\kappa}_{\mathrm{rv}}/{\nu}_{\mathrm{v}}\right)} $$
(37)

where κrw and κrv are the relative permeabilities of water and vapor, respectively, and νw and νv are their kinematic viscosities.

The relative permeability of each phase in the porous medium is generally simplified to an exponential function of the liquid phase saturation s. In order to simplify the model and reduce the computational cost, we adopted Wang et al.’s (1994) suggestion to simplify the relative permeability of each phase to a linear function of liquid saturation:

$$ {\kappa}_{\mathrm{rw}}\approx s,\kern1.1em {\kappa}_{\mathrm{rv}}\approx 1-s $$
(38)

and thus

$$ {\mu}_{\mathrm{w}\mathrm{v}}\approx \frac{\rho_{\mathrm{w}}s+{\rho}_{\mathrm{v}}\left(1-s\right)}{\left(s/{\nu}_{\mathrm{w}}\right)+\left(\left(1-s\right)/{\nu}_{\mathrm{v}}\right)} $$
(39)

As described earlier, there may be three states of pore water in the shear band, namely, water, water-vapor mixture, and vapor, which correspond to different thermodynamic stages. In the first stage, the pore water has not started to vaporize before the temperature reaches the boiling point; the vaporizing expansion coefficient is hw-v = 0. In the second stage, after the temperature reaches the boiling point, and before the pore water completely vaporizes, the heat of the system increases, but the temperature remains unchanged. In this stage, ∂T/∂t = 0. In the third stage, the supersaturated state in thermodynamics is reached, and the pore water is completely evaporated into vapor. In this stage, there is no vaporization, so the vaporizing expansion coefficient is hw-v = 0. Therefore, in different thermodynamic stages, the pore pressure Eq. (36) can be simplified to different forms.

In the first and third stages, the pore pressure equation is simplified to

$$ \left(n{\alpha}_{\mathrm{wv}}+{m}_{\mathrm{v}}\right)\frac{\partial p}{\partial t}=\frac{\kappa }{\mu_{\mathrm{wv}}}\frac{\partial^2p}{\partial {z}^2}+\left(n{\beta}_{\mathrm{wv}}+\left(1-n\right){\beta}_{\mathrm{s}}\right)\frac{\partial T}{\partial t} $$
(40)

and in the second stage, it is simplified to the following:

$$ \left(n{\alpha}_{\mathrm{w}\mathrm{v}}+{m}_{\mathrm{v}}\right)\frac{\partial p}{\partial t}=\frac{\kappa }{\mu_{\mathrm{w}\mathrm{v}}}\frac{\partial^2p}{\partial {z}^2}+n{h}_{\mathrm{w}-\mathrm{v}}\frac{\partial H}{\partial t} $$
(41)

Numerical implementation

In each shear band, the heat Eq. (11) and the pore pressure Eqs. (40) and (41) at different stages can be numerically solved by the finite difference method. The coefficients of these equations are replaced by algebra, and the simplified heat equation is given by Eq. (42), and the pore pressure equation is given by Eqs. (43) and (44):

$$ \hat{a}\frac{\partial H}{\partial t}=\hat{b}\frac{\partial^2H}{\partial {z}^2}+\hat{c}p+\hat{d} $$
(42)
$$ \hat{e}\frac{\partial p}{\partial t}=\hat{f}\frac{\partial^2p}{\partial {z}^2}+\hat{g}\frac{\partial T}{\partial t} $$
(43)
$$ \hat{e}\frac{\partial p}{\partial t}=\hat{f}\frac{\partial^2p}{\partial {z}^2}+\hat{h}\frac{\partial H}{\partial t} $$
(44)

The coefficients in the above equations are expressed as follows:

$$ \hat{a}=n+{\rho}_{\mathrm{s}}{c}_{\mathrm{s}}\left(1-n\right)\frac{dT}{dH}; $$
$$ \hat{b}=\left({k}_{\mathrm{s}}\left(1-n\right)+{k}_{\mathrm{w}} ns+{k}_{\mathrm{v}}n\left(1-s\right)\right)\frac{dT}{dH}; $$
$$ \hat{c}=-\frac{\tan \varphi \cdotp {v}^m}{d}; $$
$$ \hat{d}={\sigma}_{n,0}^{\prime}\frac{v^m}{d}\tan \varphi; $$
$$ \hat{e}=n\left({\alpha}_{\mathrm{w}}s+{\alpha}_{\mathrm{v}}\left(1-s\right)\right)+{m}_{\mathrm{v}}; $$
$$ \hat{f}\approx \frac{\kappa }{\frac{\rho_{\mathrm{w}}s+{\rho}_v\left(1-s\right)}{\left(s/{\nu}_{\mathrm{w}}\right)+\left(\left(1-s\right)/{\nu}_{\mathrm{v}}\right)}}; $$
$$ \hat{g}=n\left({\beta}_{\mathrm{w}}s+{\beta}_{\mathrm{v}}\left(1-s\right)\right)+\left(1-n\right){\beta}_{\mathrm{s}}; $$
$$ \hat{h}=n\frac{\left({v}^{{\prime\prime} }-{v}^{\prime}\right)}{h_{-\mathrm{fg}}}. $$

The implicit method of backward-time centered-space (BTCS) is adopted to solve these partial differential equations. In the shear band i, which is located at the bottom of the slide block i, the heat equation is discretized into the following format using the BTCS difference method:

$$ \hat{a}\frac{H_j^k-{H}_j^{k-1}}{\varDelta t}=\hat{b}\frac{H_{j+1}^k-2{H}_j^k+{H}_{j-1}^k}{\varDelta {z}^2}+\hat{c}{p}_j^k+\hat{d} $$
(45)

where the subscripts denote the spatial position of each shear band in the z-axis direction; the superscripts denote the time; Δt and Δz denote the size of the time step and the space step, respectively. The current time and space are represented by k and j, respectively.

The pore pressure equations at different stages are discretized into the following formats:

$$ \hat{e}\frac{p_j^k-{p}_j^{k-1}}{\varDelta t}=\hat{f}\frac{p_{j+1}^k-2{p}_j^k+{p}_{j-1}^k}{\varDelta {z}^2}+\hat{g}\frac{T_j^k-{T}_j^{k-1}}{\varDelta t} $$
(46)
$$ \hat{e}\frac{p_j^k-{p}_j^{k-1}}{\varDelta t}=\hat{f}\frac{p_{j+1}^k-2{p}_j^k+{p}_{j-1}^k}{\varDelta {z}^2}+\hat{h}\frac{H_j^k-{H}_j^{k-1}}{\varDelta t} $$
(47)

Initial and boundary conditions are similar to those in Zhao et al.’s (2018) study. The initial temperature in the shear band is denoted by Tinitial, and the initial excess pore pressure and the initial velocity are both zero. Thus, the initial conditions can be expressed as

$$ T\left(z,0\right)={T}_{\mathrm{initial}};\kern1.2em p\left(z,0\right)=0;\kern1.2em v\left(z,0\right)=0 $$
(48)

The initial value of the heat H can be directly obtained by the temperature T (from Eq. (16)).

The dissipation boundary of heat and excess pore pressure is assumed to be located χd from the boundary of the shear band, where d denotes the thickness of the shear band. Thus, the boundary conditions are described as follows:

$$ {T}_i\left(\pm \chi d,t\right)={T}_{\mathrm{initial}};\kern1.2em {p}_i\left(\pm \chi d,t\right)=0 $$
(49)

The boundary condition of the heat H can be directly obtained by the temperature T (from Eq. (16)).

As described above, the velocity at the upper boundary of shear band is equal to velocity of the overlying block; the lower boundary of the shear band is fixed; within the shear band, the velocity is assumed to have a linear distribution. Therefore, the shear rate of the shear band can be expressed as

$$ \left\{\begin{array}{l}{v}_i=0\kern4.099998em z=0\\ {}{v}_i={v_i}^m(t)\frac{z}{d}\kern1.5em z\in \left(0,d\right)\\ {}{v}_i={v_i}^m(t)\kern2.4em z=d\end{array}\right. $$
(50)

where z denotes the coordinate axis parallel to the thickness direction of the shear band, and the starting point of this coordinate axis is at the lower boundary of the shear band; vim (t) is the velocity of the overlying block i.

Case study

Vaiont landslide

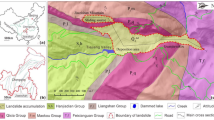
The Vaiont landslide has been frequently used as an example for analysis of the thermal pressurization mechanism of high-speed landslides, such as in the studies of Vardoulakis (2002), Veveakis et al. (2007), and Zhao et al. (2018). For comparison, this paper also uses the Vaiont landslide as an example. The calculation profile we have selected is shown in Fig. 7. As in Zhao et al.’s (2018) study, in order to take into account the real spatial morphological characteristics of the slide body, it is divided into 24 vertical blocks, and each block corresponds to a small shear band at the bottom. In each shear band, there are 11 nodes and 10 elements. Additional 30 elements in each of the area adjacent to the upper and lower boundaries of the shear band are considered for diffusion of pore pressure and heat. As stated above, during the startup of the landslide, interactions happen constantly between adjacent slide blocks, as well as between the slide block and the corresponding shear band, thus forming a quasi two-dimensional dynamic model with thermo-hydro-vapor-mechanical coupling. The time window of the model is still within 10 s from the startup of the landslide.

Fig. 7
figure 7

Critical failure circle of the Vaiont landslide (after Vardoulakis (2002))

Full size image

Input parameters

The parameters inputted in the model are shown in Table 1, most of which are derived from Vardoulakis (2002) and Zhao et al. (2018). Additional parameters include thermodynamic parameters of vapor. It is assumed that the specific heat capacity, heat transfer coefficient, thermal expansion coefficient, and compression coefficient of a single-phase medium are constant, and these properties of the water-vapor mixture are affected by the saturation s of pore water.

Table 1 Input parameters in the Vaiont landslide model
Full size table

Results

The numerical results show that, at 2.7 s after the startup of the Vaiont landslide model, the pore water in the shear band 16 first vaporizes to form a water-steam mixture; at 3.2 s, the excess pore pressure in the shear band 16 first exceeds the initial effective normal stress applied by the overlying block, reaching the maximum of 4.5 MPa. Friction-induced heat production no longer occurs in this shear band, and the highest temperature is 295 °C. In the following section, the numerical results are described and analyzed in detail.

Temperature and excess pore pressure in the shear band

Figures 8 and 9 show the evolution of the maximum temperature and pore pressure over time in a representative number of shear bands distributed along the slide (4, 7, 10, 13, 16, 19, 22). In Fig. 8, the solid line denotes the maximum temperature Tmax within the shear band; the dotted line denotes the critical temperature Tcr in the corresponding shear band, and when the critical temperature is exceeded, the excess pore water pressure is generated; the dotted line denotes the thermodynamic saturation temperature Tsat or the boiling point at which pore water vaporizes. The results show that the temperature in each shear band begins to increase gradually from the start of the overlying slide mass, and the temperature evolution in each shear band is asynchronous. During the period of the 1st to 3rd second, the temperature changes significantly. What is more, the temperature in the middle shear bands rises the fastest, such as the shear bands 10, 13, 16, and 19. After the temperature has risen to a certain value, it remains stable, and the highest temperature is within the shear band 16, which is 295 °C. The time taken to reach the highest temperature varies with different shear bands; for example, the temperature in the shear band 16 reaches the maximum at 3 s, and that in the shear band, 22 reaches the maximum at 4.3 s. In addition, after 1.2 s, the highest temperature in each shear band begins to exceed the corresponding critical temperature Tcr, and thereafter, the excess pore water pressure begins to be generated, which is be reflected from Fig. 9. Subsequently, the temperature in each shear band starts to reach the boiling point Tsat at about 2.7 s.

Fig. 8
figure 8

The maximum temperature Tmax, critical temperature Tcr and boiling point Tsat in each shear band change with time

Full size image
Fig. 9
figure 9

The maximum excess pore pressure in each shear band changes with time

Full size image

The evolution of pore pressure in Fig. 9 can be divided into four stages. In the first stage, before the temperature reaches the critical temperature Tcr, no excess pore pressure is generated in the shear band, and this stage corresponds to the period of 0 to 1.2 s. In the second stage, the temperature exceeds the critical temperature Tcr and is lower than the boiling point Tsat; the excess pore water pressure is generated, and the curve increases rapidly; this stage corresponds to 1.2 to 2.7 s. In the third stage, the temperature exceeds the boiling point Tsat; the pore water in the shear band vaporizes, and the curve increases rapidly, reaching the maximum value in a very short time; this stage occurs almost instantaneously. The fourth stage is the stable stage of excess pore pressure, in which the excess pore pressure no longer increases. This is because the frictional resistance between the overlying slide block and the shear band has disappeared, and the thermal pressurization no longer occurs, which will be further elaborated later.

Figure 10a and b show the spatial distribution of temperature and excess pore pressure at different moments in the shear band 16 and adjacent areas. The green area represents the shear band. In the vicinity of the shear band, a range that is 3 times the thickness of the shear band is taken as a dissipating region of heat and excess pore pressure. The results show that within the first 3 s, the temperature inside the shear band rises rapidly, and within 3 to 10 s, the temperature does not increase significantly, and the maximum temperature reaches 295 °C. For the pore pressure in the shear band, it grows rapidly in the first 3 s, especially in the period of 2.5th to 3rd second; after that, the pore pressure no longer increases significantly, and the maximum pore pressure is 4.5 MPa. It can be preliminarily judged from the figure that after about 2.5 s, the temperature in the shear band has reached the saturation temperature Tsat; after the 3rd second, the excess pore pressure has substantially offset the initial effective normal stress from the overlying block; no more heat is generated in the shear band, and the excess pore pressure no longer increases.

Fig. 10
figure 10

Temporal and spatial distribution of temperature and excess pore pressure in the shear band 16 and its adjacent areas. a Temperature. b Excess pore pressure. The green area represents the shear band

Full size image

Figure 11 shows the change of saturation at the center of the representative shear bands with time. The results show that within 2.7 s after the startup of the landslide, the saturation is s = 1 in all shear bands, that is, the pores are all filled with liquid water, and vaporization has not yet occurred; thereafter, the saturation within the shear band 16 first drops and begins to vaporize, and then, vaporization gradually occurs in adjacent shear bands. The closer the shear band is to the middle of the landslide, the lower its saturation is and the higher the degree of vaporization is. The variation characteristics of saturation are closely related to the friction-induced heat generation mechanism in the shear band. More friction work in the shear band leads to higher heat generated, more obvious vaporization effect, and smaller saturation s; when the excess pore pressure exceeds the initial effective normal stress from the overlying block, no heat is generated in the shear band, the vaporization process no longer occurs, and the saturation no longer decreases.

Fig. 11
figure 11

The saturation at the midpoint of each shear band changes with time

Full size image

Dynamic characteristics of slide blocks

Figures 12, 13, 14, and 15 show the evolution of the interslice force, acceleration, velocity and displacement of the blocks 4, 7, 10, 13, 16, 19, and 22, respectively. The results show that the variation law of interslice force, acceleration, velocity, and displacement is similar to that of Zhao et al.’s (2018) thermo-hydro-mechanical coupling model, such as the periodic fluctuation of interslice force and acceleration, the stepwise growth of velocity, and the exponential growth of displacement. However, these indicators are slightly different in value. As for the maximum velocity and the total displacement, at 10 s, the velocity of each block is in the range of 24~31 m/s; the displacement of each block along the sliding surface is about 110~140 m.

Fig. 12
figure 12

The interslice force of each block changes with time

Full size image
Fig. 13
figure 13

The acceleration of each block along the sliding surface changes with time

Full size image
Fig. 14
figure 14

The velocity of each block along the sliding surface changes with time

Full size image
Fig. 15
figure 15

Displacement of each block along the sliding surface changes with time

Full size image

Discussions

Vaporization process of pore water in the shear band and its influence on the slide mass

The saturation of pore water in the shear band is an intuitive variable that reflects the vaporization process. As is seen from the saturation evolution process in Fig. 11 above, the vaporization process of pore water is very short, almost instantaneous from the beginning of vaporization to the time when the saturation no longer changes. It shows that the pore pressure generated by vaporization of pore water is much larger than the pore pressure generated by thermal expansion, and the pore pressure in the shear band rises sharply in a very short time until it exceeds the initial effective normal stress of the overlying slide mass. The vaporizing expansion coefficient hw-v (Eq. (28)) is an important variable controlling the process, which determines the relationship between the absorption of heat and the volume of the water-vapor mixture, resulting in a change in the pore pressure. In Eq. (28), the volume ratios of water and vapor vary with the pressure. Therefore, the vaporization process is affected not only by the temperature or heat but also by the pressure state in the shear band.

In the previous analysis, the whole evolution process of the excess pore pressure is divided into four stages. Here, taking the shear band 16 as an example, the saturation, temperature, excess pore pressure at the center point of this shear band, and velocity of the overlying slide block in each stage are comparatively analyzed, as shown in Fig. 16. In the figure, the color filling areas represent pressurization stages, wherein the yellow area is the thermal expansion pressurization stage, and the green area is the vaporizing pressurization stage. In the thermal expansion pressurization stage, the pore water is in a saturated state, and the temperature exceeds the critical temperature Tcr; in this stage, the velocity of the slide block begins to increase significantly, and the duration of this stage is about 1.5 s. During the vaporizing pressurization stage, part of the pore water begins to evaporate, the saturation decreases, and the water-vapor mixture appears in the pores. During this stage, the temperature remains constant at the boiling point Tsat. Due to the liquid-to-gas conversion, the excess pore pressure increases sharply, and the velocity of the overlying block also increases significantly. The vaporizing pressurization process lasts only 0.5 s because the excess pore pressure reaches the maximum value instantaneously, and then the overlying block slides without resistance. Since the heat and the excess pore pressure in the shear band are difficult to dissipate in a very short time, the temperature and the excess pore pressure remain stable in the next few seconds, and the acceleration of the slide block changes more and more dramatically.

Fig. 16
figure 16

Pressurization process of the shear band 16 and its influence. The yellow area represents the thermal expansion pressurization stage and the green area represents the vaporizing pressurization phase

Full size image

What controls the vaporization process?

It has been described that there may be three different states of pore water in the shear band, and some variables have different expressions under different thermodynamic states, such as the temperature T in Eq. (16) and the saturation s in the Eq. (17). When H ≤ − ρw(2hvsat − hwsat), the pore water is in a liquid state; it turns into the water-vapor mixed state when − ρw(2hvsat − hwsat) < H ≤ − ρvhvsat. Therefore, starting from the initial state of the model, vaporization occurs once H > − ρw(2hvsat − hwsat) is satisfied. From this condition, it is known that the occurrence of vaporization is related not only to the heat H, but also to the specific enthalpy hvsat and hwsat, which vary with pressure as shown in Fig. 4. Therefore, vaporization process is essentially controlled by heat H and excess pore pressure p, and these two variables interact with each other, as described above. According to this analysis, the parameters affecting heat H and excess pore pressure p will undoubtedly affect the vaporization process. These parameters are mainly the thickness of sliding mass and shear band and the permeability, compressibility, thermal conductivity, and thermal expansion coefficient of the material in shear band, as shown in Fig. 17.

Fig. 17
figure 17

The main parameters and variables that control the vaporization process, where H is the heat of unit volume; p is the excess pore pressure; h and d are respectively the thickness of sliding mass and shear band; and κ, α, k, and β are respectively the permeability, compressibility, thermal conductivity, and thermal expansion coefficient of the material in shear band

Full size image

Comparison of thermo-hydro-mechanical model and thermo-hydro-vapor-mechanical model

To simplify the description, the thermo-hydro-mechanical model of Zhao et al. (2018) is referred to as model I, and the thermo-hydro-vapor-mechanical model is referred to as model II. Model II is evolved from model I, and these two models have many similarities. First, both models adopt the slice method to divide the sliding mass and the shear band. Secondly, the two models are controlled by three sets of equations describing the motion of sliding mass and the temperature and excess pore pressure in the shear band respectively. In addition, the material frictional softening mechanism described by Vardoulakis (2002) and Zhao et al. (2018) is also considered in both models.

Compared with model I, model II considers the vaporization process of pore water in the shear band under high temperature condition. In addition, in the vaporization stage, the heat equation of model II takes the heat per unit volume as the main variable; the heat equation of model I, which does not consider vaporization, takes the temperature as the main variable.

The numerical results of the two models applied to the Vaiont landslide are now analyzed by comparison. The temperature and excess pore pressure inside the shear band 16 and the velocity and acceleration of the block 16 are selected as the comparison indexes, as shown in Figs. 18 and 19, respectively. According to Fig. 18a, at 10 s, the temperature Tmax of model I reaches 201 °C, and that of model II is 295 °C, that is, the final temperature of model II is higher than that of model I. The temperature growth rate of model I changes more uniformly throughout the process, while that of model II increases sharply about 2 s after startup, and then remains stable during vaporization. From the perspective of excess pore pressure, as shown in Fig. 18b, at 10 s, the excess pore pressure pmax of model I is 4.1 MPa, and that of model II is 4.5 MPa, that is, the final excess pore pressure of model II is slightly higher than that of model I. The rate of increase in excess pore pressure of model II is significantly greater than that of model I. By comparing the temperature and the excess pore pressure of the two models, it is not difficult to find that model II reaches the maximum excess pore pressure earlier, which means frictionless sliding occurs earlier. This is mainly the result of high-temperature induced vaporizing pressurization of pore water in the shear band.

Fig. 18
figure 18

Comparison of the changes in temperature and excess pore pressure in the shear band 16 of the two models. a The evolution of temperature. b The evolution of excess pore pressure

Full size image
Fig. 19
figure 19

Comparison of the changes in velocity and acceleration of the block 16 of the two models

Full size image

As for the velocity and acceleration in Fig. 19, after vaporization occurs in the shear band of model II, the acceleration and velocity of the overlying block begin to be slightly higher than those of model I. In model I, the final velocity of the block 16 is about 23 m/s at 10 s, while in model II, it is about 24 m/s. It can be seen that the high-temperature induced vaporization of pore water in the shear band has a certain influence on the dynamic process of the overlying slide mass, but the effect is not significant for the Vaiont landslide.

Conclusions

The heat-induced pressurization mechanism in the shear band is an important reason for the transition of motion state of landslides from creeping to high-speed sliding during their initial startup phase. Friction inside the shear band generates heat, which causes the temperature to rise. Once it exceeds the boiling point of the pore water, vaporization will occur, which will affect the excess pore pressure in the shear band and the dynamic process of the overlying slide mass. Based on the thermal-hydro-mechanical coupling model of Vardoulakis (2002) and Zhao et al. (2018), and considering the high-temperature induced vaporization of pore water in the shear band, a dynamic model for the startup phase of high-speed landslides with thermo-hydro-vapor-mechanical coupling is established and applied to the Vaiont landslide for case study.

The model consists of three governing equations: the equation of motion derived from Newton’s second law of motion, which controls the motion of the overlying slide mass; the heat equation derived from the law of conservation of energy, which controls the heat or temperature change in the shear band at the bottom; and the pore pressure equation derived from the law of conservation of mass, which controls the change of excess pore pressure in the shear band. The main variables of these equations interact with each other. There are three states of pore water in the shear band at different stages: it is initially in a saturated liquid water state; once the temperature exceeds the boiling point, it is in a water-vapor coexisting state; and when the liquid water completely vaporizes, it is in a complete vapor state.

The analysis results of the model applied to the Vaiont landslide show that, at 10 s, the excess pore pressure in the shear band is up to 4.5 MPa; the maximum temperature is 295 °C; the velocity of each block is in the range of 24~31 m/s; and the maximum displacement along the sliding surface is about 140 m. The evolution of excess pore pressure can be divided into four stages: (i) there is no excess pore pressure before the temperature reaches the critical temperature Tcr; (ii) when the temperature exceeds Tcr and is lower than the boiling point Tsat, excess pore water pressure is generated; (iii) when the temperature reaches Tsat, vaporization occurs in the pores of the shear band, and the excess pore pressure increases sharply; (iv) when the initial effective normal stress from the overlying slide block is offset by the excess pore pressure, friction-induced heat is no longer generated in the shear band, and the temperature and excess pore pressure remain stable for a short time.

Compared with the thermo-hydro-mechanical model of Zhao et al. (2018), the thermo-hydro-vapor-mechanical model presented in this paper considers the vaporization process of pore water in the shear band. From the numerical results of the two models applied to the Vaiont landslide, it can be seen that as a result of vaporizing pressurization, frictionless sliding occurs earlier. High-temperature induced vaporization of pore water in the shear band has a certain influence on the dynamic process of the overlying slide mass, but the effect is not significant for the Vaiont landslide.

In conclusion, the thermo-hydro-vapor-mechanical model established in this paper can reflect the physical mechanism of thermal pressurization inside the shear band of high-speed landslides during their startup process to a certain extent, and it could also explain why some landslides quickly turn to catastrophic high-speed sliding after they start. However, due to the huge difference in thickness between the shear band and the slide mass, the model presented in this paper is still quasi-two-dimensional, without considering the transfer of heat and excess pore pressure between adjacent shear bands, which result in a more concentrated temperature and excess pore pressure within some shear bands; thus, the velocity of the overlying sliding mass may be somewhat greater than the actual value. In addition, the model does not consider internal energy dissipation within the sliding mass during its movement; otherwise, the vibration amplitude of the interslice force and acceleration of slide blocks will be smaller, as well as its velocity, and the temperature and excess pore pressure in the shear band will not reach the maximum so quickly. What is more, the model has many parameters and some of them are difficult to obtain accurately, which may affect the accuracy of the model.