Dynamic three-dimensional displacement analysis of small-scale granular flows by fringe projection and digital image correlation

Abstract

In this work, we present experimental results that show the feasibility of measuring three-dimensional displacement in models of dry granular avalanches. For this purpose, we have used a technique that is capable to measure simultaneously the three involved mutually perpendicular components of displacement on the free surface of the granular flow. The approach comprises two simultaneously used optical techniques: fringe projection, FP, and digital image correlation, DIC; the first technique yields the out-of-plane component of displacement, and the second one, the two in-plane components. Combination of both techniques is achieved by color encoding, which consists in using different color illumination sources for the two optical techniques, in conjunction with a camera recording in RGB. The resulting combination is robust since the illumination sources are non-coherent between them, avoiding any optical interference. This contribution shows the potentiality of the method to analyze dynamic events, by presenting temporal full-field sequences of displacement of small-scale granular flows down an inclined plane, at camera speeds up to 2000 fps. These types of measurements are valuable for validation of physical and numerical models related with the analysis of the dynamic behavior of granular flows in the earth. Because these phenomena, which include rock avalanches, debris avalanches, debris flows, and pyroclastic density currents, are among the most dangerous natural hazards in mountainous and volcanic areas, the possibility to foresee their behavior in a more precise way is extremely important in order to elaborate more rigorous physical models and improve the predictive capacity of the simulation software.

Introduction

Granular avalanches are a common phenomenon in nature; when they occur on a large scale, they represent major geological hazards (Pudasaini and Hutter 2007; De Blasio 2011). Examples of granular avalanches are debris avalanches, sturzstrom, debris flows (Marui et al. 1997; Jakob and Hungr 2005) and pyroclastic density currents (Doyle et al. 2011; Sulpizio et al. 2014; Breard et al. 2016), mixtures of lithic particles, gas, and occasionally water that move across the landscape, at high speed, under the effect of gravity. Their nature is very hostile, because they are unpredictable, dangerous, very dynamic events, often wrapped by fine particles or ash that limits their observation. For these reasons, their direct field-based observations are generally rare, incomplete, and uncertain (Sulpizio et al. 2014). Since they cannot be observed and studied on a large scale, a very effective alternative way is to study them on a reduced scale, through experimental flumes, in controlled, repeatable environments and in total safety. Similar experiments allow us to develop more detailed kinematic and rheological models, as well as more efficient simulation algorithms. Therefore, observations derived from experiments may contribute to the understanding of the formation and development of particular transitory structures such as free-surface waves, Kelvin-Helmholtz, or Von Karman instabilities (Shkadov 1967; Forterre and Pouliquen 2003; Gray and Edwards 2014; Pollock et al. 2019).

We present new experimental results that indicate the feasibility to measure three-dimensional displacement in small-scale geological modeling of granular flows. Three-dimensional displacement can be regarded as the addition of the three mutually perpendicular components of the displacement vector: the out-of-plane component that is along the observation direction, and the in-plane components, which are generally contained by the mean plane of the free surface. In geological analogue modelling, generally, the two in-plane components of displacement are preferred to obtain when the interest is focused on strain evolution of the model surface (Tatsuoka et al. 1990; Pudasaini et al. 2005; Nilforoushan and Koyi 2007; Graveleau et al. 2012; Schellart and Strak 2016; Ritter et al. 2018); other authors have shown the importance to further measure the topography or morphology (out-of-plane component), for example, for carrying out analyses of synkinematic sedimentation and temporal vertical uplift (Graveleau et al. 2008; Pichot and Nalpas 2009; Martinez et al. 2016; Gracia et al. 2018). Furthermore, velocity and depth are important physical quantities to describe the dynamics of avalanches (Pudasaini et al. 2005). For the measurement of the three components of displacement, researchers have commonly resorted to the use of an optical stereoscopic setup, which consists of two simultaneous different views of an object under test (Beynet and Trampczynski 1977; Desrues et al. 1985; Prasad 2000; White et al. 2003; Genovese et al. 2013). These types of setups, however, imply a laborious process of cross-matching the two views. An upgrading of this approach was presented by Barrientos et al. (2008) and Shi et al. (2013), where only one camera was used in conjunction with a digital projector; however, the proposed techniques were limited to the analysis of static tests or relatively slow events, such as in physical modeling of tectonic processes (Barrientos et al. 2008). In that case, the duration of the events is on the order of several minutes and it is possible to employ two separate optical techniques sequentially: fringe projection, FP, and digital image correlation, DIC. Fringe projection is based on the projection of a spatially varying illuminating pattern, which is deformed according to the out-of-plane changes of the surface under observation (Takeda et al. 1982; Wust and Capson 1991; Gasvik 2003). On the other hand, in DIC, the surface is illuminated by a uniform beam, and by measuring the displacements of the local texture in the observation plane, in-plane displacements can be inferred (Peters and Ranson 1982; Willert and Gharib 1991; Sjodahl and Benckert 1993). Due to the fact that in both FP and DIC, the observation direction of a recording camera is generally perpendicular to the mean plane of the object; it is possible to employ only one camera for the two techniques, which simplifies the optical setup. A further simplification is the use of only one source of light, such as a digital projector, which generates the necessary light beams sequentially.

For relatively rapid phenomena, such as granular avalanches, which take place in just a few seconds, there is the need to perform measurements by FP and DIC simultaneously, rather than sequentially. In recent works (Siegmann et al. 2011; Mares et al. 2011; Sesé et al. 2014a, b), a technique based on the aforementioned FP-DIC combination that incorporates the latter capability (measurements of dynamic events) has been proposed. It is based on color encoding, where a RGB camera and two different illuminating colors are used. A unique illumination source, such as a digital projector, may be used in both techniques, but illumination by two separate light sources is preferred due to the availability of larger illumination intensity levels and the ability to enable the analysis of multi-colored objects and to boost the in-plane sensitivity—particularly, for objects with relatively low surface rugosity (Mares et al. 2018). Use of non-coherent light sources enables us to count with a technique that is robust to environment noise sources; besides, apart from being non-disturbing, the technique is of whole-field type. The technique can provide pixel-wise measurements for both the out-of-plane and the in-plane components of displacement, with an accuracy of around 1% (Mares et al. 2011); this value is on the same order as that reported by Siegmann et al. 2011.

Most of the methods for displacement measurement used nowadays are based on particle image velocimetry obtained in two dimensions. The method proposed here is completely new, because it is based on measurements provided by instant digital models reconstructed by means of high-speed images (captured up to 2000 fps). Such digital elevation models permit the capture of three-dimensional movements of the particles as a whole.

The aim of this work is to show the applicability of the combined technique (FP-DIC) to the measurement of displacement in rapid phenomena, such as small-scale avalanches. We show that when the complete state of deformation is obtained for these types of events, important spatiotemporal features can be identified, such as flattening and slowing of the granular stream, which are apparently related to the level of clustering of the materials and the speed of the flow.

This work is organized as follows. The fundamental theory of the optical techniques, FP and DIC, is presented in the “Description of the used optical techniques” section. In the “Experimental layout” section, we include experimental results for two different granular media, where the granular compositional mixture is varied. Finally, in the “Conclusions” section, the main conclusions of the work are included.

Description of the used optical techniques

Fringe projection, FP

Optical setup

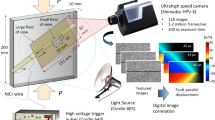
A schematic diagram of the setup for FP is depicted in Fig. 1. FP is a technique that enables the measurement of the out-of-plane component of displacement (along the z-direction in Fig. 1) of an object surface when the object is subjected to deformation. In this technique, the object is illuminated by a beam of structured light. The structure of the light generally corresponds to a pattern of periodic straight fringes, where half the fringe width is white and the rest is black.

Fig. 1.

Optical layout for fringe projection technique. a 3D schematic diagram. b Side view

As shown in Fig. 1, the light pattern produced by a digital projector P1 is cast firstly onto the surface of object, before deformation; we assume that this undisturbed surface corresponds to a reference plane RP. Then, an image (called the reference image) is taken by using a camera C and an imaging lens L (the camera is focused on RP and maintains this condition throughout the test). In Fig. 1a, two fringes projected onto RP are shown, F1 and F2. As depicted, straight fringes are projected onto RP. Subsequently, as the object surface is deformed, a second image (called the displaced image) is acquired. In this case, the fringes move transversely a distance Δx(x, y) in accordance with the local out-of-plane displacement w(x, y) of the object—(x, y) are the spatial coordinates. For example, when the objects are deformed, F1 (line segment ab) will intersect the object surface along segment a’b’, and this intersection is imaged by the camera as segment a”b”, which is the projection of a’b’ onto RP.

In Fig. 1, the displacement of the surface is assumed to vary only along the x-coordinate; therefore, in this particular case, after deformation, the projected lines remain straight but laterally displaced. The setup incorporates a second projector P2; this projector will enable the implementation of the complementary technique, digital image correlation.

From Fig. 1, the local out-of-plane displacement w can be obtained as follows. By using the similar triangles aa’a” and P1a’L, we find that w/Δx = (D − w)/B, where the variables are defined in Fig. 1b; in parameters w and Δx, the dependence on the spatial coordinate variables has been omitted for clarity. Therefore (Gasvik 2003),

$$ w=\frac{D\varDelta x}{B+\varDelta x}=\frac{\varDelta x}{\tan \alpha +\varDelta x/D}, $$

(1)

where α denotes the mean angle between projector P1 and optical axis of the camera, and D is the camera-to-reference plane distance; these two last parameters can be selected as described next.

Selection of the angle of projection should prevent the production of shadows by the relief itself; therefore, shallow angles are preferred. Besides, as the sensitivity of the setup depends on this parameter as well, as it can be seen from Eq. (1), the smaller the value of the angle, the lower the sensitivity (in this case, for particular w values, relatively small values of transverse displacement are observed). Consequently, by considering the two latter effects, it would seem that a compromise regarding the projection angle should be met. However, since the fringe signal is suppressed in zones with shadows, the measurement is restrained in those zones, and the condition of shallow projection angles prevails over the sensitivity issue (yet the axial resolution may be moderately low). On the other hand, selection of the distance from reference plane to camera D is directly related with the field of view, which in turn, is inversely proportional to the lateral resolution.

If the projector is sufficiently far away from the object, the spatial period P of the projected fringe pattern can be considered practically constant throughout the field of view. In this case, the local change of phase Δϕ(x, y) of a fringe point can be related as

$$ \varDelta x\left(x,y\right)=\frac{\varDelta \phi \left(x,y\right)}{2\pi }P $$

(2)

Thus, if Δϕ(x, y) is known, as described in the “Numerical example” section, then the out-of-plane displacement map can be readily calculated. The change of phase can be obtained automatically through any of the existing phase-extraction methods (Malacara et al. 2005); however, when we consider the analysis of rapid events, e.g., the deformation dynamics of an avalanche, the selection of the phase method is restricted to the use of only one image to recover the phase information of a certain state of the object. This restriction can be adequately handled by the Fourier method (Takeda et al. 1982).

For the Fourier method to be used, a carrier frequency signal should be incorporated into the setup. In fringe projection, this carrier is naturally available via the projected fringe pattern itself. Then, by taking into account these considerations, the intensity I(x, y) of a registered image can be expressed (for the reference state and the displaced state, respectively) as (Gasvik 2003; Mares et al. 2011)

$$ {\displaystyle \begin{array}{l}{I}_r\left(x,y\right)=a\left(x,y\right)+b\left(x,y\right)\cos \left[{\phi}_r\left(x,y\right)+2\pi {f}_0x\right],\\ {}{I}_d\left(x,y\right)=a\left(x,y\right)+b\left(x,y\right)\cos \left[{\phi}_d\left(x,y\right)+2\pi {f}_0x\right],\end{array}} $$

(3)

where (x, y) are pixel coordinates on the sensor plane of the camera, and a(x, y) and b(x, y) refer to the background level of illumination and the modulation amplitude of the resulting fringes, respectively; these two latter parameters are assumed to hold unchanged during the measurements. The terms appearing in the argument of the cosine functions are the phase information ϕ_r(x, y) and ϕ_d(x, y), which are related with the height distribution of the reference and the displaced images, respectively. Besides, f₀ is the carrier frequency that represents the signal of the projected fringes. Notice that the direction of the carrier fringes is along the y-axis. The corresponding spatial period of the fringes at the center of the field of view is P = 1/f₀.

When the object is deformed, the reference phase ϕ_r(x, y) is changed by Δϕ(x, y), so that the phase of the displaced image becomes ϕ_d(x, y) = ϕ_r(x, y) + Δϕ(x, y). As described in the “Numerical example” section, by applying the Fourier method to both the reference and the displaced images, the arguments of the cosine functions in Eq. (3) can be computed. Thus, their difference can be readily obtained as Δϕ(x, y) = [ϕ_d(x, y) + 2πf₀x] − [ϕ_r(x, y) + 2πf₀x], where we can notice that the carrier frequency term is automatically discarded. According to Eqs. (1) and (2), the change of phase Δϕ(x, y) is proportional to the out-of-plane component of displacement.

Numerical example

A representative numerical example of Eq. (3) is presented in Fig. 2a and b, where the change of phase is specified as a parabolic distribution Δϕ(x, y) = 6π(x² + y²)/(0.92s_x/2)², with s_x being the size of the field of view in the horizontal direction, and −0.92(s_x/2) ≤ x, y ≤ 0.92(s_x/2)—this interval defines the deformation zone, which corresponds to a circle of radius 0.92(s_x/2). The background and the modulation are set to be equal and they are let to vary as a Gaussian function $a\left(x,y\right)=b\left(x,y\right)=\exp \left[-2\left({x}^2+{y}^2\right)/\left({s}_x^2/2\right)\right]$. This function represents an illuminating beam that fades away towards the edges.

Fig. 2

Numerical example of the phase-extraction Fourier method. a Reference image (it only includes the carrier signal and Gaussian variations of both the background level of intensity and the modulation amplitude). b Displaced image additionally incorporates a parabolical distribution of out-of-plane displacement. Amplitude of the Fourier transform of: c reference image and d displaced image. e Recovered wrapped phase map (a horizontal cross section through the center of the figure is shown complementarily. f Recovered unwrapped phase map (it also includes corresponding horizontal cross sections of the recovered wrapped phase (in yellow line), the recovered unwrapped phase (in green line), and the prescribed phase (in black dashed line)). Units are described as follows: au, arbitrary units; GL, gray level; pix, pixel

On applying the Fourier method to the displaced image, for example, first the Fourier transform of the image is taken (Mares et al. 2018),

$$ {\displaystyle \begin{array}{c}\mathrm{\Im}\left\{{I}_d\left(x,y\right)\right\}={I}_F\left({f}_x,{f}_y\right)=\mathrm{\Im}\left\{a\left(x,y\right)\right\}+\mathrm{\Im}\left\{\frac{1}{2}b\left(x,y\right)\exp \left[i{\phi}_d\left(x,y\right)\right]\exp \left(i2\pi {f}_0x\right)\right\}+\\ {}\mathrm{\Im}\left\{\frac{1}{2}b\left(x,y\right)\exp \left[-i{\phi}_d\left(x,y\right)\right]\exp \left(-i2\pi {f}_0x\right)\right\},\end{array}} $$

(4)

where the cosine term has been replaced by exponential functions and ℑ{} stands for the Fourier transform operator, and (f_x, f_y) are frequency coordinates in the Fourier domain. Notice that the third term corresponds to the complex conjugate of the second one, where it is assumed that b(x, y) is real. Generally, the frequency of the spatial variations of the background term is less than the carrier frequency; hence, the Fourier transform of the first term in Eq. (4) produces a narrow halo around the origin in the complex plane, as seen in Fig. 2c and d—these two figures correspond to the Fourier transform of Fig. 2a and b, respectively. In these last two figures, we have plotted the natural logarithm of the complex amplitude in order to reduce the dynamic range of resulting values and thus permitting all features to be visible.

The last two terms in Eq. (4), in turn, yield wider side lobes centered at the carrier frequency ±f₀, as shown in Fig. 2c and d. Other side lobes located at odd multiples of the carrier frequency are shown as well. These side lobes arise from the fact that the fringe pattern in consideration does not have a sinusoidal profile as implied by Eq. (3), but, as mentioned above, it encompasses a profile with straight edges (rectangle function). The side lobes at higher frequencies than the carrier can be neglected as long as they do not overlap with the first lobe, as it is described by the next step.

Equation (4) gives,

$$ {I}_F\left({f}_x,{f}_y\right)=A\left({f}_x,{f}_y\right)+B\left({f}_x-{f}_0,{f}_y\right)+{B}^{\ast}\left(-{f}_x-{f}_0,{f}_y\right), $$

(5)

where A(f_x, f_y) = ℑ{a(x, y)} and $B\left({f}_x,{f}_y\right)=\mathrm{\Im}\left\{\frac{1}{2}b\left(x,y\right)\exp \left(i{\phi}_d\right)\exp \left(i2\pi {f}_0x\right)\right\}$.

The next step of the Fourier method has to do with the application of a band-pass filter to Eq. (5) to isolate one of its side lobes, centered at the carrier frequency f₀, which produces—by arbitrarily selecting the right lobe

$$ {I}_{FP}\left({f}_x,{f}_y\right)=B\left({f}_x-{f}_0,{f}_y\right). $$

(6)

The filter considered in the current numerical example is indicated by the magenta rectangle in Fig. 2d.

In a further step, we take the inverse Fourier transform of Eq. (6),

$$ {\displaystyle \begin{array}{l}{\mathrm{\Im}}^{-1}\left\{B\left({f}_x-{f}_0,{f}_y\right)\right\}={I}_{rec,d}\left(x,y\right)={\mathrm{\Im}}^{-1}\left\{\mathrm{\Im}{\left\{\frac{1}{2}b\left(x,y\right)\exp \left(i{\phi}_d\right)\exp \left(i2\pi {f}_0x\right)\right\}}_{f_x,{f}_y}\right\}\\ {}\kern5em =\frac{1}{2}b\left(x,y\right)\exp \left[i\left({\phi}_d+2\pi {f}_0x\right)\right]\\ {}\kern5em =\mathrm{\Re}\left\{{I}_{rec,d}\left(x,y\right)\right\}+ iI\left\{{I}_{rec,d}\left(x,y\right)\right\},\end{array}} $$

(7)

where $\Re \left\{{I}_{rec,d}\left(x,y\right)\right\}=\frac{1}{2}b\left(x,y\right)\cos \left({\phi}_d+2\pi {f}_0x\right)$ and $I\left\{{I}_{rec,d}\left(x,y\right)\right\}=\frac{1}{2}b\left(x,y\right)\sin \left({\phi}_d+2\pi {f}_0x\right)$, with ℜ and I representing the operators for taking the real and imaginary part of a complex number, respectively. Therefore, the argument can be obtained by ϕ_d + 2πf₀x = tan⁻¹[I{I_{rec, d}(x, y)}/ℜ{I_{rec, d}(x, y)}]. In these expressions, I_{rec, d}(x, y) designates the recovered complex intensity.

The argument of the reference image, (ϕ_r + 2πf₀x), can be calculated by following a similar procedure as above; then, as a final step of the Fourier method, the desired phase term related to the out-of-plane displacement can be obtained by subtracting the two computed arguments,

$$ {\displaystyle \begin{array}{c}\varDelta {\phi}_w=\left({\phi}_d+2\pi {f}_0x\right)-\left({\phi}_r+2\pi {f}_0x\right)\\ {}={\tan}^{-1}\left[I\left\{{I}_{rec,d}\right\}/\Re \left\{{I}_{rec,d}\right\}\right]-{\tan}^{-1}\left[I\left\{{I}_{rec,r}\right\}/\Re \left\{{I}_{rec,r}\right\}\right],\end{array}} $$

(8)

where ${I}_{rec,r}\left(x,y\right)=\frac{1}{2}b\left(x,y\right)\exp \left[i\left({\phi}_r+2\pi {f}_0x\right)\right]$ is related to the reference image. Equation (8) can be recast in order to be computed in one step, by using a trigonometric identity, as

$$ \varDelta {\phi}_w={\tan}^{-1}\frac{I\left\{{I}_{rec,d}\right\}\Re \left\{{I}_{rec,r}\right\}-I\left\{{I}_{rec,r}\right\}\Re \left\{{I}_{rec,d}\right\}}{\Re \left\{{I}_{rec,d}\right\}\Re \left\{{I}_{rec,r}\right\}+I\left\{{I}_{rec,d}\right\}I\left\{{I}_{rec,r}\right\}}. $$

(9)

For the numerical example, the result of this step is presented in Fig. 2e. As it can be observed (particularly by the horizontal cross-sectional view that passes along the center of the image, in yellow line), the phase map presents jumps of 2π rad at certain locations. This arises from the fact that the values obtained by the inverse tangent function are wrapped in the interval 0 − 2π rad. By using integration-like methods, values outside this range may be computed by assuming smoothness of the phase distribution—that is, that differences of the phase of two neighboring pixels should be less than π rad. The integration-like methods compensate for the phase jumps automatically, and these methods are known as unwrapping phase methods (Malacara et al. 2005). When the wrapped phase map is relatively free from noise, we can apply a simple unwrapping technique that resembles a numerical integration method; that is, a method that first unwraps a line of pixels (horizontally, for instance), by the iterative routine (Malacara et al. 2005),

$$ \varDelta {\phi}_u\left(1,n+1\right)=\varDelta {\phi}_u\left(1,n\right)+{\tan}^{-1}\left\{\tan \left[\varDelta {\phi}_w\left(1,n+1\right)-\varDelta {\phi}_u\Big(1,n\Big)\right]\right\}, $$

(10)

with Δϕ_u representing the resulting unwrapped phase. The dummy index n runs from 1 to N − 1, with N being the total number of pixels of the images, in the horizontal direction. Normally, we set the initial value as Δϕ_u(1, 1) = 0. In a subsequent step, the integration in column-wise direction can then be performed as

$$ \varDelta {\phi}_u\left(m+1,n\right)=\varDelta {\phi}_u\left(m,n\right)+{\tan}^{-1}\left\{\tan \left[\varDelta {\phi}_w\left(m+1,n\right)-\varDelta {\phi}_u\Big(m,n\Big)\right]\right\} $$

(11)

for 1 ≤ m ≤ M − 1 and 1 ≤ n ≤ N, with M being the total number of pixels in the vertical direction. For the current numerical example, the unwrapped phase map is shown in Fig. 2f, along with corresponding profile lines passing through the center that respectively correspond to the wrapped phase (in yellow), the recovered unwrapped phase (in green), and the prescribed parabolical phase (in black dashed line).

In summary, the Fourier method includes the following tasks. For both the reference and displaced image: (1) take their Fourier transform, (2) apply a band-pass filter, (3) take the inverse Fourier transform of step (2); to get the wrapped phase map, apply Eq. (9); and finally, if needed, apply an unwrapping algorithm as that represented by Eqs. (10) and (11).

Once that the change of phase Δϕ_u is assessed, the out-of-plane displacement can be readily computed as indicated by Eqs. (1) and (2). In Eq. (1), however, it is assumed that both the projector and the camera are at infinity. When this situation is not met, spatial variations of the local period of the projected pattern have to be considered, and a compensation factor to P should be applied (Gasvik 2003), as P '  = P(1 + x sin α/l)², where l represents the distance between the exit pupil of P1 and the object.

By measuring the phase of two consecutive images, via double application of Fourier method, the general expression for out-of-plane displacement w can be obtained by (Gasvik 2003; Mares et al. 2018)

$$ w=\frac{\varDelta \phi}{2\pi}\frac{P\hbox{'}\cos \alpha }{\sin \alpha +\left(D-l\cos \alpha \right)x/(lD)}, $$

(12)

where D is the camera-to-object distance and α the projection angle at the center of the field of view (at x = 0). Notice that w depends on the x-position through both the projected period P' and the term appearing in the denominator, which is equivalent to a modified local transverse displacement—by comparison with Eqs. (1) and (2). To avoid the x-dependence regarding the denominator, the projector lens and the camera lens can be positioned at the same height above RP (Gasvik 2003)—as depicted in Fig. 1; hence, D = l cos α and $w=\frac{\varDelta \phi}{2\pi}\frac{P\hbox{'}}{\tan \alpha }$.

Digital image correlation, DIC

The DIC technique permits us to estimate the in-plane component of displacement, which is perpendicular to the out-of-plane component. The in-plane component is generally analyzed as the addition of two mutually perpendicular components. DIC relies on the comparison of two white-speckle images of the object, which correspond to two different states of deformation (reference and displaced images, as in FP). The object is illuminated by a uniform beam of white light so that a speckle signal is formed by the natural texture of the surface (Mares et al. 2018)—for non-granular objects, the speckle distribution can even be painted directly on the surface when dealing with solid objects (Siegmann et al. 2011). In Fig. 1, the DIC illuminating source is indicated by P2, which may be any type of non-coherent light source as it is only necessary that the object is illuminated uniformly. By using spectrally separated light sources, P1 and P2, and a color camera, FP and DIC can be implemented simultaneously (Mares et al. 2018).

The relative in-plane displacement between the reference and displaced images can be obtained by cross correlation. The images are divided into subimages, generally of size 24 × 24 pix, and these subimages are then correlated (Raffel et al. 1998). If the intensity subimages, related to the reference and displaced images, are denoted by I₁(x, y) and I₂(x, y), then the displaced image may be expressed as I₂(x, y) = I₁(x − u, y − v), where constancy of intensity is assumed. The displacement vector v→ = (u, v) can be found by means of the two-dimensional correlation function defined as (Blanco et al. 2016)

$$ h\left(u,\mathrm{v}\right)={\int}_{-\infty}^{\infty }{\int}_{-\infty}^{\infty }{I}_1\left(x,y\right){I}_1\left(x-u,y-\mathrm{v}\right) dxdy, $$

(13)

which can be evaluated through the Fourier transform,

$$ h\left(u,\mathrm{v}\right)={\mathrm{\Im}}^{-1}\left\{{F}_1\left({f}_x,{f}_y\right){F}_2^{\ast}\left({f}_x,{f}_y\right)\right\}, $$

(14)

where F₁(f_x, f_y) and F₂(f_x, f_y) designate the Fourier transform of I₁ and I₂, respectively. The position of the maximum of the correlation map defines directly the unknown displacements.

Subpixel resolution of the displacements can be achieved by fitting analytical surface functions to the region that contains the maximum peak of the correlation map (Raffel et al. 1998). If the time between two consecutive images (reference and displaced images) is known, then the computation of the velocity vector field is straightforward.

The Fourier correlation method produces in-plane displacement results at each subwindow. If results are to be obtained at each pixel, then we may resort to optical flow techniques (Horn and Schunck 1981). In this latter case, the matching of the images is achieved by rewriting the expression of intensity constancy, as $\nabla \cdot \overrightarrow{v}=-\mathit{\partial I}/\mathit{\partial t}$, which describes the temporal evolution of the apparent movement of any spatial structure in an image.

Simultaneous implementation of FP and DIC

In Mares et al. (2011, 2018), the implementation of simultaneous FP and DIC is described. The main idea is to capture the signals of FP and DIC in the different color channels of an RGB camera. The major consideration is to avoid any degrading of the contrast of the images caused by cross-talk between the two signals; the level of cross-talk is related to the spectral response of each color pixel of the camera (the camera sensor has 3 types of pixels: sensitive to red, to green, and to blue, respectively). Consequently, search of an optimum combination of light sources is of great importance. For neutral-colored objects, which is the case of the present application, the best combination of light sources is to use for DIC, a red uniform light beam, produced for example by either a projector or a matrix of LEDs, and for FP, a pattern of blue fringes (embedded in a black background) generated by a projector or by a combination of laser-grating.

For FP, in this report, we use a digital projector P1 that casts a square-profile (or sinusoidal) fringe pattern onto the object surface, half the fringe width is blue and the rest is black. This signal is received on the blue channel of color camera C (see Fig. 1). Regarding DIC, a matrix of 20 × 25 red LEDs is employed; the resulting image is received on the red channel of C. It is then observed that the images are almost free of any residual information. To further decrease the level of cross-talk, we may resort to color compensation. The signal that is received by the camera can be modeled as $\left[\begin{array}{c}R\\ {}B\end{array}\right]=\left[\begin{array}{cc}{a}_{RR}& {a}_{RB}\\ {}{a}_{BR}& {a}_{BB}\end{array}\right]\left[\begin{array}{c}R\hbox{'}\\ {}B\hbox{'}\end{array}\right]$, where [R B]^T is the received signal by the camera (on the red and blue channels, respectively) and the primed letters represent the prescribed signal (the red and blue values fed to the digital projector, with no cross-talking); the cross-talk matrix A considers the effect of each illumination color onto each camera channel, for example, a_BR is the value of the intensity detected by the blue channel while illuminating by the red light source.

The cross-talk matrix can be measured by illuminating the object by the separate light sources (red and blue) one at a time, and registering the detected values on each channel of the camera. Therefore, to obtain the prescribed values of intensity for each channel (without overlapping) from the corresponding measured values, we need only to solve for the primed values (for each pixel of a raw color image) via the inverse of A.

In the case of DIC, for objects with relatively smooth surfaces, contrast of the images may be too low. To overcome this situation, the DIC light source is oriented at a relatively small angle with respect to the reference plane RP, although care should be taken to avoid any production of shadows by the object surface.

Additionally, as shown in Fig. 3, the resulting out-of-plane displacement w produces an in-plane displacement $\varDelta \overrightarrow{r}=\left(\varDelta u,\varDelta \mathrm{v}\right)$, caused by the viewing angle of the object from camera C (Sutton et al. 2008; Sesé et al. 2014a, b). This in-plane displacement affects the in-plane measurements given by DIC. From Fig. 3, the introduced error is given by $\varDelta \overrightarrow{r}=w\overrightarrow{r}/D$, where $\overrightarrow{r}=\left(x,y\right)$ contains the radial coordinates of an object point, in the reference plane. In this way, the compensated values of the in-plane displacement (u_c, v_c) become u_c = u − Δu = u − wx/D and v_c = v − Δv = v − wy/D.

Fig. 3.

Biased in-plane error, $\varDelta \overrightarrow{r}=\left(\varDelta u,\varDelta \mathrm{v}\right)$, arising from the out-of-plane component of displacement w

Experimental layout

Optical setup

The optical setup incorporates a RGB high-speed camera (Photron Mini UX100) operating at 2000 fps, with a spatial resolution of 1280 × 1024 pix. The camera includes a RGB Bayer filter. Additionally, two light sources are integrated, a 3000-lumen WXGA projector (Epson PowerLite 1776W), and a matrix of 20 × 25 40-mW red LEDs, for FP and DIC, respectively. Besides, an imaging lens of focal distance of 17 mm is used (Canon TS-E 17mm). The lens-to-reference plane distance is specified as 93 cm, so that a field of view of 70 cm is attained. The mean angle of projection is 14°. The period of the projected period is chosen as 6 mm, so that it is slightly larger than the average size of granular sieved material (which is −2ϕ, where ϕ =  − log₂d, with d being the diameter of the particle).

The out-of-plane displacement is obtained by Eq. (12), and for the calculation of the in-plane component, a commercial software package is employed (proVision-XS PIV, from IDT), where subimages of 24 × 24 pix are used. Color correction and in-plane correction are implemented as described in the “Simultaneous implementation of FP and DIC” section.

Flume geometry and small-scale model of granular avalanches

We performed two series of flow experiments on a straight flume facility with two lengths. The large flume (see Fig. 4) is an inclined plane (34°) of 500 cm long and 30 cm wide (Sulpizio et al. 2016). The floor surface of the channel consists of a layer of polyurethane (thickness, 2 mm). The small flume length is 100 cm, its width 12.5 cm, and the inclination is 37°; the base is a piece of cardboard (thickness of 0.1 cm). Both flumes include lateral transparent walls (made of acrylic) that maintain the flow laterally confined. In both cases, the region of interest is located in the middle part of the length of the channel.

Fig. 4

The large flume facility of the Image Analysis and Analog Modeling Laboratory (LAIMA-lab), Geology Institute, Universidad Autónoma de San Luis Potosí, Mex

Experimental results for two very different granular mixtures are reported: Material 1, a 65–35 mixture of crushed marble (bulk density of 1600 kg m⁻³) and commercial cornstarch—this latter material has a particle size of a few μm (Jane et al. 1992) and a bulk density of 1100 kg m⁻³—mixture density of 1400 kg m⁻³; and material 2, natural volcanic pumice with a quasi-monodisperse 4–5 mm grain size with a bulk density of 500 kg m⁻³. These two very different types of mixtures serve to consider the differences in size of level of clustering, which may affect the rheology and dynamics of the granular flows (analysis of the level of clustering is beyond the scope of this work). A mass of 2.6 kg of material 1 was used for the test in the small flume, whereas a mass of 23 kg of material 2 was used for the large flume. Friction coefficients for materials 1 and 2 are tan25 °  = 0.47 and tan34 °  = 0.67, respectively. The inclination angle of the channel is chosen in such a way that tanγ (where γ is the flume slope) is greater or equal than the friction coefficient. The shape of the initial state of the object corresponds to the floor surface of each flume, that is to say, the flume without granular flow.

In the initial state, the reference image is recorded and only contains the projected fringes on the flat flume base and the uniform light produced by the LED matrix. The material is released instantly by using an electromagnet-activated gate (which corresponds to the bottom lid of a square recipient), permitting vertical material discharging on the flume. About 1 s before activating the gate, the camera is enabled to register images continuously for 5 s. For the marble-cornstarch mixture, the rate of frame recording is 1000 fps and for the pumice 2000 fps.

Experimental results

In this section, we present the results obtained from the application of the optimized setup to the analysis of the granular flow in an open-air flume. These experiments and their measurements may serve to collect the necessary data to validate the performance of numerical simulation packages and geophysical models.

Regarding material 1 (mixture of marble and cornstarch, small flume) in Fig. 5, we present images related with a particular displaced state, at t = 475ms after arrival of the material to the region of observation. In Fig. 5a, the raw image is included; the upper and bottom parts of the image correspond to lateral views of the flume that are realized by using two plane mirrors positioned at 45° with respect to the flume base (two intensity-saturated lobes are caused by spurious reflection of the light sources). Notice the large leaping of the grains at the avalanche front and the well-formed protuberances on the surface. From this latter image, the central section is selected and then we obtain the color-separated images (FP image from blue channel and DIC image from red channel), which are shown in Fig. 5b and c. Figure 5d illustrates the magnitude of the Fourier transform of Fig. 5b, where the filtering mask (in magenta) is shown superimposed.

Fig. 5.

Processing steps of a color raw image (a). Separated blue and red images—in gray levels, GL—b and c, respectively. d Amplitude of the Fourier transform of Fig. 5b—arbitrary units

By taking the inverse Fourier transform of the Fourier-domain-filtered image (Fig. 5d), we can recover the phase of the current snapshot. The Fourier method can be applied to the reference image to get the reference phase as well. Comparison of displaced phase maps with the reference phase allows us to obtain the corresponding out-of-plane components of displacement. Likewise, by comparing a pair of consecutive DIC images, as that shown in Fig. 5c, the in-plane components of displacement can be computed. For the present exemplary snapshot, the resulting three-dimensional displacement is illustrated in Fig. 6a; the out-of-plane component is indicated by the color graph and the in-plane component by the arrows. In the title of the figure, we include the maximum values of the stream-wise in-plane velocity (u-component, in m/s) and the out-of-plane component, in mm. The range of values for the out-of-plane map, in mm, is indicated by a color bar and by the blue numbers which are located on the right of the figure. The horizontal and vertical axes denote the dimensions of the region of observation, in mm.

Fig. 6

Time series of three-dimensional displacement for cornstarch. The scale of the axes and that of the color bar is in mm. The maximum value of the in-plane velocity and the out-of-plane displacement are included in the titles of each plot

In general, the dynamics of the granular material of the experiments resembles that of a fluid stream. As it can be noticed, the cross-stream in-plane speed, v, is generally close to zero—(u, v) is used indistinctly to designate in-plane displacements and in-plane velocities. Other results of the time series are presented in Fig. 6. The displacement of particles in the forefront is characterized by rolling and saltation (Bagnold 1972); this chaotic behavior of the particles induces high variations in the measurements. The cornstarch tends to agglomerate and to slow down the flow, and this produces some lumps that are observed during the whole event. We can also see the presence of a gradient in the in-plane stream-wise velocity, characteristic of fluid streams down an inclined plane; the gradient tends to flatten out any irregularities of the free surface, such as lumps and pits. Besides, the maximum velocity remains practically constant as the flow evolves.

To gain further insight into the dynamic behavior of the stream-wise velocity, this component is shown separately in Fig. 7a to d, and for some of the snapshots in Fig. 6. The existence of two zones with distinct gradient of velocity is noticed, divided at about x =  − 150 mm; on the left, the granular material is decelerated. This effect may initiate wave-like features of the flow; further experiments should be carried out to confirm this hypothesis.

Fig. 7

a–d Stream-wise velocity, in m/s, for some snapshots of Fig. 5. e, f Swirling indicator, in s⁻², and superimposed streamlines for a and c

Regarding the two components of in-plane velocity, complementary derived parameters can be determined, such as swirling (Raffel et al. 1998) and streamlines (Granger 1995). Swirling is defined as $S=-\frac{\partial u}{\partial y}\frac{\mathrm{\partial v}}{\partial x}$, where positive values are related to the local swirling of the flow and negative values to in-plane shearing strain. On the other hand, the streamlines can be calculated by integration of $\frac{dy}{dx}=\frac{\mathrm{v}}{u}$, with starting points selected by the user; they indicate the actual stream flow pattern. These two derived variables are represented in Fig. 7 e to f for two snapshots. As inferred by the swirling indicator, the instabilities are larger at the initial front of the stream than when the region of observation is full with granular material. Also, the streamlines show that the cross-stream velocity is relatively small.

For the case of material 2 (pumice, large flume) in Fig. 8, we present two snapshots of the displacement maps with their corresponding stream-wise velocity maps and swirling maps—in Fig. 8g, a photograph of an on-going test along the facility is presented (the forefront has passed the region of observation). From the out-of-plane results (Fig. 8a, b), we observe that the surface is free of any protuberances, as a result of less level of clustering of the material and more importantly as a result of greater values of speed, in comparison with the marble-starch mixture.

Fig. 8

a, b Displacement distribution for two snapshots, for pure pumice. c, d Stream-wise velocity, in m/s, for a and b. e, f Swirling indicator, in s⁻², and streamlines for c and d. g An avalanche produced along the flume facility (the red rectangle indicates the region of observation). For visualization of low values of swirling, the values corresponding to t = 300 ms are clipped to 0.1 times the maximum value

As shown by the stream-wise velocity image corresponding to the slide forefront (Fig. 8c), some minute zones show high local values of speed. These zones correspond to grains which are gliding above the free surface; random jumping of around 4 cm has been registered by photographs taken laterally (the jumping cannot be registered by FP since it is beyond the continuity condition of a π-rad difference between neighbor pixels). Besides, as exhibited in Fig. 8c and d, the maps of velocity are more uniform than in the case of the cornstarch. This is due to the greater relative amount of employed granular material and to the larger values of speed registered in this case. In addition, in the lower part of Fig. 8d, a zone of relatively low velocity values is reported. This distinctive zone is caused by the presence of a small protuberance composed of glue—6 mm of average width—running along the height of one of the lateral walls. The perturbed zone is shown as well in the corresponding out-of-plane result (Fig. 8b).

As inferred by the swirling results (Fig. 8e–f), the level of instabilities in this case is much greater than in the cornstarch case; once again, the greater values of speed and the less level of clustering are the possible causes. The aforementioned perturbed lower zone in this case can also be noticed in Fig. 8f. Additionally, a greater level of straightness of the streamlines is illustrated.

As a third experiment, a variation in the experiment with material 2 (pumice) is done: the large channel is replaced by the small channel, of length 1 m. The new conditions are an inclination of 37°, material load of 1 kg, grain size of 4–5 mm, and coefficient of friction of tan30 °  = 0.58; the coefficient of friction is in this case is greater than the case with the mixture of marble and cornstarch—the cornstarch provides a slip layer for the mixture. Notice that the new friction coefficient is smaller than the case of pumice with large flume; this effect is due to the differences in the materials of the flume base. The resulting three-dimensional displacement maps for experiment 3 are not shown because they are similar to those obtained with the longest channel.

Comparisons of the results of the 3 experiments—material 1 (mixture of cornstarch and marble, channel length of 1 m, denoted as starch), material 2 (pumice, channel length of 5 m, denoted as Pum L5), and material 3 (pumice, channel length of 1 m, designated by Pum L1)—are exhibited by plotting the displacement of the center line along the length of the channel as a function of time (streak-displacement image) (Fig. 9). Figures on the left (Fig. 9a, c, and e), report the temporal evolution of the out-of-plane displacement, for the 3 experiments (in mm); and, in the right column, the stream-wise in-plane velocity is presented (in m/s). In all figures, the slope of the lower and upper parts of the plots is inversely proportional to the speed of the event; the upper and lower slopes may differ slightly because the trailing edge of the stream flow is slower than the forefront. Out of the 3 experiments, the slowest one is the cornstarch (for a quantitative comparison of the speed between the plots, it is necessary to consider the distinct durations of the events).

Fig. 9

Evolution of the displacement for the center line along the length of the region of observation. Cornstarch: a out-of-plane and b in-plane; pumice L1: c out-of-plane and d in-plane; pumice L5: e out-of-plane and f in-plane

In connection with the out-of-plane results (figures in left column), moving spatial features downstream are rendered as slightly sloped streaks (it is useful to remember that a horizontal line indicates the distribution of out-of-plane displacement at a particular time and that a vertical line in turn indicates the passing of bumps and pits through a particular point of the examined profile line). For experiments regarding starch and pumice L1 (Fig. 9a and c), the profile height (out-of-plane displacement) decreases markedly in a short interval of time (about 250 ms); this feature is clearly evidenced by the color variation in the vertical direction; for pumice L5, this interval is on the order of 1 s. The difference in time durations has to do mainly with the distinct material loads, which for pumice L5 is relatively greater (for completeness, consider that L5 channel width is 2.4 times greater than L1 channel width, but the load in L5 is 23 times greater than that in L1—besides, the regions of observation are 14% and 70% of their total lengths, respectively). Effects of the length difference can also be appreciated by the stronger gradient of w in the horizontal direction of the plots—compare Fig. 9a and c with e.

As to the in-plane speed (figures in right column), for pumice L5, the stream-wise speed holds almost constant along the entire region of observation at any instant; unlike this, in the cases of the cornstarch (starch) and pumice L1 (Pum L1), a strong gradient downstream is readily noticed. The gradient is accentuated in the case of pumice L1, at about x = 0 mm. Apparently, the deceleration of the granular flow at this position is manifested as an accumulation of material, which is reflected as an increasing of the height surface (note the zone of relatively large out-of-plane displacement in Fig. 9c, at position x = 0 mm).

It is worth noting as well that for the cornstarch, the speed values at the exiting edge of the region of interest remain practically constant during the whole event, irrespective of the amount of material, which remind us of the presence of strong clustering effects.

Another result that is interesting to note is the greater speed values for pumice L1 than cornstarch (ratio 2.3:1), despite the fact that the friction coefficient for cornstarch is smaller than for pumice (for the cornstarch-marble mixture, despite a slip layer is produced by the starch, the clustering effect prevails over the sliding).

Figure 10 contains the temporal evolution of 5 points with different position along the center line of the channel, for the 3 experiments (the sampled points are not uniformly spaced, but cover almost the whole field of view). These types of plots reveal the presence of protuberances and information on the relative delays of displacement. From the out-of-plane plots (Fig. 10a, c, and e), the cornstarch and pumice L1 present greater differences in height for the 5 sampled points than for pumice L5. This is a consequence of the differences in in-plane speed gradients and in the amount of granular material. The relatively large height of ripples seen in the cornstarch has to do with the large size of the registered protuberances.

Fig. 10

Temporal evolution of 5 sampled points located along a line running stream-wise (for cornstarch, pumice L1, and pumice L5). a, c, and e Out-of-plane component of displacement. b, d, and f Stream-wise velocity

Concerning the in-plane speed (Fig. 10b, d, and f), the differences in the plots of the five sampled points make evident the presence of a relatively large gradient of stream-wise speed. In Fig. 10d, the difference in in-plane speed observed at x = 0 mm with respect to its two neighboring sampled points (x = − 123 mm and x = 123 mm) is different; this fact implies a deceleration of the material and, as shown in Fig. 10c, as an increase of the out-of-plane deformation for curve x = 0; notice that the out-of-plane displacement values for curve x = 0 are larger than for any other sampled point. The resulting slowing behavior arises from the presence of a small convex deformation of one of the walls.

Additionally, in Fig. 10f, in the case of pumice L5, it is readily noticed the presence of two zones corresponding to distinct speed value (the change occurs at about 1200 ms); these speed values may be seen as the equivalent to a terminal velocity in free fall. A consequence of the speed change at 1500 ms is a slight increase of the out-of-plane displacement at (see Fig. 10e) around the same instant. Then, a strong relationship between the in-plane and the out-of-plane information is observed.

As a last observation, the two experiments with pumice (Fig. 10d and f) exhibit an overall similar evolution for both components of displacement.

The data in Fig. 10 allows us to roughly estimate the scaling and the dynamic regime of the three experiments by the use of the Froude number (Gray et al. 2003), which is given by $Fr=u/\sqrt{gw\cos \gamma }$, where u and w correspond to the values observed at full cavity. For cornstarch, pumice L1, and pumice L5, the Froude number yields 2.1, 6.0, and 7.1, respectively; all of these values are within the supercritical range of flow, which implies the appearance of slight jumps in velocity and thickness of the free stream surface. Additionally, we notice a close scaling between the two experiments with pumice.

In order to further compare the evolution of the out-of-plane component of displacement for the three current experiments, next, we calculate two parameters derived from that displacement component (for each snapshot): the ensemble spatial average of displacement ($\overline{w}$), for a particular image, and the standard deviation of the time derivative of displacement (${\sigma}_{\dot{w}}$). These results are shown in Fig. 11, for the three current experiments. The first parameter, $\overline{w}$, is proportional to the granular material volume in the flume (the time at which the cavity gets full is indicated by the position of the maximum peak). The second parameter, ${\sigma}_{\dot{w}}$, is related to the level of temporal instabilities of the height distribution.

Fig. 11

Time-derived parameters for the out-of-plane component of displacement: average of displacement (material volume) and standard deviation of time derivative of displacement

Considering the average curves, $\overline{w}$, positive values of their slope indicate that the cavity is being filled and negative values that the cavity is being drained. Unlike the experiments with pumice, the cornstarch curve shows a positive plateau that is related to a relatively long time in the full state; this behavior stems primarily from the quasi-rigid-body motion of the granular flow. As to the standard deviation of the time derivative, ${\sigma}_{\dot{w}}$, the three experiments show significant differences, which are mainly due to their overall velocities and their level of agglomeration. The distinct values of speed also affect the time at which the cavity gets full, as shown by the average curves. We can also observe that for pumice (L5 and L1), at the trailing edge of the stream, the level of instabilities is on the order than at the forefront.

The afore-described technique can be implemented under real-scale conditions as long as the following conditions are met. First, for a large observation area, the illumination levels have to be large enough. In this case, the fringe pattern can be either produced by a high-power projector, such as those used for cinema projection, or by the combination of a laser and a grating (Mares et al. 2018). This latter option could be used under any light conditions, such as day or night (under day conditions, a dichroic filter may be utilized in order to enhance the red and blue signals). For generating high levels of uniform illumination, a set of several light sources can be used simultaneously since the position of the sources does not influence the in-plane results. Considering the imaging components, camera, and lens, large fields of view can be obtained by using full-frame (35-mm) sensors and wide-angle lenses. Besides, the distance between camera and object can be adequately selected by varying the focal distance of the imaging lens, for example, a distance value of 10 m with a focal distance of 18 mm. Additionally, considering the period of the fringe pattern, it is necessary to maintain a constant number of pixels per fringe, which is about 10 pix/fringe for any condition (also, the fringe period varies according to the field of view).

In real-world conditions, the weather may be severe, and in the presence of rain, the contrast of the granular material is reduced; this problem may be addressed by considering the power level of the light sources.

Conclusions

We have presented experimental results that show the feasibility to measure dynamic three-dimensional displacement fields in a small-scale flume. This has been done by using a technique that is able to simultaneously measure the three components of displacement by color-encoding the signals of two optical techniques: fringe projection and digital image correlation. To contrast different temporal behaviors, two types of granular materials have been used, which presented different levels of clustering. In this regard, the high-clustering level material evolved resembling a quasi-rigid body motion, and the low-clustering level material resembled a granular flow. Additionally, two lengths of flumes were tested, and in the preliminary results, similar displacement dynamics for the two were observed.

The presented technique not only allows us to observe dynamic phenomena invisible to the naked eye by means of revealing slow motion videos but also lets us calculate the particle’s movement indicators, such as streamlines and swirling, which provide the degree of turbulence (present in the flow in a quantitative way), as well as the presence of wave systems or surface patterns related to internal instability conditions (Kelvin-Helmoltz and Von Karman instabilities) which can provide paramount information about the rheology and fluid-dynamics of the granular flows.