Introduction

It is essential to determine the shear strength parameters c and φ on a sliding surface for stability evaluation and engineering analysis of a landslide. Presently, these parameters are mainly determined by the test, engineering experience analogy method, and back analysis method (Sonmez et al. 1998). Among these methods, the back analysis method can accurately determine the shear strength parameters while considering the most important factors. The back analysis value is a reliable index that coincides well with the real shear strength parameter (Tang et al. 1999). Consequently, the parameter back analysis method is being used increasingly widely in the field of geotechnical engineering (Sonmez et al. 1998; Deng and Lee 2001; Saneio 1981).

In the traditional deterministic back analysis method, the shear strength parameters are determined by changing the values of c and φ to make the factor of safety Fs be equal to 1.0 (Tang et al. 1999; Wang et al. 2013). Either c or φ is assumed to be a certain value by experience for a selected slope cross section; the value of the other parameter is then calculated. This approach is greatly influenced by the experience of the engineer. At present, the physical model and the statistical result remain uncertain in the field of slope engineering, and the geotechnical properties exist with great spatiotemporal variations. Therefore, the traditional deterministic analysis method cannot accurately reflect the uncertainty and complexity of geotechnical properties when using only the mean parameter values of geotechnical materials for calculation.

To account for the uncertainties associated with the shear strength parameters, the limit analysis method based on the reliability theory is used along with the probability theory and mathematics statistics. It can well reflect the actual slope condition while considering the mean parameter values of geotechnical materials as well as the covariance matrix of random variables. Consequently, the reliability index is considered as a more reasonable and effective approach for slope stability analysis compared with the traditional factor of safety analysis method in the field of civil engineering (Low and Tang 1997). Many studies have already applied the reliability theory for back analysis for shear strength parameters (Tang et al. 1999; Wang et al. 2013; Low and Tang 1997, 2004; Zhang et al. 2009, 2010; Low 2014). Low and Tang (1997, 2004, 2014) proposed a new concept to explain the reliability theory by making 1-σ elliptic in the basic random variable space. However, most of the published literatures about the reliability analysis of slopes did not consider the influence of parameter correlation. Statistical data and experimental results increasingly reveal a negative correlation between the shear strength parameters c and φ that will subsequently influence the back analysis results (Cherubini 2000; Low 2007; Li and Low 2010; Lü and Low 2011; Wu 2013; Fenton and Griffiths 2008). Meanwhile, the 2D analysis method is still widely used for the stability analysis of a slope in the field of geotechnical engineering; however, this method cannot properly simulate 3D characteristics for slopes with complex and nonplane-strain configurations. Therefore, it is necessary to establish a 3D analysis model for slope stability evaluation for application to more engineering practices (Chen et al. 2001a, b; Hisatake and Hieda 2008; Stark and Eid 1998; Chen et al. 2013).

Therefore, in this study, a new parameter back analysis method is proposed by combining the 2D/3D upper bound method of limit analysis and reliability theory to accurately determine the shear strength parameters for a 3D slope with a single failure surface. Owing to the adoption of the reliability theory, several variables can be optimized simultaneously. The optimized values of c and φ can be determined by establishing a single equilibrium equation based on a selected failure surface. The 3D analysis method, which considers the influence of the lateral restraint and spatial variability of a sliding body on a factor of safety, can well reflect the 3D real failure behavior of a slope compared with the 2D analysis method. Studies on reliability indexes and the back analysis values of parameters with different correlation coefficients have already indicated the importance of accurate prior information for parameter determination.

Slope stability analysis based on upper bound theory

2D slope stability analysis based on upper bound theory

The upper bound limit analysis method is known as the energy method. The equations for the energy consumption balance of internal and external forces in the failure system can be established based on the principle of virtual work (Chen 1975; Chen and Liu 1990). Combined with the strength reduction technique, the values of c and φ are reduced to decrease the internal energy consumption. Then, the shear strength parameters c and φ can be determined by back analysis when the internal energy consumption is equal to the energy produced by the external force. When the factor of safety of the slope becomes 1.0, the back analysis values of the shear strength parameters are defined as the limit values in the strength reduction technique. The strength reduction factor (i.e., factor of safety) is used to evaluate the slope stability (Ausilio et al. 2001; Taylor 1948), which is defined as F s = c/c f or F s = tan φ/tan φ f. Here, F s is the shear strength reduction factor, c and φ are the original shear strength parameters, and c f and φ f are the shear strength parameters after reduction.

Kinematically admissible velocity field

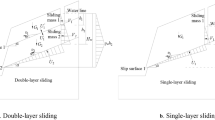
It is important to establish a failure model that satisfies a kinematically admissible velocity field in limit analysis. In this study, a vertical slice with a broken line failure surface is selected for analysis (Michalowski 1995), as shown in Fig. 1a.

Fig. 1
figure 1

2D slope stability analysis: a failure mechanism of slope with broken line sliding surface divided into vertical slices and b the pore water pressure on slice

Full size image

The relative velocity [υ] i − 1,i is defined as the vector difference of υ i to υ i − 1, which are the velocity vectors in adjacent slices. The velocity vectors υ i , υ i − 1, and [υ] i − 1,i satisfy the closure relations, as shown in Fig. 1a. The velocity formula can be established as follows based on Fig. 1a.

$$ {\upsilon}_i={\upsilon}_{i-1}\frac{ \cos \left({\alpha}_{i-1}-{\varphi}_{i-1}-{\left[\varphi \right]}_{i-1,i}\right)}{ \cos \left({\varphi}_i+{\left[\varphi \right]}_{i-1,i}-{\alpha}_i\right)} $$
(1)
$$ {\left[\upsilon \right]}_{i-1,i}={\upsilon}_i\frac{ \sin \left({\varphi}_i-{\varphi}_{i-1}-{\alpha}_i+{\alpha}_{i-1}\right)}{ \cos \left({\alpha}_{i-1}-{\varphi}_{i-1}-{\left[\varphi \right]}_{i-1,i}\right)} $$
(2)

Here, υ i and υ i − 1 are the velocities of a slice on the sliding surface, φ i and φ i − 1 are the internal friction angles of a slice on the sliding surface, α i and α i − 1 are the inclination angles of the sliding surface, and [υ] i − 1,i and [φ] i − 1,i are, respectively, the relative velocity and internal friction angle in the vertical direction of slices.

Formula for factor of safety

The upper bound solution of the factor of safety of the slope can be obtained by establishing virtual work equations based on the upper bound theory of limit analysis. In this study, the pore water pressure and soil weight are considered. The former is taken as an external force in the virtual work equations.

The virtual work equations can be established by assuming that internal work is equal to external work (i.e., D int = W ext) when the slope is in the limit state. The equations can be expressed as follows for a homogeneous slope:

$$ {F}_{\mathrm{s}}=\frac{{\displaystyle \sum_{i=1}^n{l}_i{\upsilon}_ic \cos {\varphi}_{\mathrm{f}}}+{\displaystyle \sum_{i=2}^n{\left[h\right]}_{i-1,i}{\left[\upsilon \right]}_{i-1,i}c \cos {\left[\varphi \right]}_{\mathrm{f}}}}{{\displaystyle \sum_{i=1}^n{W}_i{\upsilon}_i \sin \left({\alpha}_i-{\varphi}_i\right)}+{\displaystyle \sum_{i=1}^n{U}_i{\upsilon}_i \sin {\varphi}_{\mathrm{f}}}+{\displaystyle \sum_{i=2}^n{\left[\upsilon \right]}_{i-1,i}{P}_{\mathrm{W}\left(i-1,i\right)} \sin {\left[\varphi \right]}_{\mathrm{f}}}} $$
(3)

Here, φ f = arctan(tan φ/F s).

3D slope stability analysis based on the upper bound theory

The characteristic of solving an unknown in one equation (upper bound solution of the factor of safety) is retained when the limit analysis of the 2D slope is extended to the 3D condition. The most important issue is to determine the 3D velocity field of a hexahedral column by a certain method (Chen et al. 2001a). Similar to the upper bound method in 2D limit analysis, the slope is assumed to be in the limit state, and the slope failure body is divided into a series of vertical or inclined columns, as shown in Fig. 2 (Chen et al. 2001a). A 3D velocity field can be built in the failure body, which comprises a series of columns. The upper bound solution of slope stability can be obtained by 3D limit analysis using the principle of virtual work.

Fig. 2
figure 2

3D slope stability analysis: a the failure mass divided by columns with vertical interfaces and b hexahedral prism

Full size image

Figure 2b shows a hexahedral column in the slope failure body. ABCD and EFGH represent a part of the sliding surface and the ground surface, respectively; the front side ABFE and the back side DCGH are both perpendicular to the plane xoy, which is represented by the symbol “↔” and called the line interface. The left side ADHE and the right side BCGF are perpendicular to the plane yoz, which is represented by symbol “↕” and called the column interface.

According to the principle of virtual work, the energy equation in the 3D field can be established as follows:

$$ {\displaystyle \sum {D}_{i\leftrightarrow j}^{\ast }}+{\displaystyle \sum {D}_{i\updownarrow j}^{\ast }}+{\displaystyle \sum {D}_{i,j}^{\ast }}=W{V}^{\ast }+{T}^{\ast }{V}^{\ast } $$
(4)

The three terms on the left of the equation represent the internal energy dissipations on the line interface, column interface, and bottom-sliding surface. The two terms on the right of the equation represent the works done by the self-weight of the landslide and external force. Here, W is the volume force in the plastic zone; T *, the external load in the plastic zone; and V *, the plastic displacement velocity induced by the incremental external load.

Similar with the 2D limit analysis method, the shear strength parameters are reduced and are expressed as c f = c/F s and tan φ f = tan φ/F s. Consequently,

$$ {\displaystyle \sum {D}_{i\leftrightarrow j,\mathrm{f}}^{\ast }}+{\displaystyle \sum {D}_{i\updownarrow j,\mathrm{f}}^{\ast }}+{\displaystyle \sum {D}_{i,j,\mathrm{f}}^{\ast }}=W{V}^{\ast }+{T}^{\ast }{V}^{\ast } $$
(5)

Here, the three terms with subscript “f” on the left-hand side of the equation represent physical quantities after strength reduction. The limit state of the slope can be reached by solving the factor of safety F s, which is implicitly embodied in c f and φ f.

The determination of the upper bound solution in 3D limit analysis can be transformed as a problem to solve the velocity field of a column system with a vertical or inclined interface. The solving process is shown in published literature (Chen et al. 2001a, b).

Comparison calculations with classical examples

To show the validity of the present approach, the contrast calculation with Michalowski’s (2010) example is adopted: a uniform 1:1 slope of overconsolidated soil with φ = 20° and c = 20 kPa is built; the unit weight of the soil is γ = 18 kN/m3. The height of the slope is 15 m, and its width is restrained to 30 m by rock formations. The factor of safety calculated by different methods is presented in Table 1.

Table 1 Contrast calculations of the F s values of slope
Full size table

The comparative analysis shows that the used method in this paper is effective for evaluating slope stability. In addition, it is seen that the factor of safety for slope in the 2D model is lower than that in the 3D analysis due to the fact that the 3D analysis method takes into account the influence of the lateral restraint. The corresponding explanation has already been made by Michalowski (2010).

Parameter back analysis of reliability method

The slope reliability index (i.e., slope stability probability) refers to the probability of a slope that completes the predetermined function under the specified condition and time. The function equation is adopted to represent the limit state of slope for reliability analysis in slope engineering. The factor of safety F s is commonly used to evaluate the slope stability. When F s ≤ 1, the slope fails because of instability; when F s = 1, the slope is in the limit state. The function equation is given as follows:

$$ Z=g\left({X}_1,{X}_2,{X}_3\cdots {X}_n\right)={F}_{\mathrm{s}}-1 $$
(6)

Here, X 1, X 2, X 3 ⋯ X n are random variables. The slope stability can be evaluated by the values of Z. When Z < 0, the structure fails; when Z = 0, the structure is in the limit state; and when Z > 0, the structure works reliably.

The basic calculation process of the reliability index is as follows. A new normal variable is used, which is expressed as \( \overset{\wedge }{X_i}=\frac{X_i-{\overline{X}}_i}{\sigma_i}\left(i=1,2,\cdots, n\right) \). The limit state surface is transformed in the standard normal distribution space. Subsequently, the new limit state surface is represented as a multidimensional curved surface in this space. A special point can be explored in a curved surface that makes the shortest distance from the origin point in coordinate to the tangent surface, which passes by this special point. Such special point is defined as the designed checking point P *, and the shortest distance is defined as the reliability index β (Verma et al. 2010), as shown in Fig. 3.

Fig. 3
figure 3

The reliability index β and the checking point P *

Full size image
$$ \beta =\sqrt{\overset{\wedge }{{X_1}^2}+\overset{\wedge }{{X_2}^2}+\cdots +\overset{\wedge }{{X_n}^2}}=\sqrt{{\displaystyle \sum_{i=1}^n\overset{\wedge }{{X_i}^2}}} $$
(7)

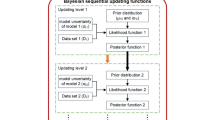
The failure model is mainly established based on the limit state of a slope in the back analysis of the shear strength parameter based on the reliability theory. A series of geotechnical parameter values is obtained by back analysis by assuming a critical factor of safety as the back analysis objective. The final back analysis result is determined as the one that results in the minimum reliability index (Sun et al. 2012). When the reliability theory is used for slope stability analysis, the influence of uncertain factors on the slope can be considered by calculating the reliability index and failure probability. Therefore, the reliability method can reveal the slope stability behavior in a more realistic scenario. In this paper, the spreadsheet method, constrained optimization method, and Monte Carlo simulation are described as follows.

Spreadsheet method

The spreadsheet-based method adopted in this study is a type of Low and Tang’s first-order reliability method (FORM). In this method, Microsoft Excel is used to determine the reliability of nonnormal variables (Low and Tang 1997, 2004, 2007). The Hasofer-Lind reliability index is expressed as follows (Low 2007; Lü and Low 2011):

$$ \beta =\underset{x\in F}{ \min}\sqrt{{\left(\theta -{\mu}_{\theta}\right)}^T{C}_{\theta}^{-1}\left(\theta -{\mu}_{\theta}\right)} $$
(8)

The reliability index determined by Eq. (8) can also be expressed by a 1-σ ellipse in the 2D random variable space when β = 1. Thus, the reliability value can be defined as the ratio of the axial length of the smallest ellipse that is tangent to the limit state curve to that of the 1-σ ellipse, as shown in Fig. 4 (Low and Tang 1997, 2004, 2014; Mollon et al. 2009). If the parameters are not interrelated, the 1-σ ellipse is a standard ellipse that is parallel to the coordinate, and the center of the ellipse lies at the point with a mean value. Otherwise, the ellipse will be inclined (Low and Tang 1997).

Fig. 4
figure 4

1-σ ellipse

Full size image
$$ \beta =\frac{R}{r} $$
(9)

The reliability index and optimal solution are obtained by solving Eq. (8) by the optimization algorithm tool in Microsoft Excel.

Constrained optimization method

The constrained optimization method is another type of FORM; it is implemented by using Matlab in this study to explore the minimum value of the objective function under the actual required constraint conditions. When the reliability theory is adopted for slope stability analysis, the minimum reliability index should be explored to evaluate the slope stability, which can be determined by the constrained optimization method. The minimum reliability under the constraint condition can be solved easily by the optimization toolbox in Matlab software (Song and Guan 2001).

The checking point, which is unknown initially, can be determined by optimizing the reliability index β. β is assumed as a function of the point P(X 1, X 2, X 3 ⋯ X n ) in the limit state surface. The minimum value of β can be searched in this area, which is called the reliability index. The corresponding point P*(X 1*, X 2*, X 3* ⋯ X n *) is the checking point, as shown in Fig. 3.

Based on the limit state equation (4) and the expression of reliability index β (Eq. (5)), the constraint optimization model for determining the reliability index β can be represented as follows (Zhang 2007):

$$ \left\{\begin{array}{l} \min {\beta}^2={\displaystyle \sum_{i=1}^n{\left(\frac{X_i-{\overline{X}}_i}{\sigma_i}\right)}^2}\\ {}s.t.Z=g\left({X}_1,{X}_2,{X}_3\cdots {X}_n\right)={F}_{\mathrm{s}}-1=0\end{array}\right. $$
(10)

Monte Carlo simulation

The Monte Carlo simulation is considered as stochastic simulation method or statistical experimental method. It is developed as a numerical method to solve uncertainty or certainty problems. The traditional Monte Carlo simulation can be used to determine the failure probability of a structure and to obtain the reliability index β. However, the traditional Monte Carlo simulation cannot be used to determine the checking point P *. In this study, the results of the failure probability, checking point, and reliability index of the structure are obtained according to a random number generated by the Matlab statistics toolbox using the Monte Carlo simulation based on the optimum principle. When the Monte Carlo simulation is used to optimize the solution, the random variable in the limit state surface is sampled, and the distance from the sampling point to the original point is calculated. The minimum distance is defined as the reliability index.

For N random variables, only N − 1 random variables should be sampled to ensure that the sampling points are located in the limit state surface. The others can be obtained by the limit state equation (Fenton and Griffiths 2008):

$$ g\left({x}_1,{x}_2,{x}_3\cdots {x}_n\right)=0 $$
(11)
$$ {x}_i={g}^{\prime}\left({x}_1,{x}_2,{x}_3\cdots {x}_{i-1},{x}_{i+1},\cdots, {x}_n\right) $$
(12)

When the Monte Carlo simulation is adopted for reliability analysis, the value of φ is randomly generated, and the corresponding c values can be determined by solving the limit state equations. Subsequently, the reliability index (checking point) can be obtained. The number of simulations is a key point in the Monte Carlo simulation. Existing studies have taken different simulations in Monte Carlo simulation for special requirements (Zhang et al. 2010; Fenton and Griffiths 2008). To analyze the effect of the number of simulations, a comparative analysis is presented in Fig. 5.

Fig. 5
figure 5

The frequency distribution plot of the simulation samples: a 1000 times of simulation, b 10,000 times of simulation, and c 100,000 times of simulation

Full size image

Figure 5 shows that the distribution of simulation samples is more concentrated with an increase in the number of simulations. The results determined by the Monte Carlo simulation are close to the real value. When the number of simulations reaches 103, 104, and 105, the average values of φ are 12.95°, 12.99°, and 13.00° with standard deviations of 1.02°, 1.00°, and 1.00°, respectively. The results after 105 simulations are almost equal to the test value of 13°, especially in terms of the standard deviation (1°). Consequently, the results after 105 simulations are used for calculations in this study.

Process of parameter back analysis by the reliability method

  1. 1.

    Determine the different velocity of vertical slices or hexahedral prisms.

  2. 2.

    Calculate the factor of safety of the slope according to the principle of virtual work.

  3. 3.

    Optimize the values of c and φ, and explore the minimum reliability index. The minimum value of the reliability index can be obtained by solving the objective function within the constraint condition of F s = 1.0 by the FORM. In the Monte Carlo simulation, the value of c is solved by the limit state equation with a φ value that is simulated with the probability distribution. The combined solution of c and φ is explored to obtain the minimum reliability index.

Case study

Background of the Zhuquedong landslide

At around 1:00 AM on July 27, 2007, a massive landslide was triggered by rainwater after several days of rain in Zhuquedong village, Luxi town, Xiangxi County, Hunan Province, China. This landslide induced the substantial slide of an embankment in the landslide area with vertical and horizontal displacement of 20 and 60 m, respectively. The culvert was broken, and the drainage and slope protection structures were deformed greatly. The landslide boundary, which had a chair shape, is controlled by the geological structure, and the Danqing River is in front of the landslide area. The landslide body mainly comprises gravel soil and strong or weak weathered rock. The weathered rock softens after being soaked and shows poor anti-erosion ability. The attitude of the rock is gentle, which can easily induce creep deformation. The weak interlayer and intercalated clay layer make it possible to trigger a landslide. The total length of the landslide area is 448 m. The average width and average thickness of the landslide are 450 and 15 m, respectively. The volume of the landslide body is about 2,600,000 m3, as shown in Fig. 6.

Fig. 6
figure 6

Zhuquedong landslide

Full size image

Figure 7 shows a plane graph of the landslide. The landslide area is divided as area I and area II for 3D parameter back analysis. The typical sections A, B, and C are selected for 2D parameter back analysis.

Fig. 7
figure 7

A partition plan for landslide sections

Full size image

It is necessary to accurately determine the strength parameters c and φ beforehand to take effective measures to harness landslides. According to the saturated three triaxial test, the mean values of the cohesion and internal frictional angle of the soil mass in the Zhuquedong landslide were 7 kPa and 13° with standard deviations of 3 kPa and 1°, respectively.

The statistic and spatial uncertainties are neglected in this paper because of the lack of satisfactory evaluation (which is a shortcoming of this paper). In this paper, the mean values of the cohesion and frictional angle on the sliding surface are taken as statistical values for shear strength parameter back analysis (Zhang et al. 2009). The types of probability distributions of the parameters also affect the calculation of the reliability index. Hoek (1998) and Lü and Low (2011) presented a normal distribution of soil shear strength parameters. Langejan (1965) and Wu and Kraft (1900) took the lognormal distribution of c and φ according to their own experience or study. Lumb (1970) and Harrop-williams (1986) stated that the β-distribution could well reflect the actual condition. Fenton and Griffiths (2008) showed that c conforms to the logarithmic normal distribution and φ, to the β-distribution. For briefness and practicality, the normal distribution is adopted in this study. Back analysis is conducted by assuming that c and φ are interindependent because the correlation between them was not recorded in the investigation report of the Zhuquedong landslide. Finally, the influences of the correlation of c and φ back analysis are discussed and illustrated.

Back analysis of shear parameters based on 2D condition

Parameter back analysis based on the reliability method

Three typical sections (called sections A, B, and C) are selected for shear strength parameter back analysis of the Zhuquedong landslide. The dividing slices and calculation models are shown in Fig. 8.

Fig. 8
figure 8

The calculation model of the Zhuquedong landslide: a section A, b section B, and c section C

Full size image

The typical reliability analysis of shear strength parameter back analysis is performed on sections A, B, and C for the Zhuquedong landslide by the different methods. The results are shown in Table 2.

Table 2 Results determined by the different methods
Full size table

In addition to the Excel table used in the spreadsheet method for reliability analysis (as shown in Fig. 9), the 1-σ ellipse is also adopted for analysis (Low and Tang 1997, 2004, 2014). The typical calculation case is performed on section B, as shown in Fig. 10. The limit state surface is a curve when F s = 1. The 1-σ ellipse will be tangent to the limit state surface through a transformation. The tangent point (i.e., checking point) is (8.31, 13.51) with the reliability index β = 0.67. The results coincide well with the results shown in Table 2. The graph shows the reliability more intuitively.

Fig. 9
figure 9

Back analysis data sheet on section B in landslide

Full size image
Fig. 10
figure 10

The 1-σ ellipse and β ellipse with correlation coefficient of 0 (ρ c,φ  = 0)

Full size image

Analysis and comparison of back analysis parameters with the traditional method

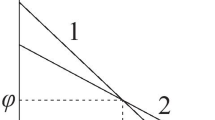
In the traditional back analysis method, several c-φ curves are plotted based on at least two slope cross sections. After that, the back analysis value of the shear strength parameter is determined according to the intersection point of the curves. However, the slope section is uncertain and is assumed subjectively, and even the c-φ curves may not intersect at one point in the traditional back analysis method. Figure 11 shows the calculation results determined by the traditional back analysis method. The three c-φ curves intersect at three points: a, b, and c. The uncertainty of the intersection points influences the correct determination of the back analysis value. Actually, the c-φ curve presents different shapes for different assumed slope cross sections. Thus, several back analysis values are obtained without a real value.

Fig. 11
figure 11

The back analysis by c-φ curves

Full size image

Figure 11 shows the checking points determined by the reliability method. The checking points P * determined by the spreadsheet method, constrained optimization method, and Monte Carlo simulation nearly intersect at one point. The feasibility and effectiveness of the above three methods are well validated. The checking points of each slope section determined by these three methods are close to the c-φ curve. The results show that the back analysis method based on the reliability theory coincides with the traditional back analysis method. Irrespective of either the traditional back analysis methods or the parameter back analysis method based on the reliability theory is used, the back analysis results are affected by the selected slope cross section. Consequently, the final determination of the back analysis value in the traditional 2D analysis model assumes the greatest importance for preventing landslides.

It is assumed that a variety of prior information is accurately known and that the uncertainty of other factors is neglected. For a small landslide, the back analysis can be processed based on the most dangerous sliding surface, and the results are considered the values of the shear strength parameter for engineering design. For a large or secondary landslide, the back analysis values determined by the most dangerous sliding surface are too conservative to prevent landslide disasters economically, especially for landside areas with good geological conditions. For this case, the landslide area can be divided into several areas based on the geological conditions. In areas with similar geological conditions, the shear strength parameters can be back-analyzed based on the most dangerous sliding surface, and the back analysis results are used as design values for this area.

Back analysis of shear parameters based on 3D condition

Owing to the obvious 3D features of a landslide in nature, the actual slope behavior can be more accurately reflected by 3D stability analysis than the 2D method, especially when the failure surface has been determined (Chen et al. 2001a, b). With the consideration of groundwater, the pore water pressure should be calculated using the virtual power equation (12). To satisfy the requirement of the traditional back analysis method, the 3D calculation model for a landslide body is established based on zones I and II in the Zhuquedong sliding body. Meanwhile, the model of the whole landslide (combined with zones I and II) was established for back analysis. Figure 12 shows the plane configuration of the landslide.

Fig. 12
figure 12

Plans for the Zhuquedong landslide discretization: a area I and b area II

Full size image

Parameter back analysis based on the reliability method

The factor of safety can be solved using Matlab and Microsoft Excel based on the virtual power equation (12). Subsequently, the limit state equations are established for the reliability back analysis of shear strength parameters. The back analysis results of shear strength parameters as determined by the spreadsheet method, constrained optimization method, and Monte Carlo simulation are shown in Table 3. Figure 13 shows the computational procedure of the spreadsheet method. The limit state equations derived from the 3D failure model are very complex, and the programming workload is large. Consequently, the increased number of samples requires long computation time in the Monte Carlo simulation.

Table 3 The effect of c, φ correlation on back analysis
Full size table
Fig. 13
figure 13

The spreadsheet of 3D back analysis

Full size image

Taking area I in the landslide body as an example, the checking point is determined as (6.25, 12.79) with the reliability index of 0.32 (β = 0.32) by combining 1-σ ellipse (Fig. 14). These results coincide well with those determined by the above three methods. The results of the reliability index and checking point P * determined by the different methods in different areas are nearly the same, as shown in Table 4.

Fig. 14
figure 14

The 1-σ elliptic and β elliptic of area I with ρ c,φ  = 0

Full size image
Table 4 Summary table of 3D results
Full size table

The checking points are distributed near the corresponding c-φ curves, as shown in Fig. 15. Consequently, the feasibility and effectiveness of the back analysis method based on the reliability theory are well verified. The back analysis values of c and φ in the 3D model are smaller than those determined by the 2D method. Actually, the back analysis result based on the 3D upper bound theory is close to the real values. The 3D analysis method is recommended to determine the range of parameters.

Fig. 15
figure 15

Back analysis by c-φ curve

Full size image

Analysis and comparison of back analysis parameters with the traditional method

Figure 15 shows the relation curves between c and φ as determined by the traditional parameter back analysis method. The c-φ curves do not intersect at one point, which means that the parameter cannot be obtained by the traditional back analysis method. When the reliability theory is applied to parameter back analysis, the randomness and uncertainty of geotechnical parameters on slope stability evaluation are considered, although an unexpected impact may still exist. The reliability-based method is accurate and efficient compared with the traditional method. The optimized values of c and φ can be determined by solving a single equilibrium equation based on the reliability theory, which is subsequently used to solve the strength parameter back analysis with a single sliding surface. Actually, there is only one landslide area for most slopes, which means that the parameter back analysis method based on the reliability theory can be widely used for most landsides.

Correlation analysis of shear strength parameters on sliding surface

The above calculations are all performed under the assumption that c and φ are independent. Studies have revealed a negative correlation between c and φ, and the correlation coefficient is in the range of −0.24 to −0.7 (Cherubini 2000; Wolff 1985). To study the influence of the correlation of c and φ on the determination of the parameter or the reliability analysis, the correlation coefficients (ρ c,φ ) are set as −0.3, −0.5, −0.7, and −0.9, respectively, for evaluation. The spreadsheet method is adopted for reliability back analysis by taking area I in the 3D analysis model and section B in the 2D model as examples. The corresponding matrix of correlation coefficients is as follows:

$$ \left[\begin{array}{cc}\hfill 1\hfill & \hfill {\rho}_{c,\varphi}\hfill \\ {}\hfill {\rho}_{c,\varphi}\hfill & \hfill 1\hfill \end{array}\right] $$
(13)

The back analysis values of parameters are shown in Table 4. When the negative correlation of c and φ is considered, the results of section B and area I, whose checking points deviate greatly from the original point, are different from those obtained without consideration of such correlation, especially when the negative correlation of c and φ increases. As for the area II model and the whole landslide model, whose checking points are close to the original point, the back analysis value of the parameter is not greatly affected by the negative correlation, especially for the whole landslide model.

Figure 16 shows the different 1-σ ellipses for different correlation coefficients. The inclination degree of the ellipse increases with the negative correlation. In an inclined ellipse, more transformations are needed to make it tangent to the limit state surface, which will subsequently increase the value of the reliability index. For example, when ρ c,φ  = 0, the reliability index of section B is 0.67; when ρ c,φ  = −0.9, the reliability index increases to 2.02, as shown in Fig. 17. Even for the whole landslide with a small reliability index, the reliability index with ρ c,φ  = −0.9 is more than two times of that with ρ c,φ  = 0. The prior distribution and posterior distribution, shown in Fig. 18, indicate that the distribution of the parameters after back analysis changes greatly with the change in the correlation coefficients. Based on the above analysis, the value of the reliability index is conservative in the parameter reliability analysis if the negative correlation of the shear strength parameters is not considered, and the back analysis values of parameters may differ greatly. Consequently, to make the back analysis value more close to the real value, it is important to obtain accurate information about the prior distribution (Zhang et al. 2009).

Fig. 16
figure 16

The 1-σ elliptic with different correlation coefficients

Full size image
Fig. 17
figure 17

The effects of negative correlation on reliability index

Full size image
Fig. 18
figure 18

The contrast diagram of prior distribution and posterior of section B by the spreadsheet method: a c and b φ

Full size image

In probability back analysis, the distributions of all basic random variables are improved. However, the change in the probability density distribution differs for different parameters. The prior distribution of the internal frictional angle φ differs from that after improvement, and the probability density distribution of cohesion c does not change greatly, as shown in Fig. 18. The uncertainty of the factor of safety is influenced by different parameters with different intensities. The parameter that significantly influences the factor of safety will induce a great change in the probability density distribution (Zhang et al. 2009; Wang et al. 2013). Furthermore, the posterior distribution is more concentrated than the prior distribution, which is due to the result that the uncertainty of the input parameter is reduced in the back analysis proposed in this study.

Discussion

In some cases, the parameter cannot be determined accurately by the traditional back analysis method since there is no intersection for different sections of a landslide when the 2D failure model is used. When the 3D failure model is adopted in traditional back analysis, two c-φ curves do not even intersect, which means that the traditional back analysis method cannot determine the back analysis value of the shear strength parameters for some cases. The existing problems greatly restrict the application of the traditional back analysis method. However, the problem of selecting an intersection point can be solved when the reliability theory is used for the back analysis of shear strength parameter. Consequently, the back analysis can be processed by selecting a cross section of a slope or a landslide zone, and the result can be easily obtained with a comprehensive consideration of the randomness and uncertainty of geotechnical parameters.

The back analysis value differs for different cross sections or landslide zones even though the back analysis based on the reliability theory is adopted. In 2D failure model, the three c-φ curves corresponding to the three cross sections do not intersect at a single point, but the curves intersect in a small area. Consequently, the checking points determined by the reliability theory on these three cross sections will not differ greatly. The error of the results will not be great irrespective of which cross section is selected for back analysis. In the 3D failure model, the c-φ curves differ greatly for different landslide zones, which result in different checking points. Consequently, there is a great error irrespective of the revision value used for the design. The determination of the cross section or landslide zone for the stability analysis of a slope becomes difficult. For a small slope, the most dangerous sliding surface can be selected in 2D parameter back analysis without considering the effect of other factors on the inversion results. In the 3D model, the whole landslide failure model can be used for parameter back analysis, and the back analysis values are used as the final design values of the shear strength parameter. For a large or secondary landslide, the back analysis value is too conservative to prevent landslide disasters economically if only the most dangerous sliding surface is selected for back analysis, especially for a landside area with good geological conditions. The results determined by the 3D failure model (see “Back analysis of shear parameters based on 3D condition” section) show that the back analysis value derived from the whole landslide failure model is between the values determined by the two landslide zones. These results do not well reflect the characteristic of the parameters in these two zones. In this case, the landslide body can be divided into different zones based on the geological conditions, and the back analysis value of the parameter can be used as a design value for each divided zone.

The back analysis of the shear strength parameters is performed for both 2D and 3D failure models in this study. The results show that the value of the parameter determined by the 3D upper bound theory is smaller than that determined by the 2D theory. In the former, the whole landslide failure model is established with the consideration of the lateral constraint, which well reflects the real failure model of landslides. Consequently, the results are more close to the real values. In 2D upper bound back analysis, a few cross sections in the landslide area are selected subjectively for analysis, which will subsequently induce a random result. Consequently, 3D stability analysis method is recommended to reveal the real behavior of a slope with a complicated ground surface or 3D features.

In this paper, the total stress is used to analyze the effect of the groundwater, which makes the virtual power equation more simple and intuitive. This method has already been validated by many researchers (Michalowski 1995, 2013; Kim et al. 1999; Viratjandr and Michalowski 2006).

The key point for the prevention of the landslide disaster is to determine the shear strength parameters c and φ on the sliding surface, and the main purpose of this paper is to solve the problem of back analysis of shear strength parameters on the sliding surface for 3D condition. In the process, the 3D slope body is divided into a series of prisms having rectangular inclined side faces with an assumption that the shear strength parameters on the interfaces between two adjacent prisms are consistent with those on the sliding surface. By making this assumption, the velocity field in three dimensions can be well satisfied (Chen et al. 2001a, b). However, it will obviously influence the results of back analysis for a landslide in engineering practice when groundwater exists. For example, an unsaturated zone above the water table may develop matric suction, contributing to the soil’s shear strength and consequently enhancing the slope stability, although such a stabilizing factor will dramatically decrease and eventually diminish with an increase in the moisture content/degree of saturation due to rain or flood. Consequently, it is necessary to further study how to accurately evaluate the influence of the real shear strength parameters of the unsaturated zone on the back analysis of shear strength on the sliding surface.

Conclusions

  1. 1.

    With reference to the traditional back analysis of shear strength parameters for landsides, 2D and 3D back analysis methods of shear strength parameters are proposed based on the upper bound theory of limit analysis. By combining the reliability analysis method with the 2D and 3D upper bound method in limit analysis, a new, simple, and practical reliability back analysis method for shear strength parameters is proposed. In this method, the optimized values of c and φ can be solved by establishing a single equilibrium equation in consideration of the influence of the randomness and uncertainty of the geotechnical parameters on the slope stability. The proposed method can be used for strength parameter back analysis of a landslide with a single sliding surface under 2D or 3D conditions.

  2. 2.

    Take the Zhuquedong landslide with a broken line surface for example. The corresponding limit state equations are established based on the reliability theory for both the 2D and 3D failure models. The back analysis values of c and φ determined by the reliability theory using a combination of the spreadsheet method, constrained optimization method, and Monte Carlo simulation are nearly the same. These results verified the feasibility and effectiveness of the parameter back analysis method based on the reliability theory in this study. The proposed method also provides a reference for further study on the back analysis method based on the probability reliability theory.

  3. 3.

    The back analysis values of shear strength parameters can be obtained by both the 2D and the 3D failure model. However, the 3D upper bound theory can consider the lateral restraint of the landslide body that reflects the real failure model of landslides. Consequently, the 3D analysis method is recommended to determine the shear strength parameters for natural landslides.

  4. 4.

    The back analysis results and reliability index are discussed by assuming different correlation coefficients of c and φ. These results show that the reliability index is conservative when the negative correlation of c and φ is neglected. Information about the prior distribution greatly influences the back analysis of the shear strength parameters.

  5. 5.

    For a simple slope model, the back analysis value of the strength parameter can be quickly and accurately obtained by the spreadsheet method, constrained optimization method, or Monte Carlo simulation. However, the limit state equations in the constrained optimization method and Monte Carlo simulation become difficult to solve when the stability analysis model of the slope is complicated, which leads to a large workload for programming. For instance, when the sampling times increase in the Monte Carlo simulation, such calculations would be too time consuming and require a great deal of computing power. In the spreadsheet method, the calculating process is intuitive with small calculation workload, and the heavy programming workload can be avoided. Furthermore, this method is not greatly affected by the external conditions. Consequently, the spreadsheet method is found to be more convenient than the constrained optimization method and Monte Carlo simulation. The spreadsheet method can be used effectively to determine the back analysis value of the shear strength parameters of a slope.