1 Introduction

Third-generation semiconductor materials, such as zinc oxide (ZnO), silicon carbide (SiC), and gallium nitride (GaN), also known as piezoelectric semiconductors (PSs), exhibit significant advantages and potential over traditional semiconductors in the fields of optoelectronics and microelectronics [1,2,3,4,5,6]. These materials, known as wide bandgap semiconductors due to their larger bandgaps (Eg > 2.3 eV) compared to traditional semiconductors, are well-suited for the fabrication of high-frequency, high-power, high-temperature, and radiation-resistant electronic and optoelectronic devices. They have found extensive applications in various fields, including radio frequency communication, radar, satellite technology, automotive industry, and industrial power electronics. ZnO semiconductor materials and structures, as representatives of the third-generation semiconductors, have attracted considerable attention for their great potential application in the field of piezoelectric electronics and piezoelectric optoelectronics. Generally, commonly used ceramic-based piezoelectric materials such as BaTiO3 and PZT have a limitation on electronic devices because of their nonconductive property. ZnO materials and structures combine the advantages of both piezoelectric and semiconductor properties, thus enabling the utilization of piezoelectric coupling effect in novel electronic devices such as nanogenerators [7, 8] and field-effect transistors [1, 9]. To understand the underlying mechanism behind the application of ZnO in novel electronic devices, researchers have conducted some theoretical investigations on the multi-field coupling responses of the extension [10,11,12], bending [13,14,15], and static buckling [16] of ZnO nanofibers under mechanical loads, providing theoretical support for the design and application of ZnO PS devices.

There is a rising trend toward miniaturization in the development of smart and functional electronic devices with the advancement of micro/nanotechnology. However, with the reduction in the size of devices to the micro/nanoscale, flexoelectricity, referring to the polarization phenomenon induced from strain gradient or non-uniform strain [17], has a considerable effect on the macroscopic physical and mechanical behaviors of devices. Flexoelectricity can exist in any dielectric material due to symmetry breaking caused by the strain gradient. It should be noted that the symmetry of the material determines the flexoelectric coefficient tensor. Cross [18] found that cubic crystals possess only three independent nonzero flexoelectric coefficients. Quang and He [19] analyzed the number and types of all possible rotational symmetries of the flexoelectric coefficient tensor. Shu et al. [20] presented the nonzero flexoelectric coefficients in different crystal systems based on the fundamental tensor relations governing flexoelectric coefficients. This understanding of the flexoelectric coefficient’s symmetry and its relation to the crystal structure allows researchers to explore the flexoelectric properties of various materials.

The circular plate structure is commonly employed in various fields, including semiconductor devices such as wafers, civil engineering, machinery, and aerospace [21,22,23]. Some researchers have studied PS nanofibers and nanobeams and found that the flexoelectric field resulting from the strain gradient has a significant influence on their macroscopic multi-field coupling responses [24,25,26]. However, there is a lack of research into circular PS nanoplate structures considering flexoelectricity. In this paper, we investigate the multi-field coupling behaviors of a bending circular PS nanoplate. The study takes into consideration the flexoelectric effect, which means that the total polarization induced in the plate is influenced not only by the strain but also by its gradient. The paper is organized as follows. In Sect. 2, we provide a summary of the three-dimensional (3D) basic equations for PS structures with flexoelectricity. In Sect. 3, the two-dimensional (2D) equations for a circular PS plate considering flexoelectricity are derived based on the Kirchhoff thin plate model. The analytical expressions of physical fields in the static bending of circular PS plates under a central force are presented. Some numerical results and discussions are given in Sect. 4. Finally, we draw a conclusion in Sect. 5.

2 Three-Dimensional Equations for PSs with Flexoelectricity

In this section, we outline the three-dimensional equations for PSs with flexoelectricity. The continuum theory of flexoelectricity has been given in [27, 28], which is an extension of Toupin’s piezoelectric theory [29] by taking strain gradient and polarization gradient into account. For PS structures considering flexoelectricity, the constitutive equations can be given, according to [30, 31], as

$$ \begin{gathered} T_{ij}^{{}} = c_{ijkl}^{p} S_{kl} + d_{ijk} P_{k} \hfill \\ T_{ijk} = f_{lijk} P_{l} \hfill \\ E_{k}^{l} = - (a_{ki}^{s} P_{i} + d_{ijk} S_{ij} + f_{kjil}^{{}} S_{ji,l} ) \hfill \\ J_{i}^{p} = qp\mu_{ij}^{p} E_{i} - qD_{ij}^{p} p_{,i} \hfill \\ J_{i}^{n} = qn\mu_{ij}^{n} E_{i} + qD_{ij}^{n} n_{,i} \hfill \\ \end{gathered} $$
(1)

where the physical field quantities of Tij, Tijk, \(E_{k}^{l}\), \(E_{i}^{{}}\), \(J_{i}^{p}\), \(J_{i}^{n}\), \(S_{kl}\), \(P_{k}\), p, and n denote stress, higher-order stress, effective local electric field, electric field, hole current density, electron current density, strain, polarization, hole concentration, and electron concentration, respectively. The Toupin-type material constants \(a_{ij}^{s}\), \(c_{ijkl}^{p}\), and dijk in Eq. (1) can be obtained from the Voigt-type elastic constants \(c_{ijkl}^{E}\) and piezoelectric constants \(d_{ijk}^{E}\) at constant electric field, and the permittivity \(\varepsilon_{ij}^{{}}\) at constant strain. The relationships [29] between them are:

$$ \begin{gathered} a_{ij}^{s} = \chi_{ij}^{s} /\varepsilon_{0} \hfill \\ c_{ijkl}^{p} = c_{ijkl}^{E} + \chi_{mn}^{s} d_{mij}^{E} d_{nkl}^{E} /\varepsilon_{0} \hfill \\ d_{ijk}^{{}} = - \chi_{ij}^{s} d_{ijk}^{E} /\varepsilon_{0} \hfill \\ \end{gathered} $$
(2)

where \(\chi_{ij}^{s}\) is the reciprocal of susceptibility \(\eta_{ij}^{s}\) at constant strain, \(\eta_{ij}^{s} = \varepsilon_{ij}^{{}} /\varepsilon_{0} - \delta_{ij}\), \(\delta_{ij}\) the Kronecker delta. \(\mu_{ij}^{n}\)/\(D_{ij}^{n}\) and \(\mu_{ij}^{p}\)/\(D_{ij}^{p}\) represent the carrier mobility/diffusion constant for electrons and holes, respectively. q = 1.6 × 10−19 C is the element charge. The last two of Eq. (1) are the constitutive equations of current densities for both holes and electrons, commonly known as the drift–diffusion model. In this model, the current of carriers includes both the drift current driven by the electric field and the diffusion current caused by the concentration gradient of carriers.

The governing equations for PS structures with donors of \(N_{{\text{D}}}^{ + }\) and acceptors of \(N_{{\text{A}}}^{ - }\) read.

$$ \begin{gathered} T_{ij,j} - T_{ijk,jk} + f_{i} = \rho \ddot{u}_{i} \hfill \\ E_{i}^{l} - \varphi_{,i} + E_{i}^{0} = 0 \hfill \\ D_{i,i} = q\left( {p - n + N_{\text{D}}^{+} - N_{\text{A}}^{ - } } \right) \hfill \\ J_{i,i}^{p} = - q\dot{p} \hfill \\ J_{i,i}^{n} = q\dot{n} \hfill \\ \end{gathered} $$
(3)

where fi is the body force, \(E_{i}^{0}\) is the external electric field, and \(\varphi\) is the electric potential. It should be noted that the electric displacement is given by \(D_{i} = - \varepsilon_{0} \varphi_{,i} + P_{i}\), the classical definition in electromagnetics in Toupin’s piezoelectric theory. Additionally, in the absence of an external electric field, we have \(E_{i}^{0} = 0\), and \(E_{i} = - \varphi_{,i} = - E_{i}^{L}\). We write the concentrations of holes and electrons as follows

$$ p = p_{0} + \Delta p,\quad n = n_{0} + \Delta n $$
(4)

where

$$ p_{0} = N_{{\text{A}}}^{ - } ,\quad n_{0} = N_{{\text{D}}}^{ + } $$
(5)

In this paper, we consider PS structures with uniform impurities, where \(N_{{\text{D}}}^{ + }\) and \(N_{{\text{A}}}^{ - }\) are constants. With this assumption, the last three equations of Eq. (3) can be rewritten as

$$ \begin{gathered} D_{i,i} = q(\Delta p - \Delta n)\; \hfill \\ q\frac{\partial }{\partial t}(\Delta p) = - J_{i,i}^{p} \hfill \\ q\frac{\partial }{\partial t}(\Delta n) = J_{i,i}^{n} \hfill \\ \end{gathered} $$
(6)

Assuming that holes and electrons in PS structures experience small disturbances of \(\Delta p\) and \(\Delta n\), Eq. (2) can be linearized as

$$ \begin{gathered} J_{i}^{p} = qp_{{0}} \mu_{ij}^{p} E_{i} - qD_{ij}^{p} (\Delta p)_{,i} \hfill \\ J_{i}^{n} = qn_{{0}} \mu_{ij}^{n} E_{i} + qD_{ij}^{n} (\Delta n)_{,i} \hfill \\ \end{gathered} $$
(7)

3 Static Bending Analysis of Circular PS Plates

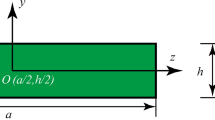
Consider an n-type circular PS plate as shown in Fig. 1, where R and h denote the radius and thickness of the circular plate, respectively. The polarized direction of the circular PS plate is upward along the thickness direction, and the bending deformation can be treated as a classical axisymmetric bending problem. To derive the plate equations, we employ the cylindrical coordinate system \(\left( {r,\theta ,z} \right)\). The coordinate origin is selected at the center point of the middle plane of the considered circular PS plate. In addition, the cylindrical coordinate system \(\left( {r,\theta ,z} \right)\) used here corresponds to the commonly used Cartesian coordinate system \(\left( {x_{1} ,x_{2} ,x_{3} } \right)\).

Fig. 1
figure 1

Schematic diagram of a circular PS plate

Full size image

According to the Kirchhoff thin plate theory, the midplane nonzero displacements of the circular PS plate can be written as

$$ u_{1} = u_{r} = zu_{1}^{(1)} ,\quad u_{3} = u_{z} = u_{3}^{(0)} $$
(8)

where \(u_{1}^{(1)}\) and \(u_{3}^{(0)}\), respectively, represent the extensional and flexural deformations. The corresponding strain components are given as

$$ S_{11} = zu_{1,1}^{(1)} ,\quad S_{22} = \frac{1}{r}zu_{1}^{(1)} ,\quad S_{13} = S_{31} = \frac{1}{r}(u_{1}^{(1)} + u_{3,1}^{(0)} ) $$
(9)

Thus, the nonzero strain gradients can be obtained as

$$ \begin{gathered} S_{11,1} = zu_{1,11}^{(1)} ,\quad S_{11,3} = u_{1,1}^{(1)} ,\quad S_{22,1} = \frac{1}{r}zu_{1,1}^{(1)} - \frac{1}{{r^{2} }}zu_{1}^{(1)} , \hfill \\ S_{22,3} = \frac{1}{r}u_{1}^{(1)} ,\quad S_{13,1} = S_{31,1} = \frac{1}{r}(u_{1,1}^{(1)} + u_{3,11}^{(0)} ) - \frac{1}{{r^{2} }}(u_{1}^{(1)} + u_{3,1}^{(0)} ) \hfill \\ \end{gathered} $$
(10)

For the thin plate model considered in this paper, the shear strain S31 can be ignored, that is

$$ S_{13} = S_{31} = \frac{1}{r}(u_{1}^{(1)} + u_{3,1}^{(0)} ) = 0 $$
(11)

As a result, there is the relation of \(u_{1}^{(1)} = - u_{3,1}^{(0)}\). From Eqs. (9), (10), and (11), the nonzero strains and nonzero strain gradients expressed in terms of displacement of \(u_{3}^{(0)}\), respectively, are

$$ S_{11} = - zu_{3,11}^{(0)} ,\quad S_{22} = - \frac{1}{r}zu_{3,1}^{(0)} $$
(12)
$$ \begin{gathered} S_{11,1} = - zu_{3,111}^{(0)} ,\quad S_{11,3} = - u_{3,11}^{(0)} \hfill \\ S_{22,1} = - \frac{1}{r}zu_{3,11}^{(0)} + \frac{1}{{r^{2} }}zu_{3,1}^{(0)} ,\quad S_{22,3} = - \frac{1}{r}u_{3,1}^{(0)} \hfill \\ \end{gathered} $$
(13)

Substituting Eqs. (12) and (13) into the stress constitutive relations of Eq. (1), we obtain

$$ \begin{gathered} T_{11} = c_{11} S_{11} + c_{12} S_{22} + d_{31} P_{3} \hfill \\ T_{22} = c_{21} S_{11} + c_{22} S_{22} + d_{32} P_{3} \hfill \\ T_{113} = f_{3113} P_{3} ,\quad T_{223} = f_{3223} P_{3} \hfill \\ \end{gathered} $$
(14)

According to Eq. (1), the electric field in the circular PS plate is

$$ \begin{gathered} E_{3} = a_{33}^{{}} P_{3} + d_{31} S_{11} + d_{32} S_{22} + f_{3113} S_{11,3} + f_{3223} S_{22,3} \\ = a_{33}^{{}} P_{3} - (d_{31} z + f_{3113} )u_{3,11}^{(0)} - \frac{1}{r}(d_{32} z + f_{3223} )u_{3,1}^{(0)} \\ \end{gathered} $$
(15)

Next, we derive the mechanical equilibrium equations of the circular PS plate using Hamilton’s variational principle. The elastic potential energy \(U\) of a circular PS plate is

$$ U = \frac{1}{2}(T_{11} S_{11} + T_{22} S_{22} + 2T_{13} S_{13} + T_{113} S_{11,3} + T_{223} S_{22,3} ) $$
(16)

The work done by the applied force is

$$ W = \int\limits_{\Omega } {qu_{3}^{(0)} } \text{d}V $$
(17)

With Hamilton’s variational principle, namely \(\int\limits_{\Omega } {\delta (U - W){\text{d}} V} = 0\), we can obtain

$$ \begin{gathered} \frac{\partial Q}{{\partial r}} + \frac{Q}{r} = rq \hfill \\ Q = \frac{{\partial M_{{\text{r}}} }}{\partial r} + \frac{{M_{{\text{r}}} - M_{\theta } }}{r} \hfill \\ \end{gathered} $$
(18)

where \(Q\) is the shear force, Mr and Mθ denote the radial and circumferential bending moments, and there are

$$ \begin{aligned} & M_{{\text{r}}} = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {(T_{113} + zT_{11} ){\text{d}}x_{3} } , \\ & M_{\theta } = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {(T_{223} + zT_{22} ){\text{d}}x_{3} ,} \quad Q = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {T_{13} {\text{d}}x_{3} } \end{aligned} $$
(19)

Now, we consider the clamped boundary conditions of the circular PS plate under an upward concentrated force F acting on the top surface’s center and the electrically insulated conditions at the top and bottom surfaces. The electric displacement D3 is given as

$$ \begin{gathered} D_{3} = P_{3} + \varepsilon_{0} E_{3} \hfill\\ \qquad= \left( {1 + \varepsilon_{0} a_{33}^{{}} } \right)P_{3} - \varepsilon_{0} \left( {d_{31} z + f_{3113} } \right)u_{3,11}^{(0)} - \frac{1}{r}\varepsilon_{0} \left( {d_{32} z + f_{3223} } \right)u_{3,1}^{(0)} \\ \end{gathered} $$
(20)

For electrically insulated conditions, there is \(J_{3}^{n} = 0\). Thus, from Eq. (7), we have

$$ q\Delta n = qn_{0} \frac{{\mu_{33}^{n} }}{{D_{33}^{n} }}\varphi + C_{1} $$
(21)

where C1 is an unknown constant. From Eq. (6), we obtain

$$ \left( {1 + \varepsilon_{0} a_{33}^{{}} } \right)P_{3,3} - \varepsilon_{0} d_{31} u_{3,11}^{(0)} - \frac{1}{r}\varepsilon_{0} d_{32} u_{3,1}^{(0)} = - qn_{0} \frac{{\mu_{33}^{n} }}{{D_{33}^{n} }}\varphi - C_{1} $$
(22)

From Eq. (15), we have,

$$ - \varphi_{,3} = E_{3} = a_{33}^{{}} P_{3} - \left( {d_{31} z + f_{3113} } \right)u_{3,11}^{(0)} - \frac{1}{r}\left( {d_{32} z + f_{3223} } \right)u_{3,1}^{(0)} $$
(23)

Immediately, from Eq. (23), we can obtain

$$ P_{3} = \frac{1}{{a_{33}^{{}} }}\left[ {\left( {d_{31} z + f_{3113} } \right)u_{3,11}^{(0)} + \frac{1}{r}\left( {d_{32} z + f_{3223} } \right)u_{3,1}^{(0)} - \varphi_{,3} } \right] $$
(24)

Substituting \(P_{3}\) given in Eq. (24) into Eq. (22), we have

$$ \frac{{1 + \varepsilon_{0} a_{33}^{{}} }}{{a_{33}^{{}} }}\left( {d_{31} u_{3,11}^{(0)} + \frac{1}{r}d_{32} u_{3,1}^{(0)} - \varphi_{,33} } \right) - \varepsilon_{0} d_{31} u_{3,11}^{(0)} - \frac{1}{r}\varepsilon_{0} d_{32} u_{3,1}^{(0)} = - qn_{0} \frac{{\mu_{33}^{n} }}{{D_{33}^{n} }}\varphi - C_{1} $$
(25)

Here, we consider the case where both the top and bottom surfaces are deposited electrodes in practical engineering. As a result, the electric potential in the plate can be approximated as a function of x3. Consequently, Eq. (26) can be rewritten as a second-order ordinary differential equation for the electric potential φ, which is given by,

$$ \varphi_{,33} - \kappa^{2} \varphi = C $$
(26)

where \(\kappa^{2} = qn_{0} \frac{{a_{33}^{{}} }}{{1 + \varepsilon_{0} a_{33}^{{}} }}\frac{{\mu_{33}^{n} }}{{D_{33}^{n} }}\) and \(C = \frac{{d_{31} }}{{1 + \varepsilon_{0} a_{33}^{{}} }}u_{3,11}^{(0)} + \frac{1}{r}\frac{{d_{32} }}{{1 + \varepsilon_{0} a_{33}^{{}} }}u_{3,1}^{(0)} + \frac{{a_{33}^{{}} C_{1} }}{{1 + \varepsilon_{0} a_{33}^{{}} }}\). Then, from Eq. (26), we have

$$ \varphi = C_{2} \sinh \kappa z + C_{3} \cosh \kappa z + \frac{C}{{\kappa^{2} }} $$
(27)

where C2 and C3 Eq. (27) into Eq. (24), we have

$$\begin{aligned} P_{3} &= \frac{1}{{a_{33}^{{}} }}\left[ \left( {d_{31} z + f_{3113} } \right)u_{3,11}^{(0)}\right. + \frac{1}{r}\left( {d_{32} z + f_{3223} } \right)u_{3,1}^{(0)}\\& \left. - C_{2} \kappa \cosh \kappa z - C_{3} \kappa \sinh \kappa z \right] \end{aligned}$$
(28)

From Eqs. (14), (19), and (28), the moments of \(M_{{\text{r}}}\) and \(M_{\theta }\) can be given as

$$ \begin{aligned} & M_{{\text{r}}} = A_{1} u_{3,11}^{(0)} + \frac{1}{r}A_{2} u_{3,1}^{(0)} + A_{3} , \\ & M_{\theta } = A_{2} u_{3,11}^{(0)} + \frac{1}{r}A_{4} u_{3,1}^{(0)} + A_{5}\end{aligned} $$
(29)

where

$$ \begin{gathered} A_{1} = \frac{{d_{31}^{2} }}{{a_{33} }}\frac{{h^{3} }}{12} + \frac{{f_{3113}^{2} }}{{a_{33}^{{}} }}h - c_{11} \frac{{h^{3} }}{12}\hfill \\ A_{2} = \frac{{d_{31} d_{32} }}{{a_{33}^{{}} }}\frac{{h^{3} }}{12} + \frac{{f_{3113} f_{3223} }}{{a_{33}^{{}} }}h - c_{12} \frac{{h^{3} }}{12}\hfill \\ A_{3} = - \frac{{2f_{3113} }}{{a_{33}^{{}} }}\sinh \frac{\kappa h}{2}C_{2} - \frac{{d_{31} }}{{a_{33}^{{}} }}\left( {h\cosh \frac{\kappa h}{2} - \frac{2}{\kappa }\sinh \frac{\kappa h}{2}} \right)C_{3}\hfill \\ A_{4} = \frac{{d_{32}^{2} }}{{a_{33}^{{}} }}\frac{{h^{3} }}{12} + \frac{{f_{3223}^{2} }}{{a_{33}^{{}} }}h - c_{22} \frac{{h^{3} }}{12}\hfill \\ A_{5} = - \frac{{2f_{3223} }}{{a_{33}^{{}} }}\sinh \frac{\kappa h}{2}C_{2} - \frac{{d_{32} }}{{a_{33}^{{}} }}\left( {h\cosh \frac{\kappa h}{2} - \frac{2}{\kappa }\sinh \frac{\kappa h}{2}} \right)C_{3}\hfill \\ \end{gathered} $$
(30)

Substituting Eq. (29) into Eq. (18), we can obtain the shear force Q

$$ Q = A_{1} u_{3,111}^{(0)} + \frac{1}{r}A_{1} u_{3,11}^{(0)} - \frac{1}{{r^{2} }}A_{4} u_{3,1}^{(0)} + \frac{1}{r}\left( {A_{3} - A_{5} } \right) $$
(31)

Then, substituting Eq. (31) into Eq. (18)1, we have

$$ A_{1} u_{3,1111}^{(0)} + \frac{2}{r}A_{1} u_{3,111}^{(0)} - \frac{1}{{r^{2} }}A_{4} u_{3,11}^{(0)} + \frac{1}{{r^{3} }}A_{4} u_{3,1}^{(0)} = 0 $$
(32)

Equation (32) has the following general solution

$$ u_{3}^{(0)} = C_{4} + C_{5} r^{2} + C_{6} \ln r + C_{7} r^{2} \ln r $$
(33)

where C4 ~ C7 are unknown constants. For the circular plate, when r approaches 0, the deflection at the center of the plate cannot be physically infinite. Hence, C6 has to be 0, thus we have

$$ u_{3}^{(0)} = C_{4} + C_{5} r^{2} + C_{7} r^{2} \ln r $$
(34)

At the same time, for an element with radius r and height h taken from the center of the circular plate, there is the following equilibrium relation

$$ Q(r) = - \frac{F}{2\pi r} $$
(35)

Then, from Eqs. (31) and (35), we have

$$ C_{7} = - \frac{F}{{8\pi A_{1} }} $$
(36)

Hence, the basic physical quantities such as the flexural deformation \(u_{3}^{(0)}\), the strain gradient \(S_{11,3}\), the polarization \(P_{3}\), and the incremental concentration of electrons \(\Delta n\) are expressed as

$$ \begin{gathered} u_{3}^{(0)} = C_{4} + C_{5} r^{2} - \frac{F}{{8\pi A_{1} }}r^{2} \ln r \hfill \\ S_{11,3} = \frac{F}{{4\pi A_{1} }}\ln r - 2C_{5} + \frac{3F}{{8\pi A_{1} }} \hfill \\ P_{3} = \frac{ - 1}{{a_{33}^{{}} }}\left\{ {\left( {d_{31} z + f_{3113} } \right)\left[ {\frac{F(\ln r + 1)}{{2\pi A_{1} }} - 4C_{5} } \right] + C_{2} \kappa \cosh \kappa z + C_{3} \kappa \sinh \kappa z} \right\} \hfill \\ \Delta n = n_{0} \frac{{\mu_{33}^{n} }}{{D_{33}^{n} }}\left\{ \begin{gathered} \frac{1}{{\kappa^{2} }}\frac{1}{{1 + \varepsilon_{0} a_{33}^{{}} }}\left[ {a_{33}^{{}} C_{1} + 4d_{31} C_{5} - \frac{{d_{31} F}}{{2\pi A_{1} }}\left( {\ln r + 1} \right)} \right] \hfill \\ + C_{2} \sinh \kappa z + C_{3} \cosh \kappa z\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \hfill \\ \end{gathered} \right\} + \frac{{C_{1} }}{q} \hfill \\ \end{gathered} $$
(37)

There are still five unknown constants C1 ~ C5, which can be determined with the five boundary conditions. For the clamped boundary conditions, there is

$$ u_{3}^{(0)} \left( R \right) = 0,\quad u_{3,1}^{(0)} \left( R \right) = 0 $$
(38)

For the circuit boundary conditions, we consider the electrical grounding conditions for the top and bottom surfaces of the circular PS plate, namely

$$ \varphi \left( {\frac{h}{2},r} \right) = 0,\quad \varphi \left( { - \frac{h}{2},r} \right) = 0 $$
(39)

In addition to the circuit boundary conditions, the electrical neutrality condition is also necessary. This condition ensures that the net charge within the circular plate is zero, maintaining electrical neutrality, namely

$$ \int {\int {\int {\Delta n} } } r{\text{d}}\theta {\text{d}}r{\text{d}}z = 0 $$
(40)

4 Numerical Results and Discussion

In this section, we employ the derived plate model to numerically investigate the bending deformation of an n-type circular ZnO plate with clamped boundary conditions and electrical neutrality conditions. The radius of the circular plate is R = 2.5 μm, the flexoelectric coupling coefficient of ZnO is f3113 = f3223 = 5 V [30], and the initial electron concentration is n0 = 1023 m−3. Table 1 contains the Voigt-type material constants of ZnO given in [32]. Using Eq. (2), we can obtain the corresponding Toupin-type material constants of ZnO, which are listed in Table 2.

Table 1 The Voigt-type material constants of ZnO [32]
Full size table
Table 2 The Toupin-type material constants of ZnO
Full size table

Firstly, we study the multi-field coupling response of a circular plate with a thickness h = 200 nm under different concentrated forces. Figure 2 shows the variations of the deflection u3, strain gradient S11,3, polarization P3, and incremental concentration of electrons Δn, respectively, at z = h/2 with the radial coordinate. Figure 2a illustrates the deflection distribution, showing that the maximum deflection occurs at the center of the circular plate. The deflection gradually increases with the applied load, while the displacement at the surrounding region with a radius of r = 2.5 µm remains zero. This behavior aligns with the clamped boundary conditions. Figure 2b displays the strain gradient distribution. The strain gradient is highest at the center and increases with the applied load. The change in the strain gradient is more pronounced along the radial direction. Figure 2c depicts the electric polarization distribution. The maximum polarization is observed at the center of the circular plate, decreasing as we move away from the center. With an increase in the applied force, both the strain and strain gradient of the circular plate increase, leading to an increase in electric polarization. Figure 2d shows the distribution of the incremental concentration of electrons Δn. It can be seen that electrons move away from the center of the circular plate, and a larger force results in a higher degree of electron movement.

Fig. 2
figure 2

The distributions of physical fields in the circular PS plate under different central loads along r when the thickness is h = 200 nm: a deflection u3; b strain gradient S11,3; c electric polarization P3; d incremental concentration of electrons Δn

Full size image

Next, we study the influence of different thicknesses (h = 100 nm, 200 nm, and 300 nm) on the multi-field coupling responses in the circular plate subjected to a concentrated force F = 100 nN. Figure 3a and b shows the variation curves of deflection u3 and strain gradient S11,3 with respect to the radius r, respectively. When the thickness is h = 100 nm, significant changes in both deflection and strain gradient are observed, which are much more pronounced compared to h = 200 nm and h = 300 nm. Additionally, Fig. 3c demonstrates that as the thickness decreases, the distribution trend of polarization along the radius remains largely unchanged. However, there is a substantial variation in the numerical values, confirming the size effect of flexoelectricity. Figure 3d displays the distribution of the incremental concentration of electrons along the radial coordinate r, from which we can observe that the incremental concentration of electrons varies greatly with the thickness. This is because of the size-dependent property of the flexoelectric effect.

Fig. 3
figure 3

The distributions of physical fields in the circular PS plate with different thicknesses along r when loading F = 100 nN: a deflection u3; b strain gradient S11,3; c electric polarization P3; d incremental concentration of electrons Δn

Full size image

Finally, we investigate the influence of different initial electron concentrations (n0 = 1022, 1023, and 1024 m−3) on the multi-field coupling response of the circular PS plate with h = 200 nm under the concentrated force F = 100 nN. Figure 4 shows the variation curves of deflection u3, strain gradient S11,3, polarization P3, and incremental concentration of electrons Δn with respect to radius r. It can be seen from Fig. 4a and b that the initial electron concentration has almost no effect on the deflection and strain gradient. From Fig. 4c, we can observe that as the initial electron concentration decreases, the polarization distribution maintains a similar trend along the radial coordinate r, with a slight change in value. The initial electron concentration has a significant influence on the incremental concentration of electrons, which can be seen from Fig. 4d.

Fig. 4
figure 4

The distributions of physical fields in the circular PS plate with a thickness h = 200 nm under different initial electron concentrations n0 along r when loading F = 100 nN: a deflection u3; b strain gradient S11,3; c electric polarization P3; d incremental concentration of electrons Δn

Full size image

5 Conclusions

In summary, a 2D deformation-polarization-carrier coupling model for PS plates incorporating flexoelectricity is presented based on the 3D basic equations of PSs. Using the established plate model, we obtain analytical solutions for the bending of the clamped circular PS plates subjected to an upward concentrated force. With the analytical solutions, we investigate the influence of mechanical forces and plate thicknesses on macroscopic multi-field coupling responses of the circular PS plate. The numerical results show that the flexoelectric effect significantly impacts the multi-field coupling behaviors of circular PS plates, highlighting the significance of considering the flexoelectric effect in the design and engineering of PS devices. However, the proposed coupling plate model for PS structures considering flexoelectricity should be verified by experiment in the future.