1 Introduction

Ductile inorganic electronic devices show great promise in information and medical applications with their unique ductility [1]. Research on the mechanics and structural design of ductile inorganic flexible electronic devices has become a new focus for scholars worldwide [2]. There are six main design options for the structural design of ductile inorganic flexible electronic devices [3, 4]: (1) corrugated structure, (2) straight interconnected island-bridge structure, (3) serpentine interconnected island-bridge structure, (4) fractal interconnected island-bridge structure, (5) origami structure, and (6) paper-cut structure. The corrugated structure has been widely used in electronic skin [5, 6] and flexible human health detectors [7, 8], and this paper will also discuss corrugated flexible electronic devices.

Several studies have been carried out on the mechanical formation mechanism of corrugated structures. Khang et al. [9] first proposed a microscale, periodic, corrugated, ductile form of silicon that can be reversibly stretched or compressed without damage when supported by an elastic substrate; Sun et al. [10] and Wu et al. [11] improved this structure by proposing a corrugated structure with controlled buckling geometry of semiconductor films, which can be stretched by 20% to 30%. The above studies are all for structures with planar corrugated morphology. A recent study by Ma et al. [12] found that not only did the films adhered to pre-stretched substrates of finite thickness wrinkle, but the structure also bent as a whole. Yan et al. [13] proposed a flexible structure design based on a bent wrinkle structure based on Ma et al., and noted that the stretchability of the structure could reach up to 309%. Bent wrinkle structures have higher ductility than flat wrinkle structures, but the mechanical formation mechanism of bent wrinkle structures and the way the pattern evolves are still unclear.

In practical applications, the performance of the bonding interface between the film and substrate in flexible electronic devices plays a vital role in the stable realization of product functions [14, 15]. When flexible electronic devices work, they are subjected to mechanical loads [16], such as tension and compression, and bend into various forms. Once the interface is damaged or destroyed, it can cause serious damage to the integrity of the bonding structure and the reliability of the device. Therefore, it is an essential theoretical guidance for studying device bonding interface damage behavior. Zhang et al. [17] explored the formation and evolution mechanism of spontaneous buckling-driven periodic delamination of a thin film on a large pre-strained soft substrate; Chen et al. [18] established a theoretical analysis model for interfacial failure in flexible electronic devices based on fracture mechanics, pointing out that the film always slips first and then delaminates as the applied load increases. Although interfacial failure is now explained theoretically and experimentally, the evolutionary paths of the delamination patterns of flexible electronic devices still need to be clarified.

Previous studies have primarily focused on analyzing the interfacial failure of bonded structures composed of thin films and substrates using a single factor. Therefore, based on the Euler–Bernoulli beam theory and considering the von Karman nonlinearity with the finite thickness of the substrate, the effects of pre-strain, interfacial adhesion coefficient, Young’s modulus, and thickness of the film and substrate on the instability characteristics of the film/substrate structure are discussed in detail in this paper and verified using the finite element method.

2 Instability Patterns of Thin-Film/Finite-Thickness-Substrate Structures

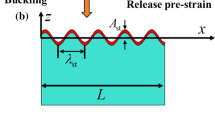
As shown in Fig. 1a, the film adheres to a pre-stretched and deformed finite-thickness substrate. The film has a length \(L\), a thickness \(h\), and the substrate has a thickness \(H\). Because of the limited thickness of the substrate, its tensile stiffness is lower than that of the film. Therefore, when the pre-tensile strain \(\varepsilon_{{{\text{pre}}}}\) on the flexible substrate is released, the substrate cannot shrink back to its initial length, causing the film/substrate structure to bend as a whole, with four patterns. (1) Pure bending structure (Fig. 1b): When the pre-strain is small, the film adheres perfectly to the upper surface of the soft substrate. (2) Bent wrinkle structure [12, 13] (Fig. 1c): As the pre-strain increases, the film remains perfectly adhered to the substrate surface but develops wrinkles on its own surface. (3) Partial delamination structure (Fig. 1d): With further increase in pre-strain, part of the film delaminates from the substrate. (4) Total delamination structure (Fig. 1e): When the pre-strain continues to increase, the film completely detaches from the substrate.

Fig. 1
figure 1

Film/substrate structure: a pre-stretched structure; b pure bending; c bent wrinkle; d partial delamination; e total delamination

Full size image

First, it is assumed that the wavelength of the film after destabilization is much larger than its thickness. In this way, the nonlinear Euler–Bernoulli beam theory is used to model the film in this paper, and the displacement–strain relationship of the film and its instanton equation can be expressed as [19, 20]

$$ \varepsilon_{x}^{{\text{f}}} = \varepsilon_{{{\text{membrane}}}}^{{\text{f}}} + \varepsilon_{{{\text{bending}}}}^{{\text{f}}} , \, \varepsilon_{{{\text{membrane}}}}^{{\text{f}}} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \kappa \left( {z - H} \right), \, \varepsilon_{{{\text{bending}}}}^{{\text{f}}} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(1)
$$ \sigma_{x}^{{\text{f}}} = E_{{\text{f}}} \left( {\varepsilon_{{{\text{membrane}}}}^{{\text{f}}} + \varepsilon_{{{\text{bending}}}}^{{\text{f}}} } \right)$$
(2)

where \(u\) and \(w\) are the in-plane displacement of the film along the \(x\)-axis and the out-of-plane displacement along the \(z\)-axis, respectively; \(\sigma_{x}^{{\text{f}}}\) is the axial stress in the film; \(E_{{\text{f}}}\) is Young’s modulus of the film; and \(\kappa\) is the curvature of the substrate.

The range of values for the \(z\)-axis in Eq. (1) is \(H \le z \le H + h\), i.e., \(0 \le z - H \le h\). Since the film's thickness \(h\) is very small, the strain in the film due to overall bending is ignored. The membrane strain \(\varepsilon_{{{\text{membrane}}}}^{{\text{f}}}\) in Eq. (1) can be re-expressed as \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0pt} {\partial x}} + \left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)^{2} /2\).

According to Hooke’s law, the expressions for the axial force \(N_{x}^{{\text{f}}}\) of the film and the shear force \(T_{1}\) at the film/substrate structure interface are [21, 22]

$$ N_{x}^{{\text{f}}} = E_{{\text{f}}} h\varepsilon_{{{\text{membrane}}}}^{{\text{f}}} , \, T_{1} = \frac{{\partial N_{x}^{{\text{f}}} }}{\partial x}$$
(3)

Assume that the out-of-plane displacement \(w\) of the film at the time of instability is [23,24,25]

$$ w = \frac{A}{2}\left[ {1 + \cos \left( {\frac{{2{\uppi }x}}{\lambda }} \right)} \right]$$
(4)

where \(A\) and \(\lambda\) are the buckling wave amplitude and wavelength to be determined.

To obtain an analytical solution, we assume that the shear force \(T_{1}\) at the interface between the film and substrate is zero [26,27,28]. The rationale for this simplification will be specified in Appendix A. Combined with the equilibrium Eq. (3), it is known that the axial force \(N_{x}^{{\text{f}}}\) of the film is uniformly distributed, i.e., \({{\partial \varepsilon_{{{\text{membrane}}}}^{{\text{f}}} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{{{\text{membrane}}}}^{{\text{f}}} } {\partial x}}} \right. \kern-0pt} {\partial x}} = 0\). According to Eqs. (1) and (4), the in-plane displacement of the film can be obtained as [27]

$$ u = \frac{{\pi A^{2} }}{16\lambda }\sin \left( {\frac{4\pi }{\lambda }x} \right) + C_{1} x + C_{2}$$
(5)

The parameters \(C_{1}\) and \(C_{2}\) in Eq. (5) can be determined from the boundary conditions. By ignoring the rigid-body displacement of the film, \(C_{2} = 0\) can be obtained; by considering the continuity between the film and substrate, we can get \(C_{1} = - \left| \varepsilon \right|\), where \(\varepsilon\) denotes the shrinkage strain to be determined in the film, and the negative sign indicates that the film is compressed [27]. In this way, Eq. (5) can be re-expressed as

$$ u = \frac{\pi }{16\lambda }A^{2} \sin \left( {\frac{4\pi }{\lambda }x} \right) - \left| \varepsilon \right|x$$
(6)

2.1 Total Energy of the Bent Wrinkle Structure

The total energy \(U_{{{\text{wrinkle}}}}\) of the system is composed of the strain energy \(U_{{{\text{film}}}}^{{{\text{wrinkle}}}}\) of the film, the strain energy \(U_{{{\text{sub}}}}^{{{\text{wrinkle}}}}\) of the substrate, and the interfacial adhesion energy \(U_{{{\text{adhesion}}}}^{{{\text{wrinkle}}}}\):

$$ U_{{{\text{wrinkle}}}} = U_{{{\text{film}}}}^{{{\text{wrinkle}}}} + U_{{{\text{sub}}}}^{{{\text{wrinkle}}}} + U_{{{\text{adhesion}}}}^{{{\text{wrinkle}}}}$$
(7)

The strain energy \(U_{{{\text{film}}}}^{{{\text{wrinkle}}}}\) of the film is

$$ U_{{{\text{film}}}}^{{{\text{wrinkle}}}} = \frac{L}{2\lambda }\int_{0}^{\lambda } {\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h/ 2}}} {\sigma_{x}^{{\text{f}}} \left( {\varepsilon_{{{\text{membrane}}}}^{{\text{f}}} + \varepsilon_{{{\text{bending}}}}^{{\text{f}}} } \right)} } {\text{d}}z{\text{d}}x $$
(8)

The strain \(\varepsilon_{{{\text{sub}}}}\) in the substrate can be expressed as

$$ \varepsilon_{{{\text{sub}}}} = \varepsilon_{{{\text{pre}}}} + \varepsilon - \kappa \left( {H - z} \right)$$
(9)

The strain energy \(U_{{{\text{sub}}}}^{{{\text{wrinkle}}}}\) of the substrate is

$$\begin{aligned}U_{{{\text{sub}}}}^{{{\text{wrinkle}}}} &= \frac{1}{2}E_{{{\text{sub}}}} L\int_{0}^{H} {\left[ {\varepsilon_{{\text{pre }}} + \varepsilon - \kappa (H - z)} \right]^{2} } {\text{d}}z\\ &\quad+ \frac{\pi }{8\lambda }E_{{{\text{sub}}}} LA^{2} g\left( {{{2\pi H} \mathord{\left/ {\vphantom {{2\pi H} \lambda }} \right. \kern-0pt} \lambda }} \right)\end{aligned}$$
(10)

where \(E_{{{\text{sub}}}}\) is Young’s modulus of the substrate, the last term of the above equation is the strain energy of the substrate due to wrinkling, and the function \(g\) is [29]

$$ g\left( x \right) = \frac{{\cosh (2x) + 1 + 2x^{2} }}{2\sinh (2x) - 4x}$$
(11)

The adhesion energy \(U_{{{\text{adhesion}}}}^{{{\text{wrinkle}}}}\) of the interface between the film and substrate is

$$ U_{{{\text{adhesion}}}}^{{{\text{wrinkle}}}} = - \gamma L $$
(12)

where \(\gamma\) is the interfacial adhesion coefficient.

Substituting Eqs. (8), (10), and (12) into Eq. (7) yields the total energy \(U_{{{\text{wrinkle}}}}\):

$$ \begin{aligned} U_{{{\text{wrinkle}}}} & = \frac{1}{2}E_{{\text{f}}} Lh\varepsilon^{2} + \frac{{\pi^{2} }}{{4\lambda^{2} }}E_{{\text{f}}} Lh(f - |\varepsilon |)A^{2} + \frac{{\pi^{4} }}{{32\lambda^{4} }}E_{{\text{f}}} LhA^{4} \\ & \quad \quad + \frac{{E_{{{\text{sub}}}} LH\left[ {\kappa^{2} H^{2} + 3\left( {\varepsilon + \varepsilon_{{{\text{pre}}}} } \right)^{2} - 3\kappa \left( {\varepsilon + \varepsilon_{{{\text{pre}}}} } \right)H} \right]}}{6} - \gamma L \\ \end{aligned} $$
(13)

where

$$ f = \frac{{\pi^{2} h^{2} }}{{3\lambda^{2} }} + \frac{{\lambda E_{{{\text{sub}}}} g\left( {{{2\pi H} \mathord{\left/ {\vphantom {{2\pi H} \lambda }} \right. \kern-0pt} \lambda }} \right)}}{{2{\uppi }E_{{\text{f}}} h}}$$
(14)

The critical wave amplitude \(A\) and wavelength \(\lambda\) of the bent wrinkle structure can be obtained based on the principle of minimum energy as

$$ \frac{{\partial U_{{{\text{wrinkle}}}} }}{\partial A} = 0, \, \frac{{\partial U_{{{\text{wrinkle}}}} }}{\partial \lambda } = 0$$
(15)

Thus, by solving Eq. (15), the expressions for \(A\) and \(\lambda\) are

$$ \begin{aligned} & A = \frac{2\lambda }{\pi }\sqrt {\left( {\left| \varepsilon \right| - f} \right)} \\ & \lambda^{3} g\left( {{{2\pi H} \mathord{\left/ {\vphantom {{2\pi H} \lambda }} \right. \kern-0pt} \lambda }} \right) - 2\pi H\lambda^{2} g^{\prime}\left( {{{2\pi H} \mathord{\left/ {\vphantom {{2\pi H} \lambda }} \right. \kern-0pt} \lambda }} \right) = \frac{{4\pi^{3} h^{3} E_{\text{f}} }}{{3E_{{{\text{sub}}}} }}\\ \end{aligned} $$
(16)

Similarly, according to the principle of minimum energy, \({{\partial U_{{{\text{wrinkle}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{wrinkle}}}} } {\partial \varepsilon }}} \right. \kern-0pt} {\partial \varepsilon }} = 0\) and \({{\partial U_{{{\text{wrinkle}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{wrinkle}}}} } {\partial \kappa }}} \right. \kern-0pt} {\partial \kappa }} = 0\), the expressions for the shrinkage strain \(\varepsilon\) and the curvature \(\kappa\) of the substrate can be obtained as

$$ \varepsilon = \frac{{4E_{{\text{f}}} hf}}{{E_{{{\text{sub}}}} H}} - \varepsilon_{{{\text{pre}}}} ,\quad \kappa = \frac{{6E_{{\text{f}}} hf}}{{E_{{{\text{sub}}}} H^{2} }}$$
(17)

It is worth noting that the curvature \(\kappa\) is independent of the pre-strain \(\varepsilon_{{{\text{pre}}}}\). This is because as the pre-strain increases, the excess strain energy is converted into energy for the buckling instability of the film and substrate due to wrinkling. In contrast, the strain energy for the overall bending of the structure remains constant.

The amplitude in Eq. (16) needs to satisfy \(A \ge 0\), i.e., \(\left| \varepsilon \right| \ge f\). Substituting this into Eq. (17) gives \(\varepsilon_{{{\text{pre}}}} \ge f(E_{{{\text{sub}}}} H + 4E_{{\text{f}}} h)/(E_{{{\text{sub}}}} H)\). The bent wrinkle structure exists only when the pre-strain is greater than this critical value.

Substituting Eqs. (16) and (17) into Eq. (13), the total energy \(U_{{{\text{wrinkle}}}}\) of the bent wrinkle structure can be re-expressed as

$$ U_{{{\text{wrinkle}}}} = E_{{\text{f}}} Lhf\varepsilon_{{{\text{pre}}}} - \frac{{2Lh^{2} E_{{\text{f}}}^{2} f^{2} }}{{E_{{{\text{sub}}}} H}} - \frac{{E_{{\text{f}}} Lhf^{2} }}{2} - \gamma L $$
(18)

When the flexural stiffness of the substrate is much greater than the flexural stiffness of the film (\({{E_{{\text{f}}} h^{3} } \mathord{\left/ {\vphantom {{E_{{\text{f}}} h^{3} } {\left( {E_{{{\text{sub}}}} H^{3} } \right) < \sim0.01}}} \right. \kern-0pt} {\left( {E_{{{\text{sub}}}} H^{3} } \right) < \sim0.01}}\)) [12], Eq. (18) can be simplified to

$$ U_{{{\text{wrinkle}}}} = \frac{1}{4}E_{{\text{f}}} Lh\varepsilon_{{{\text{pre}}}} \left( {\frac{{3E_{{{\text{sub}}}} }}{{E_{{\text{f}}} }}} \right)^{2/3} - \frac{{Lh^{2} E_{{\text{f}}}^{2} }}{{8E_{{{\text{sub}}}} H}}\left( {\frac{{3E_{{{\text{sub}}}} }}{{E_{{\text{f}}} }}} \right)^{4/3} - \frac{{E_{{\text{f}}} Lh}}{32}\left( {\frac{{3E_{{{\text{sub}}}} }}{{E_{{\text{f}}} }}} \right)^{4/3} - \gamma L$$
(19)

2.2 Total Energy of Partial Delamination Structure

For film/substrate structures where partial delamination occurs, \(n\) buckling instability morphology is assumed to occur in the delaminated portion; it is also assumed that these \(n\) buckling forms have the same wavelength and length of the delaminated part, all of which is \(l\). Define the total strain in the delaminated region of the film as \(\varepsilon_{n}\) and the membrane strain in the adhesive region as \(\varepsilon_{{{\text{membrane}}}}^{{{\text{adhesion}}}}\). Then they have the following relationship [24],

$$ - L\left| \varepsilon \right| = nl\varepsilon_{n} + (L - nl)\varepsilon_{{{\text{membrane}}}}^{{{\text{adhesion}}}} $$
(20)

where the total strain \(\varepsilon_{n}\) in the delaminated region of the film consists of the bending strain \(\varepsilon_{{{\text{bending}}}}^{n} = - z{{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}\) of the film and the membrane strain \(\varepsilon_{{{\text{membrane}}}}^{n} = {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0pt} {\partial x}} + \left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)^{2} /2\). As derived in Sect. 2.1, the out-of-plane and in-plane displacements of the delaminated part of the buckling can be obtained as

$$ w = \frac{{A_{n} }}{2}\left[ {1 + \cos \left( {\frac{2\pi x}{l}} \right)} \right],\quad u = \frac{{\uppi }}{16l}A_{n}^{2} \sin \left( {\frac{4\pi }{l}x} \right) - \varepsilon_{{{\text{pre}}}} x$$
(21)

where \(A_{n}\) is the buckling magnitude. Substituting Eq. (21) into Eq. (1), the membrane strain in the delaminated region can be obtained as \(\varepsilon_{{{\text{membrane}}}}^{n} = {\uppi }^{2} A_{n}^{2} /\left( {4l^{2} } \right) - \varepsilon_{n}\). Due to the continuity of the film axial force, the membrane strain \(\varepsilon_{{{\text{membrane}}}}^{{{\text{part.delam}}}}\) of the film is also continuous, which means that the membrane strain of the film in the delaminated region is equal to the membrane strain in the adhesive region,

$$ \varepsilon_{{{\text{membrane}}}}^{n} = \varepsilon_{{{\text{membrane}}}}^{{{\text{adhesion}}}} = \varepsilon_{{{\text{membrane}}}}^{{{\text{part.delam}}}}$$
(22)

From Eqs. (20) and (22), the membrane strain \(\varepsilon_{{{\text{membrane}}}}^{{{\text{part.delam}}}}\) for the partial delamination structure and the total strain \(\varepsilon_{n}\) in the delaminated region can be obtained as

$$ \varepsilon_{{{\text{membrane}}}}^{{{\text{part.delam}}}} = \frac{{\pi^{2} A_{n}^{2} }}{{4l^{2} }} \cdot \frac{nl}{L} - \varepsilon_{{{\text{pre}}}} ,\quad \varepsilon_{n} = \frac{{\pi^{2} A_{n}^{2} }}{{4l^{2} }}\left( {\frac{nl}{L} - 1} \right) - \varepsilon_{{{\text{pre}}}}$$
(23)

For a film/substrate structure with partial delamination, the total energy \(U_{{{\text{part.delam}}}}\) is also composed of the strain energy \(U_{{{\text{film}}}}^{{{\text{part.delam}}}}\) of the film, the strain energy \(U_{{{\text{sub}}}}^{{{\text{part.delam}}}}\) of the substrate, and the interfacial adhesion energy \(U_{{{\text{adhesion}}}}^{{{\text{part.delam}}}}\) of the adhesive region,

$$ U_{{{\text{part.delam}}}} = U_{{{\text{film}}}}^{{{\text{part.delam}}}} + U_{{{\text{sub}}}}^{{{\text{part.delam}}}} + U_{{{\text{adhesion}}}}^{{{\text{part.delam}}}}$$
(24)

where the strain energy \(U_{{{\text{film}}}}^{{{\text{part.delam}}}}\) of the film is

$$ U_{{{\text{film}}}}^{{{\text{part.delam}}}} = \int_{0}^{L} {\frac{{N_{x}^{{\text{f}}} \varepsilon_{{{\text{membrane}}}}^{{{\text{part.delam}}}} }}{2}} {\text{d}}x + n\int_{0}^{l} {\frac{{E_{{\text{f}}} h^{3} }}{24}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} {\text{d}}x}$$
(25)

the strain energy \(U_{{{\text{sub}}}}^{{{\text{part.delam}}}}\) of the substrate is

$$ U_{{{\text{sub}}}}^{{{\text{part.delam}}}} = \frac{1}{2}E_{{{\text{sub}}}} L\int_{0}^{H} {\left[ {\varepsilon_{{\text{pre }}} + \varepsilon - \kappa (H - z)} \right]^{2} } {\text{d}}z\\ $$
(26)

the interfacial adhesion energy \(U_{{{\text{adhesion}}}}^{{{\text{part.delam}}}}\) in the adhesive region is

$$ U_{{{\text{adhesion}}}}^{{{\text{part.delam}}}} = - \gamma (L - nl)$$
(27)

Then, according to the principle of minimum energy, \({{\partial U_{{{\text{part.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{part.delam}}}} } {\partial A_{n} }}} \right. \kern-0pt} {\partial A_{n} }} = 0\) and \({{\partial U_{{{\text{part.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{part.delam}}}} } {\partial l}}} \right. \kern-0pt} {\partial l}} = 0\), the amplitude \(A_{n}\) and the length \(l\) of the delaminated part can be solved for as

$$ A_{n} { = }\frac{2}{\pi }\sqrt {\frac{lL}{n}\left( {\left| \varepsilon \right| - \frac{{L^{2} }}{{l^{2} }}\varepsilon_{{\text{c}}} } \right)}$$
(28)

and

$$ \frac{n\gamma }{{2E_{{\text{f}}} h\varepsilon_{{\text{c}}}^{{2}} }}\left( \frac{l}{L} \right)^{5} - \left( {\frac{\left| \varepsilon \right|}{{\varepsilon_{{\text{c}}} }}} \right)\left( \frac{l}{L} \right)^{2} + 1 = 0$$
(29)

where \(\varepsilon_{{\text{c}}} = {{\pi^{2} h^{2} } \mathord{\left/ {\vphantom {{\pi^{2} h^{2} } {3L^{2} }}} \right. \kern-0pt} {3L^{2} }}\) is the critical strain for Euler buckling. In order for \(A_{n} > 0\), \(l\) must satisfy the following conditions,

$$ L\sqrt {\frac{{\varepsilon_{{\text{c}}} }}{\left| \varepsilon \right|}} \le l \le \frac{L}{n}$$
(30)

Again, based on the principle of minimum energy, \({{\partial U_{{{\text{part.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{part.delam}}}} } {\partial \varepsilon }}} \right. \kern-0pt} {\partial \varepsilon }} = 0\) and \({{\partial U_{{{\text{part.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{part.delam}}}} } {\partial \kappa }}} \right. \kern-0pt} {\partial \kappa }} = 0\), the shrinkage strain \(\varepsilon\) and the substrate curvature \(\kappa\) can be solved for as

$$ \varepsilon = \frac{{4{\uppi }^{2} E_{{\text{f}}} h^{3} }}{{3E_{{{\text{sub}}}} Hl^{2} }} - \varepsilon_{{{\text{pre}}}} ,\quad \kappa = \frac{{2{\uppi }^{2} h^{3} E_{{\text{f}}} }}{{E_{{{\text{sub}}}} H^{2} l^{2} }}$$
(31)

Substituting Eq. (30) into Eq. (31) gives \(\varepsilon_{{{\text{pre}}}} \ge {{\left( {4{\uppi }^{2} E_{{\text{f}}} h^{3} + {\uppi }^{2} E_{{{\text{sub}}}} Hh^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {4{\uppi }^{2} E_{{\text{f}}} h^{3} + {\uppi }^{2} E_{{{\text{sub}}}} Hh^{2} } \right)} {\left( {3E_{{{\text{sub}}}} Hl^{2} } \right)}}} \right. \kern-0pt} {\left( {3E_{{{\text{sub}}}} Hl^{2} } \right)}}\). The partial delamination structure exists only when the pre-strain is greater than this critical value.

Substituting Eqs. (28) and (31) into Eq. (24), the total energy \(U_{{{\text{part.delam}}}}\) of the partial delamination structure is

$$ U_{{{\text{part.delam}}}} = \frac{{E_{{\text{f}}} hL^{3} }}{{l^{2} }}\varepsilon_{{\text{pre }}} \varepsilon_{{\text{c}}} - \frac{{2E_{{\text{f}}}^{2} h^{2} L^{5} }}{{E_{{{\text{sub}}}} Hl^{4} }}\varepsilon_{{\text{c}}}^{{2}} - \frac{{E_{{\text{f}}} hL^{5} }}{{2l^{4} }}\varepsilon_{{\text{c}}}^{{2}} + nl\gamma - L\gamma $$
(32)

From Eq. (32), it is clear that the total energy of the structure is related to the number of delaminated regions \(n\). Minimizing the energy \({{\partial U_{{{\text{part.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{part.delam}}}} } {\partial n}}} \right. \kern-0pt} {\partial n}} = 0\), one can find \(n = l\gamma > 0\), which shows that the energy monotonically increases as the number of delaminated regions increases. It can be found from Fig. 2 that the total energy of the film/substrate structure is lowest when \(n = 1\). Therefore, \(n\) takes the value of 1 in the subsequent study.

Fig. 2
figure 2

Effect of the number of delaminated regions \(n\) on the total energy of partial delamination structure

Full size image

Then, the total energy of the partial delamination structure can be re-expressed as

$$ U_{{{\text{part.delam}}}} = E_{{\text{f}}} hL\varepsilon_{{\text{c}}} \varepsilon_{{\text{pre }}} \left( \frac{l}{L} \right)^{ - 2} - \frac{{2LE_{{\text{f}}}^{2} h^{2} \varepsilon_{{\text{c}}}^{{2}} }}{{E_{{{\text{sub}}}} H}}\left( \frac{l}{L} \right)^{ - 4} - \frac{{E_{{\text{f}}} hL\varepsilon_{{\text{c}}}^{{2}} }}{2}\left( \frac{l}{L} \right)^{ - 4} + \gamma L\left( {\frac{l}{L} - 1} \right) $$
(33)

where the value of \({l \mathord{\left/ {\vphantom {l L}} \right. \kern-0pt} L}\) is determined by solving the value of Eq. (29).

2.3 Total Energy of the Delamination Structure as a Whole

For the delamination structure as a whole, the wavelength of buckling is assumed to be \(L\), such that the in-plane and out-of-plane displacements of the film are

$$ w = \frac{A}{2}\left[ {1 + \cos \left( {\frac{{2{\uppi }x}}{L}} \right)} \right],\quad u = \frac{{\uppi }}{16L}A^{2} \sin \left( {\frac{{4{\uppi }}}{L}x} \right) - \left| \varepsilon \right|x$$
(34)

In the case of the delamination structure as a whole, the total energy consists only of the strain energy of the film and substrate,

$$\begin{aligned}U_{{{\text{tot.delam}}}} &= \frac{1}{2}\int_{0}^{L} {\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\sigma_{x}^{{\text{f}}} \left( {\varepsilon_{{{\text{membrane}}}}^{{\text{f}}} + \varepsilon_{{{\text{bending}}}}^{{\text{f}}} } \right)} } {\text{d}}z{\text{d}}x \\ &\quad+ \frac{1}{2}E_{{{\text{sub}}}} L\int_{0}^{H} {\left[ {\varepsilon_{{\text{pre }}} + \varepsilon - \kappa (H - z)} \right]^{2} } {\text{d}}z\end{aligned}$$
(35)

Minimizing the energy, \({{\partial U_{{{\text{tot.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{tot.delam}}}} } {\partial A}}} \right. \kern-0pt} {\partial A}} = 0\), \({{\partial U_{{{\text{tot.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{tot.delam}}}} } {\partial \varepsilon }}} \right. \kern-0pt} {\partial \varepsilon }} = 0\), and \({{\partial U_{{{\text{tot.delam}}}} } \mathord{\left/ {\vphantom {{\partial U_{{{\text{tot.delam}}}} } {\partial \kappa }}} \right. \kern-0pt} {\partial \kappa }} = 0\), the solution gives the amplitude \(A\), the contraction strain \(\varepsilon\), and the base curvature \(\kappa\) of the structure,

$$ A = \frac{2L}{{\uppi }}\sqrt {\left| \varepsilon \right| - \varepsilon_{{\text{c}}} } ,\quad \varepsilon = \frac{{4{\uppi }^{2} E_{{\text{f}}} h^{3} }}{{3E_{{{\text{sub}}}} HL^{2} }} - \varepsilon_{{{\text{pre}}}} ,\quad \kappa = \frac{{2E_{{\text{f}}} {\uppi }^{2} h^{3} }}{{E_{{{\text{sub}}}} H^{2} L^{2} }} $$
(36)

where the amplitude needs to satisfy \(A \ge 0\), i.e., \(\varepsilon_{{{\text{pre}}}} \ge {{\left( {4{\uppi }^{2} E_{{\text{f}}} h^{3} + {\uppi }^{2} E_{{{\text{sub}}}} Hh^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {4{\uppi }^{2} E_{{\text{f}}} h^{3} + {\uppi }^{2} E_{{{\text{sub}}}} Hh^{2} } \right)} {\left( {3E_{{{\text{sub}}}} HL^{2} } \right)}}} \right. \kern-0pt} {\left( {3E_{{{\text{sub}}}} HL^{2} } \right)}}\). The delamination structure as a whole exists only when the pre-strain is greater than this critical value.

Substituting Eq. (36) back into Eq. (35), the total energy of the delamination structure as a whole can be re-expressed as

$$ U_{{{\text{tot.delam}}}} = E_{{\text{f}}} hL\varepsilon_{{\text{c}}} \varepsilon_{{{\text{pre}}}} - \frac{{E_{{\text{f}}} hL\varepsilon_{{\text{c}}}^{{2}} }}{2} - \frac{{2L\varepsilon_{{\text{c}}}^{{2}} E_{{\text{f}}}^{2} h^{2} }}{{E_{{{\text{sub}}}} H}}$$
(37)

Letting the amplitude \(A = 0\) in Eq. (35) and considering the interfacial adhesion energy \(- \gamma L\), the total energy \(U_{{{\text{bend}}}}\) of the pure bending structure can be obtained as

$$ U_{{{\text{bend}}}} = \frac{{E_{{{\text{sub}}}} E_{{\text{f}}} LHh\varepsilon_{{{\text{pre}}}}^{2} }}{{2\left( {E_{{{\text{sub}}}} H + 4E_{{\text{f}}} h} \right)}} - \gamma L$$
(38)

Similarly, by setting the amplitude \(A = 0\), the energy of the bent wrinkle structure and the partial delamination structure can be degraded to the energy of the pure bending structure using the procedure described in Appendix B.

2.4 Total Energy Normalization of Film/Substrate Structure

For analytical convenience, this section will normalize the total energy of the previous film/substrate structure by introducing new dimensionless parameters,

$$\begin{aligned}&\overline{\varepsilon }_{{{\text{pre}}}} = \frac{{\varepsilon_{{{\text{pre}}}} }}{{\varepsilon_{{\text{c}}} }},\;\; \, \overline{\gamma } = \frac{\gamma }{{8E_{{\text{f}}} h\varepsilon_{{\text{c}}}^{{2}} }},\;\; \, \overline{E}_{{{\text{sub}}}} { = }\frac{1}{{4\varepsilon_{{\text{c}}} }}\left( {\frac{{3E_{{{\text{sub}}}} }}{{E_{{\text{f}}} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\;\; \,\\ &\overline{h} = \frac{{hE_{{\text{f}}} }}{{HE_{{{\text{sub}}}} }},\quad \overline{l} = \frac{l}{L},\;\overline{U} = \frac{U}{{E_{{\text{f}}} hL\varepsilon_{{\text{c}}}^{{2}} }}\end{aligned}$$
(39)

Substituting the dimensionless parameters of Eq. (39) into Eqs. (19), (33), (37), and (38), the total energy of the four instability patterns in dimensionless form is obtained as

$$ \overline{U}_{{{\text{wrinkle}}}} = \, \overline{E}_{{{\text{sub}}}} \overline{\varepsilon }_{{{\text{pre}}}} - \frac{1}{2}\overline{E}_{{{\text{sub}}}}^{2} - 2\overline{E}_{{{\text{sub}}}}^{2} \overline{h} - 8\overline{\gamma }$$
(40)
$$ \overline{U}_{{{\text{part.delam}}}} { = }\overline{\varepsilon }_{{{\text{pre}}}} \overline{l}^{ - 2} - \frac{1}{2}\overline{l}^{ - 4} - 2\overline{h} \, \overline{l}^{ - 4} + 8\overline{\gamma }\left( {\overline{l} - 1} \right)$$
(41)

where \(\overline{l}\) needs to satisfy \(4\overline{\gamma }\overline{l}^{5} - \overline{\varepsilon }_{{{\text{pre}}}} \overline{l}^{2} + 4\overline{h} + 1 = 0,\;\;\;\sqrt {{{\left( {4\overline{h} + 1} \right)} \mathord{\left/ {\vphantom {{\left( {4\overline{h} + 1} \right)} {\left( {\overline{\varepsilon }_{{{\text{pre}}}} } \right)}}} \right. \kern-0pt} {\left( {\overline{\varepsilon }_{{{\text{pre}}}} } \right)}}} \le \overline{l} \le 1\).

$$ \overline{U}_{{{\text{tot.delam}}}} = \overline{\varepsilon }_{{{\text{pre}}}} - 2\overline{h} - \frac{1}{2}$$
(42)
$$ \overline{U}_{{{\text{bend}}}} { = }\frac{1}{{2 + 8\overline{h}}}\overline{\varepsilon }_{{{\text{pre}}}}^{2} - 8\overline{\gamma }$$
(43)

When \(\overline{U}_{{{\text{bend}}}} = \overline{U}_{{{\text{wrinkle}}}}\), this equation can be solved to obtain the critical strain for the evolution of pure bending and bent wrinkle structures as

$$ \overline{\varepsilon }_{{\text{bend-wrinkle}}} = \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right)$$
(44)

Similarly, the critical strain for the evolution of the other five patterns can be obtained as

$$ \overline{\varepsilon }_{{{\text{bend-tot.delam}}}} = 4\overline{h} + 1 + 4\sqrt {4\overline{\gamma }\overline{h} + \overline{\gamma }} $$
(45)
$$ \overline{\varepsilon }_{{{\text{bend-part.delam}}}} = 5\left( {1 + 4\overline{h}} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}}$$
(46)

at this point \(\overline{l}_{{{\text{bend-part.delam}}}} = \left[ {{{\left( {1 + 4\overline{h}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + 4\overline{h}} \right)} {\overline{\gamma }}}} \right. \kern-0pt} {\overline{\gamma }}}} \right]^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}}\),

$$ \overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}} { = }\frac{{\overline{E}_{{{\text{sub}}}}^{2} + 16\overline{\gamma } - 1}}{{2\overline{E}_{{{\text{sub}}}} - 2}} + \frac{{2\overline{E}_{{{\text{sub}}}}^{2} \overline{h} - 2\overline{h}}}{{\overline{E}_{{{\text{sub}}}} - 1}}$$
(47)
$$ \overline{\varepsilon }_{{{\text{part.delam-tot.delam}}}} = 4\overline{\gamma } + 4\overline{h} + 1$$
(48)
$$\begin{aligned}&\overline{\varepsilon }_{{{\text{wrinkle - part.delam}}}}\\ &\quad= \frac{{c \cdot 5\left( {4\overline{h} + 1} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} - \left( {4\overline{h} + 1} \right)\overline{E}_{{{\text{sub}}}}^{2} - 25\left( {4\overline{h} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{4 \mathord{\left/ {\vphantom {4 5}} \right. \kern-0pt} 5}}} }}{{c - 2\overline{E}_{{{\text{sub}}}} }}\end{aligned}$$
(49)

where \( c = \left[ {24\overline{\gamma } + 4\overline{h} + 1 - 25\left( {4\overline{h} + 1} \right)^{{1/5}} \overline{\gamma }^{{4/5}} } \right]/\left( 4\overline{\gamma } + 1\right.\break\left. - 5\overline{\gamma }^{{2/5}} \right) \).

3 Results and Discussion

In this section, the effects of material and geometric parameters on the pattern evolution of the film/substrate structure are discussed, and the validity of the theoretical analysis is verified through finite element simulations using the commercial finite element software ABAQUS. Table 1 shows the material and geometric parameters [30] of the film/substrate structure. To improve efficiency, only half of the model shown in Fig. 1 is used for simulation analysis due to its symmetry. The film and substrate are meshed using CPE8R cells. The interface between the film and substrate is defined as the cohesive cell, and the damage evolution of the interface follows the B-K criterion.

Table 1 Material and geometric parameters of the film/substrate structure [30]
Full size table

Figure 3 depicts the relationship between dimensionless substrate curvature and dimensionless pre-strain when the material and geometric parameters are shown in Table 1. The theoretical result (solid line) matches well with the finite element result (hollow circle), confirming the accuracy of our theoretical model. It is worth noting that the substrate’s curvature changes abruptly when the structure transforms from the bent wrinkle pattern to the partial delamination pattern. This is because most of the strain energy is converted into energy that breaks the adhesion at the film/substrate interface, thereby reducing the substrate’s curvature.

Fig. 3
figure 3

Relationship between dimensionless substrate curvature and dimensionless pre-strain

Full size image

From previous theoretical analysis and existing studies [31], it is known that the normalized substrate Young’s modulus is an important parameter affecting the instability of the film/substrate structure. In this paper, the substrates are classified into four categories based on the effect of the normalized substrate Young’s modulus on the total energy of the film/substrate system as follows: (1) extremely soft substrate (\(0 < \overline{E}_{{{\text{sub}}}} \le 1\)), (2) soft substrate (\(1 < \overline{E}_{{{\text{sub}}}} \le 3\)), (3) stiff substrate (\(3 < \overline{E}_{{{\text{sub}}}} \le 5\)), and (4) extremely stiff substrate (\(\overline{E}_{{{\text{sub}}}} > 5\)). It is worth noting that the Young’s modulus of the extremely stiff substrate here is also three to four orders of magnitude lower than the Young’s modulus of the film.

(I) \(0 < \overline{E}_{{{\text{sub}}}} \le 1\): Extremely soft substrate. Figure 4a presents the curves of total energy of the film/extremely-soft-substrate system versus pre-strain, where \(\overline{E}_{{{\text{sub}}}} = 1\) is used in the numerical calculation. The results in Fig. 4a show that as the pre-strain \(\overline{\varepsilon }_{{{\text{pre}}}}\) increases, the film/substrate structure undergoes pure bending and bent wrinkle sequentially according to the principle of minimum energy. The solid pentagon in Fig. 4a represents the critical pre-strain for the evolution from pure bending to bent wrinkle, and its analytical expression is given by Eq. (44). In this way, we can obtain a criterion for determining the pattern evolution of the structure under extremely soft substrate conditions,

$$ {\text{for }}0 < \overline{E}_{{{\text{sub}}}} \le 1,\quad \, \left\{ \begin{array}{ll} {\text{pure bending, }}\quad {\text{when }}\overline{\varepsilon }_{{{\text{pre}}}} < \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \hfill \\ {\text{bent wrinkle, }}\quad {\text{when }}\overline{\varepsilon }_{{{\text{pre}}}} \ge \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \hfill \\ \end{array} \right. $$
(50)
Fig. 4
figure 4

a Total energy versus pre-strain for the film/extremely-soft-substrate structure; b phase diagram for the film/extremely-soft-substrate structure

Full size image

According to Eq. (50), Fig. 4b depicts the phase diagram of the pattern evolution of the film/extremely-soft-substrate structure. It can be found that in the case of extremely soft substrates, the destabilization mode of the structure is not affected by changes in the adhesion strength \(\overline{\gamma }\) at the film/substrate interface. In addition, it can be found from Fig. 4b that the finite element results (upper and lower triangles) match well with the theoretical analysis of this paper, which verifies the correctness of our theoretical analysis.

(II) \(1 < \overline{E}_{{{\text{sub}}}} \le 3\): Soft substrate. The reason for \(\overline{E}_{{{\text{sub}}}} = 3\) being the upper boundary of Young’s modulus for the soft substrate is explained here. Numerically, when \(\overline{U}_{{{\text{wrinkle}}}} = \overline{U}_{{{\text{tot.delam}}}} = \overline{U}_{{{\text{part.delam}}}}\), that is, when these three energy curves intersect at a point, \(\overline{\varepsilon }_{{{\text{wrinkle-part.delam}}}} = \overline{\varepsilon }_{{{\text{part.delam-tot.delam}}}}\), so \(\overline{E}_{{{\text{sub}}}} = 3\) can be found. The critical pre-strain Eqs. (44)–(49) of the pattern evolution and the available research results [32, 33] indicate that the adhesion coefficient \(\overline{\gamma }\) at the film/substrate interface is another key control parameter affecting the instability pattern. For a soft substrate, if \(\overline{\varepsilon }_{{\text{bend-wrinkle}}} \ge \overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}}\), which is \(\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /16\), as shown in Fig. 5a, the pattern evolution path is pure bending → total delamination. Therefore, the adhesion strength is defined as weak adhesion when \(\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /16\). To investigate the effect of adhesion strength on the instability characteristics of the film/substrate structure, Fig. 5b shows the system’s total energy versus pre-strain under strong adhesion conditions. It can be found that, for strong adhesion, the instability pattern of the film/substrate structure transforms from pure bending to bent wrinkles when the pre-strain increases to \(\overline{\varepsilon }_{{\text{bend - wrinkle}}}\) (solid pentagon); when the pre-strain exceeds \(\overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}}\), the structure is in total delamination pattern. In summary, the criteria for determining the pattern evolution of the structure under soft substrate conditions can be obtained as follows,

$$ \begin{aligned} & {\text{for}}\;{1} < \;\overline{E}_{{{\text{sub}}}} \le 3{, }\;\;{\text{weak adhesion}}: \, \overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /16, \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < 4\overline{h} + 1 + 4\sqrt {4\overline{\gamma }\overline{h} + \overline{\gamma }} \hfill \\ {\text{total delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge 4\overline{h} + 1 + 4\sqrt {4\overline{\gamma }\overline{h} + \overline{\gamma }} \hfill \\ \end{array} \right. \\ & {\text{for 1}} < \;\overline{E}_{{{\text{sub}}}} \le 3,\;{\text{ strong adhesion}}: \, \overline{\gamma } > \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /16, \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \hfill \\ {\text{bent wrinkle,}}\;\; \, \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \le \, \overline{\varepsilon }_{{{\text{pre}}}} < \overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}} \hfill \\ {\text{total delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge \overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(51)
Fig. 5
figure 5

a Total energy versus pre-strain for the film/soft-substrate structure under weak adhesion; b total energy versus pre-strain for the film/soft-substrate structure under strong adhesion; c phase diagram of the film/soft-substrate structure

Full size image

According to Eq. (51), Fig. 5c depicts the phase diagram of the pattern evolution of the film/soft-substrate structure. From this figure, it can be found that changing the pre-strain \(\overline{\varepsilon }_{{{\text{pre}}}}\) and the adhesion coefficient \(\overline{\gamma }\) can regulate the instability pattern of the structure; the strength of adhesion determines the path of pattern evolution, and there are two paths of pattern evolution in soft substrate conditions.

(III) \(3 < \overline{E}_{{{\text{sub}}}} \le 5\): Stiff substrate. The reason for the upper boundary of Young’s modulus of the stiff substrate to be determined as 5 is explained here. According to Eq. (46), the length of the delaminated region must satisfy \(l < L\) due to the partial delamination pattern, i.e., \(\overline{l}_{{{\text{bend-part.delam}}}} < 1\). Then the adhesion coefficient needs to satisfy \(\overline{\gamma } > 4\overline{h} + 1\) for the film/stiff-substrate structure to achieve the evolution of pure bending with partial delamination, so the critical pre-strain \(\overline{\varepsilon }_{{{\text{bend-part.delam}}}}\) satisfies the relation \(\overline{\varepsilon }_{{{\text{bend-part.delam}}}} = 5\left( {1 + 4\overline{h}} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} > 5\left( {4\overline{h} + 1} \right)\). From a numerical perspective, when \(\overline{U}_{{{\text{wrinkle}}}} = \overline{U}_{{{\text{bend}}}} = \overline{U}_{{{\text{part.delam}}}}\), which is when these three energy curves intersect at a point, then \(\overline{\varepsilon }_{{\text{bend-wrinkle}}} = \overline{\varepsilon }_{{{\text{bend-part.delam}}}}\), which is equivalent to \(\overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) = 5\left( {1 + 4\overline{h}} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} > 5\left( {4\overline{h} + 1} \right)\), so \(\overline{E}_{{{\text{sub}}}} > 5\) can be found. This means the critical pre-strain \(\overline{\varepsilon }_{{{\text{part.delam-tot.delam}}}}\) exists when \(\overline{E}_{{{\text{sub}}}}\) is greater than or equal to 5.

For the stiff substrate, if \(\overline{\varepsilon }_{{{\text{part.delam-tot.delam}}}} \ge \overline{\varepsilon }_{{{\text{wrinkle-tot.delam}}}}\), which means \(\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /\left( {8\overline{E}_{{{\text{sub}}}} - 24} \right)\), the pattern evolution of the film/stiff-substrate structure is the same as case (II), as shown in Figs. 6a and 6b, and the paths of pattern evolution are pure bending → total delamination and pure bending → bent wrinkle → total delamination. Therefore, a weak adhesion state at the film/stiff-substrate interface is defined when the adhesion coefficient satisfies \(\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /\left( {8\overline{E}_{{{\text{sub}}}} - 24} \right)\). When the interface is in the strong adhesion state at \(\overline{\gamma } > \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /\left( {8\overline{E}_{{{\text{sub}}}} - 24} \right)\), as shown in Fig. 6c, the path of pattern evolution is pure bending → bent wrinkle → partial delamination → total delamination. In summary, the evolution and regulation laws of the pattern under stiff substrate conditions can be obtained as

$$ \begin{aligned} & {\text{for}}\;{3} < \;\overline{E}_{{{\text{sub}}}} \le 5{,}\;\;{\text{ weak adhesion}}: \,\\ &\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /\left( {8\overline{E}_{{{\text{sub}}}} - 24} \right), \\ & {\text{same as Case (II),}} \\ & {\text{for 3}} < \;\overline{E}_{{{\text{sub}}}} \le 5,\;\;{\text{ strong adhesion}}: \,\\ & \overline{\gamma } > \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} - 1} \right)^{2} /\left( {8\overline{E}_{{{\text{sub}}}} - 24} \right), \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \hfill \\ {\text{bent wrinkle,}}\;\; \, \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \le \overline{\varepsilon }_{{{\text{pre}}}} < \overline{\varepsilon }_{{{\text{wrinkle-part.delam}}}} \hfill \\ {\text{partial delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{wrinkle-part.delam}}}} \le \overline{\varepsilon }_{{{\text{pre}}}} < 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ {\text{total delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(52)
Fig. 6
figure 6

a Total energy versus pre-strain for the film/stiff-substrate structure under extremely weak adhesion; b total energy versus pre-strain for the film/stiff-substrate structure under weak adhesion; c total energy versus pre-strain for the film/stiff-substrate structure under strong adhesion; d phase diagram for the film/stiff-substrate structure

Full size image

According to Eq. (52), Fig. 6d depicts the phase diagram of the pattern evolution of the film/stiff-substrate structure. It can be seen that there are three paths for pattern evolution under this condition, and the magnitude of the adhesion coefficient \(\overline{\gamma }\) determines the choice of the path.

(IV) \(\overline{E}_{{{\text{sub}}}} > 5\): Extremely stiff substrate. According to Eq. (46), when the adhesion coefficient \(\overline{\gamma } \le 4\overline{h} + 1\), the critical pre-strain \(\overline{\varepsilon }_{{{\text{bend-part.delam}}}}\) does not exist, and the adhesion strength at this time is defined as extremely weak adhesion. Figure 7a shows the curves of total energy versus pre-strain of the system under extremely weak adhesion conditions. It can be seen that the mode transformation is in the form of pure bending → total delamination. For an extremely stiff substrate, if \(\overline{\varepsilon }_{{\text{bend-wrinkle}}} \ge \overline{\varepsilon }_{{{\text{bend-part.delam}}}}\), which means \(\overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} /5} \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}}\), as shown in Fig. 7b, the pattern evolution at is pure bending → partial delamination → total delamination. Therefore, the adhesion coefficient is defined to satisfy \(4\overline{h} + 1 < \overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} /5} \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}}\) as the weak adhesion state at the film/extremely-stiff-substrate interface. Figure 7c depicts the relationship between the total energy of the system and pre-strain in the strong adhesion state, where the pattern transformation is pure bending → bent wrinkle → partial delamination → total delamination. In summary, the pattern evolution law of the film/extremely-stiff-substrate structure can be obtained as

$$ \begin{aligned} & {\text{for}}\;\overline{E}_{{{\text{sub}}}} > 5{,}\;\;{\text{ extremely weak adhesion}}: \, \overline{\gamma } \le 4\overline{h} + 1, \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < 4\overline{h} + 1 + 4\sqrt {4\overline{\gamma }\overline{h} + \overline{\gamma }} \hfill \\ {\text{total delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge 4\overline{h} + 1 + 4\sqrt {4\overline{\gamma }\overline{h} + \overline{\gamma }} \hfill \\ \end{array} \right. \\ & {\text{for }}\;\overline{E}_{{{\text{sub}}}} > 5,\;\;{\text{ weak adhesion}}: \, 4\overline{h} + 1 < \overline{\gamma } \le \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} /5} \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} , \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < 5\left( {1 + 4\overline{h}} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} \hfill \\ {\text{partial delamination,}}\;\; \, 5\left( {1 + 4\overline{h}} \right)^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} \overline{\gamma }^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} \le \overline{\varepsilon }_{{{\text{pre}}}} < 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ {\text{total delamination,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ \end{array} \right. \\ & {\text{for }}\;\overline{E}_{{{\text{sub}}}} > 5,\;\;{\text{ strong adhesion}}: \, \overline{\gamma } > \left( {4\overline{h} + 1} \right)\left( {\overline{E}_{{{\text{sub}}}} /5} \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} , \\ & \left\{ \begin{array}{ll} {\text{pure bending,}}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} < \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \hfill \\ {\text{bent wrinkle,}}\;\; \, \overline{E}_{{{\text{sub}}}} \left( {4\overline{h} + 1} \right) \le \overline{\varepsilon }_{{{\text{pre}}}} < \overline{\varepsilon }_{{{\text{wrinkle-part.delam}}}} \hfill \\ {\text{partial delamination, }}\;\; \, \overline{\varepsilon }_{{{\text{wrinkle-part.delam}}}} \le \overline{\varepsilon }_{{{\text{pre}}}} < 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ {\text{total delamination, }}\;\; \, \overline{\varepsilon }_{{{\text{pre}}}} \ge 4\overline{\gamma } + 4\overline{h} + 1 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(53)
Fig. 7
figure 7

a Total energy versus pre-strain for the film/extremely-stiff-substrate with extremely weak adhesion; b total energy versus pre-strain for the film/extremely-stiff-substrate with weak adhesion; c total energy versus pre-strain for the film/extremely-stiff-substrate with strong adhesion; d phase diagram of the film/extremely-stiff-substrate structure

Full size image

According to Eq. (53), Fig. 7d depicts the phase diagram of the pattern evolution of the film/extremely-stiff-substrate structure. It can be seen that there are three paths for the evolution of the structural instability pattern under extremely stiff substrate conditions, and the magnitude of the adhesion coefficient \(\overline{\gamma }\) determines the choice of the path.

In order to comprehensively evaluate the normalized adhesion coefficient \(\overline{\gamma }\), normalized substrate Young’s modulus \(\overline{E}_{{{\text{sub}}}}\), normalized thickness \(\overline{h}\), and normalized pre-strain \(\overline{\varepsilon }_{{{\text{pre}}}}\), as well as their effects on the instability characteristics of the film/substrate structure, a four-dimensional phase diagram of the structure is shown in Fig. 8, where Figs. 8a-d represent the phase diagrams of the extremely soft substrate, soft substrate, stiff substrate, and extremely stiff substrate, respectively. By comparing these four phase diagrams, it can be found that the higher is the substrate Young’s modulus, the smaller is the region where the film/substrate structure undergoes bent wrinkling, i.e., a soft substrate is more likely to contribute to the formation of bent wrinkles. The partial delamination structure only occurs in stiff substrate and extremely stiff substrate conditions, and the higher is the substrate Young’s modulus (the stiffer is the substrate), the larger is the area where the partial delamination structure occurs.

Fig. 8
figure 8

Four-dimensional phase diagram of the film/substrate structure: a extremely soft substrate; b soft substrate; c stiff substrate; d extremely stiff substrate

Full size image

The phase diagram shown in Fig. 8 is an important engineering guide for the design of flexible electronic devices. The four-dimensional results in Fig. 8 provide parameter design intervals for the four instability patterns of the film/substrate structure, i.e., the ability to predict and regulate the instability patterns of the film/substrate structure by adjusting material parameters, geometric parameters, and adhesion parameters. A critical aspect of this information is the partitioning between regions, especially between partial and total delamination structures and the other two structures. These partitioning interfaces indicate that the film will begin to detach from the substrate, which will have an impact on the overall stability of the structure. Therefore, the theoretical analysis model in this paper will help to optimize the design of this type of electronic devices.

4 Conclusions

For the delamination instability characteristics of the film/substrate structure, this paper firstly establishes mechanical models for pure bending, bent wrinkle, partial delamination, and total delamination of the film/finite-thickness-substrate structure based on the elastic film and finite-thickness substrate; the critical strains for the four destabilization patterns of the film/substrate structure are then obtained based on the energy approach and the principle of minimum energy. The results show that by adjusting material parameters (Young’s modulus), geometric parameters (thickness), interfacial adhesion strength, and pre-strain of the structure, the delamination of the film/substrate structure interface can be avoided, and the prediction and regulation of the structural instability characteristics can be achieved. The greater is the substrate Young’s modulus, the larger is the parameter region where partial delamination of the film/substrate structure occurs, and the smaller is the parameter region where bent wrinkle occurs. This theoretical models and conclusions of this paper contribute to the structural design and optimization of flexible electronic devices.