1 Introduction

Spacecraft systems are subjected to harsh vibration environments before they enter their intended orbit. As a result, the spacecraft structure and the instruments in it may be easily damaged. Whole-spacecraft vibration reduction is an effective method to overcome this problem, and it has been widely used in recent years [1]. Johnson et al. [2] reported that vibration reduction in the SoftRide MultiFlex whole-spacecraft vibration isolation system is effective. Liu et al. [3, 4] optimized the design of an octo-strut platform to improve low longitudinal stiffness, which could effectively improve the dynamic vibration environment of spacecraft. Hu et al. [5] designed a control system that effectively suppresses system vibration and achieves accurate attitude control of spacecraft. However, the natural frequencies of most whole-spacecraft vibration reduction systems have changed, and these systems have limited vibration reduction effects.

The nonlinear energy sink (NES) is a new type of nonlinear vibration absorber that uses target energy transfer to suppress vibration. NES can remarkably reduce vibration without changing the natural frequency [6,7,8,9]. Georgiades et al. [10] studied the vibration of NES connected to a damped and forced dispersive linear finite rod and discovered that NES is highly effective as a passive broadband energy absorber. Ahmadabadi and Khadem [11] investigated the effect of grounded and ungrounded NES on the vibration reduction of a cantilever beam and obtained 89% energy dissipation of the ungrounded system by optimizing the NES parameters. Chen et al. [12] proved that the vibration of a truss-core sandwich beam combined with NES exhibits excellent vibration suppression. Gourc et al. [13] analyzed the dynamic response of NES under harmonic excitation through experiments and confirmed the good vibration reduction effect of NES. Zang and Chen [14] revealed the dynamic complexity of NES by employing the harmonic balance approach and pseudo-arclength continuation algorithm. Dai et al. [15] studied the effects of NES on the amplitude of an elastically mounted square prism subjected to a galloping force and concluded that NES with optimized parameters can effectively reduce vibration. In addition, NES can effectively reduce the vibration of the transmission input shaft in an automotive drivetrain over a wide frequency range [16]. NES absorbs the vibration energy of the system to reduce vibration effectively. Moreover, the vibration energy can be absorbed as electric energy, which presents a meaningful research direction.

Researchers have also conducted extensive research on vibration-type energy harvesters [17,18,19]. Designed by Ferrari et al. [20], a nonlinear bistable piezoelectric converter for vibration reduction was tested on a cantilever beam and eventually harvested large amounts of energy during broadband vibration. Tao et al. [21] designed an electret-based micro-electro-mechanical system (MEMS) energy harvester that enables energy harvesting over a wider bandwidth compared with traditional linear systems. The flexible longitudinal zigzag structure of piezoelectric materials can efficiently collect energy at low frequencies [22]. Liu et al. [23] studied an electromagnetic energy harvester that generates current in copper coils through the law of electromagnetic induction. The highest open circuit voltage is 2.64 V. Zhou and Zuo [24] analyzed an asymmetric tristable energy harvester by using the harmonic balance approach, and the performance of the energy harvester was improved by changing the unstable equilibrium point. Chtiba et al. [25] connected NES to a piezoelectric device in a linear main structure; the system absorbed the vibrational energy of the simply supported beam, while the vibrational energy was converted into electrical energy. A system that consists of NES and a piezoelectric harvester can reduce vibration and harvest large amounts of energy if the system parameters are optimized [26]. Fang combined NES with a giant magnetostrictive material to reduce vibration and harvest energy. The highest voltage (1.79 V) was obtained at the resonant frequency, but no electrical energy was harvested at other frequencies [27, 28]. The capability of an energy harvesting system with NES was verified through an experiment by Kremer and Liu [29, 30]. In these studies, the systems can only harvest energy at natural frequency or low frequencies and have low output voltage. Therefore, the power-generating capability and frequency range of energy harvesters should be improved in the future.

In this work, we study the integration of NES and a novel levitation magnetoelectric energy harvester (MEEH) for vibration control and energy harvesting in whole-spacecraft systems. The MEEH consists of a magnetoelectric laminate and three ring magnets. It generates power on the resistive load through the magnetostrictive effect and the piezoelectric effect [31]. The laminated structure is a piezoelectric layer (PZT) bonded between two magnetostrictive layers (Terfenol-D) [32]. This system exhibits good vibration reduction and achieves a high voltage over a wide frequency range. A simplified mathematical model of the system is established in Sect. 2. Section 3 analyzes the response of the system and the harvested energy by using the harmonic balance approach and pseudo-arclength continuation algorithm. Section 4 discusses the effects of different parameters on system vibration response and energy harvesting. Section 5 provides the conclusions of this work.

2 Whole-Spacecraft Model with NES and MEEH

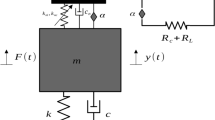
The equivalent simplified model of a whole spacecraft with NES and MEEH is shown in Fig. 1, where \(m_1\) and \(m_2\) are, respectively, the masses of the primary system and the subsystem [33]; \(k_i \) and \(c_i \) (\(i=1,2)\) are the linear stiffness and damping coefficients, respectively. NES is attached to mass \(m_2 \) and includes mass \(m_3 \), cubic nonlinear stiffness coefficient \(k_3 \), and damping coefficient \(c_3 \). The energy harvester is placed on mass \(m_3 \), and the intermediate magnet is rigidly connected to mass \(m_2 \). Mass \(m_2 \) includes the mass of the middle magnet, and mass \(m_3 \) includes the mass of the energy harvester except for the middle magnet.

Fig. 1
figure 1

Model of the whole-spacecraft system with NES and MEEH

Full size image

The dynamic equation of the system is expressed as follows:

$$\begin{aligned}&m_1 \ddot{x}_1 +c_1 (\dot{x}_1 -\dot{x}_2 )+k_1 (x_1 -x_2 )+m_1 \ddot{x}_\mathrm{b} =0 \nonumber \\&m_2 \ddot{x}_2 +c_1 (\dot{x}_2 -\dot{x}_1 )+c_2 \dot{x}_2 +c_3 (\dot{x}_2 -\dot{x}_3 )+k_1 (x_2 -x_1 )+k_2 x_2 +k_3 (x_2 -x_3 )^{3}-F_\mathrm{m} +m_2 \ddot{x}_\mathrm{b} =0 \nonumber \\&m_3 \ddot{x}_3 +c_3 (\dot{x}_3 -\dot{x}_2 )+k_3 (x_3 -x_2 )^{3}+F_\mathrm{m} +m_3 \ddot{x}_\mathrm{b} =0 \end{aligned}$$
(1)

where \(x_\mathrm{b} \) is the excitation acceleration and \(F_\mathrm{m} \) is the magnetic field force of the intermediate magnet [31].

$$\begin{aligned}&x_\mathrm{b} =\frac{A_\mathrm{b} }{(2\pi f)^{2}}\sin ( {2\pi ft} ) \nonumber \\&\dot{x}_\mathrm{b} =\frac{A_\mathrm{b} }{2\pi f}\cos ( {2\pi ft} ) \nonumber \\&\ddot{x}_\mathrm{b} =-A_\mathrm{b} \sin ( {2\pi ft} ) \end{aligned}$$
(2)
$$\begin{aligned} F= & {} Az+Bz^{3}=A(x_2 -x_3 )+B(x_2 -x_3 )^{3} \end{aligned}$$
(3)

where \(A_\mathrm{b} =0.3\,\hbox {g}\), \(A=6.39\,\hbox {N/m}\), and \(B=1.66\times \hbox {10}^{5}\,\hbox {N/m}\); f is the excitation frequency; and z is the central magnet relative displacement.

The output voltage and power of MEEH are

$$\begin{aligned} V= & {} \frac{\varphi _\mathrm{m} \varphi _\mathrm{p} R_{\mathrm{load}} H}{\varphi _\mathrm{p}^2 R_{\mathrm{load}} +(1+\hbox {j}\omega R_{\mathrm{load}} C_0 )Z} \end{aligned}$$
(4)
$$\begin{aligned} P= & {} \frac{V^{2}}{R_{\mathrm{load}} } \end{aligned}$$
(5)

where \(\varphi _\mathrm{m} \) is the magnetoelastic coupling factor; \(\varphi _\mathrm{p} \) is the electromechanical coupling factor; \(C_0 \) is the static capacitance of PZT; Z is the equivalent mechanical impedance of the laminate composite; \(R_{\mathrm{load}} \) is the resistive load; and H is the magnetic field strength, which can be expressed as \(H=f( z )=f( {x_2 -x_3 } )\) [31].

The energy harvested by the harvester is an alternating current. Its instantaneous voltage value is the real part of the complex voltage.

$$\begin{aligned}&\displaystyle V_{\mathrm{real}} =\frac{-A_1 A_2 H}{A_2^2 +\frac{A_3^2 }{(2\pi f)^{2}}} \end{aligned}$$
(6)
$$\begin{aligned} A_1= & {} 2bt_\mathrm{p}^2 d_{33,\mathrm{m}} d_{31,\mathrm{p}} R_{\mathrm{load}} s_{11}^\mathrm{E} l \nonumber \\ A_2= & {} 2lR_{\mathrm{load}} b\left( {\left( {t_\mathrm{m} s_{11}^\mathrm{E} +\frac{1}{2}t_\mathrm{p} s_{33}^\mathrm{H} } \right) \left( {k_{31}^2 -1} \right) s_{11}^\mathrm{E} \varepsilon _{33}^\mathrm{T} -\frac{1}{2}t_\mathrm{p} d_{31,\mathrm{p}}^2 s_{33}^\mathrm{H} } \right) \nonumber \\ A_3= & {} 2s_{11}^{\mathrm{E}^{2}}t_\mathrm{m} t_\mathrm{p} +s_{11}^\mathrm{E} s_{33}^\mathrm{H} t_\mathrm{p}^2 \end{aligned}$$
(7)

where b is the PZT layer width, \(t_\mathrm{p} \) is the PZT layer thickness, \(d_{33,\mathrm{m}} \) is a longitudinal piezomagnetic constant, \(d_{31,\mathrm{p}} \) is a transverse piezoelectric constant, \(t_\mathrm{m} \) is the Terfenol-D layer thickness, \(s_{11}^\mathrm{E} \) is piezoelectric elastic compliance, l is the PZT layer length, \(s_{11}^\mathrm{E} \) is piezoelectric elastic compliance, \(s_{33}^\mathrm{H} \) is piezomagnetic elastic compliance, \(k_{31} \) is the piezoelectric electromechanical coupling coefficient, and \(\varepsilon _{33}^\mathrm{T} \) is piezoelectric permittivity [31].

Fig. 2
figure 2

Comparison of the approximate analytical method with Ode45

Full size image
Fig. 3
figure 3

Harvested energy across a \(10^{7}\,\Omega \) load resistance: a maximum voltage and b maximum power

Full size image
Fig. 4
figure 4

Magnetic field strength H

Full size image
Fig. 5
figure 5

Output voltage: a\(f=20\,\hbox {Hz}\), b\(f=40\,\hbox {Hz}\), and c\(f=60\,\hbox {Hz}\)

Full size image
Fig. 6
figure 6

Comparative analysis of the response with or without NES and MEEH

Full size image
Fig. 7
figure 7

Amplitude–frequency response curves as the mass changes: a total figure, b enlargement figure near 20 Hz, and c enlargement figure near 90 Hz

Full size image

3 Simulations

The approximate analytical method combines the harmonic balance approach and the pseudo-arclength continuation algorithm. Initially, \(x_i\ (i=1,2,3)\) in Eq. (1) are represented by the assumption of three harmonic functions as follows:

$$\begin{aligned} \begin{aligned} x_1 ( t )=a_{11} \cos ( {\omega t} )+b_{11} \sin ( {\omega t} )+a_{31} \cos ( {3\omega t} )+b_{31} \sin ( {3\omega t} ) \\ x_2 ( t )=a_{12} \cos ( {\omega t} )+b_{12} \sin ( {\omega t} )+a_{32} \cos ( {3\omega t} )+b_{32} \sin ( {3\omega t} ) \\ x_3 ( t )=a_{13} \cos ( {\omega t} )+b_{13} \sin ( {\omega t} )+a_{33} \cos ( {3\omega t} )+b_{33} \sin ( {3\omega t} ) \end{aligned} \end{aligned}$$
(8)

where \(\omega =2\pi f\) is a variable parameter. By substituting Eq. (8) into Eq. (1), we derive 12 equations. Then, the pseudo-arclength continuation algorithm is used to solve the equations. This study defines vector \({\varvec{x}}\) consisting of \(a_{ij} \) and \(b_{ij}\ (i,j=1,2,3)\) to write the 12 equations abstractly as \(f( {x,\omega } )=0\). We set an extension vector \({\varvec{y}}=(x,\omega )^\mathrm{T}\) and introduce vector \({\varvec{y}}_\mathrm{1}\) and a fairly small arc length s. We then obtain a new equation, \(\parallel {\varvec{y}}_1 -{\varvec{y}}\parallel -s=0\). Ultimately, we have 13 equations and 13 unknowns. The Newton–Raphson method is used to solve these equations [34, 35].

Fig. 8
figure 8

Amplitude–frequency response curves as the stiffness changes: a total figure, b enlargement figure near 20 Hz, and c enlargement figure near 90 Hz

Full size image
Fig. 9
figure 9

Amplitude–frequency response curves as the damping changes: a total figure, b enlargement figure near 20 Hz, and c enlargement figure near 90 Hz

Full size image
Fig. 10
figure 10

Amplitude–frequency response curves as the excitation amplitude varies: a total figure, b enlargement figure near 20 Hz, and c enlargement figure near 90 Hz

Full size image

The system parameters are \(m_1 =60\hbox { kg}\), \(k_1 =1.8677\times 10^{6}\,\hbox {N}/\hbox {m}\), \(c_1 =600\,\hbox {Ns}/\hbox {m}\), \(m_2 =12\,\hbox {kg}\), \(k_2 =2.1346\times 10^{6}\,\hbox {N}/\hbox {m}\), \(c_2 =20\,\hbox {Ns}/\hbox {m}\), \(m_3 =7\,\hbox {kg}\), \(k_3 =7\times 10^{9}\,\hbox {N}/\hbox {m}^{3}\), \(c_3 =600\, \hbox {Ns}/\hbox {m}\) [28, 33].

In Fig. 2a, b, the solid black line is the amplitude–frequency response obtained by the harmonic balance approach and pseudo-arclength continuation algorithm, and the dashed red line is the amplitude–frequency response obtained by the fourth-order Runge–Kutta method (Ode45) under 0.3-g base excitation. The results of approximate analysis are nearly consistent with those of the numerical simulation. Figure 2b is an enlargement figure that uses \(\log _{10} (x_1)\) as the y-axis. A small peak caused by the second natural frequency of the system is observed at 90 Hz.

3.1 Harvested Energy Analysis

The maximum output voltage and power are shown in Fig. 3, and the magnetic field strength is shown in Fig. 4. The system can harvest energy in the entire frequency range. As the frequency increases, the output voltage value remains stable at 70 V. However, the variation trends of voltage and power differ from that of magnetic field strength. This result can be explained by Eq. (6). Voltage is determined by magnetic field strength H, excitation frequency f, resistive load \(R_{\mathrm{load}} \), and other parameters with determined values. In Fig. 4, the numerical value of magnetic field strength H varies only slightly, and the value of magnetic field strength is too small for \(A_1 \), \(A_2 \), and \(A_3 \) in Eq. (7). Therefore, the change in magnetic field strength has no obvious influence on voltage. Meanwhile, a change in excitation frequency and resistive load changes the voltage considerably. As shown in Fig. 3, output voltage and power increase as the excitation frequency increases across a \(10^{7}\,\Omega \) load resistance. In Fig. 5, the voltages at three frequencies are \(60\,\hbox {Hz}>40\,\hbox {Hz}>20\,\hbox {Hz}\), and the result is consistent with Fig. 3.

3.2 Comparative Analysis of the Response With or Without NES and MEEH

In Fig. 6, the amplitude–frequency responses with or without NES and MEEH are compared under a 0.3-g base excitation. The whole-spacecraft system with NES and MEEH can effectively reduce vibration. The amplitude of the system decreases most at 20 Hz, which is the natural system frequency. The peak of the second natural system frequency disappears in Fig. 6b.

4 Parametric Study

The choice of parameters is crucial to system performance. In this work, the variations in base excitation amplitude \(A_\mathrm{b}\), NES (\(m_3 \), \(k_3 \), \(c_3\)), and resistive load \(R_{\mathrm{load}}\) of the system are analyzed. The influence of the change in \(m_3\) on the vibration of the system is examined firstly. Figure 7 depicts the relationship between the amplitude frequency response and NES mass \(m_3 \), with the values of other parameters unchanged. With the increase in NES mass, the response amplitude decreases near 20 Hz and hardly changes at a high frequency. When the value of NES mass is larger, the effect of reducing vibration becomes smaller. As reported in the previous section, the parameters of NES and the base excitation amplitude exert nearly no effect on voltage. Hence, the voltage change is not discussed here.

In Fig. 8, the effect of the variation of NES stiffness coefficient \(k_3 \) on the amplitude frequency response is compared. When NES stiffness coefficient \(k_3 \) increases, the response amplitude decreases near 20 Hz. Figure 8c is an enlargement figure near 90 Hz, where the amplitude is almost unchanged.

The effects of different NES damping coefficients \(c_3 \) on the amplitude frequency response are presented in Fig. 9. The effect of NES damping coefficient on amplitude is different from NES mass and NES stiffness coefficient. The response amplitude increases when NES damping coefficient increases near 20 Hz but hardly changes at a high frequency.

Fig. 11
figure 11

Maximum voltage curves as the resistive load varies

Full size image

Figure 10 shows the effect of the change in acceleration excitation amplitude \(A_\mathrm{b}\) on the amplitude frequency response. The effect of \(A_\mathrm{b}\) on the amplitude is very obvious at low frequencies. The response amplitude increases when excitation amplitude \(A_\mathrm{b}\) increases near 20 Hz but hardly changes at a high frequency.

In Fig. 11, as base excitation f increases, the output voltage increases. When resistive load \(R_{\mathrm{load}} \) increases, the output voltage increases at low frequencies. After the frequency is greater than 40 Hz, the change of resistive load has little effect on the voltage. The voltage changes very little when resistive load exceeds \(1\times 10^{8}\,\Omega \). The two curves of \(R_{\mathrm{load}} =3\times 10^{8}\,\Omega \) and \(R_{\mathrm{load}} =5\times 10^{8}\,\Omega \) are very close, and the highest voltage 70 V can be harvested at low frequencies in these two cases. Therefore, the optimal resistance range is selected as \(\hbox {3}\times 10^{8}\,\Omega {-}\hbox {5}\times 10^{8}\,\Omega \).

5 Conclusion

We propose a new integrated device that combines NES and MEEH to achieve whole-spacecraft vibration reduction and energy harvesting. The dynamic equation of the system is analyzed with an approximate analytical method that combines the harmonic balance approach and pseudo-arclength continuation algorithm. The results are then compared with those of the Runge–Kutta algorithm for numerical simulation. The dynamic response, output voltage, and output power of the system after reaching the steady-state response under acceleration excitation are also calculated.

The following conclusions are derived.

  1. (1)

    The integration of NES and MEEH can effectively reduce system vibration while harvesting large amounts of electrical energy over a wide range of frequencies.

  2. (2)

    The approximate analytical solution of the dynamic equation obtained by the harmonic balance approach and pseudo-arclength extension algorithm is nearly consistent with the Runge–Kutta algorithm solution.

  3. (3)

    The harvested electrical energy is inconsistent with the change in magnetic field strength. The harvested electrical energy increases as the excitation frequency and resistive load increase because the influence of magnetic field strength on voltage is extremely small.