Viscometric Detection in Size-Exclusion Chromatography: Principles and Select Applications

Abstract

Size-exclusion chromatography (SEC) has benefitted from commercially available on-line viscometers for 30 years now. Initial (and continued) interest was mostly in applying the universal calibration concept to obtain molar mass averages and distributions of macromolecules for which no appropriate calibration standards existed, and in obtaining long-chain branching information such as branching number and frequency. During the last three decades, viscometry has shown itself to be able to do much more than this, especially (but not exclusively) when employed in multi-detector set-ups which include light scattering photometers. The purpose of this review is to demonstrate the power of viscometry detection in SEC, through applications which showcase the extreme or, simply, the unusual, oftentimes as encountered by the author. A brief review of history and theory is thus followed by examples of the role of viscometry in the SEC characterization of, among others, solutions with negative viscosity, polymers which undergo morphological transformations during growth, polysaccharides with molar mass distributions extending into the hundreds of millions of g mol⁻¹, and spectroscopically invisible macromolecules.

Introduction

In the three decades since the commercial introduction of on-line viscometers for size-exclusion chromatography (SEC), the use of this detection technique has become widespread. This is especially so in the analysis of synthetic polymers and polysaccharides, less pronounced in the study of proteins and peptides. Most applications of viscometric detection have involved one of two topics: Either the determination of absolute, calibrant-independent molar mass averages and distributions, based on applying Benoit’s concept of universal calibration, and/or the use of on-line viscometry (VISC) to establish the presence of long-chain branching in macromolecules. The realized potential of viscometry, however, greatly exceeds just these two applications.

The author has employed viscometry almost continuously for the last 24 years. As such, the purpose of this review is to highlight the versatility and power of the technique, mostly (but not exclusively) from a personal perspective. Case studies will balance the worlds of synthetic and biopolymers, with the latter emphasizing the characterization of polysaccharides. In most cases, examples have been chosen based on the ability of SEC/VISC to confront obdurate or simply unusual problems, be these polymer or property related.

We begin, however, with a brief historical background, taking a somewhat different perspective than that usually employed when discussing viscometry.

Historical Background: How Did We Get Here From There-and Where, Exactly, was “There”?

As happens so often in physics, the origins of viscometry can be traced back to Isaac Newton (1642–1726). In 1687, in his Principia Mathematica, Newton wrote that “The resistance which arises from the lack of slipperiness originating in a fluid, other things being equal, is proportional to the velocity by which the parts of the fluid are being separated from each other” [1] (Differences among translations of the Principia will lead to slightly different texts, though the meaning remains identical. This particular translation is by Markus Reiner [2], also known for having proposed the Deborah number and its moniker [3]). This statement by Newton merits some attention [4]. The “resistance” of a fluid, i.e., its opposition to an applied force, gives rise to a local stress τ. In accordance with rheological convention, stress is defined as a force (more specifically, the force per unit area). As regards “the velocity by which the parts of the fluid are being separated:” For separation to occur, different parts of the fluid must move at different velocities, i.e., there must exist a velocity gradient in the fluid. We refer to this as the strain rate $\dot{\gamma }$ which, being a change in velocity with position in the fluid, is an acceleration. Stress is thus seen to be proportional to strain; in one dimension $\tau_{yx} \propto \dot{\gamma }$, or $\tau_{yx} \propto {\text{d}}v_{x} /{\text{d}}y$. The coefficient of proportionality between these properties is the “lack of slipperiness” of the fluid, which is the fluid’s viscosity η (which is the reason why η is sometimes referred to, especially in the much older polymer literature, as the “coefficient of viscosity”). The one-dimensional relation between stress and strain can now be written as the equality:

$$ \tau_{yx} = \eta \dot{\gamma } $$

(1)

which given the definitions of stress and strain, can be seen as a form of Newton’s second law, force = mass × acceleration, or F = ma.

While the above may make our understanding of viscosity appear as a fait accompli, the extension of Newton’s viscosity law to three dimensions took over one-and-a-half centuries after the one-dimensional formulation implicit in the Principia. This was ultimately accomplished in 1845 by George Gabriel Stokes (1819–1903), relying on work by, among others, Claude-Louis Navier (1785–1836). (These “others” include the names of a number of notables in the fields of hydraulics, fluid mechanics, and mathematics, including Cauchy, Poisson, Saint–Venant, and Airy. The reader is referred to the excellent Ref. [5] for a more detailed account of the subject.) Under the assumptions that the stress in a fluid is the sum of a diffusing viscous term and a pressure term, and that the fluid has a constant density and viscosity, Newton’s viscosity law in three dimensions can be formulated as [6, 7]:

$$ \rho \left( {\frac{{\partial {\mathbf{v}}}}{\partial t} + {\mathbf{v}} \cdot \nabla {\mathbf{v}}} \right) = - \nabla p + \rho {\mathbf{g}} + \eta \nabla^{2} {\mathbf{v}} $$

(2)

At first inspection, the above equation, which is the famous Navier–Stokes equation written in Gibbs notation, may not seem to resemble F = ma. A visual definition and grouping of the terms in the equation helps:

As can be seen, the bottom row of the above now presents us with an equivalency between the Navier–Stokes equation and Newton’s second law.

In his classic book Chaos: Making a New Science [8], James Gleick writes that “In fluid dynamics, everything boils down to one canonical equation, the Navier–Stokes equation. It is a miracle of brevity, relating a fluid’s velocity, pressure, density, and viscosity, but it happens to be nonlinear” (italics mine). It is exactly this nonlinearity, with its accompanying sensitive dependence on initial conditions, which makes it, more often than not, impossible to accurately quantitate the interrelationships between the various terms in the Navier–Stokes equation and to obtain exact solutions to it [9]. Gleick, not surprisingly, states the case more elegantly: “Analyzing the behavior of a nonlinear equation like the Navier–Stokes equation is like walking through a maze whose walls rearrange themselves with each step you take” [8]. In many analyses the nonlinear terms of the equation can be ignored, as they tend to cancel each other out. This is not always the case, however, and the consequences can be quite profound, such as the case of rogue waves and freak seas [10].

Exact solutions to the Navier–Stokes equation can be obtained for certain special cases, and/or if certain assumptions are made. Let us make the following assumptions for fluid flow through an open cylinder with constant cross-section [6]:

• 1. Flow is laminar (i.e., the Reynolds number Re is less than 2100).

• 2. The fluid density is constant (“incompressible flow”).

• 3. Flow is time-independent (“steady state”).

• 4. The fluid is Newtonian.

• 5. End effects are neglected (an “entrance length” is actually required, to allow for development of a parabolic flow profile. The value of this length depends on the diameter of the tube and the Reynolds number of the fluid).

• 6. The fluid behaves as a Newtonian continuum (usually a concern only when dealing with very dilute gases, plasmas, or when employing very small diameter tubes, i.e., when the diameter is comparable to the molecular mean free path).

• 7. No wall slip.

In such a case, a parabolic flow profile with the characteristics shown in Fig. 1 will develop, where the arrows within the parabola are meant to represent the streamlines of flow.

Fig. 1

Parabolic flow profile in a tube of constant cross-section. Blue arrows represent streamlines of flow

The equation which described the flow in Fig. 1 is given as:

$$ Q = \int_{0}^{2\pi } {\int_{0}^{{r_{0} }} {v_{z} r{\text{ d}}r{\text{ d}}\theta = \frac{{\pi \, r_{0}^{4} \Delta P}}{8\eta L}} } $$

(3)

where ΔP is the pressure drop across the tube (i.e., between entrance and exit), Q is the volumetric flow rate, r ₀ is the inner radius of the cylinder and L its length, and η is the viscosity of the fluid. Equation (3) is generally known as Poiseuille’s law [or as the Hagen-Poiseuille law, after Jean Léonard Marie Poiseuille (1797–1869) and Gottfried Heinrich Ludwig Hagen (1797–1884)], the history of which is elegantly recounted in Ref. [11].

It is Eq. (3) which provides the cornerstone for on-line viscometric detection.

Viscometry Principles and Instrumentation: A Brief Overview

Because the principles by which the various types of viscometers operate are presented in detail in a number of recent publications [12–14], only a cursory overview is given here.

The simplest type of viscometer is the single-capillary viscometer, in which a pressure transducer is attached to a capillary of known length and internal diameter. With the voltage V from the transducer being converted into pressure P at each SEC elution slice i, the viscosity of each slice is calculated by applying Poiseuille’s law, yielding the specific viscosity η _sp of the solution via:

$$ \eta_{{{\text{sp}},i}} = \frac{{\eta_{i} - \eta_{0} }}{{\eta_{0} }} = \frac{{P_{i} - P_{0} }}{{P_{0} }} = \frac{{V_{i} - V_{0} }}{{V_{0} }} $$

(4)

The subscript “0” is meant to denote baseline (solvent) values. Particular advantages of single-capillary viscometers are their simplicity (only a tube and a transducer are needed) and the fact that no transducer calibration is necessary due to the fact that only one transducer is present. The extreme sensitivity of this type of viscometer to even the most minor flow rate fluctuations in the laboratory is the main reason it has fallen into disuse. It is, however, a detector which can be home-made easily and its principles of operation apply equally to the differential viscometers described next.

By far the most popular type of viscometer is that shown in Fig. 2a, which is the fluid flow analog of the classic Wheatstone bridge electrical circuit [15, 16]. Flow in each of the four capillaries (R ₁ through R ₄) in this viscometer follows Poiseuille’s law. The inlet pressure transducer IP measures the pressured drop across the bridge, and the differential pressure transducer DP measures the drop through the bridge. The “Delay Volume” is a hold-up reservoir which can either be of a single volume or, in newer instruments, can take on any of several discretely adjustable values through the use of a series of hold-up columns. The advantages and disadvantages of this type of viscometer, as compared to its single-capillary counterpart, have been the subject of recent discussion [14]. For the Wheatstone bridge type viscometer, the specific viscosity at each elution slice is calculated according to [12–19]:

$$ \eta_{{{\text{sp}},i}} = \frac{{4{\text{DP}}_{i} }}{{\text{IP}_{i} - 2{\text{DP}}_{i} }} = \frac{{4K_{\text{DP}} V_{{{\text{DP}},i}} }}{{K_{\text{IP}} V_{{{\text{IP}},i}} - 2K_{\text{DP}} V_{{{\text{IP}},i}} }} $$

(5)

where IP _i and DP _i are the slicewise signals from the inlet and differential pressure transducers, respectively; K _IP and K _DP are the calibration constants of these transducers (needed to convert the voltage from each transducer into the respective pressure drop); and V _IP,i and V _DP,i are the voltages associated with the respective transducer responses at each chromatographic slice.

Fig. 2

Differential viscometers. a Wheatstone bridge type, where R ₁–R ₄ represent individual capillaries, DP is the differential pressure transducer, and IP is the inlet pressure transducer. b Triple-capillary type. b Courtesy of Waters Corp

The three-capillary viscometer, shown schematically in Fig. 2b, is found only in certain models of high-temperature SEC instruments. According to the manufacturer, its advantages over other types of commercial viscometers include solution always flowing through all components (i.e., no fluid dead ends), a relative viscosity output independent of both low and high frequency components of viscometer flow, and no need for capillary balancing or matching [20]. For the type of triple-capillary set-up shown in the figure, after entering the viscometer from the SEC columns (or from an additional detector, e.g., a light scattering photometer or a refractometer, placed intermediate to the columns and the viscometer), flow is split into two paths. In one path, the solution flows through the First Capillary into the First Delay Volume, then through the Third Capillary and, finally, to either waste or to another detector placed downstream from the viscometer (e.g., a differential refractometer). In the second path, the solution flows directly through the Second Delay Volume to the Second Capillary and, then, to either waste or a downstream detector. The First and Second Transducers measure the pressures in the First and Second Capillaries (and other fluidic elements), respectively. As with the other viscometers discussed above, flow through each capillary follows Eq. (3). Given the limited availability of this type of viscometer, and the lengthier mathematics involved, the reader is referred to Ref. [20] for a detailed description of how η _sp is calculated from triple-capillary measurements.

Select Applications of SEC/VISC

Universal Calibration

The concept of universal calibration, originally proposed by Grubisic et al. in the 1960s [13, 21, 22], relates the logarithm of the hydrodynamic volume of a polymer to its SEC retention volume, with hydrodynamic volume defined as the product of the intrinsic viscosity [η] and the molar mass M. The intrinsic viscosity, in turn, is defined as:

$$ \left[ \eta \right] \equiv \mathop {\lim }\limits_{c \to 0} \frac{{\eta_{\text{sp}} }}{c} $$

(6)

where c is the concentration of polymer in the near-infinitely dilute solution. To determine [η] a concentration-sensitive detector (most commonly, but not exclusively, a differential refractive index detector or DRI) is needed, and the intrinsic viscosity is thus recognized as the ratio of the signal from the viscometer, which measured η _sp, to that of the concentration-sensitive detector, which measures c, subsequent to correction for interdetector delay or split, depending on whether the two detectors are being used in series or parallel, respectively [12, 13].

Grubisic et al. determined that, regardless of monomeric identity or architectural variability, the data for different polymers all fell on a single curve when plotting log([η] × M) versus retention volume [21]. This conclusion proved invaluable for the determination of the absolute, non-calibrant-relative molar mass averages and distributions of polymers for which no well-characterized narrow dispersity standards exist of the same monomeric composition and architecture as those of the analyte (see e.g., the next two subsections, on cellulose and on poly(amido amine) dendrimers). While certain exceptions to the universal calibration concept have been uncovered over the years, in general this approach has proven itself quite robust across a variety of chemical and structural motifs.

Cellulose

A particular macromolecule for which narrow dispersity standards are nonexistent is cellulose, which is the most abundant biopolymer on Earth. As shown in Fig. 3, the cellulose chain is composed of (1 → 4)-β-d-anhydroglucose units covalently linked to one another in linear fashion. Non-covalent linkages in this molecule include an extensive network of inter- and intramolecular hydrogen bonds (not shown in Fig. 3), which render cellulose dissolution quite challenging. A preferred solvent for the dissolution and analysis of it and related polysaccharides is N,N-dimethyl acetamide with lithium chloride, DMAc/LiCl. The mechanism of dissolution of cellulose in this solvent has been discussed at length elsewhere [23, 24].

Fig. 3

Structures of several of the macromolecules discussed, in order of appearance in this paper. a Cellulose (shown without hydrogen bonds), b polystyrene, c pullulan, d alternan, e third generation (G3) PAMAM dendrimer (core shown in blue and each successive generation shown in a different color; for numbering in PAMAMs, the core is given a generation number of zero), f N-acetylchitooligosaccharides. (Structure of G3 PAMAM reprinted with permission from [57]. Copyright 2005 American Chemical Society)

Given the aforementioned lack of cellulose calibration standards, absolute molar mass averages and distributions of this polysaccharide were obtained using the universal calibration curve in Fig. 4, created employing well-characterized, commercially available narrow dispersity polystyrene (PS) standards [25], the structure of which is shown in Fig. 3.

Fig. 4

Universal calibration plot of narrow dispersity PS standards dissolved in DMAc/0.5 % LiCl, at 80 °C, obtained by SEC/VISC/DRI. “IV” corresponds to intrinsic viscosity [η]. (Reprinted with permission from Ref. [25]. Copyright 1995 American Chemical Society)

In cotton plants, fiber development begins on the day of flowering, botanically referred to as the day of anthesis. Up to approximately 21 days post anthesis (DPA), rapid elongation of the outer cell wall occurs; this is the primary wall stage of cotton. Subsequent to this stage, the secondary cell wall develops, with major cellulose deposition. Mature fiber is usually harvested from cotton plants at around 60 DPA. Given that length is considered among the most important properties of the fiber and that, for a linear macromolecule such as cellulose, molar mass is directly related to fiber length, determining the molar mass distribution of mature cellulose is of great interest. So, too, is determining the molar mass distribution of the primary cell wall components, as difficulties in monitoring changes in cell wall development has hindered research into the biochemical composition of the walls. As seen in Fig. 5, the primary cell wall components have a lower molar mass than do components (primarily cellulose) of the secondary wall. Moreover, high-M cellulose, characteristic of mature cotton fiber, was detected in the 10 DPA sample (as part of these same experiments, cellulose was actually detected as early at 8 DPA). The abundance of high-M cellulose in mature, 60 DPA cotton fiber is also shown in Fig. 5, where it is observed that the differential weight fraction of secondary wall components greatly exceeds that of primary wall components in mature cotton, in contradistinction to what is observed to occur at 10 DPA, during the early stages of fiber development [25].

Fig. 5

Overlay of differential molar mass distributions (MMDs, also known as molecular weight distributions) of cotton fiber at different stages of development: Primary wall stage (10 DPA) versus mature fiber (60 DPA). MMDs obtained by SEC/VISC/DRI in DMAc/0.5 % LiCl at 80 °C, applying universal calibration curve shown in Fig. 4. (Reprinted with permission from Ref. [25]. Copyright 1995 American Chemical Society)

Poly(amido amine) Dendrimers

The above provided an example of the absolute molar mass of a natural polymer, namely cellulose, being obtained through a universal calibration curve constructed using standards of a synthetic polymer, namely polystyrene. Now, we demonstrate the opposite scenario, where pullulan oligo- and polysaccharide standards were employed to construct a universal calibration curve to then obtain the molar mass of poly(amido amine), also known as PAMAM or Starburst^®, dendrimers (The structures of both pullulan and of a generation 3 PAMAM dendrimer are shown in Fig. 3).

For dendrimers, the theoretical average molar mass M _theor can be calculated using Eq. (7) [26]:

$$ M_{\text{theor}} = M_{c} + N_{c} \left[ {M_{\text{RU}} \left( {\frac{{N_{b}^{G + 1} - 1}}{{N_{b} - 1}}} \right) + M_{t} N_{b}^{G + 1} } \right] $$

(7)

where M _c , M _RU, and M _t are, respectively the molar masses of the initiator core, repeat unit, and terminal unit; N _c and N _b are, respectively, the initiator core and branch-juncture multiplicity; G is the dendrimer generation; and N _RU is the number of repeat units in the dendrimer, i.e., the dendrimer degree of polymerization, which can be calculated according to:

$$ N_{\text{RU}} = N_{c} \left( {\frac{{N_{b}^{G + 1} - 1}}{{N_{b} - 1}}} \right) $$

(8)

For the PAMAM dendrimers examined in our study, the M _theor values are given in the second column of Table 1 [27]. As can be seen, the molar mass values obtained by SEC/VISC/DRI using universal calibration differ minimally from the theoretical values, attesting to the accuracy of this type of calibration even in the case of such architecturally extreme structures (dendrimers are potentially the most highly branched structures that can exist [28]).

Table 1 Molar mass and intrinsic viscosity of PAMAM Starburst dendrimers

On-line viscometry detection also allows for another interesting observation in the case of the PAMAM dendrimers. As seen in the last column of Table 1, the intrinsic viscosity of the dendrimers decreases with increasing generation, corresponding to a decrease in [η] with increasing M. This is contrary to the case for most other types of polymers, where [η] increases as a function of M (constancy of [η] with increasing M is addressed below, when discussing the SEC/MALS/VISC/DRI analysis of pullulan; MALS: multi-angle static light scattering). The reason behind this seemingly paradoxical behavior, which has been previously documented for other types of dendrimers [29], is as follows: Initially, at early generations, dendrimers adopt a disclike structure, and their intrinsic viscosity increases with increasing generation (increasing M). Because the growth in density occurs at a faster pace than does radial growth, eventually these materials undergo a so-called “morphological transformation” [27] from disclike to sphere like structures. The point at which this transformation occurs provides the maximum in the [η] versus M relationship. After this, intrinsic viscosity decreases with increasing M, as a result of dendrimer volume increasing cubically, whereas mass increases exponentially (see Eqs. (7), (8)).

Long-Chain Branching Influence on Macromolecular Size: the Viscometric Radius of an Ultra-High-M Polysaccharide

The polysaccharide alternan, the structure of which is shown in Fig. 3, is an ultra-high molar mass macromolecule (M » 1 × 10⁶ g mol⁻¹) with potential applications as a coating for time-released pharmaceuticals, as a binder for inks and paints, as a bulking agent for food and beverages, and as a domestic substitute for gum Arabic. Its characterization is made challenging by the fact that, in addition to having very high M, it aggregates in aqueous solutions; it possesses long-chain branching (LCB) and, most likely, branch-on-branch type structures; it has a broad MMD; and it has two different types of glycosidic linkages, its structure being statistically alternating (1 → 3)-α-d- and (1 → 6)-α-d-anhydroglucose units [30, 31].

The magnitude of the molar mass of alternan, as well as the breadth of its MMD, is demonstrated in Fig. 6. As a matter of fact, the M of alternan is so high, and the macromolecule so fragile (likely as a result of the abundance of (1 → 6) glycosidic linkages in its structure) that it could not be accurately characterized by SEC [31, 32]; rather, hydrodynamic chromatography (HDC [33, 34]), which is a substantially gentler separation method, was employed.

Fig. 6

Differential (blue line) and cumulative (red line) MMD of alternan B-1335, obtained by HDC/MALS/DRI in DMSO at 50 °C. See Ref. [31] for details

To demonstrate the influence of LCB on macromolecular size in solution, we examine the viscometric radius R _η of alternan. The viscometric radius can be thought of as the radius of a homogeneous hard sphere (hard sphere of constant density and composition) which changes the viscosity of the solvent by the same amount as the change imparted by the analyte [12, 13, 35]. Mathematically, R _η is defined as [13, 35]:

$$ R_{\eta } \equiv \left( {\frac{3\left[ \eta \right]M}{{10\pi N_{\text{A}} }}} \right)^{1/3} $$

(9)

where N _A is Avogadro’s number and the other symbols retain their same meaning as above.

The R _η of two different alternans are given in Table 2 (the names “B-1335” and “B-21297” refer to the types of enzymes used to produce each alternan; see Ref. [30] for details). Also tabulated, for comparison, are results for two pullulans. Pullulan was chosen for comparison as it is a linear d-anhydroglucose polysaccharide with two (1 → 4)-α linkages per (1 → 6)-α linkage (Fig. 3); while it is not a perfect linear analog for alternan, it serves for demonstrating the influence of branching on size. In the fourth row of Table 2 are the data for a pullulan of approximately the same viscometric radius as the alternans. As can be seen, the molar mass of this pullulan is over an order of magnitude smaller than are the molar masses of the two alternans examined. More strikingly, the last row of the table gives calculations for a “theoretical” pullulan of molar mass intermediate to those of the two alternans (to this author’s knowledge, no pullulans exist with a molar mass this high; hence, then need for resorting to calculations). The intrinsic viscosity of this pullulan was estimated from the Mark–Houwink relation for pullulan in DMSO/LiBr at 50 °C (courtesy of Peter Kilz, PSS Polymer Standards Service), i.e., at solvent/temperature conditions very similar to those employed to characterize alternan. As can be seen, a pullulan of molar mass similar to alternan would have a viscometric radius of ≈330 nm, compared to only ≈46 nm for alternan! These comparisons serve to demonstrate the great extent to which long-chain branching can compress the hydrodynamic volume of a branched polymer as compared to a linear macromolecule of the same molar mass and monomeric composition [31].

Table 2 Molar mass, intrinsic viscosity, and viscometric radius of alternans and pullulans

Long-Chain Branching: Molar Mass Between Branches

The determination of long-chain branching parameters, such as branching number and branching frequency, employing SEC with MALS and/or VISC detection is based on the theory developed by Bruno Zimm (1920–2005) and Walter Stockmayer (1914–2004) in their classic 1949 paper [36]. The requirements for accurate quantitation of LCB using this theory have been laid out in detail in [37] and in Section 11.2 of [13], while the types of errors that can be incurred by not paying proper attention to these requirements has been demonstrated in [38, 39]. Here, a somewhat different and, perhaps, less widely known LCB metric is discussed.

In 1999, Lusignan et al. applied percolation theory to their SEC/MALS/VISC/DRI results and demonstrated that, for randomly branched polymers, the average molar mass between branches is given by the point of intersection of the power laws describing the linear and branched portions of the polymer in a Mark–Houwink plot (where intrinsic viscosity is plotted versus molar mass, with each axis on a logarithmic scale) [40]. This conclusion was later arrived at, independently, by combining frictional arguments with Zimm–Stockmayer theory and multi-detector SEC results [41]. As seen in Fig. 7 for a randomly branched polyester, the Mark–Houwink plot of the linear portion of the molecule can be fit to a straight line of slope (power law exponent) of 0.80, while the straight line describing the long-chain branched portion of the polyester has a slope of 0.45. The two power laws intersect at M _x  = 66,000 g mol⁻¹, which corresponds to the average molar mass between long-chain branches in this polyester [40]. It should be noted that the same conclusion can be arrived at, in general more accurately but less precisely, employing a conformation plot of the radius of gyration versus molar mass (with each axis, again, plotted logarithmically) [41]. Given the proper choice of standard for comparison, this approach also serves to determine the average molar mass between crosslinks in a lightly crosslinked macromolecule, though without any indication as to whether branch-on-branch structures may exist [41].

Fig. 7

Mark–Houwink plot of a randomly branched polyester. The solid lines with slopes of 0.80 and 0.45 correspond, respectively, to the linear and randomly branched portions of the polymer. The point of intersection of the two lines, M _x , corresponds to the average molar mass between branches (M _x  = 66,000 g mol⁻¹). (Reprinted with permission from [40] Copyright 1999 by the American Physical Society)

Solution Aggregation: Pullulan

As mentioned earlier when discussing the analysis of cellulose, use of the complex solvent DMAc/LiCl has been extended to a large variety of polysaccharides [23, 42, 43], including pullulan (which, it should be noted, is water-soluble). Solutions of pullulan in DMAc/LiCl at 80 °C were analyzed by SEC/MALS/VISC/DRI; results are shown in Fig. 8 [44].

Fig. 8

SEC/MALS/VISC/DRI analysis of pullulan (M _w  = 112,000 g mol⁻¹) in DMAc/0.5 % LiCl at 80 °C. In both top and bottom panels, magenta symbols correspond to signal from 90^o photodiode of MALS detector. In top panel, purple symbols correspond to DRI signal while, in lower panel, purple symbols correspond to differential pressure signal from VISC. (Adapted with permission from [44]. Copyright 1996 American Chemical Society)

Static light scattering experiments such as MALS measure the so-called “excess Rayleigh scattering ratio,” ΔR(θ), which corresponds to the amount of light scattered by a polymer solution in excess of that scattered by the neat solvent. The relation between ΔR(θ) and the molar mass of the polymer being analyzed is given by the Rayleigh–Gans–Debye approximation [13, 45]:

$$ \frac{{K^{*} c}}{\Delta R(\theta )} = \left( {\frac{1}{P(\theta )}} \right)\left( {\frac{1}{{M_{w} }} + 2A_{2} c + \ldots } \right) $$

(10)

where c is the concentration of polymer in solution, P(θ) is a form factor meant to account for angular dissymmetry (i.e., for the angular dependence of the scattered light), A ₂ is the second virial coefficient of the solution, and K* is an optical constant defined as:

$$ K^{*} = \frac{{4\pi^{2} n_{0}^{2} \left( {{{\partial n} \mathord{\left/ {\vphantom {{\partial n} {\partial c}}} \right. \kern-0pt} {\partial c}}} \right)^{2} }}{{\lambda_{0}^{4} N_{\text{A}} }} $$

(11)

where n ₀ is the refractive index of the solvent at the experimental temperature and wavelength, λ ₀ is the vacuum wavelength of the incident radiation, N _A is Avogadro’s number, and ∂n/∂c is the specific refractive index increment of the polymer solution (this term may be considered the refractometric equivalent of the absorptivity in Beer’s law experiments). From these relations, one notes that the signal from a light scattering photometer, which corresponds to ΔR(θ), is directly proportional to the molar mass of the analyte, i.e., a light scattering photometer is a molar-mass-sensitive detector [12, 17]. Because, all other factors being equal, aggregates of an analyte in dilute solution will have a larger molar mass than do the unaggregated moieties, static light scattering detectors such as MALS prove to be very useful in detecting the aggregation of polymers in solution.

As seen in Fig. 8 [44], the traces from all three detectors, MALS, VISC, and DRI, show a common peak eluting with a retention volume of ≈21 mL, which corresponds to unaggregated pullulan. Observed only with the MALS, but not with the VISC and DRI, is also an earlier-eluting peak at a retention volume of ≈18 mL. This early peak is due to aggregation of pullulan at the solvent/temperature conditions of the experiment and is observable by MALS due to the above-mentioned M-sensitivity of this detector. However, viscosity is related to molar mass through the well-known Mark–Houwink equation:

$$ \left[ \eta \right] = KM^{a} $$

(12)

where K and a are empirically determined constants which correspond, respectively, to the intercept (which is, actually, log K) and slope of a Mark–Houwink plot. This means that the viscometer may also be considered a molar-mass-sensitive detector [17]. Given this sensitivity, the absence of a VISC signal for the pullulan aggregate appears paradoxical. To explain this observation, let us examine Eq. (12) a bit more closely.

Table 3 shows the values of the Mark–Houwink exponent a for a few well-defined structures. Pertinent to the present case of pullulan aggregation is the fact that, for homogeneous hard spheres (i.e., hard spheres of constant density and composition), the theoretical value of a is 0. For such a case, the molar mass dependence of intrinsic viscosity disappears and Eq. (12) simplifies to [η] = K (this means that homogeneous hard spheres of one polymer, e.g., PS, will have a different Mark–Houwink intercept than will hard spheres of a different polymer, e.g., PMMA, even though they will both have the same Mark–Houwink slope of 0). Figure 9 shows that this relation does, indeed, hold in reality, for the case of poly(methyl methacrylate) latexes in water where, over the course of more than two orders of magnitude in M, [η] was found to be essentially statistically invariant [46]. Others have also noted similar invariance in [η] as a function of M for star polymers with a large number of arms (see e.g., Section 6.3 of Ref. [47]), meaning that the spheres do not have to be that “hard” for their solutions to display M-independent intrinsic viscosity.

Table 3 Theoretical values of Mark–Houwink exponent a for select well-defined structures

Fig. 9

Mark–Houwink plot of PMMA latexes in aqueous solution at room temperature. Error bars represent one standard deviation based on quadruplicate injections, two each from separate dissolutions. Solid line represent a non-weighted first-order fit to the data, with slope = 0.0003. Based on results from experiments presented in Ref. [46]

The above provides a glimpse into some of the information obtainable from a multi-detector SEC experiment which includes a viscometer in the experimental set-up. SEC separates the aggregates from the unaggregated pullulan, allowing for measurement of the molar mass averages, etc. of the latter. The on-line MALS detector, with its M sensitivity, provides evidence of the existence of pullulan aggregates in solution, aggregates which must be present at a very low concentration (because the DRI shows negligible response to them) and which appear to adopt a fairly spherical, fairly compact solution structure (given the lack of viscometer signal for the aggregate).

The Viscometer as an Orthogonal Detector: “Spectroscopic Invisibility”

Several of the above case studies, in particular the previous one dealing with pullulan aggregation, provide examples of the synergy between viscometry and other methods of detection such as MALS and DRI. This subsection examines a different type of relation between these detectors.

Shown in Fig. 10a–c are the results of the quadruple-detector SEC analysis of poly(dimethyl siloxane), PDMS, samples, either as single samples or as blends [48]. SEC/MALS/QELS/VISC/DRI (QELS: quasi-elastic light scattering, also known as dynamic light scattering) was employed to analyze solutions of PDMS 116 (M _w of 116,000 g mol⁻¹); of a blend of two PDMS samples, PDMS 116 and PDMS 440 (M _w of 116,000 g mol⁻¹ and 440,000 g mol⁻¹, respectively); and of a blend of PDMS 440 and PS 18 (a polystyrene with M _w of 18,000 g mol⁻¹) (see Ref. [48], where additional examples can be found). As can be observed, the signals from the MALS, QELS, and DRI lead to the conclusion that PDMS has been irreversibly adsorbed onto the column packing material, as no signal beyond baseline noise is observed with any of these three detectors (that this observation is not due to faulty columns or detectors is corroborated by the fact that PS 18 elutes as expected and is detected by MALS, QELS, and DRI). The viscometer, however, contradicts this conclusion: Employing this detector, the PDMS is observed in all solutions (as is the PS in the appropriate blend). Moreover, in both blends (Fig. 10b, c), the larger analyte is observe to elute before the smaller one, as expected in an SEC experiment. Also, PDMS 440 elicits a larger response from the viscometer than do the smaller PDMS 116 or PS 18, in accordance with the viscometer being a molar-mass-sensitive detector.

Fig. 10

SEC/MALS/QELS/VISC/DRI analysis of PDMS: a PDMS 116, b ≈2:1 blend of PDMS 116 and PDMS 440, c ≈1.5:1 blend of PS 18 and PDMS 440. In all panels, DRI in black, MALS in blue, QELS in magenta, and VISC in red. Except for normalized responses in c, all MALS, DRI, and VISC signals are in volts, V, whereas the QELS signals are in Hertz, Hz. (Reprinted with permission from [48]. Copyright 2015 Springer)

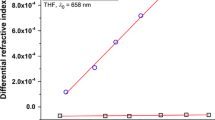
Why is PDMS observable with VISC but not with MALS, QELS, or DRI? Briefly (the subject is treated more fully in Ref. [48]), MALS, QELS, and DRI are spectroscopically based detectors, whereas the viscometer’s response in based on hydrodynamic transport properties of solutions. As seen in Eqs. (10) and (11) above, the light scattering detectors’ responses depend on the specific refractive index increment ∂n/∂c of the solutions being analyzed. This same is true of the differential refractometer, the response of which is proportional to the product of ∂n/∂c and concentration (DRI α (∂n/∂c × c) [13, 45], with the proportionality converted into equality using the calibration constant for the particular refractometry hardware employed in the measurements). The ∂n/∂c plots of both PS and PDMS, at the experimental conditions, are shown in Fig. 11. As can be seen, while the ∂n/∂c of PS is quite large, that of PDMS is almost zero. For the particular detectors employed, at the particular solvent/temperature conditions, solutions of PDMS may be considered to be “spectroscopically invisible.” The principle of operation of VISC being orthogonal to those of the other detectors employed explains why PDMS is not invisible to viscometry. (It should be noted that “visibility” by viscometry but not by refractometry does not affect the measurement of η _sp, as given by Eq. (4), but it does preclude the determination of [η] by SEC/VISC/DRI, because of the inability to determine the denominator in Eq. (6)).

Fig. 11

Specific refractive index increment (∂n/∂c) plot of PDMS 116 at 20 °C (open black squares) and PS of M _w 200000 (Р= 1.06) g mol⁻¹ at 25 °C (open blue circles), both in THF and both with λ ₀ = 658 nm. Instrumental standard deviations are smaller than data markers and, therefore, not shown. Solid red lines represent the first-order, non-weighted linear fits of the data, without forcing through the origin (for PDMS, Pearson’s r = 0.798; for PS, Pearson’s r = 0.999). The slopes of these lines correspond to the ∂n/∂c of the respective polymers, (0.1964 ± 0.0019) mL g⁻¹ for PS, (0.0016 ± 0.0006) mL g⁻¹ for PDMS. (Reprinted with permission from [48]. Copyright 2015 Springer)

SEC/VISC of Oligomers

Being a molar-mass-sensitive detector, the response of the viscometer increases as a function of increasing analyte molar mass (certain special cases, discussed above, notwithstanding). Conversely, the opposite is true, i.e., as molar mass decreases, so does the viscometer’s response [49]. For this reason, the viscometer is not usually considered a choice detector for studies of oligomer solutions which, by definition, are low-M species. Here, we demonstrate the sensitivity of VISC in the analysis of oligosaccharides and the insights attainable via SEC/VISC into the seemingly counterintuitive behavior of solutions of synthetic oligomers.

Oligosaccharides

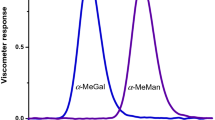
Size-exclusion chromatography with on-line viscosity detection was recently shown to be an excellent way to analyze oligosaccharides in aqueous solution at quasi-physiological conditions (human body temperature and pH) [14]. As seen in Fig. 12 for the case of N-acetylchitooligosaccharides, even for disaccharides the viscometer response is excellent (it should be noted that analysis conditions were typical, i.e., solution concentration was 1 mg mL⁻¹ and, using a four-column set, injection volume was 100 μL per column). Analyses were also conducted on two additional oligosaccharide series, namely cello- and mannooligosaccharides, with similar results (see Ref. [14] for details].

Fig. 12

Overlay of SEC/VISC chromatograms of N-acetylchitooligosaccharide dimer through hexamer (numbers above peaks), at quasi-physiological conditions. Ordinate represents response from the VISC differential pressure transducer. (Reprinted with permission from [14]. Copyright 2014 Elsevier)

Negative Viscosity of Oligomer Solutions

The fact that solutions of oligomers, and even of polymers, can possess a negative viscosity (i.e., η < 0) has been known for some time. However, the conditions under which this behavior occurs can be fairly extreme: under high frequency oscillatory electric birefringence conditions [50, 51], or in the case of magnetic fluids flowing through capillaries placed inside solenoids through which passed an alternating magnetic field [52]. In general, these are conditions far removed from those of an SEC/VISC experiment. Under fairly standard SEC conditions, however, the viscosity of solutions of ethylene oligomers and styrene monomers has been shown to be less than zero.

Shown in Fig. 13a are the traces from the VISC differential pressure transducer for high-temperature (135 °C) SEC experiments in 1,2,4-trichlorobenzene (TCB) of the polyethyelene oligomers octadecane (PE 282) and dodecane (PE 170) [53]. The larger oligomer, PE 282, behaves as expected, its solution displaying a larger viscosity than that of the neat solvent, as exemplified by the positive peak in the SEC/VISC trace of this oligomer (for comparison, the traces of the respective solvent blanks have been overlaid upon the oligomer traces in Fig. 13a–c). In sharp contrast to this, the VISC peak for PE 170 is negative. The same type of behavior as for PE 170 was observed for PS 162, an n-butyl-terminated styrene monomer, but not for larger PS oligomers, at the same experimental conditions as the PEs (Fig. 13b). In DMAc/LiCl at 35 °C, however, solutions of PS 162 display a positive VISC peak, while solutions of non-functionalized styrene monomer (“Styrene” in figure) display a negative peak (Fig. 13c; it should also be noted that, under the experimental conditions of this figure, the styrene oligomers elute by a non-size-exclusion mechanism, most markedly so for the non-functionalized styrene monomer, as seen by it eluting earlier than PS 162 and at approximately the same retention volume as a trimer of styrene) [53].

Fig. 13

Negative viscosity of oligomer solutions. a, b in TCB at 135 °C, c in DMAc/0.5 % LiCl at 35 °C. Ordinates in all graphs correspond to signal from the differential pressure transducer of a Wheatstone bridge type viscometer, proportional to the specific viscosity η _sp of the solutions. (Adapted with permission from Ref. [53]. Copyright 2002 Taylor and Francis)

As noted earlier, the signal from the differential pressure transducer of the Wheatstone bridge type differential viscometer is directly proportional to the specific viscosity η _sp of analyte solutions. The intrinsic viscosity [η] of these solutions is calculated from η _sp via Eq. (6). In turn, the viscometric radius R _η of the analytes is calculated from [η] using Eq. (9). As can be seen from Table 4, this corresponds to analytes with solutions of negative viscosity having a negative size, at least as R _η is concerned.

Table 4 Intrinsic viscosities and viscometric radii of select oligomers in Fig. 13

A detailed explanation of the above behavior can be found in Ref. [53]. Briefly, for the case of non-functionalized styrene monomer (“Styrene,” M = 104 g mol⁻¹) in DMAc/LiCl at 35 °C, solutions appear to follow the predictive mixing rule for one-phase binary mixtures [54]:

$$ \eta = \eta_{A} \phi_{A} + \eta_{B} \phi_{B} + P\phi_{A} \phi_{B} $$

(13)

where η _A and η _B are the viscosities of the individual components of the mixture (in the present case, Styrene and DMAc/LiCl), ϕ _A and ϕ _B are the volume fractions of these components, and P is an interaction parameter such that the last set of terms on the right-hand side of Eq. (13) is meant to represent the concentration-dependent interaction between two different chemical species (for these particular experiments, P was calculated to be 0.129 mPa s). Using literature values for the 20 °C viscosities of Styrene (0.76 mPa s) and DMAc (0.97 mPa s) [55], the solid-line relation in Fig. 14 was calculated from Eq. (13). As can be seen, this relation agrees quite well with concentric-cylinder rheometry data for the viscosity of solutions of Styrene in DMAc/LiCl at various volume fractions (experimental points in Fig. 14). Thus, the SEC/VISC behavior of solutions of Styrene in DMAc/LiCl has been corroborated by an independent experimental method.

Fig. 14

Viscosity of Styrene-DMAc/0.5 % LiCl solutions versus volume fraction of Styrene, at 35 °C. Experimental points obtained by concentric cylinder rheometry employing a Couette geometry. Error bars represent one standard deviation based on replicate measurements, except for 0.5 volume fraction styrene, which are based on quadruplicate measurements from two separate dissolutions (see original reference for experimental details). Solid blue line, for which r ² = 0.992, represents prediction from Eq. (13). (Adapted with permission from Ref. [53]. Copyright 2002 Taylor and Francis)

As to why the solutions display a negative viscosity, this appears to be a result of the analytes having a lower viscosity than the solvents at the experimental temperatures (as seen in the previous paragraph, at room temperature η _Styrene < η _DMAc). While solutions follow the mixing rule for one-phase binary mixtures (Eq. 13), the small oligomeric or monomeric “solutes” are, essentially, becoming the diluents for the solvent, i.e., qualitatively one can think of this scenario as solute and solvent exchanging their roles with one another.

There is also nothing anomalous or paradoxical in having negative values of R _η . Indeed, this is in agreement with the qualitative definition of this radius, given above, as “the radius of a homogeneous hard sphere which changes the viscosity of the solvent by the same amount as the change imparted by the analyte.” Italics have now been added, to highlight the fact that the “change” may not necessarily be toward an increase in viscosity. When the change is to a viscosity decrease then, per force, R _η  < 0.

It should be noted that other macromolecular radii, such as the thermodynamic radius R _T, can also possess negative values. The explanation for this, which is beyond the topic of this discussion, can be found along with examples in Ref. [35].

Conclusions

The principles and applications of viscometry as an on-line detection method in SEC (and related size-based methods) have been highlighted. It is hoped that the variety of examples presented attest to the power and versatility of VISC as a detection method, especially in combination with other physical and chemical detectors (for an example of VISC used in combination with both types of detectors, the reader is referred to Ref. [56]). As stated in the Introduction, beyond determining M averages and distributions using the universal calibration approach, and LCB parameters using Zimm–Stockmayer theory, the uses of VISC, for both natural and synthetic macromolecules, range from the monomeric and oligomeric to ultra-high M; across linear, branched, hyperbranched, and dendritic architectures; into the realm of latexes and aggregates; and even into the negative size regime. Its synergy with other types of SEC detectors helps provide topological information about macromolecules vital to processing and end-use, while the orthogonality of VISC with respect to spectroscopically based detectors allows for analytes to be viewed from a different, oftentimes unique, perspective subsequent to their chromatographic separation.

A final, unusual, albeit quite informative, piece of information regarding the utility of viscometry is that traditional leading manufacturers of light scattering photometers have, for over a decade now, also become manufacturers and vendors of on-line viscometers—recognizing and embracing the need for this type of detector, on a commercially viable scale.