Introduction

Furrow irrigation is the most common method of surface irrigation. In this irrigation type, the flow is both spatially varied and unsteady that depends on infiltrating water. Mathematical models of surface irrigation include either mass conservation or both mass conservation and momentum equation, namely the Saint–Venant equations. These models can be applied for analyzing the flow hydraulics and managing surface irrigation. To solve these equations, which are also known as the Saint–Venant equations, the full equation system or a simplified version of them might be considered. Regarding the applied form, developed models are categorized into four main groups, including the full hydrodynamic model, the zero-inertia model, the kinematic-wave model and the volume balance model. The full hydrodynamic model is the complete form of Saint–Venant equations (Wallender and Rayej 1990). This model is the most complex and accurate among all models. The zero-inertia model is suggested by Strelkoff and Katopodes (1977) for borders and then utilized for furrow irrigation by Elliott et al. (1982). This model neglects the acceleration and inertia terms in the momentum equation, whereas the volume balance model ignores entire momentum equation (Wallender 1986; Valiantzas 2000). The kinematic-wave model is normally utilized to steep slopes and used uniform flow assumptions (Walker and Humpherys 1983).

Over the past years, several numerical models from hydrodynamic models (Wallender and Rayej 1990; Bautista and Wallender 1992; Tabuada et al. 1995; Banti et al. 2011), zero-inertia models (Schmitz and Seus 1990; Schwankl et al. 2000; Abbasi et al. 2003; Zerihun et al. 2008; Soroush et al. 2013), kinematic-wave models (Walker and Humpherys 1983; Ram and Singh 1985; Clemmens and Strelkoff 2011) and volume balance models (Alazba 1999; Guardo et al. 2000; Weihan and Wenying 2011) have been developed in the field of surface irrigation researches. Banti et al. (2011) simulated advance in the furrow irrigation using a coupled finite difference technique for the surface flow and finite element method for the subsurface flow. Their model developed based on the Saint–Venant equation for surface flow and the Richards equations for infiltration. They showed that the proposed coupling model managed to prevent numerical instabilities and convergence problems.

Shayya et al. (1993) discussed the obtained results of a kinematic-wave model to simulate flow in furrow irrigation. Their model was built on using one-dimensional finite element method. The Kostiakov–Lewis formula is used to estimate infiltration. The model tested with measured data from three farm sites. The results showed that the proposed model could be effectively used in analyzing sloping furrows.

Clemmens and Strelkoff (2011) presented a kinematic-wave model that used a zero-inertia approximation to the water-surface profile at cutoffs. They indicated that this approximation could alter the estimation of recession time. Soroush et al. (2013) developed a model by applying slow-change/slow-flow equations that are a combination of mass conservation and momentum equation. The Saint–Venant equations were solved using a method based on explicit Euler and implicit Crank–Nicolson methods. They claimed that the applied model is a suitable and simple approach for modeling and evaluation of furrow irrigation. All in all, studying and exploring the related literature show that the zero-inertia models are capable for giving promising results as the complex full hydrodynamic models (Zerihun et al. 1996; abbasi et al. 2003; Ebrahimian and Liaghat 2011).

In this paper, the authors created and developed zero-inertia finite element model (ZIFEM) to simulate furrow irrigation phases of advance, storage and recession. To achieve this purpose, the equations were discretized by the finite element method. ZIFEM was used to solve the Saint–Venant equations based on the nonuniform spatial elements. The variation of element sizes in space dimension could lead to lower computational expense, especially if the furrow length is fairly large. In this regard, at first a system of equations was developed by using the Galerkin finite element method and then ZIFEM was determined the element length for each time step. Finally, the system of equation was solved numerically by using the Gauss elimination approach. A computer model was expanded to utilize the mathematical procedure. The accuracy of the model was verified by data set gathered from the experimental furrows in Kerman as well as some of the reported data. In addition, the results were also compared with the output of the WinSRFR and Sirmod numerical models.

Governing equations

In this study, the zero-inertia equations, which are a popular form of governing equations for flow simulation in irrigation furrows, have been applied. These equations can be given as follows:

$$\frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} + I = 0$$
(1)
$$\frac{\partial y}{\partial x} = S_{o} - S_{f}$$
(2)

where A is the cross-sectional area; Q represents the flow rate; I is the infiltration rate; y stands for the flow depth; S o is the field slop; S f denotes the hydraulic resistance slop; t is the time; and x is the distance along the field.

Of the abovementioned parameters, the estimation of infiltration rate was achieved by the Kostiakov–Lewis equation.

$$I = ka\tau^{a - 1} + f_{0}$$
(3)

where τ is the opportunity time; f 0 is the final infiltration rate; and k and a are empirical constants. f 0 is computed using the inflow rate and runoff data as follows (Walker and Skogerboe (1987):

$$f_{0} = \frac{{(\bar{Q}_{\text{in}} - Q_{{{\text{ro}}\,}} )*\psi }}{L.W}$$
(4)

where \(\bar{Q}_{\text{in}}\) is the average inflow rate up to the cutoff time, Q ro is the runoff rate measured at or prior to cutoff time, L stands for the furrow length, and W is the furrow spacing. The value of Q ro was assumed to measure at steady-state condition. The actual system is not at steady state, and the value of f 0 should be reduced by applying the empirical parameter ψ = 0.5 (Bautista et al. 2012a, b). In this research, the Sipar_ID model was applied to estimate the infiltration parameter of Kostiakov–Lewis. The Sipar_ID model was developed by Rodriguez and Martos in 2007. This model combines a volume balance model with artificial neural networks (ANN) to estimate infiltration parameters (Rodriguez and Martos 2010). Also, the Merriam–Keller procedure of the WinSRFR model was utilized to calibrate infiltration parameter. It is worth noting that the Merriam–Keller procedure is a method for estimating the final infiltration depth profile and the average infiltration characteristics of the evaluated furrow, border or basin from a post-irrigation volume balance (Merriam and Keller 1978). The precision of the estimated parameters can be achieved via a trial-and-error method which is used to calculate the infiltration function (Bautista et al. 2012a, b).

The Manning equation was used to calculate the hydraulic resistance slope. The manning formula can be expressed by:

$$S_{f} = \frac{{Q\left| Q \right|n^{2} }}{{\rho_{1} A^{{\rho_{2} }} }}$$
(5)

The power–law relationships can also be written in flow cross section and flow depth as follows (Abbasi et al. 2003):

$$y = \sigma_{1} A^{{\sigma {}_{2}}}$$
(6)

By using Eqs. (2), (5) and (6), the momentum equation can be rewritten as:

$$Q = CA^{{\frac{{\rho {}_{2}}}{2}}}$$
(7)

where ρ 1, ρ 2, σ 1 and σ 1 are furrow cross-sectional parameters and C is equal to \(\left( {S_{o} - \left( {\sigma_{1} \sigma_{2} A^{{\sigma_{2} - 1}} \frac{\partial A}{\partial x}} \right)} \right)^{{\frac{1}{2}}} \frac{{\rho_{1}^{{\frac{1}{2}}} }}{n}\).

Formulation and finite element implementation of the equations

In this section, the process of linearization and application of the applied finite element method is outlined. For linearity, we considered the Galerkin formulation and linear elements for the continuity equation as follows:

$$\int {\psi (x)\left( {\frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} + I} \right){\text{d}}x = 0}$$
(8)

where ψ(x) is the weighting function.

By selecting a linear element, there are two equations for one element. The finite element approach is used to approximate the parameters of Eq. (8). Therefore, the parameters in Eq. (8) can be written as:

$$\left\{ {\begin{array}{*{20}l} {A(x,t) = N_{i} A_{i} (t) + N_{j} A_{j} (t)} \hfill \\ {Q(x,t) = N_{i} Q_{i} (t) + N_{j} Q_{j} (t)} \hfill \\ {I(t) = I_{i} (t) + I_{j} (t)} \hfill \\ \end{array} } \right.$$
(9)

where N i and N j are shape functions at node i and j.

For linear element, the shape functions in the local coordinate system are represented as:

$$N_{i} = 1 - \frac{s}{L},\quad N_{j} = \frac{s}{L}$$
(10)

where L is the length of the element and s = x − X i .

Then, by substituting Eq. (9) in Eq. (8), we have:

$$\int_{0}^{l} {\left[ N \right]^{\text{T}} \left[ N \right]\left[ {\dot{A}} \right] + \left[ N \right]^{\text{T}} \left[ B \right]\left[ Q \right] + \left[ N \right]^{\text{T}} \left[ I \right]{\text{d}}x} = 0$$
(11)

where t is time and \(\left[ B \right] = \left[ {\frac{{\partial N_{i} }}{\partial x}\,\,\,\,\,\frac{{\partial N_{j} }}{\partial x}} \right] = \left[ { - \frac{1}{L}\,\,\,\,\,\frac{1}{L}} \right]\), \(\left[ {\dot{A}} \right] = \frac{\partial A}{\partial t}\). Substituting shape function into Eq. (11) and simplifying, we can write the discrete form of Eq. (1) as follows:

$$\left[ {C_{\text{e}} } \right]\left[ {\dot{A}} \right] + \left[ {K_{\text{e}} } \right]\left[ Q \right] + \left[ {F_{\text{e}} } \right] = 0$$
(12)

where

$$C_{\text{e}} = \frac{L}{6}\left[ {\begin{array}{*{20}c} 2 & 1 \\ 1 & 2 \\ \end{array} } \right],\quad K_{\text{e}} = \left[ {\begin{array}{*{20}c} {\frac{ - 1}{2}} & {\frac{1}{2}} \\ {\frac{ - 1}{2}} & {\frac{1}{2}} \\ \end{array} } \right],\quad F_{\text{e}} = \left[ {\begin{array}{*{20}c} {\frac{ - L}{2}} \\ {\frac{ - L}{2}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{i} } & {I_{j} } \\ \end{array} } \right]$$
(13)

K e is the stiffness matrix of each element. The finite difference approach is used to approximate \(\frac{\partial A}{\partial t}\), Q and F e in Eq. (12):

$$\left[ {\frac{\partial \varphi }{\partial t}} \right] = \frac{{\left[ \varphi \right]_{n + 1} - \left[ \varphi \right]_{n} }}{\Delta t}$$
(14)
$$\left[ \varphi \right] = (1 - \theta )\left[ \varphi \right]_{n} + \theta \left[ \varphi \right]_{n + 1}$$
(15)

where Δt = t n+1−t n , [φ] n and [φ] n+1 are the nodal values of parameters such as A, Q and I at the time t n and t n+1. To estimate θ in Eq. (15), the central scheme of the finite difference method (θ = 0.5) is chosen. It should be noted that the backward difference is used to approximate \(\frac{\partial A}{\partial x}\) in Eq. (7). By substituting Eqs. (14, 15) into Eq. (12) and assembling element into a global system of equation using the direct stiffness procedure, we get:

$$\left[ {C_{\text{g}} } \right]\left( {\left[ A \right]_{n + 1} - \left[ A \right]_{n} } \right) + \frac{1}{2}\Delta t\left[ {K_{\text{g}} } \right]\left( {\left[ Q \right]_{n + 1} - \left[ Q \right]_{n} } \right) - \frac{1}{2}\Delta t\left( {\left[ F \right]_{n + 1} + \left[ F \right]_{n} } \right) = 0$$
(16)

where K g is the global stiffness matrix and F is the global force vector. In the first time step, the element and global matrices are the same. At the each next time step, one element is added to the solution process, until the summation of the lengths of elements equals to the length of the furrow.

To solve this equation, we consider a hypothetical advanced distance and then by assuming equal discharge at two time step ([Q] n+1=[Q] n ), the cross-sectional area of each node was calculated. The flow rate at each node was estimated by Eq. (7). Initial and boundary conditions for the irrigation advance phase are:

$$\left\{ {\begin{array}{*{20}l} {A\left( {x,0} \right) = 0, \, Q\left( {x,0} \right) = 0} \hfill & {0 \le x \le L} \hfill \\ {Q\left( {0,t} \right) = Q_{0} ,A(0,t) = A_{0} } \hfill & {0 \le t \le t_{\text{co}} } \hfill \\ {Q\left( {x_{\text{adv}} ,t_{\text{adv}} } \right) = 0,A(x_{\text{adv}} ,t_{\text{adv}} ) = 0} \hfill & {0 \le t \le t_{\text{co}} } \hfill \\ \end{array} } \right.$$
(17)

where Q 0 is the flow rate in the first node at the beginning of the furrow, x adv and t adv are the location and time of the advancing waterfront, and t co is time of cutoff.

We drive the advanced distance at each time step (L i ) from Eq. (16) by considering the boundary condition of the tip cell in advance phase.

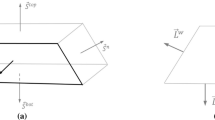
$$L_{i} = \frac{{1.5\theta \Delta tQ_{i} }}{{A_{i} + 1.5\theta \Delta tI_{i} }}$$
(18)

where i index presents the upstream node of the tip cell (Fig. 1). With the results of Eq. (16), we calculate the advanced distance by using Eq. (18). At the beginning of irrigation, the advanced distance from one time step is more than other time steps. So, we have maximum advanced distance in first time step and minimum advanced distance in the last time step. This advanced distance will be compared with hypothetical one and corrected by trial-and-error method. The process will be continued until the distance is equivalent to the length of the furrow.

Fig. 1
figure 1

Typical surface and subsurface profile expansion under surface-irrigated conditions (Walker and Skogerboe 1987)

Full size image

The algorithm below describes ZIFEM advance phase:

ZIFEM algorithm

1. Input Δt, Lfurrow;

2. i = 0, t = Δt, n = 0, L total  = 0, ε = 0.00001; % ε is the accuracy.

3. Assume advanced distance (Li s );

4. Built the matrices in Eq (16);

5. By assuming \(\left[ Q \right]_{n + 1} = \left[ Q \right]_{n}\), calculate \(\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} } \right]_{n + 1}\) from Eq (16);

6. Calculate [Q] n+1 from Eq (7);

7. Calculate [A] n+1 using Eq(16);

8. If \(\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} - A} \right|_{n + 1} \le \varepsilon\)

  From Eq (18), estimate Li;

  else

   \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{n + 1} = A_{n + 1}\) and go to step 6;

  End if

9. If \(\left| {L_{is} - L_{i} } \right| \le \varepsilon\)

    L i is correct, L total  = L total  + L i ;

  else

    L is  = Li and go to step 4;

  End if

10. If L total  < L Furrow

   Print L total and t (advance time),

   % new element is added.

   t = t + Δt, n = n + 1, i = i + 1, go to step 3;

   else

   Print t % t is the total time of advance

   End

Once waterfront reaches end of the furrow, storage phase begins. After completing the advance phase, the number of elements in the storage and depletion phases remains constant. Upstream boundary condition is similar to advance phase. In the storage phase, the downstream boundary condition is fixed by free discharge at the end of the furrow.

When the inflow of the furrow cuts, the depletion phase starts. The governing equations are similar to the storage phase. The only condition that imposed in this phase is Q 0 = zero. The depletion phase stops when the cross-sectional area at the first node is smaller than 10% of the initial cross-sectional area and the recession phase starts.

In the recession phase, when the cross-sectional area at one node is smaller than 10 percent of the initial cross-sectional area, this node removes from computations. In this phase, the water wave is moved to the end of the furrow. To simulate the phases in furrow irrigation, a computer code was written in MATLAB based on the previous formulas. It should be added that ZIFEM is from order of O(Δt) + O(Δx 2).

Model verification

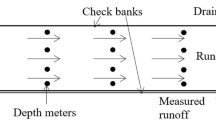
The ability of the ZIFEM model to simulate furrow irrigation was verified with seven sets of field observed data. Two data sets were obtained from field experiment during 2015 at the Agricultural Research Farm of Shahid Bahonar University of Kerman, Iran. The research farm is located in the southeast of Kerman (57°10′E, 30°20′N) on sandy loam soil at 1750 m above sea level. The experiments were conducted on the furrows of 72 m in length and 0.7 m in space. The inflow and outflow discharge was measured by V-notch weir and 1-in. Parshall flume, respectively. The furrows were divided into fourteen stations with stakes, and the advance time and recession time were measured at each station. Figure 2 shows the schematic view of the experimental furrows.

Fig. 2
figure 2

a Sketch of the furrow layout in the experimental farm, b a landscape photograph of the furrow during storage phase

Full size image

In addition to the field experiments, five data sets were collected from the literature (see Table 1). The selected irrigation events cover a wide range of soil infiltration parameter, furrow lengths and field slops. One of the furrow data sets (Isfahan) could be found in Moravejalahkami et al. (2012). The Dezfool data set was published by Abbasi et al. (2003). Two data sets were Printz 8-2-3 and Kimberly wheel that were reported in Walker and Skogerboe (1987). The last data sets (Matchett 1-4-5) were derived from Elliott et al. (1982). General geometric characteristics and infiltration parameters of data sets are shown in Table 1.

Table 1 Data sets of furrow irrigation
Full size table

To evaluate the suitability of the ZIFEM, three statistical criteria were computed to analyze the model’s goodness of fit. These statistics are: (1) the root-mean-square error (RMSE), (2) the percentage error (E) and (3) the relative error (ε) as the following:

$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {(t_{i} - t_{i}^{\prime } )^{2} } }}{N}}$$
(19)
$$E = \left| {\frac{{t_{i} - t_{i}^{\prime } }}{{t_{i} }}} \right| \times 100$$
(20)
$$\varepsilon = \frac{{V_{\text{Runoff}}^{\prime } - V_{\text{Runoff}} }}{{V_{\text{Runoff}} }}$$
(21)

where N is the number of measurements, t and t′ are the measured and predicted values of advance and recession times, respectively, \(V_{\text{Runoff}}^{\prime }\) and V Runoff are the predicted and measured values of the runoff volume, respectively.

Results and discussion

Accuracy of the proposed ZIFEM model was assessed with observed furrow data. Also, the results were compared with the WinSRFR 4.1.3 model. The WinSRFR software package is an integrated surface irrigation analysis tool. The USDA Natural Resources Conservation Service developed this model (Bautista et al. 2010). The WinSRFR model uses finite volume method to discrete the governing equations and solves the system of equations by double-sweep method (Bautista et al. 2012a, b). The performance of the ZIFEM and the WinSRFR models in predicting advanced and recession trajectories and outflow hydrographs is tabulated in Tables 2 and 3. Noting that in the present study the zero-inertia engine of WinSRFR was used for all simulation runs.

Table 2 Statistical indices of simulated parameters for ZIFEM
Full size table
Table 3 Statistical indices of simulated parameters WinSRFR 4.1.3 model
Full size table

Table 2 indicates that the RMSE values between the experimental data versus the modeled results are less than 10%. Figure 3 illustrates a good fit of the simulated advance and recession times and observed data over the entire length of the furrow in Kerman1 and Kerman2 irrigation events. However, the ZIFEM advance times resulted in lower RMSE values compared to those obtained from the WinSRFR model.

Fig. 3
figure 3

Simulated and measured advance and recession trajectories for Kerman1 and Kerman2 furrows

Full size image

From Fig. 3 and Table 2, it is clear that the ZIFEM slightly overestimated the recession times. This matter was expected as a result of difficulties in observing the recession times. Runoff volume and outflow hydrographs are closely matched with the experimental data with small relative error values of 0.1 and 0.12 (Fig. 4; Table 2). It can be viewed (Fig. 4) that the tailwater runoff increased with time because the infiltration rate decreased.

Fig. 4
figure 4

Measured and simulated runoff rate for Kerman1 and Kerman2 furrows

Full size image

According to relative error, the ZIFEM and WinSRFR model overpredicted the runoff volume in the same level (Tables 2, 3).

The simulated advance and recession times compared with measured values for Isfahan and Dezfool farms have been shown in Fig. 5. The percentage errors of the total advance and recession times of ZIFEM for Isfahan and Dezfool farms were 3.32, 3.66, 5.53 and 1.56%, respectively, which are less than WinSRFR model (Tables 2, 3).

Fig. 5
figure 5

Simulated and measured advance and recession trajectories for Isfahan and Dezfool furrows

Full size image

The Isfahan farm resulted in a lower RMSE value (0.38) of the advance times as compared to those obtained with other irrigation events. The ZIFEM simulated the runoff of Isfahan farm in good agreement with observed data (Fig. 6). The deviations between the measured and simulated runoff were related to assume steady-state conditions, and accuracy of the Parshall flume is used for measuring outflow hydrograph.

Fig. 6
figure 6

Measured and model-simulated runoff for different data sets

Full size image

The observed and simulated advance and recession trajectories for Matchett 1-4-5 farm have been shown in Fig. 7. The RMSE and percentage error of advance and recession times of the ZIFEM for Matchett farm are 8.06 and 9.31, respectively, which were less than WinSRFR model (Table 3).

Fig. 7
figure 7

Simulated and measured advance and recession trajectories for Matchett 1-4-5 furrow

Full size image

For Printz 8-2-3 and Kimberly wheel furrows, the model-simulated and observed data of advance and recession curves are presented in Fig. 8. In Printz 8-2-3 farm, the ZIFEM resulted a lower RMSE and percentage error as compared to those obtained using the WinSRFR model. Thus, in general the ZIFEM is superior to WinSRFR and performed in an acceptable way for estimating the advance and recession times.

Fig. 8
figure 8

Simulated and measured advance and recession trajectories for Printz 8-2-3 and Kimberly wheel furrows

Full size image

On the Kiemberely wheel farm, the inflow was cutted before the advancing waterfront reached at the end of the furrow. Therefore, there was no storage phase in this irrigation event. Advance and recession curves were fitted well by the model with RMSE of 10.09 and 6.66%, respectively. Minor discrepancies between ZIFEM and WinSRFR model were due to different methods of solving the governing equations.

Abbasi et al. (2003) developed a zero-inertia model based on finite difference method. They used Dezfool furrow data for their assessment. This data set also adopted in our research. The average error for their model to predict advance and recession times was 4.4 and 2.6%, respectively, while in the proposed model (ZIFEM) the average error was 3.4 and 1.5%, respectively. So, it can be concluded that ZIFEM has increased precision in this case. Soroush et al. (2013) expanded a zero-inertia model based on reducing the Saint–Venant equations and solving them by finite difference method. They compared their results to those from WinSRFR model. Their results showed that in 28% of the total number of events, their model could simulate satisfactorily compared with the WinSRFR model. ZIFEM simulates 78% of the total number of events satisfactorily in comparison with the WinSRFR model.

Having a better and profound insight of the proposed model, the ZIFEM results were also compared with those from zero-inertia model in Sirmod package. Surface irrigation simulation model (Sirmod) was developed by Walker at Utah University, USA. This model solves the Saint–Venant equation by using the method of characteristics with deformed cell (Walker 2003). The values of RMSE and relative error of the simulated events of this study from Sirmod package are presented in Table 4.

Table 4 Statistical indices of simulated parameters for Sirmod
Full size table

The values of RMSE for Sirmod model are varied between 1.34 and 17.89 and for ZIFEM are varied between 0.38 and 12.58. All models simulated the advance times for Isfahan event more accurate than those from the other irrigation events. This is because the Isfahan irrigation event has a short furrow length. ZIFEM predicted 64% of total number of events better than Sirmod model. In overall, the average values of RMSE of advance times for the seven data sets for ZIFEM, WinSRFR and Sirmod models are 4.62, 6.05 and 5.03, respectively, and these values for recession times are 5.81, 12.51 and 9.5, respectively. According to these results, ZIFEM was simulated the advance and recession times more precisely than other models. As a general conclusion, it should be noted that all of the three models predicted the advance times better than the recession times. Similar results were reported by Abbasi et al. (2003).

According to Tables 2, 3 and 4, the runoff volume predicted using the WinSRFR model in Kerman2 irrigation event was more accurate than ZIFEM and Sirmod models. All in all, in irrigation events of lower inflow rate, the results simulated using WinSRFR model are better than other models. The differences between the ZIFEM, WinSRFR and Sirmod models’ outcomes might be due to application of different methods in solving the governing equation. The ZIFEM uses the finite element method to simulate furrow irrigation system, whereas the Sirmod and WinSRFR models use the finite difference method and finite volume method, respectively.

Conclusion

A numerical model, namely ZIFEM, was presented to predict furrow irrigation phases including advance, storage, depletion and recession phases and runoff rate. The zero-inertia equations were discretized with linear elements. The model was set up by using the Galerkin formulation of the finite element method. The governing equations of Saint–Venant were solved using the Gaussian elimination technique. The Kostiakov–Lewis formula was also implemented to estimate the infiltration process. The evaluation of the model in simulating the advance, recession and runoff phases revealed that the proposed model agreed well with the field measurements and even was superior to the results of the WinSRFR and Sirmod models. The computer programming of ZIFEM was straight, and boundary conditions were easily incorporated in the solution processes. The limitation of ZIFEM is that the discretization of the governing equations was based on a piecewise representation of the solution in terms of the linear basis functions. The results indicated that the ZIFEM could be successfully used in predicting advance and recession curves for almost all furrow-type irrigation events with various agricultural soil types. Further investigations are recommended to study the effects of another basis functions such as wavelet basis or quadratic elements, different inflow hydrograph shapes and using a cropped field on simulating furrow irrigation system.