Introduction

High-precision time transfer is the basis for the time laboratory to establish and maintain standard time scale and time synchronization. With the development of space technology, the precision of time transfer is getting higher and higher. Precise point positioning (PPP) has the advantages of high-precision, wide-area coverage, and convenient data acquisition and processing. In recent years, the time transfer method based on PPP has shown superior performance in terms of precision and coverage, which has made it become one of the most popular Global Navigation Satellite System (GNSS) time transfer methods, and it was applied to the International Atomic Time Scale (TAI) in 2009 (Petit 2009; Petit and Jiang 2007; Yao et al. 2015). With the improvement of precision and timeliness of IGS precise ephemeris and clock products, PPP technology has been applied more in the GNSS time-frequency field. Petit et al. (2011) carried out PPP time transfer experiments based on GPS, and the results show that the uncertainty uA of the static PPP time transfer is 0.3ns. Harmegnies et al. (2013) analyzed the time transfer of a GPS single system and GPS + GLONASS combined PPP. The results show that the timing precision of the two schemes is similar, i.e., the precision improvement of GPS + GLONASS multi-system combination timing is rather limited.

Concerning the above studies in PPP timing, the ionospheric-free combination was widely used. Along with the modernization of GPS and GLONASS, as well as the newly launched systems BDS and Galileo (Montenbruck et al. 2017; Yang et al. 2021), multi-frequency GNSS data processing has paved the way for the undifferenced and uncombined PPP (UC-PPP) model (Zhou et al. 2018). Tu et al. (2019) analyze the time transfer performance of IF-PPP and UC-PPP models. The results show that the two models have the same accuracy and stability, and the receiver code bias is very stable that can be predicted for the next day. In undifferenced and uncombined PPP timing, ionospheric delay plays an important role (Rose et al. 2014; Su et al. 2019; Zhang et al. 2020). Ge et al. (2019) compared the time transfer performance of the ionospheric constraint model, the ionospheric correction model, and the ionospheric-free model and pointed out that the accuracy of the ionospheric constraint model is better than others. The ionospheric constraint model estimates the ionospheric delay as a parameter constrained by the Global Ionosphere Map (GIM) product, and the ionospheric correction model constraint model directly uses GIM to correct the ionospheric delay. In addition, the standard deviation (STD) values of the ionospheric constraint model time transfer are at the level of 0.5 ns at cutoff elevation angles of 10°, 20°, and 30°. Hexagon Positioning Intelligence (HPI) tested regional ionosphere models (RIM), and the results show that convergence to a 5 cm level can be obtained in several seconds and regional ionospheric products have higher reliability (Jokinen et al. 2018). However, the application of high-precision ionospheric products in time transfer and its in-depth analysis is still left for further study.

We first briefly review the basic principle of PPP time transfer technology, and the emphasis is given to the difference between the ionospheric-free PPP and undifferenced and uncombined PPP; then, the performance of time transfer with different PPP models is analyzed based on six GNSS stations equipped with H-MASERs for over 357 days.

Methods

The undifferenced and uncombined observable of the GNSS pseudorange and carrier phase is generally expressed as (Leick et al. 2015)

$$\left. {\begin{array}{*{20}c} {P_{r,f}^{s} = \rho_{r}^{s} + t_{r} + \alpha_{r}^{s} T_{r}^{s} + \beta_{f} \gamma_{r}^{s} I_{Z} + b_{r,f}^{s} + \varepsilon_{P} } \\ {\phi_{r,f}^{s} = \rho_{r}^{s} + t_{r} + \alpha_{r}^{s} T_{r}^{s} - \beta_{f} \gamma_{r}^{s} I_{Z} + \lambda_{f} N_{r,f}^{s} + \varepsilon_{\phi } } \\ \end{array} } \right\}$$
(1)

where \(r\), \(s\) and \(f\) are the receiver, satellite and frequency, respectively;\(P_{r,f}^{s}\),\(\phi_{r,f}^{s}\) are pseudorange and carrier phase from receiver \(r\) to satellites \(s\) on frequency \(f\) in length unties, respectively;\(\rho_{r}^{s}\) denotes the geometric distance between the phase center of the satellite and receiver antennas at the signal transmitting and receiving time, respectively; \(t_{r}\) is the receiver clock bias in units of length; \(T_{r}^{s}\) is the zenith tropospheric delay that can be converted to slant with the mapping function \(\alpha\); \(I_{Z}\) denotes the zenith TEC with the frequency and elevation angle dependent factor \(\beta_{f} = \frac{40.3}{{f^{2} }} \cdot {\text{mf}}\left( e \right)\),\(\gamma_{r}^{s}\) is the ionospheric mapping function; \(b_{r}^{s} = b_{r} - b^{s}\) is the frequency dependent code bias (Li et al. 2011); \(N_{r}^{s}\) is the float ambiguity in cycle units with the corresponding wave length \(\lambda_{f}\); \(\varepsilon_{P}\) and \(\varepsilon_{{\phi }}\) denote the sum of measurement noise and multipath error for the pseudorange and carrier phase, respectively. In addition, the satellite and receiver antenna phase center offsets (PCOs) and variations (PCVs), earth tides, relativistic effects, and phase wind-up have been corrected with existing models (Kouba 2009).

Ionospheric-free PPP

The IF-PPP model combines observations of different frequencies linearly to eliminate the first-order ionospheric delay term of carrier phase and pseudorange observations. In this model, only receiver coordinates, receiver clock offset, zenith tropospheric delay and ambiguity are estimated (Zhao et al. 2019)

$$\begin{array}{*{20}c} {\left. {\begin{array}{*{20}c} {P_{{{\text{IF}}}} = \rho_{r}^{s} { + }t_{r} + \alpha_{r}^{s} T_{r}^{s} + b_{{r,{\text{IF}}}}^{s} + \varepsilon_{{{\text{IF}},P}} } \\ {\phi_{{{\text{IF}}}} = \rho_{r}^{s} { + }t_{r} + \alpha_{r}^{s} T_{r}^{s} + \lambda_{{{\text{IF}}}} N_{{{\text{IF}}}} + \varepsilon_{{{\text{IF}},\phi }} } \\ \end{array} } \right\}} \\ \end{array}$$
(2)

where the subscript IF represents the ionospheric elimination combination; \(P_{{{\text{IF}}}}\), \(\phi_{{{\text{IF}}}}\) are the IF pseudorange and carrier phase in units of range, respectively, and \(P_{{{\text{IF}}}} = \gamma_{1} P_{1} - \gamma_{2} P_{2}\),\(\phi_{{{\text{IF}}}} = \gamma_{1} \phi_{1} - \gamma_{2} \phi_{2}\),\(\gamma_{i} = \frac{{f_{i}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\left( {i = 1,2} \right)\); \(b_{{r,{\text{IF}}}}^{s} = \gamma_{1} b_{r,1}^{s} - \gamma_{2} b_{r,2}^{s}\) is the IF code bias; similarly, the definition of the left terms can be obtained by IF combination and (1).

In addition, following the dual-frequency IF combination, the measurement noise of pseudorange and carrier phase is

$$\left. {\begin{array}{*{20}c} {\sigma_{{\varepsilon_{{{\text{IF}},P}} }}^{2} = \left( {\gamma_{1}^{2} + \gamma_{2}^{2} } \right)\sigma_{{\varepsilon_{P} }}^{2} } \\ {\sigma_{{\varepsilon_{{{\text{IF}},\phi }} }}^{2} = \left( {\gamma_{1}^{2} + \gamma_{2}^{2} } \right)\sigma_{{\varepsilon_{{\phi }} }}^{2} } \\ \end{array} } \right\}$$
(3)

where \(\sigma_{ \cdot }^{2}\) is the variance of the corresponding measurement noise. By substituting \(f_{1}\) and \(f_{2}\) into (3), it is derived that \(\sigma_{{\varepsilon_{{{\text{IF}},P}} }}^{2} \approx 8.87\varepsilon_{P}\) and \(\sigma_{{\varepsilon_{{{\text{IF}},\phi }} }}^{2} \approx 8.87\varepsilon_{\phi }\); thus, the noise of IF combination is much larger than that of the undifferenced and uncombined observable.

Ionospheric hardware delay in pseudorange observations will be fully absorbed by receiver clock offset through IF combination

$$t_{{r,{\text{IF}}}} = t_{r} + b_{{r,{\text{IF}}}} = t_{r} + \gamma_{1} b_{r,1} - \gamma_{2} b_{r,2}$$
(4)

where the definition of \(\gamma\) and \(b_{r}\) can be obtained by (1).

Undifferenced and uncombined PPP

Although the IF combination can eliminate the influence of the first-order term of the ionospheric, the combined observation noise would be amplified in (3). To solve this problem, the undifferenced and uncombined model is proposed in which the individual signal of each frequency is treated as an independent observation. And the basic model is written as (1). One of the main features of the undifferenced and uncombined model is that the ionospheric delay should be estimated along with the geometry parameters. Traditionally, the LOS (line of sight) ionospheric delay is treated as an independent parameter, whereas in this study, the ionospheric parameterization method DESIGN (deterministic plus stochastic ionospheric delay modeling for GNSS) is applied in the undifferenced and uncombined model (Lou et al. 2016; Shi et al. 2012)

$$\left. {\begin{array}{*{20}c} {I_{Z} = a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} } \\ {I_{{{\text{corr}}}} = a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} + \varepsilon_{I} } \\ \end{array} } \right\}$$
(5)

where \(I_{Z}\) is the zenith ionospheric delay from receiver to satellite,\(I_{{{\text{corr}}}}\) is the ionosphere delay correction from, e.g., GIM or a regional high-precision ionospheric delay model (RIM), as in this study;\(a_{i} \left( {i = 0,1,2,3,4} \right)\) are the coefficients that describe the deterministic behavior of ionospheric delay; \(r_{r}^{s}\) is the residual ionospheric effect for each satellite that describes the stochastic behavior of ionospheric delay; \(d_{L}\), \(d_{B}\) is the longitude and latitude difference between the Ionospheric Pierce Point (IPP) and the approximate location of the station, respectively; \(\varepsilon_{I}\) is the ionospheric parameter fitting estimation noise.

In addition, to eliminate the linear dependence of receiver clock offset and code bias, we have the following assumption

$$\begin{array}{*{20}c} {t_{r,{\text{UC}}} = t_{r} + b_{r,1} } \\ \end{array}$$
(6)

where \(t_{r,UC}\) is the receiver clock solved by the undifferenced and uncombined PPP model.

By substituting (5) and (6) into (1), the dual-frequency undifferenced and uncombined PPP model based on DESIGN is written as

$$\left. {\begin{array}{l} {P_{r,1}^{s} = \rho_{r}^{s} { + }t_{r,{\text{UC}}} { } + \alpha_{r}^{s} T_{r}^{s} + \beta_{1} \gamma_{r}^{s} \left( {a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} } \right) + b^{s} + \varepsilon_{P} } \\ {P_{r,2}^{s} = \rho_{r}^{s} { + }t_{r,{\text{UC}}} - b_{r,12} + \alpha_{r}^{s} T_{r}^{s} + \beta_{2} \gamma_{r}^{s} \left( {a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} } \right) + b^{s} + \varepsilon_{P} } \\ {\phi_{r,1}^{s} = \rho_{r}^{s} { + }t_{r,{\text{UC}}} + \alpha_{r}^{s} T_{r}^{s} - \beta_{1} \gamma_{r}^{s} \left( {a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} } \right) + \lambda_{1} N_{r,1}^{s} + \varepsilon_{{\phi }} } \\ {\phi_{r,2}^{s} = \rho_{r}^{s} { + }t_{r,{\text{UC}}} + \alpha_{r}^{s} T_{r}^{s} - \beta_{2} \gamma_{r}^{s} \left( {a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} } \right) + \lambda_{1} N_{r,2}^{s} + \varepsilon_{\phi } } \\ {I_{{{\text{corr}}}} = a_{0} + a_{1} d_{L} + a_{2} d_{L}^{2} + a_{3} d_{B} + a_{4} d_{B}^{2} + r_{r}^{s} + \varepsilon_{I} } \\ \end{array} } \right\}$$
(7)

where parameters definitions can be obtained from (1) and (5); \(b^{s}\) is the satellite code bias that can be corrected with IGS products; concerning the receiver code bias, though \(b_{r,1}\) is absorbed by the receiver clock as (6), the code bias on the second frequency is \(b_{r,12} = b_{r,1} - b_{r,2}\) to make model (7) hold. \(b_{r,12}\) is usually known as differential code bias (DCB) and usually rather stable.

Recall (4) and (6), the difference of receiver clock between IF-PPP and undifferenced and uncombined PPP can be derived as

$$t_{{r,{\text{IF}}}} = t_{r,{\text{UC}}} + \gamma_{2} b_{r,12}$$
(8)

where the bias is due to the different parameterization and rank deficiency elimination strategy are used for IF-PPP and undifferenced and uncombined PPP.

Assessment of clock stability with PPP

Considering the linear relationship between the receiver and the satellite clock, the extensive constraint on the satellite clock is (Yang et al. 2019) :

$$\mathop \sum \limits_{s = 1}^{k} t^{{s,{\text{sys}}}} = 0$$
(9)

where \(t^{{s,{\text{sys}}}}\) is satellite clock belonging to \({\text{sys}} \in \left( {G R C E} \right)\). In addition, considering the linear relationship between the satellite clock and carrier phase ambiguity, as well as the additional bias generated by satellites in the same system, the satellite clock estimate can be written:

$$\widehat{t}^{{s,{\text{sys}}}} = t^{{s,{\text{sys}}}} - t^{{0,{\text{sys}}}} + \varepsilon^{{s,{\text{sys}}}}$$
(10)

where \(t^{{0,{\text{sys}}}}\) is the reference clock offset caused by the linear relationship among the system satellite clock, receiver clock, and ambiguities;\(\varepsilon^{{s,{\text{sys}}}}\) is the estimation noise.

Considering the reference clock in PPP, \(t^{{0,{\text{sys}}}}\) , would be absorbed by the receiver clock,

$$\hat{t}_{r}^{{{\text{sys}}}} = t_{r}^{{{\text{sys}}}} - t^{{0,{\text{sys}}}} + \varepsilon_{r}$$
(11)

where \(t_{r}^{{{\text{sys}}}}\) is the receiver clock belonging to \({\text{sys}} \;{\text{and}} \varepsilon_{r}\) is the estimation noise, then the time difference between two receivers using the same satellite system:

$$\Delta \hat{t}_{{r_{i} ,r_{j} }}^{{{\text{sys}}}} = \hat{t}_{{r_{i} }}^{{{\text{sys}}}} - \hat{t}_{{r_{j} }}^{{{\text{sys}}}} = t_{{r_{i} }}^{{{\text{sys}}}} - t_{{r_{j} }}^{{{\text{sys}}}} + \varepsilon_{{r_{i} }} - \varepsilon_{{r_{j} }} \left( {i \ne j} \right)$$
(12)

The symbols meaning on the right of the equal sign are the same as (14).

The overlapping Allan deviation is used to evaluate the stability of the receiver clock. Based on (11) and (12), considering that the receivers used in this experiment are equipped with the external H-MASER, the effect of \(t_{r}^{{{\text{sys}}}}\) can be ignored, then we can obtain:

$$\left. {\begin{array}{*{20}c} {\delta_{y}^{2} \left( {\tau ,\hat{t}_{r}^{{{\text{sys}}}} } \right) \approx \delta_{y}^{2} \left( {\tau ,t^{{0,{\text{sys}}}} } \right) + \delta_{y}^{2} \left( {\tau ,\varepsilon_{r} } \right)} \\ {\delta_{y}^{2} \left( {\tau ,\Delta \hat{t}_{{r_{i} ,r_{j} }}^{{{\text{sys}}}} } \right) = \delta_{y}^{2} \left( {\tau ,\hat{t}_{{r_{i} }}^{{{\text{sys}}}} } \right) + \delta_{y}^{2} \left( {\tau ,\hat{t}_{{r_{j} }}^{{{\text{sys}}}} } \right) \approx 2\delta_{y}^{2} \left( {\tau ,\varepsilon_{r} } \right)\left( {i \ne j} \right)} \\ \end{array} } \right\}$$
(13)

the symbolic meaning on the right of the equal sign can be found from (10) to (12).

When tested with k receivers, we can get \(k\) receivers and \(k - 1\) time synchronization overlapping Allan deviation. We can use the following model to obtain \(\delta^{2} \left( {\tau ,\varepsilon_{r} } \right)\):

$$\left( {\begin{array}{*{20}c} {\delta_{y}^{2} \left( {\tau ,\hat{t}_{{r_{1} }}^{{{\text{sys}}}} } \right)} \\ \vdots \\ {\delta_{y}^{2} \left( {\tau ,\hat{t}_{{r_{k} }}^{{{\text{sys}}}} } \right)} \\ {\delta_{y}^{2} \left( {\tau ,\Delta \hat{t}_{{r_{1} ,r_{2} }}^{{{\text{sys}}}} } \right)} \\ \vdots \\ {\delta_{y}^{2} \left( {\tau ,\Delta \hat{t}_{{r_{1} ,r_{k} }}^{{{\text{sys}}}} } \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\varvec{u}}_{{\varvec{k}}} } & {{\varvec{u}}_{{\varvec{k}}} } \\ {2{\varvec{u}}_{{{\varvec{k}} - 1}} } & {{\varvec{z}}_{{{\varvec{k}} - 1}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\delta_{y}^{2} \left( {\tau ,\varepsilon_{r} } \right)} \\ {\delta_{y}^{2} \left( {\tau ,t^{0} } \right)} \\ \end{array} } \right)$$
(14)

where \({\varvec{u}}_{{\varvec{k}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } & {\begin{array}{*{20}c} \cdots & 1 \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}}\) is a \(k \times 1\) vector with one entry; \({\varvec{z}}_{{\varvec{k}}} = \left( {0,0 \ldots 0} \right)^{{\text{T}}}\) is a \(k \times 1\) vector with zero entries.

Ionospheric modeling

Based on (5) and (7), we can obtain the vertical TEC of the ionospheric pierce point (IPP) and convert it to slant TEC (STEC) by the ionospheric mapping function \(\gamma\). Then, the ionospheric variations can be fitted by the Quasi-4-Dimension Ionospheric Modeling (Q4DIM) (Gu et al. 2022). For the Q4DIM users, the ionospheric delay corrections are obtained as:

$${\text{STEC}}_{r}^{s} = I_{o}^{s} + r_{r}^{s}$$
(15)

where \(I_{o}^{s}\) is ionospheric delay deterministic part; it can be either interpolated from grids or calculated with the Spherical Harmonic Function (SHF) of GIM with a mapping function.\(r_{r}^{s}\) is obtained according to the key values in the Q4DIM map.

Experimental data and processing strategies

To assess the performance of PPP time transfer, all the above-mentioned algorithms, i.e., IF-PPP, undifferenced and uncombined PPP, RIM products are realized with the FUSING (FUSing IN GNSS) software. Up to now, FUSING is capable of real-time multi-GNSS precise POD, satellite clock estimation, atmosphere modeling, and multi-sensor navigation.(Gong et al. 2018; Shi et al 2019; Luo et al. 2020; Gu et al. 2021).

Data and strategy

The experiment is carried out with six GNSS stations of EUREF Permanent Network (EPN), BRUX, OP71, PTBB, ROAG, SPT0, and WAB2. These stations are involved in Bureau International des Poids et Mesures (BIPM) TAI maintenance and are equipped with H-MASER (iMaser 3000 active hydrogen maser standards for BRUX and OP71; VCH-1003M active hydrogen maser standards for PTBB; MHM-2010 active H-MASER standards for ROAG; CH1-95 hydrogen maser standard for SPT0; pHMaser 1008 passive hydrogen maser standards for WAB2;), and the specifications of these clocks are given in Table 1; thus, the stability of the receiver clock frequency standard itself is relatively negligible in PPP clock estimation noise evaluation. In addition, 202 stations are selected for the regional ionospheric model (Wang et al. 2021; Geng et al. 2021). To extract regional ionospheric products, the spatial and temporal resolution of bins of 5° × 3° and 1 minute, respectively, have been selected. The observation is collected for DOY (day of year) 009 to 365, 2020 with an interval of 30s. Though the signals of BDS+GPS+Galileo+GLONASS are tracked by these stations, only the receiver clock of the GPS is used since the receiver clocks of different systems are estimated as individual parameters. Precise orbit and clock products are provided by the Helmholtz-Centre Potsdam-German Centre for Geoscience Research (GFZ), which are calculated from data from the Multi-GNSS Experiment (MGEX) in the global region (Montenbruck et al. 2017). And the final precise orbit and clock products of GFZ, i.e., GBM provide multi-system satellite products, and the satellite clock product is consistent with the ionospheic-free combination of L1 and L2. Table 2 presents the details of the stations. In addition, Table 3 lists the details of PPP processing strategies; the receiver DCB uses the smooth convergence value of the previous day as a constraint. Note that the undifferenced and uncombined PPP in this work is constrained by GIM and RIM products, so we name them GIM-PPP and RIM-PPP, respectively. Except for the orbit and clock, regional ionospheric products and PPP are processed in forward-filtering decoding mode with Square Root Information Filter (SRIF).

Table 1 Specification and ADEV (s)
Full size table
Table 2 Summaries of the station information
Full size table
Table 3 Details of PPP processing strategy
Full size table

Performance analysis

In the following analysis, we first demonstrate the precision of regional ionospheric products. Then, the performance of GNSS timing based on a different algorithm, i.e., IF-PPP, GIM-PPP, and RIM-PPP is analyzed in terms of Allan deviation.

Efficiency of regional ionospheric product and ambiguity resolution

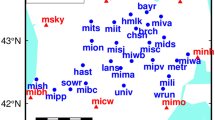
High-precision ionospheric delay correction is the key to improving the convergence speed and positioning accuracy of the undifferenced and uncombined PPP model (Song et al. 2021). The distribution of these base stations is shown in Fig. 1. In order to evaluate the precision of the regional ionospheric High-precision products, the post-processed ionospheric delay of the six laboratories with maser-equipped GNSS receivers with fixed coordinates was used as the reference.

Fig. 1
figure 1

Geographical distribution of 202 selected GNSS tracking stations in blue for ionospheric delay modeling, and six time laboratory stations in red for PPP timing

Full size image

Fig. 2 shows the time series of the ionosphere delay differences at the zenith between the regional ionospheric product and the reference value within one day, with a cutoff angle of 10°. The result of BRUX is selected arbitrarily as an example. We can see that the ionosphere delay differences are almost all less than 0.2 m. In addition, Fig. 3 presents the average RMS of GPS satellites for 357 consecutive days at BRUX, OP71, PTBB, ROAG, SPT0, and WAB2. The ionospheric delays in the zenith direction at the stations are obviously better than 0.10 m. Comparing the RMS of the RIM product at day and night, it can be seen that the accuracy of the RIM products at day and night is comparable, which is highly significant for the RIM-PPP model.

Fig. 2
figure 2

Time series of ionospheric delay differences at the zenith of satellite G01 to G32 between regional ionospheric products and post-processing model on frequency L1 for BRUX at DOY 010, 2020.

Full size image
Fig. 3
figure 3

Day and night RMS of the ionospheric delay differences at the zenith between regional ionospheric products and post-processing value on frequency L1 from DOY 009 to 365, 2020 for BRUX, OP71, PTBB, ROAG, SPT0, and WAB2, respectively

Full size image

Fig. 4 presents the percentage of available satellites at the cutoff elevation angle of 10°for BRUX, OP71, PTBB, ROAG, SPT0, and WAB2. As presented, we usually have 6 to 11 satellites available; the average number of available satellites is (8.76, 8.38, 8.62, 8.53, 8.95, 8.48), respectively. This is acceptable for PPP time transfer. In addition, the data integrity rates of observations during the experiment are (99.90%, 99.99%, 99.74%, 99.90%, 99.99%, 99.63%), and the data integrity rate of all stations is better than 99.50%.

Fig. 4
figure 4

Percentage of available satellites for BRUX, OP71, PTBB, ROAG, SPT0, and WAB2, respectively

Full size image

PPP one-way timing analysis

Figure 5 shows the clock series of the solution IF-PPP (black), GIM-PPP (red), and RIM-PPP (blue) for 357 consecutive days of the experimental period. As presented, there is a bias between IF-PPP and GIM-PPP/ RIM-PPP due to the receiver code bias in Fig. 6. Note that BRUX changed the receiver on DOY 56, 2020 and SPT0 changed the antenna on DOY 226, 2020 (https://www.igs.org/). Overall, the clocks of these stations are rather stable with an amplitude of 2.5 ns intraday and 8 ns in a year, as the high-quality atomic frequency standards data. The fluctuation in the series was mainly due to the noise in the satellite clock datum and PPP processing. As the same satellite clock product is used, the performance comparison revealed the noise of one-way timing with different PPP algorithms. The series suggests that, overall, the PPP noise of different algorithms is similar to each other. The receiver code bias between P1 and P2 is plotted in Fig. 6 for GIM-PPP, and RIM-PPP, respectively. As we can see, these biases are rather stable, with an amplitude of 1 ns in a year, and have similar performance for different stations. In addition, we note that there are similar fluctuations in the receiver P1-P2 code bias estimated value series for different stations, and ​the STD of the receiver P1-P2 code bias series is slightly larger for the RIM-PPP model than for the GIM-PPP model. With (7), this is mainly due to the strong correlation between ionospheric delay and DCB. Thus, the fluctuation of the P1-P2 DCB estimation sequence is similar for different stations, and the STD of the P1-P2 DCB series for the RIM-PPP model is larger than that of the GIM-PPP model due to the higher accuracy of RIM and the stronger constraint on DCB.

Fig. 5
figure 5

Receiver clock series of IF-PPP, GIM-PPP, and RIM-PPP model timing from DOY 009 to 365, 2020 for BRUX, OP71, PTBB, ROAG, SPT0, and WAB2, respectively.

Full size image
Fig. 6
figure 6

Series of the receiver P1P2 DCB estimated values over DOY 009 to 365, 2020 with GIM-PPP model in red and RIM-PPP model in green for BRUX, OP71, PTBB, ROAG, SPT0, and WAB2, respectively.

Full size image

With (8), the receiver estimated clock bias for IF-PPP and UC-PPP models should be zero. Table 4 shows the 357d average difference between the GIM-PPP and RIM-PPP models compared to the IF-PPP model at different stations during the test period of the experiment. As shown in Table, the receiver estimated clock bias for the GIM-PPP and the RIM-PPP models is extremely small compared to the IF-PPP model, in addition, we note that the deviation between the RIM-PPP model and the IF-PPP model is slightly larger for the ROAG and WAB2 stations than for the other stations. According to Fig. 3, it can be seen that the ionospheric accuracy of the two stations is slightly worse than that of the other stations and fluctuates considerably over the year, which affects the accuracy of the PPP one-way timing.

Table 4 Model biases of GIM-PPP and RIM-PPP compared to IF-PPP model for one-way timing (units: ns)
Full size table

Stability of PPP time transfer

To assess the stability of PPP time transfer, Fig. 7 presents the 357d average overlapping Allan deviations of PPP one-way timing, i.e., \(\delta_{y}^{2} \left( {\tau ,\hat{t}_{r}^{sys} } \right)\) in (13), of BRUX, OP71, PTBB, ROAG, SPT0, and WAB2 at different time intervals with IF-PPP, GIM-PPP, and RIM-PPP, respectively. As shown in this figure, RIM-PPP presents the best result for stability. This is most likely due to the fast convergence of RIM-PPP when compared to IF-PPP and GIM-PPP, and regional ionospheric products are more stable. The results of GIM-PPP are slightly better than that of IF-PPP.

Fig. 7
figure 7

Modified Allan deviations of IF-PPP, GIM-PPP, and RIM-PPP model receiver clock series from DOY 009 to 365, 2020 for BRUX, OP71, PTBB, SPT0 and WAB2, respectively

Full size image

With (14), we can derive the Allan deviations of data processing noise \(\delta_{y}^{2} \left( {\tau ,\varepsilon_{r} } \right)\) for different PPP solutions. And the results are presented in Fig. 8. As we can see, the Allan deviations of estimated noise in IF-PPP, GIM-PPP, and RIM-PPP models have a similar trend. Because the IF-PPP model uses an unsmoothed linear combination of observations, the overall Allan deviation of the IF-PPP model is worse than that of the other solutions. In addition, since RIM-PPP uses high-precision regional ionospheric products, its stability is obviously better than that of the IF-PPP and GIM-PPP models.

Fig. 8
figure 8

Modified Allan deviations of PPP data processing noise with IF-PPP, GIM-PPP, and RIM-PPP model

Full size image

Conclusions

This study assesses the PPP time transfer performance with different solutions, i.e., IF-PPP, GIM-PPP, and RIM-PPP in simulated real-time mode. The experiment is carried out with EPN observations from six maser-equipped laboratory stations and GBM products from DOY 009 to 365, 2020. To enable the RIM-PPP solution, 202 stations of EPN are collected for the estimation of the regional ionospheric model.

​For PPP one-way timing, the GIM-PPP and the RIM-PPP models have comparable accuracy compared to the IF-PPP model. In terms of time transfer stability, we separated the PPP estimation noise for the evaluation and the results show that both the GIM-PPP and RIM-PPP models show improvements over the traditional IF-PPP model. The short-term stabilities of GIM-PPP and RIM-PPP models are significantly improved; the improvement is about 20% and 50%, respectively. The long-term stabilities for GIM-PPP and RIM-PPP are improved by about 17 and 29%, respectively.