Ephemeris monitor with ambiguity resolution for CAT II/III GBAS

Abstract

In safety-critical applications, such as the Ground-Based Augmentation System for precision approaches in civil aviation, it is important to safeguard users under the case of ephemeris failures. For CAT II/III approaches, different ephemeris monitors with approaches for ambiguity resolution are proposed with the double differenced carrier phase as the test statistics. The continuity risks introduced by the ambiguity resolution are addressed by deriving the required averaging time for new, acquired, and re-acquired satellites. Since the ephemeris fault is closely related with the baseline length between ground stations, the minimum baseline length is derived to meet the probability of missed detection region. Current methods are compared with both the averaging time and the ground baseline length. It is demonstrated that a combination of two methods is able to achieve the best performance with 94 averaging epochs and 218 m ground baseline length.

Introduction

The Ground-Based Augmentation System (GBAS) is used for precision approaches in civil aviation to improve both the accuracy and integrity of the Global Navigation Satellite System (GNSS) (Annex-10 2018). With accuracy improved by a local area differential positioning scheme between the ground and airborne receivers, how to guarantee the safety of aviation users within the required integrity level is a more challenging task. Integrity monitoring is implemented in airborne and ground subsystems for incidents that may result in large position errors. Failure of ranging source failure is one of the causes. Five types of threats are characterized in GBAS, including ionospheric anomaly, code-carrier divergence, signal deformation, satellite clock, and ephemeris failure (Brenner and Liu 2010; Jiang et al. 2017). It is within the responsibility of the ground subsystem to detect the ranging faults and remove the satellite before it is incorporated in the airborne solution.

In the early history of GPS, the ephemeris error greater than 50 m has occurred on 24 occasions. A more recent case was observed on GPS SV54 with errors larger than 350 m in 2014 (Gratton et al. 2007). In GBAS, the ephemeris threat occurs when the broadcast ephemeris parameters yield excessive satellite position errors perpendicular to the ground subsystem’s line of sight (LOS) to the satellite (SARPs 2009; Pervan and Chan 2003). It has been proved that only satellite position errors perpendicular to LOS contributes to the differential range error (Matsumoto et al. 1999). The GBAS ephemeris threat is categorized as type A and type B threats, where the type A threat involves a satellite maneuver and type B does not. Type A is further categorized as type A1 and type A2, where the maneuver of type A1 is scheduled and A2 is not. For CAT I approaches, a YE-TE (Yesterday-minus-Today Ephemeris) test is used to monitor the Type B ephemeris threat where the ephemeris is compared with a previously validated ephemeris (Matsumoto et al. 1999; Pullen et al. 2001; Gratton et al. 2004; Pervan and Gratton 2005). The difference between the computed and predicted range and range rates with pseudorange corrections is also used for this purpose (Tang et al. 2010). Due to the limited precision of the test statistics, it can only be used for CAT I approaches.

For CAT II/III approaches with more stringent requirements, aviation users also need protection against type A threat, for which the YE-TE approach is not applicable. The double differenced (DD) phase observations are commonly used as the test statistics in the ephemeris monitor for CAT II/III approaches (Pervan and Chan 2003; Khanafseh et al. 2017; Patel et al. 2020), which is also used for monitoring the ionosphere threat (Khanafseh et al. 2012). With dual-frequency signals available for civil aviation, e.g., GPS L1 and L5, a second test statistics is proposed using the Wide-Lane (WL) combination (Patel et al. 2020). The purpose is to enlarge the wavelength, and the cost is the 4.9 times inflated standard deviation. With less noise in test statistics, the monitor is able to detect smaller ephemeris faults. Therefore, the DD phase observation is a preferred choice to achieve better performance.

The critical issue using the high precision phase observations for integrity monitoring is the ambiguity resolution (AR). With the DD observation as the test statistics, the WL ambiguity is estimated by the difference between WL phase and DD code combinations, and the single-frequency ambiguity is fixed afterward (Pervan and Chan 2003). More recently, the single difference (SD) observation between two ground stations is used to estimate the unknown ambiguity in the carrier phase for a single satellite (Khanafseh et al. 2017; Patel et al. 2020). Although the SD code noise is smaller than the DD code noise, the remaining receiver clock error is not separable with the ambiguity for single epoch solutions. With the WL phase combination as the test statistics, the WL ambiguity is fixed by the ionospheric-free (IF) Hatch–Melbourne–Wübbena (HMW) combination (Patel et al. 2020) as the difference between the WL phase and Narrow Lane (NL) code observations. Generally, if the wavelength is larger compared with the total noise in cycles, the ambiguity can be fixed more easily. In order to avoid possible ephemeris failure in AR, the combination used to estimate the ambiguity should be geometry-free (GF).

Since ambiguity fixing and ephemeris failure are not distinguishable, the probability of wrong ambiguity (PWA) fixing poses an extra risk to ephemeris monitoring. The ambiguity resolution should be considered in overbounding both the continuity risk and the integrity risk. The required number of epochs for averaging new, acquired, and re-acquired satellites, and the minimum length of baselines on the ground are proposed to satisfy the allocated continuity risk and integrity risk (Pervan and Chan 2003). The satellite availability risk for GBAS bounds the continuity risk, and the probability of false alarm (PFA) with the wrong ambiguity fixed is considered negligible. The more recent work analyzed the compliance of the probability of missed detection (PMD) (Khanafseh et al. 2017; Patel et al. 2020), where the test statistic is a mixed distribution containing both the possibilities of correct and wrong ambiguities. However, the process is over-complicated, considering the PMD with the wrong ambiguity. We proved that the PMD under the wrong ambiguity does not need overbounding since the prior probability of PWA is constrained by the continuity risk to a level much lower than the required PMD region. Furthermore, the minimum ground baseline is also derived based on the PMD requirement. Current methods are compared, considering both the required number of epochs and the minimum ground baselines.

The ephemeris error in GBAS differential positioning is introduced first, followed by the single-frequency and dual-frequency test statistics of the ephemeris monitor. Current AR approaches are described next, including an alternative approach proposed. Then, the required number of epochs is derived based on the allocated continuity risk, and the minimum length of ground baselines is derived based on the allocated PMD. Finally, numerical results are shown to illustrate the difference between various AR methods.

Ephemeris fault in differential range

The GBAS differential range error Er is the residual error in the airborne smoothed pseudorange after applying corrections from the ground receivers. With the common errors from satellite and ground receiver removed, one of the residual errors is the ephemeris error. If the ephemeris data contains erroneous information, the ephemeris error becomes large enough to be considered as the ephemeris fault. The ephemeris fault $\Delta E_{p}$ from satellite j is expressed as a projection of baseline vector $\varvec{b}$ between airborne antenna and geometric centroid of the ground antennas onto the vector $\Delta \varvec{e}_{\varvec{j}}^{\varvec{T}}$, which is the error in the LOS unit vector from ground to satellite j caused by the erroneous ephemeris. Another way to interpret the ephemeris fault is by the satellite position error $\Delta \varvec{r}_{\varvec{j}}^{\varvec{T}}$, with which the baseline vector becomes the scalar (Matsumoto et al. 1999),

$$\Delta E_{Er} = \Delta \varvec{e}_{\varvec{j}}^{\varvec{T}} \varvec{b} = \frac{{\Delta \varvec{r}_{\varvec{j}}^{\varvec{T}} \left( {\varvec{I} - \varvec{e}_{\varvec{j}} \varvec{e}_{\varvec{j}}^{\varvec{T}} } \right)b}}{{\rho_{j} }}$$

(1)

where $\varvec{e}_{\varvec{j}}$ is the LOS unit vector from ground station to satellite j, $\varvec{I}$ is the identity matrix, and $\rho_{j}$ is the range from ground station to satellite j. It can, therefore, be concluded that only the satellite position error orthogonal to the LOS, i.e., $\Delta \varvec{r}_{\varvec{j}}^{\varvec{T}} \left( {\varvec{I} - \varvec{e}_{\varvec{j}} \varvec{e}_{\varvec{j}}^{\varvec{T}} } \right)$, contributes to the differential range error.

Ephemeris monitor

To meet the stringent requirements of CAT II/III approaches and protect users against both types of ephemeris faults, the DD phase observation is used as the test statistic. With the coordinates of ground stations precisely surveyed and the satellite position computed by the broadcast ephemeris data, the geometric range is compensated beforehand. The first test statistics is the single-frequency DD phase observation (Pervan and Chan 2003; Khanafseh et al. 2017; Patel et al. 2020),

$$ts_{1} = \emptyset_{1}^{ij} = \lambda_{1} N_{1}^{ij} + I_{1}^{ij} + \Delta E_{ts} + Tr^{ij} + \varepsilon_{dd\_p1}$$

(2)

where the satellite with the highest elevation angle is used as the reference satellite i. The subscripts 1 and 5 are used for noting the frequency of L1 and L5, $\lambda_{1}$ is the L1 wavelength, and $N_{1}^{ij}$ is the L1 DD ambiguity. $\Delta E_{ts} = - \left( {\tilde{\varvec{e}}_{\varvec{i}} - \tilde{\varvec{e}}_{\varvec{j}} } \right)^{\varvec{T}} \varvec{x}_{{\varvec{ab}}}$ is the residual ephemeris error, where $\tilde{\varvec{e}}_{\varvec{i}}$ is the difference between the true LOS and the one computed by the broadcast ephemeris data for satellite i and $\tilde{\varvec{e}}_{\varvec{j}}$ is for satellite j. $\varvec{x}_{{\varvec{ab}}}$ is the baseline vector between two antennas of the ground receivers. The residual atmospheric errors include the L1 ionospheric error $I_{1}^{ij}$ and the tropospheric error $Tr^{ij}$, which are influenced by the baseline length. Further, $\varepsilon_{dd\_p1}$ is the residual DD phase error due to multipath and noise, whose standard deviation $\sigma_{dd\_p}$ is assumed the same for L1 and L5. The second test statistics is the dual-frequency WL combination (Patel et al. 2020),

$$ts_{2} = \emptyset_{w}^{ij} = \frac{{f_{1} \emptyset_{1}^{ij} - f_{5} \emptyset_{5}^{ij} }}{{f_{1} - f_{5} }} = \lambda_{w} N_{w}^{ij} + I_{w}^{ij} + \Delta E_{ts} + Tr^{ij} + \varepsilon_{w\_p}$$

(3)

where $\lambda_{w} = \frac{c}{{f_{1} - f_{5} }}$ is the WL wavelength with $c$ as the speed of light, $N_{w}^{ij} = N_{1}^{ij} - N_{5}^{ij}$ is the WL ambiguity, $\varepsilon_{w\_p}$ is the WL phase noise whose standard deviation $\sigma_{w\_p}$ is $\frac{{\sqrt {f_{1}^{2} + f_{5}^{2} } \sigma_{dd\_p} }}{{f_{1} - f_{5} }}$ assuming L1 and L5 carrier observations are independent. The WL ionosphere is $I_{w}^{ij} = \frac{{f_{1} I_{1}^{ij} - f_{5} I_{5}^{ij} }}{{f_{1} - f_{5} }}$. If there is an ephemeris failure in satellite j, then

$$\Delta E_{ts} = \Delta \varvec{e}_{\varvec{j}}^{\varvec{T}} \varvec{x}_{{\varvec{ab}}} = \frac{{\Delta \varvec{r}_{\varvec{j}}^{\varvec{T}} \left( {\varvec{I} - \varvec{e}_{\varvec{j}} \varvec{e}_{\varvec{j}}^{\varvec{T}} } \right)x_{ab} }}{{\rho_{j} }}$$

(4)

where the ephemeris failure in the test statistics is proportional to $x_{ab}$. It is observed from (1) and (4) that the only difference between the ephemeris failure in the differential range and the DD phase observation is the baseline length, i.e., $b$ vs. $x_{ab}$. Therefore, $ts_{1}$ and $ts_{2}$ can be used for monitoring the ephemeris fault in the differential range. However, they can only be used when the ambiguity is correctly fixed with high success rate and in a timely manner, since the ambiguity is not separable with the ephemeris failure.

It was observed that the residual troposphere ${\text{Tr}}^{ij}$ can become abnormal (Guilbert et al. 2017), triggering false alarms with both $ts_{1}$ and $ts_{2}$. Considering that the impact of the troposphere is a local error, two baselines $x_{ab}$ and $x_{cd}$ parallel to the runway are used whose distance is long enough to cancel this effect. Only when the test statistics of both baselines exceed the threshold T, e.g., $\left| {ts_{1}^{ab} } \right| > T$ and $\left| {ts_{1}^{cd} } \right| > T$, the alarm is generated (Patel et al. 2020). Similarly, this approach can also reduce the false alarms caused by the residual ionosphere $I^{ij}$/$I_{w}^{ij}$.

Ambiguity resolution methods

Currently, there are two AR methods proposed for $ts_{1}$. The first method used the SD between two ground stations to estimate the SD ambiguity $\hat{N}_{1}^{i}$ by rounding (5). The DD ambiguity is obtained by differencing two SD ambiguities $N_{1}^{ij} = N_{1}^{i} - N_{1}^{j}$, which is referred to as the KPSF method (Khanafseh et al. 2017; Patel et al. 2020),

$$\frac{{\emptyset_{1}^{i} - R_{1}^{i} }}{{\lambda_{1} }} = N_{1}^{i} + \frac{{2I_{1}^{i} }}{{\lambda_{1} }} + \frac{{\varepsilon_{sd\_p} }}{{\lambda_{1} }} - \frac{{\varepsilon_{sd\_c} }}{{\lambda_{1} }}$$

(5)

where $\emptyset_{1}^{i}$ is the SD phase observation between ground stations a and b for satellite i, $R_{1}^{i}$ is the SD code observation, $I_{1}^{i}$ is the residual SD phase ionospheric error, $\varepsilon_{sd\_p}$ is the SD phase noise, and $\varepsilon_{sd\_c}$ is the SD code noise whose standard deviation is $\sigma_{sd\_c}$. The second method needs the estimation of two ambiguities referred as the method by Pervan and Chan (2003), i.e., PC method. The WL ambiguity $\hat{N}_{w}^{ij}$ is estimated first by rounding the difference between the WL phase and DD code,

$$\frac{{\emptyset_{w}^{ij} - R_{1}^{ij} }}{{\lambda_{w} }} = N_{w}^{ij} + \frac{{I_{w}^{ij} + I_{1}^{ij} }}{{\lambda_{w} }} + \frac{{\varepsilon_{w\_p} }}{{\lambda_{w} }} - \frac{{\varepsilon_{dd\_c} }}{{\lambda_{w} }}$$

(6)

where $R_{1}^{ij}$ is the L1 DD code observation with the residual multipath and noise as $\varepsilon_{dd\_c}$, whose standard deviation is $\sigma_{dd\_c}$. The L1 DD ambiguity is then obtained by

$$\frac{{\emptyset_{1}^{ij} - \emptyset_{5}^{ij} - \lambda_{5} \hat{N}_{w}^{ij} }}{{\lambda_{1} - \lambda_{5} }} = N_{1}^{ij} + \frac{{I_{1}^{ij} - I_{5}^{ij} }}{{\lambda_{1} - \lambda_{5} }} + \frac{{\varepsilon_{dd\_p1} }}{{\lambda_{1} - \lambda_{5} }} - \frac{{\varepsilon_{dd\_p5} }}{{\lambda_{1} - \lambda_{5} }}$$

(7)

where the standard deviation is $\sqrt 2 \sigma_{dd\_c}$ and the residual ionosphere is the dominating error. The AR method for $ts_{2}$ uses the HMW combination referred as the KPDF method (Patel et al. 2020). The WL ambiguity is estimated by

$$\frac{{\emptyset_{w}^{ij} - R_{n}^{ij} }}{{\lambda_{w} }} = N_{w}^{ij} + \frac{{\varepsilon_{w\_p} }}{{\lambda_{w} }} - \frac{{\varepsilon_{n\_c} }}{{\lambda_{w} }}$$

(8)

where $R_{n}^{ij} = \frac{{f_{1} R_{1} + f_{5} R_{5} }}{{f_{1} + f_{5} }}$ is the NL code combination with residual multipath and noise as $\varepsilon_{n\_c}$, whose standard deviation $\sigma_{n\_c}$ is $\frac{{\sqrt {f_{1}^{2} + f_{5}^{2} } \sigma_{dd\_c} }}{{f_{1} + f_{5} }}$, assuming the L1 and L5 code observations are independent. An alternative AR method is proposed for $ts_{1}$ with the WL ambiguity estimated by (8) and the single-frequency ambiguity estimated by (7), which is referred as the PC_ALT method. It is compared with other methods in the following sections considering both the criteria of the required number of epochs $n_{t}$ and the minimum baselines of GBAS ground stations $x_{ \hbox{min} }$.

Required number of epochs

With the antennas phase variation calibrated, it was demonstrated that $\sigma_{dd\_p}$ is overbounded as 0.6 cm (Khanafseh et al. 2012) and $\sigma_{dd\_c}$ is overbounded as 84 cm (Khanafseh et al. 2017). The PFA allocated for the ephemeris monitor is 10⁻⁸ for CAT II/III GBAS (Annex-10 2018), which is expressed as a combination of probabilities under correct ambiguity (CA) and wrong ambiguities (WA) with prior probabilities as $P_{\text{CA}}$ and $P_{\text{WA}}$ separately,

$$P_{\text{FA}} = P({\text{FA}}|{\text{CA}})P_{\text{CA}} + P({\text{FA}}|{\text{WA}})P_{\text{WA}}$$

(9)

where $P_{\text{FA}}$ is allocated to CA and WA equally. The PFA under correct ambiguity $P({\text{FA}}|{\text{CA}})$ is bounded as 0.5 × 10⁻⁸ with $P_{CA}$ close to 1. $P({\text{FA}}|{\text{CA}})$ is defined with $ts_{1}$ as an example,

$$P\left( {\text{FA|CA}} \right) = P(\left| {ts_{1}^{ab} } \right| > T \cap \left| {ts_{1}^{cd} } \right| > T|H_{0} )$$

(10)

where $ts_{1}^{ab}$ is the test statistics $ts_{1}$ of baseline $x_{ab}$ with ambiguity resolved, and $ts_{1}^{cd}$ is similarly defined for baseline $x_{cd}$. To evaluate $P({\text{FA}}|{\text{WA}})$, the residual ambiguities in the test statistics with WA are analyzed first. Assuming the rounding of (5–8) generates maximum $\pm$ 1 wrong ambiguity, the residual ambiguity in the test statistic is derived in the Appendix, e.g., 5N₁ with the PC_ALT method. Other methods are derived in similar ways, including 2N₁ with the KPSF method, 5N₁ with the PC method, and N_w with the KPDF method. Therefore, the thresholds are far larger than the bias in test statistics caused by the wrong ambiguities. It is thereby reasonable to assume that $P({\text{FA}}|{\text{WA}})$ is bounded by 1. Therefore, 0.5 × 10⁻⁸ is allocated to $P_{\text{WA}}$. For cascaded ambiguity resolution with PC and PC_ALT methods, half of the risk is allocated for $P_{\text{WA}}$ of N_w and N₁ each as 0.25 × 10⁻⁸ (Pervan and Chan 2003). The corresponding K-value $K_{\text{AR}}$ is 5.85 for the KPDF and KPSF methods and 5.96 for PC and PC_ALT methods. The required standard deviation $\sigma_{t}$ of the combinations in (5, 6) is derived in Table 1 with the following inequation,

$$K_{\text{AR}} \sigma_{t} \le \frac{1}{2}$$

(11)

where $\sigma_{t}$ is achieved by averaging within the required number of epochs $n_{t}$. The original standard deviation $\sigma_{o}$ can be expressed as $\sqrt {n_{t} } \sigma_{t}$ assuming each epoch is independent with each other, which is used to derive $n_{t}$ in Table 1. With the combinations in (5), (6), and (8) dominated by the code noise, the standard deviations are derived in Table 1 together with $n_{t}$ for each approach. Considering the correlation between two SD phase observations, it is derived that $\sigma_{dd\_c} \le \sqrt 2 \sigma_{sd\_c}$. Therefore, $\sigma_{sd\_c} \ge \frac{{\sigma_{dd\_c} }}{\sqrt 2 }$ is used to derive the minimum $n_{t}$ in Table 1. It should be noted that since $\sigma_{sd\_c}$ is not bounded, the resulting $n_{t}$ can only serve the purpose of comparison. As shown in Table 1, the required epochs for new rising, acquired, and re-acquired satellites with the PC, KPDF, and PC_ALT methods are 181, 87, and 94, respectively. The KPSF method requires more than 1322 epochs for a single satellite, and for two satellites, it can even be longer.

Table 1 Required number of epochs $n_{t}$

$n_{t}$ is derived in Table 1, assuming independence in time. However, there is a correlation in time for both code and phase observations with residual multipath. The time constant is characterized as 2 s for code observations (Patel et al. 2020). For the phase observations, it may be slightly larger than 2 s. This implies more time required for (7) to estimate DD N₁ in both PC and PC_ALT methods. However, since their required number of independent epochs is only 3, the slight inflation of time with 3 epochs does not change the comparison results, i.e., the required time maintains the sequence of KPDF < PC_ALT < PC < KPSF.

PMD compliance

Although the PWA is constrained as 0.5 × 10⁻⁸, the ambiguity with $\pm$ 1 difference from the correct ambiguity may still be rounded when $K_{\text{AR}} \sigma_{t}$ is close to 0.5. Therefore, the impact of the residual ambiguities should be accounted for in integrity monitoring. The PMD under the faulty hypothesis $H_{j}$ is defined in a similar way (Patel et al. 2020),

$$P_{\text{MD}} = P({\text{MD}}|{\text{CA}})P_{\text{CA}} + P({\text{MD}}|{\text{WA}})P_{\text{WA}}$$

(12)

where $P({\text{MD}}|{\text{WA}})$ is caused by the masking effect of the residual ambiguity on the ephemeris fault is considered (Khanafseh et al. 2017; Patel et al. 2020). With $P_{\text{WA}}$ bounded at 0.5 × 10⁻⁸ by averaging within the required number of epochs, $P({\text{MD}}|{\text{WA}})P_{\text{WA}}$ is also guaranteed to be lower than 0.5 × 10⁻⁸. As shown in the PMD required region in Fig. 1, there is no requirement on PMD values below 0.5 × 10⁻⁸. Therefore, $P({\text{MD}}|{\text{WA}})$ can be neglected in the PMD compliance analysis and only $P({\text{MD}}|{\text{CA}})$ is considered, which is expressed as

$$P\left( {\text{MD|CA}} \right) = P(\left| {ts_{1}^{ab} } \right| \le T \cup \left| {ts_{1}^{cd} } \right| \le T|H_{a} )$$

(13)

where the correlation coefficient between $ts_{1}^{ab}$ and $ts_{1}^{cd}$ is $\rho$, which is caused by common satellites with correlated ionospheric, tropospheric, and multipath errors. Since $\rho$ varies as satellite moves, the relevant risks are bounded for an arbitrary $\rho$,

$$P\left( {\text{FA|CA}} \right) \le \alpha$$

(14)

$$\beta \le P\left( {\text{MD|CA}} \right) \le 1 - \left( {1 - \beta } \right)^{2}$$

(15)

where $\alpha = P(\left| {ts_{1}^{ab} } \right| > T|H_{0} )$, $\beta = P\left( {\left| {ts_{1}^{ab} } \right| < T |H_{a} } \right)$. The extreme values are obtained by $\rho$ = 0 and $\rho$ = 1. With $P\left( {\text{FA|CA}} \right)$ bounded by $\alpha$, the threshold $T$ is therefore obtained by $\alpha$, which is 3.5 cm for $ts_{1}$ and 17.2 cm for $ts_{2}$. Also, the PMD compliance is conducted with the bounded value of $1 - \left( {1 - \beta } \right)^{2}$.

Fig. 1

PMD with $ts_{1}$ at LTP when ${\text{x}}_{\text{ab}} =$ 218 m

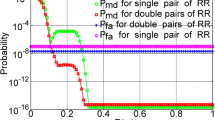
The PMD requirement for the integrity monitor is given as a function of $\Delta E_{er}$ (Brenner and Liu 2010). Since $\Delta E_{ts}$ and $\Delta E_{er}$ is a ratio of $x_{ab}$ and $b$, PMD versus $\Delta E_{ts}$ can be mapped to PMD versus $\Delta E_{er}$. $x_{ab}$ is fixed at certain airports, and b varies when the aircraft is approaching the ground station. The maximum distance between a landing aircraft and the ground station at the decision height of CAT II/III approaches is 5 km as the Landing Threshold Point (LTP), and the PMD required region applies within this distance. With a given ephemeris fault, Er is smaller with the decrease of b, making it easier to satisfy the PMD requirement. Therefore, b = 5 km is considered as the driving value for PMD compliance analysis. If the ground baseline is too long, the residual ionosphere and troposphere might decrease the sensitivity of the test statistics toward the ephemeris fault, and the residual ionosphere might increase the difficulty of estimating the correct ambiguity. However, when the ionospheric and tropospheric errors are not dominating factors, the ephemeris fault can be more easily detected with longer ground baseline $x_{ab}$, and larger $x_{ab}$ is easier to satisfy the PMD requirement. By varying the value of $x_{ab}$, the minimum $x_{ab}$ to satisfy the PMD required region is obtained as shown in Fig. 1, where the red curve is the PMD required region and the blue line is obtained when $b$ = 23 $x_{ab}$ for $ts_{1}$ with b = 5 km.

It is observed from Fig. 1 that the monitor can satisfy the PMD requirement when $x_{ab}$ is not less than 218 m at the LTP. A similar conclusion can be obtained with $ts_{2}$ with 1.1 km minimum baseline as listed in Table 2, where $\sigma_{ts}$ is the standard deviation of the test statistics.

Table 2 $x_{min}$ to satisfy the PMD requirements

Simulation results

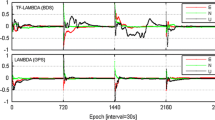
The AR is further demonstrated by the 0.2 Hz SatRef data on Oct 10, 2019 in Hong Kong. Two stations HKKT and HKLT, with a baseline of 7.8 km, are used to form the DD observations. Due to the limitation of GPS L5 signals, L2 signals are used for the purpose of demonstration with similar results. For $ts_{1}$, three AR methods are compared with the real-time float ambiguity results (Figs. 2, 3, 4).

Fig. 2

Float SD-L1 ambiguity with KPSF method

Fig. 3

Float WL ambiguity with PC method

Fig. 4

Float WL ambiguity with PC_ALT method

As shown in the above figures, the noise level is consistent with the standard deviations assumed in Table 1. Comparing the results in Figs. 3 and 4, the PC_ALT method contains less noise than the PC method for estimation of the WL ambiguity. It should be noted that this numerical result is only used for the purpose of comparison. The overbounding of test statistics requires data from GBAS testbeds with the multipath limiting antennas.

Conclusion

The ephemeris monitors in GBAS for CAT II/III approaches are compared together with procedures for ambiguity resolution. Both PFA and PMD are accommodated, considering the risks introduced by the ambiguity resolution. The PWA is constrained by the required number of epochs for averaging the new, acquired, and re-acquired satellites. With the ephemeris fault closely related to the baseline length, the minimum ground baseline length is derived by the PMD requirement, which is obtained by fixing airborne to ground baseline length and varying the ground baseline length. It has been demonstrated that the best performance is achieved by the PC_ALT method considering both the requirement of the 94 averaging epochs for new satellites and the 218 m minimum baseline for GBAS ground stations.

Appendix: residual ambiguities

For the PC_ALT method under WA,

$$\hat{N}_{w}^{ij} - N_{w}^{ij} = \left| {\left[ {\frac{{\emptyset_{w}^{ij} - R_{n}^{ij} }}{{\lambda_{w} }}} \right]_{\text{round}} - N_{w}^{ij} } \right| \le 1$$

(a1)

the maximum residual N_w bounded by (9) is assumed to be 1. Similarly,

$$\left| {\left[ {\frac{{\emptyset_{1}^{ij} - \emptyset_{5}^{ij} - \lambda_{5} N_{w}^{ij} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} - N_{1}^{ij} } \right| \le 1$$

(a2)

where the maximum residual N₁ is also 1 assuming the correct $N_{w}^{ij}$ input. Therefore, the residual ambiguity in the test statistics is 5N₁ with the PC_ALT method,

$$\begin{aligned} & \left| {\left[ {\frac{{\emptyset_{1}^{ij} - \emptyset_{5}^{ij} - \lambda_{5} \hat{N}_{w}^{ij} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} - N_{1}^{ij} } \right| \le \left| {\left[ {\frac{{\emptyset_{1}^{ij} - \emptyset_{5}^{ij} - \lambda_{5} N_{w}^{ij} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} \pm \left[ {\frac{{\lambda_{5} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} - N_{1}^{ij} } \right| \\ & \quad \le \left| {\left[ {\frac{{\emptyset_{1}^{ij} - \emptyset_{5}^{ij} - \lambda_{5} N_{w}^{ij} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} - N_{1}^{ij} } \right| \pm \left| {\left[ {\frac{{\lambda_{5} }}{{\lambda_{1} - \lambda_{5} }}} \right]_{\text{round}} } \right| \le 5 \\ \end{aligned}$$

(a3)