Modeling and prediction of flow-induced hemolysis: a review

Abstract

Despite decades of research related to hemolysis, the accuracy of prediction algorithms for complex flows leaves much to be desired. Fundamental questions remain about how different types of fluid stresses translate to red cell membrane failure. While cellular- and molecular-level simulations hold promise, spatial resolution to such small scales is computationally intensive. This review summarizes approaches to continuum-level modeling of hemolysis, a method that is likely to be useful well into the future for design of typical cardiovascular devices. Weaknesses are revealed for the Eulerian method of hemolysis prediction and for the linearized damage function. Wide variations in scaling of red cell membrane tension are demonstrated with different types of fluid stresses when the scalar fluid stress is the same, as well as when the energy dissipation rate is the same. New experimental data are needed for red cell damage in simple flows with controlled levels of different types of stresses, including laminar shear, laminar extension (normal), turbulent shear, and turbulent extension. Such data can be curve-fit to create more universal continuum-level models and can serve to validate numerical simulations.

1 Introduction

This article focuses on flow-induced hemolysis, in particular on experiments that have quantified hemolysis for different fluid stress conditions, and on the development of mechanistic models that seek to interpret these results. Such models are essential to achieving the ultimate goal of creating reliable hemolysis prediction algorithms applicable to a wide range of flow fields for use in designing new blood-contacting devices.

1.1 Types of hemolysis

Hemolysis is characterized by damage, whether transient or permanent, that causes release of hemoglobin from red cells. Mechanical, thermal, chemical, and biological factors can all cause blood damage in blood-contacting devices (Lokhandwalla and Sturtevant 2001; Offeman and Williams 1976; Sutera 1977). Mechanical damage can be further categorized as by surface interactions, such as cells squashed between the walls of a roller pump, or in the bulk flow. While each of these damage factors may be important in particular patients and applications, flow-induced hemolysis has proven to be a persistent challenge across a wide range of devices.

Red blood cells (RBCs) passing through the cardiovascular system and through prosthetic devices experience combinations of different types of stresses for a range of exposure times. Under normal conditions in the natural circulation, these stresses are for the most part below the critical values for hemolytic damage to RBCs. However, irregular blood flow around complex geometries in cardiovascular devices and in abnormal conditions in the natural circulation may create combinations of high stress and long duration of stress in regurgitant jets, rapidly converging flows, and turbulent and vortical flows. Such flows may cause complete or partial rupture of membranes that allows immediate release of hemoglobin. Alternatively, accumulated damage to the cell membrane may result in delayed hemoglobin release or premature elimination of red cells from the circulation by the spleen and kidney (sublytic damage) (Girdhar and Bluestein 2008; Lippi 2012). Model development in both areas will be discussed.

1.2 Hemolysis in cardiovascular devices

Hemolysis has been observed since the earliest application of intracardiac prosthetic material into the body (Andersen et al. 1965; Brodeur et al. 1965; Rodgers and Sabiston 1969; Sayed et al. 1961). Although improved knowledge about the dynamics of blood flow, enhanced engineering design of cardiovascular devices, and the introduction of more biocompatible materials have reduced the rate of severe hemolysis (AbouRjaili et al. 2012; Shapira et al. 2009; Shivakumaraswamy et al. 2006), mild hemolysis and sub-hemolytic damage remain clinical concerns for modern mechanical circulatory support devices, including cardiopulmonary bypass, extracorporeal membrane oxygenation (ECMO), percutaneous cardiopulmonary system, and left ventricular assist devices (Cardoso et al. 2013; Cowger et al. 2014; Dewitz et al. 1977; Fraser et al. 2012; Shapira et al. 2009).

2 Red blood cells

Mechanistic hemolysis prediction logically involves the red cell and its membrane. Therefore, properties of red cells are briefly reviewed. Dimensional and other information about human RBCs is listed in Table 1. Red cells, also called erythrocytes, are the most numerous type of cells in the blood, comprising nearly half of the blood volume. Consequently, mechanical and rheological behavior of the blood is usually dominated by RBCs. Owing to their biconcave shape (Fig. 1), RBCs have 44% greater surface area than that required to enclose a sphere of the same volume, thus providing more surface area for gas exchange (Skalak et al. 1989) and allowing the cells to squeeze through capillaries and other passages smaller than their unstressed dimensions (Arwatz and Smits 2013).

Table 1 Typical values for RBC properties (Fung 1993; Surgenor and Bishop 1974; Walker et al. 1990)

Fig. 1

Shape and statistical dimensions of the RBC

RBCs lack a cell nucleus as well as most other common intracellular elements, which helps maximize space for hemoglobin, a protein molecule responsible for carrying oxygen. The total amount of hemoglobin in blood (intracellular plus extracellular) is typically 12–13.5 g/dl. However, the normal level of extracellular hemoglobin, called plasma free hemoglobin (PfHb), is very small (0.008 g/dl). PfHb of more than 0.03–0.05 g/dl is considered clinically dangerous and may cause physiologic complications, particularly hemolytic anemia and renal impairment, or even multiple organ failure (Omar et al. 2015; Sakota et al. 2008).

2.1 Red cell membrane structure

The RBC membrane, which is composed of an outer lipid bilayer, an underlying spectrin network, and transmembrane proteins, is a very flexible viscoelastic material (Fig. 2). The thickness of the lipid bilayer is about h = 5 nm (Boal 2012; Hochmuth et al. 1983), and that of the whole membrane is about 40 nm (Yoon et al. 2008). It is generally held that the lipid bilayer acts as the viscous component while RBC elasticity is primarily attributed to the spectrin network (Fedosov et al. 2010). The lipid bilayer is composed of lipid molecules, each with a hydrophilic head and two hydrophobic tails. The tails interdigitate to form the bilayer, but the molecules are mostly free to move tangentially, allowing the membrane to behave like a two-dimensional fluid. The cytoskeleton, a filamentous hexagonal protein network, has a significant role in RBC shape, flexibility, deformability, and lipid organization (Zhang et al. 2013). Spectrin, which is the dominant component in the cytoskeleton, is a long and flexible protein (Smith 1987). Spectrin tetramers can stretch to approximately 200 nm in length when fully extended and can contract to a length as short as 70 nm (Kodippili et al. 2010).

Fig. 2

[adopted from Lux and Palek (1995)]

Schematic diagram of the RBC membrane structure

Conceptually, there are two types of interactions between components of the cell membrane: tangential and normal (Fig. 2). The tangential interactions include those among the spectrin skeleton components themselves and are responsible for the structural integrity of the RBC, whereas the normal interactions stabilize the membrane by linking the cytoskeleton to the bilayer (Tse and Lux 1999). It has become well established that disruptions in tangential and normal interactions can result in elliptocytes (abnormally oval-shaped RBCs) and spherocytes (abnormally sphere-shaped RBCs), respectively. For more information about these interactions and connections among different proteins in the RBC membrane, which also affect the cell’s final shape and behavior, readers are encouraged to refer to Burton and Bruce (2011).

Deformability of the red cell has been measured by several experimental methods, including micropipette aspiration, optical tweezer stretching, flow visualization, and recently atomic force microscopy (AFM) (Barns et al. 2017; Buys et al. 2013). The contribution of the bilipid layer to several properties of the membrane can be traced to the hydrophobicity of the phospholipid tails, which have a surface tension relative to water of $\gamma \approx 50 \;{{\text{mN}} \mathord{\left/ {\vphantom {{\text{mN}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}$. Biaxial stretching of the layer exposes the tails to water on both sides (plasma and cytoplasm are aqueous), which by simplified models leads to an area expansion modulus of $\kappa \approx \left( {4 - 6} \right)\gamma = 200 - 300 \;{{\text{mN}} \mathord{\left/ {\vphantom {{\text{mN}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}$ (Boal 2012). Experimental measurements of the area modulus, which include stretching of the spectrin network, are higher (Table 2). The area modulus is the important property for quasi-steady cell deformation near the hemolytic limit. Bending of the layer compresses heads on one side and exposes tails on the other, giving $B \approx \frac{{\kappa h^{2} }}{24} = \left( {2 - 3} \right) \times 10^{ - 19} \;{\text{Nm}}$. This value is higher than experimental measurements, which may be explained by the bumpiness of the unstressed layer, which allows some bending deformation without expanding the distance between lipid molecules (Boal 2012). When an edge of the layer is exposed, such as around a pore, the hydrophilic heads form a U from one side to the other to protect the tails. This is analogous to bending a single layer around 180°, giving edge tension $\Lambda \approx \frac{B}{h} = 40 - 60 \;{\text{pN}}$, which is close to the range measured for several types of bilipid layers (Akimov et al. 2017). Flow-induced forces exerted on the layer must be larger than Λ to grow a pore. The lipid bilayer being largely fluid in nature, the shear modulus arises primarily from the spectrin network. The membrane viscosity has contributions from both the bilipid and spectrin layers. The membrane relaxation time, which is given by the ratio of the shear modulus and the membrane viscosity, is important for unsteady deformation.

Table 2 Mechanical properties of the human RBC (Tomaiuolo 2014)

Many models have been developed to simulate the structural properties of the membrane (Boal et al. 1992; Boey et al. 1998; Li and Lykotrafitis 2014). Hemoglobin content of the cells can be released into the blood plasma either due to complete rupture of the cell membrane or through temporary pores created in the membrane when the cell is deformed. Because the size of hemoglobin is about 5 nm, the pores must be this size or larger for hemoglobin to exit the cell (Erickson 2009). Since hemolysis is fundamentally a structural failure phenomenon within the RBC membrane, incorporating the mechanical properties of the membrane and its response to different flow dynamics seems central to providing an accurate hemolysis prediction model.

2.2 Human RBC versus other species

Although human blood samples are necessary for final hemolysis testing, animal samples, especially ovine, bovine, and porcine, are alternatives for other purposes because of their ease of accessibility and low cost (Ding et al. 2015). Rheological properties and sensitivity to hemolysis vary among species, which can be expected in light of different morphological properties, including diameter and excess surface area, which is the larger surface area the red cell has compared to a sphere of the same volume (Table 3) (Adili et al. 2014; Baskurt and Meiselman 2013; Zhu 2000). For instance, the diameter of bovine red cells is around half of that for human, with its surface area being almost an order of magnitude smaller than the human red cell.

Table 3 Typical values for size of RBC among different species

Further, deformability of the red blood cell membrane, which is an important factor in response of the cell to different stresses, as well as in mass transport across the membrane, is different among species (Baskurt 1996).

2.3 RBC damage and platelet activation

Although red cells and platelets have many biochemical and physical interactions as they move through the cardiovascular system (Vallés et al. 2002), only a few of them that are relevant to hemolysis are discussed in this review paper. Fluid stresses also cause platelet activation, both directly and indirectly. In fact, early studies on platelet activation suggested that, just like red cell damage, level of shear stress and exposure time are the main factors (Nobili et al. 2008; Shadden and Hendabadi 2013). Stress levels that are not considered harmful to RBCs can activate platelets and ultimately cause thrombosis (Dewitz et al. 1977; Sharp and Mohammad 1998). The formed thrombus can in turn change the flow dynamics within the cardiovascular pathways and contribute to RBC damage, for example by creating restrictions where fluid stresses are high. On the other hand, red cells contain adenosine diphosphate (ADP) that is released during RBC deformation and damage. Once in the plasma, ADP can activate platelets (Hellem 1960; Helms et al. 2013). RBCs also play a role in platelet-initiated coagulation, which depends on hematocrit, red cell deformability, and shear rate (Brown et al. 1975; Iuliano et al. 1992). Additionally, in vitro studies have shown that nitric oxide (NO), an endothelium-derived relaxing factor that reduces the platelet activation, fails to protect platelets in the presence of Hb released from red cell damage (Villagra et al. 2007).

Furthermore, von Willebrand factor (vWF) is a blood plasma glycoprotein that has been shown to mediate platelet adhesion, activation, and aggregation under excessive fluid dynamical stresses occurring in the mechanical blood-contacting devices (Da et al. 2015). While normal concentration of vWF in the circulating blood plasma is 5–10 µg/ml, higher concentration is associated with a risk of thrombosis (Hudzik et al. 2015). The plasma free hemoglobin due to flow-induced hemolysis promotes thrombosis via vWF (Valladolid et al. 2018). Therefore, by better understanding the mechanism of mechanical blood damage, thus reducing thrombosis and consequently preventing clotting, clinical outcomes of cardiovascular assist devices may be improved.

2.4 Index of hemolysis

To compare among investigations, it is useful to be aware that many different measures of hemolysis have been applied, all of which are based on plasma free hemoglobin (PfHb) (Naito et al. 1994). An early index of hemolysis (IH) used units of milligrams of PfHb released per deciliter of blood (mg/dl) and is given simply by

$${\text{IH}} = \Delta {\text{PfHb}}$$

(1)

where $\Delta {\text{PfHb}}$ is the increase in PfHb relative to pre-trial measurements. The so-called normalized index of hemolysis (NIH) is normalized by hematocrit (H), which is the dimensionless volume percentage of red cells in whole blood. NIH is expressed as

$${\text{NIH}} = \Delta {\text{PfHb}} \times \frac{100 - H}{100}$$

(2)

NIH takes into account that the maximum amount of hemoglobin that can be released into the plasma is proportional to the concentration of red cells in the blood, but still has dimensions (mg/dl). The dimensionless modified index of hemolysis (MIH) is formed by normalizing NIH by the total blood hemoglobin ${\text{Hb}}$ (intracellular and extracellular, in mg/dl)

$${\text{MIH}} = \frac{{\Delta {\text{PfHb}}}}{{\text{Hb}}} \times \frac{100 - H}{100}$$

(3)

[Because MIH with equivalent units of ΔPfHb and Hb is very small, a factor of 10⁶ is added for convenience (Mueller et al. 1993)]. Additional red cell damage functions will be introduced in Sect. 6.

Although a high level of PfHb is an indication that hemolysis has occurred, a normal level of PfHb does not guarantee that the RBCs are healthy. A more comprehensive index of hemolysis would characterize hemolytic damage as well as accumulation of sublytic damage (Yeleswarapu et al. 1995) (see Sect. 6.2), which is defined as damage to the cell that does not result in hemoglobin release. The greater susceptibility of aged cells to lysis may be evidence of sublytic damage (Yeleswarapu et al. 1995). Sublytic damage from repeated exposure to stress, which is broadly analogous to fatigue in metals, may depend on threshold stresses, strains, and/or exposure times that are lower than those for hemolysis. Whether an accurate model of sublytic damage is otherwise similar to that for membrane rupture remains to be validated. Interestingly, red cells also exhibit characteristics similar to strain hardening in metals. Cells subjected to a period of constant shear (Lee et al. 2004; Mizuno et al. 2002) or to cyclic shear (Lee et al. 2007) have dramatically decreased deformability. The change is associated with increased band 3 protein (Fig. 2) in the cell membrane (Mizuno et al. 2002). The effect on stress/strain thresholds for lysis has not been investigated, and the reversibility of the alteration is unclear, but both have potentially important impacts on hemolysis prediction. For instance, to the extent that hardening and recovery occur, stress cannot be simply integrated along pathlines to predict hemolysis. Rather, thresholds of hemolytic stress and duration may be reset based on the stress history along the pathline.

3 Fluid stresses in blood flow

The types of fluid stresses that may be exerted on red cells include all possible categories (Fig. 3). The Reynolds number in the normal cardiovascular system varies from less than 1 in small capillaries to around 4000 in the aorta. In the former case, viscous forces are dominant, while in the latter case, inertial forces dictate the flow dynamics (Ku 1997). Blood flow in the cardiovascular system is mostly laminar; however, disease states and cardiovascular devices can induce transitional or turbulent flow (Quinlan 2014). True turbulence can occur in large arteries, and disturbances with turbulence-like characteristics¹ have been documented at branches, in narrowed arteries, across stenotic heart valves, and in regurgitant aortic valves, as well as in blood pumps and other mechanical cardiovascular devices. Turbulent stresses have been categorized in the Reynolds average sense as viscous (due to the mean velocity) and fluctuating (due to fluctuation of the velocity about the mean) (Fig. 3). One characterization of the fluctuations is the Reynolds stresses. Other characterizations, particularly based on energy conservation, have been proposed for blood flow. As a foundation for more detailed models, the traditional viscous and Reynolds stresses, as well as energy dissipation rate, will be defined in the following subsections.

Fig. 3

Different types of stresses encountered by the RBC in blood flow. 2D stresses shown (overbar denotes time average, and there are several ways of quantifying fluctuating stresses)

3.1 Viscous stresses

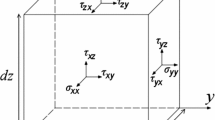
The viscous stress tensor is symmetric, with the diagonal components representing normal stresses, which tend to compress or extend the fluid element, while its off-diagonal components represent the shear stress acting on the fluid element (Çengel and Cimbala 2006)

$$\varvec{\sigma}= \left( {\begin{array}{*{20}c} {2\mu \frac{\partial u}{\partial x}} & {\mu \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right)} & {\mu \left( {\frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}} \right)} \\ {''} & {2\mu \frac{\partial v}{\partial y}} & {\mu \left( {\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}} \right)} \\ {''} & {''} & {2\mu \frac{\partial w}{\partial z}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma_{xx} } & {\tau_{xy} } & {\tau_{xz} } \\ {\tau_{yx} } & {\sigma_{yy} } & {\tau_{yz} } \\ {\tau_{zx} } & {\tau_{zy} } & {\sigma_{zz} } \\ \end{array} } \right)$$

(4)

where µ is the viscosity of the fluid, u, v, and w are velocities in x, y, and z directions, respectively, and σ and τ are the normal and shear (viscous) stresses, respectively.

3.1.1 Principal stresses

Like stresses in solid material, the viscous fluid stress tensor can be transformed to its principal orientations. The transformed principal stresses represent the viscous momentum flux due to velocity gradients in the directions of the principal axes. The reason for devoting the mathematical effort is the hope that following the example of solid mechanics, these fluid principal stress values may correlate with red cell membrane stresses and membrane failure. Considering a two-dimensional viscous stress tensor, the values of which are based on the measurement coordinates x and y:

$$\varvec{\sigma}= \left( {\begin{array}{*{20}c} {\sigma_{xx} } & {\tau_{xy} } \\ {\tau_{yx} } & {\sigma_{yy} } \\ \end{array} } \right)$$

(5)

By rotating the measurement axes by the angle

$$\theta_{\text{P}} = \frac{1}{2}{ \tan }^{ - 1} \left( {\frac{{2\tau_{xy} }}{{\sigma_{xx} - \sigma_{yy} }}} \right),$$

(6)

one can derive the principal viscous normal stresses using the relations already known from solid mechanics (Popov et al. 1976)

$$\varvec{\sigma}_{ 1,2} = \frac{{\sigma_{xx} + \sigma_{yy} }}{2} \pm \sqrt {\left[ {\frac{{\sigma_{xx} - \sigma_{yy} }}{2}} \right]^{2} + \tau_{xy}^{2} }$$

(7)

The last term on the right side of the above equation is the principal viscous shear stress

$$\tau_{ \hbox{max} } = \sqrt {\left[ {\frac{{\sigma_{xx} - \sigma_{yy} }}{2}} \right]^{2} + \tau_{xy}^{2} } ,$$

(8)

the orientation of which is 45° to that of principal viscous normal stress.

For a 3-D flow with stress tensor as shown in Eq. (4), the three principal stresses can be expressed as

$$\sigma_{1} = \frac{{I_{1} }}{3} + \frac{2}{3}\left( {\sqrt {I_{1}^{2} + 3I_{2} } } \right){ \cos }\phi$$

(9)

$$\sigma_{2} = \frac{{I_{1} }}{3} + \frac{2}{3}\left( {\sqrt {I_{1}^{2} - 3I_{2} } } \right)\cos \left( {\phi - \frac{2}{3}\pi } \right)$$

(10)

$$\sigma_{3} = \frac{{I_{1} }}{3} + \frac{2}{3}\left( {\sqrt {I_{1}^{2} - 3I_{2} } } \right)\cos \left( {\phi - \frac{4}{3}\pi } \right)$$

(11)

where

$$\phi = \frac{1}{3}\cos^{ - 1} \left( {\frac{{2I_{1}^{3} - 9I_{1} I_{2} + 27I_{3} }}{{2\left( {I_{1}^{2} - 3I_{2} } \right)^{{\frac{3}{2}}} }}} \right)$$

(12)

and the stress invariants are

$$I_{1} = \sigma_{xx} + \sigma_{yy} + \sigma_{zz}$$

(13)

$$I_{2} = \sigma_{xx} \sigma_{yy} + \sigma_{xx} \sigma_{zz} + \sigma_{yy} \sigma_{zz} - \tau_{xy}^{2} - \tau_{xz}^{2} - \tau_{yz}^{2}$$

(14)

$$I_{3} = \sigma_{xx} \sigma_{yy} \sigma_{zz} - \sigma_{xx} \tau_{yz}^{2} - \sigma_{yy} \tau_{xz}^{2} - \sigma_{zz} \tau_{xy}^{2} + 2\tau_{xy} \tau_{xz} \tau_{yz}$$

(15)

The three direction cosines of each principal stress are, then, obtained by solving the following system of equations:

$$\begin{aligned} (\sigma_{xx} - \sigma_{i} )n_{1} + \tau_{xy} n_{2} + \tau_{xz} n_{3} & = 0 \\ \tau_{yx} n_{1} + (\sigma_{yy} - \sigma_{i} )n_{2} + \tau_{yz} n_{3} & = 0 \\ \tau_{zx} n_{1} + \tau_{zy} n_{2} + (\sigma_{zz} - \sigma_{i} )n_{3} & = 0 \\ \end{aligned}$$

(16)

where $\sigma_{i}$ is the principal stress and $n_{1}$, $n_{2}$ and $n_{3}$ are the direction cosines of each corresponding principal stress.

The usefulness of the principal stress transformation to characterize fluid stresses for hemolysis prediction is uncertain and may depend on the type of flow exerted on the cells (see Sect. 4). For extensional flow, cells are deformed into approximately prolate ellipsoids along the first principal axis (Lee et al. 2009b), and for compressive flow are deformed into oblate ellipsoids (Lokhandwalla and Sturtevant 2001). But for high shear flow, cells are more or less aligned with the flow direction (Goldsmith and Marlow 1972), rather than the first principal axis, which is 45° to the flow. These differences in cell response in simple flows could mean that hemolysis prediction in complex flows may require additional information beyond the principal stresses.

3.1.2 Resultant scalar stress

An even more drastic simplification of the stress state has been applied. Many authors have used a resultant scalar stress, similar to the von Mises stress in solid mechanics, to represent the combined state of stress. In particular, the following scalar stress [though with some inconsistency, see Faghih and Sharp (2016)] has often been used in the popular power-law hemolysis prediction model, which was developed from data for shear stress only (e.g., Alemu and Bluestein 2007; Bludszuweit 1995a, b; Fraser et al. 2012).

$$\sigma = \frac{1}{\sqrt 3 } \left( {\sqrt {\sigma_{xx}^{2} + \sigma_{yy}^{2} + \sigma_{zz}^{2} - \left( {\sigma_{xx} \sigma_{yy} + \sigma_{xx} \sigma_{zz} + \sigma_{yy} \sigma_{zz} } \right) + 3\left( {\tau_{xy}^{2} + \tau_{xz}^{2} + \tau_{yz}^{2} } \right)} } \right)$$

(17)

This resultant scalar stress has similarities to the square root of the second invariant I₂, but gives normal stresses one-third the weight of shear stresses. The appropriateness of this weighting remains to be validated.

3.2 Turbulent stresses

Direct numerical simulation (DNS) of turbulent flow uses exactly the same Navier–Stokes equations as laminar flow. Because of the often small dimensions and timescales of turbulence, DNS is computationally intensive. With faster computers and more sophisticated algorithms, the use of DNS is increasing for hemolysis prediction (e.g., Ezzeldin et al. 2015). Other computational techniques, such as lattice Boltzmann, dissipative particle dynamics, smoothed particle hydrodynamics, and smoothed dissipative particle dynamics, have been applied to laminar blood flow in relatively small regimes, yielding valuable results (Fedosov et al. 2014; Ju et al. 2015; Li et al. 2013), but to the authors knowledge have not yet been attempted for hemolytic flows. To understand historical work on hemolysis modeling, as well as its potential improvements, this review will also outline the Reynolds average approach that decomposes turbulent velocities into mean and fluctuating parts. Fluctuating velocities in turbulent flow are not technically random, because statistical measures of the fluctuations are consistent for particular locations within particular flows. This consistency provides the potential for prediction of hemolysis based on these statistical indices. Two that have been tested for hemolysis prediction, Reynolds stress and energy dissipation rate, are outlined in Sects. 3.2.1 and 3.2.3. Two turbulent vortex size scales by Kolmogorov and Taylor are discussed in Sect. 3.2.2.

3.2.1 Reynolds stress

The Reynolds-averaged Navier–Stokes (RANS) equation is the time-averaged equation of motion for fluid flow, which assumes that each velocity and the pressure in a turbulent flow may be decomposed into mean, $\bar{u}$, and fluctuating, $u'$, components, $u = \bar{u} + u'$. After applying the Reynolds decomposition, the Navier–Stokes equations for a compressible fluid can be written in tensor form as

$$\rho \frac{{D\overline{{u_{i} }} }}{Dt} = - \frac{{\partial \bar{P}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\underbrace {{\left( {\mu \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} - \rho \overline{{u'_{i} u'_{j} }} } \right)}}_{{{\text{Total}}\;{\text{stress}}}}$$

(18)

where $\frac{D }{Dt}$ is the material derivative, $\rho$ is the fluid density, and $\bar{P}$ is time-averaged hydrostatic pressure acting on the fluid element. The first term in the parenthesis is the (time-averaged) viscous stress tensor, while the second term is the well-known Reynolds stress tensor, due to the velocity fluctuations. In the averaging operation for the RANS equation, the viscous terms associated with the fluctuating velocity disappear because they are statistically symmetric about the mean. However, the fluctuating convective inertia terms scale with products of velocity fluctuations, which do not average to zero. Traditionally, they are moved from the left- to the right-hand side of the equation with the average viscous stresses (as shown in Eq. 18) and are called the Reynolds stresses. Because of their origin as convective inertia, they are not true viscous stresses, but are nonetheless terms that represent real and physical motion of the fluid in which the cells are immersed. In typical turbulent flows, the Reynolds stresses are much larger than the viscous stresses, except near the wall in wall-bounded flows. Closure models can be employed to relate the Reynolds stresses to the mean velocities, but the fluctuating velocities and, therefore, the Reynolds stresses can also be characterized statistically in terms of magnitude and frequency. It is still unclear how turbulence models for continuum flows apply to suspensions of deformable particles such as red cells and, in particular, whether Reynolds stresses constitute an appropriate scale for the fluid dynamic forces applied to cells.

The total stress can be written as

$$\varvec{\sigma}_{t} = \bar{\varvec{\sigma }} + \varvec{\sigma^{\prime}}$$

(19)

where $\bar{\varvec{\sigma }}$ and $\varvec{\sigma^{\prime}}$ are viscous and Reynolds stresses, respectively. The Reynolds stress tensor has the following matrix form:

$$\varvec{\sigma^{\prime}} = - \rho \left( {\begin{array}{*{20}c} {\overline{{u^{'2} }} } & {\overline{{u^{\prime}v^{\prime}}} } & {\overline{{u^{\prime}w^{\prime}}} } \\ {''} & {\overline{{v^{'2} }} } & {\overline{{v^{\prime}w^{\prime}}} } \\ {''} & {''} & {\overline{{w^{'2} }} } \\ \end{array} } \right)$$

(20)

Note that both diagonal (normal) and off-diagonal (shear) components are included in Eq. (20). It has been shown that under some flow conditions, normal components of Reynolds stress may become greater than the Reynolds shear stress at some particular locations in the flow cross section (Baldwin et al. 1993; Maymir et al. 1998; Quinlan and Dooley 2007; Shakeri et al. 2012). For example, the maximum Reynolds shear stress immediately downstream of an artificial aortic valve was estimated to be half of the maximum Reynolds normal stress (Nyboe et al. 2006; Nygaard et al. 1990). However, it still remains unresolved how the components and ratios of Reynolds stresses affect blood damage. For instance, two estimates of the stress actually applied to red cells in or between turbulent eddies are 0.12 (Quinlan and Dooley 2007) to 0.30 (Antiga and Steinman 2009) times the Reynolds stress. Modeling of such reduced effects of Reynolds stress versus viscous stress can be accomplished empirically by simply applying a coefficient smaller than one to the Reynolds stress term in Eq. (19) (Goubergrits et al. 2016). To answer this question, experiments must be carried out and, subsequently, mathematical models can be developed to capture the detailed response of RBC membrane to different indices of the fluctuating stresses, which may include Reynolds stresses, energy dissipation rate or other measures.

Similar to the viscous stress tensor, the Reynolds stress at any point within the flow geometry is a second-order tensor and is not invariant to coordinate transformation. The experimentally measured Reynolds stresses are usually reported based on the measurement axes, which may be misleading (Baldwin et al. 1990; Ge et al. 2008). It may be useful to determine the eigenvalues of the Reynolds stress tensor (i.e., principal stresses) at any point of measurement, which quantify the maximum Reynolds normal and shear stresses and their directions (Baldwin et al. 1993; Barbaro et al. 1997a, b; Travis et al. 2002). Considering only a two-dimensional flow field, the Reynolds stress can be written as

$$\varvec{\sigma^{\prime}} = - \rho \left( {\begin{array}{*{20}c} {\overline{{u^{'2} }} } & {\overline{{u^{\prime}v^{\prime}}} } \\ {\overline{{u^{\prime}v^{\prime}}} } & {\overline{{v^{'2} }} } \\ \end{array} } \right)$$

(21)

Then, the principal Reynolds and maximum shear stresses are (Popov et al. 1976)

$$\varvec{\sigma^{\prime}}_{1,2} = \frac{{\rho \overline{{u^{'2} }} + \rho \overline{{v^{'2} }} }}{2} \pm \underbrace {{\sqrt {\left[ {\frac{{\rho \overline{{u^{'2} }} - \rho \overline{{v^{'2} }} }}{2}} \right]^{2} + \left( {\rho \overline{{u^{\prime}v^{\prime}}} } \right)^{2} } }}_{{\tau '_{ \hbox{max} } }}$$

(22)

$$\varvec{\tau^{\prime}}_{ \hbox{max} } = \sqrt {\left[ {\frac{{\rho \overline{{u^{'2} }} - \rho \overline{{v^{'2} }} }}{2}} \right]^{2} + \left( {\rho \overline{{u^{\prime}v^{\prime}}} } \right)^{2} }$$

(23)

and the angle that the measurement coordinate must be rotated to give the maximum Reynolds normal stresses is

$$\theta^{\prime}_{\text{P}} = \frac{1}{2}{ \tan }^{ - 1} \left( {\frac{{2\rho \overline{{u^{\prime}v^{\prime}}} }}{{\rho \overline{{u^{'2} }} - \rho \overline{{v^{'2} }} }}} \right)$$

(24)

The same expressions for 3-D principal stresses as discussed for the viscous stress tensor (Eqs. 9–11) can also be developed for the turbulent stress tensor.

Therefore, the representative scalar stress including both viscous and Reynolds stresses may be written as (Ishii et al. 2015)

$$\sigma_{t} = \frac{1}{\sqrt 3 } \left( {\sqrt {\sigma_{xx,t}^{2} + \sigma_{yy,t}^{2} + \sigma_{zz,t}^{2} - \left( {\sigma_{xx,t} \sigma_{yy,t} + \sigma_{xx,t} \sigma_{zz,t} + \sigma_{yy,t} \sigma_{zz,t} } \right) + 3\left( {\tau_{xy,t}^{2} + \tau_{xz,t}^{2} + \tau_{yz,t}^{2} } \right)} } \right)$$

(25)

where Eq. (25) is the same as Eq. (17), except that $\sigma_{xx,t}$ and $\tau_{xy,t}$ are the total normal and total shear stresses, respectively, which comprise both viscous and Reynolds components (Eq. 19).

3.2.2 Kolmogorov and Taylor scales

Inherent to turbulence is the presence of swirling eddies of different time and length scales. During the energy cascade, energy is transferred from larger eddies, with higher kinetic (inertial) energy, to smaller eddies. This continues to eddies of the smallest (Kolmogorov) size, in which viscous dissipation takes place. The Kolmogorov scale, $\eta_{\text{k}}$, is given by

$$\eta_{\text{k}} = \left( {\nu^{3} /\varepsilon } \right)^{1/4}$$

(26)

where $\varepsilon$ is the kinetic energy dissipation rate and $\nu$ is kinematic viscosity. This scale was developed for a continuum fluid, and thus, its applicability to the flow of particles (red cells) with size that is significant compared to $\eta_{\text{k}}$ has been questioned. With arguments relating the energy dissipation rate to energy supply rate, which must be equal in steady state, the Kolmogorov scale depends on the Reynolds number

$$\frac{{\eta_{\text{k}} }}{L} = Re^{ - 3/4}$$

(27)

where L is the large scale of the flow regime (such as the diameter of the artery). Therefore, $\eta_{\text{k}}$ decreases with an increase in velocity in a given flow geometry. For instance, $\eta_{\text{k}}$ has been reported to vary from 20 to 70 µm in a bileaflet mechanical heart valve (BMHV) (Ge et al. 2008).

It has been proposed that only eddies with length scales similar to those of the red cell are capable of damaging the cell (Ellis et al. 1998; Liu et al. 2000; Lu et al. 2001).This idea can be traced back at least as far as Kawase and Moo-Young (1990) and Kunas and Papoutsakis (1990). Kunas and Papoutsakis (1990) took high-speed photographs of hybridoma cells in an impeller-agitated bioreactor. No velocity measurements of any kind were performed. They noted, with support from previous authors, that cell damage occurred as the Kolmogorov eddy size (based on scaling estimates) approached the size of the cell. However, the intensity of eddies across the entire spectrum increases as the Kolmogorov scale decreases. Accordingly, they cautioned that “Although the ratio of (Kolmogorov scale) to the cell size may be used as a predictor of cell damage, it provides no details as to how cells are damaged by their interactions with these eddies, or even a proof that there is indeed a direct cell to eddy interaction.” A lack of damage in large vortices is consistent only with the oversimplified notion that large vortices exhibit only translation and rigid body rotation (Liu et al. 2000). On the contrary, Quinlan and Dooley (2007) showed that shear is applied to cells in large eddies and may be more responsible for cell damage than Kolmogorov eddies. This idea also neglects that cells may experience stresses between eddies (Antiga and Steinman 2009). Shear between large eddies causes the largest membrane tension among several possible cell locations in turbulent flow (Faghih and Sharp (2018a), see Sect. 7.3).

An alternative scale that to our knowledge has yet to be applied to blood flow is the Taylor microscale (Tennekes and Lumley 1972)

$$\lambda_{t}^{2} = \frac{{u^{'2} }}{{\left( {\frac{{\partial u^{\prime}}}{\partial x}} \right)^{2} }}$$

(28)

where $\lambda_{t}$ is a measure of the distance over which strain energy is dissipated. Because cell membrane strain, which is a precursor to membrane failure, has a logical connection to surrounding fluid strain, $\lambda_{t}$ may be relevant to hemolysis. Equation (28) can also be rearranged to show that the Taylor microscale provides an estimate of the fluctuating velocity gradients within the flow $\left( {\partial u^{\prime}/\partial x} \right)^{2} = u^{'2} /\lambda_{t}^{2}$, which multiplied by viscosity are the fluctuating stresses. With similar assumptions in continuum flow, the Taylor microscale can also be related to the Reynolds number

$$\frac{{\lambda_{t} }}{L} = \sqrt {10} Re^{ - 1/2}$$

(29)

In the downstream wakes of three different prosthetic heart valves, the Taylor microscale varied from 100 to 500 µm (Liu et al. 2000), compared to the Kolmogorov scale of 26.7 µm [revised from that reported by Liu et al. (2000) by Faghih and Sharp (2018b)] and highest energy vortex size of 8.5–17 mm. The Taylor microscale represents the intermediate vortex size above which turbulent motions are inertial and below which are viscous. Given the clear mathematical differences between $\eta_{\text{k}}$ and $\lambda_{t}$ [a different coefficient and different exponent, Eqs. (27) and (29)], the relationships of the two to hemolysis could be readily compared in experiments quantifying both turbulent velocity fluctuations and PfHb.

3.2.3 Energy dissipation rate

The dissipation rate of kinetic energy, which represents the energy flux converted into heat by viscous forces in both laminar and turbulent flows, has also been suggested as a quantity to scale blood damage (Bluestein and Mockros 1969; Morshed et al. 2014). The instantaneous dissipation rate for a 3-D flow field is (Pope 2000)

$$\varepsilon = \nu \varvec{ }\left\{ {\begin{array}{*{20}c} { \left[ {\frac{\partial u}{\partial x}} \right]^{2} + \left[ {\frac{\partial u}{\partial y}} \right]^{2} + \left[ {\frac{\partial u}{\partial z}} \right]^{2} } \\ { + \left[ {\frac{\partial v}{\partial x}} \right]^{2} + \left[ {\frac{\partial v}{\partial y}} \right]^{2} + \left[ {\frac{\partial v}{\partial z}} \right]^{2} } \\ { + \left[ {\frac{\partial w}{\partial x}} \right]^{2} + \left[ {\frac{\partial w}{\partial y}} \right]^{2} + \left[ {\frac{\partial w}{\partial z}} \right]^{2} } \\ \end{array} } \right\} + \nu \varvec{ }\left\{ {\begin{array}{*{20}c} { \left[ {\frac{\partial u}{\partial x}} \right]^{2} + \left[ {\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}} \right] + \left[ {\frac{\partial u}{\partial z}\frac{\partial w}{\partial x}} \right]} \\ { + \left[ {\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}} \right] + \left[ {\frac{\partial v}{\partial y}} \right]^{2} + \left[ {\frac{\partial v}{\partial z}\frac{\partial w}{\partial y}} \right]} \\ { + \left[ {\frac{\partial u}{\partial z}\frac{\partial w}{\partial x}} \right] + \left[ {\frac{\partial v}{\partial z}\frac{\partial w}{\partial y}} \right] + \left[ {\frac{\partial w}{\partial z}} \right]^{2} } \\ \end{array} } \right\}$$

(30)

Note that for the dissipation rate of turbulent fluctuations ($\varepsilon '$), the velocities in Eq. (30) must be replaced by velocity fluctuations. Furthermore, for local homogeneity of the turbulent flow, the second bracket in Eq. (30) reduces to zero (Moulden and Frost 1977).

Equivalently, Eq. (30) can be rewritten in terms of the normal and shear stresses as

$$\varepsilon = \frac{1}{\rho \mu }\left[ {\frac{1}{2}\left( {\sigma_{xx}^{2} + \sigma_{yy}^{2} + \sigma_{zz}^{2} } \right) + \left( {\tau_{xy}^{2} + \tau_{xz}^{2} + \tau_{yz}^{2} )} \right)} \right]$$

(31)

However, measuring all the components in Eq. (30) in an experiment is not an easy task. Therefore, simplifications are usually adopted. For instance, based on Kolmogorov’s theory of local isotropy of small-scale structures in a turbulent flow, the mean viscous dissipation rate and an isotropic homogenous turbulence can be simplified as (Kolmogorov 1991)

$$\varepsilon ' = 15 \nu \overline{{\left( {\frac{{\partial u^{\prime}}}{\partial x}} \right)^{2} }}$$

(32)

Additionally, a useful approximation of Eq. (32) is based on (Tennekes and Lumley 1972)

$$\varepsilon^{\prime} = 15 \nu \frac{{\mathop {u_{\text{rms}}^{'} }\nolimits^{2} }}{{\lambda_{t}^{2} }}$$

(33)

where $u_{\text{rms}}^{'}$ is the root-mean-square of the velocity fluctuations.

Using Eq. (31), the effective scalar stress becomes

$$\sigma_{\text{e}} = \sqrt {\rho \mu \varepsilon } = \sqrt {\frac{1}{2}\left( {\sigma_{xx}^{2} + \sigma_{yy}^{2} + \sigma_{zz}^{2} } \right) + \left( {\tau_{xy}^{2} + \tau_{xz}^{2} + \tau_{yz}^{2} } \right)}$$

(34)

This stress is proportional to what Jones (1995) called “turbulent viscous shear stress.” Comparing this equation to the scalar stress in Eq. (17) reveals that the two indices are broadly similar. σ_e lacks the normal stress cross products, but the other two groups of terms are the same, though with different coefficients.

4 Red cell motion

4.1 Motion in viscous shear flow

Previous investigations of red cell behavior have concentrated largely on shear stress. This historic emphasis on shear stress led to considerable literature on bulk and single-cell flow of RBCs in shear flows (e.g., Abkarian et al. 2007; Dupire et al. 2012; Viallat and Abkarian 2014). Based on the level of the applied shear, RBCs exhibit several characteristic motions within the plasma. Under very small shear rate (< 1 s⁻¹), isolated RBCs maintain a biconcave disk shape and are observed to tumble (Fig. 4a). On the other hand, concentrated RBCs tend to aggregate, so long as the shear is not too large (< 50 s⁻¹), into rod-shaped structures called rouleaux, which dramatically increase the apparent viscosity of the red cell suspension. These aggregates are dynamically reversible such that the rouleaux break apart when shear increases, and reform when shear decreases.

Fig. 4

Cell motion in a low shear stress and low viscosity medium, b moderate shear stress and high viscosity, and c high shear stress and high viscosity. The black dot indicates circulation of the membrane in the tank-treading case

It has been shown that among other factors, the ratio of internal (cytoplasmic) viscosity to external viscosity has an important effect on RBC deformation in shear flow (Kon et al. 1987). As the shear rate increases, RBCs in low viscosity suspending media continue to tumble with increasing deformation into irregular shapes (Dupire et al. 2012; Goldsmith and Marlow 1972). At moderate shear rates, the cells are found to undergo a swinging motion with periodic change of inclination and shape deformation, with superimposed tank-treading motion (Fig. 4b). In highly viscous suspending media, cells take on an elongated shape with their long axis more or less aligned with the flow direction, but with their downstream end angled toward higher velocity, and the membrane rotating about the cytoplasm, in a motion commonly referred to as tank-treading (Keller and Skalak 1982) (Fig. 4c). With further increase in the shear rate, the RBCs continue to elongate (Becker and Kuznetsov 2015; Galdi et al. 2008). This area-preserving elongation is reversible, i.e., RBCs demonstrate shape memory (up to a certain areal strain) (Cardenas et al. 2012; Dupire et al. 2012).

As introduced in Sect. 2.1, beyond a threshold elongation, the RBC membrane area must increase to contain a constant volume of cytoplasm. Because the membrane is much more resistant to area dilation than to shear deformation, substantial increases in flow-induced stresses are required for this to occur. As the membrane area is stretched, the potential increases for leakage of the cell contents, for permanent damage to the membrane structure, and for catastrophic membrane rupture. In some cases, the RBCs biological function is compromised, which consequently leads to the premature need to remove the cell from the circulation. This places an added demand on the erythropoietic system that it may or may not be capable of fulfilling.

Vesicles are composed of a viscous liquid encapsulated by a lipid bilayer membrane, which have been extensively used in both experimental studies and simulations as a simplified model to better understand RBC motion (Yazdani and Bagchi 2012). Their behavior is different from that of RBCs mainly due to lack of a spectrin network in vesicles, so their shape in the flow is mainly governed by the bending rigidity of their membrane (Abkarian and Viallat 2008). Based on numerical studies of vesicles, it has been shown that by decreasing the ratio of intracellular to extracellular viscosity in a uniform shear flow, three modes of motion similar to that of RBCs occur, starting in low shear with unsteady tumbling, changing in moderate shear to swinging, trembling and/or vacillating-breathing, and ending in high shear with steady tank-treading (Misbah 2006). Lacking the shear elasticity provided by the spectrin network, vesicles tank-tread when the shear is weak and the ratio of internal viscosity to external viscosity is near unity, whereas RBCs tumble under the same condition. This is because in the case of RBCs, the weak shear cannot overcome the cytoskeletal stiffness. However, when the shear is stronger, the shear stress can overcome the resistance to network deformation and tank-treading occurs (Misbah 2012).

In the more complex dynamics of Poiseuille flow that has a nonuniform shear rate (Coupier et al. 2008; Hiroshi and Gerhard 2005; Shi et al. 2012), particles migrate away from the walls and toward the centerline due to the wall effect and the curvature in the velocity profile. Numerical analysis has predicted that vesicles in a noninertial Poiseuille flow in a narrow capillary may develop three shapes: bullet-like, parachute-like, and slipper-like, depending on the initial conditions of cell orientation in the flow, as well as the flow conditions and properties of the membrane (Fig. 5) (Danker et al. 2009; Shi et al. 2012). Experiments and simulations show that when the ratio of internal to external viscosities is about 5, the transition from parachute mode to slipper mode occurs with increasing shear rate (Misbah 2012). The vesicle may also assume either parachute- or bullet-like shapes depending on the confinement of the flow and the flow rate (Fedosov et al. 2010).

Fig. 5

Different modes of RBC motion in Poiseuille capillary flow: (a) parachute mode, (b) slipper mode, and (c) bullet mode

4.2 Motion in viscous extensional flow

While shear stress has long been the focus for damage to RBCs, the extensional component of viscous stress has also been noted to play a significant role in inducing cell damage (Down et al. 2011). RBCs are initially highly deformable under extensional flow conditions; however, as the extensional stress increases, deformation reaches a plateau that corresponds to a shape beyond which areal strain of the membrane is required for further elongation (Chen and Sharp 2011; Yaginuma et al. 2013).

RBCs may experience extensional (elongational) stresses in contractions entering blood vessels and/or blood-contacting devices (Lee et al. 2009b). Extension occurs when different parts of an RBC are subjected to different velocity magnitudes, for example, when there is a spatial acceleration in the flow due to changes in the cross-sectional area (converging flow) where the leading tip of the RBC is surrounded by higher velocity than that surrounding the trailing end. Similarly, the RBC may also be oriented in a shear velocity profile in such a way that the leading and trailing ends experience different velocities, resulting in an extensional tension in the cell membrane (Fig. 6). In fact, a combination of shear and extensional stresses may often act on the cell. A cell in a simple shear flow may rotate (i.e., tumble or tank-tread), thereby partially mitigating the tension caused by shear stress. On the other hand, during a uniaxial extensional flow, the cell is stretched without rotation or other tension-mitigating mechanisms. This sustained extensional stress may stretch cells more readily and be more damaging to the membrane than shear. Such behavior has also been observed in polymer solutions (Fuller and Leal 1980). For this reason, it is important to also study the behavior of the RBCs within extensional flow.

Fig. 6

Extensional stress applied to the RBC in a steep velocity gradient

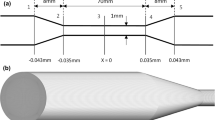
Researchers have used different devices, including opposed jets (Fig. 7) and hyperbolic micro-contractions (Fig. 8), to evaluate cell deformability and cell membrane behavior within extensional flow (Bae et al. 2015; Bento et al. 2018; Faghih and Sharp 2018c; Faustino et al. 2014; Gossett et al. 2012; Mcgraw 1992; Rodrigues et al. 2013; Yaginuma et al. 2011, 2013). One of the earliest studies on the behavior of RBCs in extensional flow used two concentrically opposed suction jets that created a stagnation point at which symmetric extensional stresses were exerted on the cell (Fig. 7) (Mcgraw 1992). At a bulk stress of 5.2 dyne/cm² in the high-viscosity suspending medium, the ratio of the major axis to minor axis of the cell was observed to reach a value of 4.8, which McGraw claimed to be the maximum area-preserving threshold.

Fig. 7

Extensional stress applied to the RBC by suction jet

Fig. 8

Extensional stress applied to the cell by hyperbolic microchannel contraction

The hyperbolic micro-contraction (Fig. 8) is popular because it provides a nearly constant strain rate at the centerline of the channel and is capable of producing a quasi-homogenous extensional flow condition (Bento et al. 2018; Oliveira et al. 2007; Sousa et al. 2011). Within the stress range of 1–200 dyne/cm² in such a channel, extensional stress was shown to produce more cell deformation than shear stress of the same level (Lee et al. 2009b).

4.3 Motion in combined shear and extensional flow

Pure shear and pure extensional flows are uncommon occurrences in typical cardiovascular devices. While these two flows may provide limits that bound the relationship between fluid stresses and cell membrane tension (step 2 for hemolysis prediction, Sect. 6.1), it could also be that additional cell motions appear that impact this relationship that is so important for predicting blood damage. Zeng and Ristenpart (2014) provide a glimpse into phenomena that may complicate hemolysis modeling. In a straight-tapered converging channel, cells were observed with a high-speed camera not only on the central streamline where shear is zero, but also on streamlines closer to the wall with combined extension and shear. Tumbling and stretching were observed, consistent with Sects. 4.1 and 4.2 and with the low suspending medium viscosity used in the experiments. Rolling was observed, which has not been previously discussed in this paper (Dupire et al. 2012). Complex motions were observed that combined these simple motions, which might to be expected when two types of stress are simultaneously applied to the cell. However, a new motion called “twisting” was discovered. This motion involves rotation of the cell around an axis aligned with the longitudinal axis of the channel. Furthermore, it was also found that a particular cell could exhibit nearly any type of motion on any given streamline. Stretching was more prevalent near the center of the channel, but tumbling and rolling were observed across the entire channel. Twisting occurred on all streamlines except the central one. These results show that fluid stress history alone on a particular streamline is not deterministic of cell motion. Similar to other biological research in which sample variability can be large, hemolysis may need to be predicted based on statistical distributions of cell behaviors.

A caveat is that these experiments were performed with a flow rate that resulted in mean shear and extensional stresses of only about 5 and 10 dyn/cm², respectively, and the standard deviation of cell shape deformation was limited to about 15%. Cell behavior may correlate more consistently with fluid stresses when cell deformation is large, i.e., that fluid stresses dominate over viscoelastic characteristics of individual cells. Additional imaging of cells subjected to stresses closer to hemolytic levels would be valuable in this regard.

4.4 Motion in turbulent flow

The only experimental study of the response of red cells flowing in turbulent flow is that of Sutera and Mehrjardi (1975). RBCs exposed to turbulent shear stress ranging from 100 to 2500 dyne/cm² were chemically “frozen” by glutaraldehyde to observe deformation and fragmentation of the cells. Based on their observations, RBCs began to lose their biconcave shape at 500 dyne/cm², with the first signs of fragmentation occurring at 2500 dyne/cm². They also found that by increasing the turbulent shear stress, the cells first underwent a recoverable deformation and then deformed irreversibly until they assumed a dumbbell-like shape, after which the cell finally ruptured into two crenated cells. Due to the method of fixing and subsequent image acquisition, cell orientation with respect to the flow and temporal history of motion could not be determined. Shakeri et al. (2012) also imaged red cell motions in turbulent flow up to Reynolds number of 3000 through a square channel of 0.8 mm × 0.8 mm. It was concluded that Reynolds number of up to 3000, which is likely not fully turbulent, was not sufficient to significantly deform cells. To the best of the authors’ knowledge, there exist no other experimental studies revealing the behavior of red cells in turbulent flow.

5 Previous hemolysis measurements in controlled flows

Threshold values for the initiation of hemolysis have been demonstrated across a range of stresses, flow regimes (laminar and turbulent), exposure times, experimental setups, hematocrit, species, and suspending medium viscosities. Early studies included interaction of red cells with a turbulent free jet (Forstrom 1969), as well as locally laminar flows generated around an oscillating wire (Williams et al. 1970) and a pulsating gas bubble (Rooney 1970) (Table 4). Later, concentric cylinders, cone-and-plate, Couette flow, and capillary flow were commonly used to study the effects of shear stress and exposure time on hemolysis. Each of these devices is associated with its own advantages, as well as uncertainties, limitations, and inaccuracies (Paul et al. 2003). For example, Couette flow can generate secondary flows (Taylor vortices) at high shear rates and, thus, is typically used for low shear rates (Paul et al. 2003). However, Leverett et al. (1972) used Couette flow to investigate the secondary flow effects that, in combination with primary shear stress, might cause hemolysis.

Table 4 Experimental studies on threshold level of RBC hemolysis in laminar flow

Results initially seemed inconsistent, because studies reported significantly different threshold stress. Furthermore, in a study that used capillary tubes of different lengths, and thus different residence times, incipient blood damage was observed at a minimum wall shear stress of about 40–50 dyne/cm² for residence time of around 70 s (Laugel and Beissinger 1983). The inconsistencies might be partly due to different experimental conditions, including blood from different species. However, the proposed theory that appeared to resolve these inconsistencies is that hemolysis is caused by surface and bulk-flow effects. In particular, at high shear stress, cell membrane rupture occurs mainly in the bulk flow, whereas under low shear stress, hemolysis is dominated by surface properties (Nakahara and Yoshida 1986; Sutera and Mehrjardi 1975).

5.1 Hemolysis threshold in laminar viscous shear flow

It is widely accepted that lysis of RBCs depends on shear stress and exposure time. For duration of less than 1 µs, RBCs can withstand shear stress of about 10⁵ dyne/cm² (Polaschegg 2009). When the exposure time is about 1 s, the threshold for laminar flow has been reported to be 20,000 dyne/cm². For exposure time in the range of minutes (≥ 100 s), the threshold in laminar flow has been suggested as 1500 dyne/cm² (Polaschegg 2009).

Many authors have already attempted to estimate a threshold value of laminar shear stress for the onset of red cell damage using different apparatus (Table 4).

5.2 Hemolysis in viscous extensional flow

The importance of extensional stress in causing cell lysis was shown in a computational fluid dynamics (CFD) analysis of laminar flow through a capillary tube with a contraction (Down et al. 2011). The investigators used the geometry and hemolysis threshold value from Keshaviah (1976) to compare the effect of shear and extensional stresses on cell damage. Results showed that the shear stress as well as the gradient of the shear stress anywhere in the flow domain failed to reach the threshold value consistent with the level of hemolysis reported by Keshaviah (1976), but the extensional stress at the entrance region reached or exceeded the stress threshold for hemolysis of 30,000 dyne/cm² for duration of the order of microseconds. Similarly, greater fractions of the flow volumes in two rotary blood pump CFD models reached the estimated hemolytic extensional stress threshold than the hemolytic shear stress threshold (the threshold for hemolysis is lower for extensional stress than for shear stress) (Khoo et al. 2018). Experiments comparing flow in tubes with sharp and tapered entrances found that hemolysis correlated better with extensional stress than either shear stress or scalar stress (Yen et al. 2015). These results suggest that the historical focus on shear stress has been misplaced and that the scalar stress (Eq. 17) does not adequately weigh extensional stresses.

In typical cardiovascular devices, quasi-steady viscous fluid forces exerted on cells are assumed to be larger than unsteady viscous forces; thus, they have been the focus of hemolysis modeling for these devices. Even in turbulent flow, unsteady viscous effects appear to be an order of magnitude smaller than quasi-steady effects (Quinlan and Dooley 2007). However, hemolysis has also been observed due to shock waves, such as those used to break up kidney stones by shock wave lithotripsy (SWL). Shock waves represent much more rapidly varying flow; thus, for completeness, the difference in the associated mechanism of hemolysis is outlined here. Shock waves propagate radially from the focal point of SWL, and cells sufficiently far from the focal point experience strong, but brief, extensional forces associated with fluid compression/expansion due to the pressure wave (Lokhandwalla and Sturtevant 2001). The fluid motion constitutes a balance between pressure and inertial terms in the Navier–Stokes equation, with viscous terms being small by comparison. The force resulting from this inertial motion may be larger than the tension in the cell membrane, in which case the deformation of the cell is the same as that of a continuum fluid, had the cell not been there. This is fundamentally different from the viscous mode, in which the inertial force is small and cell membrane tension balances the fluid viscous force. It was found that the momentary extensional surface tension (force per meter) of around 64 mN/m for exposure time of 3 ns created by the shock wave lithotripsy caused an areal strain of approximately 10⁻⁵ in the membrane (Lokhandwalla and Sturtevant 2001). Although this level of strain is less than the critical level [order of magnitude of 10⁻² (Evans et al. 1976)] for viscous mode hemolysis, it was sufficient to produce energetically reversible pores in the RBC membrane. It is apparent, then, that a hemolysis model developed for viscous flows may not apply to SWL.

5.3 Hemolysis in turbulent flow

Although under normal conditions blood flow within most of the circulation is laminar, local turbulence that may occur in vivo [e.g., in the ascending aorta (Stein and Sabbah 1976)] and in adverse flow conditions in medical devices has been suggested as a contributing factor in RBC trauma (Quinlan 2014; Sallam and Hwang 1984). Therefore, many studies have attempted to determine a threshold for RBC damage in turbulent blood flow (Table 5). One of the earliest studies on the effect of turbulence found the threshold of viscous stress for RBC lysis in free turbulent jets to be nearly 40,000 dyne/cm² for short exposure time (10⁻⁶ s) (Forstrom 1969).

Table 5 Experimental studies on threshold level of RBC hemolysis in turbulent flow

In an important later study, RBCs exposed in Couette flow to 4 min of turbulent viscous shear stresses varying from 100 to 4500 dyne/cm² were fixed by glutaraldehyde to observe cell response (Sutera and Mehrjardi 1975). Cells fragmented in the bulk flow starting at 2500 dyne/cm². The cell fragments had continuous membranes without holes. Cells stressed at 2000 dyne/cm² were deformed into elongated spindle-like shapes, but if left unfixed, largely recovered their original shape after the applied stress was discontinued.

In an attempt to overcome weaknesses of previous experiments, Sallam and Hwang (1984) designed a new setup to fully survey the velocity field within a free submerged axisymmetric turbulent jet and used laser Doppler anemometer to quantify the turbulence intensities in the flow field (Sallam and Hwang 1984). They used an aspirator to collect human blood samples for hemoglobin measurements at locations in the jet where the streamwise mean velocity, turbulence intensities, and Reynolds shear stresses were experimentally predetermined. It was concluded that Reynolds shear stress of more than 4000 dyne/cm² for duration of 10⁻⁵ s is needed to cause RBC lysis. To provide a better defined shear field and to compare the effect of laminar and turbulent flows of the same flow rate and wall shear stress on hemolysis rate, Kameneva et al. (2004) used a simple capillary geometry to demonstrate that turbulent stresses contribute strongly to blood trauma, generating exponential increases in hemolysis as Reynolds number increased. They postulated that local stretching/deformation of RBCs due to interaction with small-scale turbulent eddies and/or fatigue loading due to cyclical stretching of cells by the fluctuating velocity field may cause the increased hemolysis. Flow through an orifice has also been used to investigate the effect of Reynolds shear stress on hemolysis (Tamagawa et al. 1996). Reynolds shear stress at the edge of the orifice was found to be several hundred times greater than that of turbulent viscous shear stress and should not be neglected when predicting hemolysis for devices containing geometries with flow similar to an orifice. The hemolytic threshold for Reynolds shear stress in the orifice was reported to be 18,000 dyne/cm⁻² with a corresponding exposure time of 10⁻⁶–10⁻⁵ s.

Based on a theoretical analysis of the experimental values of Reynolds shear stress reported by Sallam and Hwang (1984), Grigioni et al. (1999) stated that the threshold values in Sallam and Hwang’s paper could be underestimated because they did not consider the peak shear stress through calculation of principal axes and principal stress. Using a relationship between velocity fluctuations in measurement axis and the principal axes as mentioned in Barbaro et al. (1997a, b), they established a correlation between values of Reynolds shear stress measured by Sallam and Hwang (1984) with the actual measurable values and found that the maximum measurable value for Reynolds shear stress in Sallam and Hwang (1984) should be 6000 dyne/cm² (instead of 4000 6000 dyne/cm² reported by Reynolds shear stress, thresholds for initial hemolysis have more recently been reported to be 5170 dyne/cm² for exposure time of 10⁻⁵ s in porcine blood (Yen et al. 2014) and 30,000 dyne/cm² in bovine blood (Jhun et al. 2018).

In contrast to studies that regard the Reynolds stress as the main mechanism of turbulence-mediated hemolysis (Lee et al. 2009a), others have suggested that turbulent viscous stress at scales similar to or smaller than the RBC size is more responsible for hemolysis (Ge et al. 2008; Jones 1995; Yen et al. 2014). To explore this question, Yen et al. (2014) used particle image velocimetry (PIV) to compare the two terms in turbulent jet flow. At each point, PIV measurements were used to calculate the Reynolds shear stress and to estimate the energy dissipation rate, from which the viscous shear stress was obtained. Then, they conducted experimental tests on fresh porcine red cells to experimentally calculate the incremental increase in hemolysis between two adjacent points in the flow field using the two-point sampling technique of Sallam and Hwang (1984). They concluded that the threshold value for incipient hemolysis due to turbulent viscous shear stress is one order of magnitude smaller than that due to Reynolds shear stress (600 dyne/cm² for the turbulent viscous shear stress vs. 5170 dyne/cm² for Reynolds shear stress).

Additional comparisons between Reynolds and viscous stresses, both shear and extensional, are needed to test the universality of this conclusion. Identifying the conditions under which one predominates over the other may be important in understanding hemolysis in particular devices (Travis et al. 2002).

As an alternative to turbulent mean and Reynolds stress, energy dissipation has been suggested as the more appropriate and physically meaningful criteria for RBC damage in turbulent flow (Bluestein and Mockros 1969; Hund et al. 2010; Jones 1995; Morshed et al. 2014). This idea will be discussed further in Sect. 6.3 and evaluated in Sect. 7.3.

5.4 Models of the hemolysis threshold

One of the earliest attempts to provide a predictive model for mechanical hemolysis was a simple equation (Blackshear et al. 1966) involving threshold shear stress and exposure time

$$\tau_{t} E^{0.5} = {\text{const}}$$

(35)

where $\tau_{t}$ is a threshold shear stress (scalar). An additional term—a stress below which no hemolysis occurs—was added by Sharp and Mohammad (1998)

$$\left( {\tau_{t} - \tau_{0} } \right) E^{0.5} = {\text{const}}$$

(36)

These equations do not quantify hemolysis; rather, they only describe the threshold at which hemolysis begins. The threshold of Eq. (35) is compared to experimental results as well as to threshold values predicted by some of the most common hemolysis models in Fig. 9, i.e., the Heuser and Opitz (1980), Giersiepen et al. (1990), and Richardson (1975) models, which are presented in Sect. 6, used 1% hemolysis to characterize the threshold. As can be seen in Fig. 9, viscous stress in turbulent flow and extensional stress in laminar flow have received little attention. It is also evident that the hemolysis prediction models could be improved with a fluid stress threshold below which no hemolysis occurs, like that of the Sharp and Mohammad (1998) threshold model.

Fig. 9

Threshold values reported by experimental studies and theoretical hemolysis prediction models

6 Hemolysis prediction models

Aside from the threshold equations of Sect. 5.4, only correlations between hemolysis and various flow parameters have been discussed. Such correlations are entirely empirical and lack the physics-based explanation that it appears may be necessary to make progress on this problem. In this section, a number of previous models with varying levels of remaining empiricism will be discussed in Sects. 6.2-6.4. But first, the components necessary to fully represent the mechanics of hemolysis are listed in Sect. 6.1.

6.1 Components of a mechanistic hemolysis prediction model

The following steps can be categorized to provide a comprehensive and mechanistic hemolysis prediction model.

• 1. First, the velocity field for the flow domain must be calculated/measured with sufficient temporal and spatial resolution to accurately describe the stress history exerted on the cells likely to be lysed. This process may be iterative to focus the greatest accuracy on the hemolytic regions of the flow. For turbulent flow, the question of sufficient accuracy takes on layers of additional meaning, since viscous and Reynolds stresses, eddy size, timescales, and spectral distribution of energy may be important. (An implicit assumption of this step is that continuum flow fields are sufficient as a basis for characterizing the processes heading to hemolysis. If fluid/cell and cell/cell interactions significantly modify the balance of stresses on the cell, then an additional step may be needed to model the relationship of continuum flow field stresses to those local to the cells).

• 2. Second, the fluid stress must be related to the membrane tension. Scaling laws, rather than fully resolved simulations of concentrated suspensions of deformable cells, would seem to be necessary for efficient algorithms for clinical use. The use of a scalar resultant fluid stress is an attractive means to simplify the model, but its application to complex flows is questionable (see Sect. 3.1.2). The scaling laws may need to accommodate cell shape, the semipermeable and viscoelastic properties of the RBC membrane and plasma, and cytoplasm properties (e.g., extracellular and intracellular viscosity, Hb concentration, etc.). Furthermore, for some applications, the model may need to be capable of predicting sub-hemolytic damage.

• 3. Third, based on the calculated membrane tension, a constitutive law for the cell membrane must be applied to model the formation of pores and/or catastrophic failure of the membrane. Large and long-lasting holes in cells with nearly complete loss of hemoglobin, such as occurring due to osmotic stress, may be uncommon. Rather, cells may cleave by pinching off in the middle of dumbbell shapes (Sutera and Mehrjardi 1975) or shed blebs from high-stress areas (Koleva and Rehage 2012), with small loss of hemoglobin. A number of models have involved determination of strain and prediction of failure at a threshold strain, without explicit modeling of the type of failure.

• 4. Fourth, the amount of hemoglobin release must be determined. This part of the model may need to include a spectrum of membrane disruption from reversible poration to complete failure, with associated differences in transport of hemoglobin to the plasma. At lower stress levels, hemoglobin can be transported through pores in the membrane by diffusion (due to a transmembrane concentration gradient) and/or by advection (due to a pressure gradient). For larger holes, the internal and external flow regions are joined, creating a fundamentally distinct modeling problem. While Vitale et al. (2014) included diffusion in their model, advection has yet to be explicitly incorporated into a hemolysis prediction model.

In the last several decades, computational fluid dynamics (CFD) has been extensively utilized for analysis and estimation of blood damage in blood-contacting devices. By providing the velocity field within the blood-handling device, CFD conveniently accomplishes the first of the four steps outlined above. A range of approaches have been applied to address the last three steps, including fluid stress-based, membrane strain-based, and computational biomechanics methods addressed in subsequent sections. For a complete review of hemolysis prediction models specifically for CFD applications, readers are referred to the recent review article by Yu et al. (2017).

6.2 Fluid stress-based models

Fluid stress-based models skip steps 2 and 3, to empirically correlate hemolysis directly to fluid stress. The advantage is simplicity and computational speed. However, due to the variability in cell response to different types of fluid stresses (see Sect. 4), it seems unlikely that this approach can lead to predictions that are universally accurate across all types of flows. A power-law model (Laugel and Beissinger 1983) was proposed for low shear stress flows (≤ 300 dyne/cm²), in which the damage was related to shear rate and tube length (thus, the residence time)

$$D_{\text{LB}} = K_{i} \dot{\gamma }^{n}$$

(37)

where D_LB is the dimensionless damage index (ratio of PfHb concentration after the test to that before the test), $\dot{\gamma }$ is the wall shear rate (s⁻¹), K_LB is the rate constant (dependent on tube length), and n is the constant related to the slope of the curve.

In the most widely used power-law model (Giersiepen et al. 1990; Heuser and Opitz 1980), the hemoglobin release is related to the levels of shear stress (scalar) and exposure time by the following regression equation

$$D = \frac{{\Delta {\text{PfHb}}}}{{\text{Hb}}} \times 100 = C E^{\alpha } \tau^{\beta } .$$

(38)

where D is the damage function, τ is the shear stress (N/m²), and C, α, and β are experimentally determined constants (Table 6). The damage function is related to the traditional index of hemolysis (Eq. (1))

$$D = \frac{{\Delta {\text{PfHb}}}}{{\text{Hb}}} \times 100 = \frac{{\text{TIH}}}{{\text{Hb}}} \times 100$$

(39)

Table 6 Values of empirical constants in power-law model

Note that based on Figs. 11 and 12 in the original paper, the correct value of C for the Heuser and Opitz (1980) model is 1.8 × 10⁻⁴, as correctly cited by Song et al. (2003) and Faghih and Sharp (2016). However, some authors used 1.8 × 10⁻⁶ either due to confusion between percent and nonpercent ratio of $\frac{{\Delta {\text{PfHb}}}}{\text{Hb}}$ or a better curve-fit with their data.

Extensions that have been applied to Eq. (38) include using a scalar stress in place of the shear stress in 2D and 3D laminar flows and using a similar scalar representing turbulent stresses. While many authors have suggested Reynolds stress as an empirical predictor of cell damage (Giersiepen et al. 1989, 1990; Nygaard et al. 1992), others have argued against it, noting that Reynolds stress is not a true viscous stress, but rather originates from convective acceleration due to the fluctuating part of the local velocity (Jones 1995). Based on an energy balance approach, Jones reasoned that the resultant turbulent viscous stress, which is proportional to the square root of energy dissipation, could be a more meaningful criterion for hemolysis prediction.

Damage accumulation has been interpreted from Eq. (38) by differentiation in time alone (Bludszuweit 1995a, b; Grigioni et al. 2004, 2005; Zimmer et al. 2000)

$$\Delta D_{i} = \alpha C E_{i}^{\alpha - 1} \tau_{i}^{\beta } \Delta t_{i}$$

(40)

where $\Delta D_{i}$ is the incremental damage, E_i is the exposure time from the beginning of the stress event and $\Delta t_{i}$ is the time step at iteration i, and τ_i is the shear stress during the time step. The questionable validity of Eq. (40) is evident by considering different stress histories leading up to a particular time step. Whether the previous stresses were small or large, Eq. (40) gives the same contribution to the total blood damage for that time step.

The time derivative of Eq. (38) is

$$\frac{\text{d}}{{{\text{d}}t}}\left( D \right) = \alpha C E^{\alpha - 1} \tau^{\beta } \frac{{{\text{d}}E}}{{{\text{d}}t}} + \beta C E^{\alpha } \tau^{\beta - 1} \frac{{{\text{d}}\tau }}{{{\text{d}}t}}$$

(41)

There is an inconsistency in using the total derivative. When decreasing stress (dτ/dt < 0) is acting on the cell, the total derivative (Eq. 41) predicts negative blood damage, i.e., hemoglobin in the plasma returning to red cells, which is not plausible (Grigioni et al. 2004). Therefore, the derivative of exposure time only (Eq. 40) is recommended.

The age of RBCs flowing through cardiovascular devices also plays a part in the sensitivity of the cell to the applied shear stress. This factor motivated Yeleswarapu et al. (1995) to formulate a theoretical hemolysis model including aging

$$\tilde{D}\left( t \right) = \tilde{D}_{0} + \frac{1}{{\sigma_{0}^{r} }}\mathop \smallint \limits_{{t_{0} }}^{t} \frac{{\tau \left( \xi \right)^{r} }}{{\left[ {1 - \tilde{D}\left( \xi \right)} \right]^{k} }}{\text{d}}\xi$$

(42)

where $\sigma_{0}$, r, and k are nonnegative characteristic constants, $\tau \left( \xi \right)$ and $\tilde{D}\left( \xi \right)$ are shear stress and damage histories, respectively, while $\widetilde{{D_{0} }}$ is the initial damage at $t = t_{0}$. $\tilde{D}$ for a single cell is considered to be $\widetilde{{D_{0} }}$ initially and increases as the cell enters the circulation and experiences fluid forces. Thereafter, damage accumulates until it reaches a pre-defined threshold value at which hemolysis occurs.

The methods discussed so far bridge the gap between fluid stresses and Hb release from red cells with a variety of simplifications, but all more or less follow the paths of individual cells through the flow regime and use the fluid stress history along these paths to determine how much hemolysis occurs; i.e., the methods are Lagrangian (Mitoh et al. 2003; Wu et al. 2005; Yano et al. 2003). This method adds a significant postprocessing step to calculate pathlines and to verify sufficient density of pathlines in hemolytic regions of the flow to achieve acceptable resolution of hemolysis. An alternative that is simpler, but decidedly more empirical, is to correlate the fluid stress field directly to hemolysis values (Farinas et al. 2006; Garon and Farinas 2004; Goubergrits 2006; Zhang et al. 2006). For example, the Eulerian method of Garon and Farinas uses a source term

$$\zeta = C^{1/\alpha } \tau^{\beta /\alpha }$$

(43)

that is derived from the material derivative of a linearized damage function based on the power law

$$D_{L} = D^{1/\alpha } = C^{1/\alpha } E\tau^{\beta /\alpha }$$

(44)

To understand the conditions for which this source term applies, the material derivative for a general function f

$$\frac{D}{Dt}\left( f \right) = \left( {\left. {\frac{\partial }{\partial t}} \right|_{{\vec{x} = {\text{fixed}}}} + \vec{v} \cdot \left. \nabla \right|_{{t = {\text{fixed}}}} } \right)f$$

(45)

becomes for the linearized damage function for steady flow [and inserting Eq. (43), Faghih and Sharp (2019)]

$$\frac{D}{Dt}\left( {D_{L} } \right) = \left[ {\frac{{\partial D_{L} }}{\partial t} + \vec{v} \cdot \left( {\frac{{\partial D_{L} }}{\partial E}\frac{dE}{{d\vec{s}}}\frac{{d\vec{s}}}{{d\vec{x}}} + \frac{{\partial D_{L} }}{\partial \tau }\frac{d\tau }{{d\vec{s}}}\frac{{d\vec{s}}}{{d\vec{x}}}} \right)} \right] = C^{{\frac{1}{\alpha }}} \left[ {0 + \vec{v} \cdot \left( {\tau^{{\frac{\alpha }{\beta }}} \frac{{n_{i} \hat{i}_{i} }}{{\bar{U}_{s} }} + E\frac{\beta }{\alpha }\tau^{{\frac{\beta }{\alpha } - 1}} \frac{\partial \tau }{{\partial \vec{x}}}} \right)} \right]$$

(46)

where $\bar{U}_{\text{s}}$ is the mean velocity during time E along the streamline s passing through the fixed point. Again ignoring spatial variations in shear stress, the source term becomes

$$\zeta = \frac{D}{Dt}\left( {D_{\text{L}} } \right) = C^{1/\alpha } \tau^{\beta /\alpha } \frac{U}{{\bar{U}_{\text{s}} }}$$

(47)

where U is the local magnitude of velocity. Comparing Eqs. (47) and (43), it is evident that the source term of Eq. (43) is valid only for flows in which $\bar{U}_{s} = U$. This is the case for uniaxial flows with constant velocity along streamlines, such as Poiseuille and Couette flows. However, for more complex flows, $\bar{U}_{s}$ must be determined along streamlines, which adds a Lagrangian step to the Eulerian method.

An additional issue has been identified with the Eulerian method and, in particular, the linearized damage function. The average of the original damage function is intended to be returned by applying an exponent to the volume integral of the source term

$$\bar{D} = \left( {\frac{1}{{\hat{u}A}}\smallint \zeta {\text{d}}V} \right)^{\alpha }$$

(48)

where $\hat{u}$ and A are the average velocity and the area of the exit cross section, respectively, and V is the volume. To be valid, this average damage function should be equal to that of the original Lagrangian method, which is found by a velocity-weighted integral over the exit cross section

$$\bar{D} = \frac{1}{{\hat{u}A}}\smallint uD{\text{d}}A$$

(49)

Equating hemolysis predicted by Eqs. (48) and (49) [and using Eq. (47)] gives

$$\frac{{\smallint uD{\text{d}}A}}{{\left( {\smallint uD^{{\frac{1}{\alpha }}} {\text{d}}A} \right)^{\alpha } }} = \left( {\hat{u}A} \right)^{1 - \alpha }$$

(50)

This equation is satisfied only if $\alpha = 1$ or $D = CE^{\alpha } \tau^{\beta }$ is constant. However, $\alpha \ne 1$ for any of the power-law models (Table 6). D is constant for Couette flow, but not for Poiseuille flow nor for more complex flows. The root of this inconsistency is that exponents are not distributive across integrals, i.e., $\left( {\smallint f^{{\frac{1}{\alpha }}} {\text{d}}x} \right)^{\alpha } \ne \smallint f{\text{d}}x$ or as shown by Eq. (50), $(\smallint uD^{{\frac{1}{\alpha }}} {\text{d}}A)^{\alpha } = \smallint uD{\text{d}}A$ only for some rather limiting conditions.

In general, neither the Lagrangian nor Eulerian approaches have shown satisfactory results for hemolysis prediction in blood-contacting devices (Pauli et al. 2013; Taskin et al. 2012).

A model that blurs the distinction between fluid stress-based and membrane strain-based models is that of Poorkhalil et al. (2016), which incorporates two semiempirical components, one for diffusion of hemoglobin through pores in the membrane at low shear stress and another for catastrophic membrane rupture at higher shear. By involving equations that differentiate between these two hemoglobin release mechanisms, they achieved better agreement with existing experimental hemolysis data. Experiments using a Couette device were also conducted on both human and porcine blood samples to validate the model, and good agreement was found between the experimentally measured damage and that predicted by their model.

6.3 Energy dissipation rate-based models

An alternative to the application of the scalar stress as a parameter to quantify red cell membrane damage is the viscous energy dissipation rate, ε. Bluestein and Mockros (1969) previously showed that the rate of red cell damage ($\dot{D}_{B}$ is defined as PfHb per cm³ of red cells per unit time) can be scaled as

$$\dot{D}_{B} = k_{d} \varepsilon^{{\alpha_{d} }}$$

(51)

for flow in round tubes, orifice plates, and a venturi tube and in uniform shear in a viscometer with combined Couette and cone/plate geometry. However, empirical constants $k_{d}$ and $\alpha_{d}$ varied among the flow types, with nonuniform energy dissipation producing more hemolysis, implying that the local rate of energy dissipation should be considered if energy dissipation is to become a universal hemolysis prediction parameter.

More recently, Morshed et al. (2014) argued that the energy dissipation in blood plasma dominates the energy dissipation in the cell membrane and its intracellular content. Based on this assumption, strain occurs only in the blood plasma, and the shear stress exerted on the cell membrane ($\tau_{\text{p}}$) is

$$\tau_{\text{p}} = \frac{{\nu_{\text{B}} }}{{\eta_{\text{k}}^{2} }} \sqrt {\frac{{\mu_{\text{B}} \mu_{\text{p}} }}{{\left( {1 - H} \right)}}}$$

(52)

where $\nu_{\text{B}}$ is the kinematic viscosity of the whole blood, $\mu_{\text{B}}$ and $\mu_{\text{p}}$ are the dynamic viscosities of whole blood and plasma, respectively, and H is the hematocrit fraction. While promising correlation was found spanning laminar and turbulent shear flow in a pipe (Kameneva et al. 2004), universality for different geometries like those tested by Bluestein and Mockros (1969) would not be expected. This model assumes that cells in turbulent flow are sheared inside a vortex, much like the Quinlan and Dooley (2007) model (see Sect. 7.2.3). However, a number of other positions of the cell relative to vortices are possible (see Sect. 7.3).

6.4 Membrane strain-based models

In spite of the extensions that have been developed to broaden the applications of the power-law model (Eq. 38), validation is limited to the original experimental data and their associated ranges of simple shear stress and exposure time. Perhaps more important is that the power-law model does not incorporate physical and mechanical properties of the RBCs, nor mechanisms of the transmission of fluid stresses to the membrane. As pointed out by Ezzeldin et al. (2015), the simpler fluid stress-based models lack a strong connection with the mechanics of membrane failure, which may limit their performance in the complex, unsteady flows that often occur in cardiovascular devices. For this reason, a number of investigators have turned to membrane strain-based models as potential avenues for improving hemolysis prediction.

6.4.1 Deformation index

Strain-based models fit between the extremes of purely empirical correlation of hemolysis with fluid flow parameters [such as the power-law model (Grigioni et al. 2004)] and molecular-scale modeling of red cell membrane failure to predict hemolysis. Strain-based models utilize observations that the RBC membrane can withstand no more than 5–10% increase in area before being ruptured (Burton 1972; Rand and Burton 1964). With a model relating fluid stress conditions to membrane strain, this threshold of strain has been used to predict hemolysis (thus, the name “strain-based” models). The relationship between fluid stress and membrane strain commonly adopts a simplified model of whole-cell deformation along pathlines through the flow. A deformation index may be used as a proxy for local or uniform membrane strain. One such index is the simple ratio of major and minor radii $a/b$ of an assumed prolate ellipsoidal cell (Fig. 10). Another option, called the deformation index (DI), is expressed as

$${\text{DI}} = \frac{a - b}{a + b}$$

(53)

Fig. 10

Deformation indices of several example shapes

A third index is sphericity, which is defined as

$${\text{Sph}} = \frac{{\pi^{1/3} \left( {6V_{\text{p}} } \right)^{2/3} }}{{A_{\text{p}} }}$$

(54)

where $V_{\text{p}}$ and $A_{\text{p}}$ are the volume and surface area of the cell. For a cell beginning with mean surface area and volume of 135 µm² and 94 µm³, respectively, the initially biconcave disk can be deformed without areal strain of the membrane to a prolate ellipsoid with $a/b = 4.8895$ (2a = 8.1254 µm and 2b = 1.6618 µm), DI = 0.6604, and Sph = 0.7406. Beyond this level of cell elongation, areal strain must occur, as shown in Fig. 11. To better compare the indices, they are normalized in Fig. 11 by their unstrained values ($a/b$)₀, DI₀, and Sph₀. It is apparent that Sph is less sensitive to strain than the other two, but nonetheless, is directly (inversely) proportional to membrane area.

Fig. 11

Three deformation indices versus membrane strain

Relationships between these deformation indices and hemolysis are yet to be fully established. Validation experiments are needed to relate the indices to hemoglobin release (sublytic membrane damage is a further question).

Three uncertainties should be considered when using the above-mentioned deformation indices. First, the indices are calculated based on shape symmetry about the long axis, which is clearly not valid for all flows. Second, the deformation indices do not take into account the initial shape and size of the cell. For instance, an RBC with greater membrane surface area to volume ratio may have the same value of deformation index at a lower state of strain. Considering the range of surface area and volume among cells in a particular patient or population of cells (such as the means and standard deviations in Table 1) leads to a distribution of strain and of resulting hemolysis, even for the same flow conditions.

Still, the use of a simple deformation index is attractive, because calibration experiments involving two-dimensional, projected images of cells (e.g., from Goldsmith and Marlow (1972) to Chen and Sharp (2011)) allow straightforward quantification of the index. More complex experimental setups are required to measure angles and lengths in the third dimension. In such experiments, optical access to individual cells within the flow regime has so far required testing at low hematocrit. Herein lies the third, more fundamental, uncertainty, which is outlined in the next section.

6.4.2 Cell/cell interactions

Although hematocrit has been shown to have a negligible effect on hemolysis in a concentric cylinder viscometer under pure shear stress (Leverett et al. 1972), low hematocrit may not fully capture the bulk-flow behavior of RBCs in the more complex fluid dynamics in cardiovascular devices. Specifically, because the low concentration of cells largely eliminates cell/cell interactions, the behavior of individual RBCs may be different from those experiencing collisions under physiologic hematocrit. An obvious question is what suspending medium viscosity should be used to most closely model these physiologic fluid stresses? Using plasma viscosity may underestimate the stresses transferred from the concentrated suspension. Is whole blood viscosity the answer? This question applies not only to the interpretation of results from microrheographic experiments, but also to step 2 for hemolysis prediction, i.e., the development of a model for the transfer of fluid stresses to the cell membrane. This important question remains unanswered.

An example of red cell behavior that depends on cell–cell interactions is the compaction of cell layers resulting in plasma release (Thurston 1989). This behavior has not been directly observed, but rather inferred from light transmission measurements and rheometry (Klose et al. 1972; Thurston 1990). Startup and relaxation of the layers depends on the viscoelasticity of the cells. It can be expected that flows in complex geometries could involve Deborah² and Weissenberg-number-dependent breakup and reformation of the layers, which would impact the fluid stress history exerted on the cells. With the limited observations that have been accomplished so far because of the difficulties associated with optical access in concentrated suspensions of opaque cells, details of theorized motions and perhaps entirely new motions likely remain to be discovered.

In a study on the deformation of RBCs flowing through a microchannel (Zhao et al. 2006), it was observed that under laminar shear stress as high as 50,000 dyne/cm² for duration of around 23 ms, the deformation index of cells reached a plateau at DI= 0.54, and the cells surprisingly exhibited no cell lysis/rupture and returned to their original shape after removal of the stress. These experiments used a very low hematocrit in order to capture images of individual cells, as well as a suspending medium viscosity more than ten times that of normal plasma to achieve a high shear stress at reasonable flow rate. This tactic has been used by others for the same reasons, as well as to maintain laminar flow (Chen and Sharp 2011; Lee et al. 2004; Rooney 1970; Williams et al. 1970). However, it has been demonstrated that cell deformation is a function of suspending medium viscosity (Morris and Williams 1979); thus, it may impact the combination of fluid stress and exposure time at which lysis occurs. This finding reinforces the question about which suspending medium viscosity best models the stresses exerted on cells.

6.4.3 Models

Membrane strain-based models, defined strictly, utilize the first three steps in Sect. 6.1, but also typically include the fourth step, as well. This category of models, therefore, includes those that simplify cell deformation and treat hemoglobin release empirically, and others that use a cell-scale or molecule-scale computational models for deformation and hemoglobin diffusion.

Using Rand’s model of the cell membrane (Rand 1964) as well as membrane shell theory, Richardson (Richardson 1974, 1975) modeled the RBC as an isolated spheroid with flexible membrane in a uniform shear field to obtain the stresses on the cell surface, with the goal of developing a model for hemolysis in high shear-rate experiments. He showed that membrane strain of the cell in a uniform shear flow is composed of three terms: a term linear in time, a periodic term, and an exponentially decreasing term. It was then concluded that the time it takes for hemolysis to occur is dictated by the linear term and is equal to

$$t_{\text{R}} = \frac{{C_{\text{R}} }}{{\mu \dot{\gamma }^{2} }}$$

(55)

where $C_{\text{R}}$ is an experimental constant equal to 6.7 × 10⁴ dyn/cm² based on Rand’s critical strain value. By treating the red cell as a particle rather than as part of a continuum, this model represented a major step forward toward more mechanistic modeling, but the limitations of the spheroidal shape and applicability to shear flow only are disadvantages.

Modeling the red cell as a deformable liquid droplet and assuming that instantaneous Hb leakage through the RBC membrane depends on instantaneous RBC shape distortion, Arora et al. (2004) proposed a tensor-based hemolysis model to estimate the time- and space-dependent straining by individual RBC under steady shear stress. They used a constitutive equation for the deformation of the initially spherical droplet to an ellipsoidal shape by balancing the interfacial tension with the fluid stresses on both sides of the interface (Barthès-Biesel and Rallison 1981; Maffettone and Minale 1998). Then, a deformation function is used as the stress term in the power-law model format (Eq. 38)

$$D = C t^{\alpha } \left( {\mu \frac{{2f_{1} \left( {\text{DI}} \right)}}{{f_{2} \left( {1 - \left( {\text{DI}} \right)^{2} } \right)}} } \right)^{\beta }$$

(56)

where D is the damage function, as previously described by Eq. (38) and DI is the deformation index previously expressed by Eqs. (53). $f_{1}$ is a parameter that in the original work of Maffettone and Minale (1998) depends on the viscosity ratio between the liquid droplet and the suspending fluid, and f₂ depends on the viscosity ratio and the flow intensity. However, $f_{1}$ and $f_{2}$ were taken as constants that apply only for shear flow at the hemolytic threshold of whole-cell strain. Therefore, the model does not account for lysis by extensional stresses, which is important in at least some cardiovascular devices (see Sect. 5.2). Gesenhues et al. (2016) found that the model predicts slower response to transient shear than the stress-based power law, which is physically consistent with the time required to stretch cells from a low-strain state to the hemolytic threshold. The deficit in predicted hemolysis that persisted to long exposure times was addressed by recalibrating the power-law constants to the experimental data of Zhang et al. (2011). This model adds mechanistic fidelity, but hemolysis was scaled to the power-law model; thus, it shares the limitations of that empirical model. The liquid droplet model has been improved upon by models that treat the cell as a capsule with a surrounding membrane (see the following paragraphs).

Chen and Sharp (2011) developed a scaling model to relate membrane stress to the von Mises-like scalar stress in the fluid and used a viscoelastic model for the RBC membrane that fails at a critical strain (Rand 1964)

$$\frac{S}{{S_{\text{c}} }} = T\left[ { \frac{1}{{S_{\text{c}} hY_{2} }} + \frac{1}{{S_{\text{c}} hY_{1} }}\left( {1 - e^{{\left( { - \frac{{Y_{1} }}{{\eta_{1} }} t} \right)}} } \right) + \frac{1}{{S_{\text{c}} h \eta_{2} }} t } \right]$$

(57)

where S is the membrane strain, S_c is the critical strain [taken as 0.064 (Rand 1964)], $T$ is the biaxial tension in the RBC membrane, h is the membrane thickness and Y and η are parameters related to elastic and viscous properties of the modeled RBC, respectively. Importantly, this work included new experimental data that documented red cell deformation in pure shear flow, but due to limitations of the equipment, tests could not be run all the way to membrane failure. Thus, the model includes extension of the experimental results to the hemolysis threshold. This model was compared with two power-law models, namely the Heuser and Opitz (1980) and Giersiepen et al. (1990) models, in the flow through needles of different entrance geometries, i.e., standard, beveled, and rounded (Chen et al. 2013). Chen and Sharp’s strain-based model provided good trends for hemolysis in the three different needles with subtle variations in entrance geometry compared to the power-law-based models, which produced opposite trends. This comparison of needle geometries is emblematic of the types of problems bioengineers would like to solve in the course of optimizing the flow within a blood-contacting device. To develop a reliable and accurate hemolysis prediction algorithm, more work like this is needed in comparing the performance of models in such problems, which also means that more experimental validation data are needed for cases that involve incremental changes in device geometry and flow conditions. A limitation of this model is that to calculate membrane tension, it assumes alignment of the cell with the first principal stress, which is true more for extensional flows than for high shear flows. This is unique among other models that are developed for shear flow only. Another limitation is that hemoglobin transport was treated as constant for all conditions beyond the hemolytic membrane strain threshold. Dependence of hemoglobin release on fluid stresses or, similarly, that the fraction of cells damaged depends on fluid stresses (Poorkhalil et al. 2016), might improve accuracy across ranges of fluid stress magnitudes.

Arwatz and Smits (2013) modified the theoretical model proposed by Rand (1964) by using a viscoelastic strain-based model with two time constants. The first time constant is related to the short timescale during which the deformed RBC releases part of its hemoglobin (change in membrane permeability/poration). The second, longer time constant represents the decay of elastic behavior of membrane. The resulting formulation is

$$\frac{D}{100} = \frac{{A_{\text{AR}} \tau }}{G}\left[ {2 - \left( {e^{{ - \frac{t}{{T_{1} }}}} + e^{{ - \frac{t}{{T_{2} }}}} } \right) + \frac{t}{{T_{2} }}} \right]$$

(58)

G is the membrane shear modulus, T₁ and T₂ are the first and second time constants, and A_AR is an empirical constant. This model, which was fit to experimental hemolysis measured in Couette flow, improves hemolysis prediction particularly for long-duration exposure (by incorporating the second time constant). However, the model was developed and validated only for shear flow.

Vitale et al. (2014) added an important factor, namely membrane poration, into their model. Their multiscale biophysical model involved all four steps: (1) calculating the flow field, (2) determining membrane stress from the calculated flow field; (3) finding areal strain and modeling membrane poration due to deformation; and (4) calculating Hb mass transfer through the pores due to transmembrane Hb concentration difference. For the third step, they used the tensor-based model of Arora et al. (2004) to define cell deformation and morphology along its trajectory. Then, energy changes on the membrane governed by two forces, namely hydrophobic attraction of lipid tails and headgroup repulsion, were considered to determine nucleation of pores in the membrane. For the last step, the rate of mass transport J of Hb out of the cell through the pores

$$J = K_{\text{c}} \left( {{\text{Hb}}_{\text{in}} - {\text{Hb}}_{\text{ex}} } \right),$$

(59)

where $Hb_{in}$ and $Hb_{ex}$ are internal and external hemoglobin, respectively, was modeled with an empirical mass-transfer coefficient K_c correlated with shear rate

$$K_{\text{c}} = h_{\text{c}} \dot{\gamma }^{{k_{\text{c}} }}$$

(60)

where h_c and k_c are empirical coefficients. Advective Hb transport induced by transmembrane pressure difference was not included. The damage function was approximated by:

$$D\left( t \right) \approx 1 - \exp \left[ { - \mathop \smallint \limits_{0}^{t} R\left( {\alpha_{\text{s}} \left( t \right),K_{\text{c}} } \right) {\text{d}}t} \right]$$

(61)

where R is a parameter representing transmembrane Hb transport that depends on K_c and the size of the pores, which depends on membrane areal strain $\alpha_{\text{s}}$. In deriving the above relation, it was assumed that damage is zero at t = 0. The transport-based model predicted much lower hemolysis in a low-Reynolds-number (Re = 100) flow in a curved tube than the strain-based model of Arora et al. (2004) and the power-law model of Giersiepen et al. (1990). However, it shares the limitation of the Arora et al. (2004) model that it is valid only for shear flow.

In a more recent study (Ezzeldin et al. 2015), a coarse-grained molecular model incorporating triangulated networks of 600–1200 nodes was used to model the lipid membrane and the spectrin cytoskeleton (Discher et al. 1998). In contrast to the model by Arora et al. (2004), which used the instantaneous strain tensor of an assumed ellipsoidal cell to obtain the RBC deformation, Ezzeldin et al. (2015) solved the fluid/solid interaction problem for the complex membrane shape and then employed the eigenvalues of the instantaneous moment of the inertia tensor of the membrane to calculate the simplified deformation index (Eq. 53). The rest of the procedure was the same as that as Arora et al. (2004); i.e., the deformation index was used to calculate an effective fluid shear stress that was inserted into the power law (Eq. 56) to estimate blood damage. The model was applied to simple shear flow and compared to the results of previous models. They found that in one-dimensional flow, fluid stress-based models predict hemolysis reasonably well, while in multi-dimensional flows, they may either over-estimate or underestimate hemolysis, depending on the frequency of cell loading and other conditions. For instance, in multi-dimensional flow, the strain-based model of Arora et al. (2004) predicts lower damage compared to the multiscale model of Ezzeldin et al. (2015). To validate these numerical findings, they conducted a simple experiment of flow in an aortic graft that was equipped with a bileaflet mechanical valve and found good agreement between the experimental and numerical results. While the molecular-scale model is an advancement, in the end the procedure regresses to algorithms that presume simple shear flow and uses the empirical power law based on shear flow for hemolysis prediction. Incorporating poration and hemoglobin transport into the membrane model would be a logical next step to avoid these limitations.

Such a model was developed by Sohrabi and Liu (2017), who modeled poration based on local membrane strain. Based on the support of the bilipid membrane by the spectrin network, pores were limited in size to that of a stretched spectrin molecule. Hemoglobin was transported through the pores by diffusion, including steric hinderance and increased hydrodynamic drag due to the size of the hemoglobin molecule being a significant fraction of the pore size. The resulting mass transport coefficient was in the same range as that of Vitale et al. (2014), but is less empirical. The model was demonstrated only to shear flow, but could presumably be applied for more complex flows.

As suggested by the curve-fits of Poorkhalil et al. (2016), hemoglobin release may occur by at least two phenomena, which were presumed to be diffusion through pores and complete hemoglobin release by catastrophic membrane rupture. The first mechanism was incorporated into the models of Vitale et al. (2014) and Sohrabi and Liu (2017), and a modified version of the second was used by Chen and Sharp (2011). The results of Poorkhalil et al. (2016) suggest that accuracy of hemolysis prediction could be improved by incorporating both mechanisms. Regarding the second mechanism, images of cells after exposure to high shear (Sutera and Mehrjardi 1975) suggest that full hemoglobin release may not occur, even when the cell is completely torn apart. The interpretation of the latter mechanism may benefit from some refinement, and though the problem is challenging, membrane-level models would seem to be a valuable tool for exploring this and other mechanisms of hemoglobin release in complex flows.

Accurately representing fluctuating fluid stresses in turbulent flow is also a challenge. Stress-based models typically use Reynolds-average statistics, such as scalar Reynolds stress or energy dissipation rate, both of which are questionable. While strain-based models can also use similar statistics, more mechanistic models require sufficient spatial and temporal resolution of velocity profiles with which to calculate cell deformation. Ezzeldin et al. (2015) used direct numerical simulation (DNS) in a turbulent flow at Reynolds number of 6200, but this approach may be impractical in terms of computational time for larger flow regimes and higher Reynolds number. It is perhaps logical that vortices smaller than red cells are substantially suppressed by the cells (Antiga and Steinman 2009). Resolution to the scale of red cells would nonetheless be computationally intensive for typical cardiovascular devices (Cristini and Kassab 2005), but the Kolmogorov scale is typically larger than the red cell. Velocity fluctuations exist down to and below the Kolmogorov scale, but only the most important scales may be necessary for hemolysis prediction. In particular, the models of Quinlan and Dooley (2007) and Faghih and Sharp (2018a) (Sect. 7.3) suggest that large-scale fluctuations with the highest energy content produce the greatest membrane tension; however, this result remains to be experimentally verified. Such response has the potential to ease the computational burden by eliminating the need to resolve the entire spectrum of turbulent fluctuations. If so, large eddy simulation (LES) may be a suitable alternative to DNS. Another proposed alternative is reconstructing velocity fluctuations using assumed distributions after RANS simulations (Goubergrits et al. (2016) used a Gaussian distribution), which also takes less computer time. However, turbulence has been shown to be non-Gaussian. This characteristic is important especially with regard to the question of which size of eddies is most hemolytic. For accurate hemolysis prediction in turbulent flows, the distribution of eddies would need to match the actual distribution, at least in the most hemolytic sizes (see, for instance, the distributions estimated by Quinlan and Dooley (2007) and Faghih and Sharp (2018a) for the flow downstream of a prosthetic valve).

For modeling hemoglobin release, it is logical to argue that resolution is needed to at least the cellular level; however, multiscale models could also be applied for more efficient computations. Fundamental questions remain about how the presence of red cells affects the distribution of turbulence scales, as well (Sect. 6.4.2). Certainly, the continuum model breaks down as grid size approaches the size of the cell. Yet, even smaller scales contain physics essential to hemolysis modeling. At the subcellular level, the opening of pores in the membrane is a molecular-scale phenomenon that greatly expands computation effort. For example, molecular dynamics modeling of the biaxial stretching of a small patch of the bilipid membrane (not including the spectrin network) took 3840 CPU hours (Koshiyama and Wada 2011), but yielded insights into thresholds and patterns of pore formation under quasi-steady and unsteady conditions.

Perhaps most remarkable about the hemolysis modeling that has been done to date is the lack of attention to extensional stresses. All of the models discussed in this section were developed for shear flow only or are traceable to empirical curve-fits that were derived only from shear flow. With the modern recognition of the importance of extensional flows in causing hemolysis (see Sect. 5.2), it is time to devote more research effort to incorporating extensional stresses into hemolysis prediction algorithms.

7 A fresh approach: greater accuracy through more mechanistic models

While cellular- and molecular-level simulations have the potential to provide accurate predictions of flow and of cellular responses, including membrane deformation and failure and hemoglobin release, it remains a formidable challenge to resolve all the necessary scales to solve the problem in real cardiovascular devices. With this in mind, this section will discuss opportunities for improving models that are within the current capacity of modern computers, in particular, modifications that may be required to address differences in the responses of cells to different components of the fluid stress tensor and to turbulent versus laminar flow. First, a full description of the physics of flow-induced hemolysis will be outlined parametrically, to our knowledge for the first time, in a reasonably comprehensive list of independent and dependent variables in Sect. 7.1. Then in Sect. 7.2, estimates of membrane tension will be developed and compared that exemplify how models of cell motion that are specific to particular types of laminar and turbulent flow might be incorporated to improve hemolysis prediction.

7.1 Dimensional analysis

A potentially important avenue for improving the accuracy of hemolysis models is reevaluating the mapping between fluid stresses and membrane stresses across different types of cell motion (step 2 in Sect. 6.1). Once membrane stresses are known, the next challenge is to model the mechanical response of the cell membrane up to and including failure that results in loss of hemoglobin from the cell.

The independent variables that may influence this response include external fluid density $\rho_{\text{ex}}$, internal fluid (cytoplasm) density $\rho_{\text{in}}$, external fluid viscosity $\mu_{\text{ex}}$, internal fluid viscosity $\mu_{\text{in}}$, red cell shape at rest (array $\varvec{D}_{0}$ of several dimensions, represented by the major diameter $a_{0}$ in Fig. 12 left), membrane mechanical properties (array $\varvec{\psi}$, represented by membrane surface viscosity $\eta_{\text{m}}$ and membrane edge tension $\Lambda$ in Fig. 12 left), the initial internal ${\text{Hb}}_{{{\text{in}}0}}$ and external ${\text{Hb}}_{{{\text{ex}}0}}$ hemoglobin, and the external fluid stress tensor $\varvec{\sigma}_{\text{ex}}$ applied to the cell (Fig. 12 left) (the strain rate tensor is a suitable alternative that eliminates the external fluid viscosity, which is already included separately).

Fig. 12

Schematic of unstressed cell (left) and stressed (right) cell with independent variables on the left and dependent variables on the right

The dependent variables that result from flow-induced stress include the distorted cell shape ($\varvec{D}_{{\mathbf{s}}}$), cell orientation in the flow (array $\varvec{\theta}$, represented by the angle $\theta_{1}$ in the yz plane in Fig. 12 right), cell motion parameters ($\varvec{\omega}$), membrane tension (T), cytoplasmic stress tensor ($\varvec{\sigma}_{\text{in}}$), pore properties (number and sizes, represented by $\varvec{\beta}_{{\mathbf{p}}}$ in Fig. 12 right), and the external ${\text{Hb}}_{\text{ex}}$ hemoglobin for the stressed condition (Fig. 12 right). Note that internal hemoglobin ${\text{Hb}}_{\text{in}}$ has not been included, since by conservation of mass, total hemoglobin remains the same ${\text{Hb}} = {\text{Hb}}_{\text{in}} + {\text{Hb}}_{\text{ex}} = {\text{Hb}}_{{{\text{in}}0}} + {\text{Hb}}_{{{\text{ex}}0}}$. Hence, the relationship of the variables in dimensional form is

$$\left( {\varvec{T},\varvec{\theta},\varvec{\omega},\varvec{D}_{{\mathbf{s}}} ,\varvec{\beta}_{{\mathbf{p}}} ,\varvec{\sigma}_{\text{in}} ,{\text{Hb}}_{\text{ex}} } \right) = f\left( {\rho_{\text{ex}} ,\rho_{\text{in}} ,\mu_{\text{ex}} ,\mu_{\text{in}} ,\varvec{D}_{0} ,\varvec{\psi},\varvec{\sigma}_{\text{ex}} ,{\text{Hb}}_{\text{ex0}} ,{\text{Hb}}_{\text{in0}} } \right)$$

(62)

By expanding some of the arrays, the relationship becomes

$$\left\{ {\varvec{T},\varvec{\theta},\underbrace {{\left( {\varvec{V},\dot{\varvec{\theta }},\varvec{f}} \right)}}_{\varvec{\omega}},\underbrace {{\left( {a,b,c} \right)}}_{{\varvec{D}_{{\mathbf{s}}} }},\varvec{\beta}_{{\mathbf{p}}} , \sigma_{\text{in}} ,{\text{Hb}}_{\text{ex}} } \right\} = f\left\{ {\rho_{\text{ex}} ,\rho_{\text{in}} ,\mu_{\text{ex}} ,\mu_{\text{in}} ,\varvec{D}_{0} ,\underbrace {{\left( {\eta_{\text{m}} ,\Lambda } \right)}}_{\varvec{\psi}}\text{,}\varvec{\sigma}_{{{\mathbf{ex}}}} ,{\text{Hb}}_{\text{ex0}} ,{\text{Hb}}_{\text{in0}} } \right\}$$

(63)

where $\varvec{V}$ is the cell linear (translational) velocity vector, $\dot{\varvec{\theta }}$ is the cell rotational velocity vector, $\varvec{f}$ is the tank-treading frequency vector, and a, b, and c are the dimensions of an assumed ellipsoidal cell in its deformed state. Note that the membrane bending (B) and area expansion ($\kappa$) moduli are dependent on the membrane thickness ($h$), which is considered a constant here for simplicity) and membrane edge tension $\Lambda$; thus, neither are included as independent variables (Boal 2012) (see Sect. 2.1). Also note that membrane shear modulus, which is an important parameter in characterizing cell motion in shear flow (the ratio of shear elastic modulus $\mu_{\text{s}}$ and bending stiffness B forms the Koeppl-von Karman number $Kv = 4\mu_{\text{s}} a_{0}^{2} /B$, which is a determinant of the transition from tumbling to tank-treading in shear flow (Fedosov et al. 2014), and in the capillary number ${\text{Ca}} = \sigma_{\text{ex}} a_{0} /\mu_{\text{s}}$, which has been shown to scale membrane tension in shear flow (Omori et al. 2012)), is neglected here within the ellipsoidal shape assumption for the models employed in this study.

Counting the vectors and $\varvec{\beta}_{{\mathbf{p}}}$ as single variables, there are 21-dimensional independent and dependent variables. By the Buckingham Pi theorem with three fundamental units, the number of dimensionless ratios can be reduced to 18. Candidate dimensionless groups are listed in Table 7, along with existing dimensionless numbers in many cases. The number of dimensionless ratios is reduced by two more (to 16), because all three hemoglobin variables are combined into one ratio,${\varvec{\Pi}}_{{{\mathbf{10}}}}$, that compares the change in external hemoglobin (caused by hemolysis) to the total hemoglobin. This ratio can be applied to whole blood and becomes MIH (Eq. 3) by adjusting by the hematocrit $\frac{{100 - {\text{Hct}}}}{100}$. The first vector of ratios ${\varvec{\Pi}}_{{\mathbf{1}}}$ weighs the components of membrane tension versus viscous forces in the extracellular fluid. The orientation angles ${\varvec{\Pi}}_{{\mathbf{2}}}$ are already dimensionless. ${\varvec{\Pi}}_{{\mathbf{3}}}$ represents primary and secondary flow cell Reynolds numbers, which might be reduced to a scalar by using the resultant velocity. ${\varvec{\Pi}}_{{\mathbf{4}}}$ and ${\varvec{\Pi}}_{{\mathbf{5}}}$ are Roshko numbers comparing whole-cell rotational and membrane tank-treading forces to external fluid viscous forces. Deformed cells are nondimensionalized by the unstressed major radius, ${\varvec{\Pi}}_{{\mathbf{6}}}$, ${\varvec{\Pi}}_{{\mathbf{7}}}$, and ${\varvec{\Pi}}_{{\mathbf{8}}}$. An example of ${\varvec{\Pi}}_{{\mathbf{9}}}$ is the Litster number, which compares the pore radius $\varvec{\beta}_{{\mathbf{p}}}$ to the critical pore radius $\Lambda /T$, above which the pore grows unstably and below which it shrinks. Other components might be added to characterize the number of pores and distribution of sizes. ${\varvec{\Pi}}_{{{\mathbf{11}}}}$ is the Reynolds number for cytoplasmic flow based on internal fluid stresses, which compares convective to viscous forces.

Table 7 Dimensionless groups for modeling mechanical hemolysis

For the independent variables, ${\varvec{\Pi}}_{{{\mathbf{12}}}}$ is the Reynolds number for external flow based on external fluid stresses, which again compares convective to viscous forces. Because of the small size of the red cell, the Reynolds number may always be small for flows in cardiovascular devices, but fluctuating stresses will indicate the effects of turbulence. ${\varvec{\Pi}}_{{{\mathbf{13}}}}$ is the ratio of internal to external fluid viscosities, which has been shown to be important in regulating the type of cell motion, particularly in shear flow (tumbling tends to occur when the cytoplasm is more viscous than the surrounding fluid, and tank-treading when the surrounding fluid is more viscous). ${\varvec{\Pi}}_{{{\mathbf{14}}}}$ is a ratio of membrane edge tension to membrane viscosity, but because the membrane area expansion modulus is proportional to edge tension, it also characterizes this expansion modulus with respect to membrane viscosity. As such, it is a factor in determining how rapidly the membrane is stretched and in the growth of pores. ${\varvec{\Pi}}_{{{\mathbf{15}}}}$ compares membrane surface viscosity and external fluid viscous forces; thus, it affects the deformation of cells in viscous flow (which is the predominant flow at the cellular level in cardiovascular devices, as opposed to the inertial flow in shock wave lithotripsy, see Sect. 5.2). Finally, ${\varvec{\Pi}}_{{{\mathbf{16}}}}$ is a ratio of internal to external fluid densities, which is important in sedimentation and in inertial flows.

The variables in Table 7 represent a first attempt to characterize hemolysis generally for any kind of cell motion under any flow condition. A benefit of dimensional analysis is in establishing a context within which specific solutions can be understood as a part of the whole. For instance, modeling of stable poration of the membrane applies only in the low Litster number regime and is just a part of an overall solution for all Litster numbers, which also includes catastrophic failure of membranes at high Litster number. Another example is the restriction of solutions to viscous (and not inertial) flow, which reduces complexity by allowing ${\varvec{\Pi}}_{{{\mathbf{16}}}}$ to be neglected.

Another benefit is in reducing the matrix of experimental or computational cases that must be tested to completely explore the effects of independent variables. For demonstration purposes, consider a simplified flow with one component of the external fluid stress tensor, or a scalar stress that represents multiple components. Also for simplicity, let the cell shape and membrane property arrays be represented by one value each. Thus, the dimensional Eq. (63) has nine independent variables. With ten values of each variable to test the effect of each, the set of experimental or computational cases to blindly quantify the relationships of these variables to the dependent variables would be 10⁹. Using dimensional analysis, however, the set of nondimensional independent variables is immediately reduced to four (Table 7 with only one membrane property variable, i.e., the ratio of membrane variables ${\varvec{\Pi}}_{{{\mathbf{14}}}}$ vanishes). Further, let us say that through the insight gained by performing the dimensional analysis, we also recognize that the flow is viscous so that ${\varvec{\Pi}}_{{{\mathbf{16}}}}$ can be ignored. By doing so, the number of cases is reduced to 10³. In the latter case, if three cases could be tested per day, the matrix could be completed in about one year. However, the dimensional set of independent variables would take over 2.7 million years! Clearly, dimensional analysis reduced the necessary effort.

7.2 Improved modeling of membrane tension

Continuum-based models of hemolysis have so far been unsuccessful in providing useful hemolysis prediction results that are universal across a wide range of flows. For turbulent flow, which is especially problematic, correlations have been attempted with turbulent viscous stress, Reynolds stress, and energy dissipation, as discussed in Sects. 3.2.1 and 3.2.3. Here, an attempt will be made to go beyond correlations between hemolysis and scalar representations of fluid stress and to evaluate the scaling of red cell membrane tension with fluid stress in a range of simplified flows. These relationships, which represent step 2 of Sect. 6.1, are the current and arguably the greatest bottleneck toward more accurate continuum-based hemolysis prediction. The following subsections will present scaling models that connect fluid stress to membrane tension in simple laminar and turbulent flows. By more clearly defining this problem, there is hope that progress will be made toward universal hemolysis prediction.

7.2.1 Modeling membrane tension in laminar extensional flow

Using dimensional analysis and applying a force balance on a prolate ellipsoidal cell (Fig. 13), the membrane tension around the circumference of the middle of the cell is (Chen and Sharp 2011):

$$T = K \frac{4}{5} b \left( {\sigma - \sigma_{\text{c}} } \right)$$

(64)

where $T$ is the membrane tension (force per unit length), b is the characteristic length of the RBC (minor axis of the 2-D projected RBC), $\sigma$ is the extensional stress, $\sigma_{\text{c}}$ is the critical stress (1500 dyne/cm²), and $K$ is an empirical constant. Assuming the absence of circulation of the membrane (tank-treading or tumbling), the membrane tension is constant.

Fig. 13

Schematic diagram of the ellipsoidal RBC model under extensional stress

The dimensional analysis used to develop Eq. (64) arose from a significantly reduced set of independent variables compared to Eq. (63)

$$\left\{ {T,a,b} \right\} = f\left( {\sigma_{\text{ex}} - \sigma_{\text{c}} } \right)$$

(65)

Of the independent variables in Eq. (63), all unstressed cell shape and membrane properties were assumed to be averages and, thus, are parameters (constants) rather than variables. The deformed cell was assumed to be axisymmetric, c = b. Internal fluid viscosity is unimportant because internal velocities are negligible for quasi-steady extension. External fluid viscosity is part of the fluid stress, but otherwise does not influence cell deformation in quasi-steady extensional flow. Internal and external fluid densities are neglected for viscous flow. Hemoglobin variables are involved later (in step 4) in hemoglobin release, but are assumed to not influence membrane tension (step 2). Note that a critical stress is incorporated in Eq. (65) that is not in Eq. (63). This critical stress is the stress required to deform the cell to the isoarea prolate ellipsoidal shape beyond which membrane area must be expanded. It represents an interpretation of the nonlinear deformation of the cell that occurs relatively freely up to the critical stress, but is more difficult for area expansion above the critical stress. While this model is not accurate for low stress deformation, it is a reasonable simplification for hemolytic stress levels. It serves as a reminder that for hemolysis prediction, accurate cell response is required only in the hemolytic range, and that similar refinements of the basic dimensional analysis relationship of Eq. (63) may be found for other steps in the hemolysis modeling process.

Equation (65) can be recognized in dimensionless form as $\frac{{{\varvec{\Pi}}_{{\mathbf{1}}} }}{{{\varvec{\Pi}}_{{\mathbf{6}}} }} = {\text{constant}}$, where we allow the critical stress to be incorporated into ${\varvec{\Pi}}_{{\mathbf{1}}}$. This reduction, in principle, allows the constant to be evaluated by one experiment. However, dimensional analysis cannot, in general, predict the quantitative form of the relationship between dependent and independent variables.

7.2.2 Modeling membrane tension in laminar shear flow

In laminar shear flow with sufficient ratio of suspending media viscosity versus cytoplasmic viscosity, an approximately ellipsoidal cell tank-tread with its downstream end elevated with respect to the shear field (Fig. 14). Using this assumed shape and with orientations matched to experiments, and with assumed internal and external velocity fields (Keller and Skalak 1982), Tran-Son-Tay et al. (1987) calculated the stress tensors acting on the outer and inner surfaces of the membrane, $\tau^{o}$ and $\tau^{i}$, respectively. Then, with assumed tank-treading motion of the cell membrane (Keller and Skalak 1982) and ignoring bending stress, a force balance provided, at any point on the membrane, two in-plane extensional tensions $T_{\alpha }$ and $T_{\varphi }$ and an in-plane shear tension $S_{\text{m}}$ (Fig. 15). The maximum extensional tension occurs on the central strip C₀, where shear within the membrane is also zero.

Fig. 14

An ellipsoidal model of RBC tank-treading in a pure shear flow with corresponding external shear rate, velocity, and pressure, having internal velocity and pressure denoted as u_i and p_i

Fig. 15

One in-plane shear stress and two in-plane extensional stresses acting on a massless elemental cell membrane

Embedded in this analytical solution is the internal cytoplasmic overpressure $\left( {\Delta P} \right)$ that is solved using a Kelvin–Vogt viscoelastic model for the RBC membrane. Because the mathematics of the solution is extensive, readers are referred to the original article for details (Tran-Son-Tay et al. 1987).

This model involves more variables than the extensional flow model of Sect. 7.2.1, but is still reduced compared to the full set of Eq. (63). Neglecting inertial flow eliminates the fluid densities, and hemoglobin and pore formation are not involved in this step. Cell orientation, shape, and motion are prescribed based on previous experiments. The solution for internal pressure involves the membrane shear modulus $\mu_{\text{s}}$ and the shear viscosity $\eta_{\text{s}}$, but the membrane edge tension and area viscosity are not used. However, on the central strip $c_{0}$, where maximum tension is located, the viscous effect vanishes due to symmetry. The external fluid stress is represented by the external viscosity and the shear rate $\dot{\gamma }$. Thus, the relationship between dependent and independent variables reduces to

$$\left\{ {T,\sigma_{\text{in}} } \right\} = f\left( {a_{0} ,\mu_{\text{ex}} ,\mu_{\text{in}} ,\mu_{\text{s}} ,\dot{\gamma }} \right)$$

(66)

where one unstressed cell dimension is retained to represent different cell sizes. (Tran-Son-Tay et al. (1987) calculated the results for two sizes characterizing young and old cells.) With three independent units, this relationship can be nondimensionalized, for instance, as

$$\left( {\frac{T}{{a_{0} \mu_{\text{ex}} \dot{\gamma }}},\frac{{\sigma_{\text{in}} }}{{a_{0}^{2} \mu_{\text{ex}} \dot{\gamma }}}} \right) = f^{*} \left( {\frac{{\mu_{\text{in}} }}{{\mu_{\text{ex}} }},\frac{{\mu_{\text{s}} }}{{a_{0} \mu_{\text{ex}} \dot{\gamma }}}} \right)$$

(67)

Five independent variables have been reduced to two, for a substantially reduced investigative effort to explore this model. A caution, however, is that the prescribed cell shapes and motion for this model were derived from limited ranges of variables.

7.2.3 Modeling membrane tension in turbulent flow

Because of the chaotic nature of turbulence, there is not a consensus on the fluid stress that is applied to the red cell, even in simple turbulent flows. Therefore, this section will discuss models for the relevant fluid stress, as well as those for the membrane tension that results.

First, Quinlan and Dooley (2007) recognized that the distribution of turbulent energy across the spectrum from microscopic to macroscopic length scales may impact the characteristic fluid stress that can be used to scale hemolysis. They used order of magnitude estimates to approximate the shear stress (1) on a cell with a uniform, oscillating velocity field surrounding it, and (2) on a cell sheared inside a rotating turbulent eddy. In both cases, the flow near the cell was considered laminar due to the small spatial scale, even though the global Reynolds number is turbulent. Because the stress for the first case was about an order of magnitude smaller than for the second case across the spectrum of frequencies relevant to the experimental data to which they were applied (Liu et al. 2000), and the same data will be used here, this case will not be further analyzed. From the second case, they concluded that Reynolds stress is at least an order of magnitude higher than the shear stress experienced by the cell.

Expanding their previous model, Dooley and Quinlan (2009) used the immersed boundary method to investigate the interaction of an isolated, tank-treading, 2D circular cell with flexible and deformable membrane with idealized 2D turbulent eddies of varying sizes from 4 to 40 µm. They used an elastic circle as a 2-D model of the red cell and adopted the constitutive equation by Hochmuth and Waugh (1987) to model the cell membrane tension. They found peak membrane tension nearly identical to the 3D model of Tran-Son-Tay et al. (1987), which validates its use for comparisons here. They concluded that the RBC damage is independent of the Kolmogorov scale, suggesting that the Kolmogorov scale may not be the most important factor for hemolysis prediction in turbulent flow. They also raised the question of whether the hypothesis of local homogenous and isotropic turbulent motion in Kolmogorov theory is valid under the typical cardiovascular blood flow that is associated with significant inhomogeneity and anisotropy.

Second, Antiga and Steinman (2009) developed scaling for the shear experienced by cells in adjacent 100-μm-diameter corotating eddies separated by a distance estimated from the packing density of aligned prolate ellipsoidal cells at a physiologic hematocrit of 45%. Applying the model to the data of Liu et al. (2000), a viscous shear stress of around 160 dyn/cm² was estimated to be applied on the cell, which is larger than the 60 dyn/cm² found by Dooley and Quinlan (2009) for a cell inside a Kolmogorov-size eddy and smaller than the 520 dyn/cm² Reynolds stress.

In a computational analysis, total surface area (or total volume) of all the turbulent eddies of critical size (up to 10 µm) was correlated with hemolysis measured in Couette and capillary tube viscometers (Ozturk et al. 2015). Results suggested that Kolmogorov scale smaller than the RBC size promotes cell damage.

7.3 Comparison of membrane tension for the same scalar stress and the same energy dissipation rate

Faghih and Sharp (2018a) compared the cell membrane tension for the same value of scalar stress reported by Liu et al. (2000) for turbulence downstream of prosthetic valve in the following cases: (a) laminar shear, (b) laminar extension, (c) turbulent shear with the cell tank-treading inside an eddy, (d) turbulent shear with the cell between two corotating eddies, and (e) turbulent extension with the cell is between two counter-rotating eddies (Fig. 16).

Fig. 16

Different encounters of a cell with turbulent eddies, (I) a cell rotating inside an eddy; (II) a cell tank-treading between two corotating eddies, and (III) a cell stretching between two counter-rotating eddies

For the shear cases, they used the membrane tension model proposed by Tran-Son-Tay et al. (1987), while for extensional cases, model by Chen and Sharp (2011) was adopted for estimation of membrane tension. The calculations were carried out for both eddies of highest energy content and for Kolmogorov eddies. The resulting membrane tensions varied by more than two orders of magnitude among the different cases, concluding that scalar stress may not be a good predictor of hemolysis. The large eddies of highest energy content produced the greatest membrane tension (for cells sheared between corotating eddies), as well as the longest exposure time.

The same order of magnitude estimate as above was also done by Faghih and Sharp (2018b) for the same dissipation rate. In addition to the five cases, they also added the recent model by Morshed et al. (2014) in order to find out whether the same viscous dissipation rate would cause almost the same membrane tension for the different cases. The results of membrane tension for the same dissipation rate also show a variation of around two orders of magnitude among the studied cases (Fig. 17). Therefore, it was concluded that neither the viscous energy dissipation rate nor the scalar stress has proven to be universal scaling parameters for prediction of mechanical hemolysis.

Fig. 17

Comparison of RMS value of membrane tension obtained based on the same scalar stress versus the same energy dissipation rate

8 Conclusions

Cells traveling in either physiologic pathways or mechanical devices experience a wide range of stresses (Fig. 3), yet hemolysis modeling efforts have focused largely on laminar shear stress. Further, validation data for simple flows at hemolytic levels of fluid stresses are available only for laminar shear. To accomplish a truly universal hemolysis prediction model, more accurate representations are needed of the responses of cells to the full range of flows that can be encountered in cardiovascular devices, and new experiments are needed to validate the models.

For laminar shear stress, a number of measurements of hemolysis at physiologic hematocrits have been made that provide validation data for hemolysis prediction. Real-time microscopic observations of cell motion have also been accomplished, but not for physiologic hematocrit and internal/external viscosity ratio, nor for shear and exposure time that produce membrane lysis. Therefore, in spite of the relative wealth of information for this flow type compared to others, important fundamental information is lacking.

For laminar extensional flow, no experimental hemolysis results exist (in terms of increase in PfHb in pure extensional flow), and images of red cell have only been captured for limited hematocrit and fluid extensional stress (Sousa et al. 2011; Yaginuma et al. 2013). Cell motion under these conditions is very different from shear flow, leading to the expectation that hemolysis scales differently, as well. Cell images and hemolysis measurements at hemolytic levels of laminar extensional stress are needed for all types of hemolysis prediction methods.

Similar results are needed for combined shear and extensional flow (Zeng and Ristenpart 2014a), which compounds the challenge of modeling. Such information may be particularly helpful in developing better alternatives to scalar stress and energy dissipation for continuum-based models.

For turbulent flow, distinctions between the effects of shear and extensional fluid stresses have not been explored experimentally. Observation of cells in real time has only been accomplished at low Reynolds number (Shakeri et al. 2012). Hypotheses have been forwarded for the stresses that are exerted on cells that arise from the fluctuating component of velocity, as well as for the resulting cell motion and deformation, but none have been validated. Important information might be gained from such experiments, since hemolysis results differ in uniform shear, orifice flow, venturi flow, and pipe flow at the same energy dissipation rate, suggesting that cells respond differently to turbulent shear and extensional stresses (Bluestein and Mockros 1969).

While this review has focused on the earlier steps leading to cell deformation, modeling of poration, rupture, and hemoglobin release are also essential components of hemolysis prediction. These processes may depend on the type of flow. For instance, membrane strain is periodic in shear flow, but steady in extensional flow. Fatigue may also be a factor in membrane failure.

The mechanisms by which hemoglobin is transferred out of the cell also need more thorough investigation. Hemoglobin may be driven from the cell by either a concentration difference or a pressure difference across the cell membrane. Recent microscale models have employed empirical mass transport based on concentration difference (Vitale et al. 2014) or diffusive transport only (Sohrabi and Liu 2017). Pressure-driven advection, which typically causes greater transport for large molecules with low diffusivity, may be important and may vary according to the type of fluid stress applied to the cell. Considering the difficulty of measuring the pressure inside a moving cell and the flow of hemoglobin through the membrane, computational models may be an effective means of comparing these transport mechanisms.