1 Introduction

Wave dissipation over fluid mud is widespread in a number of coastal regions including coastal waters of Surinam, Guyana coast, Kumamoto Port at the Ariake Sea of Japan, coast of Kerala in India, Cassino Beach in Brazil, and the northwest part of the Persian Gulf in Iran. The wave dissipation due to fluid mud depends on the rheological behavior of mud, wave characteristics, water depth, and mud thickness. Although the characteristics of the irregular waves can be influenced by the presence of a mud layer, there are only a limited number of experimental and numerical studies on irregular wave transformation over muddy beds (e.g., Zhao and Li 1994; Zhang and Zhao 1999; Soltanpour et al. 2007; Niu and Yu 2008; de Boer et al. 2009).

One of the earliest field measurements on muddy coasts was reported by Tubman and Suhayda (1976) in the east bay of Louisiana. The energy lost to the bottom by the waves at their field site was found to be at least an order of magnitude greater than that resulting from the processes of percolation or that caused by normal frictional effects. Another early effort was made by Wells and Kemp (1986) who measured wave spectra at three stations at 21.1, 11.7, and 4.3 km offshore of Surinam. They reported 88 % wave energy dissipation over a distance of about 9.4 km onshore and 96 % dissipation at the most nearshore station. Investigating the dynamics of mudbanks of the southwest coast of India, Mathew et al. (1995) indicated 95 % wave energy attenuation onshore from the 5-m isobath off the coast of Kerala. Sheremet and Stone (2003) observed significantly smaller wave heights at a muddy station, compared with another station covered with sand, in the Gulf of Mexico considering the same incident wave condition at two stations. They reported that wave damping occurred throughout the entire wave spectra. Sheremet et al. (2005) stressed the possible effect of nonlinear wave–wave interactions on wave–mud interaction. The dissipation rate function was presented by Elgar and Raubenheimer (2008) through field measurements at 5- and 2-m water depths across the muddy continental shelf of Louisiana. Rogers and Holland (2009) studied the impact of mud seafloor on the wave climate at Cassino Beach, Brazil, and deduced considerable wave dissipation by the nonrigid bed. The inverse spectral modeling was used to extract unknown mud parameters. Safak et al. (2013) showed by wave and boundary layer modeling that mud dissipation is maximum during the hindered settling of fluid mud after a storm. Their modeling results were compared with the obtained wave measurements in the central Chenier Plain coast, western Louisiana shelf, USA.

Zhang and Zhao (1999) investigated regular and irregular wave–mud interaction in a wave flume and used natural dredged soil as mud layer. The laboratory results were compared with a multi-layered model similar to the numerical model of Maa and Mehta (1990). De Boer et al. (2009) performed some experiments in a flume in order to investigate regular and irregular wave damping due to the presence of a 10-m-long fluid mud patch with a thickness of 20 cm. Their experimental results were used to test the validity of the dispersion relation of Kranenburg (2008). Although the dissipation rates of wave spectra were investigated in these studies, the effects of applying different incident wave spectra and the continuous changes of the shapes of wave spectra along the mud layer were not investigated.

The existence of steady current also affects wave–mud interaction. An and Shibayama (1994) performed a series of wave flume experiments for regular wave–current–mud interaction. Their results indicated higher rates of wave dissipation and mud mass transport due to the existence of opposing currents, where the process was attributed to the change of water pressure gradient at the water–mud interface. In their numerical treatment, the deformation of waves due to currents is modeled and the deformed wave was applied on fluid mud layer and the linearized Navier–Stokes equations for a system of water layer, and fluid mud sub-layers were solved. Including a uniform current in the water layer, Nakano (1994) also solved Navier–Stokes equations for the water layer and fluid mud sub-layers assuming a simple Newtonian viscous behavior for fluid mud. Another study by De Wit and Kranenburg (1996) offered both theoretical and experimental investigations of wave dissipation on fluid mud layer using two artificial muds. A net flow was also generated in the wave–current flume over mud layer. Modifying the Gade (1958) model, they obtained a good agreement between the calculated wave attenuation rates and wave-induced velocities and measurements. Zhao et al. (2006) proposed an eddy viscosity model for wave and current in order to close the equations of wave motion or of current motion in a combined flow, respectively.

Soltanpour et al. (2008) proposed an integrated wave–mud–current interaction model to simulate energy dissipation of traveling waves over nonrigid muddy beds and mud mass transport in the presence of current. Assuming the viscoplastic rheological behavior for mud layer, they compared the results of their numerical model with the laboratory data of An and Shibayama (1994), showing a good agreement. Kaihatu and Tahvildari (2012) developed a phase-resolving nonlinear frequency domain model with both wave–current interaction and viscous mud-induced energy dissipation. The dissipation of the random waves was enhanced by opposing currents and reduced by following currents in the numerical model. Comparisons of the modeled dissipation rates to laboratory works of An and Shibayama (1994) and Zhao et al. (2006) were also presented.

The present study investigates the wave transformation and attenuation along soft mud layers as one of the major components of irregular wave–mud interaction through a large series of wave flume laboratory experiments with different incident wave spectra. The wave height attenuation and the changes of wave spectral shape along fluid mud layer were studied. Another series of wave flume tests was employed to investigate the effect of following and opposing currents on regular and irregular wave propagation over muddy beds. Three different wave spectra are adopted in this study to investigate irregular wave–mud and wave–current–mud interactions in wave flume experiments, namely, JONSWAP—the Joint North Sea Wave Project by Hasselmann et al. (1973); Pierson and Moskowitz (1964); and Neumann (1953). The effect of bandwidth on wave attenuation is studied here by comparing the laboratory results of energy dissipation of different wave spectra.

2 Wave–current–mud interaction

Wave–current interaction is a complex phenomenon in coastal and estuarine waters. In a simple treatment, Bretherton and Garrett (1968) simplified the wave–current interaction by applying the wave action equation (i.e., wave energy density/wave frequency relative to the current).

$$ {\left(\omega -kU\right)}^2-gk\kern.2em \tanh \kern.2em kd=0 $$
(1)

where ω is the angular frequency, U is the mean depth-averaged current velocity, k is the wave number, d is the water depth, and g is the acceleration due to gravity. In order to define the constant value, the reference level is specified as the no-current condition.

The more complicated irregular wave–current interaction has also been studied (e.g., Tayfun et al. 1976, Hedges et al. 1985). Here, the changes in deformed wave spectrum are obtained based on the simple equation proposed by Huang et al. (1972). Considering the wave action as

$$ \frac{\partial }{\partial x}\left[\frac{E\left({C}_{gr}+U\right)}{\omega_r}\right]= 0 $$
(2)

where ω r is the angular wave frequency in the frame of reference moving with current (intrinsic angular wave frequency). After the current action, Eq. (2) can be rewritten as

$$ \frac{E\left({C}_{gr}+U\right)}{\omega_r}=\frac{E_0{C}_{g0}}{\omega_a} $$
(3)

where the subscript “0” refers to no current condition and ω a is the angular wave frequency in the stationary frame of reference (apparent angular wave frequency). The group velocities are defined by the linear wave theory as

$$ {C}_{g0}=\frac{1}{2}\left(1+\frac{2{k}_0d}{ \sinh \kern.2em 2{k}_0d}\right)\frac{\omega_a}{k_0} $$
(4)
$$ {C}_{gr}=\frac{1}{2}\left(1+\frac{2kd}{ \sinh \kern.2em 2kd}\right)\frac{\omega_r}{k} $$
(5)

Inasmuch as the value of ω a of each component will remain constant from no-current to current condition, the spectral density in this transition condition can be written as follows:

$$ \frac{S_{\eta \eta}\left({\omega}_a,U\right)}{S_{\eta \eta}\left({\omega}_a\right)}=\frac{S_{\eta \eta}\left({\omega}_a,U\right)d{\omega}_a}{S_{\eta \eta}\left({\omega}_a\right)d{\omega}_a}=\frac{E}{E_0}=\frac{\omega_r\left[1+\left(\frac{2{k}_0d}{ \sinh \kern.2em 2{k}_0d}\right)\right]}{2{k}_0\left\{U+\left[1+\left(\frac{2kd}{ \sinh \kern.2em 2kd}\right)\right]\frac{\omega_r}{2k}\right\}} $$
(6)

Assuming that the waves are not refracted by current and the water depth is sufficiently deep, the deformed spectrum can be defined as (Huang et al. 1972):

$$ \frac{S_{\eta \eta}\left({\omega}_a,U\right)}{S_{\eta \eta}\left({\omega}_a\right)}=\frac{\omega_r^2}{\omega_a^2}\frac{1}{\left(1+\frac{2U{\omega}_r}{g}\right)}=\frac{1}{{\left(1+\frac{U{\omega}_r}{g}\right)}^2\left(1+\frac{2U{\omega}_r}{g}\right)} $$
(7)
$$ =\frac{4}{{\left[1+{\left(1+\frac{4U{\omega}_a}{g}\right)}^{1/2}\right]}^2{\left(1+\frac{4U{\omega}_a}{g}\right)}^{1/2}} $$

The interactive effects of wave–current field on muddy beds are of considerable practical interests. In this study, it is assumed that the wave attenuation process will take place after regular/irregular waves are deformed due to the currents. This assumption has been already justified by the laboratory experiments of Otsubo and Muraoka (1986) and An and Shibayama (1994) under regular wave. They observed that when currents flow over a fluid mud bed, sediments are transported only in the water layer by the current if they are suspended or if the bed surface is massively destroyed. There was no mass transport due to the current action without wave.

The current is included to obtain the changed regular wave height following Thomas (1981). In the case of an irregular wave, the deformed wave spectrum due to current action is calculated based on Huang et al. (1972). Following the numerical model of An and Shibayama (1994), the dissipation of regular waves and the attenuated wave spectra at different sections along the fluid mud layer are modeled using the extended numerical model of Soltanpour et al. (2007) in the presence of currents.

3 Methods

3.1 Numerical model

The extended multi-layered numerical model of Soltanpour et al. (2007) is used for simulating wave–fluid mud interaction and the calculation of attenuation of both regular waves and harmonic components of spectral waves. The governing equations for the system of water and fluid mud sub-layers are the linearized Navier–Stokes equations, neglecting the convective accelerations, and the continuity equation. Considering the boundary conditions and using the periodic solutions for particle velocities, the wave attenuation coefficient for each wave component, k i

$$ a(x)={a}_0 \exp \left(-{k}_ix\right) $$
(8)

is computed. The details of the wave–mud interaction model have been provided by Soltanpour et al. (2007).

The spectral wave is presented as superposition of many simple, regular harmonic wave components having their own amplitudes and periods using the Fourier theory. The modeled wave spectra can be determined as

$$ {\widehat{S}}_x\left({f}_n\right)={\widehat{S}}_0\left({f}_n\right) \exp \left(-2{k}_{in}x\right) $$
(9)

where Ŝ x (f n ) is the modeling spectra at point x, Ŝ(f n ) is the average wave spectra at x = 0 in the range of (f n , f n  + Δf), and f n and k in are the frequency and wave attenuation coefficient for each wave component, respectively. Choosing Δf is crucial in this method where larger values result in a smaller number of regular waves with higher wave heights. This will highly affect the results of simulations depending on the adopted rheological model.

The effect of the current is also included in the numerical model to obtain the changed regular wave height following Thomas (1981). In the case of a spectral wave, the deformed wave spectrum due to the current is calculated based on Huang et al. (1972).

3.2 Laboratory experiments

Two series of wave flume laboratory experiments on commercial kaolinite were conducted in order to investigate irregular wave–mud and also wave–current–mud interactions. Two types of kaolinite (K and J) were used in these experiments. Table 1 shows the characteristics of used kaolinite.

Table 1 Characteristics of used commercial kaolinite
Full size table

The rheological parameters of oscillatory tests better represent the wave–mud interaction because of the oscillatory nature of the waves, although for some other cases, such as gravitational flow of fluid mud over a mild slope, rotary tests are more relevant. Here, the rheological parameters of the adopted viscoelastic rheological model of fluid mud, i.e., viscosity μ and elastic modulus G of used kaolinite K and kaolinite J, were adopted from the oscillatory tests of Soltanpour and Samsami (2011), where they studied different rheological models and their performances for the application in modeling of wave dissipation. No sensitivity test was conducted on the viscosity and elasticity modulus because of extracting of these rheological parameters out of direct laboratory tests.

3.2.1 Wave–mud interaction

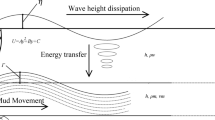
In order to investigate the propagation of irregular waves over fluid mud layers, the first series of experiments were carried out in the wave flume of the Hydraulic Model Laboratory of the Department of Civil Engineering at K. N. Toosi University of Technology. The glass-sided tilting flume with a stainless steel bed has a cross section of 30 cm wide by 45 cm deep and a working length of 12.5 m. The total length of flume including inlet and outlet tanks is 15.75 m. Two false beds were placed in the flume to confine the beginning and the end of the mud section. The well mixture of commercial kaolinite (kaolinite K) with tap water was used as muddy bed. Figure 1a shows a schematic diagram of the experimental setup. The waves were generated by a flap-type wave maker (the paddle is hinged at the bottom of the flume). Different wave heights and periods can be generated by the forward and/or backward movements of the flap as a function of the stroke and speed of the actuator. In order to avoid sudden jumps in the paddle position on starting/stopping, the ramp up/down time for the wave maker is about 25 s. Eight conductive wave gauges at every 1.2 m were simultaneously employed to measure rapid changes of surface water levels along the wave flume.

Fig. 1
figure 1

Sketch of the wave flume experimental setup: a the first series of experiments at K. N. Toosi University of Technology and b the second series of experiments at Waseda University (dimensions in m)

Full size image

Using a wave generation control program to generate irregular waves, three various wave spectra of Pierson-Moskowitz, JONSWAP, and Neumann with different significant wave heights and frequencies were employed. Random waves of JONSWAP and Pierson-Moskowitz wave spectra can be directly produced by the wave maker. Input parameters are directional spreading functions (including cos2 θ, cos6 θ, cosn θ, Mitsuyasu, exponential), modal period, significant wave height, and spectral shape for JONSWAP spectra and directional spreading functions, and modal period for Pierson-Moskowitz spectra. Neumann spectra were defined based on the peak frequency. The value of spectral shape, γ, was set as 3.3 in JONSWAP spectra.

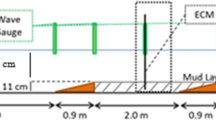
Three water depths were selected above the muddy bed (i.e., 10, 15, and 20 cm), and the thickness of the mud was kept at 10 cm in all runs. Totally, 140 wave cases were conducted. Incident wave conditions for Pierson-Moskowitz (PT), JONSWAP (JT), and Neumann (NT) test cases at the water depth of 15, 20, and 25 cm are listed in Table 2.

Table 2 Incident wave conditions measured at gauge No. 1 of the first series of laboratory experiments
Full size table

3.2.2 Wave–current–mud interaction

The second series of laboratory experiments were carried out in the wave flume of the Coastal Engineering Laboratory of the Department of Civil and Environmental Engineering at Waseda University, Japan, measured 40.5 cm wide by 60 cm deep in cross section and 13.8 m in length. The well mixture of commercial kaolinite (kaolinite J) with tap water was used as fluid mud bed at the 2-m-long mud section with a thickness of 10 cm in the flume. Regular monochromatic waves and irregular waves with JONSWAP spectra were produced by a flap-type wave generator installed at the beginning of the flume. Wave heights were recorded by three capacitance wave gauges, where the data of gauge 2 presents the measured deformed irregular waves due to currents and gauge 3 shows the wave under effects of both current and fluid mud. A pump system was employed to generate the following and opposing currents through an inlet and outlet, located at the bottom of the flume. The current velocity was recorded by an electro-magnetic current meter at a fixed location about 12 cm above the mud layer (Fig. 1b).

Table 3 presents the measured wave characteristics, current velocities (positive and negative indicate following and opposing currents, respectively), and the values of the wave attenuation rate of the conducted test runs based on Eq. (8).

Table 3 Measured data of the second series of laboratory experiments
Full size table

4 Results and discussions

The viscoelastic rheological model was selected for the rheological behavior of the used mud layer in laboratory experiments. The input parameters of the numerical model are the amplitude and frequency of each discrete wave component of the incident wave spectrum, water depth, and mud thickness. In spite of the sensitivity of the numerical results to the rheological parameters, no calibration on viscoelastic parameters was performed.

4.1 Spectral wave–mud interaction (first series of experiments)

The wave spectra at each wave gauge along the muddy bed based on initial JONSWAP, Pierson-Moskowitz, and Neumann wave spectra were recorded, where the wave spectra at first gauge represent the initial wave conditions before the mud layer. The observations indicate that the fluid mud bed absorbs the wave energy of wave spectra resulting in the energy dissipation along the wave flume. Figure 2 presents the wave height attenuations for the three sample cases (i.e., JT4, PT9, and NT1). Despite several known issues with the data (e.g., multiple reflections of the waves, nonuniformity of the mud bed thickness, etc.) that cause the observed fluctuations, an exponential decay can be a reasonable approximation for the measured data. Similar fluctuations of measured wave heights along the mud bed have been observed in the wave flume laboratory results of other researchers (Tsuruya et al. 1987; Sakakiyama and Bijker 1988; De Boer et al. 2009).

Fig. 2
figure 2

The wave heights decay over the muddy bed (test cases JT4, PT9, and NT1)

Full size image

The effects of spectral bandwidth parameters on wave attenuation can also be investigated. Spectral parameters of waves may be expressed based on spectral shape or bandwidth (e.g., ε, υ, Q p ). These parameters can be calculated by using spectral moments which are defined as

$$ {m}_n={\displaystyle {\int}_0^{\infty }{f}^nS(f)df} $$
(10)

The zeroth order, m 0 (which is the area under the spectral curve); the first order, m 1; the second order, m 2; and the fourth order, m 4, are the most used moments for calculation of wave parameters.

Cartwright and Longuet-Higgins (1956) and Longuet-Higgins (1975) proposed the spectral bandwidth parameter, ε, and spectral width, υ, respectively. The spectral width, υ, is also called “spectral narrowness parameter” (Rye and Svee 1976). The spectral bandwidth parameter and spectral width range from 0 to 1 are defined as

$$ \varepsilon =\sqrt{1-\frac{m_2^2}{m_0{m}_4}} $$
(11)
$$ \upsilon =\sqrt{\frac{m_0{m}_2}{m_1^2}-1} $$
(12)

Due to the existence of high-order moments in the spectral bandwidth parameter ε, the use of the spectral width parameter υ is preferred. υ 2 → 0 when all wave energy is concentrated in a single frequency. On the contrary, υ 2 increases when wave energy is broadly distributed among frequencies. Another shape parameter, i.e., spectral peakedness parameter Q p , can be defined as (Goda 1970)

$$ {Q}_p=\frac{2}{m_0^2}{\displaystyle {\int}_0^{\infty }f{S}^2(f)df} $$
(13)

The values of Q p are normally more than 1.0. High values of Q p correspond to narrow band and sharply peaked spectra.

Figure 3 presents the spectral peakedness parameter, Q p , of incident waves at the first gauge for all conducted test cases at different water depths. The corresponding wave height attenuations shown on the vertical axes were extracted based on the measured waves at the beginning and the end of mud section, i.e., wave gauges No. 1 and No. 8. In spite of the discrepancy of data points, linear trend lines, representing the increase of the wave attenuation rate k i by the increase of the spectral peakedness parameter Q p , are observed in three water depths. Thus, the narrow band and sharply peaked spectra traveling over muddy beds show higher energy dissipation rates. This can be attributed to the frequency dependency of wave energy dissipation on the mud layer. A nonlinear wave interaction might also be responsible as another possible mechanism, as hypothesized by Sheremet et al. (2005). It may also result in a shift in the peak frequency of a wave spectrum traveling on real muddy coasts. However, this shift was not observed on the short mud section of this experimental study.

Fig. 3
figure 3

Spectral peakedness parameter versus wave height attenuation coefficient at different water depths

Full size image

It was expected that the trend line of h = 15 cm shows the highest slope, compared to the other two water depths of 20 and 25 cm, as the wave attenuation rate generally increases by the decrease of water depth. However, considering that similar input waves were applied for the three water depths, the occurred wave breaking of higher incident irregular waves at 15-cm water depth resulted to lower wave heights in this case at gauge No.1.

Figure 4 shows the comparisons between the spectral width, υ, at the end and the beginning of the mud section for all test cases. The slight increase of the spectral width parameter along the muddy bed can be related to different energy dissipation rates of irregular wave components, which results in the unbalanced changes of spectral moments m 0, m 1, and m 2. However, it is observed that the spectral width along the soft mud section does not significantly change with wave characteristics or water depth.

Fig. 4
figure 4

Spectral width at gauge No. 1 versus gauge No. 8 at different water depths

Full size image

Figures 5, 6, and 7 show comparisons of measured and simulated wave spectra along the wave flume for the three sample cases of JT4, PT9, and NT1, respectively, where the wave spectra at first gauge represent the initial wave conditions before the mud layer. The observations reveal the reduction of wave energy on the muddy bed along the wave flume. The observed discrepancies between the model results and data are due to the uncontrolled fluctuations of the measured wave heights along the wave flume, as mentioned before. The small reflected wave from the absorber at the end of the flume, which is reflected again by the wave paddle, will end up to the generation of a standing long wave in the flume affecting the traveling wave. The uneven mud bed due the wave action, which results in the local change of dissipation rate because of the changes of fluid mud thickness and water depth, also seems to be partially responsible for these fluctuations.

Fig. 5
figure 5

Comparisons of measured and simulated wave spectra (test case JT4)

Full size image
Fig. 6
figure 6

Comparisons of measured and simulated wave spectra (test case PT9)

Full size image
Fig. 7
figure 7

Comparisons of measured and simulated wave spectra (test case NT1)

Full size image

It should be noted that some data show the appearance of what looks like a second harmonic of the spectral peak. This can be due to either the undesirable laboratory conditions such as the small vibrations of wave gauges or the nonlinear effects which cannot be captured by our linear wave–mud interaction model.

The quantitative comparisons between measured and calculated results for the aforementioned test cases are listed in Table 4. The relative error is also listed in the table. Figure 8 shows the comparisons between the computed and measured representative wave heights. In spite of slight overall underestimation of simulated wave heights, the accuracy of predicting the attenuated irregular waves is acceptable.

Table 4 Measured and calculated representative wave parameters (JT4, PT9, and NT1)
Full size table
Fig. 8
figure 8

Comparisons between spectral measured and computed wave heights at all gauges of the first series of experiments

Full size image

4.2 Irregular wave–current–mud interaction (second series of experiments)

Figure 9 shows the measured regular wave and JONSWAP wave spectrum in gauge No. 2 with following and opposing currents. The obtained spectral shapes are not fully developed because of the short duration of the experiments (about 60–90 s). The necessary time to generate a full spectrum depends on the type of the wave spectrum and also the wave characteristics. Applying the same input incident wave in all three conditions (i.e., opposing, following, and no currents), it is observed that the wave energy increases due to opposing currents and decreases in the case of following currents. It should be added that choosing the same initial input parameters will not result in the completely similar generated wave spectra because of the limitations of the flap-type wave maker. Therefore, the incident regular/irregular waves of each set of laboratory runs (i.e., three cases of opposing, following, and no-current conditions) are not exactly similar.

Fig. 9
figure 9

Measured waves in gauge No. 2 with opposing, following, and no-current conditions (second series of experiments)

Full size image

A sample of measured wave spectra at gauge 2 (beginning of the mud section) and gauge 3 (the attenuated wave height) is illustrated in Fig. 10. The difference of the wave spectra at these two gauges is small because of their short distance, due to a relatively small mud section. However, the data of wave attenuation rates in Table 3 reveal that the highest and lowest dissipation of wave heights occurs in the opposing and following currents, respectively.

Fig. 10
figure 10

Measured wave spectra at gauges No. 2 and No. 3 with opposing (JTN1 and JTN4) and following currents (JTN3 and JTN6)

Full size image

Using the discretization method, the wave spectral deformation due to current effect is calculated based on the theory of Huang et al. (1972). Comparisons of measured wave spectra (in gauge 2) and calculated wave spectra are shown in Fig. 11. The observed discrepancy between the simulated and measured wave spectra is mainly due to slight differences in applied waves as it is not possible to exactly repeat the same incident wave characteristics for the corresponding three test cases of opposing, following, and no current by the flap-type wave maker. Calculating the representative waves of the measured and calculated wave spectra due to opposing and following currents at gauge 2, Table 5 shows the quantitative comparisons of the corresponding representative waves. Similarly, the wave characteristics with the no-current condition were assumed as the incident wave. The comparisons of regular waves are also presented in Table 5.

Fig. 11
figure 11

Comparisons of calculated and measured wave spectra (at gauge 2) with following and opposing currents

Full size image
Table 5 Comparisons of measured and calculated representative waves at gauge 2 (second set of experiments)
Full size table

Similar to the first set of laboratory experiments, the spectral wave transformation was used to calculate the attenuated wave spectra using the deformed wave spectra at the beginning of the mud section. Figure 12 shows the comparisons between the measured and modeled wave spectra at gauge 3. The selected values of Δf in the discretization method affect the shape of wave spectra. Choosing the value of Δf = 0.078 Hz in this series of experiments has resulted to smooth modeling wave spectra here. The representative wave parameters obtained from the attenuated spectra are also compared to measured data and listed in Table 6. The comparisons indicate that the attenuated wave height can be predicted by the model.

Fig. 12
figure 12

Comparison of measured and modeled wave spectra on the muddy bed (at gauge 3)

Full size image
Table 6 Comparison of measured and modeled representative wave heights on the muddy bed (second set of laboratory experiments)
Full size table

5 Summary and conclusion

The spectral evolution of irregular waves propagating over a muddy bed is studied in two series of wave flume experiments with and without currents. The laboratory experiments showed that the representative wave heights follow a nearly exponential decay pattern over the muddy bed. The measurements of wave spectra along the mud layer show that there is no significant change or shift in peak frequencies due to propagation of irregular waves over the muddy bed. The study on the spectral bandwidth shows that higher values of spectral peakedness parameters, which correspond to narrow band or sharply peaked wave spectra, generally result in higher wave height attenuation rates.

The extended multi-layered numerical model of Soltanpour et al. (2007) was also verified using the new data set of irregular waves. Comparisons between the measured and simulated waves confirmed the earlier studies that wave spectral modeling can be employed to predict the irregular wave height decay on the fluid mud layer.

The wave–current–mud interaction was studied by simple models of wave deformation due to currents. The second series of experimental investigation was conducted to find out the irregular and regular wave–mud interaction with opposing and following currents. It was concluded that in general, the wave dissipation increases due to opposing currents and it decreases in the case of following currents.

The numerical model of Soltanpour et al. (2007) was extended for the simulation of irregular wave–mud–current interaction by taking the spectral wave deformation into consideration. To simulate the wave–current–mud interaction, it was assumed that the dynamic pressure of wave propagation on the mud surface is more important than the shear stress at the interface between the water layer and mud layer. This assumption means that the mud bed responds only to the deformed wave resulting in the wave–current interaction. In a mathematical formulation, the irregular wave attenuation process takes place after the deformation of wave. The wave spectrum is deformed first due to current action, and the deformed spectral wave is then applied on the fluid mud layer.

However, in spite of the capability of the model to predict the energy dissipation on the mud layer, it should be added that natural phenomena have been treated in a simplified manner in the present study and there are many imperfections in the numerical model. In addition to the general simplifications of applying linear wave theory, the assumption of linear superposition of regular wave components in the wave spectra is a simplified approach in modeling of the transformation of actual wave spectra on the mud layer. Moreover, modeling of the wave–mud–current interaction was reduced to the action of current on the wave and the interaction of deformed wave with mud. Further theoretical and numerical studies are necessary to include more realistic formulations for spectral wave transformation on muddy beds and a full wave–current–mud interaction.