Rough filters based on residuated lattices

Abstract

The paper is devoted to introduce the notion of rough sets within the context of residuated lattices. By considering the notion of a residuated lattice, we concern a relationship between rough sets theory and residuated lattices theory. We shall introduce the notion of rough subalgebra (resp. filter) with respect to a filter of a residuated lattice, which is an extended notion of subalgebra (resp. filter) in a residuated lattice and investigate some of their properties.

1 Introduction

Formal concept analysis (FCA) and rough set theory (RST), introduced in the early 1980s by Wille [47] and Pawlak [35], respectively, have become today leading theories of knowledge acquisition from data tables. This fact has resulted in a rapid growth of interest in their formal relationships and possible unifications. Generally, both theories are based on Galois connections and cluster data into coherent and meaningful entities called concepts. Both the theory of formal concept analysis (FCA) and that of rough set (RST) are useful tools for qualitative data analysis.

The theory of rough set was introduced as a tool for dealing with granularity in knowledge. It has found practical applications in many areas such as knowledge discovery, machine learning, data analysis, approximate classification, conflict analysis. Rough set theory is an extension of set theory. In the theory of rough set, it is important to construct a pair of upper and lower approximation operators based on available information. The Pawlak approximation operators are defined by an equivalence relation. The equivalence classes are the building blocks for the construction of the lower and upper approximations.

Some researches studied algebraic properties of rough sets. Iwinski [26] suggested a lattice theoretic approach to rough set. Bonikowaski [4] and Bonikowaski et al. [5] studied some algebraic and set-theoretical properties of rough sets. Pomykala [36] showed that the set of rough sets forms a Stone algebra. A natural question is what will happen if we substitute an algebraic system instead of the universe set. Biswas and Nanda [2] applied the notion of rough sets to algebra and introduced the notion of rough subgroups. Kuroki and Wang [30] gave some properties of the lower and upper approximations with respect to the normal subgroups. Kuroki [31] introduced the notion of a rough ideal in a semigroup. Davvaz [9] studied the properties of rough subring with respect to ideals of ring. Rough modules [10] have been investigated by Davvaz and Mahdavipour. Rasouli and Davvaz [38] introduced and studied the notion of rough ideals in an MV algebra. Fuzzy rough sets were defined by Dubois and Prade [14]. Yao [50] introduced the concept of generalized rough sets based on relations. Feng et al. proposed another type of rough sets, in which lower and upper approximations of a subset are obtained with the help of soft sets [18], also see [11, 25, 32, 39, 44, 48, 49].

It is well known that certain information processing, especially inferences based on certain information, is based on the classical logic (classical two-valued logic). Naturally, it is necessary to establish some rational logic systems as the logical foundation for uncertain information processing. For this reason, various kinds of non-classical logic systems have been extensively proposed and researched. In fact, non-classical logic has become a formal and useful tool for computer science to deal with uncertain information and fuzzy information. On the other hand, various logical algebra have been proposed as the semantical systems of non-classical logic systems, for example, residuated lattices, MV algebras, BL algebras, G$\ddot{o}$del algebras, lattice implicational algebras, MTL algebras, NM algebras and $R_0$ algebras. Among these logical algebras, residuated lattices are very basic and important algebraic structures because the other logical algebras are all particular cases of residuated lattices.

Commutative residuated lattices are the algebraic counterpart of logics without contraction rule. The concept of commutative residuated lattice firstly introduced by W. Krull in [29] who discussed decomposition into isolated component ideals. After him, they were investigated by M. Ward and R. P. Dilworth in [46], as the main tool in the abstract study of ideal lattices in ring theory. The properties of residuated lattices were presented in [19, 20, 23, 24, 28, 34]. For a survey of residuated lattices we refer to [27].

Non-commutative residuated lattices, sometimes called pseudo-residuated lattices, biresiduated lattices or generalized residuated lattices, are the algebraic counterparts of substructural logics, i.e., logics which lack at least one of the three structural rules, namely contraction, weakening and exchange. Complete studies on non-commutative residuated lattices were developed in [1, 7, 8, 27, 41, 42]. In this paper, a residuated lattice will be a $FL_w$ algebra. We denote by ${{\mathcal {RL}}}$ the class of residuated lattices. Following the results of Blount and Tsinakis [3], we deduce that the class ${\mathcal {RL}}$ of residuated lattices is equational, hence it forms a variety. A subclass ${\mathcal {V}}$ of the variety ${\mathcal {RL}}$ which is also a variety is called a subvariety of ${\mathcal {RL}}$.

The deductive system theory of the logical algebras plays an important role in studying these algebras and the completeness of the corresponding non-classical logics. From a logical point of view, various deductive systems correspond to various sets of provable formulas. Since deductive systems correspond to subsets closed with respect to Modus Ponens, they are sometimes called (implicative) filters.

Recently, some researchers studied the rough sets in the context of logical algebras [37, 38, 43]. The filter theory of the logical algebras plays an important role in studying these algebras. From algebraic point of view, filters induced equivalence relations on logical algebras. Therefore, in the paper we study approximation spaces in residuated lattices based on their filters.

This paper is organized in five sections. In Sect. 2 we recall some definitions, properties and results relative to residuated lattices and give some examples of residuated lattices which will be used in the following sections of the paper. In Sect. 3, we introduce the notion of rough approximation sets based on residuated lattices and give some examples of them. We study them under co-annihilators, homomorphisms and quotients. In Sect. 4 we introduce the notion of rough subalgebra (resp. filter) with respect to a filter of a residuated lattice, which is an extended the notion of subalgebra (resp. filter) in a residuated lattice and investigate some of their properties. Section 5 is the conclusion.

2 A brief excursion into residuated lattices

In this section we recall some definitions, properties and results relative to residuated lattices, which will be used in the following sections of the paper.

Definition 2.1

[27] A residuated lattice is an algebra ${\mathfrak {A}}=(A;\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,1)$ of type (2, 2, 2, 2, 2, 0) satisfying the following conditions:

• $(A;\vee ,\wedge )$ is a lattice.

• $(A;\odot ,1)$ is a monoid.

• $x\odot y\le z$ iff $x\le y\rightarrow _l z$ iff $y\le x\rightarrow _r z$ for $x,y,z\in A$.

The operations $\rightarrow _l$ and $\rightarrow _r$ are referred to as the left and right residual of $\odot$, respectively. Note that, in general, 1 is not the top element of the lattice reduct of ${\mathfrak {A}}$, $\ell ({\mathfrak {A}})$. A residuated lattice with a constant 0 (which can denote any element) is called a pointed residuated lattice or a full Lambek algebra (FLalgebra). If 1 is a top element of $\ell ({\mathfrak {A}})$, then ${\mathfrak {A}}$ is called an integral residuated lattice. A FL algebra ${\mathfrak {A}}$ in which $(A;\vee ,\wedge ,0,1)$ is a bounded lattice is called a $FL_w$algebra. A $FL_w$ algebra is sometimes called a bounded integral residuated lattice. In this paper, a residuated lattice will be a $FL_w$ algebra. A residuated lattice ${\mathfrak {A}}$ is non-trivial if and only if $0\ne 1$. A residuated lattice ${\mathfrak {A}}$ is called commutative if $\rightarrow _l=\rightarrow _r$. It is obvious that ${\mathfrak {A}}$ is a commutative residuated lattice if and only if $\odot$ is a commutative binary operation.

In a residuated lattice ${\mathfrak {A}}$, for any $a\in A$, we put $\lnot _la:=a\rightarrow _l 0$ and $\lnot _ra:=a\rightarrow _r 0$. Also, $\lnot _l\lnot _la$, $\lnot _l\lnot _ra$, $\lnot _r\lnot _la$ and $\lnot _r\lnot _ra$ are denoted by $\lnot _{ll}a$, $\lnot _{rl}a$, $\lnot _{lr}a$ and $\lnot _{rr}a$, respectively.

A residuated lattice ${\mathfrak {A}}$ is called a pseudo-MTL algebra [17] if it satisfies the pseudo-pre-linearity condition (denoted by pprel):

$$\begin{aligned} {(pprel)}\quad (x\rightarrow _l y)\vee (y\rightarrow _l x)=(x\rightarrow _r y)\vee (y\rightarrow _r x)=1. \end{aligned}$$

It is easy to see that each linearly ordered residuated lattice is a pseudo-MTL algebra. We denote by ${\mathcal {PMTL}}$ the class of pseudo-MTL algebras. Obviously, the class ${\mathcal {PMTL}}$ of pseudo-MTL algebras is equational; hence, it forms a subvariety of the variety ${\mathcal {RL}}$.

${\mathfrak {A}}$ is called a divisible pseudo-residuated lattice [15] (or a bounded R$\ell$monoid in [37]) if it satisfies the pseudo-divisibility condition (denoted by pdiv):

$$\begin{aligned} {(pdiv)}\quad x\odot (x\rightarrow _r y)=(x\rightarrow _l y)\odot x=x\wedge y. \end{aligned}$$

We denote by ${\mathcal {R}}\ell$ the class of bounded R$\ell$ monoids. Obviously, the class ${\mathcal {R}}\ell$ of bounded R$\ell$ monoids is equational, hence it forms a subvariety of the variety ${\mathcal {RL}}$. A residuated lattice ${\mathfrak {A}}$ in which $x\odot y=x\wedge y$ (or equivalently, $x^2=x$) for all $x,y\in A$ is called a Heyting algebra or pseudo-Boolean algebra [45]. A Heyting algebra is a particular case of divisible commutative residuated lattice.

${\mathfrak {A}}$ is called a pseudo-BL algebra [12, 22] if it satisfies both pprel and pdiv. Denote by ${\mathcal {PBL}}$ the class of pseudo-BL algebras. A residuated lattice is called proper if it is not a pseudo-MTL algebra, a bounded R$\ell$ monoid or a pseudo-BL algebra, i.e., if pprel and pdiv do not hold. A pseudo-MTL algebra is called proper if it is not a pseudo-BL algebra, i.e., if pdiv does not hold. A bounded R$\ell$ monoid is called proper if it is not a pseudo-BL algebra, i.e., if pprel does not hold. Note that ${\mathcal {PMTL}}$, ${\mathcal {R}}\ell$, ${\mathcal {PBL}}$ are all subvarieties of ${\mathcal {RL}}$, connected as next figure shows (Fig. 1).

Fig. 1

Subvarieties of $\mathcal {RL}$

An element a of a residuated lattice ${\mathfrak {A}}$ is said to be regular if and only if $\lnot _{lr}a=\lnot _{rl}a=a$. The set of all regular elements of ${\mathfrak {A}}$ is denoted by $Reg({\mathfrak {A}})$. ${\mathfrak {A}}$ is called involutive if $Reg({\mathfrak {A}})=A$.

The following proposition provides some rules of calculus in a residuated lattice (see [1, 6, 12]).

Proposition 2.1

Let ${\mathfrak {A}}$ be a residuated lattice. Then the following rules of calculus hold for any $a,b,c\in A$.

• 1. $a\rightarrow _l(b\rightarrow _l c)=(a\odot b)\rightarrow _l c$;

• 2. $a\rightarrow _r(b\rightarrow _r c)=(b\odot a)\rightarrow _r c$;

• 3. $a\le b$ if and only if $a\rightarrow _l b=1$ if and only if $a\rightarrow _r b=1$;

• 4. $a\odot b\le a\wedge b$. In particular, $a\odot b=1$ implies $a=b=1$;

• 5. $a\le b$ implies $a\odot c\le b\odot c$ and $c\odot a\le c\odot b$. In particular, $a\le b$ and $c\le d$ imply $a\odot c\le b\odot d$ and $c\odot a\le d\odot b$;

• 6. $a\rightarrow _l b\le \lnot _lb\rightarrow _r\lnot _la$, $a\rightarrow _r b\le \lnot _rb\rightarrow _l\lnot _ra$;

• 7. $\lnot _{lrl}a=\lnot _la$, $\lnot _{rlr}a=\lnot _ra$;

• 8. $(b\rightarrow _l c)\odot (a\rightarrow _l b)\le a\rightarrow _l c$, $(a\rightarrow _r b)\odot (b\rightarrow _r c)\le a\rightarrow _r c$;

• 9. $a\rightarrow _l \lnot _rb=b\rightarrow _r \lnot _la$;

• 10. $1\rightarrow _l a=1\rightarrow _r a=a$;

• 11. If $a\le b$ then $c\rightarrow _l a\le c\rightarrow _l b$ and $c\rightarrow _r a\le c\rightarrow _r b$;

• 12. If $a\le b$ then $b\rightarrow _l c\le a\rightarrow _l c$ and $b\rightarrow _r c\le a\rightarrow _r c$;

• 13. $(a\vee c)\odot (b\vee c)\le (a\odot b)\vee c$.

In the following, we give some examples of residuated lattice.

Example 2.1

Assume that R is a ring with unit and let I(R) be the collection of all ideals of R. This set, ordered by inclusion, is a lattice. The meet of two ideals is their intersection, and their join is the ideal generated by the union. We define multiplication of two ideals I, J in the usual way

$$\begin{aligned} I\odot J:=\left\{ \sum _{x\in X,y\in Y}xy:~X,Y~\text {are finite subsets of}~I,J,~\text {respectivly}\right\} . \end{aligned}$$

Also, we put $I\rightarrow _l J:=\{k:Ik\subseteq J\}$ and $I\rightarrow _r J:=\{k:kI\subseteq J\}$. Then $(I(R);\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,0,R)$ forms a residuated lattice.

Example 2.2

[7] Let $A_5=\{0,a,b,c,1\}$ be a lattice whose Hasse diagram is below (see Fig. 2). Define $\odot$, $\rightarrow _l$ and $\rightarrow _r$ on $A_5$ as follows:

$\begin{array}{c|ccccc} \odot &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \\ \hline 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ a &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad a &{}\quad a \\ b &{}\quad 0 &{}\quad a &{}\quad b &{}\quad a &{}\quad b \\ c &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad c &{}\quad c \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \end{array}$      $\begin{array}{c|ccccc} \rightarrow _l &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad c &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad c &{}\quad c &{}\quad 1 &{}\quad c &{}\quad 1 \\ c &{}\quad 0 &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \end{array}$      $\begin{array}{c|ccccc} \rightarrow _r &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad 0 &{}\quad c &{}\quad 1 &{}\quad c &{}\quad 1 \\ c &{}\quad b &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 \end{array}$

Fig. 2

The Hasse diagram of ${\mathfrak {A}}$

Routine calculation shows that ${\mathfrak {A}}_5=(A_5;\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,0,1)$ is a proper pseudo-MTL algebra, because the property 2 does not hold:

$$\begin{aligned} c\odot (c\rightarrow _r a)=c\odot b=0\ne a=c\wedge a. \end{aligned}$$

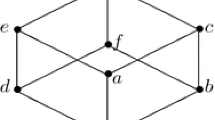
Example 2.3

[33] Let $A_7=\{0,a,b,c,d,e,1\}$ be a lattice whose Hasse diagram is below (see Fig. 3). Define $\odot$, $\rightarrow _l$ and $\rightarrow _r$ on $A_7$ as follows:

$\begin{array}{c|ccccccc} \odot &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \\ \hline 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ a &{}\quad 0 &{}\quad a &{}\quad a &{}\quad a &{}\quad a &{}\quad a &{}\quad a \\ b &{}\quad 0 &{}\quad a &{}\quad a &{}\quad a &{}\quad a &{}\quad a &{}\quad b \\ c &{}\quad 0 &{}\quad a &{}\quad a &{}\quad c &{}\quad c &{}\quad c &{}\quad c \\ d &{}\quad 0 &{}\quad a &{}\quad a &{}\quad c &{}\quad c &{}\quad c &{}\quad d \\ e &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad e \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \end{array}$      $\begin{array}{c|ccccccc} \rightarrow _l &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1\\ a &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1&{}\quad 1 \\ b &{}\quad 0 &{}\quad d &{}\quad 1 &{}\quad d &{}\quad 1 &{}\quad 1&{}\quad 1\\ c &{}\quad 0 &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1\\ d &{}\quad 0 &{}\quad b &{}\quad b &{}\quad d &{}\quad 1&{}\quad 1&{}\quad 1\\ e &{}\quad 0 &{}\quad b &{}\quad b &{}\quad d &{}\quad d&{}\quad 1&{}\quad 1\\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \end{array}$      $\begin{array}{c|ccccccc} \rightarrow _r &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1\\ a &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1&{}\quad 1 \\ b &{}\quad 0 &{}\quad e &{}\quad 1 &{}\quad e &{}\quad 1 &{}\quad 1&{}\quad 1\\ c &{}\quad 0 &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 1\\ d &{}\quad 0 &{}\quad b &{}\quad b &{}\quad e &{}\quad 1&{}\quad 1&{}\quad 1\\ e &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad 1 \end{array}$

Fig. 3

The Hasse diagram of ${\mathfrak {A}}$

Routine calculation shows that ${\mathfrak {A}}_7=(A_7;\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,0,1)$ is a proper residuated lattice, because the property 2 does not hold: $(b\rightarrow _l c)\vee (c\rightarrow _l b)=d\vee b=d\ne 1$ and the property 2 also does not hold: $d\odot (d\rightarrow _r b)=d\odot b=a\ne d\wedge b$.

Example 2.4

[33] Let $A_{10}=\{0,a,b,c,d,e,f,g,h,1\}$ be a lattice whose Hasse diagram is below (see Fig. 4). Define $\odot$, $\rightarrow _l$ and $\rightarrow _r$ on $A_{10}$ as follows:

$\begin{array}{c|cccccccccc} \odot &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \hline 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ a &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad a \\ b &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad b &{}\quad b &{}\quad b \\ c &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad c &{}\quad 0 &{}\quad c &{}\quad c \\ d &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad c &{}\quad b &{}\quad d &{}\quad d \\ e &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad e &{}\quad e &{}\quad e &{}\quad e &{}\quad e \\ f &{}\quad 0 &{}\quad 0 &{}\quad b &{}\quad 0 &{}\quad b &{}\quad e &{}\quad f &{}\quad e &{}\quad f &{}\quad f \\ g &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad c &{}\quad c &{}\quad e &{}\quad e &{}\quad g &{}\quad g &{}\quad g \\ h &{}\quad 0 &{}\quad 0 &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad h \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \end{array}$   $\begin{array}{c|cccccccccc} \rightarrow _l &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad h &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad g &{}\quad g &{}\quad 1 &{}\quad g &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ c &{}\quad f &{}\quad f &{}\quad f &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ d &{}\quad e &{}\quad e &{}\quad f &{}\quad g &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ e &{}\quad d &{}\quad d &{}\quad d &{}\quad d &{}\quad d &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ f &{}\quad b &{}\quad b &{}\quad b &{}\quad d &{}\quad d &{}\quad g &{}\quad 1 &{}\quad g &{}\quad 1 &{}\quad 1 \\ g &{}\quad c &{}\quad c &{}\quad d &{}\quad c &{}\quad d &{}\quad f &{}\quad f &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ h &{}\quad a &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \end{array}$   $\begin{array}{c|cccccccccc} \rightarrow _r &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad h &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad f &{}\quad f &{}\quad 1 &{}\quad f &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ c &{}\quad g &{}\quad g &{}\quad g &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ d &{}\quad e &{}\quad e &{}\quad g &{}\quad f &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ e &{}\quad d &{}\quad d &{}\quad d &{}\quad d &{}\quad d &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ f &{}\quad c &{}\quad c &{}\quad d &{}\quad c &{}\quad d &{}\quad g &{}\quad 1 &{}\quad g &{}\quad 1 &{}\quad 1 \\ g &{}\quad b &{}\quad b &{}\quad b &{}\quad d &{}\quad d &{}\quad f &{}\quad f &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ h &{}\quad a &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad g &{}\quad h &{}\quad 1 \\ \end{array}$

Fig. 4

The Hasse diagram of ${\mathfrak {A}}$

Routine calculation shows that ${\mathfrak {A}}_{10}=(A_{10};\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,0,1)$ is a proper involutive residuated lattice, because the property 2 does not hold: $(b\rightarrow _l c)\vee (c\rightarrow _l b)=g\vee f=h\ne 1$ and the property 2 also does not hold: $b\odot (b\rightarrow _l c)=b\odot g=0\ne a=b\wedge c$.

Let ${\mathfrak {A}}$ be a residuated lattice. A subset S of A is called a subalgebra of ${\mathfrak {A}}$ if it is closed under the fundamental operations of ${\mathfrak {A}}$. The set of all subalgebras of ${\mathfrak {A}}$ is denoted by $S({\mathfrak {A}})$.

Example 2.5

Consider the proper pseudo-MTL algebra ${\mathfrak {A}}_5$ from Example 2.2. Then $S({\mathfrak {A}}_5)=\{\{0,1\},A_5\}$.

Example 2.6

Consider the proper residuated lattice ${\mathfrak {A}}_7$ from Example 2.3. Then $S({\mathfrak {A}}_7)=\{\{0,1\},\{0,a,1\},\{0,c,1\},\{0,e,1\},A_7\}$.

Example 2.7

Consider the proper involutive residuated lattice ${\mathfrak {A}}_{10}$ from Example 2.4. Then $S({\mathfrak {A}}_{10})=\{\{0,1\},\{0,a,h,1\},A_{10}\}$.

It is obvious that $(A;S({\mathfrak {A}}))$ is an algebraic closed set system. The closure operator associated with the closed set system $(A;S({\mathfrak {A}}))$ is denoted by $Sg^{{\mathfrak {A}}}:{\mathcal {P}}(A)\longrightarrow {\mathcal {P}}(A)$. Thus, for any subset X of A, $Sg^{{\mathfrak {A}}}(X)=\cap \{S\in S({\mathfrak {A}})|X\subseteq S\}$ is the smallest subalgebra of ${\mathfrak {A}}$ contains X. $Sg^{{\mathfrak {A}}}(X)$ is called the subalgebra of ${\mathfrak {A}}$ generated by X. When there is no ambiguity, we will drop the superscript ${\mathfrak {A}}$.

Example 2.8

Consider Example 2.7 and let $X=\{0,a\}$. Then $Sg(X)=\{0,a,h,1\}$.

Let ${\mathfrak {A}}$ be a residuated lattice. The set of all complemented elements in the lattice reduct ${\mathfrak {A}}$ is denoted by $B({\mathfrak {A}})$, and it is called the Boolean center of ${\mathfrak {A}}$. Complements are generally not unique unless the lattice is distributive. In residuated lattices, however, although the underlying lattices need not be distributive, according to [8], the complements are unique.

Proposition 2.2

[8] Let ${\mathfrak {A}}$ be a residuated lattice and $e_1,e_2\in B({\mathfrak {A}})$. The following assertions hold:

• 1. $e^c=\lnot _le=\lnot _re$.

• 2. $(e_1\vee e_2)^c=e^{c}_{1}\wedge e^{c}_{2}$ and $(e_1\wedge e_2)^c=e^{c}_{1}\vee e^{c}_{2}$

• 3. $e_1\odot e_2=e_1\wedge e_2$.

• 4. $e_{1}\rightarrow _{l} e_2=e_{1}\rightarrow _{r} e_2=(e_{1}\odot e_{2})^c$.

Let ${\mathfrak {A}}$ be a residuated lattice. A non-void subset F of A is called filter if it satisfies the following conditions:

• $x,y\in F$ implies $x\odot y\in F$;

• $x\le y$ and $x\in F$ implies $y\in F$.

The set of filters of a residuated lattice ${\mathfrak {A}}$ will be denoted by $F({\mathfrak {A}})$. Trivial examples of filters are ${\mathbf {1}}=\{1\}$ and A. A filter F of ${\mathfrak {A}}$ is proper if $F\ne A$. Clearly, F is a proper filter if and only if $0\notin F$.

Proposition 2.3

[7] Let ${\mathfrak {A}}$ be a residuated lattice and F be a non-empty subset of A. F is a filter if and only if it satisfies the following assertions:

• $x,y\in F$ implies $x\odot y\in F$;

• $x\in F$ and $y\in A$ implies $x\vee y\in F$.

Example 2.9

Consider the proper pseudo-MTL algebra ${\mathfrak {A}}_5$ from Example 2.2. Then $F({\mathfrak {A}}_5)=\{F_1=\mathbf {1},F_2=\{b,1\},F_3=\{c,1\},F_4=A_5\}$.

Example 2.10

Consider the proper residuated lattice ${\mathfrak {A}}_7$ from Example 2.3. Then $F({\mathfrak {A}}_7)=\{F_1=\mathbf {1},F_2=\{e,1\},F_3=\{c,d,e,1\},F_4=\{a,b,c,d,e,1\},F_5=A_7\}$.

Example 2.11

Consider the proper involutive residuated lattice ${\mathfrak {A}}_{10}$ from Example 2.4. Then $F({\mathfrak {A}}_{10})=\{F_1=\mathbf {1},F_2=\{h,1\},F_3=\{f,h,1\},F_4=\{g,h,1\},F_5=\{e,f,g,h,1\},F_6=A_{10}\}$.

Let ${\mathfrak {A}}$ be a residuated lattice. It is obvious that $(A;F({\mathfrak {A}}))$ is an algebraic closed set system. The closure operator associated with the closed set system $(A;F({\mathfrak {A}}))$ is denoted by $Fi^{{\mathfrak {A}}}:{\mathcal {P}}(A)\longrightarrow {\mathcal {P}}(A)$. Thus, for any subset X of A, $Fi^{{\mathfrak {A}}}(X)=\cap \{F\in F({\mathfrak {A}})|X\subseteq F\}$ is the smallest filter of ${\mathfrak {A}}$ contains X. $Fi^{{\mathfrak {A}}}(X)$ is called the filter generated by X. When there is no ambiguity, we will drop the superscript ${\mathfrak {A}}$.

If $\{F_i\}_{i\in I}$ is a family of all filters of ${\mathfrak {A}}$, we define $\wedge _{i\in I}F_i=\cap _{i\in I}F_i$ and $\vee _{i\in I}F_i=Fi(\cup _{i\in I}F_i)$. According to [7], $(F({\mathfrak {A}}),\wedge ,\vee )$ is a complete Brouwerian algebraic lattice.

Example 2.12

Consider Example 2.7 and let $X=\{f\}$. Then $Fi(X)=\{f,h,1\}$.

Proposition 2.4

[7] Let ${\mathfrak {A}}$ be a residuated lattice and X be a subset of A. Then we have

$$\begin{aligned} Fi(X)=\{a\in A|x_1\odot \cdots \odot x_n\le a, for~some~integer~n,~x_1,\ldots ,x_n\in X\}. \end{aligned}$$

Proposition 2.5

Let ${\mathfrak {A}}$ be a residuated lattice, F be a filter of ${\mathfrak {A}}$, and S be a subalgebra of ${\mathfrak {A}}$. Then $F\cap S$ is a filter of the residuated lattice S.

Proof

It is clear that $1\in F\cap S$ so $F\cap S$ is a non-empty set of S. also, for any $x,y\in F\cap S$ we have $x\odot y\in F\cap S$. Now, assume that $x\in F\cap S$ and $y\in S$. It implies that $x\vee y\in F\cap S$ and by Proposition 2.3 we conclude the result. $\square$

Let ${\mathfrak {A}}$ be a residuated lattice. An element a of A is said to be the left (right) dense element of ${\mathfrak {A}}$ if and only if $\lnot _{l}a=0(\lnot _{r}a=0)$. We denote by $D_{s}^{l}({\mathfrak {A}})$ and $D_{s}^{r}({\mathfrak {A}})$ the sets of the left and the right dense elements of ${\mathfrak {A}}$, respectively. Also, the intersection of the left and the right dense elements of ${\mathfrak {A}}$ is said to be the dense elements of ${\mathfrak {A}}$ and denoted by $D_s({\mathfrak {A}})$. One can check that $D_s({\mathfrak {A}})=\{a\in A|\lnot _{lr}a=1=\lnot _{rl}a\}$. Obviously, if ${\mathfrak {A}}$ is an involutive residuated lattice then $D_{s}^{l}({\mathfrak {A}})=D_{s}^{r}({\mathfrak {A}})=D_{s}({\mathfrak {A}})=\{1\}$.

Proposition 2.6

[7] Let ${\mathfrak {A}}$ be a residuated lattice. Then $D_{s}^{l}({\mathfrak {A}})$ and $D_{s}^{r}({\mathfrak {A}})$ are proper filters of ${\mathfrak {A}}$. In particular, $D_s({\mathfrak {A}})$ is a proper filter of ${\mathfrak {A}}$.

Let ${\mathfrak {A}}$ be a residuated lattice and F be a filter of ${\mathfrak {A}}$ and X be a subset of A. The co-annihilator of X relative to F is denoted by (F : X) and defined as follows:

$$\begin{aligned} (F:X)=\{a\in A|x\vee a\in F,\forall x\in X\}. \end{aligned}$$

If $X=\{x\}$, then $(F:\{x\})$ is denoted by (F : x).

Proposition 2.7

Let ${\mathfrak {A}}$ be a residuated lattice, F, G be filters of ${\mathfrak {A}}$, and X, Y be subsets of A. The following assertions hold:

• 1. (F : X) is a filter of ${\mathfrak {A}}$;

• 2. $F\subseteq (F:X)$;

• 3. $x\le y$ implies $(F:x)\subseteq (F:y)$;

• 4. $X\subseteq Y$ implies $(F:Y)\subseteq (F:X)$;

• 5. $F\subseteq G$ implies $(F:X)\subseteq (G:X)$.

Proof

• 1. It is obvious that $1\in (F:X)$. Let $a,b\in (F:X)$. Thus, for any $x\in X$ we have $a\vee x,b\vee x\in F$ and it implies that $(a\vee x)\odot (b\vee x)\in F$. By Proposition 2.1(12), we have $(a\vee x)\odot (b\vee x)\le (a\odot b)\vee x$. Therefore, we have $(a\odot b)\vee x\in F$, for any $x\in X$. It shows that $a\odot b\in (F:X)$. Also, it is easy to check that $a\le b$ and $a\in (F:X)$ implies $b\in (F:X)$. Hence, (F : X) is a filter of ${\mathfrak {A}}$.

• 2. Let $a\in F$. Then $a\vee x\ge a\in F$ and it implies $a\in (F:X)$.

• 3. Let $a\in (F:x)$. Thus, $a\vee x\in F$. Since $a\vee x\le a\vee y$, we deduce that $a\vee y\in F$ and it shows that $a\in (F:y)$.

• 4. Let $a\in (F:Y)$. Then for any $x\in X$ we have $x\in Y$ and it implies $a\vee x\in F$. Hence, $a\in (F:Y)$.

• 5. Let $a\in (F:X)$. Hence, for any $x\in X$ we have $a\vee x\in F\subseteq G$ and it states that $a\in (G:X)$.

$\square$

For any subset X of the residuated lattice ${\mathfrak {A}}$, $(\mathbf 1 ,X)$ is called the co-annihilator of X and it is denoted by $X^{\perp }$. It is easy to see that $A^{\perp }=\{1\}$ and $\emptyset ^{\perp }=\{1\}^{\perp }=A$. If $X=\{x\}$, then $X^{\perp }$ is denoted by $x^{\perp }$.

Let ${\mathfrak {A}}$ be a residuated lattice. We put $d^l(a,b)=(a\rightarrow _l b)\odot (b\rightarrow _l a)$ and $d^r(a,b)=(a\rightarrow _r b)\odot (b\rightarrow _r a)$, for any $a,b\in A$.

Proposition 2.8

Let ${\mathfrak {A}}$ be a residuated lattice. For any $a,b\in A$ the following conditions hold:

• 1. $d^l(a,b)=1$ iff $d^l(b,a)=1$ iff $d^r(a,b)=1$ iff $d^r(b,a)=1$ iff $a=b$;

• 2. $d^l(a,1)=d^l(1,a)=d^r(a,1)=d^r(1,a)=a$;

• 3. $d^l(a,0)=d^l(0,a)=\lnot _la$, $d^r(a,0)=d^r(0,a)=\lnot _r a$;

• 4. if $a\le b$ then $d^l(a,b)=d^l(b,a)=b\rightarrow _l a$ and $d^r(a,b)=d^r(b,a)=b\rightarrow _r a$;

• 5. $d^l(a,b)\le d^r(\lnot _l b,\lnot _l a)$, $d^r(a,b)\le d^l(\lnot _r b,\lnot _r a)$;

• 6. $d^l(\lnot _r a,\lnot _r b)=d^r(\lnot _{lr} b,\lnot _{lr} a)$ and $d^r(\lnot _l a,\lnot _l b)=d^l(\lnot _{rl} b,\lnot _{rl} a)$. In particular, if $a,b\in Reg({\mathfrak {A}})$ we have $d^l(a,b)=d^r(\lnot _l b,\lnot _l a)$ and $d^r(a,b)=d^l(\lnot _rb,\lnot _ra)$.

Proof

• 1. $d^l(a,b)=1$ conclude that $(a\rightarrow _l b)\odot (b\rightarrow _l a)=1$. So by Proposition 2.1(4), we get $a\rightarrow _l b=1$ and $b\rightarrow _l a=1$. By Proposition 2.1(3), we have $a\le b$ and $b\le a$ and it implies $a=b$. Also, it is obvious that $d^l(a,a)=1$. Similarly, we can show the result holds in other cases.

• 2. By Proposition 2.1(3,10), we have $d^l(a,1)=(a\rightarrow _l 1)\odot (1\rightarrow _l a)=1\odot a=a$.

• 3. $d^l(a,0)=(a\rightarrow _l 0)\odot (0\rightarrow _l a)=\lnot _l a\odot 1=\lnot _l a$. Similarly, we can show $d^l(0,a)=\lnot _la$ and $d^r(a,0)=d^r(0,a)=\lnot _r a$.

• 4. Let $a,b\in A$ such that $a\le b$. By Proposition 2.1(3), we have $d^l(a,b)=(a\rightarrow _l b)\odot (b\rightarrow _l a)=1\odot (b\rightarrow _l a)=b\rightarrow _l a$. Also, we have $d^l(b,a)=(b\rightarrow _l a)\odot (a\rightarrow _l b)=(b\rightarrow _l a)\odot 1=b\rightarrow _l a$. Similarly, we can show that $d^r(a,b)=d^r(b,a)=b\rightarrow _r a$.

• 5. By Proposition 2.1(5,6), we have $d^l(a,b)=(a\rightarrow _l b)\odot (b\rightarrow _l a)\le (\lnot _lb\rightarrow _r \lnot _la)\odot (\lnot _la\rightarrow _r \lnot _lb)=d^r(\lnot _lb,\lnot _la)$. Similarly, we can show $d^r(a,b)\le d^l(\lnot _r b,\lnot _r a)$.

• 6. By part 5, we have $d^l(\lnot _r a,\lnot _r b)\le d^r(\lnot _lr b,\lnot _lr a)\le d^l(\lnot _rlr a,\lnot _rlr b)$. On the other hand, by Proposition 2.1(7), we obtain that $d^l(\lnot _rlr a,\lnot _rlr b)=d^l(\lnot _r a,\lnot _r b)$ and it shows the result holds. Similarly, we can show that $d^r(\lnot _l a,\lnot _l b)=d^l(\lnot _{rl} b,\lnot _{rl} a)$. Also, if $a,b\in Reg({\mathfrak {A}})$ we have $\lnot _{lr} a=\lnot _{rl} a=a$ and $\lnot _{lr} b=\lnot _{rl} b=b$ and it concludes $d^l(a,b)=d^r(\lnot _l b,\lnot _l a)$ and $d^r(a,b)=d^l(\lnot _rb,\lnot _ra)$.

$\square$

With any filter of a residuated lattice ${\mathfrak {A}}$, we associate two binary relations $\equiv ^{l}_{F}$ and $\equiv ^{r}_{F}$ on A by defining

$$\begin{aligned}&(a,b)\in \equiv ^{l}_{F} \hbox { if and only if } d^l(a,b)\in F;\\&(a,b)\in \equiv ^{r}_{F} \hbox { if and only if } d^r(a,b)\in F. \end{aligned}$$

By Proposition 2.1, it is easy to check that the binary relations $\equiv ^{l}_{F}$ and $\equiv ^{r}_{F}$ are equivalence relations on A. $\equiv ^{l}_{F}$ and $\equiv ^{r}_{F}$ are called the right equivalence relation and the left equivalence relation induced by F, respectively. In the following, for any $a\in A$ the equivalence classes $a/\equiv ^{l}_{F}$ and $a/\equiv ^{r}_{F}$ are denoted by $[a]^{l}_{F}$ and $[a]^{l}_{F}$, respectively.

Proposition 2.9

Let ${\mathfrak {A}}$ be a residuated lattice and F be a filter of ${\mathfrak {A}}$. For any $a\in A$ and $f\in F$ the following assertions hold:

• 1. $[f]^{l}_{F}=[f]^{r}_{F}=F$;

• 2. $\lnot _l[a]^{l}_{F}\subseteq [\lnot _l a]^{r}_{F}$ and $\lnot _r[a]^{r}_{F}\subseteq [\lnot _ra]^{l}_{F}$. In particular, if ${\mathfrak {A}}$ is involutive we have $\lnot _l[a]^{l}_{F}=[\lnot _l a]^{r}_{F}$ and $\lnot _r[a]^{r}_{F}=[\lnot _ra]^{l}_{F}$;

• 3. $\lnot _l[0]^{l}_{F}\cup \lnot _r[0]^{r}_{F}\subseteq F$.

Proof

• 1. Let $a\in [f]^{l}_{F}$. Then $d^l(a,f)\in F$ and it implies that $f\rightarrow _l a\in F$. Since F is a filter and $f\in F$, we obtain that $a\in F$ and it shows that $[f]^{l}_{F}\subseteq F$. Now, assume that $a\in F$. Thus, $f\rightarrow _l a\in F$ and since $f\in F$ we have $a\rightarrow _l f\in F$ and these imply that $d^l(a,f)\in F$. Therefore, $a\in [f]^{l}_{F}$ and it shows that $F\subseteq [f]^{l}_{F}$. Hence, $[f]^{l}_{F}=F$. Analogously, we can show that $[f]^{r}_{F}=F$.

• 2. Let $b\in \lnot _l[a]^{l}_{F}$. So there is $c\in [a]^{l}_{F}$ such that $b=\lnot _lc$. We have $d^l(a,c)\in F$ and by Proposition 2.8(5) we obtain that $d^l(a,c)\le d^r(\lnot _lc,\lnot _la)$ and it implies that $d^r(b,\lnot _la)\in F$. Therefore, $b\in [\lnot _l a]^{r}_{F}$ and it proves the result. Similarly, we can show that $\lnot _r[a]^{r}_{F}\subseteq [\lnot _ra]^{l}_{F}$. Now, let ${\mathfrak {A}}$ is involutive and consider $b\in [\lnot _l a]^{r}_{F}$. Then $d^r(b,\lnot _la)\in F$ and it implies $d^l(a,\lnot _rb)=d^l(\lnot _{rl}a,\lnot _rb)\in F$. Thus, $\lnot _rb\in [a]^{F}_{l}$ and it concludes that $b=\lnot _{lr}b\in \lnot _l[a]^{F}_{l}$. Therefore, $[\lnot _l a]^{r}_{F}\subseteq \lnot _l[a]^{l}_{F}$ and it proves the result. Similarly, we can show that $\lnot _r[a]^{r}_{F}=[\lnot _ra]^{l}_{F}$ when ${\mathfrak {A}}$ is involutive.

• 3. By parts 1 and 2, we have $\lnot _l[0]^{l}_{F}\subseteq [\lnot _l 0]^{r}_{F}=[1]^{r}_{F}=F$. Similarly, we can conclude that $\lnot _r[0]^{r}_{F}\subseteq F$ and it holds the result.

$\square$

By the following example, we show that we cannot replace the inclusion symbol $\subseteq$ by an equal sign in Proposition 2.9(2).

Example 2.13

[33] Let $A_6=\{0,a,b,c,d,1\}$ be a lattice whose Hasse diagram is below (see Fig. 5). Define $\odot$, $\rightarrow _l$ and $\rightarrow _r$ on A as follows:

$\begin{array}{c|cccccc} \odot &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \\ \hline 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ a &{}\quad 0 &{}\quad 0 &{}\quad a &{}\quad 0 &{}\quad a &{}\quad a \\ b &{}\quad 0 &{}\quad 0 &{}\quad b &{}\quad 0 &{}\quad b &{}\quad b \\ c &{}\quad 0 &{}\quad a &{}\quad a &{}\quad c &{}\quad c &{}\quad c \\ d &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad d \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \end{array}$      $\begin{array}{c|cccccc} \rightarrow _l &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad 0 &{}\quad c &{}\quad 1 &{}\quad c &{}\quad 1 &{}\quad 1 \\ c &{}\quad b &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ d &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \end{array}$

$\begin{array}{c|cccccc} \rightarrow _r &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \\ \hline 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ a &{}\quad c &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ b &{}\quad c &{}\quad c &{}\quad 1 &{}\quad c &{}\quad 1 &{}\quad 1 \\ c &{}\quad 0 &{}\quad b &{}\quad b &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ d &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad a &{}\quad b &{}\quad c &{}\quad d &{}\quad 1 \end{array}$   

Fig. 5

The Hasse diagram of ${\mathfrak {A}}_6$

Routine calculation shows that ${\mathfrak {A}}_6=(A_6;\vee ,\wedge ,\odot ,\rightarrow _l,\rightarrow _r,0,1)$ is a proper residuated lattice, because the property (pprel) does not hold: $(b\rightarrow _l c)\vee (c\rightarrow _l b)=c\vee b=d\ne 1$ and the property (pdiv) also does not hold: $b\odot (b\rightarrow _l c)=b\odot c=0\ne a=b\wedge c$. One can check that $F=\{b,d,1\}$ is a filter of ${\mathfrak {A}}_6$. We have

$$\begin{aligned} A_6/\equiv _{F}^{l}=\{\{0,a,c\},\{b,d,1\}\}. \end{aligned}$$

Also, we have

$$\begin{aligned} A_6/\equiv _{F}^{r}=\{\{0\},\{a,c\},\{b,d,1\}\}. \end{aligned}$$

Now, we have $\lnot _l[a]^{l}_{F}=\{b,1\}$ and $[\lnot _la]^{r}_{F}=[b]^{r}_{F}=\{b,d,1\}$ and it shows that $[\lnot _la]^{r}_{F}\nsubseteq \lnot _l[a]^{l}_{F}$, in general.

The following example shows that $[a]^{l}_{F}$ and $[a\odot f]^{l}_{F}$ are not equal, in general, for any $a\in A$ and $f\in F$.

Example 2.14

Consider the proper involutive residuated lattice ${\mathfrak {A}}_{10}$ from Example 2.4. By Example 2.11, we have $F_3=\{f,h,1\}\in F({\mathfrak {A}}_{10})$. We have

$$\begin{aligned} A_{10}/\equiv _{F_3}^{l}=\{\{0,a,c\},\{b,d\},\{e,g\},\{f,h,1\}\}. \end{aligned}$$

Also, we have

$$\begin{aligned} A_{10}/\equiv _{F_3}^{r}=\{\{0,a,b\},\{c,d\},\{e,g\},\{f,h,1\}\}. \end{aligned}$$

Now, we have $[b]^{l}_{F}=\{b,d\}$ and $[b\odot f]^{l}_{F}=[0]^{l}_{F}=\{0,a,c\}$ and it shows that $[a]^{l}_{F}\cap [a\odot f]^{l}_{F}=\emptyset$.

Corollary 2.1

Let ${\mathfrak {A}}$ be an involutive residuated lattice and F be a filter of ${\mathfrak {A}}$. Then $card(A/\equiv _{F}^{l})=card(A/\equiv _{F}^{r})$.

Proof

We define the mapping $f:A/\equiv _{F}^{l}\longrightarrow A/\equiv _{F}^{r}$ by $f([a]^{l}_{F})=[\lnot _la]^{r}_{F}$. By Proposition 2.9(2), we have

$$\begin{aligned}{}[a]^{l}_{F}=[b]^{l}_{F}\Leftrightarrow \lnot _l[a]^{l}_{F}=\lnot _l[b]^{l}_{F}\Leftrightarrow [\lnot _la]^{r}_{F}=[\lnot _lb]^{r}_{F}. \end{aligned}$$

It shows that f is an injection. Also, we have $f([\lnot _ra]^{l}_{F})=[\lnot _{lr}a]^{r}_{F}=[a]^{r}_{F}$ and it implies that f is a bijection. $\square$

Let F be a filter of an involutive residuated lattice ${\mathfrak {A}}$. By Corollary 2.1, we know that $card(A/\equiv _{F}^{l})=card(A/\equiv _{F}^{r})$. In the following, this cardinal is named the index of F in ${\mathfrak {A}}$ and denoted by $[{\mathfrak {A}}:F]$.

A subset X of a poset ${\mathfrak {A}}$ is named a convex subset of ${\mathfrak {A}}$ if for any $x,z\in X$ and $y\in A$ such that $x\le y\le z$ we have $y\in X$.

Proposition 2.10

Let ${\mathfrak {A}}$ be a residuated lattice and F be a filter of ${\mathfrak {A}}$. Then for any $a\in A$, $[a]^{l}_{F}$ and $[a]^{r}_{F}$ are convex subsets of ${\mathfrak {A}}$.

Proof

Let $x,z\in [a]^{l}_{F}$ and $x\le y\le z$. Therefore, we have $d^l(x,a),d^l(z,a)\in F$ and it implies that $z\rightarrow _l x=d^l(x,z)\in F$. Since $y\le z$, by Proposition 2.1(11) we obtain that $z\rightarrow _l x\le y\rightarrow _l x$ and it shows that $y\rightarrow _l x=d^l(y,x)\in F$. Thus, $d^l(y,x),d^l(x,a)\in F$ and it implies that $d^l(y,a)\in F$ and consequently $y\in [a]^{l}_{F}$. Similarly, we can show that $[a]^{r}_{F}$ is a convex subset of ${\mathfrak {A}}$. $\square$

Definition 2.2

[13] Let ${\mathfrak {A}}$ be a residuated lattice. A filter F of ${\mathfrak {A}}$ is called normal if $x\rightarrow _l y\in F$ if and only if $x\rightarrow _r y\in F$, for any $x,y\in A$. We shall denote by $F_n({\mathfrak {A}})$ the set of normal filters of ${\mathfrak {A}}$.

Example 2.15

Consider the proper involutive residuated lattice ${\mathfrak {A}}_{10}$ from Example 2.4. Then we have $F_n({\mathfrak {A}}_{10})=\{F_1=\mathbf {1},F_2=\{h,1\},F_5=\{e,f,g,h,1\},F_6=A_{10}\}$

Proposition 2.11

[7] Let ${\mathfrak {A}}$ be a residuated lattice and $\{F_i\}_{i\in I}$ be a non-empty family of normal filters of ${\mathfrak {A}}$. Then $\wedge _{i\in I}F_i$ and $\vee _{i\in I}F_i$ are normal filters of ${\mathfrak {A}}$.

As a consequence of Proposition 2.11 we conclude $(F_n({\mathfrak {A}}),\wedge ,\vee )$ is a complete sublattice of $(F({\mathfrak {A}}),\wedge ,\vee )$.

It is obvious that if F is a normal filter of the residuated lattice ${\mathfrak {A}}$ then the right and the left equivalence relations induced by F are equal and both of them are denoted by $\equiv _F$. So $(x,y)\in \equiv _F$ if and only if $d^l(x,y)\in F$ if and only if $d^r(x,y)\in F$. According to [22], if F is a normal filter of a residuated lattice ${\mathfrak {A}}$ then $\equiv _{F}$ is a congruence relation on ${\mathfrak {A}}$. In this case, For any $a\in A$, let a / F be the equivalence class $a/\equiv _{F}$ and $A/F=\{a/F|a\in A\}$. A / F becomes a residuated lattice with the natural operations induced from those of ${\mathfrak {A}}$ and it is denoted by ${\mathfrak {A}}/F$. If $a,b\in A$, then $a/F\le b/F$ if and only if $a\rightarrow _l b\in F$ if and only if $a\rightarrow _r b\in F$.

Remark 2.1

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. By Proposition 2.5, $F\cap S$ is a filter of S. Also, one can check that $F\cap S$ is a normal filter of S.

Let ${\mathfrak {A}}$ and ${\mathfrak {B}}$ be residuated lattices. A mapping $h:A\longrightarrow B$ is called a homomorphism, in symbols $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$, if it preserves the fundamental operations. If $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ is a homomorphism we put $coker(h)=h^{\leftarrow }(1)$. It is easy to check that coker(h) is a normal filter of ${\mathfrak {A}}$. Also, it is obvious that h is a monomorphism if and only if $coker(h)=\{1\}$.

Proposition 2.12

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be a homomorphism.

• 1. If h is onto and $F\in F({\mathfrak {A}})(F\in F_n({\mathfrak {A}}))$ such that $coker(h)\subseteq F$ then $h(F)\in F({\mathfrak {B}})(h(F)\in F_n({\mathfrak {B}}))$.

• 2. If $F\in F({\mathfrak {B}})(F\in F_n({\mathfrak {B}}))$ then $h^\leftarrow (F)\in F({\mathfrak {A}})(h^\leftarrow (F)\in F_n({\mathfrak {A}}))$ and $coker(h)\subseteq h^\leftarrow (F)$.

Proof

It is easy. $\square$

Lemma 2.1

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be an epimorphism and F be a filter of ${\mathfrak {A}}$ containing coker(h). Then for any $a\in A$ we have $h([a]^{l}_{F})=[h(a)]^{l}_{h(F)}$ and $h([a]^{r}_{F})=[h(a)]^{r}_{h(F)}$

Proof

According to Proposition 2.12(2) we know that h(F) is a filter of ${\mathfrak {B}}$. It is easy to see that $h([a]^{l}_{F})\subseteq [h(a)]^{l}_{h(F)}$. Now, consider $b\in [h(a)]^{l}_{h(F)}$. It implies that there is $a_b\in A$ such that $b=h(a_b)$ and it means $h(d^l(a_b,a))\in h(F)$. Let $f\in F$ such that $h(d^l(a_b,a))=h(f)$. Therefore, $h(f)\rightarrow _l h(d^l(a_b,a))=h(f)\rightarrow _l h(f)$ and by substitution property of h we obtain that $h(f\rightarrow _l d^l(a_b,a))=h(f\rightarrow _l f)=h(1)=1$. Thus, $f\rightarrow _l d^l(a_b,a)\in coker(h)\subseteq F$ and it implies that $d^l(a_b,a)\in F$. Thus, $a_b\in [a]^{l}_{F}$ and it shows that $b\in h([a]^{l}_{F})$. Hence, we obtain that $h([a]^{l}_{F})=[h(a)]^{l}_{h(F)}$. Similarly, we can show that $h([a]^{r}_{F})=[h(a)]^{r}_{h(F)}$. $\square$

Corollary 2.2

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be an epimorphism and F be a normal filter of ${\mathfrak {A}}$ containing coker(h). Then for any $a\in A$ we have $h(a/F)=h(a)/h(F)$.

Proof

By Proposition 2.12(2), h(F) is a normal filter of ${\mathfrak {A}}$. Also, by Lemma 2.1, the result holds. $\square$

Lemma 2.2

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be a homomorphism and F be a filter of ${\mathfrak {B}}$. Then for any $a\in A$ we have $[a]^{l}_{h^{\leftarrow }(F)}=h^{\leftarrow }([h(a)]^{l}_{F})$ and $[a]^{r}_{h^{\leftarrow }(F)}=h^{\leftarrow }([h(a)]^{r}_{F})$. Moreover, we have $h([a]^{l}_{h^{\leftarrow }(F)})\subseteq [h(a)]^{l}_{F}$ and $h([a]^{r}_{h^{\leftarrow }(F)})\subseteq [h(a)]^{r}_{F}$.

Proof

According to Proposition 2.12(1) we know that $h^{\leftarrow }(F)$ is a filter of ${\mathfrak {A}}$. Therefore, we have

$$\begin{aligned} \begin{array}{ll} x\in [a]^{l}_{h^{\leftarrow }(F)}&{}\Longleftrightarrow d^l(x,a)\in h^{\leftarrow }(F)\\ &{} \Longleftrightarrow h(d^l(x,a))\in F\\ &{} \Longleftrightarrow d^l(h(x),h(a))\in F\\ &{} \Longleftrightarrow h(x)\in [h(a)]^{l}_{F}\\ &{} \Longleftrightarrow x\in h^{\leftarrow }([h(a)]^{l}_{F}). \end{array} \end{aligned}$$

It shows that the equality holds. Also, for each $a\in A$ we can conclude that $h([a]^{l}_{h^{\leftarrow }(F)})=h(h^{\leftarrow }([h(a)]^{l}_{F}))\subseteq [h(a)]^{l}_{F}$. Similarly, we can show that $[a]^{r}_{h^{\leftarrow }(F)}=h^{\leftarrow }([h(a)]^{r}_{F})$ and $h([a]^{r}_{h^{\leftarrow }(F)})\subseteq [h(a)]^{r}_{F}$. $\square$

Corollary 2.3

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be a homomorphism and F be a normal filter of ${\mathfrak {B}}$. Then for any $a\in A$ we have $a/h^{\leftarrow }(F)=h^{\leftarrow }(h(a)/F)$. Moreover, we have $h(a/h^{\leftarrow }(F))\subseteq h(a)/F$.

Proof

By Proposition 2.12(1), $h^{\leftarrow }(F)$ is a normal filter of ${\mathfrak {A}}$. Also, by Lemma 2.2, the result holds. $\square$

3 Rough approximation sets based on residuated lattices

Rough set theory and formal concept analysis offer related and complementary approaches for data analysis. Both theories are useful tools for qualitative data analysis. Formal contexts provide a common framework for both theories. A formal context is a triple $(A,B;\mathfrak {R})$, where A and B are sets and $\mathfrak {R}\subseteq A\times B$ is a relation from A to B. In a formal context $(A,B;\mathfrak {R})$, A is interpreted as the set of objects, B the set of properties, and $(a,b)\in \mathfrak {R}$ reads as that the object a has property b. Given a formal context $(A,B;\mathfrak {R})$, there are two Galois connections between the powersets of A and B [16]. The relation between rough set theory and formal concept analysis studied by some researchers [21, 33, 51]

In the theory of rough sets, presented by Pawlak [35], equivalence relations are very important. Equivalence classes are basic building blocks for lower and upper approximations of a subset of the universe set.

Let U be a non-empty finite set called the universe set and let $\theta$ be an equivalence relation on U. Then, $(U,\theta )$ is called an approximation space. By a rough approximation in $(U,\theta )$ we mean a mapping $Apr^{U}_{\theta }:{\mathcal {P}}(U)\longrightarrow {\mathcal {P}}(U)\times {\mathcal {P}}(U)$ defined for every $X\in {\mathcal {P}}(U)$ by

$$\begin{aligned} Apr^{U}_{\theta }(X)=(\underline{Apr}^{U}_{\theta }(X),{\overline{Apr}}^{U}_{\theta }(X)), \end{aligned}$$

where $\underline{Apr}^{U}_{\theta }(X)=\{u\in U:[u]_{\theta }\subseteq X\}$ and ${\overline{Apr}}^{U}_{\theta }(X)=\{u\in U:[u]_{\theta }\cap X\ne \emptyset \}$. $\underline{Apr}^{U}_{\theta }(X)$ and ${\overline{Apr}}^{U}_{\theta }(X)$ are called the lower rough approximation and the upper rough approximation of X in $(U,\theta )$, respectively. When there is no ambiguity, we will drop the superscript U. A subset X of U is called definable with respect to $\theta$ if $\underline{Apr}_{\theta }(X)={\overline{Apr}}_{\theta }(X)$.

Now, let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. In the following, the approximation space $(A;\equiv _F)$ is denoted by $({\mathfrak {A}};F)$ and it is named the approximation space induced by F. Also, $\underline{Apr}^{A}_{\equiv _F}(X)$ and ${\overline{Apr}}^{A}_{\equiv _F}(X)$ are denoted by $\underline{Apr}^{{\mathfrak {A}}}_{F}(X)$ and ${\overline{Apr}}^{{\mathfrak {A}}}_{F}(X)$ and they are called the lower rough approximation and the upper rough approximation on ${\mathfrak {A}}$ induced by F, respectively. When there is no ambiguity we will drop the superscript ${\mathfrak {A}}$.

By a rough approximation in $({\mathfrak {A}},F)$ we mean a mapping $Apr_{F}:{\mathcal {P}}(A)\longrightarrow {\mathcal {P}}(A)\times {\mathcal {P}}(A)$ defined for every $X\in {\mathcal {P}}(A)$ by

$$\begin{aligned} Apr_{F}(X)=(\underline{Apr}_{F}(X),{\overline{Apr}}_{F}(X)). \end{aligned}$$

A subset X of A is called definable with respect to F if $\underline{Apr}_{F}(X)={\overline{Apr}}_{F}(X)$.

Proposition 3.1

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. For any subsets X and Y of A the following assertions hold:

• 1. $\underline{Apr}_{F}(X)\subseteq X\subseteq {\overline{Apr}}_{F}(X)$;

• 2. X is definable with respect to F if and only if X is the union of equivalence classes of $\equiv _F$. In particular, A, $\emptyset$; ${\overline{Apr}}_{F}(X)$, $\underline{Apr}_{F}(X)$ and x / F are definable sets with respect to F;

• 3. X is definable with respect to F if and only if $\underline{Apr}_{F}(X)=X$ or $X={\overline{Apr}}_{F}(X)$;

• 4. if $X\subseteq Y$, then $\underline{Apr}_{F}(X)\subseteq \underline{Apr}_{F}(Y)$ and ${\overline{Apr}}_{F}(X)\subseteq {\overline{Apr}}_{F}(Y)$;

• 5. $\underline{Apr}_{F}(X)=({\overline{Apr}}_{F}(X^{c}))^{c}$ and ${\overline{Apr}}_{F}(X)=(\underline{Apr}_{F}(X^{c}))^{c}$;

• 6. $\underline{Apr}_{F}(X\cap Y)=\underline{Apr}_{F}(X)\cap \underline{Apr}_{F}(Y)$;

• 7. ${\overline{Apr}}_{F}(X\cap Y)\subseteq {\overline{Apr}}_{F}(X)\cap {\overline{Apr}}_{F}(Y)$;

• 8. $\underline{Apr}_{F}(X)\cup \underline{Apr}_{F}(Y)\subseteq \underline{Apr}_{F}(X\cup Y)$;

• 9. ${\overline{Apr}}_{F}(X\cup Y)={\overline{Apr}}_{F}(X)\cup {\overline{Apr}}_{F}(Y)$;

• 10. $Apr_{A}(X)=(\emptyset ,A)$ if $X\ne A$;

• 11. $Apr_0(\mathbf {1})=(X,A)$.

Proof

The proof is similar to the proof of [38, Theorem 3.1.1]. $\square$

The following example shows that the converse of Proposition 3.1 part 7 and 8 don’t hold.

Example 3.1

Consider the residuated lattice ${\mathfrak {A}}_{10}$ from Example 2.4. By Example 2.15, $F_3=\{h,1\}\in F_n({\mathfrak {A}}_{10})$. The set of equivalence classes induced by $F_5$ on ${\mathfrak {A}}_{10}$ is

$$\begin{aligned} A_{10}/F_3=\{\{0,a\},\{b\},\{c\},\{d\},\{e\},\{f\},\{g\},\{h,1\}\}. \end{aligned}$$

Let $X=\{0,b,h\}$ and $Y=\{a,b,h,1\}$. Therefore, we obtain

• $\underline{Apr}_{F_3}(X)=\{b\}$;

• $\underline{Apr}_{F_3}(Y)=\{b,h,1\}$;

• $\underline{Apr}_{F_3}(X\cup Y)=\{0,a,b,h,1\}$;

• ${\overline{Apr}}_{F_3}(X)=\{0,a,b,h,1\}$;

• ${\overline{Apr}}_{F_3}(Y)=\{0,a,b,h,1\}$;

• ${\overline{Apr}}_{F_3}(X\cap Y)=\{b,h,1\}$.

It shows that $\underline{Apr}_{F}(X\cup Y)\nsubseteq \underline{Apr}_{F}(X)\cup \underline{Apr}_{F}(Y)$ and ${\overline{Apr}}_{F}(X)\cap {\overline{Apr}}_{F}(Y)\nsubseteq {\overline{Apr}}_{F}(X\cap Y)$.

Proposition 3.2

Let ${\mathfrak {A}}$ be a residuated lattice and F be a filter of ${\mathfrak {A}}$. Then for any subset X of A the following conditions hold:

• 1 $\lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)\subseteq {\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)$. In particular, if F is normal then $\lnot _l{\overline{Apr}}_{F}(X)\subseteq {\overline{Apr}}_{F}(\lnot _l X)$;

• 2 $\lnot _r{\overline{Apr}}_{\equiv ^{r}_{F}}(X)\subseteq {\overline{Apr}}_{\equiv ^{l}_{F}}(\lnot _rX)$. In particular, if F is normal then $\lnot _r{\overline{Apr}}_{F}(X)\subseteq {\overline{Apr}}_{F}(\lnot _r X)$.

Proof

• 1. Let $u\in \lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)$. So there is an element $a\in {\overline{Apr}}_{\equiv ^{l}_{F}}(X)$ such that $u=\lnot _l a$. We have $[a]^{l}_{F}\cap X\ne \emptyset$ and it implies that there is $x\in X$ such that $d^l(x,a)\in F$. By Proposition 2.8(5), we get that $d^r(\lnot _l x,\lnot _l a)\in F$ and it implies that $[\lnot _l a]^{r}_{F}\cap \lnot _l X\ne \emptyset$. Hence, $u\in {\overline{Apr}}_{F}(\lnot _l X)$.

• 2. Its proof is similar to part 3.2.

$\square$

The following example shows that we cannot replace the inclusion symbol $\subseteq$ by an equal sign in Proposition 3.2. Also, it shows that the same inequalities don’t hold for the lower rough approximation

Example 3.2

Consider the proper residuated lattice ${\mathfrak {A}}_{6}$ from Example 2.13 and let $X=\{a,c\}$. We have $\lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)=\{b,1\}$ and ${\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)=\{b,d,1\}$. It shows that ${\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)\nsubseteq \lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)$. Also, $\lnot _r{\overline{Apr}}_{\equiv ^{r}_{F}}(X)=\{0,c\}$ and ${\overline{Apr}}_{\equiv ^{l}_{F}}(\lnot _rX)=\{0,a,c\}$. It shows that ${\overline{Apr}}_{\equiv ^{l}_{F}}(\lnot _r X)\nsubseteq \lnot _r{\overline{Apr}}_{\equiv ^{r}_{F}}(X)$.

Corollary 3.1

Let ${\mathfrak {A}}$ be an involutive residuated lattice and F be a filter of ${\mathfrak {A}}$. Then for any subset X of A the following conditions hold:

• 1. $\lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)={\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)$;

• 2. $\lnot _r{\overline{Apr}}_{\equiv ^{r}_{F}}(X)={\overline{Apr}}_{\equiv ^{l}_{F}}(\lnot _rX)$.

In particular, if F is normal then we have

$$\begin{aligned} \lnot _l{\overline{Apr}}_{F}(X)= & {} {\overline{Apr}}_{F}(\lnot _l X)~\hbox {and}\\ \lnot _r{\overline{Apr}}_{F}(X)= & {} {\overline{Apr}}_{F}(\lnot _r X). \end{aligned}$$

Proof

According to Proposition 3.2, we have $\lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)\subseteq {\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)$. Now, consider $a\in {\overline{Apr}}_{\equiv ^{r}_{F}}(\lnot _l X)$. So $[a]^{r}_{F}\cap \lnot _lX\ne \emptyset$ and it implies that $\lnot _r[a]^{r}_{F}\cap X\ne \emptyset$. Thus, by Proposition 2.9(2), we obtain that $[\lnot _ra]^{l}_{F}\cap X\ne \emptyset$. Therefore, $\lnot _ra\in {\overline{Apr}}_{\equiv ^{l}_{F}}(X)$ and it shows that $a\in \lnot _l{\overline{Apr}}_{\equiv ^{l}_{F}}(X)$. Similarly, we can prove the remind. $\square$

Proposition 3.3

Let ${\mathfrak {A}}$ be a residuated lattice and F be a filter of ${\mathfrak {A}}$. For any filter G of ${\mathfrak {A}}$ and any subset X of A we have

• 1. $(G:{\overline{Apr}}_{\equiv _{F}^{l}}(X))\subseteq (G:X)\subseteq (G:\underline{Apr}_{\equiv _{F}^{l}}(X))$;

• 2. $(G:{\overline{Apr}}_{\equiv _{F}^{r}}(X))\subseteq (G:X)\subseteq (G:\underline{Apr}_{\equiv _{F}^{r}}(X))$;

• 3. $({\overline{Apr}}_{\equiv _{F}^{l}}(X))^\perp \subseteq X^\perp \subseteq (\underline{Apr}_{\equiv _{F}^{l}}(X))^\perp$;

• 4. $({\overline{Apr}}_{\equiv _{F}^{r}}(X))^\perp \subseteq X^\perp \subseteq (\underline{Apr}_{\equiv _{F}^{r}}(X))^\perp$.

In particular, if F is normal we have

• 1. $(G:{\overline{Apr}}_{F}(X))\subseteq (G:X)\subseteq (G:\underline{Apr}_{F}(X))$;

• 2. $({\overline{Apr}}_F(X))^\perp \subseteq X^\perp \subseteq (\underline{Apr}_F(X))^\perp$.

Proof

It is obvious by Proposition 2.7(4) and Proposition 3.1(1). $\square$

By the following example, we show that we cannot replace the inclusion symbols by equal signs in Proposition 3.3.

Example 3.3

Consider the residuated lattice ${\mathfrak {A}}_{5}$ from Example 2.2. By Example 2.9, we have $F_2=\{b,1\}\in F({\mathfrak {A}}_{5})$. We have

$$\begin{aligned} A_{5}/\equiv _{F_2}^{l}=\{\{0\},\{a,c\},\{b,1\}\}. \end{aligned}$$

Also, we have

$$\begin{aligned} A_{5}/\equiv _{F_2}^{r}=\{\{0,a,c\},\{b,1\}\}. \end{aligned}$$

Let, $X=\{c\}$. Thus, we have $({\overline{Apr}}_{\equiv _{F}^{l}}(X))^\perp =\{a,c\}^\perp =\{1\}$, $X^\perp =\{b,1\}$ and $(\underline{Apr}_{\equiv _{F}^{l}}(X))^\perp =\emptyset ^\perp =A_5$.

Proposition 3.4

Let ${\mathfrak {A}}$ be a residuated lattice and $F_1,F_2\in F({\mathfrak {A}})$ such that $F_1\subseteq F_2$. For any subset X of A the following conditions hold:

• 1. $\underline{Apr}_{\equiv _{F_2}^{l}}(X)\subseteq \underline{Apr}_{\equiv _{F_1}^{l}}(X)\subseteq {\overline{Apr}}_{\equiv _{F_2}^{l}}(X)$;

• 2. $\underline{Apr}_{\equiv _{F_2}^{r}}(X)\subseteq \underline{Apr}_{\equiv _{F_1}^{r}}(X)\subseteq {\overline{Apr}}_{\equiv _{F_2}^{r}}(X)$.

  In particular, if $F_1$ and $F_2$ are normal then the following conditions hold:

• 3. $\underline{Apr}_{F_2}(X)\subseteq \underline{Apr}_{F_1}(X)\subseteq {\overline{Apr}}_{F_2}(X)$.

Proof

It is straightforward by $[a]_{F_1}^{l}\subseteq [a]_{F_2}^{l}$, $[a]_{F_1}^{r}\subseteq [a]_{F_2}^{r}$ and $a/F_1\subseteq a/F_2$, for any $a\in A$. $\square$

Corollary 3.2

Let ${\mathfrak {A}}$ be a residuated lattice and $\{F_i\}_{i\in I}$ be a family of normal filters of ${\mathfrak {A}}$. Then for any subset X of A the following condition holds.

$$\begin{aligned} \cup _{i\in I}\underline{Apr}_{F_i}(X)\subseteq \underline{Apr}_{\wedge _{i\in I}F_i}(X)\subseteq \cap _{i\in I}{\overline{Apr}}_{F_i}(X). \end{aligned}$$

Proof

We have $\cap _{i\in I}F_i\subseteq F_i$, for each $i\in I$. Thus, by Proposition 3.4 we obtain that $\underline{Apr}_{F_i}(X)\subseteq \underline{Apr}_{\cap _{i\in I}F_i}(X)$, for each $i\in I$ and it implies that $\cup _{i\in I}\underline{Apr}_{F_i}(X)\subseteq \underline{Apr}_{\wedge _{i\in I}F_i}(X)$. Similarly, we can show that ${\overline{Apr}}_{\wedge _{i\in I}F_i}(X)\subseteq \cap _{i\in I}{\overline{Apr}}_{F_i}(X)$ and it holds the result. $\square$

Proposition 3.5

Let ${\mathfrak {A}}$ be a residuated lattice, $\{F_i\}_{i\in I}$ be a family of normal filters of ${\mathfrak {A}}$ and X be a non-empty subset of A. Then we have

• 1. $\underline{Apr}_{\vee _{i\in I}F_i}(X)\subseteq \cap _{i\in I}\underline{Apr}_{F_i}(X)$;

• 2. if X is a subset of $B({\mathfrak {A}})$ then ${\overline{Apr}}_{\vee _{i\in I}F_i}(X)\subseteq Fi(\cup _{i\in I}{\overline{Apr}}_{F_i}(X))$.

Proof

• 1. We have $F_i\subseteq \vee _{i\in I}F_i$, for each $i\in I$. So by Proposition 3.4, we conclude that $\underline{Apr}_{\vee _{i\in I}F_i}(X)\subseteq \underline{Apr}_{F_i}(X)$, for each $i\in I$ and it holds the result.

• 2. Let $X\subseteq B({\mathfrak {A}})$ and $a\in {\overline{Apr}}_{\vee _{i\in I}F_i}(X)$. Therefore, $a/\vee _{i\in I}F_i\cap X\ne \emptyset$. Thus, there is $x\in X$ such that $x\rightarrow _l a\in \vee _{i\in I}F_i$. It implies that there are $f_1,\ldots ,f_n\in \cup _{i\in I}F_i$, for some integer n, such that $f_1\odot \cdots \odot f_n\le x\rightarrow _l a$. Thus, $(f_1\odot \cdots \odot f_n)\odot x\le a$. On the other hand, by hypothesis and Proposition 2.2 we get $(f_1\odot \cdots \odot f_n)\odot x=(f_1\odot x)\odot \cdots \odot (f_n\odot x)$. Since, $f_i\odot x/F_i=x/F_i$, for each $1\le i\le n$, then we have $a\in Fi(\cup _{i\in I}{\overline{Apr}}_{F_i}(X))$.

$\square$

Proposition 3.6

Let ${\mathfrak {A}}$ be a residuated lattice, F be a filter of ${\mathfrak {A}}$ and X be a non-empty subset of A. Then the following assertions hold:

• 1. $X\subseteq F$ if and only if ${\overline{Apr}}_{\equiv ^{l}_{F}}(X)={\overline{Apr}}_{\equiv ^{r}_{F}}(X)=F$. In particular, if F is a normal filter of ${\mathfrak {A}}$ then we have $X\subseteq F$ if and only if ${\overline{Apr}}_F(X)=F$;

• 2. $F\subseteq X$ if and only if $F\subseteq \underline{Apr}_{\equiv ^{l}_{F}}(X)\cap \underline{Apr}_{\equiv ^{r}_{F}}(X)$. In particular, if F is a normal filter of ${\mathfrak {A}}$ then we have $F\subseteq X$ if and only if $F\subseteq \underline{Apr}_F(X)$.

Proof

• 1. Let $X\subseteq F$ and $a\in {\overline{Apr}}_{\equiv ^{l}_{F}}(X)$. Hence, there is $x\in X$ such that $[a]^{l}_{F}=[x]^{l}_{F}$. Since, $X\subseteq F$ by Proposition 2.9(1) we obtain that $a\in [x]^{l}_{F}=F$, that is, ${\overline{Apr}}_{\equiv ^{l}_{F}}(X)\subseteq F$. Conversely, let $f\in F$. Then $[f]^{l}_{F}=F$ and it shows that $[f]^{l}_{F}\cap X=X\ne \emptyset$. Therefore, $f\in {\overline{Apr}}_{\equiv ^{l}_{F}}(X)$, and hence ${\overline{Apr}}_{\equiv ^{l}_{F}}(X)=F$. The converse follows from Proposition 3.1(1). Similarly, we can prove the rest.

• 2. Let $f\in F$. Therefore, $[f]^{l}_{F}=[f]^{r}_{F}=F\subseteq X$ and it shows that $F\subseteq \underline{Apr}_{\equiv ^{l}_{F}}(X)\cap \underline{Apr}_{\equiv ^{r}_{F}}(X)$. Conversely, assume that $f\in F$. The converse follows from Proposition 3.1(1). Similarly, we can prove the rest.

$\square$

Proposition 3.7

Let ${\mathfrak {A}}$ be a residuated lattice and F, G be filters of ${\mathfrak {A}}$. Then the following assertions hold:

• 1. $F\subseteq G$ if and only if $\underline{Apr}_{\equiv _{l}^{F}}(G)=\underline{Apr}_{\equiv _{r}^{F}}(G)=G={\overline{Apr}}_{\equiv _{r}^{F}}(G)={\overline{Apr}}_{\equiv _{l}^{F}}(G)$. In particular, if F is a normal filter of ${\mathfrak {A}}$ we have $F\subseteq G$ if and only if $\underline{Apr}_{F}(G)=G={\overline{Apr}}_{F}(G)$;

• 2. $F\subseteq {\overline{Apr}}_{\equiv _{r}^{F}}(G)\cap {\overline{Apr}}_{\equiv _{l}^{F}}(G)$. In particular, if F is a normal filter of ${\mathfrak {A}}$ we have $F\subseteq {\overline{Apr}}_{F}(G)$.

Proof

• 1. Let $F\subseteq G$. By Proposition 3.1(1), we have $\underline{Apr}_{\equiv _{l}^{F}}(G)\subseteq G\subseteq {\overline{Apr}}_{\equiv _{l}^{F}}(G)$. Now, let $a\in {\overline{Apr}}_{\equiv _{l}^{F}}(G)$. So $[a]^{l}_{F}\cap G\ne \emptyset$ and it implies that there is $g\in G$ such that $d^l(a,g)\in F\subseteq G$. Therefore, $a\in G$ and it shows $G={\overline{Apr}}_{\equiv _{l}^{F}}(G)$. Hence, by Proposition 3.1(3), we get the results. Similarly, we can prove the rest. Conversely, suppose that $\underline{Apr}_{\equiv _{l}^{F}}(G)=G={\overline{Apr}}_{\equiv _{l}^{F}}(G)$. If $x\in F$ then $1\in [x]^{l}_{F}\cap G$ and it means that $x\in {\overline{Apr}}_{\equiv _{l}^{F}}(G)=G$.

• 2. Let $x\in F$. Then we have $1\in [x]^{l}_{F}\cap G$ and it shows that $x\in {\overline{Apr}}_{F}(G)$.

$\square$

Proposition 3.8

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be a homomorphism. Then for any subset X of A we have

$$\begin{aligned} h({\overline{Apr}}_{coker(h)}(X))=h(X). \end{aligned}$$

Proof

According to Proposition 3.1(1), it is obvious that $h(X)\subseteq h({\overline{Apr}}_{coker(h)}(X))$. Conversely, if $b\in h({\overline{Apr}}_{coker(h)}(X))$ then there is $a\in {\overline{Apr}}_{coker(h)}(X)$ such that $b=h(a)$. It shows that there exists $x\in X$ such that $h(d^l(x,a))=1$ and it implies that $d^l(h(x),b)=1$. Thus, by Proposition 2.1(4) we obtain that $h(x)\rightarrow _l b=1$ and $b\rightarrow _l h(x)=1$. Also, by Proposition 2.1(2) we get that $h(x)\le b$ and $b\le h(x)$ and it shows that $b=h(x)\in h(X)$. $\square$

Proposition 3.9

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be an epimorphism and F be a normal filter of ${\mathfrak {A}}$ containing coker(h). Then for each subset X of A we have

• 1. $h(\underline{Apr}_{F}(X))\subseteq \underline{Apr}_{h(F)}(h(X))$;

• 2. $\underline{Apr}_{h(F)}(h(X))\subseteq h({\overline{Apr}}_{F}(X))$;

• 3. $h({\overline{Apr}}_{F}(X))\subseteq {\overline{Apr}}_{h(F)}(h(X)).$

Proof

• 1. Let $b\in h(\underline{Apr}_{F}(X))$. So there is $a\in \underline{Apr}_{F}(X)$ such that $b=h(a)$. Now, we have $h(a/F)\subseteq f(X)$ and by Corollary 2.2 we obtain that $b=h(a)\in \underline{Apr}_{h(F)}(h(X))$.

• 2. Let $b\in \underline{Apr}_{h(F)}(f(X))$. Therefore, $b/h(F)\subseteq h(X)$ and it implies that there exists $x\in X$ such that $b=h(x)$. Also, we have $x/F\cap X\ne \emptyset$ and it shows that $b\in h({\overline{Apr}}_{F}(X))$.

• 3. Let $b\in h({\overline{Apr}}_{F}(X))$. Hence, there exists $a\in {\overline{Apr}}_{F}(X)$ such that $b=h(a)$. We have $a/F\cap X\ne \emptyset$ and by Corollary 2.2 it implies that

  $$\begin{aligned} \emptyset \ne h(a/F\cap X)\subseteq h(a/F)\cap h(X)=h(a)/h(F)\cap f(X). \end{aligned}$$

  Hence, $b=h(a)\in {\overline{Apr}}_{h(F)}(h(X))$.

$\square$

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. The mapping $\pi ^{{\mathfrak {A}}}_{F}:{\mathfrak {A}}\longrightarrow {\mathfrak {A}}/F$ defined by $\pi ^{{\mathfrak {A}}}_{F}(a)=a/F$ is called the natural homomorphism. It is obvious that the natural homomorphism $\pi ^{{\mathfrak {A}}}_{F}$ is onto and $coker(\pi ^{{\mathfrak {A}}}_{F})=F$. Therefore, by Proposition 2.12 we have

$$\begin{aligned} F_n({\mathfrak {A}}/F)=\{H/F|F\subseteq H\in F_n({\mathfrak {A}})\}. \end{aligned}$$

Corollary 3.3

Let ${\mathfrak {A}}$ be a residuated lattice and $F_1,F_2\in F_n({\mathfrak {A}})$ such that $F_1\subseteq F_2$. Then for any subset X of A the following conditions hold:

• 1. $\underline{Apr}_{F_2}(X)/F_1\subseteq \underline{Apr}_{F_2/F_1}(X/F_1)$;

• 2. $\underline{Apr}_{F_2/F_1}(X/F_1)\subseteq {\overline{Apr}}_{F_2}(X)/F_1$;

• 3. ${\overline{Apr}}_{F_2}(X)/F_1\subseteq {\overline{Apr}}_{F_2/F_1}(X/F_1)$.

Proof

It is enough to consider the natural homomorphism $\pi ^{{\mathfrak {A}}}_{F_1}$ in Proposition 3.9. $\square$

Proposition 3.10

Let $h:{\mathfrak {A}}\longrightarrow {\mathfrak {B}}$ be a homomorphism and F be a normal filter of ${\mathfrak {B}}$. Then for any subset X of A and subset Y of B the following assertions hold:

• 1. $h^{\leftarrow }(\underline{Apr}_{F}(Y))\subseteq \underline{Apr}_{h^{\leftarrow }(F)}(f^{\leftarrow }(Y))$. Moreover, the equality holds if h is onto;

• 2. $\underline{Apr}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y))\subseteq h^{\leftarrow }({\overline{Apr}}_{F}(Y))$;

• 3. if h is onto then $h^{\leftarrow }({\overline{Apr}}_{F}(Y))\subseteq {\overline{Apr}}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y))$;

• 4. ${\overline{Apr}}_{h^{\leftarrow }(F)}(X)\subseteq h^{\leftarrow }({\overline{Apr}}_{F}(h(X)))$.

Proof

• 1. Let $h^{\leftarrow }(\underline{Apr}_{F}(Y))$ be a non-empty set. Consider, $a\in h^{\leftarrow }(\underline{Apr}_{F}(Y))$. Thus, $h(a)\in \underline{Apr}_{F}(Y)$ and it means that $h(a)/F\subseteq Y$. By Corollary 2.3 we have $h(a/h^{\leftarrow }(F))\subseteq Y$ and it shows that $a/h^{\leftarrow }(F)\subseteq h^{\leftarrow }(Y)$. Therefore, we obtain that $a\in \underline{Apr}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y))$. Now, let h be a surjection. By Proposition 3.9(1) we have $h(\underline{Apr}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y)))\subseteq \underline{Apr}_{h(h^{\leftarrow }(F))}(h(h^{\leftarrow }(Y))))=\underline{Apr}_{F}(Y)$ and it shows that the equality holds.

• 2. Let $\underline{Apr}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y))$ be a non-empty set. Let $a\in \underline{Apr}_{h^{\leftarrow }(F)}(h^{\leftarrow }(Y))$. So $a/h^{\leftarrow }(F)\subseteq h^{\leftarrow }(Y)$ and it concludes that $h(a/h^{\leftarrow }(F))\subseteq Y\cap h(a)/F$. Thus, $a\in h^{\leftarrow }({\overline{Apr}}_{F}(Y))$.

• 3. Let h be a surjection and $a\in h^{\leftarrow }({\overline{Apr}}_{F}(Y))$. So $h(a)\in {\overline{Apr}}_{F}(Y)$ and it concludes that $h(a)/F\cap Y\ne \emptyset$. Thus, $h^{\leftarrow }(h(a)/F)\cap h{\leftarrow }(Y)\ne \emptyset$ and it implies that $a/h^{\leftarrow }(F)\cap h^{\leftarrow }(Y)\ne \emptyset$. It shows that $a\in {\overline{Apr}}_{f^{\leftarrow }(F)}(h^{\leftarrow }(Y))$.

• 4. Let $a\in {\overline{Apr}}_{h^{\leftarrow }(F)}(X)$. So $a/h^{\leftarrow }(F)\cap X\ne \emptyset$ and it implies that $h(a)/F\cap h(X)\ne \emptyset$. It shows that $a\in h^{\leftarrow }({\overline{Apr}}_{F}(h(X)))$.

$\square$

4 Rough subalgebras and rough filters

In this section, we introduce the notion of rough subalgebras and rough filters of a residuated lattice as a generalization of the notion of subalgebras and filters of a residuated lattice.

Definition 4.1

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. A non-empty subset X of A is called an upper (resp., a lower) rough subalgebra (or filter) of ${\mathfrak {A}}$ w.r.t F, if the upper (resp., the lower) approximation of X w.r.t F is a subalgebra (or filter) of ${\mathfrak {A}}$. If X is both an upper and a lower rough subalgebra (or filter) of ${\mathfrak {A}}$ w.r.t F, we say S is a rough subalgebra (or filter) of ${\mathfrak {A}}$ w.r.t F.

Proposition 4.1

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. If S is a subalgebra of ${\mathfrak {A}}$ then S is an upper rough subalgebra of ${\mathfrak {A}}$ w.r.t F.

Proof

It is obvious that $0,1\in {\overline{Apr}}_F(S)$. Now, let $x,y\in {\overline{Apr}}_F(S)$. So there are $s_x,s_y\in S$ such that $d^l(x,s_x),d^l(y,s_y)\in F$. Since F is a normal filter, then $\equiv _F$ is a congruence relation and it states $d^l(x\wedge y,s_x\wedge s_y),d^l(x\vee y,s_x\vee s_y),d^l(x\odot y,s_x\odot s_y),d^l(x\rightarrow _l y,s_x\rightarrow _l s_y),d^l(x\rightarrow _r y,s_x\rightarrow _r s_y)\in F$. Therefore, $x\wedge y,x\vee y,x\odot y,x\rightarrow _l y,x\rightarrow _r y\in {\overline{Apr}}_F(S)$ and it shows that ${\overline{Apr}}_F(S)$ is a subalgebra of ${\mathfrak {A}}$. $\square$

The following example shows that a subalgebra of a residuated lattice may not be a lower rough subalgebra of it in general.

Example 4.1

According to Example 2.7, $S=\{0,a,h,1\}$ is a subalgebra of ${\mathfrak {A}}_{10}$. We have $\underline{Apr}_F(S)=\{0,a\}$ which clearly it is not a subalgebra of ${\mathfrak {A}}_{10}$.

Proposition 4.2

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then for each non-empty subset of X of A we obtain

$$\begin{aligned} Sg({\overline{Apr}}_F(X))\subseteq {\overline{Apr}}_F(Sg(X)). \end{aligned}$$

Proof

By definition of a generated subalgebra we have $X\subseteq Sg(X)$. Also, by Proposition 3.1(4), we conclude that ${\overline{Apr}}_F(X)\subseteq {\overline{Apr}}_F(Sg(X))$. By Proposition 4.1, we know that ${\overline{Apr}}_F(Sg(X))$ is a subalgebra of ${\mathfrak {A}}$ and it shows that $Sg({\overline{Apr}}_F(X))\subseteq {\overline{Apr}}_F(Sg(X))$. $\square$

The following example shows that we can not replace the inclusion symbol be equal sign in Proposition 4.2.

Example 4.2

Consider Example 2.7 and let $X=\{0,a\}$. Then $Sg^{{\mathfrak {A}}}(X)=\{0,a,h,1\}$ and it implies that ${\overline{Apr}}_F(Sg^{{\mathfrak {A}}}(X))=\{0,a,e,f,g,h,1\}$. On the other hand, we have $Sg^{{\mathfrak {A}}}({\overline{Apr}}_F(X))=\{0,a\}$. Hence, in general ${\overline{Apr}}_F(Sg^{{\mathfrak {A}}}(X))\nsubseteq Sg^{{\mathfrak {A}}}({\overline{Apr}}_F(X))$.

Proposition 4.3

(Third Isomorphism Theorem) Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then for any subalgebra S of ${\mathfrak {A}}$ we have

$$\begin{aligned} S/F\cap S\cong {\overline{Apr}}_F(S)/F\cap {\overline{Apr}}_F(S). \end{aligned}$$

Proof

By Remark 2.1, $F\cap S$ is a normal filter of S and $F\cap {\overline{Apr}}_F(S)$ is a normal filter of ${\overline{Apr}}_F(S)$. Now, we define the map $h:S\longrightarrow {\overline{Apr}}_F(S)/F\cap {\overline{Apr}}_F(S)$ by $h(s)=s/F\cap {\overline{Apr}}_F(S)$, for any $s\in S$. It is easy to check that h is a homomorphism of residuated lattices. Now, consider $a/F\cap {\overline{Apr}}_F(S)\in {\overline{Apr}}_F(S)/F\cap {\overline{Apr}}_F(S)$. So there is $s\in S$ such that $a/F=s/F$. Now, one can check that $h(s)=a/F\cap {\overline{Apr}}_F(S)$ and it implies that h is an epimorphism. So by the first isomorphism theorem we have

$$\begin{aligned} S/coker(h)\cong {\overline{Apr}}_F(S)/F\cap {\overline{Apr}}_F(S). \end{aligned}$$

Also, if $s\in coker(h)$ then $s/F\cap {\overline{Apr}}_F(S)=1/F\cap {\overline{Apr}}_F(S)$ and it implies that $s=d^l(s,1)\in F\cap {\overline{Apr}}_F(S)$. Thus, $s\in F$ and it shows that $coker(h)\subseteq F\cap S$. On the other hand, $F\cap S\subseteq coker(h)$ and it shows that $coker(h)=F\cap S$. It completes the result. $\square$

Proposition 4.4

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then for any filter G of ${\mathfrak {A}}$, ${\overline{Apr}}_F(G)$ is a filter of ${\mathfrak {A}}$.

Proof

Let $x,y\in {\overline{Apr}}_F(G)$. So there are $g_x,g_y\in G$ such that $d^l(x,g_x),d^l(y,g_y)\in F$. Since F is a normal filter, then we have $d^l(x\odot y,g_x\odot g_y)\in F$ and so on $x\odot y/F=g_x\odot g_y/F$ and it shows that $x\odot y\in {\overline{Apr}}_F(G)$. Now, let $x\in {\overline{Apr}}_F(G)$ and $y\in A$. So there is $g_x\in G$ such that $d(x,g_x)\in F$. Since F is a normal filter, we get that $d^l(x\vee y,g_x\vee y)\in F$ and so on $x\vee y/F=g_x\vee y/F$. On the other hand, by Proposition 2.3 we have $g_x\vee y\in G$ and it shows that $x\vee y/F\cap G\ne \emptyset$. Hence, $x\vee y\in {\overline{Apr}}_F(G)$. So we conclude that ${\overline{Apr}}_F(G)$ is a filter of ${\mathfrak {A}}$. $\square$

The following example shows that a filter of a residuated lattice may not be a lower rough filter of it in general.

Example 4.3

Consider Example 3.1. By Example 2.15 we have $F_2=\{h,1\}\in F_n({\mathfrak {A}}_{10})$. Then $\underline{Apr}_{F_5}(F_2)=\emptyset$ which clearly it is not a filter of ${\mathfrak {A}}_{10}$.

Proposition 4.5

Let ${\mathfrak {A}}$ be a residuated lattice and F be filter of ${\mathfrak {A}}$. Then

• 1. $F\subseteq {\overline{Apr}}_{\equiv _{F}^{l}}(D_{s}({\mathfrak {A}}))\subseteq \{a\in A|\lnot _{rl}a\in F\}$;

• 2. $F\subseteq {\overline{Apr}}_{\equiv _{F}^{r}}(D_{s}({\mathfrak {A}}))\subseteq \{a\in A|\lnot _{lr}a\in F\}$;

• 3. if F is a normal filter then $F\subseteq {\overline{Apr}}_{F}(D_{s}({\mathfrak {A}}))\subseteq \{a\in A|\lnot _{ll}a\odot \lnot _{rr}a\in F\}$.

Proof

According to Proposition 2.6, $D_{s}({\mathfrak {A}})$ is a proper filter of ${\mathfrak {A}}$. So by Proposition 3.7(2), we obtain that $F\subseteq {\overline{Apr}}_{\equiv _{F}^{l}}(D_{s}({\mathfrak {A}}))$. Now, consider $a\in {\overline{Apr}}_{\equiv _{F}^{l}}(D_{s}({\mathfrak {A}}))$. Therefore, $[a]_{F}^{l}\cap D_{s}({\mathfrak {A}})\ne \emptyset$ and it implies that there is an element $x\in X$ such that $d^l(a,x)\in F$ and $\lnot _lx=0$. By Proposition 2.8(5), we get $d^l(a,x)\le d^r(\lnot _lx,\lnot _la)$ and it states that $\lnot _{rl}a=d^r(\lnot _lx,\lnot _la)\in F$. Similarly, we can prove part 2. Also, part 3 is concluded by part 1 and 2. $\square$

Definition 4.2

[40] Let F be a filter of residuated lattice ${\mathfrak {A}}$.

• F is called a left (right) Boolean filter if it satisfies the following condition for any $x,y\in A$;

  $$\begin{aligned} {B^{l}} x\vee \lnot _{l(r)} x\in F; \end{aligned}$$

• F is called a left (right) Heyting filter if it satisfies the following condition for any $x\in A$;

  $$\begin{aligned} {H^{l}} (x\wedge y)\rightarrow _{l(r)}(x\odot y)\in F; \end{aligned}$$

• F is called a left (right) MV filter if it satisfies the following condition for any $x,y\in A$;

  $$\begin{aligned} {MV^{l}} ((x\rightarrow _{l(r)} y)\rightarrow _{r(l)} y)\rightarrow _{l(r)}((y\rightarrow _{l(r)} x)\rightarrow _{r(l)} x)\in F; \end{aligned}$$

• F is called a left (right) MTL filter if it satisfies the following condition for any $x,y\in A$;

  $$\begin{aligned} {MTL^{l}} (x\rightarrow _{l(r)} y)\vee (y\rightarrow _{l(r)} x)\in F; \end{aligned}$$

• F is called a left$R\ell$ filter if it satisfies the following assertion for any $x,y\in A$;

  $$\begin{aligned} {R\ell ^{l}} (x\wedge y)\rightarrow _{l}((x\rightarrow _l y)\odot x)\in F; \end{aligned}$$

  Also, F is called a right$R\ell$ filter if it satisfies the following assertion for any $x,y\in A$;

  $$\begin{aligned} {R\ell ^{r}} (x\wedge y)\rightarrow _{r}(x\odot (x\rightarrow _r y))\in F. \end{aligned}$$

Example 4.4

Consider the proper residuated lattice ${\mathfrak {A}}_6$ in Example 2.13. One check that $F_1=\{c,d,1\}$ is a right Boolean filter, a right Heyting filter of ${\mathfrak {A}}_6$ and a right MV filter. But it is not a left Boolean filter since $b\vee \lnot _{l} b=b\vee 0=b\notin F_1$, it is not a left Heyting filter since $a\rightarrow _l a^2=a\rightarrow _l 0=b\notin F_1$ and it is not a left MV filter since $((a\rightarrow _l 0)\rightarrow _r 0)\rightarrow _l ((0\rightarrow _l a)\rightarrow _r a)=c\rightarrow _l a=b\notin F_1$. Also, $F_2=\{b,d,1\}$ is a left Boolean filter, a left Heyting filter and a left MV filter. But it is not a right Boolean filter since $c\vee \lnot _{r} c=c\vee 0=c\notin F_2$, it is not a right Heyting filter since $a\rightarrow _r a^2=a\rightarrow _r 0=c\notin F_2$ and it is not a right MV filter since $((a\rightarrow _r 0)\rightarrow _l 0)\rightarrow _r ((0\rightarrow _r a)\rightarrow _l a)=b\rightarrow _r a=c\notin F_2$.

Example 4.5

Consider Example 2.10. Then $F_3=\{c,d,e,1\}$ is a left and right MTL filter of the proper residuated lattice ${\mathfrak {A}}_7$. We note that $F_2=\{e,1\}$ is a right MTL filter but it is not a left MTL filter since $(b\rightarrow _l c)\vee (c\rightarrow _l b)=d\vee b=d\notin F_2$. Also, $\{1\}$ is a filter but it is not a left MTL filter since $(b\rightarrow _l c)\vee (c\rightarrow _l b)=d\vee b=d\notin \{1\}$ and it is not a right MTL filter since $(b\rightarrow _r c)\vee (c\rightarrow _r b)=e\vee b=e\notin \{1\}$.

The extension theorem of filters is obtained from the following theorem.

Theorem 4.1

(Extension property) Let F and G be filters of a residuated lattice ${\mathfrak {A}}$ such that $F\subseteq G$. If F is a left (right) Boolean filter, a left (right) Heyting filter, a left (right) MV filter, a left (right) MTL filter or a left (right) $R\ell$ filter then G is a left (right) Boolean filter, a left (right) Heyting filter, a left (right) MV filter, a left (right) MTL filter or a left (right) $R\ell$ filter, respectively.

Proof

It is straightforward by Definition 4.2. $\square$

Corollary 4.1

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then if G is a left (right) Boolean filter, a left (right) Heyting filter, a left (right) MV filter, a left (right) MTL filter or a left (right) $R\ell$ filter of ${\mathfrak {A}}$, then ${\overline{Apr}}_F(G)$ is a left (right) Boolean filter, a left (right) Heyting filter, a left (right) MV filter, a left (right) MTL filter or a left (right) $R\ell$ filter of ${\mathfrak {A}}$, respectively.

Proof

Let G be a left Boolean filter of ${\mathfrak {A}}$. By Proposition 4.4, we conclude that ${\overline{Apr}}_F(G)$ is a filter of ${\mathfrak {A}}$. Also, by Proposition 3.1(1) we have $G\subseteq {\overline{Apr}}_F(G)$. Thus, by Theorem 4.1 we conclude that ${\overline{Apr}}_F(G)$ is a left Boolean filter of ${\mathfrak {A}}$. Analogously, we can show that the other cases. $\square$

Proposition 4.6

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then for each non-empty subset X of A we have

$$\begin{aligned} Fi({\overline{Apr}}_F(X))={\overline{Apr}}_F(Fi(X)). \end{aligned}$$

Proof

We have $X\subseteq Fi(X)$. Also, by Proposition 3.1(4), we conclude that ${\overline{Apr}}_F(X)\subseteq {\overline{Apr}}_F(Fi(X))$. By Proposition 4.4, we know that ${\overline{Apr}}_F(Fi(X))$ is a filter of ${\mathfrak {A}}$ and it shows that $Fi({\overline{Apr}}_F(X))\subseteq {\overline{Apr}}_F(Fi(X))$.

Now, assume that $a\in {\overline{Apr}}_{F}(Fi(X))$. Thus, there exists $b\in a/F\cap Fi(X)$. It implies that there are $x_1,\ldots ,x_n\in X$, for some integer n such that $x_1\odot \cdots \odot x_n\le b$. Also, we have $b\rightarrow _l a\in F$ so on there is $f\in F$ such that $b\rightarrow _l a=f$. It concludes $f\odot b\le a$ that is $b\le f\rightarrow _r a$. by hypothesis we obtain that $x_1\odot \cdots \odot x_n\le f\rightarrow _r a$ and hence $x_1\odot \cdots \odot x_{n-1}\odot (x_n\odot f)\le a$. Since F is a normal filter, we have $x_n\odot f\in {\overline{Apr}}_{F}(X)$ and it shows that $a\in Fi({\overline{Apr}}_F(X))$. $\square$

Corollary 4.2

Let ${\mathfrak {A}}$ be a residuated lattice and F be a normal filter of ${\mathfrak {A}}$. Then for any family of filters $\{F_i\}_{i\in I}$ of A we have

$$\begin{aligned} {\overline{Apr}}_F(\vee _{i\in I} F_i)=Fi(\cup _{i\in I} {\overline{Apr}}_F(F_i)). \end{aligned}$$

Proof

By Proposition 4.6, we have

$$\begin{aligned} {\overline{Apr}}_F(\vee _{i\in I} F_i)={\overline{Apr}}_F(Fi(\cup _{i\in I} F_i))=Fi({\overline{Apr}}_F(\cup _{i\in I} F_i)) \end{aligned}$$

and by Proposition 3.1(7), we have $Fi({\overline{Apr}}_F(\cup _{i\in I} F_i))=Fi(\cup _{i\in I}{\overline{Apr}}_F(F_i))$ and it get the results. $\square$

5 Conclusion

Since Pawlak [35] proposed the notion of rough sets, his idea has been applied to various algebraic structures. In this paper, we introduce the notion of the lower rough approximation and the upper rough approximation on a residuated lattice ${\mathfrak {A}}$ induced by a normal filter F. We study them under co-annihilators, homomorphisms and quotients and give some examples. Also, we introduce the notions of rough subalgebras and rough filters in a residuated lattices. We show that if ${\mathfrak {A}}$ is a residuated lattice and F is a normal filter of ${\mathfrak {A}}$ then each subalgebra of ${\mathfrak {A}}$ is an upper rough subalgebra of ${\mathfrak {A}}$ w.r.t F. We prove that for any filter G of ${\mathfrak {A}}$, ${\overline{Apr}}_F(G)$ is a filter of ${\mathfrak {A}}$ and for any left (right) Boolean filter, left (right) Heyting filter, left (right) MV filter, left (right) MTL filter or left (right) $R\ell$ filter G of ${\mathfrak {A}}$, ${\overline{Apr}}_F(G)$ is a left (right) Boolean filter, a left (right) Heyting filter, a left (right) MV filter, a left (right) MTL filter or a left (right) $R\ell$ filter of ${\mathfrak {A}}$, respectively. Also, we state that for each non-empty subset X of A we have $Fi({\overline{Apr}}_F(X))={\overline{Apr}}_F(Fi(X))$ and then we conclude that for any family of filters $\{F_i\}_{i\in I}$ of A we have ${\overline{Apr}}_F(\vee _{i\in I} F_i)=Fi(\cup _{i\in I} {\overline{Apr}}_F(F_i))$.