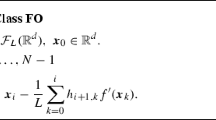Abstract
We consider minimization of a smooth nonconvex objective function using an iterative algorithm based on Newton’s method and the linear conjugate gradient algorithm, with explicit detection and use of negative curvature directions for the Hessian of the objective function. The algorithm tracks Newton-conjugate gradient procedures developed in the 1980s closely, but includes enhancements that allow worst-case complexity results to be proved for convergence to points that satisfy approximate first-order and second-order optimality conditions. The complexity results match the best known results in the literature for second-order methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the unconstrained optimization problem
where \(f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a twice Lipschitz continuously differentiable function that is nonconvex in general. We further assume that f is bounded below for all x, by some constant \(f_{\mathrm{low}}\). Although the Hessian \(\nabla ^2 f(x)\) is well defined for such functions, we assume that full evaluation of this matrix is undesirable from a computational viewpoint, though we assume that Hessian-vector products of the form \(\nabla ^2 f(x) v\) can be computed with reasonable efficiency, for arbitrary vectors v, as is often the case when n is large.
Unconstrained minimization of nonconvex smooth functions of many variables is a much-studied paradigm in optimization. Approaches such as limited-memory BFGS and nonlinear conjugate gradient are widely used to tackle (1), particularly in the case of large dimension n. Another popular approach, known as “Newton-CG,” applies the (linear) conjugate gradient (CG) method to the second-order Taylor-series approximation of f around the current iterate \(x_k\). Each iteration of CG requires computation of one Hessian-vector product of the form \(\nabla ^2 f(x_k) v\). A trust-region variant of Newton-CG, due to Steihaug [27], terminates the CG iterations when sufficient accuracy is achieved in minimizing the quadratic approximation, when a CG step leads outside the trust region, or when negative curvature is encountered in \(\nabla ^2 f(x_k)\). A line-search variant presented in [25] applies CG until some convergence criterion is satisfied, or until negative curvature is encountered, in which case the search direction reverts to the negative gradient.
Theoretical guarantees for Newton-CG algorithms have been provided, e.g. in [12, 15,16,17, 25]. Convergence analysis for such methods typically shows that accumulation points are stationary, that is, they satisfy the first-order optimality condition \(\nabla f(x)=0\). Local linear or superlinear convergence to a point satisfying second-order sufficient conditions is sometimes also proved for Newton-CG methods. Although several Newton-type methods have been analyzed from a global complexity perspective [8], particularly in terms of outer iterations and derivative evaluations, bounds that explicitly account for the use of inexact Newton-CG techniques have received less attention in the optimization literature. Meanwhile, with the recent upsurge of interest in complexity, several new algorithms have been proposed that have good global complexity guarantees. We review some such contributions in Sect. 2. In most cases, these new methods depart significantly from those seen in the traditional optimization literature, and there are questions surrounding their practical appeal.
Our aim in this paper is to develop a method that hews closely to the Newton-CG approach, but which comes equipped with certain safeguards and enhancements that allow worst-case complexity results to be proved. At each iteration, we use CG to solve a slightly damped version of the Newton equations, monitoring the CG iterations for evidence of indefiniteness in the Hessian. If the CG process terminates with an approximation to the Newton step, we perform a backtracking line search along this direction. Otherwise, we step along a negative curvature direction for the Hessian, obtained either from the CG procedure on the Newton equations, or via some auxiliary computation (possibly another CG process). In either case, we can show that significant decrease can be attained in f at each iteration, at reasonable computational cost (in terms of the number of gradient evaluations or Hessian-vector products), allowing worst-case complexity results to be proved.
The remainder of the paper is organized as follows. We position our work within the existing literature in Sect. 2. Our algorithm is described in Sect. 3. Section 4 contains the complexity analysis, showing both a deterministic upper bound on the computation required to attain approximate first-order conditions (Sect. 4.2) and a high-probability upper bound on the computation required to satisfy approximate second-order necessary conditions (Sect. 4.3). Section 5 contains some conclusions and discussion. Several technical results and proofs related to CG are gathered in the Appendix.
Assumptions, Background, Notation Our algorithm seeks a point that approximately satisfies second-order necessary conditions for optimality, that is,
for specified small positive tolerances \(\epsilon _{g}\) and \(\epsilon _{H}\). (Here and subsequently, \(\Vert \cdot \Vert \) denotes the Euclidean norm, or its induced norms on matrices.) We make the following standard assumptions throughout.
Assumption 1
The level set \(\mathcal {L}_f(x_0) = \{x | f(x) \le f(x_0)\}\) is compact.
Assumption 2
The function f is twice uniformly Lipschitz continuously differentiable on an open neighborhood of \(\mathcal {L}_f(x_0)\) that includes the trial points generated by the algorithm. We denote by \(L_H\) the Lipschitz constant for \(\nabla ^2 f\) on this neighborhood.
Note that Assumption 2 is made for simplicity of exposition; slightly weaker variants could be used at the expense of some complication in the analysis.
Under these two assumptions, there exist scalars \(f_{\mathrm{low}}\), \(U_g > 0\), and \(U_H > 0\) such that the following are satisfied for \(x \in \mathcal {L}_f(x_0)\):
We observe that \(U_H\) is a Lipschitz constant for the gradient.
For any x and d such that Assumption 2 is satisfied at x and \(x+d\), we have
Notationally, we use order notation \({{\mathcal {O}}}\) in the usual sense, whereas \({\tilde{{\mathcal {O}}}}(\cdot )\) represents \(\mathcal{O}\) with logarithmic terms omitted. We use such notation in bounding iteration count and computational effort, and focus on the dependencies of such complexities on \(\epsilon _{g}\) and \(\epsilon _{H}\). (In one of our final results—Corollary 2—we also show explicitly the dependence on n and \(U_H\).)
2 Complexity in nonconvex optimization
In recent years, many algorithms have been proposed for finding a point that satisfies conditions (2), with iteration complexity and computational complexity bounded in terms of \(\epsilon _{g}\) and \(\epsilon _{H}\). We review several works most relevant to this paper here, and relate their results to our contributions. For purposes of computational complexity, we define the unit of computation to be one Hessian-vector product or one gradient evaluation, implicitly using the observation from computational/algorithmic differentiation [18] that these two operations differ in cost only by a modest factor, independent of the dimension n.
Classical second-order convergent trust-region schemes [12] can be shown to satisfy (2) after at most \(\mathcal {O}(\max \{\epsilon _{g}^{-2}\epsilon _{H}^{-1}, \epsilon _{H}^{-3}\})\) iterations [10]. For the class of second-order algorithms (that is, algorithms which rely on second-order derivatives and Newton-type steps) the best known iteration bound is \(\mathcal {O}(\max \{\epsilon _{g}^{-3/2}, \epsilon _{H}^{-3}\})\). This bound was first established for a form of cubic regularization of Newton’s method [24]. Following this paper, numerous other algorithms have also been proposed which match this bound, see for example [3, 8, 13, 14, 23].
A recent trend in complexity analysis of these methods also accounts for the computational cost of each iteration, thus yielding a bound on the computational complexity. Two independent proposals, respectively based on adapting accelerated gradient to the nonconvex setting [6] and approximately solving the cubic subproblem [1], require \({\tilde{{\mathcal {O}}}}(\epsilon ^{-7/4})\) operations (with high probability, showing dependency only on \(\epsilon \)) to find a point x that satisfies
The difference of a factor of \(\epsilon ^{-1/4}\) with the results presented above arises from the cost of computing a negative curvature direction of \(\nabla ^2 f(x_k)\) and/or the cost of solving a linear system. The probabilistic nature of the bound is generally due to the introduction of randomness in the curvature estimation process; see [2, 28] for two recent examples. A complexity bound of the same type was also established for a variant of accelerated gradient free of negative curvature computation, that regularly adds a random perturbation to the iterate when the gradient norm is small [19].
In an interesting followup to [6], an algorithm based on accelerated gradient with a nonconvexity monitor was proposed [5]. It requires at most \({\tilde{{\mathcal {O}}}}( \epsilon ^{-7/4})\) iterations to satisfy (5) with high probability. However, if one is concerned only with satisfying the gradient condition \(\Vert \nabla f(x) \Vert \le \epsilon \), the \({\tilde{{\mathcal {O}}}}(\epsilon ^{-7/4})\) bound holds deterministically. Note that this bound represents an improvement over the \(\mathcal {O}(\epsilon ^{-2})\) of steepest descent and classical Newton’s method [7]. The improvement is due to a modification of the accelerated gradient paradigm that allows for deterministic detection and exploitation of negative curvature directions in regions of sufficient nonconvexity.
In a previous work [26], two authors of the current paper proposed a Newton-based algorithm in a line-search framework which has an iteration complexity of \(\mathcal {O}(\max \{\epsilon _{g}^{-3/2}, \epsilon _{H}^{-3}\})\) when the subproblems are solved exactly, and a computational complexity of \({\tilde{{\mathcal {O}}}}\left( \epsilon ^{-7/4}\right) \) Hessian-vector products and/or gradient evaluations, when the subproblems are solved inexactly using CG and the randomized Lanczos algorithm. Compared to the accelerated gradient methods, this approach aligns more closely with traditional optimization practice, as described in Sect. 1.
Building on [26], the current paper describes a similar line-search framework with inexact Newton steps, but uses a modified version of CG to solve the system of Newton equations, without first checking for positive definiteness of the coefficient matrix. The modification is based in part on a convexity monitoring device introduced in the accelerated gradient algorithms mentioned above. An implicit cap is imposed on the number of CG iterations that are used to solve the damped Newton system. We show that once this cap is reached, either the damped Newton system has been solved to sufficient accuracy or else a direction of “sufficiently negative curvature” has been identified for the Hessian. (A single extra CG iteration may be needed to identify the negative curvature direction, in much the same manner as in [5] for accelerated gradient.) In contrast to the previous work [26], no estimate of the smallest eigenvalue of the Hessian is required prior to computing a Newton step. In addition to removing potentially unnecessary computation, this approach allows a deterministic result for first-order optimality to be proved, as in [5].
We are deliberate in our use of CG rather than accelerated gradient as the method of choice for minimizing the quadratic objective that arises in the damped Newton step. When applied to strongly convex quadratics, both approaches have similar asymptotic linear convergence rates that depend only on the extreme eigenvalues of the Hessian, and both can be analyzed using the same potential function [20] and viewed as two instances of an underlying “idealized algorithm” [21]. However, CG has several advantages: It has a rich convergence theory that depends on the full spectrum of eigenvalues; it is fully adaptive, requiring no prior estimates of the extreme eigenvalues; and its practical performance on convex quadratics is superior. (See, for example, [25, Chapter 5] for a description of these properties.) Further, as we prove in this paper (Sect. 3.1), CG can be adapted to detect nonconvexity efficiently in a quadratic function, without altering its core properties. We show in addition (see Sect. 3.2 and Appendix B) that by applying CG to a linear system with a random right-hand side, we can find a direction of negative curvature in an indefinite matrix efficiently, with the same iteration complexity as the randomized Lanczos process of [22] used elsewhere.
The practical benefits of CG in large-scale optimization have long been appreciated. We establish here that with suitable enhancements, methods based on CG can also be equipped with good complexity properties as well.
3 Damped-Newton/Capped-CG method with negative curvature steps
We describe our algorithm in this section, starting with its two major components. The first component, described in Sect. 3.1, is a linear conjugate gradient procedure that is used to solve a slightly damped Newton system. This procedure includes enhancements to detect indefiniteness in the Hessian and to restrict the number of iterations. Because of this implicit bound on the number of iterations, we refer to it as “Capped CG.” The second component (see Sect. 3.2) is a “minimum eigenvalue oracle” that seeks a direction of negative curvature for a symmetric matrix, along with its corresponding vector. The main algorithm is described in Sect. 3.3.

3.1 Capped conjugate gradient
Conjugate Gradient (CG) is a widely used technique for solving linear equations with symmetric positive definite coefficient matrices or, equivalently, minimizing strongly convex quadratic functions. We devise a modified CG algorithm and apply it to a system of the form \({\bar{H}}y = -g\), where \({\bar{H}}= H + 2\epsilon I\) is a damped version of the symmetric matrix H, which is our notational proxy for the Hessian \(\nabla ^2 f(x_k)\).
Algorithm 1 presents our Capped CG procedure. The main loop consists of classical CG iterations. When \({\bar{H}}\succeq \epsilon I\), Algorithm 1 will generate the same iterates as a classical conjugate gradient method applied to \({\bar{H}}y=-g\), and terminate at an inexact solution of this linear system. When \({\bar{H}}\not \succeq \epsilon I\), the features added to Algorithm 1 cause a direction d to be identified along which \(d^\top {\bar{H}}d < \epsilon \Vert d\Vert ^2\) or, equivalently, \(d^\top H d < -\epsilon \Vert d\Vert ^2\)—a direction of “sufficiently negative curvature” for H. Directions d of this type are encountered most obviously when they arise as iterates \(y_j\) or search directions \(p_j\) in the CG iterations. But evidence of the situation \({\bar{H}}\not \succeq \epsilon I\) can arise more subtly, when the residual norms \(\Vert r_j \Vert \) decrease more slowly than we would expect if the eigenvalues of \({\bar{H}}\) were bounded below by \(\epsilon \). Accordingly, Algorithm 1 checks residual norms for slow decrease, and if such behavior is detected, it uses a technique based on one used for accelerated gradient methods in [5] to recover a direction d such that \(d^\top {\bar{H}}d < \epsilon \Vert d\Vert ^2\).
Algorithm 1 may be called with an optional input M that is meant to be an upper bound on \(\Vert H\Vert \). Whether or not this parameter is supplied, it is updated so that at any point in the execution of the algorithm, M is an upper bound on the maximum curvature of H revealed to that point. Other parameters that depend on M (namely, \(\kappa \), \({\hat{\zeta }}\), \(\tau \), and T) are updated whenever M is updated.
The following lemma justifies our use of the term “capped” in connection with Algorithm 1. Regardless of whether the condition \({\bar{H}}\succeq \epsilon I\) is satisfied, the number of iterations will not exceed a certain number \(J(M,\epsilon ,\zeta )\) that we subsequently show to be \({\tilde{{\mathcal {O}}}}(\epsilon ^{-1/2})\). (We write J for \(J(M,\epsilon ,\zeta )\) in some of the subsequent discussion, to avoid clutter.)
Lemma 1
The number of iterations of Algorithm 1 is bounded by
where \(J=J(M,\epsilon ,\zeta )\) is the smallest integer such that \(\sqrt{T}\tau ^{J/2} \le \hat{\zeta }\) where M, \({\hat{\zeta }}\), T, and \(\tau \) are the values returned by the algorithm. If all iterates \(y_i\) generated by the algorithm are stored, the number of matrix-vector multiplications required is bounded by
If the iterates \(y_i\) must be regenerated in order to define the direction d returned after (6), this bound becomes \(2\min \{n,J(M,\epsilon ,\zeta )\}+1\).
Proof
If the full n iterations are performed, without any of the termination conditions being tripped, the standard properties of CG (see Appendix A) ensure that the final residual \(r_n\) is zero, so that the condition \(\Vert r_n \Vert \le {\hat{\zeta }} \Vert r_0\Vert \) is satisfied, and termination occurs.
Since no more than n iterations are performed, the upper bound M is updated at most a finite number of times, so the quantity J is well defined.
Supposing that \(J<n\), we note from the definition of J that \(\sqrt{T}\tau ^{J/2} \Vert r_0 \Vert \le {\hat{\zeta }} \Vert r_0\Vert \). Thus at least one of the following two conditions must be satisfied at iteration J: \(\Vert r_{J} \Vert \le {\hat{\zeta }} \Vert r_0\Vert \) or \(\Vert r_{J} \Vert > \sqrt{T}\tau ^{J/2} \Vert r_0\Vert \). In either case, termination will occur at iteration J, unless it has occurred already at a previous iteration.
To derive (7), note that the main workload at each iteration j is computation of a single matrix-vector product \(H p_j\) after the increment of j (since matrix-vector products involving the matrices H and \({\bar{H}}\) and the vectors \(y_j\) and \(r_j\) can be computed in terms of this vector, in an additional O(n) operations). (The “\(+1\)” in (7) accounts for the initial matrix-vector multiplication \(H p_0\) performed prior to entering the loop.)
If we do not store additional information, we need to regenerate the information needed to compute the direction d satisfying (6) by re-running the iterations of CG, possibly up to the second-to-last iteration. This fact accounts for the additional cost of \(\min \{n,J(M,\epsilon ,\zeta )\}\) in the no-storage case.Footnote 1\(\square \)
Note that \(J(M,\epsilon ,\zeta )\) is an increasing function of M, since \(\hat{\zeta }\) is a decreasing function of M, while T and \(\tau \) (and thus \(\sqrt{T}\tau ^{j/2}\)) are increasing in M. If \(U_H\) is known in advance, we can call Algorithm 1 with \(M = U_H\) and use \(J(U_H,\epsilon ,\zeta )\) as the bound. Alternately, we can call Algorithm 1 with \(M=0\) and let it adjust M as needed during the computation. Since the final value of M will be at most \(U_H\), and since \(J(M,\epsilon ,\zeta )\) is an increasing function of M, the quantity \(J(U_H,\epsilon ,\zeta )\) provides the upper bound on the number of iterations in this case too.
We can estimate J by taking logs in its definition, as follows:
where we used \(\ln (1+\tfrac{1}{t}) \ge \tfrac{1}{t+1/2}\) to obtain the latest inequality. By replacing \(T,\tau ,\hat{\zeta },\kappa \) by their definitions in Algorithm 1, and using \( \frac{1}{1-\sqrt{\tau }} = \frac{1+\sqrt{\tau }}{1-\tau } \le \frac{2}{1-\tau }, \) we obtain
3.2 Minimum eigenvalue oracle
A minimum eigenvalue oracle is needed in the main algorithm to either return a direction of “sufficient negative curvature” in a given symmetric matrix, or else return a certificate that the matrix is almost positive definite. This oracle is stated as Procedure 2.

To implement this oracle, we can use any procedure that finds the smallest eigenvalue of H to an absolute precision of \(\epsilon /2\) with probability at least \(1-\delta \). This probabilistic property encompasses both deterministic and randomized instances of Procedure 2. In Sect. 4.3, we will establish complexity results under this general setting, and analyze the impact of the threshold \(\delta \). Several possibilities for implementing Procedure 2 have been proposed in the literature, with various guarantees. An exact, deterministic computation of the minimum eigenvalue and eigenvector (through a full Hessian evaluation and factorization) would be a valid choice for Procedure 2 (with \(\delta =0\) in that case), but is unsuited to our setting in which Hessian-vector products and vector operations are the fundamental operations. Strategies that require only gradient evaluations [2, 28] may offer similar guarantees to those discussed below.
We focus on two inexact, randomized approaches for implementing Procedure 2. The first is the Lanczos method, which finds the smallest eigenvalue of the restriction of a given symmetric matrix to a Krylov subspace based on some initial vector. When the starting vector is chosen randomly, the dimension of the Krylov subspace increases by one at each Lanczos iteration, with high probability (see Appendix B and [22]). To the best of our knowledge, [6] was the first paper to propose a complexity analysis based on the use of randomized Lanczos for detecting negative curvature. The key result is the following.
Lemma 2
Suppose that the Lanczos method is used to estimate the smallest eigenvalue of H starting with a random vector uniformly generated on the unit sphere, where \(\Vert H\Vert \le M\). For any \(\delta \in [0,1)\), this approach finds the smallest eigenvalue of H to an absolute precision of \(\epsilon /2\), together with a corresponding direction v, in at most
with probability at least \(1-\delta \).
Proof
If \(\frac{\epsilon }{4M} \ge 1\), we have \(-\tfrac{\epsilon }{4}I \prec -M I\preceq H \preceq M I \prec \tfrac{\epsilon }{4}I\). Therefore, letting b be the (unit norm) random start of the Lanczos method, we obtain
thus the desired conclusion holds at the initial point.
We now suppose that \(\frac{\epsilon }{4M} \in (0,1)\). By setting \({\bar{\epsilon }} = \frac{\epsilon }{4M}\) in Lemma 9, we have that when k is at least the quantity in (9), the estimate \(\xi _{\mathrm{{min}}}(H,b,k)\) of the smallest eigenvalue after k iterations of Lanczos applied to H starting from vector b satisfies the following bound, with probability at least \(1-\delta \):
as required. \(\square \)
Procedure 2 can be implemented by outputting the approximate eigenvalue \(\lambda \) for H, determined by the randomized Lanczos process, along with the corresponding direction v, provided that \(\lambda \le -\epsilon /2\). When \(\lambda >-\epsilon /2\), Procedure 2 returns the certificate that \(\lambda _{\mathrm{{min}}}(H) \ge -\epsilon \), which is correct with probability at least \(1-\delta \).
The second approach to implementing Procedure 2 is to apply the classical CG algorithm to solve a linear system in which the coefficient matrix is a shifted version of the matrix H and the right-hand side is random. This procedure has essentially identical performance to Lanczos in terms of the number of iterations required to detect the required direction of sufficiently negative curvature, as the following theorem shows.
Theorem 1
Suppose that Procedure 2 consists in applying the standard CG algorithm (see Appendix A) to the linear system
where b is chosen randomly from a uniform distribution over the unit sphere. Let M satisfying \(\Vert H\Vert \le M\) and \(\delta \in (0,1)\) be given. If \(\lambda _{\mathrm{{min}}}(H) < -\epsilon \), then with probability at least \(1-\delta \), CG will yield a direction v satisfying the conditions of Procedure 2 in a number of iterations bounded above by (9). Conversely, if CG runs for this number of iterations without encountering a direction of negative curvature for \(H + \tfrac{1}{2} \epsilon I\), then \(\lambda _{\mathrm{{min}}}(H) \ge -\epsilon \) with probability at least \(1-\delta \).
We prove this result, and give some additional details of the CG implementation, in Appendices A and B. We also present in Appendix B.3 a variant of the randomized-Lanczos implementation of Procedure 2 that does not require prior knowledge of the bound M such that \(\Vert H\Vert \le M\). In this variant, M itself is also estimated via randomized Lanczos, and the number of iterations required does not different significantly from (9). It follows from this result, together with our observation above that M can also be obtained adaptively inside Algorithm 1, that knowledge of the bound on \(\Vert \nabla ^2 f(x) \Vert \) is not needed at all in implementing our method.
3.3 Damped Newton-CG
Algorithm 3 presents our method for finding a point that satisfies (2). It uses two kinds of search directions. Negative curvature directions (that are also first-order descent steps) are used when they are either encountered in the course of applying the Capped CG method (Algorithm 1) to the damped Newton equations, or found explicitly by application of Procedure 2. The second type of step is an inexact damped Newton step, which is the other possible outcome of Algorithm 1. For both types of steps, a backtracking line search is used to identify a new iterate that satisfies a sufficient decrease condition, that depends on the cubic norm of the step. Such a criterion is instrumental in establishing optimal complexity guarantees in second-order methods [3, 13, 14, 26].

In its deployment of two types of search directions, our method is similar to Steihaug’s trust-region Newton-CG method [27], which applies CG (starting from a zero initial guess) to solve the Newton equations but, if it encounters a negative curvature direction during CG, steps along that direction to the trust-region boundary. It differs from the line-search Newton-CG method described in [25, Section 7.1] in that it makes use of negative curvature directions when they are encountered, rather than discarding them in favor of a steepest-descent direction. Algorithm 3 improves over both approaches in having a global complexity theory for convergence to both approximate first-order points, and points satisfying the approximate second-order conditions (2).
In Sect. 4, we will analyze the global complexity properties of our algorithm. Local convergence could also be of interest, in particular, it is probably possible to prove rapid convergence of Algorithm 3 once it reaches the neighborhood of a strict local minimum. We believe that such results would be complicated and less enlightening than the complexity guarantees, so we restrict our study to the latter.
4 Complexity analysis
In this section, we present a global worst-case complexity analysis of Algorithm 3. Elements of the analysis follow those in the earlier paper [26]. The most technical part appears in Sect. 4.1 below, where we show that the Capped CG procedure returns (deterministically) either an inexact Newton step or a negative curvature direction, both of which can be used as the basis of a successful backtracking line search. These properties are used in Sect. 4.2 to prove complexity results for convergence to a point satisfying the approximate first-order condition \(\Vert \nabla f(x) \Vert \le \epsilon _{g}\). Section 4.3 proves complexity results for finding approximate second-order points (2), leveraging properties of the minimum eigenvalue oracle, Procedure 2.
4.1 Properties of Capped CG
We now explore the properties of the directions d that are output by our Capped CG procedure, Algorithm 1. The main result deals with the case in which Algorithm 1 terminates due to insufficiently rapid decrease in \(\Vert r_j \Vert \), showing that the strategy for identifying a direction of sufficient negative curvature for H is effective.
Theorem 2
Suppose that the main loop of Algorithm 1 terminates with \(j={\hat{J}}\), where
(where \(J(M,\epsilon ,\zeta )\) is defined in Lemma 1 and (8)) because the fourth termination test is satisfied and the three earlier conditions do not hold, that is, \(y_{{\hat{J}}}^\top {\bar{H}}y_{{\hat{J}}} \ge \epsilon \Vert y_{{\hat{J}}}\Vert ^2\), \(p_{{\hat{J}}}^\top {\bar{H}}p_{{\hat{J}}} \ge \epsilon \Vert p_{{\hat{J}}}\Vert ^2\), and
where M, T, \(\hat{\zeta }\), and \(\tau \) are the values returned by Algorithm 1. Then \(y_{{\hat{J}}+1}\) is computed by Algorithm 1, and we have
The proof of Theorem 2 is quite technical, and can be found in Appendix C. It relies on an argument previously used to analyze a strategy based on accelerated gradient [5, Appendix A.1], itself inspired by a result of Bubeck [4], but it needs some additional steps that relate specifically to CG. The part of our proof that corresponds to [5, Appendix A.1] is simplified in some respects, thanks to the use of CG and the fact that a quadratic (rather than a nonlinear) function is being minimized in the subproblem.
Having shown that Algorithm 1 is well-defined, we summarize the properties of its outputs.
Lemma 3
Let Assumptions 1 and 2 hold, and suppose that Algorithm 1 is invoked at an iterate \(x_k\) of Algorithm 3 (so that \(\Vert \nabla f(x_k)\Vert> \epsilon _{g}>0\)). Let \(d_k\) be the vector obtained in Algorithm 3 from the output d of Algorithm 1. Then, one of the two following statements holds:
- 1.
d_type = SOL, and the direction \(d_k\) satisfies
$$\begin{aligned} d_k^\top (\nabla ^2 f(x_k)+2\epsilon _{H}I) d_k&\ge \epsilon _{H}\Vert d_k\Vert ^2, \end{aligned}$$(13a)$$\begin{aligned} \Vert d_k\Vert&\le {1.1 \epsilon _{H}^{-1} \Vert \nabla f(x_k)\Vert ,}\end{aligned}$$(13b)$$\begin{aligned} \Vert \hat{r}_k \Vert&\le {\frac{1}{2}\epsilon _{H}\zeta \Vert d_k \Vert ,} \end{aligned}$$(13c)where
$$\begin{aligned} \hat{r}_k := (\nabla ^2 f(x_k)+2\epsilon _{H}I) d_k+ \nabla f(x_k); \end{aligned}$$(14) - 2.
d_type = NC, and the direction \(d_k\) satisfies \(d_k^\top \nabla f(x_k) \le 0\) as well as
$$\begin{aligned} \frac{d_k^\top \nabla ^2 f(x_k) d_k}{\Vert d_k\Vert ^2} = -\Vert d_k \Vert \le -\epsilon _{H}. \end{aligned}$$(15)
Proof
For simplicity of notation, we use \(H=\nabla ^2 f(x_k)\) and \(g=\nabla f(x_k)\) in the proof. Suppose first that d_type = SOL. In that case, we have from the termination conditions in Algorithm 1 and (14) that
where \({\hat{\zeta }}\) was returned by the algorithm. We immediately recognize (13a) in (16a). We now prove (13b). Observe first that (16a) yields
so from (14) we have
where we used (16b) to obtain the final bound, together with the equality \(\Vert -g+\hat{r}_k\Vert ^2=\Vert g\Vert ^2+\Vert \hat{r}_k \Vert ^2\), which follows from \(g^\top \hat{r}_k = r_0^\top \hat{r}_k = 0\), by orthogonality of the residuals in CG (see Lemma 7, Property 2). Since \(\hat{\zeta } \le \zeta /(3 \kappa ) \le 1/6\) by construction, we have \(\Vert d_k \Vert \le \sqrt{37/36} \epsilon _{H}^{-1} \Vert g\Vert \le 1.1 \epsilon _{H}^{-1} \Vert g\Vert \), proving (13b).
The bound (13c) follows from (16b) and the logic below:
where M is the value returned by the algorithm. We finally use \({\hat{\zeta }} < 1/6\) to arrive at
yielding (13c).
In the case of d_type = NC, we recall that Algorithm 3 defines
where d denotes the direction obtained by Algorithm 1. It follows immediately that \(d_k^\top g \le 0\). Since \(d_k\) and d are collinear, we also have that
By using this bound together with (17), we obtain
proving (15). \(\square \)
4.2 First-order complexity analysis
We now find a bound on the number of iterations and the amount of computation required to identify an iterate \(x_k\) for which \(\Vert \nabla f(x_k) \Vert \le \epsilon _{g}\). We consider in turn the two types of steps (approximate damped Newton and negative curvature), finding a lower bound on the descent in f achieved on the current iteration in each case. We then prove an upper bound on the number of iterations required to satisfy these approximate first-order conditions (Theorem 3) and an upper bound on the number of gradient evaluations and Hessian-vector multiplications required (Theorem 4).
We start with a lemma concerning the approximate damped Newton steps.
Lemma 4
Suppose that Assumptions 1 and 2 hold. Suppose that at iteration k of Algorithm 3, we have \(\Vert \nabla f(x_k)\Vert > \epsilon _{g}\), so that Algorithm 1 is called. When Algorithm 1 outputs a direction \(d_k\) with d_type = SOL, then the backtracking line search requires at most \(j_k \le j_{sol}+1\) iterations, where
and the resulting step \(x_{k+1} = x_k + \alpha _k d_k\) satisfies
where
Proof
The proof tracks closely that of [26, Lemma 13]. The only significant difference is that equation (65) of [26], which is instrumental to the proof and requires a probabilistic assumption on \(\lambda _{\min }(\nabla ^2 f(x_k))\), is now ensured deterministically by (13a) from Lemma 3. As a result, both the proof and the result are deterministic. \(\square \)
When \(\Vert \nabla f(x_{k+1}) \Vert \le \epsilon _{g}\), the estimate (19) may not guarantee a “significant” decrease in f at this iteration. However, in this case, the approximate first-order condition \(\Vert \nabla f(x) \Vert \le \epsilon _{g}\) holds at the next iteration, so that Algorithm 3 will invoke Procedure 2 at iteration \(k+1\), leading either to termination with satisfaction of the conditions (2) or to a step that reduces f by a multiple of \(\epsilon _{H}^3\), as we show in Theorem 4 below.
We now address the case in which Algorithm 1 returns a negative curvature direction to Algorithm 3 at iteration k. The backtracking line search guarantees that a sufficient decrease will be achieved at such an iteration. Although the Lipschitz constant \(L_H\) appears in our result, our algorithm (in contrast to [5]) does not require this constant to be known or estimated.
Lemma 5
Suppose that Assumptions 1 and 2 hold. Suppose that at iteration k of Algorithm 3, we have \(\Vert \nabla f(x_k)\Vert > \epsilon _{g}\), so that Algorithm 1 is called. When Algorithm 1 outputs d_type = NC, the direction \(d_k\) (computed from d in Algorithm 3) has the following properties: The backtracking line search terminates with step length \(\alpha _k = \theta ^{j_k}\) with \(j_k \le j_{nc}+1\), where
and the resulting step \(x_{k+1} = x_k + \alpha _k d_k\) satisfies
with
Proof
By Lemma 3, we have from (15) that
The result can thus be obtained exactly as in [26, Lemma 1]. \(\square \)
We are ready to state our main result for first-order complexity.
Theorem 3
Let Assumptions 1 and 2 hold. Then, defining
some iterate \(x_k\), \(k=0,1,\cdots ,\bar{K}_1+1\) generated by Algorithm 3 will satisfy
Proof
Suppose for contradiction that \(\Vert \nabla f(x_k) \Vert > \epsilon _{g}\) for all \(k=0,1,\cdots ,\bar{K}_1+1\), so that
Algorithm 1 will be invoked at each of the first \(\bar{K}_1+1\) iterates of Algorithm 3. For each iteration \(l=0,1,\cdots ,\bar{K}_1\) for which Algorithm 1 returns d_type = SOL, we have from Lemma 4 and (24) that
For each iteration \(l=0,1,\cdots ,\bar{K}_1\) for which Algorithm 1 returns d_type = NC, we have by Lemma 5 that
By combining these results, we obtain
where we used the definition of \(\bar{K}_1\) for the final inequality. This inequality contradicts the definition of \(f_{\mathrm{low}}\) in (3), so our claim is proved. \(\square \)
If we choose \(\epsilon _{H}\) in the range \([\epsilon _{g}^{1/3},\epsilon _{g}^{2/3}]\), this bound improves over the classical \(\mathcal {O}(\epsilon _{g}^{-2})\) rate of gradient-based methods. The choice \(\epsilon _{H}=\epsilon _{g}^{1/2}\) yields the rate \(\mathcal {O}(\epsilon _{g}^{-3/2})\), which is known to be optimal among second-order methods [9].
Recalling that the workload of Algorithm 1 in terms of Hessian-vector products depends on the index J defined by (8), we obtain the following corollary. (Note the mild assumption on the quantities of M used at each instance of Algorithm 1, which is satisfied provided that this algorithm is always invoked with an initial estimate of M in the range \([0,U_H]\).)
Corollary 1
Suppose that the assumptions of Theorem 3 are satisfied, and let \(\bar{K}_1\) be as defined in that theorem and \(J(M,\epsilon _{H},\zeta )\) be as defined in (8). Suppose that the values of M used or calculated at each instance of Algorithm 1 satisfy \(M \le U_H\). Then the number of Hessian-vector products and/or gradient evaluations required by Algorithm 3 to output an iterate satisfying (23) is at most
For n sufficiently large, this bound is \( {\tilde{{\mathcal {O}}}}\left( \max \left\{ \epsilon _{g}^{-3} \epsilon _{H}^{5/2},\epsilon _{H}^{-7/2} \right\} \right) \), while if
\(J(U_H,\epsilon _{H},\zeta ) \ge n\), the bound is \({\tilde{{\mathcal {O}}}}\left( n\,\max \left\{ \epsilon _{g}^{-3} \epsilon _{H}^{3},\epsilon _{H}^{-3}\right\} \right) \).
Proof
From Lemma 1, the number of Hessian-vector multiplications in the main loop of Algorithm 1 is bounded by \(\min \left\{ n, J(U_H,\epsilon _{H},\zeta )+1 \right\} \). An additional \(\min \left\{ n, J(U_H,\epsilon _{H},\zeta ) \right\} \) Hessian-vector products may be needed to return a direction satisfying (6), if Algorithm 1 does not store its iterates \(y_j\). Each iteration also requires a single evaluation of the gradient \(\nabla f\), giving a bound of \((2 \min \left\{ n,J(U_H,\epsilon _{H},\zeta )\right\} +2)\) on the workload per iteration of Algorithm 3. We multiply this quantity by the iteration bound from Theorem 3 to obtain the result. \(\square \)
By setting \(\epsilon _{H}=\epsilon _{g}^{1/2}\), we obtain from this corollary a computational bound of \({\tilde{{\mathcal {O}}}}(\epsilon _{g}^{-7/4})\) (for n sufficiently large), which matches the deterministic first-order guarantee obtained in [5], and also improves over the \(\mathcal {O}(\epsilon _g^{-2})\) computational complexity of gradient-based methods.
4.3 Second-order complexity results
We now find bounds on iteration and computational complexity of finding a point that satisfies (2). In this section, as well as using results from Sects. 4.1 and 4.2, we also need to use the properties of the minimum eigenvalue oracle, Procedure 2. To this end, we make the following generic assumption.
Assumption 3
For every iteration k at which Algorithm 3 calls Procedure 2, and for a specified failure probability \(\delta \) with \(0 \le \delta \ll 1\), Procedure 2 either certifies that \(\nabla ^2 f(x_k) \succeq -\epsilon _{H}I\) or finds a vector of curvature smaller than \(-{\epsilon _{H}}/{2}\) in at most
Hessian-vector products, with probability \(1-\delta \), where \(\mathcal {C}_{\mathrm {meo}}\) depends at most logarithmically on \(\delta \) and \(\epsilon _{H}\).
Assumption 3 encompasses the strategies we mentioned in Sect. 3.2. Assuming the bound \(U_H\) on \(\Vert H\Vert \) is available, for both the Lanczos method with a random starting vector and the conjugate gradient algorithm with a random right-hand side, (27) holds with \(\mathcal {C}_{\mathrm {meo}}=\ln (2.75n/\delta ^2)\sqrt{U_H}/2\). When a bound on \(\Vert H\Vert \) is not available in advance, it can be estimated efficiently with minimal effect on the overall complexity of the method, as shown in Appendix B.3.
The next lemma guarantees termination of the backtracking line search for a negative curvature direction, regardless of whether it is produced by Algorithm 1 or Procedure 2. As in Lemma 4, the result is deterministic.
Lemma 6
Suppose that Assumptions 1 and 2 hold. Suppose that at iteration k of Algorithm 3, the search direction \(d_k\) is of negative curvature type, obtained either directly from Procedure 2 or as the output of Algorithm 1 and d_type = NC. Then the backtracking line search terminates with step length \(\alpha _k = \theta ^{j_k}\) with \(j_k \le j_{nc}+1\), where \(j_{nc}\) is defined as in Lemma 5, and the decrease in the function value resulting from the chosen step length satisfies
with \(c_{nc}\) is defined in Lemma 5.
Proof
Lemma 5 shows that the claim holds (with a factor of 8 to spare) when the direction of negative curvature is obtained from Algorithm 1. When the direction is obtained from Procedure 2, we have by the scaling of \(d_k\) applied in Algorithm 3 that
from which it follows that \(\Vert d_k \Vert \ge \tfrac{1}{2} \epsilon _{H}\). The result can now be obtained by following the proof of Lemma 5, with \(\tfrac{1}{2} \epsilon _{H}\) replacing \(\epsilon _{H}\). \(\square \)
We are now ready to state our iteration complexity result for Algorithm 3.
Theorem 4
Suppose that Assumptions 1, 2, and 3 hold, and define
where constants \(c_{sol}\) and \(c_{nc}\) are defined in Lemmas 4 and 5, respectively. Then with probability at least \((1-\delta )^{\bar{K}_2}\), Algorithm 3 terminates at a point satisfying (2) in at most \(\bar{K}_2\) iterations. (With probability at most \(1-(1-\delta )^{\bar{K}_2}\), it terminates incorrectly within \(\bar{K}_2\) iterations at a point for which \(\Vert \nabla f(x_k) \Vert \le \epsilon _{g}\) but \(\lambda _{\min }(\nabla ^2 f(x)) < -\epsilon _{H}\).)
Proof
Algorithm 3 terminates incorrectly with probability \(\delta \) at any iteration at which Procedure 2 is called, when Procedure 2 certifies erroneously that \(\lambda _{\min }(\nabla ^2 f(x)) \ge -\epsilon _{H}\). Since an erroneous certificate can only lead to termination, an erroneous certificate at iteration k means that Procedure 2 did not produce an erroneous certificate at iterations 0 to \(k-1\). By a disjunction argument, we have that the overall probability of terminating with an erroneous certificate during the first \(\bar{K}_2\) iterations is bounded by \(1-(1-\delta )^{\bar{K}_2}\). Therefore, with probability at least \((1-\delta )^{\bar{K}_2} \), no incorrect termination occurs in the first \(\bar{K}_2\) iterations.
Suppose now for contradiction that Algorithm 3 runs for \(\bar{K}_2\) iterations without terminating. That is, for all \(l=0,1,\cdots ,\bar{K}_2\), we have either \(\Vert \nabla f(x_l) \Vert > \epsilon _{g}\) or \(\lambda _{\mathrm{{min}}}(\nabla ^2 f(x_l)) < -\epsilon _{H}\). We perform the following partition of the set of iteration indices:
where \(\mathcal{K}_1\), \(\mathcal{K}_2\), and \(\mathcal{K}_3\) are defined as follows.
Case 1\(\mathcal{K}_1 := \{ l =0,1,\cdots ,\bar{K}_2-1 \, : \, \Vert \nabla f(x_l) \Vert \le \epsilon _{g}\}\). At each iteration \(l \in \mathcal{K}_1\), Algorithm 3 calls Procedure 2, which does not certify that \(\lambda _{\mathrm{{min}}}(\nabla ^2 f(x_l)) \ge -\epsilon _{H}\) (since the algorithm continues to iterate) but rather returns a direction of sufficient negative curvature. By Lemma 6, the step along this direction leads to an improvement in f that is bounded as follows:
Case 2\(\mathcal{K}_2 := \{ l=0,1,\cdots ,\bar{K}_2-1 \, : \, \Vert \nabla f(x_l) \Vert> \epsilon _{g}\; \text{ and } \; \Vert \nabla f(x_{l+1}) \Vert > \epsilon _{g}\}\). Algorithm 3 calls Algorithm 1 at each iteration \(l \in \mathcal{K}_2\), returning either an approximate damped Newton or a negative curvature direction. By combining Lemmas 4 and 5, we obtain a decrease in f satisfying
Case 3\(\mathcal{K}_3 := \{ l=0,1,\cdots ,\bar{K}_2-1 \, : \, \Vert \nabla f(x_l) \Vert > \epsilon _{g}\ge \Vert \nabla f(x_{l+1}) \Vert \}\). Because \(\Vert \nabla f(x_{l+1})\Vert \) may be small in this case, we can no longer bound the decrease in f by an expression such as (33). We can however guarantee at least that \(f(x_l)-f(x_{l+1}) \ge 0\). Moreover, provided that \(l<\bar{K}_2-1\), we have from \(\Vert \nabla f(x_{l+1}) \Vert \le \epsilon _{g}\) that the next iterate \(l+1\) is in \(\mathcal{K}_1\). Thus, a significant decrease in f will be attained at the next iteration, and we have
We now consider the total decrease in f over the span of \(\bar{K}_2\) iterations, which is bounded by \(f(x_0)-f_{\mathrm{low}}\) as follows:
where both sums in the final expression are nonnegative. Using first the bound (32) for the sum over \(\mathcal{K}_1\), we obtain
Applying (33) to the sum over \(\mathcal{K}_2\) leads to
Using these bounds together with (34), we have
giving the required contradiction. \(\square \)
We note that when \(\delta < 1/\bar{K}_2\) in Theorem 4, a technical result shows that \((1-\delta )^{\bar{K}_2} \ge 1-\delta \bar{K}_2\). In this case, the qualifier “with probability at least \((1-\delta )^{\bar{K}_2}\)” in the theorem can be replaced by “with probability at least \(1-\delta \bar{K}_2\)” while remaining informative.
Finally, we provide an operation complexity result: a bound on the number of Hessian-vector products and gradient evaluations necessary for Algorithm 3 to find a point that satisfies (2).
Corollary 2
Suppose that assumptions of Theorem 4 hold, and let \(\bar{K}_2\) be defined as in (30). Suppose that the values of M used or calculated at each instance of Algorithm 1 satisfy \(M \le U_H\). Then with probability at least \((1-\delta )^{\bar{K}_2}\), Algorithm 3 terminates at a point satisfying (2) after at most
Hessian-vector products and/or gradient evaluations. (With probability at most \(1-(1-\delta )^{\bar{K}_2}\), it terminates incorrectly with this complexity at a point for which \(\Vert \nabla f(x_k) \Vert \le \epsilon _{g}\) but \(\lambda _{\min }(\nabla ^2 f(x)) < -\epsilon _{H}\).)
For n sufficiently large, and assuming that \(\delta < 1/\bar{K}_2\), the bound is \({\tilde{{\mathcal {O}}}}\left( \max \left\{ \epsilon _{g}^{-3} \epsilon _{H}^{5/2},\epsilon _{H}^{-7/2} \right\} \right) \), with probability at most \(1-\bar{K}_2 \delta \).
Proof
The proof follows by combining Theorem 4 (which bounds the number of iterations) with Lemma 1 and Assumption 3 (which bound the workload per iteration). \(\square \)
By setting \(\epsilon _{H}=\epsilon _{g}^{1/2}\) and assuming that n is sufficiently large, we recover (with high probability) the familiar complexity bound of order \({\tilde{{\mathcal {O}}}}(\epsilon _{g}^{-7/4})\), matching the bound of accelerated gradient-type methods such as [1, 6, 19].
5 Discussion
We have presented a Newton-CG approach for smooth nonconvex unconstrained minimization that is close to traditional variants of this method, but incorporates additional checks and safeguards that enable convergence to a point satisfying approximate second-order conditions (2) with guaranteed complexity. This was achieved by exploiting the properties of Lanczos-based methods in two ways. First, we used CG to compute Newton-type steps when possible, while monitoring convexity during the CG iterations to detect negative curvature directions when those exist. Second, by exploiting the close relationship between the Lanczos and CG algorithms, we show that both methods can be used to detect negative curvature of a given symmetric matrix with high probability. Both techniques are endowed with complexity guarantees, and can be combined within a Newton-CG framework to match the best known bounds for second-order algorithms on nonconvex optimization [11].
Nonconvexity detection can be introduced into CG in ways other than those used in Algorithm 1. For instance, we can drop the implicit cap on the number of CG iterations that is due to monitoring of the condition \(\Vert r_j \Vert > \sqrt{T} \tau ^{j/2} \Vert r_0 \Vert \) and use of the negative curvature direction generation procedure (6) from Algorithm 1, and instead impose an explicit cap (smaller by a factor of approximately 4 than \(J(M,\epsilon ,\zeta )\)) on the number of CG iterations. In this version, if the explicit cap is reached without detection of a direction of sufficient negative curvature for \({\bar{H}}\), then Procedure 2 is invoked to find one. This strategy comes equipped with essentially the same high-probability complexity results as Theorem 4 and Corollary 2, but it lacks the deterministic approximate-first-order complexity guarantee of Theorem 3. On the other hand, it is more elementary, both in the specification of the Capped CG procedure and the analysis.
A common feature to the Capped CG procedures described in Algorithm 1 and in the above paragraph, which also emerges in most Newton-type methods with good complexity guarantees [11], is the need for high accuracy in the step computation. That is, only a small residual is allowed in the damped Newton system at the approximate solution. Looser restrictions are typically used in practical algorithms, but our tighter bounds appear to be necessary for the complexity analysis. Further investigation of the differences between our procedure in this paper and practical Newton-CG procedures is a subject of ongoing research.
Notes
Interestingly, as we show in Appendix A, the ratios on the left-hand side of (6) can be calculated without knowledge of \(y_i\) for \(i=0,1,\cdots ,j-1\), provided that we store the scalar quantities \(\alpha _i\) and \(\Vert r_i\Vert ^2\) for \(i=0,1,\cdots ,j-1\).
References
Agarwal, N., Allen-Zhu, Z., Bullins, B., Hazan, E., Ma, T.: Finding approximate local minima faster than gradient descent. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2017), PMLR (2017)
Allen-Zhu, Z., Li, Y.: NEON2: finding local minima via first-order oracles. In: Proceedings of the 32nd Conference on Neural Information Processing Systems (2018)
Birgin, E.G., Martínez, J.M.: The use of quadratic regularization with a cubic descent condition for unconstrained optimization. SIAM J. Optim. 27, 1049–1074 (2017)
Bubeck, S.: Convex optimization: algorithms and complexity. Found. Trends\(^{{\copyright }}\) Mach. Learn. 8, 231–357 (2015)
Carmon, Y., Duchi, J.C., Hinder, O., Sidford, A.: “Convex until proven guilty”: dimension-free acceleration of gradient descent on non-convex functions. In: International Conference on Machine Learning, vol. 70, 6–11 August 2017, International Convention Centre, Sydney, Australia, PMLR, pp. 654–663 (2017)
Carmon, Y., Duchi, J.C., Hinder, O., Sidford, A.: Accelerated methods for non-convex optimization. SIAM J. Optim. 28, 1751–1772 (2018)
Cartis, C., Gould, N.I.M., Toint, P.L.: On the complexity of steepest descent, Newton’s and regularized Newton’s methods for nonconvex unconstrained optimization. SIAM J. Optim. 20, 2833–2852 (2010)
Cartis, C., Gould, N.I.M., Toint, P.L.: Adaptive cubic regularisation methods for unconstrained optimization. Part I: motivation, convergence and numerical results. Math. Program. 127, 245–295 (2011)
Cartis, C., Gould, N.I.M., Toint, P.L.: Optimal Newton-type methods for nonconvex optimization. Technical Report naXys-17-2011, Department of Mathematics, FUNDP, Namur (B) (2011)
Cartis, C., Gould, N.I.M., Toint, P.L.: Complexity bounds for second-order optimality in unconstrained optimization. J. Complex. 28, 93–108 (2012)
Cartis, C., Gould, N.I.M., Toint, P.L.: Worst-case evaluation complexity and optimality of second-order methods for nonconvex smooth optimization. arXiv:1709.07180 (2017)
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. MPS-SIAM Series on Optimization. Society for Industrial and Applied Mathematics, Philadelphia (2000)
Curtis, F.E., Robinson, D.P., Samadi, M.: A trust region algorithm with a worst-case iteration complexity of \(\cal{O}\left(\epsilon ^{-3/2}\right)\) for nonconvex optimization. Math. Program. 162, 1–32 (2017)
Curtis, F.E., Robinson, D.P., Samadi, M.: An inexact regularized Newton framework with a worst-case iteration complexity of \(\cal{O}(\epsilon ^{-3/2})\) for nonconvex optimization. IMA J. Numer. Anal. (2018). https://doi.org/10.1093/imanum/dry022
Dembo, R.S., Steihaug, T.: Truncated-Newton algorithms for large-scale unconstrained optimization. Math. Program. 26, 190–212 (1983)
Fasano, G., Lucidi, S.: A nonmonotone truncated Newton–Krylov method exploiting negative curvature directions, for large-scale unconstrained optimization. Optim. Lett. 3, 521–535 (2009)
Gould, N.I.M., Lucidi, S., Roma, M., Toint, P.L.: Exploiting negative curvature directions in linesearch methods for unconstrained optimization. Optim. Methods Softw. 14, 75–98 (2000)
Griewank, A., Walther, A.: Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Frontiers in Applied Mathematics, 2nd edn. SIAM, Philadelphia (2008)
Jin, C., Netrapalli, P., Jordan, M.I.: Accelerated gradient descent escapes saddle points faster than gradient descent. In: Proceedings of the 31st Conference on Learning Theory, PMLR, pp. 1042–1085 (2018)
Karimi, S., Vavasis, S.A.: A unified convergence bound for conjugate gradient and accelerated gradient. arXiv:1605.00320 (2016)
Karimi, S., Vavasis, S.A.: A single potential governing convergence of conjugate gradient, accelerated gradient and geometric descent. arXiv:1712.09498 (2017)
Kuczyński, J., Woźniakowski, H.: Estimating the largest eigenvalue by the power and Lanczos algorithms with a random start. SIAM J. Matrix Anal. Appl. 13, 1094–1122 (1992)
Martínez, J.M., Raydan, M.: Cubic-regularization counterpart of a variable-norm trust-region method for unconstrained minimization. J. Glob. Optim. 68, 367–385 (2017)
Nesterov, Y., Polyak, B.T.: Cubic regularization of Newton method and its global performance. Math. Program. 108, 177–205 (2006)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer Series in Operations Research and Financial Engineering, 2nd edn. Springer, New York (2006)
Royer, C.W., Wright, S.J.: Complexity analysis of second-order line-search algorithms for smooth nonconvex optimization. SIAM J. Optim. 28, 1448–1477 (2018)
Steihaug, T.: The conjugate gradient method and trust regions in large scale optimization. SIAM J. Numer. Anal. 20, 626–637 (1983)
Xu, Y., Jin, R., Yang, T.: First-order stochastic algorithms for escaping from saddle points in almost linear time. In: Proceedings of the 32nd Conference on Neural Information Processing Systems (2018)
Acknowledgements
We thank sincerely the associate editor and two referees, whose comments led us to improve the presentation and to derive stronger results.
Funding
Funding was provided by National Science Foundation (Grant Nos. 1447449, 1628384, 1634597, 1740707), Air Force Office of Scientific Research (Grant No. FA9550-13-1-0138) and Argonne National Laboratory (Grant Nos. 3F-30222, 8F-30039) and DARPA (Grant No. N660011824020).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research supported by NSF Awards IIS-1447449, 1628384, 1634597, and 1740707; AFOSR Award FA9550-13-1-0138; Subcontracts 3F-30222 and 8F-30039 from Argonne National Laboratory; and Award N660011824020 from the DARPA Lagrange Program.
Appendices
Linear conjugate gradient: relevant properties
In this appendix, we provide useful results for the classical CG algorithm, that also apply to the “standard CG” operations within Algorithm 1. To this end, and for the sake of discussion in Appendix B, we sketch the standard CG method in Algorithm 4, reusing the notation of Algorithm 1.

Here and below, we refer often to the following quadratic function:
where \({\bar{H}}\) and g are the matrix and vector parameters of Algorithms 1 or 4. When \({\bar{H}}\) is positive definite, the minimizer of q is identical to the unique solution of \({\bar{H}}y = -g\). CG can be viewed either as an algorithm to solve \({\bar{H}}y = -g\) or as an algorithm to minimize q.
The next lemma details several properties of the conjugate gradient method to be used in the upcoming proofs.
Lemma 7
Suppose that j iterations of the CG loop are performed in Algorithm 1 or 4. Then, we have
Moreover, the following properties hold.
- 1.
\(y_i \in {{\,\mathrm{span}\,}}\left\{ p_0,\cdots ,p_{i-1}\right\} \), \(i=1,2,\cdots ,j\).
- 2.
\(r_i \in {{\,\mathrm{span}\,}}\left\{ p_0,\cdots ,p_i\right\} \) for all \(i=1,2,\cdots ,j\), and
$$\begin{aligned} r_i^\top v = 0, \quad \text{ for } \text{ all } v \in {{\,\mathrm{span}\,}}\left\{ p_0,\cdots ,p_{i-1}\right\} \text{ and } \text{ all } i=1,2,\cdots ,j. \end{aligned}$$(In particular, \(r_i^\top r_l = 0\) if \(0 \le l<i \le j\). If \(j=n\), then \(r_n=0\).)
- 3.
\(\Vert r_i\Vert \le \Vert p_i\Vert \), \(i=0,1,\cdots ,j\).
- 4.
\(r_i^\top p_i = -\Vert r_i\Vert ^2\), \(i=0,1,\cdots ,j\).
- 5.
\(p_i^\top {\bar{H}}p_k=0\) for all \(i,k =0,1,\cdots ,j\) with \(k \ne i\).
- 6.
\(p_i = -\sum _{k=0}^i ({\Vert r_i\Vert ^2}/{\Vert r_k\Vert ^2}) r_k\), \(i=0,1,\cdots ,j\).
- 7.$$\begin{aligned} q(y_{i+1}) = q(y_i) - \frac{\Vert r_i\Vert ^4}{2 p_i^\top {\bar{H}}p_i}, \quad i=0,1,\cdots ,j-1. \end{aligned}$$
- 8.
\(r_i^\top {\bar{H}}r_i \ge p_i^\top {\bar{H}}p_i\), \(i=0,1,\cdots ,j\).
Proof
Since CG has not terminated prior to iteration j, (39) clearly holds. All properties then follow from the definition of the CG process, and most are proved in standard texts (see, for example, [25, Chapter 5]). Property 8 is less commonly used, so we provide a proof here.
The case \(i=0\) is immediate since \(r_0=-p_0\) and there is equality. When \(i \ge 1\), we have:
(Note that if iteration i is reached, we cannot have \(\Vert r_{i-1}\Vert =0\).) It follows that
as \(p_i^\top {\bar{H}}p_{i-1} = 0\) by Property 5 above. Since iteration i has been reached, \(p_{i-1}\) is a direction of positive curvature, and we obtain \(r_i^\top {\bar{H}}r_i \ge p_i^\top {\bar{H}}p_i\), as required. \(\square \)
We next address an important technical point about Algorithm 1: the test (6) to identify a direction of negative curvature for H after an insufficiently rapid rate of reduction in the residual norm \(\Vert r_j\Vert \) has been observed. As written, the formula (6) suggests both that previous iterations \(y_i\), \(i=1,2,\cdots ,j-1\) must be stored (or regenerated) and that additional matrix-vector multiplications (specifically, \({\bar{H}}(y_{j+1}-y_i)\), \(i=0,1,\cdots \)) must be performed. We show here that in fact (6) can be evaluated at essentially no cost, provided we store two extra scalars at each iteration of CG: the quantities \(\alpha _k\) and \(\Vert r_k\Vert ^2\), for \(k=0,1,\cdots ,j\).
Lemma 8
Suppose that Algorithm 1 computes iterates up to iteration \(j+1\). Then, for any \(i \in \{0,\cdots ,j\}\), we can compute (6) as
Proof
By definition, \(y_{j+1}-y_i = \sum _{k=i}^{j} \alpha _k p_k\). By conjugacy of the \(p_k\) vectors, we have
where we used the definition of \(\alpha _k\) to obtain the last equality. Now we turn our attention to the denominator. Using Property 6 of Lemma 7, we have that
By rearranging the terms in the sum, we obtain
Using the fact that the residuals \(\{ r_{\ell } \}_{\ell =0,1,\cdots ,j}\) form an orthogonal set (by Property 2 of Lemma 7), we have that
Combining this with (40) gives the desired result. \(\square \)
Implementing Procedure 2 via Lanczos and conjugate gradient
In the first part of this appendix (Appendix B.1) we outline the randomized Lanczos approach and describe some salient convergence properties. The second part (Appendix B.2) analyzes the CG method (Algorithm 4) applied to a (possibly nonconvex) quadratic function with a random linear term. We show that the number of iterations required by CG to detect nonpositive curvature in an indefinite matrix is the same as the number required by Lanczos, when the two approaches are initialized in a consistent way, thereby proving Theorem 1. As a result, both techniques are implementations of Procedure 2 that satisfy Assumption 3, provided than an upper bound M on \(\Vert H\Vert \) is known. In the third part (Appendix B.3), we deal with the case in which a bound on \(\Vert H\Vert \) is not known a priori, and describe a version of the randomized Lanczos scheme which obtains an overestimate of this quantity (to high probability) during its first phase of execution. The complexity of this version differs by only a modest multiple from the complexity of the original method, and still satisfies Assumption 3.
1.1 Randomized Lanczos
Consider first the Lanczos algorithm applied to a symmetric, n-by-n matrix \({\bar{H}}\) and a starting vector \(b \in {\mathbb {R}}^n\) with \(\Vert b\Vert =1\). After \(t+1\) iterations, Lanczos constructs a basis of the t-th Krylov subspace defined by
The Lanczos method can compute estimates of the minimum and maximum eigenvalues of \({\bar{H}}\). For \(t=0,1,\cdots \), those values are given by
The Krylov subspaces satisfy a shift invariance property, that is, for any \(\hat{H}=a_1 I + a_2 H\) with \((a_1,a_2) \in {\mathbb {R}}^2\), we have that
Properties of the randomized Lanczos procedure are explored in [22]. The following key result is a direct consequence of Theorem 4.2(a) from the cited paper, along with the shift invariance property mentioned above.
Lemma 9
Let \({\bar{H}}\) be an \(n \times n\) symmetric matrix, let b be chosen from a uniform distribution over the sphere \(\Vert b\Vert =1\), and suppose that \(\bar{\epsilon } \in [0,1)\) and \(\delta \in (0,1)\) are given. Suppose that \(\xi _{\mathrm{{min}}}({\bar{H}},b,k)\) and \(\xi _{\mathrm{{max}}}({\bar{H}},b,k)\) are defined as in (42). Then after k iterations of randomized Lanczos, the following convergence condition holds:
provided k satisfies
A sufficient condition for (44) thus is
Similarly, we have that
for k satisfying the same conditions (45) or (46).
1.2 Lanczos and conjugate gradient as minimum eigenvalue oracles
Lemma 2 implies that using the Lanczos algorithm to generate the minimum eigenvalue of \({\bar{H}}\) from (42a) represents an instance of Procedure 2 satisfying Assumption 3. The sequence of iterates \(\{z_t\}\) given by \(z_0=b\) and
eventually yields a direction of sufficient negative curvature, when such a direction exists.
Consider now Algorithm 4 applied to \({\bar{H}}\), and \(g=-b\). By Property 2 of Lemma 7, we can see that if Algorithm 4 does not terminate with \(j \le t\), for some given index t, then \(y_{t+1}\), \(r_{t+1}\), and \(p_{t+1}\) are computed, and we have
because \(\{r_{\ell }\}_{\ell =0}^{i}\) is a set of \(i+1\) orthogonal vectors in \(\mathcal{K}_{i}(b,{\bar{H}})\). Thus \(\{p_0,\cdots ,p_i\}\), \(\{r_0,\cdots ,r_i\}\), and \(\{ b, {\bar{H}}b, \cdots , {\bar{H}}^i b \}\) are all bases for \(\mathcal{K}_{i}(b,{\bar{H}})\), \(i=0,1,\cdots ,t\). As long as they are computed, the iterates of Algorithm 4 satisfy
The sequences defined by (48) (for Lanczos) and (50) (for CG) are related via the Krylov subspaces. We have the following result about the number of iterations required by CG to detect non-positive-definiteness.
Theorem 5
Consider applying Algorithm 4 to the quadratic function (38), with \(g=-b\) for some b with \(\Vert b\Vert = 1\). Let \(J\) be the smallest value of \(t \ge 0\) such that \(\mathcal{K}_t(b,{\bar{H}})\) contains a direction of nonpositive curvature, so that \(J\) is also the smallest index \(t \ge 0\) such that \(z_{t+1}^\top {\bar{H}}z_{t+1} \le 0\), where \(\{z_j \}\) are the Lanczos iterates from (48). Then Algorithm 4 terminates with \(j=J\), with \(p_J^\top {\bar{H}}p_J\le 0\).
Proof
We consider first the case of \(J=0\). Then \(z_1 = b / \Vert b\Vert \) and \(b^\top {\bar{H}}b \le 0\), so since \(p_0=-r_0=b\), we have \(p_0^\top {\bar{H}}p_0 \le 0\), so the result holds in this case. We assume that \(J\ge 1\) for the remainder of the proof.
Suppose first that Algorithm 4 terminates with \(j=t\), for some t satisfying \(1 \le t \le J\), because of a zero residual — \(r_t=0\)—without having encountered nonpositive curvature. In that case, we can show that \({\bar{H}}^t b \in {{\,\mathrm{span}\,}}\{b,\cdots ,{\bar{H}}^{t-1}b\}\).
We can invoke (49) with t replaced by \(t-1\) since Algorithm 4 has not terminated at iteration \(t-1\). By the recursive definition of \(r_{t-1}\) within Algorithm 4, there exist coefficients \(\tau _i\) and \(\sigma _i\) such that
Since \(r_t=0\), we have again from Algorithm 4 that
The coefficient \(\alpha _{t-1} \sigma _{t-1}\) must be nonzero, because otherwise this expression would represent a nontrivial linear combination of the basis elements \(\{ b, {\bar{H}}b, \cdots , {\bar{H}}^{t-1} b \}\) of \(\mathcal{K}_{t-1}(b,{\bar{H}})\) that is equal to zero. It follows from this observation and (51) that \({\bar{H}}^t b \in {{\,\mathrm{span}\,}}\{b, {\bar{H}}b, \cdots , {\bar{H}}^{t-1} b \} = \mathcal{K}_{t-1}(b,{\bar{H}})\), as required.
Consequently,
By using a recursive argument on the definition of \(\mathcal{K}_i(b,{\bar{H}})\) for \(i=t,\cdots ,J\), we arrive at \(\mathcal{K}_{t-1}(b,{\bar{H}}) = \mathcal{K}_{J}(b,{\bar{H}})\). Thus there is a value of t smaller than \(J\) such that \(\mathcal{K}_{t}(b,{\bar{H}})\) contains a direction of nonpositive curvature, contradicting our definition of \(J\). Thus we cannot have termination of Algorithm 4 with \(j \le J\) unless \(p_j^\top {\bar{H}}p_j \le 0\).
Suppose next that CG terminates with \(j=t\) for some \(t >J\). It follows that \(p_j^\top {\bar{H}}p_j > 0\) for all \(j=0,1,\cdots ,J\). By definition of \(J\), there is a nonzero vector \(z \in \mathcal{K}_{J}(b,{\bar{H}})\) such that \(z^\top {\bar{H}}z \le 0\). On the other hand, we have \(\mathcal{K}_{J}(b,{\bar{H}}) = {{\,\mathrm{span}\,}}\{p_0,p_1,\cdots ,p_{J} \}\) by (49), thus we can write \(z = \sum _{j=0}^{J} \gamma _j p_j\), for some scalars \(\gamma _j\), \(j=0,1,\cdots ,J\). By Property 5 of Lemma 7, we then have
Since \(p_{j}^\top {\bar{H}}p_{j}>0\) for every \(j=0,1,\cdots ,J\), and not all \(\gamma _j\) can be zero (because \(z \ne 0\)), the final summation is strictly positive, a contradiction.
Suppose now that CG terminates at some \(j<J\). Then \(p_j^\top {\bar{H}}p_j \le 0\), and since \(p_j \in \mathcal{K}_j(b,{\bar{H}})\), it follows that \(\mathcal{K}_j(b,{\bar{H}})\) contains a direction of nonpositive curvature, contradicting the definition of \(J\).
We conclude that Algorithm 4 must terminate with \(j=J\) and \(p_J^\top {\bar{H}}p_J\le 0\), as claimed. \(\square \)
Theorem 5 is a generic result that does not require b to be chosen randomly. It does not guarantee that Lanczos will detect nonpositive curvature in \({\bar{H}}\) whenever present, because b could be orthogonal to the subspace corresponding to the nonpositive curvature, so the Lanczos subspace never intersects with the subspace of negative curvature. When b is chosen randomly from a uniform distribution over the unit ball, however, we can certify the performance of Lanczos, as we have shown in Lemma 2 based on Lemma 9 above. We can exploit Theorem 5 to obtain the same performance for CG, as stated in Theorem 1. We restate this result as a corollary, and prove it now.
Corollary 3
Let b be distributed uniformly on the unit ball and H be a symmetric n-by-n matrix, with \(\Vert H \Vert \le M\). Given \(\delta \in [0,1)\), define
Consider applying Algorithm 4 with \({\bar{H}}:= H + \frac{1}{2} \epsilon I\) and \(g=-b\). Then, the following properties hold:
- (a)
If \(\lambda _{\mathrm{{min}}}(H) < -\epsilon \), then with probability at least \(1-\delta \), there is some index \(j \le {\bar{J}}\) such that Algorithm 4 terminates with a direction \(p_j\) such that \(p_j^\top H p_j \le -(\epsilon /2) \Vert p_j\Vert ^2\).
- (b)
if Algorithm 4 runs for \({\bar{J}}\) iterations without terminating, then with probability at least \(1-\delta \), we have that \(\lambda _{\mathrm{{min}}}(H) \ge -\epsilon \).
Proof
We will again exploit the invariance of the Krylov subspaces to linear shifts given by (43). This allows us to make inferences about the behavior of Algorithm 4 applied to \({\bar{H}}\) from the behavior of the Lanczos method applied to H, which has been described in Lemma 2.
Suppose first that \(\lambda _{\mathrm{{min}}}(H) < - \epsilon \). By Lemma 2, we know that with probability at least \(1-\delta \), the Lanczos procedure returns a vector v such that \(\Vert v\Vert =1\) and \(v^\top Hv \le -(\epsilon /2)\) after at most \({\bar{J}}\) iterations. Thus, for some \(j \le {\bar{J}}\), we have \(v \in \mathcal{K}_j(b,H) = \mathcal{K}_j(b,{\bar{H}})\), and moreover \(v^\top {\bar{H}}v \le 0\) by definition of \({\bar{H}}\), so the Krylov subspace \(\mathcal{K}_j(b,{\bar{H}})\) contains directions of nonpositive curvature, for some \(j \le {\bar{J}}\). It then follows from Theorem 5 that \(p_j^\top {\bar{H}}p_j \le 0\) for some \(j \le {\bar{J}}\). To summarize: If \(\lambda _{\mathrm{{min}}}(H) < - \epsilon \), then with probability \(1-\delta \), Algorithm 4 applied to \({\bar{H}}\) and \(g=-b\) will terminate with some \(p_j\) such that \(p_j^\top {\bar{H}}p_j \le 0\) for some j with \(j \le {\bar{J}}\). The proof of (a) is complete.
Suppose now that Algorithm 4 applied to \({\bar{H}}\) and \(g=-b\) runs for \({\bar{J}}\) iterations without terminating, that is \(p_j^\top {\bar{H}}p_j >0\) for \(j=0,1,\cdots ,{\bar{J}}\). It follows from the logic of Theorem 5 that \(\mathcal{K}_{{\bar{J}}}(b,{\bar{H}})\) contains no directions of nonpositive curvature for \({\bar{H}}\). Equivalently, there is no direction of curvature less than \(-\epsilon /2\) for H in \(\mathcal{K}_{{\bar{J}}}(b,H)\). By Lemma 2, this certifies with probability at least \(1-\delta \) that \(\lambda _{\mathrm{{min}}}(H) \ge -\epsilon \), establishing (b). \(\square \)
1.3 Randomized Lanczos with internal estimation of a bound on \(\Vert H\Vert \)
The methods discussed in Sect. B.2 assume knowledge of an upper bound on the considered matrix, denoted by M. When no such bound is known, we show here that it is possible to estimate it within the Lanczos procedure. Algorithm 5 details the method; we show that it can be used as an instance of Procedure 2 satisfying Assumption 3 when the optional parameter M is not provided.
Algorithm 5 consists in applying the Lanczos method on H starting with a random vector b. We first run Lanczos for \(j_M\) iterations, where \(j_M\) does not depend on any estimate on the minimum or maximum eigenvalue and instead targets a fixed accuracy. After this initial phase of \(j_M\) iterations, we have approximations of the extreme eigenvalues \(\xi _{\mathrm{{max}}}(H, b, j_M)\) and \(\xi _{\mathrm{{min}}}(H, b, j_M)\) from (42). An estimate M of \(\Vert H\Vert \) is then given by:
We show below that \(\Vert H\Vert \le M \le 2\Vert H\Vert \), with high probability. This value can then be used together with a tolerance \(\epsilon \) to define a new iteration limit for the Lanczos method. After this new iteration limit is reached, we can either produce a direction of curvature at most \(-\epsilon /2\), or certify with high probability that \(\lambda _{\min }(H) \succeq -\epsilon I\)—the desired outcomes for Procedure 2.

Algorithm 5 could be terminated earlier, in fewer than \(j_{\mathrm {total}}\) iterations, when a direction of sufficient negative is encountered. For simplicity, we do not consider this feature, but observe that it would not affect the guarantees of the method, described in Lemma 10 below.
Lemma 10
Consider Algorithm 5 with input parameters H and \(\epsilon \), and internal parameters \(\delta \) and b. The method outputs a value \(\lambda \) such that
in at most
matrix-vector multiplications by H, with probability at least \(1 - \delta \).
Proof
We begin by showing that the first phase of Algorithm 5 yields an accurate estimate of \(\Vert H\Vert \) with high probability. We assume that \(\Vert H\Vert >0\) as the result is trivially true otherwise. By setting \(\delta \leftarrow \delta /3\) and \({\bar{\epsilon }} = \frac{1}{4}\) in Lemma 9, we obtain that the following inequalities hold, each with probability at least \(1-\delta /3\):
We consider the various possibilities for \(\lambda _{\mathrm{{min}}}(H)\) and \(\lambda _{\mathrm{{max}}}(H)\) separately, showing in each case that M defined by (53) has \(\Vert H\Vert \le M \le 2 \Vert H\Vert \).
When \(\lambda _{\mathrm{{max}}}(H) \ge \lambda _{\mathrm{{min}}}(H) \ge 0\), we have \(\xi _{\mathrm{{max}}}(H,b,j_M) \ge \frac{3}{4} \lambda _{\mathrm{{min}}}(H)\) and \(0 \le \xi _{\mathrm{{min}}}(H,b,j_M) \le \xi _{\mathrm{{max}}}(H,b,j_M)\), so that
$$\begin{aligned} M&= 2 \xi _{\mathrm{{max}}}(H,b,j_M) \ge \frac{3}{2} \lambda _{\mathrm{{max}}}(H) = \frac{3}{2}\Vert H\Vert , \\ M&= 2 \xi _{\mathrm{{max}}}(H,b,j_M) \le 2 \lambda _{\mathrm{{max}}}(H) = 2 \Vert H\Vert , \end{aligned}$$as required.
When \(\lambda _{\mathrm{{min}}}(H) \le \lambda _{\mathrm{{max}}}(H) \le 0\), we have \(\xi _{\mathrm{{min}}}(H,b,j_M) \le \frac{3}{4} \lambda _{\mathrm{{min}}}(H) \le 0\) and \(\xi _{\mathrm{{min}}}(H,b,j_M) \le \xi _{\mathrm{{max}}}(H,b,j_M) \le 0\), so that
$$\begin{aligned} M&= 2 | \xi _{\mathrm{{min}}}(H,b,j_M)| \ge \frac{3}{2} | \lambda _{\mathrm{{min}}}(H)| = \frac{3}{2} \Vert H\Vert , \\ M&= 2 | \xi _{\mathrm{{min}}}(H,b,j_M)| \le 2 | \lambda _{\mathrm{{min}}}(H)| = 2 \Vert H\Vert , \end{aligned}$$as required.
When \(\lambda _{\mathrm{{min}}}(H) \le 0 \le \lambda _{\mathrm{{max}}}(H)\) and \(-\lambda _{\mathrm{{min}}}(H) \le \lambda _{\mathrm{{max}}}(H)\), we have \(\lambda _{\mathrm{{max}}}(H)-\lambda _{\mathrm{{min}}}(H) \le 2 \lambda _{\mathrm{{max}}}(H)\), so from (56a), it follows that \(\xi _{\mathrm{{max}}}(H,b,j_M) \ge \frac{1}{2} \lambda _{\mathrm{{max}}}(H) = \frac{1}{2} \Vert H\Vert \), and so
$$\begin{aligned} M&\ge 2 \xi _{\mathrm{{max}}}(H,b,j_M) \ge \Vert H\Vert , \\ M&= 2 \max \left\{ |\xi _{\mathrm{{max}}}(H, b, j_M)|, |\xi _{\mathrm{{min}}}(H, b, j_M)| \right\} \\&\le 2 \max \left\{ |\lambda _{\mathrm{{max}}}(H)|,|\lambda _{\mathrm{{min}}}(H)| \right\} = 2 \Vert H\Vert , \end{aligned}$$as required.
When \(\lambda _{\mathrm{{min}}}(H) \le 0 \le \lambda _{\mathrm{{max}}}(H)\) and \(-\lambda _{\mathrm{{min}}}(H) \ge \lambda _{\mathrm{{max}}}(H)\), we have \(\lambda _{\mathrm{{max}}}(H) - \lambda _{\mathrm{{min}}}(H) \le -2 \lambda _{\mathrm{{min}}}(H)\), so from (56b), it follows that \(\xi _{\mathrm{{min}}}(H,b,j_M) \le \frac{1}{2} \lambda _{\mathrm{{min}}}(H) \le 0\), and so
$$\begin{aligned} M&\ge 2 |\xi _{\mathrm{{min}}}(H,b,j_M)| \ge | \lambda _{\mathrm{{min}}}(H)| = \Vert H\Vert , \\ M&=2 \max \left\{ |\xi _{\mathrm{{max}}}(H, b, j_M)|, |\xi _{\mathrm{{min}}}(H, b, j_M)| \right\} \\&\le 2 \max \left\{ |\lambda _{\mathrm{{max}}}(H)|,|\lambda _{\mathrm{{min}}}(H)| \right\} = 2 \Vert H\Vert , \end{aligned}$$as required.
Since each of the bounds in (56) holds with probability at least \(1-\delta /3\), both hold with probability at least \(1-2\delta /3\), by a union bound argument.
We finally consider the complete run of Algorithm 5, which requires \(j_{\mathrm {total}}\) iterations of Lanczos. If our estimate M is accurate, we have by setting \(\delta \leftarrow \delta /3\) and \(M \leftarrow 2 \Vert H\Vert \) in Lemma 2 that \(\lambda =\xi _{\mathrm{{min}}}(H,b,j_{\mathrm {total}})\) satisfies (54) with probability \(1-\delta /3\). By using a union bound to combine this probability with the probabilities of estimating M appropriately, we obtain the probability of at least \(1-\delta \).
In conclusion, Algorithm 5 runs \(j_{\mathrm {total}}\) iterations of Lanczos (each requiring one matrix-vector multiplication by H) and terminates correctly with probability at least \(1-\delta \). \(\square \)
The lemma above shows that Algorithm 5 is an instance of Procedure 2 that does not require an a priori bound on \(\Vert H\Vert \). Assuming \(\Vert H\Vert \le U_H\), we further observe that Algorithm 5 satisfies the conditions of Assumption 3 with \(\mathcal {C}_{\mathrm {meo}}= \frac{\ln (25n/\delta ^2)}{\sqrt{2}}\sqrt{U_H}\), which is within a modest constant multiple of the one obtained for the Lanczos method with knowledge of \(\Vert H\Vert \) or \(U_H\).
Proof of Theorem 2
Proof
The proof proceeds by contradiction: If we assume that all conditions specified in the statement of the theorem hold, and in addition that
then we must have
contradicting (11). Note that
by assumption, therefore we can consider (57) to hold for \(i=0,1,\cdots ,{\hat{J}}\). Moreover, recalling the definition (38) of the quadratic function q, we have for any \(i=0,1,\cdots ,{\hat{J}}\) that
Thus, (57) can be reformulated as
where we used \(\nabla q(y_i)=r_i\) and the definitions (57), (59) of strong convexity along the directions \(y_{{\hat{J}}+1}-y_i\). In the remainder of the proof, and similarly to [5, Proof of Proposition 1], we will show that (60) leads to the contradiction (58), thus proving that (12) holds.
We define the sequence of functions \(\varPhi _j\), \(j=0,1,\cdots {\hat{J}}\) as follows:
and for \(j=0,\cdots ,{\hat{J}}-1\):
Since each \(\varPhi _j\) is a quadratic function with Hessian \(\epsilon I\), it can be written as follows:
where \(v_j\) is the unique minimizer of \(\varPhi _j\), and \(\varPhi _j^* = \varPhi _j(v_j)\) is the minimum value of \(\varPhi _j\). (Note that \(v_0=y_0=0\) and \(\varPhi ^*_0 = q(y_0) = 0\).)
Defining
we give a short inductive argument to establish that
For \(j=0\), (64) holds because \(\varPhi _0(y) = q(y) + \psi (y)\) by definition. Assuming that (64) holds for some index \(j \ge 0\), we find by first applying (61) (with \(z=y_{{\hat{J}}+1}\)) and then (60) (with \(i=j\)) that
Thus, we have
which proves (64) for \(j+1\), and thus completes the inductive argument.
We next prove another technical fact about the relationship between \(q(y_j)\) and \(\varPhi _j^*\), namely,
We establish this result by an inductive argument that is quite lengthy and technical; we note the termination of this phase of the proof clearly below.
This result trivially holds (with equality) at \(j=0\). Supposing that it holds for some \(j =0,1,\cdots , {\hat{J}}-1\), we will prove that it also holds for \(j+1\).
By using Properties 7 and 8 of Lemma 7, and also \(\Vert {\bar{H}}r_j\Vert \le (M+2\epsilon )\Vert r_j\Vert \), we have
It follows from induction hypothesis \(q(y_j) \le \varPhi _j^*\) that
By taking the derivative in (61), and using (62), we obtain
By rearranging the above relation (and noting that the z terms cancel out), we obtain:
It follows from this expression together with Properties 1 and 2 of Lemma 7 that
(The result holds for \(j=1\), from (67) we have \(v_1 \in {{\,\mathrm{span}\,}}\{v_0, r_0, y_0\} = {{\,\mathrm{span}\,}}\{r_0\} = {{\,\mathrm{span}\,}}\{p_0 \}\), and an induction based on (67) can be used to establish (68) for the other values of j.) By combining the expressions (62) for \(\varPhi _j\), \(\varPhi _{j+1}\) with the recurrence formula (61) for \(\varPhi _{j+1}\), we obtain
and therefore
On the other hand, we have by (67) that
where the last relation comes from \(r_j \perp {{\,\mathrm{span}\,}}\{p_0,\cdots ,p_{j-1}\}\) (Property 2 of Lemma 7) and (68) in the case \(j \ge 1\), and immediately in the case \(j=0\), since \(y_0=v_0=0\). By combining (69) and (70), we arrive at:
where the last inequality comes from (66). By using the definitions of \(\tau \) and \(\kappa \) in Algorithm 1, we have
It therefore follows from (71) that \(q(y_{j+1}) \le \varPhi _{j+1}^*\). At this point, we have shown that when \(q(y_j) \le \varPhi _j^*\) for \(j=0,1,\cdots ,{\hat{J}}-1\), it follows that \(q(y_{j+1}) \le \varPhi _{j+1}^*\), establishing the inductive step. As a result, our proof of (65) is complete.
By substituting \(j={\hat{J}}\) into (65), we obtain \(q(y_{{\hat{J}}}) \le \varPhi _{{\hat{J}}}^*\), which in combination with (64) with \(j={\hat{J}}\), and the definition (62), yields
By substitution from (63), we obtain
We now depart from the analysis of [5], and complete the proof of this result by expressing (73) in terms of residual norms. On the left-hand side, we have
because \(r_{{\hat{J}}+1}^\top (y_{{\hat{J}}}-y_{{\hat{J}}+1}) = r_{{\hat{J}}+1}^\top (\alpha _{{\hat{J}}} p_{{\hat{J}}}) = 0\) by Lemma 7, Property 2. We thus have from (59) that
On the right-hand side of (73), because of the strong convexity condition (60) at \(i=0\), we have
Moreover, we have
where the last relation follows from the definition of \(\alpha _i\). By combining these last two bounds, and using Property 3 of Lemma 7, we obtain
because \(p_j^\top {\bar{H}}p_j \ge \epsilon \Vert p_j\Vert ^2\) for \(j=0,1,\cdots ,{\hat{J}}\) by assumption.
To bound the sum in (75), we recall that since Algorithm 1 did not terminate until iteration \({\hat{J}}\), the residual norms \(\Vert r_i \Vert \) at all iterations \(i=0,1,\cdots ,{\hat{J}}-1\) must have decreased at the expected convergence rate. In particularly, we have \(\Vert r_i\Vert \le \sqrt{T} \tau ^{i/2} \Vert r_0\Vert \) for the possibly smaller versions of \(\sqrt{T}\) and \(\tau \) that prevailed at iteration i, so certainly \(\Vert r_i\Vert \le \sqrt{T} \tau ^{i/2} \Vert r_0\Vert \) for the final values of these parameters. Thus for \(i=0,1,\cdots ,{\hat{J}}-1\), we have
where we used \(\Vert r_{{\hat{J}}}\Vert \ge \sqrt{T} \tau ^{{\hat{J}}/2} \Vert r_0\Vert \) (from (11)) for the last inequality. Observing that this bound also holds (trivially) for \(i={\hat{J}}\), we obtain by substituting in (75) that
Applying successively (74), (73) and (76) finally yields:
After rearranging this inequality and dividing by \(\Vert r_{{\hat{J}}}\Vert > 0\), we obtain
We have thus established (58) which, as we noted earlier, contradicts (11). Thus (57) cannot be true, so we have established (12), as required. \(\square \)
Rights and permissions
About this article
Cite this article
Royer, C.W., O’Neill, M. & Wright, S.J. A Newton-CG algorithm with complexity guarantees for smooth unconstrained optimization. Math. Program. 180, 451–488 (2020). https://doi.org/10.1007/s10107-019-01362-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-019-01362-7
Keywords
- Smooth nonconvex optimization
- Newton’s method
- Conjugate gradient method
- Optimality conditions
- Worst-case complexity