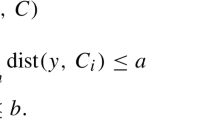Set regularities and feasibility problems

Abstract

We synthesize and unify notions of regularity, both of individual sets and of collections of sets, as they appear in the convergence theory of projection methods for consistent feasibility problems. Several new characterizations of regularities are presented which shed light on the relations between seemingly different ideas and point to possible necessary conditions for local linear convergence of fundamental algorithms.

1 Introduction

In recent years there has been a tremendous interest in first-order methods for solving variational problems. As the name suggests, these methods only use information that, in some way, encodes the gradient of a function to be minimized. Often one has in mind the following universal optimization problem for such methods

$$\begin{aligned} \underset{x\in \mathbb {E}}{\text{ minimize }} \sum _{j=1}^m f_j(x) \end{aligned}$$

(1)

where $f_j$ are scalar extended-valued functions, not necessarily smooth or convex, on a Euclidean space. This specializes to constrained optimization in the case that one or more of the functions $f_j$ is an indicator function for a set.

All of the (nonconvex) convergence results concerning local linear convergence that we have seen in the literature involve implicitly or explicitly assumptions on the regularity of the functions $f_j$ and on the relation of the functions to each other at critical points. Prominent examples of this are the assumption that the functions satisfy the Kurdyka-Łojasiewicz property [11, 12, 43, 48] or that certain constraint qualifications are satisfied at critical points, like interiority of the constraints and invertability of the Jacobian of the objective in directions normal to the constraints.

Our goal in this note is to identify common ideas and properties for a special case of (1) and to develop a general framework that both encapsulates all of these ideas and is robust enough to be applied in other settings. We focus our attention on the feasibility problem

$$\begin{aligned} {{\mathrm{\mathsf {Find}\,}}}{\overline{x}}\in \cap _{j=1}^m A_j, \end{aligned}$$

(2)

which is the specialization of (1) to the case

$$\begin{aligned} f_j(x)=\iota _{ A_j}(x):={\left\{ \begin{array}{ll}0&{} \text{ if } x\in A_j\\ +\infty &{} \text{ else }\end{array}\right. }\qquad (j=1,2,\ldots ,m). \end{aligned}$$

In the setting of the feasibility problem, regularity properties of individual sets (elemental regularity—see Sect. 3) and of their intersections (transversality and subtransversality of collections of sets—see Sect. 4) come into play. Both types of regularity have long history. A typical classical elemental regularity assumption is the convexity of the sets, while the traditional assumption that sets have a point in common on their interiors provides an example of transversal regularity in the convex setting. Another classical example of the second type of regularity is the concept of transversality of smooth manifolds.

In the last decade there has been a great deal of interest in extending the classical notions of regularity to include nonconvex and nonsmooth sets, motivated to a large extent by nonsmooth and nonconvex optimization and attendant subdifferential and coderivative calculus, optimality and stationarity conditions and convergence analysis of algorithms. Examples of modern elemental regularity concepts include Clarke regularity [58], prox-regularity (Poliquin et al. [57]), super-regularity (Lewis et al. [44]), $(A',\varepsilon ,\delta )$ -regularity and $(\varepsilon ,\delta )$ -regularity (Bauschke et al. [9]), relative ($A',\varepsilon ,\delta$)-subregularity (Hesse and Luke [26]), relative $\sigma$ -Hölder regularity (Noll and Rondepierre [53]). Among the numerous transversal regularity (regularity of intersections) concepts we mention Jameson properties (N) and (G) [32]), the conical hull intersection property (CHIP) (Chui et al. [17]), (local, bounded) linear regularity (Bauschke and Borwein [5], Zheng and Ng [59]), the strong conical hull intersection property (strong CHIP) (Deutsch et al. [20]), metric regularity (Li [47]), metric inequality (Ngai and Théra [52]), the closed intersection property, the normal property, the weak, uniform and dual normal properties, the normal conical hull intersection property (normal CHIP) (Bakan et al. [4]), the normal qualification condition (Mordukhovich [49]), regularity, strong regularity, or uniform regularity (Kruger [35–37]), the linearly regular intersection (Lewis et al. [44]), linear coherence, alliedness (Penot [55]), the (A, B)-qualification condition (Bauschke et al. [9]), inherent and intrinsic transversality (Drusvyatskiy et al. [22, 23]), separable intersection (Noll and Rondepierre [53]), transversality and subtransversality (Ioffe [30]). Some of the above concepts used under different names by different authors actually coincide.

A short survey of the recent developments in this area in the general nonsmooth and nonconvex setting with the emphasis on convergence analysis is provided in Sect. 2. The elemental and transversal regularity properties are further studied in Sects. 3 and 4, respectively.

Section 3 introduces a general framework for elemental regularity of sets that provides a common language for the many different definitions that have appeared to date. This new framework makes the cascade of implications between the different types of regularity more transparent, namely that convexity $\implies$ prox-regularity $\implies$ super-regularity $\implies$ Clarke regularity $\implies$ $(\varepsilon ,\delta )$-regularity $\implies$ $(\varepsilon ,\delta )$-subregularity $\implies$ $\sigma$-Hölder regularity see Theorem 4. The last of these implications is new.

Section 4 focuses on two local regularity properties of collections of sets which we call here subtransversality and transversality. Both properties admit several representations and characterizations: metric, dual, angle, etc, and because of that or just historically are known under various names, e.g. (local) linear regularity, metric regularity, linear coherence, and metric inequality for the first property, and strong regularity, uniform regularity, alliedness, normal qualification condition for the second one. They correspond (are in a sense equivalent) to subregularity and metric regularity of set-valued mappings, respectively. At the same time, the properties are related to certain ‘good’ mutual arrangement of several objects (sets) in space, and after a discussion with experts in variational analysis,¹ we have decided to adopt the classical ‘transversality’ terminology.

For ease of exposition, our discussion is limited to the case of just two closed subsets of Euclidean space with nonempty intersection, though most of the regularity properties discussed are easily extended to collections of more than two sets with nonempty intersection. We compare the various representations of these properties and discuss also some recently introduced ‘restricted’ regularity properties. A number of characterizations of the properties are formulated. Some characterizations are new, see Theorems 1(iii), 2(ii), (iv), 3(ii), and 4(ii), (iv). We emphasize the important dual characterization of subtransversality in Theorem 4(ii) which expands and improves (in the setting adopted in the current article) [41, Theorem 4.1]. The proof of this assertion is going to appear in the forthcoming article [39]. In contrast to dual characterizations for transversality which are necessary and sufficient, this note underscores the fact that the known dual characterizations for subtransversality are sufficient. This raises the question whether necessary dual characterizations exist.

1.1 Notation and basic definitions

Throughout our discussion $\mathbb {E}$ is a Euclidean space. Given a subset $A\subset \mathbb {E}$, d(x, A) stands for the distance from a point $x\in \mathbb {E}$ to A: $d(x,A) := \inf _{a\in A}\Vert x-a\Vert$. The projector onto the set A, $P_{A}:\,\mathbb {E}\rightrightarrows A\,$, is central to algorithms for feasibility and is defined by

$$\begin{aligned} P_{A}(x):=\underset{a\in A}{{{\mathrm{argmin\,}}}}\left\| a-x\right\| . \end{aligned}$$

A projection is a selection from the projector. This exists for any closed set $A\subset \mathbb {E}$, as can be deduced by the continuity and coercivity of the norm. Note that the projector is not, in general, single-valued, and indeed uniqueness of the projector defines a type of regularity of the set A: local uniqueness characterizes prox-regularity [57] while in finite dimensional settings global uniqueness characterizes convexity [13]. The inverse of the projector is well defined:

$$\begin{aligned} P_A^{-1}(a):=\left\{ x\in \mathbb {E}\,\left| \,a\in P_A(x)\right. \right\} . \end{aligned}$$

Following [9], we use this object to define the various normal cone mappings, which in turn lead to the subdifferential of the indicator function $\iota _ A$. This brings the theory presented here to the edge of a much broader context of descent methods for solving (1). We will, however, focus exclusively on the feasibility problem for two sets.

Given a subset $A\subset \mathbb {E}$ and a point $\overline{x}\in A$, the Fréchet, proximal and limiting normal cones to A at $\overline{x}$ are defined, respectively, as follows:

$$\begin{aligned}&\displaystyle N^F_{A}(\overline{x}):= \left\{ v\in \mathbb {E}\mid \limsup _{x\mathop {\rightarrow }\limits ^{ A}\overline{x},\,x\ne \overline{x}} \frac{\langle v,x-\overline{x}\rangle }{\Vert x-\overline{x}\Vert } \le 0 \right\} , \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle N^{\text {prox}}_{ A}(\overline{x}):={{\mathrm{{cone}}}}\left( P_{A}^{-1}(\overline{x})-\overline{x}\right) , \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle {N}_{A}({\overline{x}}):= \mathop {\mathrm{Lim\,sup}\,}_{x\mathop {\rightarrow }\limits ^{A}\overline{x}}N^{\text {prox}}_{ A}(x):=\left\{ v= \lim _{k\rightarrow \infty }v_k\mid v_k\in N^{\text {prox}}_{ A}(x_k),\; x_k\mathop {\rightarrow }\limits ^{ A} \overline{x}\right\} . \end{aligned}$$

(5)

In the above and throughout this paper, $x\mathop {\rightarrow }\limits ^{ A} \overline{x}$ means that $x\rightarrow \overline{x}$ with $x\in A$.

All these three sets are clearly cones. Unlike the first two cones, the third one can be nonconvex. It is easy to verify that $N^{\text {prox}}_{A}(\overline{x})\subseteq N^F_{A}(\overline{x})$. Furthermore, if A is closed, then

$$\begin{aligned} {N}_{A}({\overline{x}})= \mathop {\mathrm{Lim\,sup}\,}_{x\mathop {\rightarrow }\limits ^{A}\overline{x}}N^F_{A}(x). \end{aligned}$$

(6)

The last formula can serve as a definition of the limiting normal cone in more general than Euclidean normed linear spaces (e.g. Asplund spaces [49]) when the original definition (5) in terms of proximal normals is not applicable. If $\overline{x}\in \mathrm{bd}\,A$, then ${N}_{A}({\overline{x}})\ne \{0\}$. If A is a convex set, then all three cones (3)–(5) coincide and reduce to the normal cone in the sense of convex analysis:

$$\begin{aligned} {N}_{A}(\overline{x}): = \left\{ v\in \mathbb {E}\mid \langle v,x-\overline{x}\rangle \le 0 \quad \quad \text{ for } \text{ all }\quad x\in A\right\} . \end{aligned}$$

(7)

In differential geometry it is more common to work with the tangent space, but for smooth manifolds the normal cone (3) [the same as (5)] is a subspace and dual to the tangent space. Following Rockafellar and Wets [58, Example 6.8], we say that a subset $A\subset \mathbb {E}$ is a k-dimensional ($0<k<n:=\dim \mathbb {E}$) smooth manifold around a point ${\overline{x}}\in A$ if there are a neighborhood U of ${\overline{x}}$ in $\mathbb {E}$ and a smooth (i.e., of $\mathcal {C}^1$ class) mapping $F:U\rightarrow \mathbb {R}^m$ ($m:=n-k$) with $\nabla F({\overline{x}})$ of full rank m such that $A\cap U = \{x\in U\mid F(x)=0\}$. The tangent space to A at ${\overline{x}}$ is a linear approximation of A near $\overline{x}$ and is given by

$$\begin{aligned} T_{ A}({\overline{x}}) := \left\{ x\in \mathbb {E}\mid \nabla F({\overline{x}})x=0\right\} . \end{aligned}$$

The normal space to A at ${\overline{x}}$ is defined as the orthogonal complement of $T_{ A}({\overline{x}})$ and can be written as

$$\begin{aligned} N_{A}({\overline{x}}) := \left\{ \nabla F({\overline{x}})^{*}y\mid y\in \mathbb {R}^m\right\} . \end{aligned}$$

(8)

It is in a sense a dual space object. If A is a smooth manifold, then cones (3), (5) and (7) reduce to the normal space (8).

Normal cones are central to characterizations both of the regularity of individual sets as well as of the regularity (transversality) of collections of sets. For collections of sets, when dealing with projection algorithms, it is important to account for the relation of the sets to each other and so the classical definitions of the normal cones above are too blunt for a refined numerical analysis. A typical situation: two nonempty sets A and B such that the affine span of $A\cup B$ is not equal to the whole space (e.g., two distinct intersecting lines in $\mathbb {R}^3$). One would expect all projections to lie in this affine span and the convergence to depend only on the mutual arrangement of the sets within the span. However, the normals (of any kind) to this affine span are also normals to the sets. They make a nontrivial subspace and this causes problems for the regularity conditions on collections of sets discussed below. In the context of algorithms, the only regularity conditions that are relevant are those that apply to the space where the iterates lie. In the case of algorithms like alternating projections, this is often an affine subspace of dimension smaller than the space in which the problem is formulated, as the example above illustrates.

That normals to one of the sets should take into account the location of the other set was first recognized by Bauschke et al. [9, 10] and has been used by Drusvyatskiy et al. [22, 23],² and Noll and Rondepierre [53], leading to weaker “restricted” regularity conditions. The most straightforward idea is to consider only those normals to each of the sets which are directed towards the other set. Given two closed sets A and B and a point $\overline{x}\in \mathrm{bd}\,A\cap \mathrm{bd}\,B$, one can define (see [9, 10]) the following restricted analogues of the cones (3)–(5):

$$\begin{aligned} N^F_{A|B}(\overline{x}):= & {} N^F_{A}(\overline{x})\cap {{\mathrm{{cone}}}}\left( B-\overline{x}\right) ,\\ N^{\text {prox}}_{A|B}(\overline{x}):= & {} {{\mathrm{{cone}}}}\left( (P_A^{-1}(\overline{x})\cap B)-\overline{x}\right) ,\\ {N}_{A|B}(\overline{x}):= & {} \mathop {\mathrm{Lim\,sup}\,}_{x\mathop {\rightarrow }\limits ^{A}\overline{x}}N^{\text {prox}}_{A|B}(x), \end{aligned}$$

which are called, respectively, the B-Fréchet normal cone, B-proximal normal cone and B-limiting normal cone to A at $\overline{x}$. When $B=\mathbb {E}$, they coincide with the cones (3)–(5). Note that in general $N^{\text {prox}}_{A|B}(\overline{x})$ and ${N}_{A|B}(\overline{x})$ can be empty. The essence of what we call “dual regularity conditions” consists in computing appropriate normal cones (limiting, Fréchet, or proximal) to each of the sets at the reference point (or nearby) and ensuring that the cones do not contain oppositely directed nonzero vectors. Such conditions are important for many applications including convergence analysis of projection algorithms.

The regularity/transversality properties of the collection $\{A,B\}$ in $\mathbb {E}$ can be understood in terms of the corresponding properties of the set-valued mapping $F:\mathbb {E}\rightrightarrows {\mathbb {E}}^2$ defined by (cf. [23, 29, 30, 44])

$$\begin{aligned} F(x):= (A-x)\times (B-x). \end{aligned}$$

(9)

For $x \in \mathbb {E}$ and $u=(u_1,u_2) \in {\mathbb {E}}^2$, we have

$$\begin{aligned}&x \in A\cap B \iff (0,0) \in F(x),\\&\quad F^{-1}(u) = (A-u_1)\cap (B-u_2),\quad \text{ and }\quad F^{-1}(0) =A\cap B. \end{aligned}$$

The mapping (9) is not the only possibility. Another useful construction is given by the set-valued mapping $G:\mathbb {E}^2 \rightrightarrows \mathbb {E}$ (cf. [45, p. 226], [23, p. 1638], [30, Corollary 7.13]) defined as follows:

$$\begin{aligned} G(x_1,x_2):= {\left\{ \begin{array}{ll} \{x_1-x_2\}&{} \quad \text{ if } x_1\in A \text{ and } x_2\in B,\\ \emptyset &{}\quad \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(10)

Obviously,

$$\begin{aligned} 0 \in G(x_1,x_2) \quad \Longleftrightarrow \quad x_1=x_2\in A\cap B. \end{aligned}$$

Conversely, the regularity of certain set-valued mappings can be understood in terms of the corresponding properties of collections of sets. Indeed, given a set-valued mapping $F:\mathbb {E}_1\rightrightarrows \mathbb {E}_2$, its regularity properties at a point $(\overline{x},\overline{y})$ in its graph ${{\mathrm{gph}}}F:=\{(x,y)\in \mathbb {E}_1\times \mathbb {E}_2\mid y\in F(x)\}$ are connected to those of the collection of sets (cf. [35, Corollary 2.1])

$$\begin{aligned} A:={{\mathrm{gph}}}F\quad \text{ and }\quad B:=\mathbb {E}_1\times \{\overline{y}\} \end{aligned}$$

in $\mathbb {E}_1\times \mathbb {E}_2$ . One can check that $(\overline{x},\overline{y})\in A\cap B=F^{-1} (\overline{y})\times \{\overline{y}\}$.

In the next definition, we recall two common regularity properties for a set-valued mapping $F:\mathbb {E}_1\rightrightarrows \mathbb {E}_2$ between two Euclidean spaces at a point $(\overline{x},\overline{y})\in {{\mathrm{gph}}}F$.

Definition 1

• (i) F is metrically subregular at ${\overline{x}}$ for ${\overline{y}}$ if there exist $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} \alpha d\left( x,F^{-1}({\overline{y}})\right) \le d({\overline{y}},F(x))\;\; \quad \text{ for } \text{ all }\;\; x \in {\mathbb {B}}_{\delta }({\overline{x}}). \end{aligned}$$

  (11)

  If, additionally, ${\overline{x}}$ is an isolated point of $F^{-1}({\overline{y}})$, then F is called strongly metrically subregular at ${\overline{x}}$ for ${\overline{y}}$.

• (ii) F is metrically regular at ${\overline{x}}$ for ${\overline{y}}$ if there exist $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} \alpha d\left( x,F^{-1}(y)\right) \le d\left( y,F(x)\right) \;\; \quad \text{ for } \text{ all }\;\; x \in {\mathbb {B}}_{\delta }({\overline{x}}),\; y \in {\mathbb {B}}_{\delta }({\overline{y}}). \end{aligned}$$

  (12)

We use the notation $\mathrm{sr}[F](\overline{x},\overline{y})$ and $\mathrm{r}[F](\overline{x},\overline{y})$ to denote the supremum of all $\alpha$ such that conditions (11) and (12), respectively, hold for some $\delta >0$. Properties (i) and (ii) in Definition 1 are equivalent to conditions $\mathrm{sr}[F](\overline{x},\overline{y})>0$ and $\mathrm{r}[F](\overline{x},\overline{y})>0$, respectively, and the values $\mathrm{sr}[F](\overline{x},\overline{y})$ and $\mathrm{r}[F](\overline{x},\overline{y})$ characterize the corresponding properties quantitatively. Some authors use for that purpose the reciprocals of the above constants (cf. [21]):

$$\begin{aligned} {{\mathrm{subreg}}}(F;{\overline{x}}|{\overline{y}}):=\frac{1}{\mathrm{sr}[F](\overline{x},\overline{y})},\quad {{\mathrm{reg}}}(F;{\overline{x}}|{\overline{y}}):=\frac{1}{\mathrm{r}[F](\overline{x},\overline{y})}, \end{aligned}$$

which are referred to as subregularity modulus and regularity modulus, respectively. One obviously has $0\le \mathrm{r}[F](\overline{x},\overline{y})\le \mathrm{sr}[F](\overline{x},\overline{y})$, which means that metric regularity is in general a stronger property than metric subregularity.

Both regularity properties in Definition 1 are fundamental for variational analysis (especially the second one) and have found numerous applications in optimization and other fields. Several useful characterizations of these properties and the fundamental equivalences

$$\begin{aligned} \text{ Metric } \text{ regularity } \;\;\Leftrightarrow \;\; \text{ Linear } \text{ openness } \;\;\Leftrightarrow \;\; \text{ Aubin } \text{ property } \text{ of } \text{ the } \text{ inverse },\\ \text{ Metric } \text{ subregularity } \;\;\Leftrightarrow \;\; \text{ Linear } \text{ subopenness } \;\;\Leftrightarrow \;\; \text{ Calmness } \text{ of } \text{ the } \text{ inverse } \end{aligned}$$

have been established. We refer the readers to the monographs [21, 49] and surveys [1, 3, 29, 30] for a comprehensive exposition of the properties. Note that metric subregularity of F at $\overline{x}$ for $\overline{y}\in F(\overline{x})$ is equivalent to the local error bound property of the real-valued function $x\mapsto d({\overline{y}},F(x))$ at $\overline{x}$, while metric regularity of F means that the mentioned error bound property holds uniformly with respect to y in a neighborhood of $\overline{y}$.

Our other basic notation is standard; cf. [21, 49, 58]. The open unit ball and the unit sphere in a Euclidean space are denoted $\mathbb {B}$ and $\mathbb {S}$, respectively. $\mathbb {B}_\delta (x)$ stands for the open ball with radius $\delta >0$ and center x. For a subspace V of a Euclidean space $\mathbb {E}$, $V^{\perp }:=\left\{ u\in \mathbb {E}\,\left| \,\left\langle u,v\right\rangle =0 \text{ for } \text{ all } v\in V\right. \right\}$ is the orthogonal complement subspace of V. For a real number $\alpha$, $[\alpha ]_+$ denotes $\max \{\alpha ,0\}$.

2 Regularity notions and convergence results

In the definitions below, we keep the terminology coming from the original publications although the use of words obviously lacks consistency.

2.1 Elemental set regularities

The following definition is a compilation of some of the main definitions of regularities of sets.

Definition 2

(set regularities) Let $A\subset \mathbb {E}$ be closed and let the projector be with respect to the Euclidean norm.

• (i) [53, Definition 2] A is $\sigma$ -Hölder regular relative to $B\subset \mathbb {E}$ at ${\overline{x}}\in A\cap B$ with constant $c>0$ if there exists a neighborhood W of ${\overline{x}}$ such that for each $b\in B\cap W$ and $b_A\in P_A(b)\cap W$,

  $$\begin{aligned} {\mathbb {B}}_{(1+c)\left\| b-b_A\right\| }(b)\cap A\cap V =\emptyset , \end{aligned}$$

  where

  $$\begin{aligned} V:=\left\{ x\in P^{-1}_B(b)\,\left| \,\left\langle b-b_A,x-b_A\right\rangle >\sqrt{c}\left\| b-b_A\right\| ^{\sigma +1}\left\| x-b_A\right\| \right. \right\} . \end{aligned}$$

• (ii) [26, Definition 2.9] A is ($A',\varepsilon ,\delta$)-subregular relative to $B\subset \mathbb {E}$ at $\overline{x}$ if

  $$\begin{aligned} \left\langle v,b-a\right\rangle \le \varepsilon \left\| v\right\| \left\| b-a\right\| \end{aligned}$$

  (13)

  holds for all $b\in B\cap {\mathbb {B}}_\delta ({\overline{x}})$, $a\in A\cap {\mathbb {B}}_\delta ({\overline{x}})$ and $v\in N^{\text {prox}}_{ A| A'}(a)$. If $B=\{{\overline{x}}\}$, then the respective qualifier, “relative to” is dropped. If $A'=\mathbb {E}$, then A is said to be $(\varepsilon ,\delta )$ -subregular (relative to B) at ${\overline{x}}$.

• (iii) [9, Definition 8.1] If $B= A$ in (2) above, then the set A is said to be $( A', \varepsilon ,\delta )$ -regular at ${\overline{x}}$. If also $A'=\mathbb {E}$, then A is said to be $(\varepsilon ,\delta )$ -regular at ${\overline{x}}$.

• (iv) [58, Definition 6.4] A is Clarke regular at ${\overline{x}}\in A$ if ${N}_{A}(\overline{x})=N^F_{A}(\overline{x})$.

• (v) [44, Definition 4.3] A is super-regular at ${\overline{x}}\in A$ if for any $\varepsilon >0$, there is a $\delta >0$ such that

  $$\begin{aligned}&\left\langle z-z_A,x-z_A\right\rangle \le \varepsilon \left\| z-z_A\right\| \Vert x-z_A\Vert \\&\quad \text{ for } \text{ all }\;\; x\in A\cap {\mathbb {B}}_\delta ({\overline{x}}), z\in {\mathbb {B}}_\delta ({\overline{x}}), z_A\in P_A(z). \end{aligned}$$

• (vi) [57, Definition 1.1] A is prox-regular at ${\overline{x}}\in A$ for ${\overline{v}}\in {N}_{A}({\overline{x}})$ if there exist $\varepsilon ,\delta >0$ such that

  $$\begin{aligned} \left\langle v,x-a\right\rangle \le \frac{\varepsilon }{2}\left\| x-a\right\| ^2 \;\; \quad \text{ for } \text{ all }\;\; x,a \in A\cap {\mathbb {B}}_\delta ({\overline{x}}), v\in {\mathbb {B}}_{\delta }({\overline{v}}) \cap {N}_{A}(a). \end{aligned}$$

  If A is prox-regular at ${\overline{x}}\in A$ for all $v\in {N}_{A}({\overline{x}})$, then A is said to be prox-regular at ${\overline{x}}$.

Convexity, of course, implies all properties in Definition 2 globally.

2.2 Regularity of collections of sets

The origins of the concept of regular arrangement of sets in space can be traced back to that of transversality in differential geometry which deals of course with smooth manifolds (see, for instance, [25, 27]).

Given two smooth manifolds $A,B\subset \mathbb {E}$ around a point ${\overline{x}}\in A\cap B$, an important question is whether their intersection $A\cap B$ is also a smooth manifold around ${\overline{x}}$. For that to be true, the manifolds must intersect in a certain regular way. The typical sufficient regularity assumption is known as transversality: the collection $\{A,B\}$ of smooth manifolds is transversal at ${\overline{x}}\in A\cap B$ if

$$\begin{aligned} T_A({\overline{x}}) + T_B({\overline{x}}) = \mathbb {E}. \end{aligned}$$

(14)

This notion has been used in [25, 30, 45]. Under this assumption, $A\cap B$ is a smooth manifold around ${\overline{x}}$ and the following equalities hold (cf. [25, 30, 45]):

$$\begin{aligned} T_{A\cap B}({\overline{x}})&= T_A({\overline{x}}) \cap T_B({\overline{x}}), \end{aligned}$$

(15)

$$\begin{aligned} N_{A}({\overline{x}})&\cap N_{B}({\overline{x}})= \{0\}. \end{aligned}$$

(16)

Equality (15) is only a necessary condition and is in general weaker than condition (16). When A and B are convex sets, it is known as the conical hull intersection property (CHIP) [17] (cf. [4, Definition 5.1]).

Example 1

Let $\mathbb {E}=\mathbb {R}^2$, $A=B=\mathbb {R}\times \{0\}$, $\overline{x}=(0,0)$. Then $A\cap B=A=B$, $T_{A\cap B}({\overline{x}}) = T_A({\overline{x}}) =T_B({\overline{x}})$, and consequently, equality (15) holds true. At the same time, $T_A({\overline{x}})+T_B({\overline{x}})=\mathbb {R}\times \{0\}$ and $N_{A}({\overline{x}})=N_{B}({\overline{x}})=\{0\}\times \mathbb {R}$. Thus condition (16) is not satisfied.

The transversality property of a collection of two smooth manifolds can be characterized quantitatively in terms of the angle between their tangent (or normal) spaces. One can use for that purpose the Friedrichs angle (cf. Deutsch [19]).

Definition 3

(Friedrichs angle) Given two nonempty subspaces $V_1$ and $V_2$, the Friedrichs angle is a number between 0 and $\pi /2$ whose cosine is given by

$$\begin{aligned}&c(V_1,V_2) \nonumber \\&\quad := \max \left\{ \left\langle v_1,v_2\right\rangle \mid v_1\in V_1\cap (V_1\cap V_2)^{\perp }\cap \mathbb {B},\; v_2\in V_2\cap (V_1\cap V_2)^{\perp }\cap \mathbb {B}\right\} . \end{aligned}$$

(17)

The following properties provide some insight into the geometry of the intersection (cf. [9, Fact 7.10], [45, Lemmas 3.2 and 3.3]):

$$\begin{aligned}&\displaystyle c(V_1,V_2)=c(V_1^{\perp },V_2^{\perp })<1, \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle \qquad \qquad \qquad \quad \text{ and } \text{ if }\quad V_1\cap V_2=\{0\}.\nonumber \\&\displaystyle 1-c(V_1,V_2)=\min \left\{ d^2(v,V_1)+ d^2(v,V_2)\mid \left\| v\right\| =1\right\} \end{aligned}$$

(19)

The angle between two smooth manifolds A and B around a point ${\overline{x}}\in A\cap B$ is defined in [45, Definition 3.1] as the Friedrichs angle between the two tangent subspaces $T_A({\overline{x}})$ and $T_B({\overline{x}})$, or equivalently, in view of (18), the Friedrichs angle between the two normal subspaces $N_{A}({\overline{x}})$ and $N_{B}({\overline{x}})$:

$$\begin{aligned} c(A,B,{\overline{x}}) := c(T_A({\overline{x}}),T_B({\overline{x}}))= c(N_{A}({\overline{x}}),N_{B}({\overline{x}})). \end{aligned}$$

(20)

Observe that, with $V_1=N_{A}(\overline{x})$ and $V_2=N_{B}(\overline{x})$, condition $V_1\cap V_2=\{0\}$ in (19) is equivalent to (16), and thus, to the transversality of $\{A,B\}$ at ${\overline{x}}$.

Expanding our scope to the general case of two closed sets $A,B\subset \mathbb {E}$ having a common point ${\overline{x}}\in A\cap B$ the intuition behind transversality plays an important role, but it is clear that a richer vocabulary is needed to describe the many ways in which sets can intersect ‘transversally’.

Definition 4

(regularities of collections of sets) Suppose A and B are closed sets of $\mathbb {E}$ and $\overline{x}\in \mathrm{bd}\,A\cap \mathrm{bd}\,B$.

• (i) [18, p. 99] The transversality condition holds at ${\overline{x}}$ if

  $$\begin{aligned} {N}_{A}({\overline{x}}) \cap (-{N}_{B}({\overline{x}})) = \{0\}. \end{aligned}$$

  (21)

• (ii) [59, p. 62] The collection of sets $\{A,B\}$ is locally linearly regular at $\overline{x}\in A\cap B$ if there exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} \alpha d\left( x,A\cap B\right) \le \max \left\{ d(x,A),d(x,B)\right\} \;\; \quad \text{ for } \text{ all }\;\; x\in \mathbb {B}_{\delta }({\overline{x}}). \end{aligned}$$

• (iii) [9, Definition 6.6] The (A, B)-qualification condition holds at $\overline{x}$ if one of the following equivalent formulations holds:

  • (a) there exists a number $\alpha <1$ such that $-\left\langle v_1,v_2 \right\rangle <\alpha$ for all $v_1\in {N}_{A|B}(\overline{x})\cap \mathbb {S}$ and $v_2\in {N}_{B|A}(\overline{x})\cap \mathbb {S}$; or

  • (b) there exist numbers $\alpha <1$ and $\delta >0$ such that $-\left\langle v_1,v_2 \right\rangle <\alpha$ for all $a\in A\cap \mathbb {B}_{\delta }(\overline{x})$, $b\in B\cap \mathbb {B}_{\delta }(\overline{x})$, $v_1\in N^{\text {prox}}_{A|B}(a)\cap \mathbb {S}$, and $v_2\in N^{\text {prox}}_{B|A}(b)\cap \mathbb {S}$.

• (iv) [22, Definition 4.4] A and B are inherently transversal at $\overline{x}$ if there exist numbers $\alpha <1$ and $\delta >0$ such that

  $$\begin{aligned} \left\langle a_1-b_2,a_2-b_1 \right\rangle <\alpha \Vert a_1-b_2\Vert \,\Vert a_2-b_1\Vert \end{aligned}$$

  for all $a_1\in (A{\setminus } B)\cap \mathbb {B}_{\delta }(\overline{x})$, $b_1\in (B{\setminus } A)\cap \mathbb {B}_{\delta }(\overline{x})$, $b_2\in P_B(a_1)$, and $a_2\in P_A(b_1)$.

• (v) [53, Definition 1] B intersects A separably at $\overline{x}$ if there exist numbers $\alpha <1$ and $\delta >0$ such that

  $$\begin{aligned} \left\langle a_1-b,a_2-b \right\rangle <\alpha \Vert a_1-b\Vert \,\Vert a_2-b\Vert \end{aligned}$$

  for all $a_1\in (A{\setminus } B)\cap \mathbb {B}_{\delta }(\overline{x})$, $b\in (P_B(a_1){\setminus } A)\cap \mathbb {B}_{\delta }(\overline{x})$, and $a_2\in P_A(b)\cap \mathbb {B}_{\delta }(\overline{x})$.

  If A also intersects B separably at $\overline{x}$, then $\{A,B\}$ is said to intersect separately at $\overline{x}$.

• (vi) [23, Definition 3.1] A and B are intrinsically transversal at $\overline{x}$ if one of the following equivalent conditions holds:

  • (a) there exist numbers $\alpha >0$ and $\delta >0$ such that

    $$\begin{aligned} \max \biggl \{d\left( \frac{b-a}{\Vert a-b\Vert }, {N}_{A}(a)\right) , d\left( \frac{a-b}{\Vert a-b\Vert }, {N}_{B}(b)\right) \biggr \}>\alpha \end{aligned}$$

    for all $a\in (A{\setminus } B)\cap \mathbb {B}_{\delta }(\overline{x})$ and $b\in (B{\setminus } A)\cap \mathbb {B}_{\delta }(\overline{x})$; or

  • (b) there exist numbers $\alpha >0$ and $\delta >0$ such that

    $$\begin{aligned} \max \biggl \{d\left( \frac{b-a}{\Vert a-b\Vert }, N^{\text {prox}}_{A}(a)\right) , d\left( \frac{a-b}{\Vert a-b\Vert }, N^{\text {prox}}_{B}(b)\right) \biggr \}>\alpha \end{aligned}$$

    for all $a\in (A{\setminus } B)\cap \mathbb {B}_{\delta }(\overline{x})$ and $b\in (B{\setminus } A)\cap \mathbb {B}_{\delta }(\overline{x})$.

Using the Euclidean space geometry, each of the properties in Definition 4 can be reformulated equivalently in several different ways; see some reformulations in [42] including the angle characterization of intrinsic transversality in [42, Proposition 19]. Analytically, this means quantifying each of these properties. As observed in [45, Theorem 18], for two smooth manifolds the equalities (14) and (16) are actually equivalent. Properties (1) and (2) are shown in Theorems 1 and 2 below to be equivalent to what we call in this article (Definition 6) transversality and subtransversality, respectively.

A more general Hölder-type setting of property (v) with exponent $\omega \in [0,2)$ is considered in [53]. Definition 4(v) corresponds to the ‘linear’ case $\omega =0$. Note also that this notion is not symmetric: B may intersect A separably, but A need not intersect B separably.

Proposition 1

(relations between regularities of collections) The known relationships between the properties in Definition 4 are as follows:

• (a) (3) $\Rightarrow$ (4) $\Rightarrow$ (5).

• (b) (6) $\Rightarrow$ (5).

• (c) Property (6) is in general independent of each of the properties (3) and (4).

• (d) When both sets are super-regular [Definition 2(v)] at the reference point, (4) $\Rightarrow$ (6).

Proof

Implications (a) and (b) follow from the description of the properties in Definition 4. The observation (c) was demonstrated in [42, Examples 23 and 24]. Implication (d) was shown in [22, Proposition 4.5]. $\square$

2.3 Convergence results

We catalog next some of the main nonconvex convergence results making use of certain combinations of the above regularities.

Proposition 2

(linear convergence of alternating projections) For A and B closed with nonempty intersection and $\overline{x}\in A\cap B$, the alternating projections algorithm converges locally linearly if one of the following collection of conditions holds.

• (i) [45, Theorem 4.3] A and B are smooth manifolds around ${\overline{x}}$ and $\{A,B\}$ is transversal at ${\overline{x}}$.

• (ii) [44, Theorem 5.16] A is super-regular at ${\overline{x}}$ and the transversality condition (21) holds at ${\overline{x}}$.

• (iii) [9, Theorem 3.17] A is $(B,\varepsilon ,\delta )$-regular at ${\overline{x}}$ and the (A, B)-qualification condition holds at ${\overline{x}}$.

• (iv) [26, Theorem 3.11] A and B are $(\varepsilon ,\delta )$-subregular relative to $A\cap B$ at ${\overline{x}}$ and $\{A,B\}$ is locally linearly regular at ${\overline{x}}$.

• (v) [22, Theorem 2.3] $\{A,B\}$ is intrinsically transversal at ${\overline{x}}$.

• (vi) [53, Theorem 2] A is 0-Hölder regular relative to B at ${\overline{x}}$ and $\{A,B\}$ intersects separably at ${\overline{x}}$.

Proposition 3

(linear convergence of the Douglas-Rachford algorithm) For A and B closed with nonempty intersection and $\overline{x}\in A\cap B$, the Douglas-Rachford algorithm converges locally linearly if one of the following collection of conditions holds.

• (i) [26, Theorem 3.18] $\{A,B\}$ satisfies the transversality condition (21) at ${\overline{x}}$, the set B is an affine subspace, and A is $(\varepsilon ,\delta )$-subregular relative to $A\cap B$ at ${\overline{x}}$.

• (ii) [56, Theorem 4.3] $\{A,B\}$ satisfies the transversality condition (21) at ${\overline{x}}$, and A and B are $(\varepsilon ,\delta )$-subregular at ${\overline{x}}$.

3 Elemental set regularity

Elemental (sub)regularity defined next provides a unifying framework for the other notions of set regularity given in Definition 2.

Definition 5

(elemental regularity of sets) Let $\emptyset \ne A\subset \mathbb {E}$, $\overline{x}\in \mathbb {E}$ and $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$.

• (i) A is elementally subregular of order $\sigma$ relative to $B\subset \mathbb {E}$ at ${\overline{x}}$ for $\left( a,v\right)$ with constant $\varepsilon$ if there exists a neighborhood U of ${\overline{x}}$ such that

  $$\begin{aligned}&\left\langle v - \left( b-b_A\right) ,b_A - a\right\rangle \le \varepsilon \left\| v-\left( b-b_A\right) \right\| ^{1+\sigma }\left\| b_A-a\right\| \nonumber \\&\quad \text{ for } \text{ all }\;\; b\in B \cap U, b_{A}\in P_{A}(b). \end{aligned}$$

  (22)

• (ii) A is uniformly elementally subregular of order $\sigma$ relative to $B\subset \mathbb {E}$ at ${\overline{x}}$ for $\left( a,v\right)$ if for any $\varepsilon >0$, there is a neighborhood U of ${\overline{x}}$ such that (22) holds.

• (iii) A is elementally regular of order $\sigma$ at ${\overline{x}}$ for $\left( a,v\right)$ with constant $\varepsilon$ if there exists a neighborhood V of v such that, for all $u\in {N}_{A}(a)\cap V$, A is elementally subregular of order $\sigma$ relative to $B:=A$ at ${\overline{x}}$ for $\left( a,u\right)$ with constant $\varepsilon$.

• (iv) A is uniformly elementally regular of order $\sigma$ at ${\overline{x}}$ for $\left( a,v\right)$ if there exists a neighborhood V of v such that, for all $u\in {N}_{A}(a)\cap V$, A is uniformly elementally subregular of order $\sigma$ relative to $B:=A$ at ${\overline{x}}$ for $\left( a,u\right)$.

If $B=\{{\overline{x}}\}$ in (i) and (ii), then the respective qualifier, “relative to” is dropped. If $\sigma =0$, then the respective qualifier, “of order” is dropped in the description of the properties. The modulus of elemental (sub)regularity is the infimum over all $\varepsilon$ for which (22) holds.

In all properties in Definition 5, ${\overline{x}}$ need not be in B and a need not be in U, although these are the main cases of interest for us. When $\sigma =0$, the properties are trivial for any constant $\varepsilon \ge 1$, so the only case of interest is elemental (sub)regularity with constant $\varepsilon <1$.

Example 2

• (a) A cross:

  $$\begin{aligned} A=\mathbb {R}\times \{0\}\cup \{0\}\times \mathbb {R}. \end{aligned}$$

  This example is of particular interest for the study of sparsity constrained optimization. A is elementally regular at any ${\overline{x}}\ne 0$, say $\Vert {\overline{x}}\Vert>\delta >0$, for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon =0$ and neighborhood ${\mathbb {B}}_\delta ({\overline{x}})$. The set A is not elementally regular at ${\overline{x}}=0$ for any $(0,v)\in {{\mathrm{gph}}}{{N}_{A}}$ since ${N}_{A}(0)= A$. However, A is elementally subregular at ${\overline{x}}=0$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ with constant $\varepsilon =0$ and neighborhood $\mathbb {E}$ since all vectors $a\in A$ are orthogonal to ${N}_{A}(a)$.

• (b) A circle:

  $$\begin{aligned} A=\left\{ (x_1,x_2)\in \mathbb {R}^2\,\left| \, x_1^2+x_2^2=1\right. \right\} . \end{aligned}$$

  This example is of particular interest for the phase retrieval problem. The set A is uniformly elementally regular at any ${\overline{x}}\in A$ for all $({\overline{x}},v)\in {{\mathrm{gph}}}{{N}_{A}}$. Indeed, note first that for any ${\overline{x}}\in A$, ${N}_{A}({\overline{x}})$ consists of the line passing through the origin and ${\overline{x}}$. Now, for any $\varepsilon \in (0,1)$, we choose $\delta = \varepsilon$. Then for any $x\in A\cap {\mathbb {B}}_{\delta }({\overline{x}})$, it holds $\cos \angle (-{\overline{x}},x-{\overline{x}})\le \delta \le \varepsilon$. Hence, for all $x\in A\cap {\mathbb {B}}_{\delta }({\overline{x}})$ and $v\in {N}_{A}({\overline{x}})$,

  $$\begin{aligned} \left\langle v,x-{\overline{x}}\right\rangle= & {} \cos \angle (v,x-{\overline{x}})\Vert v\Vert \Vert x-{\overline{x}}\Vert \\\le & {} \cos \angle (-{\overline{x}},x-{\overline{x}})\Vert v\Vert \Vert x-{\overline{x}}\Vert \le \varepsilon \Vert v\Vert \Vert x-{\overline{x}}\Vert . \end{aligned}$$
• (c)
  $$\begin{aligned} A= & {} \left\{ (x_1,x_2)\in \mathbb {R}^2\,\left| \, x_1^2+ x_2^2\le 1,\, x_1\le |x_2|\right. \right\} \subset \mathbb {R}^2,\\ B= & {} \left\{ (x_1,x_2)\in \mathbb {R}^2\,\left| \,x_1^2+ x_2^2\le 1, x_2 \le x_1 \le 2x_2\right. \right\} \subset \mathbb {R}^2. \end{aligned}$$

  The set A is elementally subregular relative to B at ${\overline{x}}= 0$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A|B}}$ with constant $\varepsilon =0$ and neighborhood $\mathbb {E}$ since for all $b\in B$, $b_A\in P_{A}(b)$ and $v\in {N}_{A|B}(a)$, there holds

  $$\begin{aligned} \left\langle v-(b-b_A),b_A-a\right\rangle = \left\langle v,b_A-a\right\rangle -\left\langle b-b_A,b_A-a\right\rangle = 0. \end{aligned}$$

  The set A, however, is not elementally regular at ${\overline{x}}=0$ for any $(0,v)\in {{\mathrm{gph}}}{{N}_{A}}$ because by choosing $x=tv \in A$ (where $0\ne v\in A\cap {N}_{A}(0)$, $t\downarrow 0$), we get $\left\langle v,x\right\rangle =\Vert v\Vert \Vert x\Vert >0$.

Proposition 4

Let A, $A'$ and B be closed nonempty subsets of $\mathbb {E}$.

• (i) Let $A\cap B\ne \emptyset$ and suppose that there is a neighborhood W of ${\overline{x}}\in A\cap B$ and a constant $\varepsilon >0$ such that for each

  $$\begin{aligned} (a,v)\in V:=\left\{ (b_A,u)\in {{\mathrm{gph}}}{N^{\text {prox}}_{A}}\,\left| \,u=b-b_A, \begin{array}{c} \quad \text{ for } b \in B\cap W\\ \text{ and } b_A \in P_A(b)\cap W \end{array}\right. \right\} , \end{aligned}$$

  (23)

  it holds that

  $$\begin{aligned} {\overline{x}}\in {{\mathrm{int\,}}}U(a,v) \text{ where } U(a,v):={\mathbb {B}}_{(1+\varepsilon ^2)\Vert v\Vert }(a+v). \end{aligned}$$

  (24)

  Then, A is $\sigma$-Hölder regular relative to B at ${\overline{x}}$ with constant $c=\varepsilon ^2$ and neighborhood W of ${\overline{x}}$ if and only if A is elementally subregular of order $\sigma$ relative to $A\cap P^{-1}_B\left( a+v\right)$ at ${\overline{x}}$ for each $(a,v)\in V$ with constant $\varepsilon =\sqrt{c}$ and the respective neighborhood U(a, v).

• (ii) Let $B\subset A$. The set A is $(A',\varepsilon ,\delta )$-subregular relative to B at ${\overline{x}}\in A$ if and only if A is elementally subregular relative to B at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{N^{\text {prox}}_{ A| A'}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. Consequently, $(\varepsilon ,\delta )$-subregularity implies 0-Hölder regularity.

• (iii) The set A is $( A',\varepsilon ,\delta )$-regular at ${\overline{x}}\in A$ if and only if A is elementally subregular relative to A at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{N^{\text {prox}}_{ A| A'}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. If A is $( A',\varepsilon ,\delta )$-regular at ${\overline{x}}$, then A is elementally regular at ${\overline{x}}$ for all $({\overline{x}},v)$ with constant $\varepsilon$, where $0\ne v\in N^{\text {prox}}_{ A| A'}({\overline{x}})$.

• (iv) The set A is Clarke regular at ${\overline{x}}\in A$ if and only if A is uniformly elementally regular at ${\overline{x}}$ for all $({\overline{x}},v)$ with $v\in {N}_{A}({\overline{x}})$. Consequently, Clarke regularity implies $(\varepsilon ,\delta )$-regularity.

• (v) The set A is super-regular at ${\overline{x}}\in A$ if and only if for any $\varepsilon >0$, there is a $\delta >0$ such that A is elementally regular at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. Consequently, super-regularity implies Clarke regularity.

• (vi) If A is prox-regular at ${\overline{x}}$, then there exist positive constants $\overline{\varepsilon }$ and ${\overline{\delta }}$ such that, for any $\varepsilon >0$ and $\delta :=\frac{\varepsilon {\overline{\delta }}}{\overline{\varepsilon }}$ defined correspondingly, A is elementally regular at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_\delta ({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_\delta ({\overline{x}})$. Consequently, prox-regularity implies super-regularity.

• (vii) If A is convex then it is elementally regular at all $x \in A$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ with constant $\varepsilon =0$ and the neighborhood $\mathbb {E}$ for both x and v.

Proof

(i) The set A is $\sigma$-Hölder regular at ${\overline{x}}$ relative to B with constant $c=\varepsilon ^2$ and neighborhood W if and only if

$$\begin{aligned} \left\langle b-b_A,x-b_A\right\rangle \le \varepsilon \Vert b-b_A\Vert ^{1+\sigma }\Vert x-b_A\Vert \end{aligned}$$

holds for each $b\in B\cap W$, $b_A\in P_{A}(b)\cap W$, and $x\in A\cap P_{B}^{-1}(b)\cap {\mathbb {B}}_{(1+\varepsilon ^2)\Vert b-b_A\Vert }(b)$. But this is equivalent to

$$\begin{aligned} \left\langle v,x-a\right\rangle \le \varepsilon \Vert v\Vert ^{1+\sigma }\Vert x-a\Vert \end{aligned}$$

holding for each $(a,v)\in V$ and $x\in \left( A\cap P_{B}^{-1}(a+v)\right) \cap U(a,v)$. Thanks to assumption (24), this is equivalent to A being elementally subregular of order $\sigma$ relative to $A\cap P_{B}^{-1}(a+v)$ at ${\overline{x}}$ for each $(a,v)\in V$ with constant $\varepsilon$ and neighborhood U(a, v).

(ii) The set A is $( A', \varepsilon , \delta )$-subregular relative to $B\subset A$ at ${\overline{x}}$ if and only if (13) holds for all $b\in B\cap {\mathbb {B}}_{\delta }(\overline{x})$, $a\in A\cap {\mathbb {B}}_\delta ({\overline{x}})$ and $v\in N^{\text {prox}}_{A|A'}(a)$. In other words, A is elementally subregular relative to B at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{N^{\text {prox}}_{ A| A'}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_\delta ({\overline{x}})$.

(iii) The first part is a particular case of (ii) for $B=A$. For the latter part, we suppose A is $(A',\varepsilon ,\delta )$-regular at ${\overline{x}}$ and let $0\ne v\in N^{\text {prox}}_{A|A'}({\overline{x}})$. We can assume without loss of generality that ${\overline{x}}\in P_{A}(z)$ for $z:={\overline{x}}+v$ (otherwise one could rescale v so that this holds). From the variational characterization of the Euclidean projector, ${\overline{x}}\in P_{ A}(z)$ if and only if

$$\begin{aligned} \left\langle z-{\overline{x}},x-{\overline{x}}\right\rangle \le \frac{1}{2}\left\| x-{\overline{x}}\right\| ^2\;\; \quad \text{ for } \text{ all }\;\; x\in A. \end{aligned}$$

In particular,

$$\begin{aligned} \left\langle v,x-{\overline{x}}\right\rangle \le \frac{\varepsilon }{2}\left\| v\right\| \left\| x-{\overline{x}}\right\| \;\; \text{ for } \text{ all }\;\; x\in A\cap {\mathbb {B}}_{{\overline{\delta }}}({\overline{x}})\quad (\text{ where } {\overline{\delta }}=\varepsilon \left\| v\right\| >0). \end{aligned}$$

Consider the neighborhood $V:= \left\{ u\in \mathbb {E}\,\left| \,(2+\varepsilon )\Vert u-v\Vert \le \varepsilon \Vert u\Vert \right. \right\}$ of v. Then the claim holds since, for all $x\in A\cap {\mathbb {B}}_{{\overline{\delta }}}({\overline{x}})$ and $u\in V$, one has

$$\begin{aligned} \left\langle u,x-{\overline{x}}\right\rangle =\,&\left\langle v,x-{\overline{x}}\right\rangle + \left\langle u-v,x-{\overline{x}}\right\rangle \\ \le \,&\frac{\varepsilon }{2}\left\| v\right\| \left\| x-{\overline{x}}\right\| + \Vert u-v\Vert \Vert x-{\overline{x}}\Vert \\ \le \,&\frac{\varepsilon }{2}\left\| u\right\| \left\| x-{\overline{x}}\right\| + \frac{2+\varepsilon }{2}\Vert u-v\Vert \Vert x-{\overline{x}}\Vert \\ \le \,&\frac{\varepsilon }{2}\left\| u\right\| \left\| x-{\overline{x}}\right\| + \frac{\varepsilon }{2}\Vert u\Vert \Vert x-{\overline{x}}\Vert = \varepsilon \left\| u\right\| \left\| x-{\overline{x}}\right\| . \end{aligned}$$

(iv) The set A is Clarke regular at ${\overline{x}}$ if and only if for any $v\in {N}_{A}({\overline{x}})$ and $\varepsilon >0$, there is a $\delta >0$ such that

$$\begin{aligned} \left\langle v,x-{\overline{x}}\right\rangle \le \varepsilon \Vert v\Vert \Vert x-{\overline{x}}\Vert \;\; \quad \text{ for } \text{ all }\;\; x\in A\cap {\mathbb {B}}_\delta ({\overline{x}}). \end{aligned}$$

This means that A is uniformly elementally subregular relative to A at ${\overline{x}}$ for all $({\overline{x}},v)\in {{\mathrm{gph}}}{{N}_{A}}$.

(v) By [44, Proposition 4.4], A is super-regular at ${\overline{x}}$ if and only if for any $\varepsilon >0$, there is a $\delta >0$ such that

$$\begin{aligned} \left\langle v,x-a\right\rangle \le \varepsilon \left\| v\right\| \Vert x-a\Vert \;\; \quad \text{ for } \text{ all }\;\; x,a\in A\cap {\mathbb {B}}_\delta ({\overline{x}}), v\in {N}_{A}(a). \end{aligned}$$

(25)

Condition (25) just means that A is elementally regular at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. In particular, A is uniformly elementally regular at ${\overline{x}}$ for all $({\overline{x}},v)$ with $v\in {N}_{A}({\overline{x}})$. That is thanks to part (iv), A is Clarke regular at ${\overline{x}}$ confirming the fact established in [44, Corollary 4.5] that super-regularity implies Clarke regularity.

(vi) By [57, Proposition 1.2], A is prox-regular at ${\overline{x}}\in A$ if and only if A is prox-regular at ${\overline{x}}$ for 0. This means that there exist $\bar{\varepsilon },\bar{\delta }>0$ such that

$$\begin{aligned} \left\langle v,x-a\right\rangle \le \tfrac{\bar{\varepsilon }}{2}\left\| x-a\right\| ^2\;\; \quad \text{ for } \text{ all }\;\; x,a\in A\cap {\mathbb {B}}_{\bar{\delta }}({\overline{x}}), v\in {N}_{A}(a)\cap (\bar{\delta }{\mathbb {B}}). \end{aligned}$$

(26)

Let $\varepsilon >0$ be arbitrary and define $\delta = \tfrac{\varepsilon \bar{\delta }}{\bar{\varepsilon }}>0$. Then, for any $x,a\in A\cap {\mathbb {B}}_{\delta }({\overline{x}})$ and $0\ne v\in {N}_{A}(a)$, condition (26) ensures that

$$\begin{aligned} \left\langle v,x-a\right\rangle =\,&\frac{\Vert v\Vert }{\bar{\delta }}\left\langle \frac{\bar{\delta }}{\Vert v\Vert }v,x-a\right\rangle \le \frac{\Vert v\Vert }{\bar{\delta }}\frac{\bar{\varepsilon }}{2}\left\| x-a\right\| ^2 \quad \left( \text{ as } \tfrac{\bar{\delta }}{\Vert v\Vert }v\in \bar{\delta }{\mathbb {B}}\right) \\ =&\, \frac{\bar{\varepsilon }\Vert x-a\Vert }{2\bar{\delta }}\Vert v\Vert \left\| x-a\right\| \le \frac{\bar{\varepsilon }\delta }{\bar{\delta }}\Vert v\Vert \left\| x-a\right\| \quad (\text{ as } \Vert x-a\Vert \le 2\delta )\\ =\,&\varepsilon \Vert v\Vert \left\| x-a\right\| . \end{aligned}$$

This just says that A is elementally regular at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. Thanks to part (v) this, in particular, shows that prox-regularity implies super-regularity.

(vii) Since we are in a finite dimensional setting, A is nonempty closed and convex if and only if the projector is everywhere single-valued (Chebyshev [8, Theorem 3.14], [13], [19, Theorem 12.7]) and

$$\begin{aligned} \left\langle z-a,x-a\right\rangle \le 0\;\; \quad \text{ for } \text{ all }\;\; x,a\in A, z\in P^{-1}_ A(a). \end{aligned}$$

Since A is convex, then ${N}_{A}=N^{\text {prox}}_{A}$, and, in particular, $\left\{ z-a\,\left| \,z\in P^{-1}_A(a)\right. \right\} = {N}_{A}(a)$ for any $a\in A$, so the above inequality holds for all $x\in A$ and $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$. That is, A is elementally regular at all $x\in A$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ with constant $\varepsilon =0$ and the neighborhood $\mathbb {E}$ for both x and v. $\square$

Remark 1

The convex characterization can be localized. If there exists a $\rho >0$ such that $A\cap {\mathbb {B}}_{\rho }({\overline{x}})$ is convex, then for any $\delta \in (0,\rho )$ the set A is elementally regular at ${\overline{x}}$ for all $(a,v)\in {{\mathrm{gph}}}{{N}_{A}}$ where $a\in {\mathbb {B}}_{\delta }({\overline{x}})$ with constant $\varepsilon =0$ and neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$. This is relevant for the set in Example 2(a).

Remark 2

Assumption (24) seems to be a technical one. However, it is satisfied, for example, when the collection of sets $\{ A, B\}$ is strongly subtransversal at ${\overline{x}}$ with constant $\alpha \ge \tfrac{1}{1+\varepsilon ^2}$, where $\alpha$ is given below in Theorem 1(iii), since

$$\begin{aligned} \Vert (a+v)-{\overline{x}}\Vert =\Vert b-{\overline{x}}\Vert =d(b, A\cap B)\le (1+\varepsilon ^2)d(b,A) = (1+\varepsilon ^2)\Vert v\Vert . \end{aligned}$$

As a consequence, 0-Hölder regularity and elemental subregularity as specified in Proposition 4(i) are equivalent under the additional assumption of strong subtransversality of the collection of sets. This observation falls within our interest of investigating relationships amongst various regularity notions of individual sets and collections of sets.

4 Regularity of collections of sets

The following definition captures two of the central notions found (under various aliases and disguises) in the literature.

Definition 6

(transversality and subtransversality)

• (i) $\{A,B\}$ is subtransversal at ${\overline{x}}$ if there exist numbers $\alpha >0$ and $\delta >0$ such that

  $$\begin{aligned} \bigl (A+(\alpha \rho )\mathbb {B}\bigr )\cap \bigl (B+(\alpha \rho )\mathbb {B}\bigr )\cap \mathbb {B}_{\delta }({\overline{x}})\subseteq \left( A\cap B\right) +\rho \mathbb {B}\end{aligned}$$

  (27)

  for all $\rho \in (0,\delta )$.

  If, additionally, ${\overline{x}}$ is an isolated point of $A\cap B$, then $\{A,B\}$ is called strongly subtransversal at ${\overline{x}}$. The (possibly infinite) supremum of all $\alpha$ above is denoted $\mathrm{sr}[A,B](\overline{x})$ with the convention that the supremum of the empty set is zero.

• (ii) $\{A,B\}$ is transversal at ${\overline{x}}$ if there exist numbers $\alpha >0$ and $\delta >0$ such that

  $$\begin{aligned} (A-a-x_1)\cap (B-b-x_2)\cap (\rho \mathbb {B})\ne \emptyset \end{aligned}$$

  (28)

  for all $\rho \in (0,\delta )$, $a\in A\cap \mathbb {B}_{\delta }({\overline{x}})$, $b\in B\cap \mathbb {B}_{\delta }({\overline{x}})$, and all $x_1,x_2\in \mathbb {E}$ with $\max \{\Vert x_1\Vert ,\Vert x_2\Vert \}<\alpha \rho$. The (possibly infinite) supremum of all $\alpha$ above is denoted by $\mathrm{r}[A,B](\overline{x})$ with the convention that the supremum of the empty set is zero.

Remark 3

The maximum of the norms in Definition 6—explicitly present in part (ii) and implicitly also in part (i)—corresponds to the maximum norm in $\mathbb {R}^2$ employed in these definitions and subsequent assertions. It can be replaced everywhere by the sum norm (pretty common in this type of definition in the literature) or any other equivalent norm. All the assertions that follow including the quantitative characterizations remain valid (as long as the same norm is used everywhere), although the exact values $\mathrm{sr}[A,B](\overline{x})$ and $\mathrm{r}[A,B](\overline{x})$ do depend on the chosen norm and some estimates can change. Note that the currently used maximum norm is not Euclidean. These details become important in the context of applications where one norm may be more appropriate than another.

Definition 6(i) was introduced recently in [41] and can be viewed as a local analogue of the global uniform normal property introduced in the convex setting in [4, Definition 3.1(4)] as a generalization of the property (N) of convex cones by Jameson [32]. A particular case of the Jameson property (N) for convex cones A and B such that $B=-A$ and $A\cap (-A)=\{0\}$ was studied by M. Krein in the 1940s. Definition 6(ii) first appeared in [35] (see also [36, 37]) in the normed linear space setting, where the property was referred to as simply regularity (and later as strong regularity and uniform regularity). In [44], the property is called linearly regular intersection.

Example 3

If $\overline{x}\in \mathrm{int}\,(A\cap B)$, then $\{A,B\}$ is trivially transversal (and consequently subtransversal) at ${\overline{x}}$ with any $\alpha >0$. Thus, $\mathrm{r}[A,B](\overline{x})=\mathrm{sr}[A,B](\overline{x})=\infty$.

Example 4

If $A=B$ and $\overline{x}\in \mathrm{bd}\,(A\cap B)$, then $A+(\alpha \rho )\mathbb {B}= B+(\alpha \rho )\mathbb {B}$ and $A\cap B+\rho \mathbb {B}=A+\rho \mathbb {B}$. Hence, condition (27) holds (with any $\delta >0$) if and only if $\alpha \le 1$. Thus, $\{A,B\}$ is subtransversal at ${\overline{x}}$ and $\mathrm{sr}[A,B](\overline{x})=1$.

Note that, under the conditions of Example 4, $\{A,B\}$ does not have to be transversal at ${\overline{x}}$.

Example 5

Consider again the two sets in Example 1. Thanks to Example 4, $\{A,B\}$ is subtransversal at ${\overline{x}}$ and $\mathrm{sr}[A,B](\overline{x})=1$. At the same time, $A-a=B-b=\mathbb {R}\times \{0\}$ for any $a\in A$ and $b\in B$. If $x_1=(0,\varepsilon )$ and $x_2=(0,0)$, then condition (28) does not hold for any $\varepsilon >0$ and $\rho >0$. Thus, $\{A,B\}$ is not transversal at ${\overline{x}}$ and $\mathrm{r}[A,B](\overline{x})=0$.

The next two results are a catalog of the main characterizations of subtransversality and transversality, respectively.

Theorem 1

(Characterizations of subtransversality) The following statements are equivalent to $\{A,B\}$ being subtransversal at ${\overline{x}}$.

• (i) There exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} (A-x)\cap (B-x)\cap (\rho \mathbb {B})\ne \emptyset \end{aligned}$$

  for all $x\in \mathbb {B}_{\delta }({\overline{x}})$ such that $x=a+x_1=b+x_2$ for some $a\in A$, $b\in B$ and $x_1,x_2\in \mathbb {E}$ with $\max \{\Vert x_1\Vert ,\Vert x_2\Vert \}<\alpha \rho$. Moreover, $\mathrm{sr}[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ such that the condition above is satisfied.

Metric characterizations.

• (ii) There exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} \alpha d\left( x,A\cap B\right) \le \max \left\{ d(x,A),d(x,B)\right\} \;\;\quad \text{ for } \text{ all }\;\; x\in \mathbb {B}_{\delta }({\overline{x}}). \end{aligned}$$

  (29)

  Moreover, $\mathrm{sr}[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ such that (29) is satisfied.

• (iii) There exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned} \alpha d(x,A\cap B)\le d(x,B)\;\; \quad \text{ for } \text{ all }\;\; x\in A\cap \mathbb {B}_{\delta }({\overline{x}}). \end{aligned}$$

  (30)

  Moreover,

  $$\begin{aligned} \frac{\mathrm{sr}'[A,B](\overline{x})}{\mathrm{sr}'[A,B](\overline{x})+2}\le \mathrm{sr}[A,B](\overline{x})\le \mathrm{sr}'[A,B](\overline{x}), \end{aligned}$$

  (31)

  where $\mathrm{sr}'[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ such that condition (30) is satisfied.

Proof

Characterization (i) This is easily checked.

Characterization (ii) This follows from [41, Theorem 3.1].

Characterization (iii) The inequality (29) implies (30), hence, thanks to characterization (ii), subtransversality of $\{A,B\}$ implies property (30) with the same numbers $\alpha >0$ and $\delta >0$, and the second inequality in (31) holds.

Conversely, let condition (30) be satisfied with some numbers $\alpha >0$ and $\delta >0$. Choose a positive number $\alpha '<\alpha /(\alpha +2)$ and a number $\beta \in (\alpha /2,\alpha )$ such that $\alpha '<1/(\alpha /\beta +\alpha ^{-1} +\beta ^{-1} )$ which is always possible if $\beta$ is taken sufficiently close to $\alpha$. For any $x'\in \mathbb {B}_{\frac{\delta }{3}}(\bar{x})$, we choose an $x\in A$ such that $\frac{\beta }{\alpha }\left\| x'-x\right\| \le d(x',A)$. Note that $x\in \mathbb {B}_{\delta }(\bar{x})$ since

$$\begin{aligned}&\left\| x-\bar{x}\right\| \le \left\| x-x'\right\| +\left\| x'-\bar{x}\right\| \le \\&\quad \frac{\alpha }{\beta }d(x',A)+\left\| x'-\bar{x}\right\| \le \left( \frac{\alpha }{\beta }+1\right) \left\| x'-\bar{x}\right\| \le 3\left\| x'-\bar{x}\right\| \le \delta . \end{aligned}$$

Using (30), we obtain

$$\begin{aligned} d(x',A\cap B)&\le \left\| x'-x\right\| +d(x,A\cap B)\\&\le \left\| x'-x\right\| +\alpha ^{-1} d(x,B)\\&\le \left\| x'-x\right\| +\alpha ^{-1} \left( \left\| x-x'\right\| +d(x',B)\right) \\&=\left( 1+\alpha ^{-1} \right) \left\| x'-x\right\| +\alpha ^{-1} d(x',B)\\&\le \left( 1+\alpha ^{-1} \right) \frac{\alpha }{\beta }d(x',A) +\alpha ^{-1} d(x',B)\\&\le \left( \frac{\alpha }{\beta }+\beta ^{-1} +\alpha ^{-1} \right) \max \{d(x',A),d(x',B)\}\\&\le (\alpha ')^{-1} \max \{d(x',A),d(x',B)\}, \end{aligned}$$

and consequently, after passing to the limit as $\alpha '\rightarrow \alpha /(\alpha +2)$,

$$\begin{aligned} \frac{\alpha }{\alpha +2}d(x',A\cap B) \le \max \{d(x',A),d(x',B)\}. \end{aligned}$$

Hence, thanks to characterization (ii), property (30) implies subtransversality of $\{A,B\}$ with numbers $\alpha /(\alpha +2)$ and $\delta /3$. Because $\alpha$ can be chosen arbitrarily close to $\mathrm{sr}'[A,B](\overline{x})$, the first inequality in (31) holds true.

This completes the proof. $\square$

Remark 4

(Historical remarks and further relations) Thanks to characterization (ii) of Theorem 1, subtransversality of a collection of sets can be recognized as a well known regularity property that has been around for more than 20 years under the names of (local) linear regularity, metric regularity, linear coherence, metric inequality, and subtransversality; cf. [4–6, 23, 26, 28–30, 33, 46, 52, 54, 55, 59, 63]. It has been used as the key assumption when establishing linear convergence of sequences generated by cyclic projection algorithms and a qualification condition for subdifferential and normal cone calculus formulae. This property is implied by the bounded linearly regularity [6]. If A and B are closed convex sets and the collection $\{A,B\}$ is subtransversal at any point in $A\cap B$, then it is boundedly linear regular; cf. [4, Remark 6.1 (d)]. Characterization (iii) of Theorem 1 can be considered as a nonconvex extension of [50, Theorem 3.1].

One can also observe that condition (29) is equivalent to the function $x\mapsto \max \{d(x,A),d(x,B)\}$ having a local error bound [2, 24, 38]/weak sharp minimum [14–16] at $\overline{x}$ with constant $\alpha$. One can think of condition (32) as a kind of uniform local error bound/relaxed weak sharp minimum property; cf. [36].

The geometrical property (29) of a collection of sets $\{A,B\}$ can also be viewed as a certain property of a collection of distance functions $x\mapsto d(x,A)$ and $x\mapsto d(x,B)$. It is sufficient to notice that $A\cap B=\left\{ x\in \mathbb {E}\mid \max \{d(x,A),d(x,B)\}\le 0\right\}$. One can study regularity properties of collections of arbitrary (not necessarily distance) functions. Such an attempt has been made recently in the convex setting by Pang [54]. Given a collection of convex functions $\{f_1,f_2\}$, the following analogue of condition (29) is considered in [54]:

$$\begin{aligned} \alpha d\left( x,C\right) \le \max \left\{ d(x,H_1(x)),d(x,H_2(x))\right\} \;\; \quad \text{ for } \text{ all }\;\; x\in \mathbb {E}, \end{aligned}$$

where $C:=\{u\in \mathbb {E}\mid \max \{f_1(u),f_2(u)\}\le 0\}$, $H_i(x):=\{u\in \mathbb {E}\mid f_i(x)+\left\langle v_i,u-x \right\rangle \le 0\}$ for some chosen $v_i\in \partial f_i(x)$ if $f_i(x)>0$ and $H_i(x):=\mathbb {E}$ otherwise, $i=1,2$. It is easy to check that, in the case of distance functions, this property reduces to (29).

Theorem 2

(Characterizations of transversality) The following statements are equivalent to $\{A,B\}$ being transversal at ${\overline{x}}$.

Metric characterizations.

• (i) There exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned}&\alpha d\left( x,(A-x_1)\cap (B-x_2)\right) \nonumber \\&\quad \le \max \left\{ d(x,A-x_1),d(x,B-x_2)\right\} ,\;\; \quad \forall x\in \mathbb {B}_{\delta }({\overline{x}}),\;x_1,x_2\in \delta \mathbb {B}. \end{aligned}$$

  (32)

  Moreover, $\mathrm{r}[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ such that (32) is satisfied.

• (ii) There exist numbers $\delta >0$ and $\alpha >0$ such that

  $$\begin{aligned}&\alpha d(x,(A-x_1)\cap (B-x_2))\le d(x,B-x_2),\nonumber \\&\quad \forall x\in (A-x_1)\cap \mathbb {B}_{\delta }({\overline{x}}),\;x_1,x_2\in \delta \mathbb {B}. \end{aligned}$$

  (33)

  Moreover,

  $$\begin{aligned} \frac{\mathrm{r}'[A,B](\overline{x})}{\mathrm{r}'[A,B](\overline{x})+2}\le \mathrm{r}[A,B](\overline{x})\le \mathrm{r}'[A,B](\overline{x}), \end{aligned}$$

  (34)

  where $\mathrm{r}'[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ such that condition (33) is satisfied.

Dual characterizations.

• (iii) There exist numbers $\alpha >0$ and $\delta >0$ such that $\Vert v_1+v_2\Vert >\alpha$ for all $a\in A\cap \mathbb {B}_\delta (\bar{x})$, $b\in B\cap \mathbb {B}_\delta (\bar{x})$, $v_1\in N^F_{A}(a)$ and $v_2\in N^F_{B}(b)$ with $\Vert v_1\Vert +\Vert v_2\Vert =1$. Moreover, $\mathrm{r}[A,B](\overline{x})$ is the exact upper bound of all numbers $\alpha$ above.

• (iv) There exists a number $\alpha >0$ such that $\Vert v_1+v_2\Vert >\alpha$ for all $v_1\in {N}_{A}(a)$ and $v_2\in {N}_{B}(b)$ with $\Vert v_1\Vert +\Vert v_2\Vert =1$. Moreover, $\mathrm{r}[A,B](\overline{x})$ is the exact upper bound of all such numbers $\alpha$.

• (v) ${N}_{A}({\overline{x}}) \cap (-{N}_{B}({\overline{x}})) = \{0\}$.

• (vi) There is a number $\alpha >0$ such that $d^2\left( v,{N}_{A}(\bar{x})\right) + d^2\left( v,-{N}_{B}(\bar{x})\right) >\alpha ^2$ for all $v\in \mathbb {S}$. Moreover, the exact upper bound of all such numbers $\alpha$, denoted $\mathrm{r}_v[A,B](\overline{x})$, satisfies $\mathrm{r}_v[A,B](\overline{x})=\sqrt{2}\,\mathrm{r}[A,B](\overline{x})$.

• (vii) There is a number $\alpha <1$ such that $-\left\langle v_1,v_2 \right\rangle <\alpha$ for all $v_1\in {N}_{A}(\overline{x})$ and $v_2\in {N}_{B}(\overline{x})$ with $\Vert v_1\Vert =\Vert v_2\Vert =1$. Moreover, the exact lower bound of all such numbers $\alpha$, denoted $\mathrm{r}_a[A,B](\overline{x})$, satisfies $\mathrm{r}_a[A,B](\overline{x})+2(\mathrm{r}[A,B](\overline{x}))^2=1$.

Proof

Characterization (i) This follows from [41, Theorem 3.1].

Characterization (ii) Condition (32) implies (33). Hence transversality of $\{A,B\}$ implies property (33) with the same numbers $\alpha >0$ and $\delta >0$, and the second inequality in (34) holds true.

Conversely, let condition (33) be satisfied with some numbers $\alpha >0$ and $\delta >0$. Fix any $x_1,x_2\in \delta '\mathbb {B}$. Then condition (30) is satisfied with the same numbers $\alpha$ and $\delta$ and the sets $A-x_1$ and $B-x_2$ in place of A and B, respectively. As shown in the proof of Theorem 1 (iii), it holds

$$\begin{aligned}&\frac{\alpha }{\alpha +2}d\left( x',(A-x_1)\cap (B-x_2)\right) \\&\quad \le \max \left\{ d(x',A-x_1),d(x',B-x_2)\right\} \;\; \quad \text{ for } \text{ all }\;\; x'\in \mathbb {B}_{\frac{\delta }{3}}(\bar{x}). \end{aligned}$$

Since the points $x_1,x_2\in \delta \mathbb {B}$ are arbitrary, this is exactly the transversality property of $\{A,B\}$ with numbers $\alpha /(\alpha +2)$ and $\delta /3$. The first inequality in (34) follows.

Characterization (iii) This was established in [35] (in the Asplund space setting).

Characterization (iv) Thanks to the representation (6), taking limits in characterization (3) yields the result.

Characterization (v) The equivalence of conditions (iv) and (v) is straightforward since ${N}_{A}(\bar{x})$ and ${N}_{B}(\bar{x})$ are closed cones.

Characterization (vii) This has been established in [40, Theorem 2]).

Characterization (vi) Let $v\in \mathbb {S}$ be such that $d^2\left( v,{N}_{A}(\bar{x})\right) + d^2\left( v,-{N}_{B}(\bar{x})\right) =(\mathrm{r}_v[A,B](\overline{x}))^2$, and $v_1$ and $v_2$ be projections of v on ${N}_{A}(\overline{x})$ and $-{N}_{B}(\overline{x})$, respectively. It is immediate from the symmetry that $\Vert v_1\Vert =\Vert v_2\Vert$. Thus,

$$\begin{aligned} \left\langle v,v_1+v_2 \right\rangle =\Vert v_1+v_2\Vert , \quad \left\langle v,v_1 \right\rangle =\left\langle v,v_2 \right\rangle =\Vert v_1\Vert ^2=\Vert v_2\Vert ^2, \end{aligned}$$

and consequently,

$$\begin{aligned} \Vert v_1+v_2\Vert= & {} \Vert v_1\Vert ^2+\Vert v_2\Vert ^2=2\Vert v_1\Vert ^2,\\ \Vert v_1-v_2\Vert ^2= & {} 2\Vert v_1\Vert ^2-2\left\langle v_1,v_2 \right\rangle = 4\Vert v_1\Vert ^2-\Vert v_1+v_2\Vert ^2\\= & {} 4\Vert v_1\Vert ^2(1-\Vert v_1\Vert ^2). \end{aligned}$$

Let $v_1'$ and $v_2'$ be unit vectors satisfying $v_1'=v_1/\Vert v_1\Vert$ and $v_2'=-v_2/\Vert v_1\Vert$. Then $v_1'\in {N}_{A}(\overline{x})\cap \mathbb {S}$, $v_2'\in {N}_{B}(\overline{x})\cap \mathbb {S}$, and $\Vert v_1'+v_2'\Vert ^2=4(1-\Vert v_1\Vert ^2).$ At the same time,

$$\begin{aligned} (\mathrm{r}_v[A,B](\overline{x}))^2&=\Vert v-v_1\Vert ^2+\Vert v-v_2\Vert ^2= 2-2\left\langle v,v_1+v_2 \right\rangle +2\Vert v_1\Vert ^2\\&=2(1-\Vert v_1\Vert ^2)= \frac{1}{2}\Vert v_1'+v_2'\Vert ^2\ge 2(\mathrm{r}[A,B](\overline{x}))^2. \end{aligned}$$

Conversely, let $v_1' \in {N}_{A}(\overline{x})$ and $v_2' \in {N}_{B}(\overline{x})$ be such that $\Vert v_1'\Vert =\Vert v_2'\Vert =1$ and $\Vert v_1'+v_2'\Vert =2\mathrm{r}[A,B](\overline{x})$. Choose a unit vector v such that $\left\langle v,v_1'+v_2' \right\rangle = \Vert v_1'+v_2'\Vert$ and let $v_1$ and $v_2$ be projections of v on $v_1'$ and $v_2'$, respectively. We are in a situation as above.

$$\begin{aligned} 4(\mathrm{r}[A,B](\overline{x}))^2&=\Vert v_1'+v_2'\Vert ^2= 2(\Vert v-v_1\Vert ^2+\Vert v-v_2\Vert ^2)\ge 2(\mathrm{r}_v[A,B](\overline{x}))^2. \end{aligned}$$

This completes the proof of (vi). $\square$

Remark 5

(Characterization (i) and strong regularities) Characterization (i) of Theorem 2 reveals that the transversality of a collection of sets corresponds to subtransversality/linear regularity of all their small translations holding uniformly (cf. [23, p. 1638]). Property (32) was referred to in [35–37] as strong metric inequality. If A and B are closed convex sets and $\mathrm{int}\,A\ne \emptyset$, then the transversality of the collection $\{A,B\}$ is equivalent to the conventional qualification condition: $\mathrm{int}\,A\cap B\ne \emptyset$; cf. [35, Proposition 14].

Remark 6

(Characterization (iii) and Jameson’s property) Characterization (iii) in Theorem 2 can be formulated equivalently as follows:

there exist numbers $\alpha >0$ and $\delta >0$ such that $\Vert v_1+v_2\Vert \ge \alpha (\Vert v_1\Vert +\Vert v_2\Vert )$ for all $a\in A\cap \mathbb {B}_\delta (\bar{x})$, $b\in B\cap \mathbb {B}_\delta (\bar{x})$, $v_1\in N^F_{A}(a)$ and $v_2\in N^F_{B}(b)$.

This characterization can be interpreted as a strengthened version of the Jameson’s property (G) [32] (cf. [4, 7, 50]). As with all dual characterizations, it basically requires that among all admissible pairs of nonzero normals to the sets there is no pair of normals which are oppositely directed. Thanks to the representation (5), one can replace the Fréchet normals by the proximal ones.

Remark 7

(Characterization (v) and related notions) Note that, unlike the other characterizations, (v) provides only a qualitative criterion of transversality. It has the interpretation that the cones ${N}_{A}({\overline{x}})$ and ${N}_{B}({\overline{x}})$ are strongly additively regular [15], and has been described as a “concise, fundamental, and widely studied geometric property” [23] extensively used in nonconvex optimization and calculus. It is known under various names, e.g., transversality [18], normal qualification condition [49, 55], linearly regular intersection [44], alliedness property [55], and transversal intersection [23, 30].

An immediate consequence of characterization (v) is the following crucial inclusion expressed in terms of the limiting normal cones (cf. [18, p. 99], [58, Theorem 6.42], [49, p. 142]):

$$\begin{aligned} {N}_{A\cap B}({\overline{x}})\subseteq {N}_{A}({\overline{x}})+{N}_{B}({\overline{x}}), \end{aligned}$$

(35)

which can be considered as an extension of the strong conical hull intersection property (strong CHIP) [20] (cf. [4, Definition 5.1(2)]) to nonconvex sets. Indeed, since the opposite inclusion in terms of Fréchet normal cones holds true trivially:

$$\begin{aligned} N^F_{A\cap B}({\overline{x}})\supset N^F_{A}({\overline{x}})+N^F_{B}({\overline{x}}), \end{aligned}$$

(36)

and both cones reduce in the convex case to the normal cone (7), inclusion (35) is equivalent in the convex setting to the strong CHIP:

$$\begin{aligned} N_{A\cap B}({\overline{x}})= N_{A}({\overline{x}})+N_{B}({\overline{x}}). \end{aligned}$$

(37)

The last equality has proved to be a fundamental regularity property in several areas of convex optimization; see the discussion of the role of this property (and many other regularity properties of collections of convex sets) in [4, 7]. Inclusion (35) plays a similar role in nonconvex optimization and calculus. Thus, thanks to Theorem 2(v), transversality implies the extended strong CHIP (35).

In fact, it is now well recognized that inclusion (35) is ensured by the weaker subtransversality property. The next proposition is a consequence of [31, Proposition 3.2] (or [55, Theorem 6.41]) and the characterization of subtransversality in Theorem 1(ii).

Proposition 5

If $\{A,B\}$ is subtransversal at ${\overline{x}}$, then inclusion (35) holds true.

In the convex case, a nonlocal version of Proposition 5 together with certain quantitative estimates can be found in [4, 7].

If a stronger than (35) condition (37) is satisfied in the nonconvex case (with Fréchet subdifferentials), then this property is referred to in [51] as the strong Fréchet-CHIP. Since inclusion (36) always holds, this is equivalent to inclusion (35) with Fréchet subdifferentials in place of the limiting ones. A quantitative (by a positive number $\alpha$) version of the strong Fréchet-CHIP property was studied in the convex and nonconvex settings in [51, 59]:

$$\begin{aligned} N^F_{A\cap B}(\overline{x}) \cap \mathbb {B} \subseteq \alpha \left( \left( N^F_{A}(\overline{x}) \cap \mathbb {B}\right) +\left( N^F_{B}(\overline{x}) \cap \mathbb {B}\right) \right) . \end{aligned}$$

A number of important links with other regularity properties were established there, and variants of the above property involving Clarke normal cones were also considered.

The “restricted” analogue of the dual regularity characterization (v) takes the following form:

$$\begin{aligned} {N}_{A|B}({\overline{x}})\cap \left( -{N}_{B|A}({\overline{x}})\right) \subseteq \{0\}. \end{aligned}$$

(38)

This condition is, incidentally, equivalent to the constraint qualification characterization of regularity of collections of sets given in Definition 4(iii).

Remark 8

(Characterizations restricted to Euclidean settings) The following equivalent characterizations of transversality have been established in [40, Theorem 2]).

• (1) There exists a number $\alpha >0$ such that $\Vert v_1+v_2\Vert >2\alpha$ for all $v_1\in {N}_{A}(\overline{x})$ and $v_2\in {N}_{B}(\overline{x})$ with $\Vert v_1\Vert =\Vert v_2\Vert =1$. Moreover, the exact upper bound of all such numbers $\alpha$ equals $\mathrm{r}[A,B](\overline{x})$.

• (2) There exists a number $\alpha <1$ such that $\Vert v_1-v_2\Vert <2\alpha$ for all $v_1\in {N}_{A}(\overline{x})$ and $v_2\in {N}_{B}(\overline{x})$ with $\Vert v_1\Vert =\Vert v_2\Vert =1$. Moreover, the exact lower bound of all such numbers $\alpha$, denoted $\mathrm{r}_d[A,B](\overline{x})$, satisfies $(\mathrm{r}[A,B](\overline{x}))^2+(\mathrm{r}_d[A,B](\overline{x}))^2=1$.

For brevity, the characterizations above are in terms of limiting normals only. The corresponding (approximate) statements in terms of Fréchet and proximal normals can be formulated in a similar way. These characterizations as well as that of Theorem 2(vi) for the proximal normal cone only hold in Euclidean spaces.

Remark 9

Theorem 2(viii) also has analogues in terms of Fréchet and proximal normals. The expression $-\left\langle v_1,v_2 \right\rangle$ can be interpreted as the cosine of the angle between the vectors $v_1$ and $-v_2$. Note that, unlike $\mathrm{r}[A,B](\overline{x})$, $\mathrm{r}_d[A,B](\overline{x})$, and $\mathrm{r}_v[A,B](\overline{x})$, constant $\mathrm{r}_a[A,B](\overline{x})$ can be negative. Constant $\mathrm{r}_a[A,B](\overline{x})$ is a modification of another one:

$$\begin{aligned} \bar{c}:=\max&\left\{ -\left\langle v_1,v_2 \right\rangle \mid v_1\in {N}_{A}(\overline{x})\cap \mathbb {B},\; v_2\in {N}_{B}(\overline{x})\cap \mathbb {B}\right\} , \end{aligned}$$

used in [44] for characterizing transversality. It is easy to check that $\bar{c}=(\mathrm{r}_a[A,B](\overline{x}))_+$, and $\bar{c}<1$ if and only if $\mathrm{r}_a[A,B](\overline{x})<1$.

Because the representation of (sub)transversality via set-valued mappings occupies a rather special relation to these properties, we detail these separately next.

Theorem 3

(Characterizations via set-valued mappings) Subtransversality of the collection $\{A, B\}$ at a point ${\overline{x}}\in A\cap B$ has the following eqvuialent characterizations.

• (i) The set-valued mapping $F:\mathbb {E}\rightrightarrows {\mathbb {E}}^2$ given by (9) with the max norm on $\mathbb {E}^2$ is metrically subregular at ${\overline{x}}$ for (0, 0). Moreover,

  $$\begin{aligned} \mathrm{sr}[A,B](\overline{x})=\mathrm{sr}[F](\overline{x},(0,0)). \end{aligned}$$

  The mapping F is strongly metrically subregular at ${\overline{x}}$ for (0, 0) if and only if the collection $\{A, B\}$ is strongly subtransversal there.

• (ii) The set-valued mapping $G:\mathbb {E}^2 \rightrightarrows {\mathbb {E}}$ given by (10) with the Euclidean norm on $\mathbb {E}^2$ is metrically subregular at $({\overline{x}},{\overline{x}})$ for 0. Moreover,

  $$\begin{aligned} \sqrt{\frac{2}{1+(\mathrm{sr}[A,B](\overline{x}))^{-2}}}\le \mathrm{sr}[G]((\overline{x},\overline{x}),0) \le \frac{2}{[(\mathrm{sr}[A,B](\overline{x}))^{-1} -1]_+}. \end{aligned}$$

  (39)

Transversality of the collection $\{A, B\}$ at a point ${\overline{x}}\in A\cap B$ has the following equivalent characterizations.

• (i$^{\prime }$) The set-valued mapping $F:\mathbb {E}\rightrightarrows {\mathbb {E}}^2$ given by (9) with the max norm on $\mathbb {E}^2$ is metrically regular at ${\overline{x}}$ for (0, 0). Moreover,

  $$\begin{aligned} \mathrm{r}[A,B](\overline{x})=\mathrm{r}[F](\overline{x},(0,0)). \end{aligned}$$

• (ii$^{\prime }$) The set-valued mapping $G:\mathbb {E}^2 \rightrightarrows {\mathbb {E}}$ given by (10) with the Euclidean norm on $\mathbb {E}^2$ is metrically regular at $({\overline{x}},{\overline{x}})$ for 0. Moreover,

  $$\begin{aligned} \sqrt{\frac{2}{1+(\mathrm{r}[A,B](\overline{x}))^{-2}}}\le \mathrm{r}[G]((\overline{x},\overline{x}),0) \le \frac{2}{[(\mathrm{r}[A,B](\overline{x}))^{-1} -1]_+}. \end{aligned}$$

  (40)

Proof

Characterization (i) This is a consequence of [29, Proposition 3.5], [36, Proposition8] and the characterization of Theorem 1(ii).

Characterization (ii) Suppose $\{A,B\}$ is subtransversal at ${\overline{x}}$. By Theorem 1(ii), there exist numbers $\alpha >0$ and $\delta >0$ such that condition (29) holds true. Set $\alpha ':=\sqrt{\frac{2}{1+\alpha ^{-2}}}$. We show that

$$\begin{aligned} \alpha ' d((x_1,x_2), G^{-1}(0)) \le d(0, G(x_1,x_2)\} \quad \quad \text{ for } \text{ all }\quad x_1,x_2\in B_{\delta }({\overline{x}}). \end{aligned}$$

(41)

If $(x_1,x_2)\notin A\times B$, then $G(x_1,x_2)=\emptyset$ and the inequality holds trivially. Take any $(x_1,x_2)\in A\times B$ with $x_1,x_2\in B_{\delta }({\overline{x}})$. Note that $G(x_1,x_2)=x_1-x_2$ and $G^{-1}(0) = \{(x,x)\mid x\in A\cap B\}$. Set $\hat{x}:=\frac{x_1+x_2}{2}$. Then $\hat{x}\in B_{\delta }({\overline{x}})$, $x_1-\hat{x}=\hat{x}-x_2=\frac{x_1-x_2}{2}$, and, thanks to (29),

$$\begin{aligned} \alpha d(\hat{x},A\cap B)\le & {} \max \left\{ d(\hat{x},A),d(\hat{x},B)\right\} \nonumber \\\le & {} \max \left\{ \left\| \hat{x}-z\right\| ,\left\| \hat{x}-x_2\right\| \right\} =\frac{1}{2}\left\| x_1-x_2\right\| . \end{aligned}$$

(42)

For any $x\in A\cap B$, we have

$$\begin{aligned} \Vert (x_1,x_2)-(x,x)\Vert ^2&= \left\| x_1-x\right\| ^2+\left\| x_2-x\right\| ^2\\&= \left\| x_1-\hat{x}+\hat{x}-x\right\| ^2+\left\| x_2-\hat{x}+\hat{x}-x\right\| ^2\\&= \left\| x_1-\hat{x}\right\| ^2+2\left\langle x_1-\hat{x},\hat{x}-x \right\rangle + \left\| x_2-\hat{x}\right\| ^2\\&\quad +2\left\langle x_2-\hat{x},\hat{x}-x \right\rangle + 2\left\| \hat{x}-x\right\| ^2\\&= \left\| x_1-\hat{x}\right\| ^2+\left\| x_2-\hat{x}\right\| ^2+2\left\| \hat{x}-x\right\| ^2\\&=\frac{1}{2}\left\| x_1-x_2\right\| ^2 + 2\left\| \hat{x}-x\right\| ^2. \end{aligned}$$

Hence,

$$\begin{aligned} d^2((x_1,x_2), G^{-1}(0))\le \frac{1}{2}\left\| x_1-x_2\right\| ^2 + 2d^2(\hat{x},A\cap B), \end{aligned}$$

and, thanks to (42),

$$\begin{aligned} \alpha 'd((x_1,x_2), G^{-1}(0))&\le \alpha '\sqrt{\frac{1}{2}\left( 1+\frac{1}{\alpha ^2}\right) } \left\| x_1-x_2\right\| =d(0, G(x_1,x_2)). \end{aligned}$$

(43)

Conversely, suppose that G is metrically subregular at $({\overline{x}},{\overline{x}})$ for 0, i.e., (41) is satisfied for some numbers $\alpha '>0$ and $\delta >0$. Fix an arbitrary number $\alpha \in (\alpha '/2,\alpha ')$. For any $z\in A\cap \mathbb {B}_{\frac{\delta }{3}}({\overline{x}})$, we pick a $w\in B$ such that $\left\| x_1-x_2\right\| \le \frac{\alpha '}{\alpha }d(z,B)$. Note that $w\in \mathbb {B}_{\delta }({\overline{x}})$ since

$$\begin{aligned} \left\| x_2-{\overline{x}}\right\|\le & {} \left\| x_2-z\right\| +\left\| x_1-{\overline{x}}\right\| \le \frac{\alpha '}{\alpha }d(z,B)+\left\| x_1-{\overline{x}}\right\| \\\le & {} \left( \frac{\alpha '}{\alpha }+1\right) \left\| x_1-{\overline{x}}\right\|< \left( \frac{\alpha '}{\alpha }+1\right) \frac{\delta }{3}<\delta . \end{aligned}$$

Then, in view of (41), we have

$$\begin{aligned} \alpha d(z,A\cap B)&\le \alpha d((x_1,x_2),\{(x,x)\mid x\in A\cap B\})=\alpha d((x_1,x_2), G^{-1}(0))\nonumber \\&\le \frac{\alpha }{\alpha '}d(0, G(x_1,x_2)) =\frac{\alpha }{\alpha '}\left\| x_1-x_2\right\| \le d(z,B). \end{aligned}$$

(44)

By Theorem 1(iii), condition (44) implies the subtransversality of $\{A,B\}$ at $\bar{x}$ and the estimate $\mathrm{sr}[A,B](\overline{x})\ge 1/(1+2\alpha ^{-1} )$, or equivalently, $\alpha \le 2/[(\mathrm{sr}[A,B](\overline{x}))^{-1} -1]_+$. Passing to the limit in the last inequality as $\alpha \rightarrow \alpha '$ and then as $\alpha '\rightarrow \mathrm{sr}[G]((\bar{x},\bar{x}),0)$, we arrive at the second inequality in (39).

The equivalence of the strong subtransversality of $\{A,B\}$ and the strong metric subregularity of G is straightforward since x is an isolated point of $\{A,B\}$ if and only if (x, x) is an isolated point of $G^{-1}(0)$.

Characterization (i$^{\prime }$). This is a consequence of [29, Proposition 3.5], [36, Proposition 8] and the characterization Theorem 2(i).

Characterization (ii$^{\prime }$). This is a consequence of Theorem (ii) as it claims the equivalence of the uniform versions of the properties in Theorem (ii). The estimates established in Theorem (ii) are preserved; cf. the proof of Theorem 2(ii). $\square$

Remark 10

(collections of sets and set-valued mappings) The characterizations in Theorem 3 provide a one-to-one correspondence between regularity properties of collections of sets and the corresponding ones of set-valued mappings. They remain true for arbitrarily finite collections of sets.

The ‘positive part’ sign in the right-hand sides of the conditions (39) and (40) is used to accommodate for the case when $\overline{x}\in \mathrm{int}\,A\cap \mathrm{int}\,B$ and, hence, $\mathrm{r}[A,B](\overline{x})=+\infty$. In this case, conditions (39) and (40) impose no upper bound on the values $\mathrm{sr}[G](({\overline{x}},{\overline{x}}),0)$ and $\mathrm{r}[G](({\overline{x}},{\overline{x}}),0)$. Recall that in the current article the assumption $\overline{x}\in \text{ cl }\,A\cap \text{ cl }\,B$ is in forth, so the ‘positive part’ sign in the right-hand sides of the conditions (39) and (40) can be dropped.

In view of characterization (ii$^{\prime }$), the property of regular intersection of sets considered in [45, Sect.  5] is equivalent to their collection being transversal. This fact also follows from [45, Theorem 5.1]. The regularity estimate obtained in parts (ii) and (ii$^{\prime }$) coincides with $\mathrm{r}_v[A,B](\overline{x})$.

Thanks to characterizations of Theorem , when investigating regularity properties of collections of sets one can employ the well developed regularity theory of set-valued mappings, particularly, the celebrated coderivative criterion for metric regularity [21, 49, 58] (see also [34]) as well as criteria of metric subregularity based on outer coderivatives (see [31, 38, 60–62]). On the other hand, related studies in [37, Theorem 7], [41, Theorem5.1(2)] have shown that regularity criteria developed for collections of sets can be used when studying the corresponding properties of set-valued mappings. The coderivatives (Fréchet, limiting or other) of the mappings (9) and (10) employed in Theorem 3 admit simple representations in terms of the corresponding normal cones to the sets involved in their definitions; see [37, the proof of Theorem 8], [45, Lemma 5.1], [44, p. 491], and [30, Theorem 7.12 and Corollary 7.13]. As a consequence, the coderivative criteria of regularity of set-valued mappings easily translate into the dual characterizations of the corresponding regularity properties of collections of sets. Not surprisingly, this way one rediscovers (some of) the known characterizations collected in Theorem 3; see [37, Theorem 8], [45, Theorem 5.1], and [30, Theorems 7.12 and 7.15].

The characterization of subtransversality given in Theorem 1(i) and the definition of transversality shows that transversality implies subtransversality (see Theorem 4 below). Alternatively, the implication is also immediate from Theorem 1(ii) and Theorem 2(i). There are a number of other useful sufficient conditions for subtransversality, detailed in the next theorem.

Theorem 4

(sufficient conditions for subtransversality) If one of the following hold, then $\{A,B\}$ is subtransversal at ${\overline{x}}$.

• (i) The collection $\{A,B\}$ is transversal at ${\overline{x}}$. Moreover, $\mathrm{r}[A,B](\overline{x})\le \mathrm{sr}[A,B](\overline{x})$.

• (ii) There exist numbers $\alpha >0$ and $\delta >0$ such that ${\Vert v_1+v_2\Vert >\alpha }$ for all $x\in \mathbb {B}_{\delta }(\bar{x})$, $a\in A$, $b\in B$ with $a\ne b$, $0<\left\| x-a\right\| <\delta$, $0<\left\| x-b\right\| <\delta$, and all nonzero $v_1\in N^F_{A}(a)$, $v_2\in N^F_{B}(b)$ satisfying

  $$\begin{aligned} \Vert v_1\Vert +\Vert v_2\Vert =1,\quad \frac{\left\langle v_1,x-a \right\rangle }{\Vert v_1\Vert \;\Vert x-a\Vert }>1-\delta ,\quad \frac{\left\langle v_2,x-b \right\rangle }{\Vert v_2\Vert \;\Vert x-b\Vert }>1-\delta . \end{aligned}$$

  Moreover, $\mathrm{sr}[A,B](\overline{x})\ge \alpha$.

• (iii) The sets A and B are intrinsically transversal at ${\overline{x}}$—Definition 4(vi).

• (iv) The set B intersects A separably at ${\overline{x}}$ and B is 0-Hölder regular relative to A at ${\overline{x}}$ with an adequate compromise between the constants.

Proof

Condition (i) This follows immediately from Theorem 1(ii) and Theorem 2(i).

Condition (ii) This result is new. It expands and improves (in the setting adopted in the current article) [41, Theorem 4.1]. We do not have the space to provide the proof here, but refer readers to the preprint [39].

(iii) This was shown in [23, Theorem 6.2].

(iv) Suppose that B intersects A separably at ${\overline{x}}$ with constant $\alpha >0$ together with a neighborhood ${\mathbb {B}}_{\delta }({\overline{x}})$ of ${\overline{x}}$ (Definition 4(v)) and that B is 0-Hölder regular relative to A at ${\overline{x}}$ with constant $c>0$ together with the same neighborhood ${\mathbb {B}}_{\delta }(\overline{x})$ of ${\overline{x}}$ (Definition 2(i)). Suppose that $\alpha +2c<1$. We show that $\{A,B\}$ is subtransversal at $\overline{x}$. To see this, choose a number $\gamma$ satisfying $\max \left\{ \alpha +2c,\tfrac{1}{1+c^2}\right\}<\gamma <1$. Thanks to Theorem 1(iii), it suffices to check the existence of a ${\overline{\delta }}>0$ such that

$$\begin{aligned} \frac{1-\gamma }{1+\gamma } d(a,A\cap B)\le d(a,B)\;\; \quad \text{ for } \text{ all }\;\; a\in A\cap \mathbb {B}_{{\overline{\delta }}}(\overline{x}). \end{aligned}$$

(45)

Let us first check that for any $a\in A\cap \mathbb {B}_{\delta }(\overline{x})$, $b\in P_B(a) \cap \mathbb {B}_{\delta }(\overline{x})$, and $a_+\in P_A(b)\cap \mathbb {B}_{\delta }(\overline{x})$, one has

$$\begin{aligned} \Vert a_+-b\Vert \le \gamma \Vert b-a\Vert . \end{aligned}$$

(46)

If $\Vert a_+-b\Vert \le \tfrac{1}{1+c^2}\Vert b-a\Vert$, then (46) holds true since $\tfrac{1}{1+c^2}\le \gamma$. Suppose that $\Vert a_+-b\Vert > \tfrac{1}{1+c^2}\Vert b-a\Vert$. The two regularity assumptions then yield the following inequalities:

$$\begin{aligned} \left\langle a_+-b,a-b\right\rangle&\le \alpha \Vert a_+-b\Vert \Vert a-b\Vert ,\\ \left\langle b-a_+,a-a_+\right\rangle&\le c\Vert b-a_+\Vert \Vert a-a_+\Vert . \end{aligned}$$

Adding these inequalities and using $\Vert a-a_+\Vert \le 2\Vert a-b\Vert$, we get

$$\begin{aligned} \Vert a_+-b\Vert \le (\alpha +2c)\Vert b-a\Vert \le \gamma \Vert b-a\Vert . \end{aligned}$$

Hence, (46) is proved. Employing the basic routine originated in the proof of [44, Theorem 5.2] implies the existence of a number ${\overline{\delta }}>0$ such that for any $a\in A\cap \mathbb {B}_{{\overline{\delta }}}(\overline{x})$, there exists an $\tilde{x}\in A\cap B$ such that $\Vert a-\tilde{x}\Vert \le \tfrac{1+\gamma }{1-\gamma }\Vert a-b\Vert$. Since $d(a,A\cap B)\le \Vert a-\tilde{x}\Vert$ and $\Vert a-b\Vert =d(a,B)$, condition (45) is proved. $\square$

Remark 11

In light of the framework presented above, the transversality has been shown to be equivalent to properties (i) of Definition 4 and (in the case of smooth manifolds) (14), and strictly to imply the other properties in Definition 4.

Remark 12

(Entaglement of elemental regularity and regularity of collections of sets) Proposition 1(d) and Theorem 4(iv) demonstrate that regularity of individual sets has implcations for the regularity of the collection of sets. The converse entaglement has also been observed in [53, Proposition 8]: if A and B are intrinsically transversal at ${\overline{x}}$ with constant $\alpha$, then A is $\sigma$-Hölder regular at ${\overline{x}}$ relative to B for every $\sigma \in [0,1)$ with any constant $c< \frac{\alpha ^2}{1-\alpha ^2}$.

As a consequence of Proposition 4(i), if A and B are intrinsically transversal at ${\overline{x}}$ with constant $\alpha \in (0,1]$ and, in addition, there is a neighborhood W of ${\overline{x}}$ and a positive constant $\varepsilon <\frac{\alpha }{\sqrt{1-\alpha ^2}}$ such that for each $(a,v)\in V$ defined in (23), condition (24) holds true, then A is elementally subregular of any order $\sigma \in [0,1)$ relative to $A\cap P^{-1}_B\left( a+v\right)$ at ${\overline{x}}$ for each $(a,v)\in V$ with constant $\varepsilon$ and the respective neighborhood U(a, v).

4.1 Special cases: convex sets, cones and manifolds

A number of simplifications are possible in the convex setting, for cones and for manifolds.

The next representations follow from the simplified representations for $\mathrm{r}[A,B](\overline{x})$ that are possible for convex sets or cones (cf. [35, Propositions 13 and 15]).

Proposition 6

(collections of convex sets) Suppose A and B are convex. The collection $\{A,B\}$ is transversal at ${\overline{x}}$ if and only if one of the next two equivalent conditions holds true:

• (i) there exists a number $\alpha >0$ such that

  $$\begin{aligned} (A-x_1)\cap (B-x_2)\cap \mathbb {B}_{\rho }({\overline{x}})\ne \emptyset \end{aligned}$$

  (47)

  for all $\rho >0$ and all $x_1,x_2\in \mathbb {E}$ with $\max \{\Vert x_1\Vert ,\Vert x_2\Vert \}<\alpha \rho$;

• (ii) there exists a number $\alpha >0$ such that condition (47) is satisfied for some $\rho >0$ and all $x_1,x_2\in \mathbb {E}$ with $\max \{\Vert x_1\Vert ,\Vert x_2\Vert \}<\alpha \rho$.

Moreover, the exact upper bound of all numbers $\alpha$ in any of the above conditions equals $\mathrm{r}[A,B](\overline{x})$.

Proposition 7

(cones) Suppose A and B are cones. The collection $\{A,B\}$ is transversal at ${\overline{x}}$ if and only if there exists a number $\alpha >0$ such that

$$\begin{aligned} (A-a-x_1)\cap (B-b-x_2)\cap \mathbb {B}\ne \emptyset \end{aligned}$$

for all $a\in A,\;b\in B$ and all $x_1,x_2\in \mathbb {E}$ with $\max \{\Vert x_1\Vert ,\Vert x_2\Vert \}<\alpha$. Moreover, the exact upper bound of all numbers $\alpha$ in any of the above conditions equals $\mathrm{r}[A,B](0)$.

In the case when A and B are smooth manifolds, the interesting understanding established in [45, Theorem 5.2] is easily deduced.

Proposition 8

(manifolds) Let A and B be smooth manifolds around a point ${\overline{x}}\in A\cap B$. Then

$$\begin{aligned} \mathrm{r}_a[A,B](\overline{x})=c(A,B,\overline{x}). \end{aligned}$$

(48)

Proof

The equalities in Theorem 2(vi) and (vii) imply the following relation between $\mathrm{r}_a[A,B](\overline{x})$ and $\mathrm{r}_v[A,B](\overline{x})$:

$$\begin{aligned} \mathrm{r}_a[A,B](\overline{x})+(\mathrm{r}_v[A,B](\overline{x}))^2=1. \end{aligned}$$

(49)

In the case when A and B are smooth manifolds, comparing the definition of $\mathrm{r}_v[A,B](\overline{x})$ with condition (19) (with $V_1=N_A(\overline{x})$ and $V_2=N_B(\overline{x})$) and taking into account the above equality and definition (20), yields the equality (48). $\square$

Remark 13

Theorem 5.2 of [45] reduces to Proposition 8 with the regularity estimate being a direct consequence of the equality (49).

Remark 14

Some sufficient and also necessary characterizations of the subtransversality property in terms of the Fréchet subdifferentials of the function $x\mapsto d(x,A)+d(x,B)$ were formulated [52, Theorem 3.1].

The next example illustrates the computation of the constants characterizing regularity.

Example 6

Let $\mathbb {E}=\mathbb {R}^2$, $A=\mathbb {R}\times \{0\}$, $B=\{(t,t)\mid t\in \mathbb {R}\}$, $\overline{x}=(0,0)$. A and B are linear subspaces. We have $A\cap B=\{(0,0)\}$, $T_A(\bar{x})=A$, $T_B(\bar{x})=B$, $T_{A\cap B}(\bar{x}) =\{(0,0)\}$, $N_A(\bar{x})=A^{\perp }=\{0\}\times \mathbb {R}$, $N_B(\bar{x})=B^{\perp }=\{(t,-t)\mid t\in \mathbb {R}\}$. Conditions (14), (15) and (16) hold true. The collection $\{A,B\}$ is transversal at $\bar{x}$ in the classical sense and, thanks to Proposition 8, also transversal at $\bar{x}$ in the sense of Definition 6(ii). By the representations in Theorem 2(i)–(vii), after performing some simple computations, we obtain:

$$\begin{aligned} \mathrm{r}[A,B](\overline{x})&=\frac{1}{2} \left\| \left( \frac{1}{\sqrt{2}}-1,\frac{1}{\sqrt{2}}\right) \right\| = t_2,\\ \mathrm{r}_d[A,B](\overline{x})&=\frac{1}{2} \left\| \left( \frac{1}{\sqrt{2}}+1,\frac{1}{\sqrt{2}}\right) \right\| = t_1,\\ \mathrm{r}_v[A,B](\overline{x})&= \sqrt{d^2\left( \left( t_1,t_2\right) ,A\right) + d^2\left( \left( t_1,t_2\right) ,B\right) }\\&= \sqrt{\left\| \left( t_1,t_2\right) - \left( t_1,0\right) \right\| ^2+ \left\| \left( t_1,t_2\right) - \left( \frac{t_1+t_2}{2},\frac{t_1+t_2}{2}\right) \right\| ^2}= t_2\sqrt{2},\\ \mathrm{r}_a[A,B](\overline{x})&= \left\langle \left( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) , (1,0) \right\rangle =\frac{1}{\sqrt{2}}, \end{aligned}$$

where $t_1:=\frac{\sqrt{2+\sqrt{2}}}{2}$ and $t_2:=\frac{\sqrt{2-\sqrt{2}}}{2}$. It is easy to check that all the relations in Theorem 2(i)-(vii) are satisfied.

5 Conclusion

Our objective in this note has been to catalog the underlying theoretical tools behind the recent flurry of activity on local convergence results for projection-type algorithms for feasibility. Of course the theory compiled here is not limited to feasibility problems, but since most of the notions are geometrically motivated, feasibility offers the most vivid motivation for the definitions. Strong metric subregularity for set-valued mappings provides, in our opinion, the most powerful avenue toward generalizing these ideas to constrained optimization and beyond.

We conclude this note with the underlying challenge that has inspired the development of this theory: what are necessary conditions for local linear convergence of first order methods?