1 Introduction

The optimal design of a regulatory mechanism for a monopolist, such as firms that provide power, natural gas, water, and other energy., differs from one domain to another, not only because of the possibility of private information but also the feasibility and efficiency of transfers. On one hand, the theoretical literature (Baron and Myerson 1982; Laffont and Tirole 1986, 1993; Amador and Bagwell 2022) on monopoly regulation typically assumes that the regulated firm probably has private information about its costs. The study in a setting where the regulated firm has the information advantage on its demand, however, is also important and relevant to explore. As Riordan (1984) and Lewis and Sappington (1988a, 1988b) and Basso et al. (2017) argue, a regulated firm is likely to have more information about the demand for its product than the regulator, not only because the firm generally has better knowledge concerning its product’s quality and reliability, but also because they usually devote significant resources to acquire the knowledge of its markets that is hardly shared with the regulator. On the other hand, monetary transfers to the regulated firm are used by the regulator to establish the contracts of the product in most of the literature (Lewis and Sappington 1988a, 1988b; Laffont and Tirole 1993; Aguirre and Beitia 2004; Basso et al. 2017). Nevertheless, there are circumstances in which the monetary transfer instruments may be limited. Some scholars (Baron 1989; Laffont and Tirole 1993; Armstrong and Sappington 2007) argue that the regulators often do not have the authority to explicitly employ public funds to compensate the regulated firm or tax the regulated firm. For example, the “Regulations on Electric Power Supervision” promulgated by the State Council of the People's Republic of China clearly determined that the competent pricing department and the power regulator shall supervise the price of electricity by laws, administrative regulations and the provisions of the State Council. The electric power regulator shall, in accordance with the law, supervise the fair and non-discriminatory opening of the electricity market to entities engaged in electricity trading and the fair opening of the power grid by transmission enterprises. However, the regulatory authority does not have the ability to explicitly tax or pay subsidies. Also, even though the monetary transfer can be realized through positive or negative access fees, the scope for such transfers may be limited by universal service or consumers’ arbitrage behaviors in practice.

In a seminal paper, Basso et al. (2017) compare price and quantity instruments to regulate a monopoly that has private information about its demand or costs. They contribute to studying an alternative option of quantity-based mechanisms for monopoly regulation. The monetary transfers, however, are used by the regulator to the regulated firm in their paper. Based on the model of Basso et al. (2017), we study the optimal monopoly regulation under the restriction that direct monetary transfers are infeasible. We characterize the optimal screening mechanisms that provide multiple menus for the regulated firm to select and pooling mechanisms that only offer one unique contract for quantity and price instruments, and compare performances of the regulator’s social welfare. The pooling mechanisms deserve discussion for two reasons. First, the pooling mechanisms would be preferred when screening the demand information of a regulated firm is not valuable for the regulator. Second, the pooling mechanisms are easier to understand and implement for regulators in practice even though less welfare would be induced.

When the regulator is allowed to offer multiple menus for the regulated firm to self-select and the costs of the regulated firm are restricted to be linear, the quantity-floor regulation emerges as the optimal quantity regulatory policy. Sufficient conditions are provided for the optimality of this quantity-floor mechanism among all feasible delegation mechanisms. We show that this quantity-floor mechanism would be optimal when the relative concavity parameter of the regulator and utility’s welfare is large and the density of the demand information is non-increasing. This optimal quantity mechanism would never attain the first-best level, while the quantity mechanism in Basso et al. (2017) can attain the first-best level when the consumers’ welfare and the firm’s utility are equally important for the regulator. The optimal quantity delegation results from the following trade-off: the firm can tailor its flexible policy to the demand information, but the implemented quantity is too low for the regulator. Hence, the first-best level that depends on the firm’s type cannot be attained, since there is no way to utilize all information without any bias. For price regulation, when marginal costs are constant, the first-best price level that equals fixed marginal cost, however, can be achieved due to the fact that it is not dependent on the firm’s private information. When marginal costs are decreasing, the optimal screening quantity depends on the floor. The screening price involves bunching. When the realized demand is not the lowest type, the screening price mechanism creates fewer losses caused by underproduction, which leads to the preference for screening price mechanism. Therefore, we find that, with the linear costs of the regulated firm, the screening price mechanism would strictly dominate the screening quantity mechanism.

When the regulator is restricted to pooling mechanisms, both price and quantity regulation switch from menus to fixed values. Compared with the transfer-based case in Basso et al. (2017), the firm’s individual rationality constraint may not bind in our paper. With linear and decreasing marginal costs, the optimal quantity and price are both optimally set to leave the lowest firm’s demand type with zero profits due to the binding individual rationality constraint. We find that the pooling price mechanism is always preferred to the pooling quantity mechanism. For non-decreasing marginal costs, there are two cases in consideration and the equal weights to consumers’ surplus and regulated firm’s profits for the regulator are assumed for clear and convenient analysis. First, when the slope of marginal costs is slightly positive or no larger than a positive threshold, the optimal quantity is still derived by the binding individual rationality constraint for the lowest type. The optimal price, however, is optimally chosen when the price equals marginal cost with expected firm’s type since the firm’s individual rationality constraint does not bind. Hence, it shows that the optimal pooling price mechanism is still superior in this circumstance. Second, when the slope of marginal costs is large exceeding a positive threshold, we demonstrate that the individual rationality constraints in quantity and price regulation both do not bind, and thus, the optimal pooling quantity and price are both determined based on the intersection of the demand with expected firm’s type and marginal costs. In this case, we show the pooling quantity will dominate if the slope of marginal costs is great than the absolute value of the demand slope. Therefore, the pooling quantity mechanism may be suitable for public monopoly cases, such as transportation, electricity production and transmission, etc., where the demand is rather inelastic, and marginal cost is increasing because of the high volumes of traffic or electricity. High volumes exceeding the capacity would result in system congestion. In a real-world setting, the level of departure and arrival flights for each time at the airport is determined to be four slots in Chicago O’Hare and Washington National, which provides evidence that the regulator uses the pooling quantity mechanism rather than the price mechanism.

Some articles have respectively focused on the issues of asymmetric cost or demand information and infeasible transfers. For example, for the literature on asymmetric cost information, Baron and Myerson (1982) first apply mechanism design to monopoly service regulation, considering how regulators should regulate a monopoly with private cost information. In optimal regulatory policies, prices and monetary transfers as subsidies are designed as functions of firm cost reporting, thus maximizing expected social welfare under the constraint that firms have non-negative profits and no incentives to distort their costs. For the literature on asymmetric demand information, Riordan (1984) and Lewis and Sappington (1988a) first focus on transfer-based price monopoly regulation when there is asymmetric information on demand. Compared with Riordan’s (1984) case of the constant marginal cost of production, Lewis and Sappington (1988a) focus on the case where marginal cost of production varies with output. Lewis and Sappington (1988b) study the optimal price regulatory policies when regulators do not fully observe both the cost function and the demand function of the firm. The transfer payments are not feasible in some circumstances, which is a key determinant in designing the optimal regulatory policy. For the literature on infeasible transfers, Alonso and Matouschek (2008) first regard the monopoly regulation problem as an optimal delegation problem, which is first introduced by Holmström (1984), when the costs are private observed by the regulated firm and the transfer instrument is infeasible, while the participation constraint is not included in their analysis. Then, Amador and Bagwell (2022) analyze the monopoly regulation with asymmetric cost information under the restriction that transfers are infeasible by extending the Lagrangian approach to delegation problems of Amador and Bagwell (2013) to include ex-post participation constraint. It is worth mentioning that the price-cap regulation and the quantity-floor regulation are the same with asymmetric cost information in the research of Amador and Bagwell (2022) since the realized quantity induced by the optimal price is equivalent to the optimal quantity. As Basso et al. (2017) state, the quantity and price regulations are not equivalent to asymmetric demand information, although these two instruments lead to the same level of welfare with asymmetric cost information.

The pooling mechanisms of our paper are also related to the literature (Williams 2002; Moledina et al. 2003; Krysiak 2008; Krysiak and Oberauner 2010) on the comparison of price and quantity instruments under asymmetric demand or cost information that is first conducted by Weitzman (1974). The key differences in our paper are twofold: first, the firms in these papers are price takers and choose a quantity of production based on their cost functions, disregarding the demand, while the firm in our paper is a monopolist who has the market power and is faced with the whole demand, and therefore the quantity induced for the price will not be offered by profit maximization but the demand; second, the direct transfers in these papers are feasible. Therefore, the results in these papers cannot directly extend to our paper. The significant differences between several key studies are summarized in Table 1.

Table 1 Significant differences between key studies
Full size table

The rest of the paper is organized as follows. Section 2 provides the basic theoretical model. Section 3 studies the optimal screening monopoly regulation mechanism in quantity and price instruments and the comparative welfare analysis is derived. In Sect. 4, the optimal pooling quantity and price mechanisms are characterized and compared. Section 5 briefly summarizes the results and suggests opportunities for further work. Formal proofs are in the Appendix.

2 The basic model

We consider the relationship between a regulator and a regulated monopoly firm, such as firms that provide power, natural gas, water resources, and other energy. This model framework has a broad appeal and can be applied to various monopoly regulations, such as electricity, telecommunication, transportation regulation, etc. The specific regulatory environment under consideration is the following.

2.1 Cost, demand and information

The regulated firm’s cost is known to be given by the function

$$C(q) = c_{0} q + {{c_{1} q^{2} } \mathord{\left/ {\vphantom {{c_{1} q^{2} } 2}} \right. \kern-0pt} 2},$$

with marginal cost \(C^{\prime}(q) = c_{0} + c_{1} q > 0\), which can be increasing, decreasing and constant with the output. We assume that any fixed cost is normalized to zero for ease of presentation and without loss of generality. It is also common knowledge that the unit price \(p\) and quantity \(q\) follow the inverse demand function

$$p(q,\theta ) = P(q) + \theta ,$$

where the parameter \(\theta\) captures the firm’s private information about the demand, and can be regarded as the regulated firm’s type. The regulator is not informed about \(\theta\) when contracting but knows that \(\theta\) is the realization of a random variable on \(\Theta \in [\underline {\theta } ,\overline{\theta }]\) where \(\overline{\theta } > \underline {\theta } > 0\) with a cumulative distribution function \(F(\theta )\), a density \(f(\theta )\) and the monotone hazard rate \({{{{d((1 - F(\theta ))} \mathord{\left/ {\vphantom {{d((1 - F(\theta ))} {f(\theta )}}} \right. \kern-0pt} {f(\theta )}})} \mathord{\left/ {\vphantom {{{{d((1 - F(\theta ))} \mathord{\left/ {\vphantom {{d((1 - F(\theta ))} {f(\theta )}}} \right. \kern-0pt} {f(\theta )}})} {d\theta }}} \right. \kern-0pt} {d\theta }} \le 0\) for most distributions, such as uniform distribution, normal distribution, logarithmic distribution, exponential distribution, and Laplace distribution. It assumes a linear demand function which means that \(p_{q} (q,\theta ) = P^{\prime } (q) < 0 < p_{\theta } (q,\theta ) = 1,\;P^{\prime \prime } (q) = 0\) where subscripts denote partial derivatives. For every price \(p \ge 0\) and type \(\theta\), the direct demand function \(Q(p,\theta )\) obeys \(p \equiv P(Q(p,\theta )) + \theta\). Following the derivatives with respect to \(p\) and \(\theta\), we find that \(Q_{p} (p,\theta ) = {1 \mathord{\left/ {\vphantom {1 {P^{\prime}(q)}}} \right. \kern-0pt} {P^{\prime}(q)}} < 0 < Q_{\theta } (p,\theta ) = - {1 \mathord{\left/ {\vphantom {1 {P^{\prime}(q)}}} \right. \kern-0pt} {P^{\prime}(q)}}\), that is higher the realizations of \(\theta\) imply a larger quantity of output consumers demand at any nonnegative price. It assumes that \(C^{\prime\prime}(q) = c_{1} > P^{\prime}(q)\) to ensure a concave optimization problem and non-negative results when the firm’s optimal policy is executed. In words, the demand is steeper than marginal costs when the latter is downward sloping.

2.2 Contracts

For screening mechanisms, the regulator designs an effective incentive regulation to foster the firm to tell the truth about its demand type. We assume that the regulator has no access to monetary transfer payments, only restrictions on the price or quantity can be imposed. Therefore, following Holmström’s (1984) delegation mechanism, an assignment menu \(x(\theta )\) that can be a quantity \(q(\theta )\) or price \(p(\theta )\) can be stipulated by the regulator. The menu emphasizes the role that the regulator plays in limiting ex ante the possible options chosen by the firm. It is no loss of generality in restricting the analysis to such direct communication and truthful mechanism from the Revelation Principle. For pooling regulatory mechanisms without considering the incentive of a firm’s truth-telling, a unique quantity \(q^{u}\) or price \(p^{u}\) for all firm’s demand types is stipulated.

2.3 Objectives

It is straightforward to write the respective firm’s profits for quantity and price regulation as

\(u(q,\theta ) = (P(q) + \theta - c_{0} - {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2})q\) and \(u(p,\theta ) = (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta )\).

To ensure it is a concave optimization problem, we assume \(u_{qq} (q,\theta ) < 0\) which means \(c_{1} { > 2}P^{\prime}(q)\) and \(u_{pp} (p,\theta ) < 0\) which means \(c_{1} Q_{p} (p,\theta ) < 2\).

The consumer surplus for quantity and price regulation is given by

$$v(q,\theta ) = \int_{0}^{q} {(P(\tilde{q}) + \theta )} d\tilde{q} - \left( {P(q) + \theta } \right)q\;{\text{and}}\;v(p,\theta ) = \int_{p}^{\infty } {Q(\tilde{p},\theta )} d\tilde{p}.$$

The regulator’s objective is to maximize a weighted sum of consumer surplus and the firm’s profit in which the latter receives a weight \(\alpha \in [0,1]\). When \(\alpha < 1\), the consumer interest is a greater concern for the regulator. The social welfare function for quantity and price regulation can be written as

\(E_{\theta } w(q,\theta ) = E_{\theta } \left[ {\int_{0}^{q} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q) + \theta )q + \alpha (P(q) + \theta - c_{0} - {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2})q} \right]\) and \(E_{\theta } w(p,\theta ) = E_{\theta } \left[ {\int_{p}^{\infty } {Q(\tilde{p},\theta )} d\tilde{p} + \alpha (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta )} \right]\).

To ensure it is a concave optimization problem, we also assume \(w_{qq} (q,\theta ) < 0\) which means \(c_{1} > (2 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha })P^{\prime}(q)\;{\text{and}}\;w_{pp} (p,\theta ) < 0\) which means \(c_{1} Q_{p} (p,\theta ) < 2 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }.\)

3 Screening quantity and price regulatory mechanisms

In this section, we characterize the optimal screening monopoly incentive regulation in both quantities and prices, and make a comparative analysis of welfare.

3.1 Screening quantity regulation

For quantity regulation, we first define the first-best quantity mechanism under complete information as a benchmark. Under the individual rational (IR) constraint, the regulator’s problem can be written as

$$\mathop {\max }\limits_{q} \int_{0}^{q} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q) + \theta )q + \alpha (P(q) + \theta - c_{0} - {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2})q$$
$$\;{\text{s}}.{\text{t}}.(P(q) + \theta - c_{0} - {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2})q>0.$$
(1)

Note that the value of an outside option is normalized to be zero. To figure out this problem, the first step is to define the optimal quantity when the IR constraint is ignored. Then, check whether the optimal quantity satisfies the IR constraint. The regulator’s optimal quantity without considering the IR constraint.

From the first-order condition of the objective function, we find that

$$P(q^{o} ) + \theta - c_{0} - {{c_{1} q^{o} } \mathord{\left/ {\vphantom {{c_{1} q^{o} } 2}} \right. \kern-0pt} 2} = [{{c_{1} } \mathord{\left/ {\vphantom {{c_{1} } 2}} \right. \kern-0pt} 2} - ({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)]P^{ {\prime }} (q^{o} ))q^{o}.$$

We assume \(c_{1} \le - 2({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)P^{\prime } (q)\) for simplicity. Thus, the IR constraint will bind, since the quantity \(q^{o} (\theta )\) violates the firm’s IR constraint except when \(\alpha = 1,\;c_{1} = 0.\) We can deduce that the first-best quantity would be \(q^{*} (\theta )\) that depends on the firm’s type \(\theta\), such that \(P(q^{*} ) + \theta - c_{0} - {{c_{1} q^{*} } \mathord{\left/ {\vphantom {{c_{1} q^{*} } 2}} \right. \kern-0pt} 2} = 0\). We find that \(q^{*\prime } (\theta ) = {2 \mathord{\left/ {\vphantom {2 {(c_{1} - 2P^{\prime } (q))}}} \right. \kern-0pt} {(c_{1} - 2P^{\prime } (q))}} > 0.\)

We now consider the case of incomplete information on demand. First, we need to identify the firm’s quantity flexible allocation. Specifically, if the firm is flexible in choosing the quantity and unrestricted by the regulator, the regulated firm’s optimal quantity policy will be obtained as

$$q^{f} (\theta ) = \arg \mathop {\max }\limits_{q} (P(q) + \theta - c_{0} - {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2})q.$$

The first-order condition is given by \(P^{\prime } (q^{f} (\theta ))q^{f} (\theta ) + \theta - c_{0} + P(q^{f} (\theta )) - c_{1} q^{f} (\theta ) = 0.\) The quantity flexible allocation is the firm’s quantity as a function of its type. Following the derivatives with respect to \(\theta\), we find that \(q^{{f^{{\prime }} }} (\theta ) = - 1/u_{{qq}} \left( {q,\theta } \right) > 0.\) Notice as well that \(P(q^{f} (\theta )) + \theta - c_{0} - {{c_{1} q^{f} (\theta )} \mathord{\left/ {\vphantom {{c_{1} q^{f} (\theta )} 2}} \right. \kern-0pt} 2} = ({{c_{1} } \mathord{\left/ {\vphantom {{c_{1} } 2}} \right. \kern-0pt} 2} - P' (q^{f} (\theta )))q^{f} (\theta ) > 0\) and thus \(u(q_{f} (\theta ),\theta ) > 0\) for all \(\theta \in \Theta\). Therefore, we can utilize this first-order condition in the regulator’s objective and obtain the direction of the bias of the firm with type \(\theta\):

$$w_{q} (q^{f} (\theta ),\theta ) = - P^{ {\prime }} (q^{f} (\theta ))q^{f} (\theta ) > 0\;{\text{for}}\;{\text{all}}\;\theta \in \Theta .$$

Therefore, the firm would prefer lower output from the perspective of the regulator. To limit this downward bias and ensure the truth-telling of firm, the regulator would stipulate a menu of quantities \(\{ q(\hat{\theta })\}_{{\hat{\theta } \in \Theta }}\) contingent on the firm’s type announcement. The incentive compatibility (IC) constraint is given as follows

$$\theta = \mathop {\arg \max }\limits_{{\hat{\theta }}} (P(q(\hat{\theta })) + \theta - c_{0} - {{c_{1} q(\hat{\theta })} \mathord{\left/ {\vphantom {{c_{1} q(\hat{\theta })} 2}} \right. \kern-0pt} 2})q(\hat{\theta }).$$

Standard revealed preferences arguments (Samuelson 1938) indicate that \(q(\theta )\) is weakly increasing in demand information \(\theta\) and almost everywhere differentiable. The first-order condition for truth-telling can be obtained as

$$q^{ {\prime }} (\theta )[P^{ {\prime }} (q(\theta ))q(\theta ) + \theta - c_{0} - c_{1} q(\theta ) + P(q(\theta ))] = 0.$$
(2)

From this, the quantity \(q(\theta )\) is either the firm’s quantity flexible policy or independent of the information on demand. The regulator may set a floor on the permissible output satisfying this IR constraint. Thus, we can get the regulator’s optimization problem as:

$$\mathop {\max }\limits_{q(\theta )} E\left[ {\int_{0}^{q(\theta )} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q(\theta )) + \theta )q(\theta ) + \alpha (P(q(\theta )) + \theta - c_{0} - {{c_{1} q(\theta )} \mathord{\left/ {\vphantom {{c_{1} q(\theta )} 2}} \right. \kern-0pt} 2})q(\theta )} \right]\;{\text{s}}.{\text{t}}.(1)\ and\ (2).$$

To figure out this problem, we need to define an optimal quantity-floor allocation as Lemma 1 when the IR constraint is ignored, which is similar to Alonso and Matouschek (2008) with cost asymmetric information. The proof appears in the Appendix.

Lemma 1

Ignoring the individual rationality constraint, the optimal quantity-floor allocation is

\(q^{c} (\theta ) = \left\{ \begin{gathered} q^{f} (\theta_{c} ) \hfill \\ q^{f} (\theta ) \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta \in [\underline {\theta } ,\theta_{c} ]} \\ {\theta \in (\theta_{c} ,\overline{\theta }]} \\ \end{array}\) where the cut-off type \(\theta_{c}\) satisfies \(\int_{{\underline {\theta } }}^{{\theta_{c} }} {w_{q} (q^{f} (\theta_{c} ),\theta )} dF(\theta ) = 0.\)

The cut-off condition implies that the average bias among the pooled types is zero. Note that \(q^{f} (\theta ) < q^{*} (\theta ) \le q^{o} (\theta )\). Then, we need to verify whether the participation constraint holds. Under this optimal quantity-floor allocation, the IR constraint can be written as \(u^{c} (\theta ) = (P(q^{c} (\theta )) + \theta - c_{0} - {{c_{1} q^{c} (\theta )} \mathord{\left/ {\vphantom {{c_{1} q^{c} (\theta )} 2}} \right. \kern-0pt} 2})q^{c} (\theta ) \ge 0\) for all \(\theta \in \Theta\). Notice that

$$u^{{c {\prime }}} (\theta ) = \left\{ \begin{gathered} q^{f} (\theta_{c} ) > 0 \hfill \\ q^{f} (\theta ) > 0 \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta \in [\underline {\theta } ,\theta_{c} ]} \\ {\theta \in (\theta_{c} ,\overline{\theta }]} \\ \end{array} .$$

Therefore, it suffices to check whether the IR constraint for the lowest demand type is satisfied, due to the strictly increasing property of the firm’s profits with the firm’s type. Then, we get the Lemma 2 which is similar to Amador and Bagwell (2022) with cost asymmetric information. See the proof in the appendix.

Lemma 2

The individual rationality constraint is not satisfied under the optimal quantity-floor allocation.

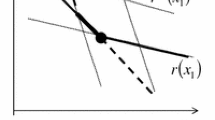
To satisfy the IR constraint, a sufficient flexible allocation is chosen so that all types would produce non-negative profit. There would exist a cut-off demand type \(\theta_{r} \in (\underline {\theta } ,\theta_{c} )\) such that the IR constraint for the lowest demand type binds (see Fig. 1). The result is summarized in the following proposition 1, which is also similar to Amador and Bagwell (2022) with cost asymmetric information.

Fig. 1
figure 1

Optimal quantity-floor mechanism where for all \(\theta \in [\underline {\theta } ,\theta_{c} ]\) the blue line is the optimal quantity-floor allocation without considering the individual rationality constraint and the red line is the optimal IR-quantity-floor allocation

Full size image

Proposition 1

The optimal IR-quantity-floor mechanism obeys:

$$q_{r} (\theta ) = \left\{ \begin{gathered} q^{f} (\theta_{r} ) \hfill \\ q^{f} (\theta ) \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta \in [\underline {\theta } ,\theta_{r} ]} \\ {\theta \in (\theta_{r} ,\overline{\theta }]} \\ \end{array}$$

where the cut-off type \(\theta_{r}\) satisfies

\(u(q^{f} (\theta_{r} ),\underline {\theta } ) = (P(q^{f} (\theta_{r} )) + \underline {\theta } - c_{0} - {{c_{1} q^{f} (\theta_{r} )} \mathord{\left/ {\vphantom {{c_{1} q^{f} (\theta_{r} )} 2}} \right. \kern-0pt} 2})q^{f} (\theta_{r} ) = 0.\) Note that

$$if\ \theta_{r} \ge \overline{\theta },q_{r} (\theta ) = q^{f} (\theta_{r} )\;{\text{for}}\;{\text{all}}\;\theta \in [\underline {\theta } ,\overline{\theta }];\;if\ \theta_{r} \le \underline {\theta } ,\;q_{r} (\theta ) = q^{f} (\theta ),\;{\text{for}}\;{\text{all}}\;\theta \in [\underline {\theta } ,\overline{\theta }].$$

Next, we proceed to determine the sufficient conditions for this IR-quantity-floor mechanism to be optimal. As the theory of optimal delegation (Holmström, 1984; Alonso and Matouschek 2008; Amador and Bagwell 2013) states, if the interval delegation is to be optimal among all feasible delegation, it must be superior for the regulator to the alternative delegation with jump discontinuities, such as the alternative allocation in Fig. 2. We adopt the “guess-and-verify” approach of Amador and Bagwell (2013) in which extended Lagrangian methods is used to verify the optimality of the guessed solution. For simplicity, we take the case \(c_{1} = 0\) as an example. See more details on the research of Anton and Andriy (2019), and focus on the comparison of the quantity and price instruments.

Fig. 2
figure 2

The alternative allocation with one jump discontinuity in which a “step” at \(\theta_{s}\), that is indifferent between \(q^{f} (\underline {\theta }_{s} )\) and \(q^{f} (\overline{\theta }_{s} )\), is induced

Full size image

The relative concavity parameter of the regulator and firm’s objective functions, which is the key to determining the optimality of the IR-quantity-floor solution, is defined as follows:

$$\kappa = \mathop {\min }\limits_{q,\theta } \left\{ {\frac{{w_{qq} (q,\theta )}}{{u_{qq} (q,\theta )}}} \right\}.$$

The resulting sufficient conditions can be summarized as follows. The proof can be seen in the appendix.

Proposition 2

If the following conditions are satisfied, the optimal solution to the regulator’s problem will be realized with the IR-quantity-floor mechanism:

$$({\text{i}})\quad \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })f(\tilde{\theta })d\tilde{\theta }} \ge 0,$$
$$\begin{aligned} ({\text{ii}})\quad & \frac{1}{{\theta_{r} - \theta }}\int_{\theta }^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } - \kappa F(\theta ) \le \frac{1}{{\theta_{r} - \underline {\theta } }} \\ & \int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })f(\tilde{\theta })d\tilde{\theta }} \;{\text{for}}\;{\text{all}}\;\theta \in [\underline {\theta } ,\theta_{r} ],\;{\text{and}} \\ \end{aligned}$$
$$({\text{iii}})\quad \kappa F(\theta ) - w_{q} (q^{f} (\theta ),\theta )f(\theta )\;{\text{is}}\;{\text{non}} - {\text{decreasing}}\;{\text{for}}\;{\text{all}}\;\theta \in \left[ {\theta_{r} ,\overline{\theta }} \right].$$

We now check the property of sufficient conditions. The left side of condition (i) shows the average quantity bias among the pooled firm which reflects the first-order condition for the optimal cut-off type. Without considering the IR constraint, the average quantity bias is equal to zero which is defined in Lemma 1. When the focus is turned to the optimal quantity allocation satisfying the IR constraint, the average quantity bias is restricted to be non-negative, which shows a lower cut-off value is feasible through the concavity of the problem. The sufficient condition (ii) and (iii) would be more easily satisfied when the relative concavity parameter of the regulator and firm’s objective functions \(\kappa\) is large, since the distribution \(F(\theta )\) is non-negative and increasing for all \(\theta \in [\underline {\theta } ,\overline{\theta }].\) We can also observe that the condition (iii) is more easily satisfied when the density \(f(\theta )\) is non-increasing, because \(w_{q} (q_{f} (\theta ),\theta )\) is positive.

To provide some intuition to interpret why the relative concavity of the regulator and firm’s objective functions and the density slope are critical, the alternative allocation with one jump discontinuity in Fig. 2 is considered. The alternative allocation has both good side and bad side as compared with the optimal IR-quantity-floor allocation. In terms of the discussion of the density slope, the higher quantity allocation for all \(\theta \in [\theta_{s} ,\overline{\theta }_{s} ]\) closer to the regulator’s preferred efficient quantity and lower quantity allocation for all \(\theta \in [\underline {\theta }_{s} ,\theta_{s} ]\) with a larger bias are induced in the alternative allocation. To make the optimal IR-quantity-floor allocation superior, the non-increasing density can induce the effect of bad side dominates the effect of good side in the regulator’s expected social welfare. Then, for the discussion of the relative concavity of the regulator and firm’s objective functions, we find that the variance of the allocation around \(q^{f} (\theta )\) for \(\theta \in [\underline {\theta }_{s} ,\overline{\theta }_{s} ]\) is increased in alternative allocation as compared with the optimal IR-quantity-floor allocation. When the regulator’s objective is more concave than the firm’s objective in which the relative concavity is large, the regulator would not benefit from the increase in variance afforded by the alternative allocation. Thus, the IR-quantity-floor allocation remains superior. Building on the above intuitive explanations, the following corollary offers conditions on the density and the relative concavity of the objective functions for Proposition 2. The proof can be seen in the appendix.

Corollary 1

If \(f^{ {\prime }} (\theta ) \le 0\) and \(\kappa \ge \frac{1}{2}\alpha\) for all \(\theta \in \Theta\) , the sufficient conditions in Proposition 2 will be satisfied, then the optimal IR-quantity-floor allocation will be the optimal solution to the regulator’s problem.

To this end, a numerical example is offered for a clear explanation. Consider a linear demand function \(P(q) = 10 - q\) with \(q \in [0,10]\), a linear cost function \(C(q) = c_{0} q\) with \(c_{0} < 10\) to ensure \(q_{f} (\theta ) = ({{10 - c_{0} + \theta )} \mathord{\left/ {\vphantom {{10 - c_{0} + \theta )} 2}} \right. \kern-0pt} 2}{ > 0}\) and \(\theta \in [1,5].\) For this numerical example, \(\kappa = \alpha - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\). \(w_{qq} (q,\theta ) < 0\) and \(w_{pp} (p,\theta ) < 0\) mean \(\alpha > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}.\) Following corollary 1, the sufficient conditions in Proposition 2 will be satisfied when \(\kappa \ge {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\alpha\), which means only when \(\alpha = 1\). Therefore, the quantity-floor mechanism, which obeys that

if \(c_{0} > 7\), \(q_{r} (\theta ) = \left\{ \begin{gathered} 11 - c_{0} \hfill \\ ({{10 - c_{0} + \theta )} \mathord{\left/ {\vphantom {{10 - c_{0} + \theta )} 2}} \right. \kern-0pt} 2} \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta \in [1,12 - c_{0} ]} \\ {\theta \in (12 - c_{0} ,5]} \\ \end{array} ,\)

and if \(c_{0} \le 7,\;q_{r} (\theta ) = 11 - c_{0} ,\;{\text{for}}\;{\text{all}}\;\theta \in [1,5],\)

can be optimal when the regulator gives equal weight to the consumers’ and firm’s utility. Otherwise, the alternative allocation with jump discontinuities will be optimal.

3.2 Screening price regulation

For price regulation, we also first define the first-best price mechanism under complete information. Under the IR constraint, the regulator’s problem can be written as

$$\mathop {\max }\limits_{p(\theta )} \int_{p}^{\infty } {Q(\tilde{p},\theta )} d\tilde{p} + \alpha (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta)$$
$$\;{\text{s}}.{\text{t}}.\quad u(p,\theta ) = (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta ) \ge 0.$$
(3)

Similar to the quantity regulation, we consider the optimal price when the IR constraint is ignored as follows:

$$p^{o} (\theta ) = \arg \mathop {\max }\limits_{p} \int_{p}^{\infty } {Q(\tilde{p},\theta )} d\tilde{p} + \alpha (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta ).$$

From the first-order condition and the assumption \(c_{1} \le - 2({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)P^{\prime } (q) = {{ - 2({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)} \mathord{\left/ {\vphantom {{ - 2({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)} {Q_{p} (p,\theta )}}} \right. \kern-0pt} {Q_{p} (p,\theta )}},\) we find that the price \(p^{o} (\theta )\) violates the firm’s IR constraint except when the weight \(\alpha = 1,c_{1} = 0,\) since

$$p^{o} (\theta ) - c_{0} - {{c_{1} Q(p^{o} (\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p^{o} (\theta ),\theta )} 2}} \right. \kern-0pt} 2} = ({{({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)} \mathord{\left/ {\vphantom {{({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha } - 1)} {Q_{p} (p^{o} (\theta ),\theta )}}} \right. \kern-0pt} {Q_{p} (p^{o} (\theta ),\theta )}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}c_{1} )Q(p^{o} (\theta ),\theta ) \le 0.$$

Thus, through the binding IR constraint, we can deduce that the first-best price would be \(p^{*} (\theta )\) that depends on the firm’s type \(\theta\) except when \(c_{1} = 0,\) such that \(p^{*} (\theta ) - c_{0} - {{c_{1} Q(p^{*} (\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p^{*} (\theta ),\theta )} 2}} \right. \kern-0pt} 2} = 0.\) Taking the deviation of \(\theta\), we find that the monotonicity of the \(p^{*} (\theta )\) depends on the slope of marginal cost \(c_{1}\), such that \(p^{*\prime } (\theta ) = \frac{{c_{1} Q_{\theta } (p^{*} (\theta ),\theta )}}{{2 - c_{1} Q_{p} (p^{*} (\theta ),\theta )}}.\)

Considering the case of incomplete information on demand, we need to identify the firm’s price flexible allocation as well. If the firm is flexible in choosing the price and unrestricted by the regulator, the regulated firm’s optimal price policy will be obtained as

$$p^{f} (\theta ) = \arg \mathop {\max }\limits_{p} (p - c_{0} - {{c_{1} Q(p,\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p,\theta )} 2}} \right. \kern-0pt} 2})Q(p,\theta ).$$

The first-order condition is given by \(\left[ {p^{f} (\theta ) - c_{0} - {{c_{1} Q(p^{f} (\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p^{f} (\theta ),\theta )} 2}} \right. \kern-0pt} 2}} \right]Q_{p}^{ {\prime }} (p^{f} (\theta ),\theta ) + (1 - {{c_{1} Q_{p} (p^{f} (\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q_{p} (p^{f} (\theta ),\theta )} 2}} \right. \kern-0pt} 2})Q(p^{f} (\theta ),\theta ) = 0.\) Following the derivatives with respect to \(\theta\), we find that \(p^{{f^{{\prime }} }} \left( \theta \right) = - \left( {1 - c_{1} Q_{p} } \right)/u_{{pp}} > 0.\) Notice as well that \(p^{f} (\theta ) - c_{0} - {{c_{1} Q(p^{f} (\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p^{f} (\theta ),\theta )} 2}} \right. \kern-0pt} 2} = - (Q_{p} (p^{f} (\theta ),\theta ) - {{c_{1} } \mathord{\left/ {\vphantom {{c_{1} } 2}} \right. \kern-0pt} 2})Q(p^{f} (\theta ),\theta ) > 0\) and thus \(u(p_{f} (\theta ),\theta ) > 0\) for all \(\theta \in \Theta\). Therefore, we can utilize this first-order condition in the regulator’s objective and obtain the direction of the bias of the firm with type \(\theta\):

$$w_{p} (p^{f} (\theta ),\theta ) = - Q(p^{f} (\theta ),\theta ) < 0\;{\text{for}}\;{\text{all}}\;\theta \in \Theta .$$

Therefore, the firm would prefer a higher price than the regulator’s first-best price. Compared to quantity instrument, further characterizing the optimal price is not easy. If marginal costs are constant, we can get that the first-best price would be \(p^{*} = c_{0}\) that depends on the firm’s type \(\theta\). Therefore, with incomplete information on demand, the first-best price mechanism is feasible. When marginal costs are decreasing, the optimal price mechanism involves complete bunching, where the regulator fixes a pooling price independent of the firm’s report. This is because the first-best price mechanism ceases to be incentive compatible. Compared to the complete bunching, using the regulated firm’s private information is not superior. Only if marginal costs are increasing, using the private information may be profitable, as only in that case the price schedule is increasing in \(\theta\). However, when \(\alpha = 1\), the IR condition may not bind, and the results are unambiguous. For simplification, we focus on the non-increasing marginal cost here. Specifically, the regulator’s optimization problem is:

$$\mathop {\max }\limits_{p(\theta )} E_{\theta } \left[ {\int_{p(\theta )}^{\infty } {Q(\tilde{p},\theta )} d\tilde{p} + \alpha (p(\theta ) - c_{0} - {{c_{1} Q(p(\theta ),\theta )} \mathord{\left/ {\vphantom {{c_{1} Q(p(\theta ),\theta )} 2}} \right. \kern-0pt} 2})Q(p(\theta ),\theta )} \right]\;{\text{s.t.}}\,{(3)}$$

The results can be summarized as following. The proof can be seen in the appendix.

Proposition 3

Assuming non-increasing marginal cost, the optimal screening price \(p_{r}\)

  1. (1)

    is the first-best price, such that \(p^{*} = c_{0}\), if marginal costs are constant \(c_{1} = 0\).

  2. (2)

    obeys \(u(p^{u} ,\underline {\theta } ) = \left( {p^{u} - c_{0} - \frac{1}{2}c_{1} Q(p^{u} ,\underline {\theta } ))Q(p^{u} ,\underline {\theta } } \right) = 0\) , if marginal costs are decreasing \(c_{1} < 0\) .

The result shows that if marginal costs are constant, the first-best price is feasible, since the price is not dependent on the firm’s information. Therefore, leaving flexibility to the firm is not necessary, since the regulator does not need to utilize firm’s private information. if marginal costs are decreasing, the optimal \(p^{u}\) is optimally set to leave the lowest type with zero profits, since \(p^{s}\) violates the IR constraint, and profits are increasing with the firm’s type. Then, it is natural to compare the social welfare of the screening quantity and price mechanism.

Corollary 2

Assuming that the transfers are not feasible and costs of firm are non-increasing, the price mechanism strictly dominates the quantity mechanism for all weight \(\alpha \in [0,1].\)

With constant marginal costs, as shown in Proposition 1, the optimal quantity mechanism would never attain the first-best level for all weight \(\alpha \in [0,1]\), while the first-best price mechanism is feasible. Thus, the price mechanism would strictly dominate the quantity mechanism for all \(\alpha \in [0,1]\). The reason is that the information of regulated firm is valuable for the regulator in quantity mechanism, while it is useless in price mechanism. Specifically, for quantity regulation, the first-best quantity depends on the firm’s type, and there exists a downward bias of firm even when the weight \(\alpha = 1\). Hence, without using the transfers, the optimal quantity delegation results from the following trade-off: the firm can tailor the flexible quantity policy to its demand information, but the implemented quantity is too low from the perspective of regulator. For price regulation, the first-best price, however, is not dependent on the information. Therefore, leaving flexibility to the firm is not necessary, since the regulator does not need to utilize firm’s private information. Compared to the result of Basso et al. (2017) who state that the transfer-based price and quantity mechanisms generate the same level of welfare when \(\alpha = 1\), we show that the price mechanism still strictly dominates the quantity mechanism when \(\alpha = 1\). This is because the transfers are not socially costly anymore when \(\alpha = 1\), and they would be the free tools to separate firm’s type. Without using the transfers, the only way to tell the firm’s type is by providing the flexibility of firm to select its preferred price or quantity with any regulator’s restriction. It, however, is costly for the regulator, since a downward bias is left.

With decreasing marginal costs, the optimal screening quantity depends on the threshold \(\theta_{r}\). If \(\theta \in (\theta_{r} ,\overline{\theta }]\), the optimal quantity is firm’s flexible policy which is optimally set based on the intersection of \(c_{0} + (c_{1} - P^{\prime}(q))q\) and the demand of the type \(\theta\). If \(\theta \in [\underline {\theta } ,\theta_{r} ]\), the optimal quantity is the quantity floor which is optimally set based on the intersection of \(c_{0} + (c_{1} - P^{\prime}(q))q\) and the demand of the threshold type \(\theta_{r}\). The screening price involves bunching, and is optimally set based on the intersection of \(c_{0} + {{c_{1} q} \mathord{\left/ {\vphantom {{c_{1} q} 2}} \right. \kern-0pt} 2}\) and the demand of the lowest type \(\underline {\theta }\). When the realized demand is not the lowest type, both the optimal screening quantity and price mechanisms induce deadweight losses caused by underproduction. Specifically, the first-best quantity of the realized demand would be larger than the realized quantity under the screening quantity and price regulation. More outputs will be induced in price regulation than the outputs in quantity regulation, since the outputs can adjust with the realized demand in price regulation. Thus, the screening price mechanism creates fewer losses, as shown in Fig. 3, which leads to the preference for screening price mechanism.

Fig. 3
figure 3

Deadweight losses of screening quantity and price mechanisms, when decreasing marginal costs are assumed. 2 is the deadweight losses of screening price mechanism, and the sum of 1 and 2 is the deadweight losses of quantity mechanism

Full size image

4 Pooling quantity and price regulatory mechanisms

We now proceed to the pooling quantity and price regulatory mechanisms in which the regulator just utilizes his incomplete information on firm’s demand type to set one unique quantity or price without incentivizing the truth-telling of firm. These pooling mechanisms would be reasonable and possible when a delegation of quantity or price choice is not valuable for the regulator for all \(\alpha \in [0,1]\), which is induced by too large bias of firm. The mechanisms also deserve discussions because they would be easier to be implemented and understood in practice. The problem of further characterizing the optimal pooling quantity and price is also non-trivial, because the IR constraints may not bind in some cases. A linear demand function \(P(q) = P(0) + P^{ {\prime }} (q)q\) is assumed to have a sharper characterization. To ensure non-negative price and quantity and clear results, it assumes that \(P(0) + E(\theta ) - c_{0} > 4(E(\theta ) - \underline {\theta } )\) and \(c_{1} \le \overline{c}_{1}\) where \(\overline{c}_{1} = - P^{\prime } (q)\left[ {{{(P(0) + E(\theta ) - c_{0} )} \mathord{\left/ {\vphantom {{(P(0) + E(\theta ) - c_{0} )} {(E(\theta ) - \underline {\theta } )}}} \right. \kern-0pt} {(E(\theta ) - \underline {\theta } )}} - 1} \right] > 0.\) When we consider the case with non-decreasing marginal costs, it is enough to consider the case where the weight is equal to one, in order to make an unambiguous comparison of pooling quantity and price regulation.

First, maximize \(w(q(\theta ),\theta )\) subject to the IR constraint \(u(q(\theta ),\theta ) \ge 0\) and maximize \(w(p(\theta ),\theta )\) subject to \(u(p(\theta ),\theta ) \ge 0.\) We can define the first-best quantity \(q(\theta )\) and price \(p(\theta )\) for all types \(\theta \in \Theta\) under complete information when marginal costs are linear, such that

\(P(q(\theta )) + \theta = c_{0} + c_{1} q(\theta )\) and \(p(\theta ) = c_{0} + c_{1} Q(p(\theta ),\theta )\) if marginal costs are increasing and the weight \(\alpha = 1;\)

\(P(q(\theta )) + \theta = c_{0} + \frac{1}{2}c_{1} (q(\theta ))\;{\text{and}}\;p(\theta ) = c_{0} + \frac{1}{2}c_{1} Q(p(\theta ),\theta )\) if marginal costs are decreasing.

Notice that the IR constraints will bind when marginal costs are decreasing, otherwise, the IR constraints will not bind.

4.1 Pooling quantity regulation

Without complete information, for pooling quantity regulation, the regulator’s problem is to choose one single \(q\) to maximize \(E_{\theta } w(q,\theta )\) subject to the IR constraint \(u(q,\theta ) \ge 0\). To solve the problem, we also consider the optimal pooling quantity when the IR constraint is ignored first, as follows:

$$q^{s} = \arg \mathop {\max }\limits_{q} E_{\theta } \left[ {\int_{0}^{q} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q) + \theta )q + \alpha (P(q) + \theta - c_{0} - \frac{1}{2}c_{1} q)q} \right].$$

From the first-order condition \(- (1 - \alpha )P^{\prime } (q^{s} )q^{s} + \alpha (P(q^{s} ) + E(\theta ) - c_{0} - c_{1} q^{s} ) = 0\) and the monotonicity of the firm’s profit with the demand information \(u_{\theta } (q,\theta ) = q > 0\), we find that the quantity \(q^{s}\) will violates the firm’s IR constraint if

$$P(q^{s} ) + \underline {\theta } - c_{0} - \frac{1}{2}c_{1} q^{s} = \left[ {\frac{1}{2}c_{1} - (1 - \frac{1}{\alpha })P^{\prime } (q^{s} )} \right]q^{s} - (E(\theta ) - \underline {\theta } ) < 0.$$

Solving this, we can obtain the following proposition. The proof can be seen in the Appendix.

Proposition 4

Assuming quadratic costs and linear demand functions, the optimal pooling quantity \(q^{u}\)

  1. (1)

    is \(q^{s}\) in which \(P(q^{s} ) + E(\theta ) = c_{0} + c_{1} q^{s} + \left( {\frac{1}{\alpha } - 1} \right)P^{\prime } (q^{s} )q^{s}\) and \(q^{s}\) depends on the weight \(\alpha\), if the slope of marginal costs \(c_{1} \in [c_{1}^{q} ,\overline{c}_{1} ];\)

  2. (2)

    obeys \(u(q^{u} ,\underline {\theta } ) = q^{u} \left( {P(q^{u} ) + \underline {\theta } - c_{0} - \frac{1}{2}c_{1} q^{u} } \right) = 0,\) in which \(q^{u}\) is independent with \(\alpha\), if the slope of marginal costs \(c_{1} \in (P^{\prime } (q),c_{1}^{q} )\).

Note that \(\overline{c}_{1} > c_{1}^{q} = 2\left( {1 - \frac{1}{\alpha } - \frac{{E(\theta ) - \underline {\theta } }}{{\alpha [P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )]}}} \right)P^{\prime } (q) > 0;\) and if the weight \(\alpha = 1\), the optimal quantity is chosen when the price with expected firm’s type equals marginal costs such that \(P(q^{s} ) + E(\theta ) = c_{0} - c_{1} q^{s} ,\) and

$$c_{1}^{q} = - P^{ {\prime }} (q)\frac{{2(E(\theta ) - \underline {\theta } )}}{{P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )}}.$$

This proposition shows that, if marginal costs are decreasing or increasing in which the slope is not too large, the binding IR constraint and the increasing profits with the firm’s type result that the optimal \(q^{u}\) is optimally set to leave the lowest type with zero profits. Otherwise, the optimal quantity \(q^{s}\) satisfies the IR constraint, and the quantity depends on the weight that the regulator assigns to the firm’s profits.

4.2 Pooling price regulation

For price regulation, the regulator’s problem is to choose one unique \(p\) to maximize \(E_{\theta } w(p,\theta )\) subject to the IR constraint \(u(p,\theta ) \ge 0\). Characterizing the optimal pooling price \(p^{s}\) when the IR constraint is ignored, we can obtain the price \(p^{s}\) will violates the firm’s IR constraint if

$$p^{s} - c_{0} - \frac{1}{2}c_{1} Q(p^{s} ,\theta ) = \left( {1 - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta )) - \frac{1}{\alpha }} \right)\frac{{Q(p^{s} ,E(\theta ))}}{{ - Q_{p} (p^{s} ,E(\theta ))}} - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta ))(E(\theta ) - \theta ) < 0{\kern 1pt} .$$

Whether the optimal pooling price \(p^{s}\) satisfies the IR constraint depends on the value of marginal costs. If the IR constraint binds, we find that the monotone property of the firm’s profit with the demand information determines which type is most reluctant to participate and left with zero profits. The solution to this optimization problem can be summarized as following. The proof can be seen in the appendix.

Proposition 5

Assuming quadratic costs and linear demand functions, the optimal pooling price \(p^{u}\).

  1. (1)

    is \(p^{s}\) in which \(p^{s} = c_{0} + c_{1} Q(p^{s} ,E(\theta ))\), if marginal costs are non-decreasing \(c_{1} \in [0,\overline{c}_{1} ]\) and the weight \(\alpha = 1;\)

  2. (2)

    obeys \(u(p^{u} ,\underline {\theta } ) = \left( {p^{u} - c_{0} - \frac{1}{2}c_{1} Q(p^{u} ,\underline {\theta } )} \right)Q(p^{u} ,\underline {\theta } ) = 0,\) in which \(p^{u}\) is independent with \(\alpha\), if marginal costs are decreasing \(c_{1} \in (P^{\prime } (q),0).\)

The result shows that if marginal costs are decreasing, the optimal \(p^{u}\) is also optimally set to leave the lowest type with zero profits, since \(p^{s}\) violates the IR constraint for all \(\alpha \in [0,1]\), and profits are increasing with the firm’s type. When marginal costs are non-decreasing and \(\alpha = 1\), the optimal price \(p^{s}\), which is based on the intersection of price and marginal costs with expected demand, will satisfy the IR constraint. Then, it is natural to compare the social welfare of the pooling quantity and price mechanism. The proof is in the Appendix.

Corollary 3

When marginal costs are decreasing, \(c_{1} < 0\) , the optimal pooling price mechanism is preferred to the quantity mechanism for all \(\alpha \in [0,1]\) . When marginal costs are non-decreasing and the weight \(\alpha = 1\) , there are two cases: (1) if \(c_{1} \in \left( {0,c_{1}^{q} } \right),\) the optimal pooling price mechanism also dominates; (2) if \(c_{1} \in [c_{1}^{q} ,\overline{c}_{1} ]\) , the price mechanism is preferred only when marginal costs \(c_{1} < - P^{\prime } (q).\)

With decreasing marginal costs, for all weight \(\alpha \in [0,1]\), both the pooling quantity and price are optimally set based on the intersection of \(c_{0} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}c_{1} q\) and the demand of the lowest type \(\underline {\theta }\). When the realized demand is not the lowest type, both the optimal pooling quantity and price mechanisms induce deadweight losses caused by underproduction. Specifically, the first-best quantity of the realized demand would be larger than the realized quantity under the pooling quantity and price regulation. More outputs will be induced in price regulation than the outputs in quantity regulation, since the outputs can adjust with the realized demand in pooing price regulation. Thus, the pooling price mechanism creates fewer losses, as shown in Fig. 4, the top panel, which leads to the preference for pooling price mechanism.

Fig. 4
figure 4

Deadweight losses of pooling quantity and price mechanisms with the weight \(\alpha = 1\). At the top, when decreasing marginal costs are assumed,\(b\) is the deadweight losses of pooling price mechanism, and the sum of \(a\) and \(b\) is the deadweight losses of quantity mechanism. In the middle, the slope of marginal costs is assumed to be slightly positive. When the demand turns out to be \(E(\theta )\), the deadweight losses of quantity and price are \(e + f + g\) and zero respectively. When the demand turns out to be \(\underline {\theta }\), the deadweight losses of quantity and price are \(d + e + f + g\) and \(c\) respectively. When the demand turns out to be \(\overline{\theta }\), the deadweight losses of quantity and price are \(f + g\) and \(f\) respectively. At the bottom, the slope of marginal costs is assumed to be heavily positive. The deadweight losses of quantity and price are \(i\) and \(h\) respectively if the demand \(\underline {\theta }\) is realized, and the deadweight losses of quantity and price are \(j\) and \(k\) respectively if the demand \(\overline{\theta }\) is realized

Full size image

If the slope of marginal costs is slightly positive, \(c_{1} \in [0,c_{1}^{q} ),\) the optimal pooling quantity is still based on the intersection of \(c_{0} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}c_{1} q\) and the demand of the lowest type \(\underline {\theta }\), while the pooling price is optimally chosen when the price equals marginal cost with expected firm’s type; see Fig. 4, the middle panel. When the realized demand is larger than expected demand, now, both the optimal pooling quantity and price mechanisms create deadweight losses caused by overproduction. Similarly, the pooling price mechanism is preferred due to a smaller overproduction. When the demand turns out to be smaller than expected demand, the deadweight losses of pooling quantity mechanism is still induced by overproduction, while the losses of pooling price mechanism are caused by underproduction. By the assumption, the slope of marginal costs is definitely lower than the absolute value of demand slope in this case. Therefore, the optimal pooling price mechanism always dominates because of lower deadweight losses.

If the slope of marginal costs is extremely positive, \(c_{1} \in [c_{1}^{q} ,\overline{c}_{1} ],\) the analysis is similar to the discussion of Basso et al. (2017) with increasing marginal costs. Both the optimal pooling quantity and price are optimally chosen when the price equals marginal cost with expected firm’s type. Now, when the realized demand is lower (resp. higher) than expected demand, the deadweight losses comparison of the quantity mechanism created by overproduction (resp. underproduction) and price mechanism caused by underproduction (resp. overproduction) depends on the slope of marginal costs and demand functions, as shown in the bottom panel of Fig. 4.

Then, it is natural to rank the social welfare of the screening and pooling mechanisms. We can obtain the following corollary.

Corollary 4

Assuming that the transfers are not feasible and costs of firm are non-increasing, the price pooling mechanism is preferred to the screening and pooling quantity mechanisms for all \(\alpha \in [0,1]\) .

5 Conclusion remarks

In practice, direct monetary transfers to the regulated firms are not feasible in some circumstances, since the regulator may have no access to the public funds or inability to tax. Based on the work of Basso et al. (2017) who compare the quantity-based and price-based instruments under asymmetric demand information, this paper examines the optimal design of monopoly regulation under the restriction that monetary transfers are infeasible. Screening mechanisms that provide multiple menus for regulate firm to select and pooling mechanisms that only offer one unique contract are characterized, and the quantity regulation and price regulation performances of regulator’s social welfare are compared.

We find that, with constant marginal costs of the regulated firm, the screening price mechanism would strictly dominate the screening quantity mechanism, since the first-best price is feasible. As compared with Basso et al. (2017), the optimal screening IR-quantity-floor mechanism would never attain the first-best level when the consumers’ welfare and the firm’s utility are equally important to the regulator. With decreasing marginal costs, the optimal screening quantity depends on the floor. The screening price involves bunching. When the realized demand is not the lowest type, the screening price mechanism creates fewer losses caused by underproduction, which leads to the preference for screening price mechanism. With pooling mechanisms, the optimal quantity and price are not always optimally chosen based on the intersection of the price and marginal cost with expected firm’s type, because the firm’s individual rationality constraint may not bind in our paper. We show that the pooling price mechanism is always superior if the slope of marginal costs is negative or slightly positive, otherwise, the ranking of quantity and price instruments would depend on the relative magnitude of the slope of marginal costs and demand functions. Furthermore, we find that the price pooling mechanism is preferred to the screening and pooling quantity mechanisms with firm’s non-increasing marginal costs.

This paper can be extended. In this paper, we normalize the fixed cost is zero. The extension is to study the possibility of shutdown with positive fixed cost, which is kept for further research.