Novel decision-making methods for the sustainable warehouse location selection problem considering the value alteration boundaries and accumulation of alternatives

Abstract

The importance of determining the appropriate location for the construction of the main centers of a company is quite tangible, so much so that the senior managers of an organization are trying to find the appropriate decision-making methods in this regard. In discrete decision-making methods, we see the existence of a decision-making matrix containing information on different options compared to the problem evaluation criteria. In this paper, a new decision-making method is presented in a way that tries to evaluate options more accurately by considering the possibility of changing the criteria's desirability in different ranges. It is not always appropriate to increase\decrease a positive\negative criterion. Even in some situations, crossing a certain limit can reduce the desirability of the desired criterion. Therefore, we will introduce the concept of value alteration boundaries for evaluation criteria in the formation of a decision matrix, which tries to examine the decision problems more realistically. Also, in the examination of alternatives, with simultaneous attention to ideal, anti-ideal and average solutions, evaluation and ranking based on accumulation and skewness of alternatives are presented. The present paper has examined the validation of methods by examining several numerical examples and also evaluating the candidate locations for the construction of a central warehouse in Gohar Zamin Mining and Industrial Company. Also, sensitivity analysis includes checking with other existing multi-criteria decision-making methods, changes in the number of problem options and checking the stability of the method, changes in the weight of the criteria and changes in the value alteration boundaries. Analysis of results shows that the proposed methods are efficient and suitable for dealing with multi-criteria decision-making problems.

Graphical abstract

Introduction

Choosing the appropriate location for establishing facilities is defined as the problem of comparing alternative locations according to a set of objectives including economic, environmental, social, access and other factors through a valid method (Sazvar et al. 2021). Facility location decisions are a strategic issue for a wide range of companies. The high costs of acquiring assets and facility construction turn location problems into long-term investment and planning. Optimal location of facilities affects numerous operational and logistical costs. Alfred Weber was the first to formally study the theory of location in 1909 for a warehouse deployment in order to minimize the total distance between it and customers (Owen and Daskin 1998). One of the most important issues for companies is the timely delivery of goods to customers, so the appropriate choice of warehouse location has a great impact on customer satisfaction and supply chain performance. Warehouses are an important part of the supply chain, so deciding on the location of warehouses is one of the most important issues in logistics problems that create competitive advantages for companies (Ulutaş et al. 2021). Deciding on the location of distribution warehouses is particularly important in the management of large industrial companies. The warehouse location problem (WLP) consists of determining one or more locations as collection, storage and distribution centers for materials or products, to serve a group of customers scattered in an area in order to achieve objectives such as the minimum total cost of transportation and maximum accessibility (You et al. 2019). Choosing the best place to establish a warehouse is a multi-criteria problem that is affected by several quantitative and qualitative criteria (Ehsanifar et al. 2021). Determining the appropriate location of warehouses is important in order to improve the efficiency of physical distribution and maximize other criteria (availability, development possibility, etc.). For this reason, the correct determination of the methods used in choosing the warehouse location is a priority condition (Gergin and Peker 2019).

Proper and timely decision-making is the key to survival in the competitive market. To gain competitive advantages, supply chain managers are always looking for the right kind of decision-making methods to meet their needs (Dey et al. 2017). In the past years, multi-criteria decision-making methods have served as an efficient and appropriate tool in the field of decision-making (Goswami et al. 2021). Multiple-Attribute Decision-Making (MADM) methods are techniques that determine the most suitable option or options by considering the criteria that can influence each other among multiple options (Emeç and Akkaya 2019). There is no single criterion that adequately describes the characteristics of an option, and there is no single solution that optimizes all problem criteria simultaneously. In such problems, the use of multi-criteria analysis methods is very useful, because, they evaluate different options by using mathematical models and considering the objective characteristics and preferences of decision-makers (Zhang 2006). In decision-making with the help of multi-criteria decision-making (MCDM) methods, possible alternatives are evaluated using different quantitative and qualitative criteria related to the problem, and how to achieve the set goal of decision-making by the alternatives is investigated. Due to the existence of a large number of MCDM methods, it is very important to choose a suitable method for the decision problem, which experts choose a method according to the type and complexity of the problem (Stević et al. 2020).

Each decision problem consists of two stages: The first stage is the evaluation of the alternatives, which depends on the opinion of decision-makers to evaluate the alternatives based on quantitative and qualitative criteria and the result is the formation of a decision matrix. The second stage is the basis for ranking alternatives by the decision matrix.

Based on multi-criteria models, assuming there are m possible alternative solutions and n evaluation criteria, the alternative o is considered better than alternative u according to the criterion j only when ${x}_{o}^{j}{>x}_{u}^{j}$. We name ${x}_{i}^{j}$ the nominal value of alternative i relative to the criterion j in the decision matrix. Although methods such as ELECTRE (ELimination Et Choix Traduisant la REalite) and PROMETHEE (Preference Ranking Organization METHod for Enrichment of Evaluations) try to better compare the alternatives according to different criteria by considering different thresholds (for example: indifference threshold, preference threshold and veto threshold), there are still shortcomings in comparing the alternatives according to their nominal value in the decision matrix. However, ${x}_{o}^{j}>{x}_{u}^{j}$ does not always indicate the superiority or indifference of alternative o over alternative u, and in some beneficial criteria, increasing the value of ${x}_{i}^{j}$ from a certain limit may not only not contribute to the superiority of alternative o but also undermine the value of this alternative. So, the value alteration boundaries (VAB) method is presented to examine the main values of the alternatives in detail.

This paper addresses two new issues in decision-making problems: First: examining the boundaries of the value change for some criteria so that a specific range is determined for taking the value of the criteria and crossing the determined limits causes a change in the actual value of the criteria. Second: paying attention to the average, ideal and anti-ideal solutions at the same time and considering the accumulation and skewness of alternatives based on different criteria, which has been named as ERASA (evaluation and ranking based on accumulation and skewness of alternatives) method. The main goal of this paper is to develop a new method of decision-making, which has a new look at the value of alternatives in the decision matrix.

The rest of the paper is organized as follow. Section 2 provides a review of the previous studies of location selection, MCDM methods and also describes the structure and causes of attention to new methods. Section 3 presents a new method for the evaluation and ranking of alternatives according to VAB in forming the decision matrix and accumulation of alternatives based on different criteria (ERASA method). In Sect. 4, several computational analyses have been used to compare the ERASA method with other existing methods and also to examine the effect of value alteration boundaries on the ranking of options. Section 5 examines a real example in selecting a sustainable warehouse location. Also, result of validation and sensitivity analysis is provided in Sect. 6. In Sects. 7 and 8, we present implications and research limitations. In the end, the overall conclusion of the study is presented in Sect. 9.

Literature review

Related works

Deciding on facility location is very important in supply chain (SC) management. Considering the impact of facility location on cost, delivery speed, service level and supply chain effectiveness, overall SC performance is affected by location decisions (Aditi et al. 2020). Mathematical programming and MCDM are common methods in choosing the appropriate facility location. Decision theory is known as a typical soft science as it deals with the judgment of decision-makers quantitatively. In the early stages, decision-making relied heavily on the experience and knowledge of the decision-makers. Obviously, this type of decision-making can lead to somewhat inaccurate results. Over time, mankind is increasingly looking for a suitable and accurate scientific decision theory (Ye et al. 2023). Experts choose a method according to the type and complexity of the problem. Due to the existence of conflicting criteria in choosing the appropriate facility location, MCDM approaches are one of the most practical methods to obtain the maximum satisfaction of the decision-maker in these problems.

Many researchers have investigated the application of MCDM methods in location selection. Wang et al. (2018) used a combination of MCDM methods to find the best place to build a solar power plant based on quantitative and qualitative criteria. Aditi et al. (2020) have evaluated the facility locations in an Indian manufacturing problem using the analytical hierarchy process (AHP) and TOPSIS (Technique of Order Preference by Similarity to the Ideal Solution) in a fuzzy environment, taking into account quality of life criteria. Fuzzy AHP is used to calculate the weight of the criteria and fuzzy TOPSIS method is used to calculate the ranking of alternatives. In the research of Karaşan et al. (2020), an integrated intuitionistic MCDM approach is applied to evaluate selected alternatives to find the most appropriate location for the electric vehicle charge station. Wang et al. (2020) propose a site selection framework for battery swapping station (BSS) to power electric vehicles based on DEMATEL (DEcision-MAking Trial and Evaluation Laboratory) and MOORA (Multi-Objective Optimization by Ratio Analysis) methods. Also, a case study in Beijing has been investigated and analyzed to select the location of BSSs. Aydin and Seker (2021) have investigated and selected the most appropriate location for an isolated hospital for epidemic-based patients using MCDM methods. In their research, five alternative locations in the European part of Istanbul have been investigated based on nine evaluation criteria with the help of Delphi, the Best–Worst Method (BWM) and the TOPSIS method. Şahin (2021) presented a hybrid approach to evaluate and select potential locations for the construction of the automotive manufacturing plant in Turkey, using MCDM methods such as ELECTRE, VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje), PROMETHEE and TOPSIS. Xuan et al. (2022) used WASPAS (Weighted Aggregates Sum Product Assessment), COPRAS (COmplex PRoportional ASsessment) and EDAS (Evaluation based on Distance from Average Solution) methods to rank the candidate sites to determine the location of solar energy for hydrogen production in Uzbekistan. Nenzhelele et al. (2023) propose a method for choosing the most appropriate facility layout plan using the AHP and TOPSIS method. The investigation of the case study of the rail car industry shows that the proposed model can effectively lead to the selection of the best facility layout plan. Using geographic information systems (GIS) and MCDM methods including CRITIC (CRiteria Importance Through Intercriteria Correlation), MABAC (Multi-Attributive Border Approximation area Comparison) and FUCOM (FUll COnsistency Method), Tulun et al. (2023) identified the best available area for establishing a biogas plant in Konya Closed Basin (KCB). Huskanović et al. (2023) developed a CRITIC-MARCOS (Measurement Alternatives and Ranking according to COmpromise Solution) model. Indeed, they used the CRITIC tool to determine values of criteria that were then applied in the MARCOS method for weighting normalized matrix. The mentioned model was used to selection of forklifts in internal transport technology. Also, Andrejić and Pajić (2023) by integrating the Best–Worst Method with the Combined Compromise Solution (CoCoSo) presented a novel decision-support model, employed to refine the recruitment process within the transportation sector. Rane et al. (2023a) presented an efficient MIF-TOPSIS (Multi Influencing Factor-TOPSIS) technique to determine the interrelated weights to solve the problems of optimal location for electric vehicle charging stations. Also, in another study, Rane et al. (2023b) have used the MIF-TOPSIS technique to evaluate the potentiality of sites for dam construction.

The warehouse location selection problem is one of the most important and key decisions in supply chain management. Therefore, various studies have been conducted to determine the best location for warehouse deployment using different MCDM methods. Ashrafzadeh et al. (2012) studied a warehouse location selection problem in an Iranian company using fuzzy TOPSIS. Day et al. (2013) evaluated and selected warehouse location under a utopian environment using a combined fuzzy MCDM model based on the SAW (Simple Additive Weighting) method and factor rating systems. Dey et al. (2016) evaluated and selected warehouse location in supply chain based on TOPSIS, SAW and MOORA methods. Sezer et al. (2016) used the MULTIMOORA method to make a group decision about warehouse location selection for hazardous materials. In research by Kabak and Keskin (2018), using a combined method including a mathematical model, MCDM and GIS, the most suitable place to create a warehouse of explosives and ammunition in the Marmara region of Turkey has been determined, with the aim of minimizing transportation costs and environmental effects. Mihajlović et al. (2019) used AHP and WASPAS methods to logistics distribution fruit center location selection in the Southern and Eastern Serbia region. Using the TOPSIS method, Ocampo et al. (2020) investigated a decision-making problem of warehouse location selection under a group decision-making structure with different priorities of experts and considering 22 different criteria. Ulutaş et al. (2021) propose an integrated gray MCDM model including gray preference selection index and gray proximity indexed value to determine the best warehouse location among 5 alternatives according to 12 criteria for a supermarket. Ak and Derya (2021), using the AHP method to evaluate the weight of the main and secondary criteria and the TOPSIS method to examine the options, have dealt with the warehouse selection problem in the humanitarian supply chain. Demircan and Özcan (2021) have evaluated and selected the best alternative for building a warehouse in cold chain logistics using the fuzzy EDAS method. Nong et al. (2022) presented an integrated MCDM model including ANP (analytic network process) to define the weights of the criteria and TOPSIS to rank the alternatives and investigated the location problem of the distribution center. Their proposed model is applied in Dong Nai province in Vietnam. Saha et al. (2023) have investigated the best warehouse location for an automobile company using Delphi techniques and the MARCOS method based on the Fermatean fuzzy sets. Mittal and Obaid (2023) used the multi-criteria decision-making approach based on the Best–Worst and TOPSIS methods, considering the aspects of sustainability, to decide on the location of aid resource warehouses in the humanitarian supply chain. In addition to the above, MCDM has also been used in warehouse management. As an example, Taletović (2023) in a review paper investigated the application of various multi-criteria decision-making methods in the context of warehouse management, considering papers published from 2010 to date.

According to the conducted studies, it can be seen that MCDM methods have been used to evaluate and choose the location of facilities in different supply chains. However, the investigation and use of MCDM methods for the establishment of facilities in the mining supply chain have not been used much. In contrast, considering the strategic role of mining companies in the economy of countries and the importance of managing the mining supply chains, optimal and appropriate establishment of facilities is necessary to increase efficiency. So, as mentioned before, in the rest of the paper, in order to increase the accuracy of decision-making, it has been tried to present two new MCDM methods. Moreover, as a case study, the issue of appropriate location selection for the construction of a central warehouse in Gohar Zamin Company has also been investigated.

Gaps and contributions

In many MCDM methods, the formation of a decision matrix is necessary as an input to solve the problem. But in some cases, the formation of a decision matrix is simply not possible. Some criteria in MCDM problems have different scores for alternatives at different bounds. For example, the suitable amount of iron in men's bodies is 65 to 175 micg/dl, which means that there is indifference to this particular suffering, while values less than 65 and more than 175 are not suitable. According to this topic, increasing the amount of iron in the body is not good, so this criterion cannot be displayed in appearance and according to its numerical amount in the decision matrix. To clarify the subject, pay attention to Fig. 1, suppose a truck is needed to carry a certain amount of building materials. One of the criteria for evaluating the alternatives available for transporting the desired materials will be the capacity of the truck. According to the expert(s), the nominal capacity of b to c will be suitable, so indifference is created for this range, i.e., trucks with a capacity between b and c have the same score of this criterion. Competition and comparison are created for capacities less than b as well as more than c. So, in the range less than b, more capacity will be more points gained. And for capacities more than c (due to the extra and unnecessary volume of the truck, the need for better machines to load the truck, increase the truck parking space, etc.) the higher the capacity, the lower the score. Boundaries a and d are also known as ‘red boundaries,’ so only alternatives with a capacity between a and d are evaluated, and crossing these boundaries means rejecting the alternative. According to Fig. 1 and based on 'capacity' criteria, the truck II is superior to the truck I. The truck III in the indifference range also has an advantage over trucks I and II, and it has the same score as the truck IV. Trucks V and VI also have lower scores than trucks III and IV due to being in the area beyond the indifference range, while the truck V will have more points than the truck VI because it is closer to indifference range. Multi-criteria models include the definition of a set of n criteria and m alternatives. If we name ${g}_{i}^{j}$ the score of alternative i relative to criterion j, we will have:

$$ga_{IV}^{capacity} = ga_{III}^{capacity} > ga_{II}^{capacity} > ga_{I}^{capacity}$$

(1)

$$ga_{III}^{capacity} = ga_{IV}^{capacity} > ga_{V}^{capacity} > ga_{VI}^{capacity}$$

(2)

Fig. 1

Value alteration boundaries

In some negative criteria, sometimes reducing the value of that criterion too much will not be desirable. For example, some people prefer to always have a certain cost to buy items, and reducing the price of a product from a certain boundary creates an unfavorable situation for the buyer. According to the raised issue, the importance of paying attention to the value alteration boundaries in the formation of the decision matrix and evaluation and ranking of alternatives is quite tangible.

In MCDM compromise methods, the best alternative is evaluated according to the distance from the ideal and anti-ideal solution. VIKOR, TOPSIS and MARCOS methods are among the MCDM compromise methods that obtain the best alternative according to the smallest distance from the ideal solution and the largest distance from the anti-ideal solution. On the other hand, the best alternative in the EDAS method is related to the distance from the average solution (AV), and in this method, there is no need to calculate the ideal and anti-ideal solutions.

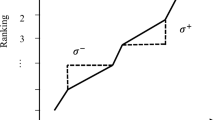
Considering the ideal, anti-ideal and average solutions at the same time, there can be a more accurate and appropriate evaluation of alternatives. Besides, the dispersion of the alternatives will be better evaluated based on each evaluation criterion by considering all three parameters (ideal, anti-ideal and average solutions). If the shape of alternatives score distribution is assumed based on a specific criterion according to one of the situations in Fig. 2, then paying attention only to the ideal and anti-ideal alternatives and not to the accumulation and skewness of the alternatives does not provide a complete evaluation. Therefore, in this paper, it has been tried to present a new method that, in addition to paying attention to the ideal and anti-ideal alternatives, also pays attention to the accumulation and skewness of the alternatives, to be a more complete evaluator in MCDM problems.

Fig. 2

Modes of alternatives score distribution

Methodology

Value Alteration Boundaries (VAB): a new method in forming the decision matrix

According to the explanations provided, the VAB method is performed through the following steps, and finally, the main decision matrix will be prepared as an input to the decision-making methods to evaluate the alternatives:

Step 1 Formation of the decision matrix (DM $={\left[{x}_{i}^{j}\right]}_{m\times n}$). This matrix represents the nominal value of each alternative relative to each quantitative and qualitative criterion.

Step 2 Specifying criteria that are sensitive to value alteration boundaries.

In this step, the criteria that have certain limits of value change are determined, which is determined based on the next step of the score of the alternatives according to the introduced score functions. According to the nature of the criteria in different issues, many criteria may not have value alteration boundaries, and according to the past methods, the points of the alternatives compared to the criteria will always be equal to the nominal value obtained.

Step 3 Determination of the value alteration boundaries (a, b, c and d) for each criterion.

Step 4 Determination of the score functions for the range c to d about beneficial and non-beneficial criteria. The criteria whose higher values are desirable, called beneficial criteria, and those criteria whose smaller values are preferable, named cost criteria or non-beneficial criteria. Due to the depreciation in the range c to d for beneficial criteria, a specific function (linear or nonlinear) is determined by the expert(s) to calculate the value of alternatives for each criterion in the range c to d. The most commonly used functions to calculate ${g}_{i}^{j}$ are expressed according to Eqs. 3 and 4. Figure 3 shows the scoring functions according to the value alteration boundaries. The scoring functions for the non-beneficial criteria are in accordance with Eqs. 5 and 6, as Fig. 4 shows these functions.

Fig. 3

Scoring functions of positive criteria according to value alteration boundaries

Fig. 4

Scoring functions of negative criteria according to value alteration boundaries

$$g_{i}^{j} ~ = \left\{ {\begin{array}{*{20}l} {x_{i}^{j} } \hfill & {~a^{j} \le x_{i}^{j} \le b^{j} } \hfill & {} \hfill & {} \hfill \\ {b^{j} } \hfill & {b^{j} \le x_{i}^{j} \le c^{j} } \hfill & {~\theta ^{j} ~ \ge 0} \hfill & {\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I} \hfill \\ { - \theta ^{j} (x_{i}^{j} - c^{j} ) + b^{j} } \hfill & {c^{j} \le x_{i}^{j} \le d^{j} } \hfill & {} \hfill & {} \hfill \\ \end{array} } \right.$$

(3)

$$g_{i}^{j} ~ = \left\{ {\begin{array}{*{20}l} {x_{i}^{j} } \hfill & {~a^{j} \le x_{i}^{j} \le b^{j} } \hfill & {} \hfill & {} \hfill \\ {b^{j} } \hfill & {b^{j} \le x_{i}^{j} \le c^{j} } \hfill & {~\theta ^{j} ~ \ge 0} \hfill & {\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I} \hfill \\ {\theta ^{j} (e^{{j^{{\left( {x_{i}^{j} - c^{j} } \right)}} }} - 1) + b^{j} } \hfill & {c^{j} \le x_{i}^{j} \le d^{j} } \hfill & {} \hfill & {} \hfill \\ \end{array} } \right.$$

(4)

$$g_{i}^{j} ~ = \left\{ {\begin{array}{*{20}l} {x_{i}^{j} } \hfill & {~a^{j} \le x_{i}^{j} \le b^{j} } \hfill & {} \hfill & {} \hfill \\ {b^{j} } \hfill & {b^{j} \le x_{i}^{j} \le c^{j} } \hfill & {~\theta ^{j} ~ \ge 0} \hfill & {\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I} \hfill \\ {\theta ^{j} \left( {c^{j} - x} \right._{i}^{j} ) + b^{j} } \hfill & {c^{j} \le x_{i}^{j} \le d^{j} } \hfill & {} \hfill & {} \hfill \\ \end{array} } \right.$$

(5)

$$g_{i}^{j} ~ = \left\{ {\begin{array}{*{20}l} {x_{i}^{j} } \hfill & {~a^{j} \le x_{i}^{j} \le b^{j} } \hfill & {} \hfill & {} \hfill \\ {b^{j} } \hfill & {b^{j} \le x_{i}^{j} \le c^{j} } \hfill & {~\theta ^{j} ~ \ge 0} \hfill & {\forall ~j~\epsilon ~J~~\& ~~i~\epsilon ~I} \hfill \\ {\theta ^{j} (\partial ^{{j^{{\left( {c^{j} - x_{i}^{j} } \right)}} }} - 1) + b^{j} } \hfill & {c^{j} \le x_{i}^{j} \le d^{j} } \hfill & {0 < \partial ^{j} < 1~} \hfill & {} \hfill \\ \end{array} } \right.$$

(6)

Step 5 Formation of the main evaluation matrix (MEM $={\left[{g}_{i}^{j}\right]}_{m\times n}$).

Evaluation and ranking based on accumulation and skewness of alternatives (ERASA): a new MCDM method

In this section, we propose a new MCDM method that is called ERASA. This method tries to examine the alternatives in a more detailed and comprehensive manner by examining the ideal, anti-ideal and average solutions at the same time and paying attention to the skewness and accumulation of alternatives based on evaluation criteria. The steps for using the ERASA method are presented as follows:

Step 1 Construction of the decision matrix. It is possible to use the main evaluation matrix (MEM) created using the VAB method as an input to the decision-making methods.

Step 2 Normalization of the decision matrix. The elements of the normalized matrix (NM $={\left[{z}_{i}^{j}\right]}_{m\times n}$) are obtained by applying Eqs. (7) and (8).

$$z_{i}^{j} = ~\frac{{g_{i}^{j} }}{{\mathop {\max }\limits_{i} g_{i}^{j} }}~~~~~~~~~if~j\epsilon ~{\text{beneficial~criteria~~~~~~~~~~~~}}\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I$$

(7)

$$z_{i}^{j} = ~\frac{{\mathop {\min }\limits_{i} g_{i}^{j} }}{{g_{i}^{j} }}~~~~~~~~~if~j\epsilon ~{\text{nonbeneficial~criteria}}~~~~~~~~~~~~~~\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I$$

(8)

Step 3 Formation of the weighted matrix (WM $={\left[{v}_{i}^{j}\right]}_{m\times n}$). The WM is obtained by multiplying the NM with the weight coefficients of the criteria (${w}^{j}$), according to Eq. (9):

$$v_{i}^{j} = z_{i}^{j} \times w^{j} ~~~~~~~~~~~~\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I$$

(9)

Step 4 Determination of the average solution for each criterion (${AV}^{j}$), according to Eq. (10):

$$AV^{j} = ~\frac{{\mathop \sum \nolimits_{I} v_{i}^{j} }}{m}~~~~~~~~~~\forall ~j~\epsilon ~J$$

(10)

Step 5 Calculation of the credibility degree of alternatives for each criterion (CM $={\left[{cd}_{i}^{j}\right]}_{m\times n}$), according to Eq. (11):

$$cd_{i}^{j} = \max ~\left\{ {\left( {v_{i}^{j} - AV^{j} } \right)\& \left( {\left( {v_{i}^{j} - \mathop {\max }\limits_{i} v^{j} } \right) + \left( {v_{i}^{j} - \mathop {\min }\limits_{i} v^{j} } \right)} \right)} \right\}~~~~~~~~~\forall ~j~\epsilon ~J~~\& ~{\text{~}}i~\epsilon ~I$$

(11)

Step 6 Determination of the excellence index (${EI}_{i}$) for each alternative, according to Eq. (12):

$$EI_{i} = ~\mathop \sum \limits_{J} cd_{i}^{j} ~~~~~~~~~~\forall ~i~\epsilon ~I$$

(12)

Step 7 Ranking of alternatives based on excellence index, so that the alternative with the highest EI will have the best rating.

Step 5 is unique compared to other existing methods and works in such a way that while paying attention to the average alternative, it is also sensitive to ideal and anti-ideal values. This makes the alternatives that have a significant superiority in a specific criterion (the options that are closest to the ideal alternative) according to the distance with the anti-ideal (the alternative with the least superiority compared to the desired criterion) get a good value of the degree of credibility. At the same time, considering the accumulation of alternatives for each criterion causes the alternatives that are far from the ideal value to be evaluated compared to the average and suffer less loss. For example, in Fig. 5, the dominant accumulation of alternatives, which causes the average solution tension toward accumulation, is shown. In such cases, Eq. (11) means the options that are even far from the ideal can be reconsidered due to their proximity to the average, and not judged solely based on the distance from the ideal. At the same time, the options that are also close to the ideal can get a good score compared to the distance from the ideal and the anti-ideal.

Fig. 5

Dominant accumulation of alternatives

According to Fig. 2, if the skewness of the distribution is zero so that the distribution of the alternative score (relative to a specific criterion) has symmetry, then if the alternative score is exactly in the center of the distribution (equal to the average), according to Eq. (11) the difference between the alternative score and the average solution, as well as the sum of the differences between the alternative score and the ideal and anti-ideal alternatives, will be equal. Also, the alternatives with a score higher than the average are evaluated based on the distance from the ideal and anti-ideal alternatives, and the alternatives with a score lower than the average are evaluated based on the distance from the average solution.

But if there is a skewness in the distribution of the alternative scores, the relationship 11 will be sensitive to the scoring of the alternatives, and by stretching the average solution toward the skewness of the distribution, it will undergo an accurate evaluation.

Computational analysis

In this section, to evaluate the ERASA method, the numerical example presented in the study of Keshavarz Ghorabaee et al. (2015) is examined. The decision matrix along with the type of each criterion is shown in Table 1. In this section, first, in order to review the proposed method, it is assumed that all the criteria are without value change boundaries (DM = MEM) so that the steps of ranking the alternatives (especially step 5 of the ERASA method) are evaluated. Then, by determining the value change boundaries, the changes in the desirability rating of the alternatives compared to other methods are checked from the decision-maker's point of view.

Table 1 Decision matrix

Evaluation of the ERASA method

In this subsection, according to the presented decision matrix and also considering the weights of the criteria according to Table 2, first the normalized, weighted and the credit matrix according to Table 3, 4 and 5 are presented and finally, by calculating the excellence index of each alternative, the ranking of the alternatives is obtained.

Table 2 Weight of criteria

Table 3 Normalized matrix

Table 4 Weighted matrix

Table 5 Credit matrix

According to the credit matrix of the alternatives and according to Eq. (12), the excellence index of the alternatives and the final ranking is according to Table 6.

Table 6 Final ranking of the alternative

Comparison with other MCDM methods

At the beginning of the validation of the proposed method, it is necessary to compare the ERASA method with other MCDM methods using a general example and evaluate the results. SAW, MARCOS, COPRAS, VIKOR, TOPSIS, EDAS, SECA (simultaneous evaluation of criteria and alternatives), WASPAS and PIV (proximity indexed value) methods have been used for this comparison. The ranking results of the ERASA method and other methods are presented in Table 7.

Table 7 Comparison of the ERASA method with other methods

Spearman's rank correlation index (r_s) is used to compare the results obtained from two different methods and calculate the degree of closeness between their results. Equation 13 shows how to calculate this index.

$${r}_{s}=1-\frac{6{\sum }_{i}{d}_{i}^{2}}{m({m}^{2}-1)}$$

(13)

In Eq. 13, m represents the number of alternatives and d represents the difference in ranks of the ith alternative in two different methods. The Spearman coefficient can take a value between + 1 to -1 where r_s =  + 1 means a perfect association of rank. According to the Spearman's rank correlation index, it can be seen that there is a strong correlation between the proposed method (ERASA) and other methods so that except for TOPSIS and VIKOR methods, this correlation is perfect (r_s =  + 1). Based on this, it can be concluded that the results of the ERASA method are valid and this method can be used as an efficient and suitable method for solving MCDM problems.

Pairwise comparison of the superiority of alternatives in different methods

In this comparison method, after ranking all alternatives simultaneously (the initial state), again in order to validate this ranking, we compare them two by two with each other in such a way that it is assumed that only two alternatives are available (the two-option state). Based on this comparison pattern and considering the different ranking of ERASA and TOPSIS methods in Sect. 4.2, these two methods have been compared.

Tables 8 and 9 present a two-by-two analysis of the alternatives in the TOPSIS and ERASA methods, respectively. The values of 1 in the table indicate the similarity of prioritization in the initial state and the two-option state, and the values of 0 indicate a shift in priorities. For example, in the TOPSIS method, after prioritizing the alternatives according to Table 7 (the initial state), alternative A1 is superior to alternative A2. However, if other alternatives are removed and we have only two alternatives A1 and A2 in the decision matrix (the two-option state), as shown in Table 8, solving the new matrix with the TOPSIS method shows the superiority of option A2 over option A1 (A2 > A1). Hence, by comparing Table 8 and 9 with Table 7, it is quite evident that the ERASA method has worked exactly according to the initial prioritization of the alternatives in the two-by-two comparison, and this shows the accuracy and stability of the ERASA method.

Table 8 Pairwise comparison of the superiority of alternatives in TOPSIS

Table 9 Pairwise comparison of the superiority of alternatives in ERASA

Validation of the ERASA method considering VAB

In this section, it is assumed that criteria C2 and C6 have value alteration boundaries, so it is assumed that the desired boundaries and scoring functions (for range c to d) are as shown in Fig. 6. For the positive criterion C2, the value alteration boundaries are equal to: a = 180, b = 245, c = 265 and d = 340, also, these values are in the case of the negative criterion C6 as a = 17,000, b = 11,000, c = 9000 and d = 3000. According to this issue, the main evaluation matrix (MEM) is according to Table 10. The weights of the criteria are considered according to Table 2. The normalized, weighted and credit matrices are shown in Table 11, 12 and 13, respectively. Also, the EI index and the final ranking of alternatives are presented in Table 14.

Fig. 6

Scoring functions (for range c to d)

Table 10 Main evaluation matrix (MEM)

Table 11 Normalized matrix

Table 12 Weighted matrix

Table 13 Credit matrix

Table 14 Final ranking of the alternative

It is evident that considering the value alteration boundaries, the final ranking of the alternatives has changed compared to the initial review (Table 6) and the ranking of alternatives 1 and 2 has shifted, this topic clearly refers to the effect of the value alteration boundaries and attention to the desirability of criteria in different intervals. So despite the nominal superiority of alternative 1 compared to alternative 2, according to the changes in the values of the criteria in different ranges from the decision-maker's point of view, alternative 2 creates more desirability than alternative 1.

Effect of change in the number of alternatives on ranking

Achieving robust ranking results is an important factor in choosing a method for multi-criteria decision-making. Meanwhile, the rank reversal phenomenon endangers the validity of the chosen method (Yang et al. 2022). In some decision-making issues, the decision-making matrix may change according to various factors, for example, removing or introducing a new alternative can affect the ranking of the alternative (Pamucar et al. 2022). For this purpose, to check the dynamics of the presented method, the alternative with the lowest rank is removed and the new decision-making matrix is checked again. This process continues until reaching two alternatives in the decision matrix. In the first scenario, despite the initial 10 alternatives (according to Table 10), the ranking is A2 > A1 > A7 > A8 > A9 > A3 > A5 > A6 > A10 > A4, where A4 has the lowest rank. Therefore, in the second scenario, it is removed from the list of alternatives and a new ranking is presented according to the new matrix. Table 15 examines different scenarios, the results of which show that the ERASA method does not change the ranking among the alternatives, and option A2 has the highest ranking in all scenarios.

Table 15 Rank alternatives according to the dynamic decision matrix

In another analysis, it is assumed that a new alternative is added to the decision matrix, so the new ranking of the alternatives is evaluated according to the new conditions of the problem. Alternative 11 with conditions according to Table 16 has been added to the previous 10 alternatives of the problem. The final ranking of alternatives is A2 > A1 > A7 > A8 > A9 > A11 > A3 > A5 > A6 > A10 > A4. This order of priority shows that no change has been made in the comparison of the previous 10 options so that by removing alternative 11 from the ranking shown, the initial order of alternatives will be visible.

Table 16 Specification of alternative 11

According to the analysis of the possible changes in the main evaluation matrix (MEM), the accuracy of the ranking of the alternatives in a dynamic environment is confirmed by the ERASA method.

Case study: sustainable warehouse location selection

Description of problem

Locating different departments is one of the most fundamental steps in establishing or expanding factories and organizations. Due to different circumstances, many companies may need to expand the area, increase production capacity and review the traditional structure of the past after a few years, so they need to change the spatial structure or create new places. In this section, a model based on the new VAB-ERASA method is used to evaluate the existing places for establishing a central warehouse in Gohar Zamin Mining and Industrial Company. This study presents an empirical illustration of how the VAB-ERASA method is used in the appropriate location selection problem. Gohar Zamin iron ore mine is located at a distance of 50 km from Sirjan city in Kerman province, Iran. Due to the dispersion of different warehouses in this company, the strategy of building a central warehouse for the integration of warehousing processes is on the agenda. In any reputable industrial organization, group decision-making is appropriate to achieve the best possible solution. Experts play a central role in choosing decision variables such as alternatives and evaluation criteria (Dey et al. 2017). Four experts among the personnel of Gohar Zamin Mining and Industrial Company (the first expert: an expert in strategic studies, the second expert: a strategic evaluation expert, the third expert: a head of strategic planning and the fourth expert: expert in statistics and warehouses) evaluate the alternatives and criteria in this study. The phases of the problem-solving method are shown in Fig. 7. After forming a specialized evaluation group, first the candidate places for establishing the warehouse have been identified. Then the various and necessary criteria for evaluating the alternatives are listed. Finally, the main work of the evaluation group begins with determining the weight of the criteria according to the company's macro strategies and the importance of different dimensions, determining the value alteration boundaries and evaluating alternatives based on set criteria. Table 17 shows the evaluation criteria. According to the evaluation group, nine alternatives and seven criteria were identified. Figure 8 also shows the location of the candidate sites in the company area.

Fig. 7

Problem-solving process

Table 17 Introducing the evaluation criteria

Fig. 8

Location of the candidate sites in the company area for the construction of the warehouse

Determination of criteria weights

In decision-making problems, determining the relative importance between criteria (criteria weight) is a key and important issue. To evaluate the weights of the criteria, several methods have been introduced in the last few decades. The BWM calculates the weights of problem criteria using relatively fewer comparisons than other methods such as AHP and ANP (Paramanik 2022). Regarding the main reasons to employ the BWM, this method has several advantages such as (i) this approach has a structured pairwise comparison, (ii) this method significantly reduces the computational burden (the AHP method needs $\frac{n(n-1)}{2}$ pairwise comparisons for n criteria, but the BWM needs $2n-3$), (iii) this work significantly enhances the reliability of outputs and (iv) this approach can easily combine with other methods, which has attracted the attention of the researchers in recent years. In this paper, BWM has been used to determine the importance and weight of the criteria. The BWM was introduced by Rezaei (2015). The following is how to calculate and determine the weight of the criteria using BWM.

Step 1 Determination of a set of decision criteria (C₁, C₂, …, C_n) by decision-maker(s).

Step 2 Determination of the best (C_B) and the worst (C_W) criteria.

Step 3 Calculation of the pairwise comparison between the best and the other criteria (BO) based on a score between 1 and 9 (a score of 1 means equal preference and a score of 9 means extreme preference). In this step, the BO vector is finally obtained, so that a_Bj indicates the preference of the best criterion over criterion j, and it is absolutely certain that a_BB = 1.

$$A_{B} = \, \left( {a_{B1} , \, a_{B2} ,..., \, a_{Bn} } \right)$$

(14)

Step 4 Calculation of the pairwise comparison between the worst and the other criteria (OW) based on a score between 1 and 9 (a score of 1 means equal preference and a score of 9 means the extreme preference). In this step, the OW vector is finally obtained, so that a_jW indicates the preference of the criterion j over the worst criterion, and it is absolutely certain that a_WW = 1.

$$A_{W} = \, \left( {a_{1W} , \, a_{2W} ,..., \, a_{nW} } \right)^{T}$$

(15)

Step 5 Calculation of the optimal weights w^* = (${w}_{1}^{*}$, ${w}_{2}^{*}$, …, ${w}_{n}^{*}$). Model (M1) is used to calculate the optimal weights of criteria.

$$\begin{gathered} Min{\text{~}}Maxj{\text{~}}\left\{ {\left| {\frac{{w_{B} }}{{w_{j} }} - a_{{Bj}} } \right|,\left| {\frac{{w_{j} }}{{w_{W} }} - a_{{jW}} } \right|} \right\} \hfill \\ s.t. \hfill \\ \mathop \sum \limits_{{{\text{j = 1}}}}^{{\text{n}}} w_{j} {\text{ = 1}} \hfill \\ w_{j} \ge 0~~~~~\forall j \hfill \\ \end{gathered}$$

(M1)

Model (M1) is equivalent to the following linear programming problem (Rezaei 2016):

$$\begin{gathered} Min\;\xi \hfill \\ s.t. \hfill \\ \left| {w_{B} - a_{{Bj}} w_{j} } \right| \le \xi \hfill \\ \left| {w_{j} - a_{{jW}} w_{W} } \right| \le \xi \hfill \\ \mathop \sum \limits_{{{\text{j = 1}}}}^{{\text{n}}} w_{j} {\text{ = 1}} \hfill \\ w_{j} \ge 0~~~~~\forall j \hfill \\ \end{gathered}$$

(M2)

To determine the weight of the criteria of the location problem, after determining the criteria with the opinion of all the experts, each of the experts independently determines the best and worst criteria, and according to steps 3 and 4, vectors A_B and A_W are determined, and in the next step, according to model (M2), the optimal weight of the criteria is determined by each expert. The average weight of each criterion determines the final weight of the criterion in our problem.

According to the weights obtained from the evaluation of each expert and according to the importance of the opinion of different experts (in this paper, the weight of the opinion of experts is considered equal), the final weight of the criteria is obtained. According to the BWM and the results of Table 18, the final weight of the criteria is shown in Table 19.

Table 18 Determination of Best-to-Others and Others-to-Worst vector

Table 19 Weight of criteria

Ranking alternatives using VAB-ERASA method

After determining the weight values of the criteria, the new VAB-ERASA method is used for alternative ranking according to the introduced criteria and alternatives. Decision-makers used five evaluation scales for quality criteria: 1 = very poor; 3 = poor; 5 = medium; 7 = good; 9 = very good.

First, the estimates of the decision-makers are aggregated and an initial decision matrix is obtained according to Table 20. According to experts, criteria 2 (ease of access) and 3 (size of the area) have value change boundaries. According to Table 21, each of the experts individually determines the boundaries of the value change, and the average obtained from the opinions of the experts indicates the final boundaries of the problem for criteria 2 and 3. According to the opinion of all experts, the score change coefficient (${\theta }^{j}$) for criteria 2 and 3 in the range c to d is equal to -0.667 and -0.5, respectively. As shown in Fig. 8, the score functions are determined for the range c to d. Then, the main decision matrix is ​​calculated, as shown in Table 22. The normalized, weighted and credit matrices are shown in Tables 23, 24 and 25, respectively. Also, the EI index and the final ranking of alternatives are presented in Table 26. The cost of construction has been checked according to the basic facilities and the smoothness of the land, also considering that all the lands are at the disposal of the company, so the land price has been determined in a relative manner according to the value of its location.

Table 20 Decision matrix

Table 21 Determination of value alteration boundaries for criteria C2 and C3

Table 22 Main evaluation matrix (MEM)

Table 23 Normalized matrix

Table 24 Weighted matrix

Table 25 Credit matrix

Table 26 Final ranking of the alternative

According to the opinion of the experts regarding criterion 2 regarding the examination of warehouse location options, more access than 7.5 creates less utility because due to the constant transportation of machinery in warehouses, high access and proximity to the main buildings of the company cause discipline and relaxation in the working space of the personnel is destroyed, also the use of lands with high access for the construction of warehouses causes the destruction of suitable spaces for the construction of strategic and important centers of the organization, so the maximum useful access for the construction of warehouses by providing a maximum of 6 to 7.5 is considered. Also, regarding criterion 3 (size of the area), it should be mentioned that according to the predicted space required for the construction of the warehouse and also the future expansion of the warehouse, spaces greater than 9000 m² reduce the usefulness of the criterion, because they reduce the maximum efficiency of the land and take away the possibility of building other centers with more required space. Figure 9 shows the score functions of criteria 2 and 3.

Fig. 9

Score functions

According to the experts' reviews and the results obtained from solving the model, the prioritization of the warehouse construction has been determined, according to which the warehouse construction proposal has been presented in alternative 5.

Results of validation and sensitivity analysis

One of the ways to test the robustness of the obtained results is to perform sensitivity analysis. The sensitivity analysis provides a subjective insight to the decision-maker about the results of the possible scenarios and how the potential changes in the input data affect the proposed solutions (Więckowski et al. 2023). In this section, several different analyzes have been used to investigate the effects of changes in the parameters of the problem on the results.

Analysis of criteria weights

To investigate the effect of changes in the weight of the criteria on the ranking of the options, the most important criterion (the criterion with the highest initial weight) is determined for sensitivity analysis requirements (Stević et al. 2020). Based on the paper by Kahraman (2002), Eqs. 16 and 17 show the proportionality of weights during sensitivity analysis.

$${w}_{j}=\left(1-{w}_{s}\right)\times \left(\frac{{w}_{j}^{0}}{\sum_{j\epsilon J-s}{w}_{j}^{0}}\right)={w}_{j}^{0}-\Delta x{\alpha }_{j}$$

(16)

$${w}_{s}={w}_{s}^{0}-\Delta x{\alpha }_{s}$$

(17)

So that, ${w}_{j}$ indicates the weight of criteria during sensitivity analysis, ${w}_{j}^{0}$ and ${w}_{s}^{0}$ indicate the original value of weights and ${w}_{s}$ indicates the weight of the most important criterion during sensitivity analysis. The parameter α is defined as the weight coefficient of elasticity. The weight coefficient of elasticity expresses the relative trade-off of hierarchy weights in relation to given changes in the weight of the most significant criterion (according to Eq. 18). The value of α_s (weight coefficient of elasticity for the most significant criterion) is defined to be one. The parameter ∆x represents the amount of change implemented to the set of weights according to their associated weight coefficient of elasticity. The parameter ∆x can be positive, which indicates an increase in the criterion weight, or negative, which indicates a decrease in the criterion weight. The bound for variable ∆x can be calculated using Eq. 19. After calculating the boundaries, by dividing the limited area by the desired number of steps, the step size is calculated to determine the new weights of the criteria.

$${\alpha }_{j}={w}_{j}^{0}/\sum_{j\epsilon J-s}{w}_{j}^{0}$$

(18)

$${-w}_{s}^{0}\le \Delta x\le min\frac{{w}_{j}^{0}}{{\alpha }_{j}}$$

(19)

After calculating $\Delta x$ and ${\alpha }_{j}$, the new weight of different criteria is calculated according to relations 16 and 17. It should be noted that the sum of the weighting coefficients of the criteria will be equal to one.

According to the initial weight of the criteria of the problem, criterion 4 (w₄ = 0.178) is considered the most important criterion, so in the first step $\Delta x$ and ${\alpha }_{4}$ are calculated and then the value of ${\alpha }_{j}$ is obtained for other weights (according to Table 27). Therefore, according to Eq. 19, the limit values of the C4 criterion, which are -0.256 ≤ $\Delta x$  ≤ 0.744, are obtained. Considering the existence of seven criteria for the problem, seven different scenarios are examined to check the changes in the weight of the criteria. Table 28 shows the weight of different criteria in the examined scenarios.

Table 27 Coefficient of elasticity for changing weights

Table 28 New weights of criteria according to different scenarios

According to the results calculated from the ranking of the alternatives according to the weight change of the criteria (Fig. 10), it is clear that the model is sensitive to weight changes.

Fig. 10

Rank of alternatives according to different scenarios

Based on this, it can be seen that in scenarios 1, 2 and 3, alternative 5 has the first rank, and gradually due to the increase in the weight of criterion 5 as the most important criterion of the problem, the rank of alternative 5 decreases to the 5th position, and the 9th alternative drops from the 9th position to it rises to the first rank at once. On the other hand, the ranking of A5 > A3 > A6 can be seen in all scenarios, which shows the absolute superiority of alternative 5 over alternatives 3 and 6. Meanwhile, in the last scenarios and due to the increase in the weight of the 4th criterion, alternatives 7, 8 and 1 gradually find a better position than alternative 5.

These changes clearly show the weighting sensitivity of the criteria. And it is quite evident that the correct selection of the weight of the criteria has a significant impact on the ranking of the alternatives.

Analysis of the score change coefficient

In this section, the effect of changes in the score change coefficient (${\theta }^{j}$) is examined. For this purpose, the ${\theta }^{j}$ for criteria 2 and 3 has been changed in the range of 0 to -2 and the ranking of the alternatives is presented in Figs. 11 and 12.

Fig. 11

Effect of changes in the score change coefficient (${\theta }^{2}$) on the ranking of options

Fig. 12

Effect of changes in the score change coefficient (${\theta }^{3}$) on the ranking of options

According to the obtained results, it is clear that with the decrease of ${\theta }^{2}$ and as the main value of alternative 3 decreases compared to criterion 2, the rank of this alternative will decrease and alternative 5 will replace alternative 3 in position 1. By reducing ${\theta }^{2}$, the main values of the alternatives in the range c to d (in the decision matrix) will decrease more, which will cause a change in the final ranking of the alternatives. Also, in the examination of criterion 3, a large change in the ranking of alternative 4 is quite evident, so that in ${\theta }^{3}$ = 0, this alternative has the first priority, and as the value of ${\theta }^{3}$ decreases, the ranking of alternative 4 changes to the 9th (last) position.

The sensitivity of the value of ${\theta }^{j}$ according to the analysis shows the importance of determining this parameter by experts.

Analysis of value alteration boundaries

To investigate the shift in the value alteration boundaries and the impact on the ranking of alternatives, ten scenarios have been examined according to Table 29. According to these scenarios, both criteria C2 (${\theta }^{2}=-0.667$) and C3 (${\theta }^{3}=-0.5$) have changed at the same time, and the ranking according to each scenario is shown in Fig. 20. In scenario 8, due to the interference between boundaries b and c, both borders are considered equal to 8100.

Table 29 Scenarios for examining displacement at the value alteration boundaries

According to the shift in the value alteration boundaries, in scenario 1, alternative 9 is not included in the range of a to d according to the red boundaries (a and d) determined for criterion 2, so it is removed from the ranking. Also, this issue occurs in scenario 2 for alternative 2, so that according to the red boundary of 5520 as the minimum acceptable amount in the case of criterion 3, the second alternative is also removed from the ranking along with alternative 9. In the third and fourth scenarios, alternatives 2, 3 and 4 are removed from the ranking according to the changes in the red boundaries. Also, in scenarios 4 and 10, alternatives 7 and 8 have jointly won the first place and other options have been placed in the third and next positions. According to Fig. 13 and the ranking of alternatives, according to different scenarios, the importance and sensitivity of determining the value alteration boundaries are quite evident, so that the smallest adjustments can be effective in the final ranking of alternatives.

Fig. 13

Rank of alternatives according to the change in value alteration boundaries

Implications

Theoretical implications

The concept of value alteration boundaries (VAB), which is examined in this paper, can be widely seen in various issues. It was discussed in detail about the positive criteria of access and land area, that their excessive increase will decrease the decision-maker's satisfaction in the case study of Gohar Zamin Company. This is also true about negative criteria. For example, in choosing many personal items, the decision-maker is sensitive to the minimum price, and by reducing the price from a certain limit regardless of other criteria, she/he feels less desire and satisfaction. For this reason, some people reject the considered option altogether when buying equipment by reducing the price from the specified limit. According to the discussions, the need to pay attention to these boundaries is quite noticeable, and it is recommended to pay attention to the value alteration boundaries in order to improve the evaluation of options. Although methods such as ELECTRE try to increase the accuracy of decision evaluations by considering different thresholds, they have never investigated the increase/decrease in the value of a positive/negative criterion about an option that may worsen the satisfaction of the option. To determine the score functions for the range of c to d in the value alteration boundaries, two linear and nonlinear functions for positive and negative criteria have been presented, and these functions can be changed according to the opinion of the decision-maker. In the sensitivity analysis, it is also quite evident that the change in the scoring functions for the range c to d can be effective in ranking the alternatives.

On the other hand, the ERASA method takes into account the ideal and anti-ideal options, as well as considering the accumulation of options, and has a broader perspective on examining alternatives than other methods. For example, TOPSIS and MARCOS methods only consider the ideal and anti-ideal options, or the EDAS method focuses on the average solution, while ERASA covers both issues at the same time. This issue can prevent the imposition of a large loss on far-from-ideal alternatives because these options are compared to the average solution. At the same time, it makes the options close to the ideal get a significant score due to the large distance to the anti-ideal alternative.

All the sensitivity analyses carried out for the validation of the ERASA method show the accuracy and appropriateness of the method in the evaluation and ranking of alternatives.

Managerial implications

As aforementioned, this study has focused on the warehouse location selection problem by considering the sustainability dimensions. In this regard, a list of criteria for evaluating the potential locations based on the sustainability indicators has been presented and then the locations are ranked. Besides the theoretical contributions of this work, it has several managerial insights that have been presented below. The present article can give a comprehensive view to practical managers regarding the importance of the warehouse location selection problem and the application of the decision-making methods in this field. Also, since the current work presented the sustainability indicators for evaluating the potential location for establishing the warehouse and also determining the most important ones, it can help managers to become familiar with the concept of sustainability and its role in the warehouse location problem. Finally, this work can help managers to understand that only focusing on the financial indicators is not acceptable in today’s competitive and modern marketplace, and they should consider a crucial principle namely sustainability to improve the efficiency of their companies.

Research limitations

Similar to other academic works, the current article has some limitations that have been presented in this section. For example, this work did not consider one of the critical challenges in the business environment named uncertainty. Also, this work did not consider some crucial features such as agility and resilience in the research problem. Additionally, another limitation of this work is the pure focus on the MCDM methods and not using data mining approaches to handle the considerable volume of data.

Conclusions

The main and primary goal of any organization in creating and using warehouses is to store different amounts of items and goods for a short or long time, so that the quality and main and basic characteristics of each type of goods are maintained, and then, they optimally provided to the consumers. Therefore, in this paper, it was shown how an organization can choose an appropriate and sustainable location to build a warehouse using MCDM methods.

This paper first deals with the concept of the value alteration boundaries to determine the decision matrix for the evaluation of alternatives, and according to the type of evaluation criteria, it presents the VAB method. By examining the nature of the criteria according to the type of problem, instead of using the nominal value of the alternatives score in relation to different criteria, this method uses the desirability and real value of the alternatives concerning each criterion in the decision matrix.

After forming the main decision matrix, the new ERASA method is presented to rank the alternatives. This method will have a more comprehensive and accurate evaluation according to the shape of the score distribution of alternatives based on each criterion and considering the accumulation and skewness in the distribution. The credibility degree of alternatives in the ERASA method is calculated based on ideal, anti-ideal and average solutions. This is while other MCDM methods evaluate alternatives based on the average solution or ideal and anti-ideal solutions, and there has been no simultaneous attention to all three parameters in any of the previous MCDM methods.

In addition, a real study based on the assumptions of Gohar Zamin Mining and Industrial Company has been developed to address the problem of choosing a sustainable warehouse location based on the ERASA method. Nine alternatives were examined according to seven criteria, taking into account the aspects of sustainability. Based on the evaluation of experts and using the BWM method, the criteria of price, land size and accessibility were the most important. Also, the score of the alternatives was measured according to the VAB method for the criteria of land size and accessibility.

The ERASA method was evaluated using different tools. First, compared to other MCDM methods, the ERASA method provided the same ranking of alternatives, and only the TOPSIS and VIKOR methods have slight deviations in the ranking of alternatives compared to other methods. In the second analysis, two-by-two alternatives have been compared with each other in such a way that it is assumed that only two alternatives are available, then by using TOPSIS and ERASA methods, the prioritization between the two alternatives has been checked and compared with the initial ranking of the two methods. Analysis of results shows that the ERASA method has worked exactly according to the initial prioritization of options in a two-by-two comparison, and this shows the accuracy and stability of the ERASA method, while the TOPSIS method shows discrepancies in some comparisons. Third, the effect of dynamic matrices on the inversion of the rank based on decreasing and increasing the number of alternatives was investigated. The results show that the ERASA method does not change the ranking among the alternatives, and option A2 has the highest ranking in all scenarios. Also, analyses of changes in the weight of criteria, changes in the score function of options based on criteria C2 and C3 and analyses of shifts in the value alteration boundaries have been investigated. According to different sensitivity analyses, the stable performance of the ERASA method has been shown in solving the MCDM problem. Therefore, this method can be used in the evaluation of various decision-making problems.

Decision-makers can use VAB and ERASA methods in several ways to rank alternatives:

• (1) Using the VAB method and converting the primary decision matrix to the main evaluation matrix and then using any of the MCDM methods as desired.

• (2) Using the primary decision matrix with the simultaneous examination of ideal, anti-ideal and average solutions (ERASA method).

• (3) Moreover, according to the investigations carried out in this paper, the simultaneous use of both parts (VAB-ERASA method) to make a more accurate decision is also suggested.

In the end, for future research, it can be suggested to use the concept of uncertainty in determining the value alteration boundaries and scoring the alternatives in the decision matrix. Also, future papers can consider other aspects, such as agility and resilience in the research problem. Also, to determine the location of warehouses and evaluating options for establishing new facilities, the MIF-TOPSIS method can be employed.