1 Introduction

To increase the collecting area, angular resolution as well as upgrade the optical performance, the next-generation optical systems are developing toward giant aperture, large off-axis, high lightweighting and superior specification in terms of mosaic primary mirror telescopes, such as the Giant Magellan Telescope (GMT) [1], James Webb Space Telescope (JWST) [2], European Extremely Large telescope (E-ELT) [3] as well as Thirty Meter Telescope (TMT) [4] project. The edge error control is widely regarded as one of the most challenging issues for manufacturing segmented mirrors in recent years, due to the unpredictable behaviors of polishing pad. Normally, the edge effect is explained as the result of excessive pressure applied by the tool when it extends beyond the workpiece; accordingly, the contact area decreases, which in turn accompanies the unpredictable non-linear pressure distribution and time-variant TIF [5]. To obtain satisfying profile at the edge, many edge-control attempts were carried out and several predictable model methods also have been demonstrated in recent researches with respect to the mechanical equilibrium model, empirical parameters optimized model or finite element analysis (FEA) model. A theoretical pressure model based on the force and momentum equations was firstly suggested by Wagner and Shannon [6], but a negative pressure distribution occurred in his pressure model. To avoid this negative pressure, Luna-Aguilar et al. proposed a skin model with non-linear pressure distribution by subdividing the contact region into two zones of continuously growing pressure region and constant pressure region [7]. But this skin model was only restricted to the square tool and square workpiece. Subsequently, Cordero-Dávila et al. modified the method to be applicable for a circular tool and circular workpiece [8]. The above predicted edge TIF is described through the pressure distribution models. However, there are few reports about the model’s validity in terms of experimental evidence. In the practice polishing process, the material removal rate (MRR) is a little complicated and is also relative to the abrasive concentration, grain size, tool stiffness, polishing pad characters, ITF stability, and so on. The hypothetical pressure distribution approach tends to ignore their contribution. Empirical parameters optimized model presented by Kim et al. accurately predicted the edge removal profile by fitting five edge parameters connected to the empirical data [9]. Subsequently, Liu et al. adopted edge parameters optimized method and pressure distribution model to verify the consistency of the edge ITF of computer-controlled active lap (CCAL) based on FEA by introducing the abrasive and slurry as the suitable soft layer during the polishing process [10]. Nevertheless, the edge-optimized parameters vary greatly with the overhang ratio of tool, so it is unrealistic without the empirical edge measured profile. Meanwhile, it is difficult to apply in the non-circular mirror, such as the hexagonal segment mirror in the E-ELT project or TMT project. as the ring TIF is only feasible in the rotated symmetrical polishing process. Li et al. developed the edge-controlled technology by utilizing the variable size influence functions through tool-lift method that practically reduces the edge effect to a large extent in the bonnet polishing (BP) for the hexagonal segment mirror [11, 12]. However, the tool-lift method would generate the time-variant TIF in the edge region, and a cost-effective process must combine TIF compensation theory and mathematical linear matrix algorithm for solving the accurate dwell time, which is time-consuming and unacceptable for large aperture mirror.

All the aforementioned methods cannot conquer the edge error completely. The precise and effective edge-suppressing method is of importance to ensure the final performance of the optical system. The non-contacted polishing (NCP) methods, for example, fluid jet polishing (FJP) [13], magnetorheological jet polishing (MJP) [14] as well as ion beam figure (IBF) [15, 16] take the advantages in the edge effect, as there are no problems of tool mismatch or wearing down. So, the TIF will not be affected by the tool-overhang ratio. Guo et al. proved that the removal function at the edge appears similar to that inside of the workpiece and the edge effect can be neglected for FJP [13]. However, the MRR of the NCP is too low. Normally, the FJP and MJP techniques are suitable for correcting the localized error of the millimeter scale mirror and the IBF technique is seen as the final phase for the high-end optical surface.

MRF, with its superb ability to control material removal, is known as an ideal method and well-established technology to fabricate state-of-the-art optical surfaces [17], whose removal mechanism mainly depends on the shear and rheological behavior of magnetorheological fluids, rather than the mechanical effect by the normal force. The fluid-based polishing pad of MRF possesses the characteristics of high removal efficiency, strong controllability, good conformability and superb polished surface quality, which endows MRF lots of advantages for application in nanometer scale, super-smoothing, and damage free process. However, there also exists the edge effect that mainly results from the fluid distortion resisted by the part edge during the process. Hu et al. researched the edge effect in MRF by adopting smaller TIF and edge TIF compensation method [18]. Nevertheless, there are still a few problems in his method. (1) Small TIF can reduce the edge error to some extent; however, the polishing time in turn increases accordingly. (2) Edge TIF compensation method, which is similar to the tool-lift method in the BP, is the time-variant TIF polishing process. It is difficult to resolve the accurate dwell time for the large aperture mirror with respect to the linear equation algorithm.

In this paper, the authors put forward a novel method to reduce the edge effect in the MRF process through further analyzing the stability of the edge TIF and correcting the post-edge algorithm of dwell time. To demonstrate the feasibility and advantages of this edge-controlled theory, two mirror substrates are taken as the experiment samples. The Φ 200 mm, R-200 mm concave sphere mirror (fused silica) is removed about 3 μm uniformly and the experiment results indicate that the edge error region can be effectively suppressed below 1.5 mm. Another Φ 610 mm, R-2100, K-1 lightweighting parabolic mirror (ULE) is verified about the actual practicability. The shape accuracy reaches RMS 6.5 nm from the original RMS 182 nm after two run iteration process, while the edge effect is well controlled to a large extent.

2 The analysis of influencing factor on the edge effect

2.1 The influence of the non-linear edge pressure distribution on the edge effect

The influence of the edge pressure distribution on the edge effect is absolutely critical and can be demonstrated by the material removal theory by Preston presented in 1927 [19]. According to Preston Eq. (1), the material removal rate (MRR) is proportional to the impacting coefficient, instantaneous pressure, and relative velocity. So, the exerting pressure at the edge of the part is non-linear increasing and the MRR is time variant with the overhang ratio, which usually leads to the roll-down edge problem, especially for the large polishing pad and high pressure processing technologies, such as computer-controlled polishing (CCP), stressed lap polishing (SLP) or bonnet polishing (BP).

$$ \Delta \mathbf{h}\left( \varvec{x,y} \right) = \varvec{K} * \varvec{P}\left( \varvec {x,y} \right)*{\varvec {V}}\left( \varvec{x,y} \right), $$
(1)

where ∆h(x, y) is the removal rate in unit time at point (x, y); K is the Preston coefficient, related to the part material, polishing tool, polishing liquid and temperature of working area; V(x, y) is the instantaneous relative velocity of polish tool at point (x, y); P(x, y) is the instantaneous pressure of polish tool at point (x, y).

2.2 The influence of edge dwell time distribution on the edge error

The error position in the workpiece can be scanned bidirectionanlly by the tool; however, as for normal contacted fabrication technologies, the tool center cannot extend the mirror edge, so the dwell time is comparatively low, which usually results in the turned-up error nearby the edge in the process. One of the most common methods is to embed the workpiece in a large domain and then discard the edge portion or utilize the small tool post-handle the turn-up edge error.

2.3 Feasibility analysis of edge error control in the MRF process

For the MRF process, the actual removal function distribution is a complex function of many factors including tool–workpiece configuration, shear force, MR fluid, immerging depth, etc. It is impossible to describe the edge removal model by means of pressure or velocity distribution. The empirical model is practicable in the process. First of all, the material removal mechanism is based on the shear force instead of normal force, so the non-linear variant pressure distribution in the edge region does not exist. Moreover, the fluid-based polishing pad is adsorbed in the polishing wheel and it can extend out of the mirror edge completely. Above the view of the point, the MRF technique is free from the shortcomings compared to the contact polishing model and the edge effect can be suppressed theoretically. However, there are still some problems that need to be resolved in-depth including the stability of the MRF edge TIF, calibrating theory of MRF TIF as well as edge post-correcting algorithm (EPCA) of dwell time.

3 Edge TIF model in MRF processing

3.1 Stability analyses of the MRF TIF by various processing parameters

According to the CCOS (Computer Controlling Optical Surfacing) theory, the time-invariant removal function is the precondition for acquiring a high accuracy surface. The MRF processing parameters mainly including the MR fluid viscosity, immerging depth, wheel speed as well as fluid flowing rate are analyzed in this paper. The Φ100 mm fused silica (Corning 7980-0F), as the witness part, is used for optimizing the best processing parameters based on the volume removal rate (VRR) and the removal rate stability (RRS). The removal spots are imprinted every 2 h and compared to the original removal spot point to point for analyzing the stability, as shown as Fig. 1. After a lot of the experimental tests, the best parameters are about MR fluid viscosity 185–190 cp, immerging depth 0.3–0.4 mm, polishing wheel speed 170–180 rpm, and fluid flowing rate 120–130 L/min, as shown as Fig. 2. The VRR is 1.8 × 10−3 mm3/s and RRS is 93%, respectively.

Fig. 1
figure 1

Stability analyses method of the MRF TIF: a the removal spots on the witness part; b the original removal spot shape; c the latter removal spot shape; d stability analyses of removal spot point to point

Full size image
Fig. 2
figure 2

Stability analyses of the MRF TIF by various processing parameters: a MR fluid viscosity (cp); b immerging depth (mm); c polishing wheel speed (rpm); d fluid flowing rate (L/min)

Full size image

3.2 Further analyzing MRF edge TIFs

Although the problems of non-linear pressure distribution and bidirectional dwell time scanning have little influence on the edge TIF in the MRF process, the edge TIF is not so much stable as the inner area because of the fluent distortion obstructed by the mirror edge. The edge TIFs of MRF in the trailing area, transitional area and leading area are analyzed based on the above optimal experimental parameters. One standard removal spot also is imprinted at the center of the spot part. The stability of MRR on the edge area illustrated that the edge effect mainly focuses on the trailing area, because the fluid ribbon is obstructed by the mirror edge and results in the distortion of MR fluid. The Stability of MRF edge TIF on the trailing area, transitional area and leading area is shown as Fig. 3. On the trailing area, the polishing point should entrance 2-4mm at least inner the edge. On the transitional area, the TIF can remain highly stable and even the polishing wheel overhangs by about 2 mm, which can be explained by the fluid ribbon being of less width and relatively steep in the horizontal direction. On the leading area, the influence of mirror geometry on the stability is negligible. The experimental results show that the stability can reach 85% and the polishing wheel overhangs by about 7 mm.

Fig. 3
figure 3

Stability of MRF edge TIF on the trailing area, transitional area and leading area

Full size image

4 Edge post-correcting algorithm (EPCA) in the MRF process

4.1 Calibrating and correcting the theory for MRF TIF

It is well known that the Gaussian removal shape is of significance because it is compatible for the high-efficiency convergence and mid-spatial frequency error (MSFR) control at the same time. But the distribution of the MRF TIF is an asymmetrical backward “D” shape and high-gradient varies along the flowing direction (or vertical direction). Sometimes because of the position error of the magnet pole structure or fluid nozzle, the removal function is asymmetrical in the horizontal direction, as shown as Fig. 4a. For increasing the convergence ratio as well as restraining the MSFR, the TIF of the MRF needs to be calibrated and compensated. According to the discrete convolution model algorithm, the surface error after polishing can be expressed as in Eq. (2):

$$ {\text{Err}}\left( {x,y} \right) = S_{{{\text{ori}}}} {\text{ori}}\left( {x,y} \right) - R_{{{\text{tif}}}} \left( {x,y} \right)**T\left( {x,y} \right), $$
(2)
Fig. 4
figure 4

a Deviation between the nozzle and the wheel middle position; b calibration of the deflected MRF influence function shape

Full size image

where \(S_{ori}\) denotes the original surface which is acquired from the interferometer. \(R_{{{\text{tif}}}} \left( {x,y} \right)\) denotes the MRF ITF on the point \(\left( {x,y} \right)\) and \(T\left( {x,y} \right)\) represents the dwell time. The double asterisks define a 2D convolution operation.

Normally, the geometry touching point “\(P_{0}\)” is on the button of the removal function area, so MRF TIF is at great asymmetry in the flowing direction, as shown in Fig. 4b. According to the simulations of residual error, the deflected TIF usually will lead to great MSFR on the surface. So, we presume the new center position \(P_{0}^{^{\prime}}\) replacing the polishing position \(P_{0}\) and reset the influence function shape for the error calculation. The deviation on the horizontal direction (DHD) is described as \(\varepsilon_{x}\) and the deviation on the flowing direction (DFD) is described as \(\varepsilon_{y}\). The influence of DHD on the residual error is shown in Fig. 5a. Normally, the deviation is below 0.5 mm. On the other hand, the influence of DFD on the residual error is shown in Fig. 5b. The deviation is between 4 and 5 mm. Through a set of simulations in terms of the different deviation, we can come to the conclusion that the corrective calibration of the MRF ITF is significant and the MSFR can be suppressed to the minimum extent.

Fig. 5
figure 5

a Influences of different DHD on the residual error. b Influence of different DFD on the simulating residual error

Full size image

4.2 Edge post-correcting algorithm (EPCA) in MRF processing

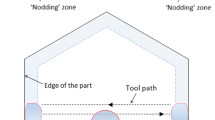
Discrete convolution model algorithm has a number of advantages, such as being fast, stable, less time consuming and without the ill-condition matrix problem compared with the linear matrix model, which is widely adopted in resolving the accurate dwell time. Nevertheless, the time-invariant TIF is the precondition for the convolution algorithm. According to the edge TIF analysis in Sects. 3.2 and 4.1, the inner distance of trailing area should be about 2–4 mm, and the DFD is about 4–5 mm, so the effective edge extension is about 2–3 mm and the polishing wheel should enter the edge at least 2 mm in the trailing area. The original surface edge, extension edge and tool path edge are shown in Fig. 6, and during the whole processing, the TIF remains relatively highly consistent.

Fig. 6
figure 6

Distribution of surface edge, extension edge and tool path edge (left)

Full size image

Pulse deconvolution iteration algorithm is widely used for resolving the dwell time. The spot size of MRF TIF is about 18 mm × 10 mm and the spot area is about 153 mm2 for our Φ 200 mm polishing wheel, which is much smaller compared to the fabricating mirror area. So the MRF processing can be supposed as the result of the small pulse impacts on the workpiece and the pulse energy PE equal to the sum of MRR of MRF TIF (\(\sum R_{{{\text{tif}}}}\)), expressed as in Eq. (3). According to the subaperture polishing principle, the dwell time for each point is proportional to the surface residual error. So, the dwell time for each residual error can be expressed as Eq. (4), (5). The material removal amount and the surface residual error can be calculated as in Eqs. (6), (7), in which we need to point out that: (1) the negative dwell time is needed to be reset as zero because the surface material is removed rather than added on the surface; (2) in the non-polishing area, the dwell time also needs to be set as zero, as the dwell time in the periphery corner also will make contribution to the surface edge, but in the practical processing, the polishing wheel should not exceed the polishing path preventing against the time-variant TIF. The convolution algorithm flowchart is shown in Fig. 7, in which the original surface error \(S\) is tested by the interferometer and the MRF removal function \(R_{{{\text{tif}}}}\) is obtained associated with the trial-and-error method.

$$ {\text{PE}} = \sum R_{{{\text{tif}}}} { }\left( {x,y} \right), $$
(3)
$$ T_{k} \left( {x_{i} ,y_{i} } \right) = {\text{Err}}_{k - 1} \left( {x_{i} ,y_{i} } \right)/{\text{PE,}} $$
(4)
$$ T_{k} = T_{k} + T_{k - 1} , $$
(5)
$$ E_{k} \left( {x,y} \right) = R_{{{\text{tif}}}} { } \otimes T_{k} \left( {x,y} \right), $$
(6)
$$ {\text{ Err}}_{k} \left( {x,y} \right) = S\left( {x,y} \right) - E_{k} \left( {x,y} \right). $$
(7)
Fig. 7
figure 7

Iterative flow of the pulse deconvolution algorithm (right)

Full size image

The mirror surfaces with turn-up and roll-down edge are simulated for verifying the feasibility of the EPCA. The simulation results illustrate that the residual error decreases to PV 24 nm, RMS 2.6 nm and PV 12 nm, RMS 0.9 nm by classical iteration algorithms (CIA) as well as EPCA, respectively. The edge error is much smoother by the latter method, as shown in Fig. 8. On the other side, the residual error decreases to PV 6.5 nm, RMS 0.74 nm by means of EPCA and the convergent ratio is almost the same as CIA for the roll-down edge, as shown in Fig. 9.

Fig. 8
figure 8

Simulation of EPCA on the turn-up surface; a original surface error; b surface error after edge extension; c simulation of residual error and dwell time by CIA and EPCA

Full size image
Fig. 9
figure 9

Simulation of EPCA on the roll-down surface; a original surface error; b surface error after edge extension; c simulation of residual error and dwell time by CIA and EPCA

Full size image

5 Experiment and verification

For further verifying the feasibility of the edge error-controlled theory in the MRF process, two mirror substrates are taken as the experiment samples. The Φ 200 mm, R-200 mm concave sphere mirror (fused silica) is removed about 3 μm uniformly based on our homemade 6 axis CNC MRF machine. The polishing wheel is Φ 200 mm and the polishing slurry is Hastilite PO (UNIVERSAL PHOTONICS 0.5μm CeO2). Polishing parameters are about: MR fluid viscosity 188 cp, immerging depth 0.3 mm, wheel speed 170 rpm, fluid flowing rate 125 L/min, magnetic field current 7A and the VRR is about 0.182 × 10−3 mm3/min. Figure 10 illustrates the mirror surface before polishing, mirror surface after polishing as well as surface error of removal amount. The experimental results indicate that the edge error region can be effectively suppressed below 1.5 mm regardless of the 0.5 mm inverted edge, which confirms the feasibility of the suppressing theory of edge effect presented in this paper. Another Φ 610 mm, R-2100, K-1 lightweighting parabolic mirror (ULE material) is taken as the practical substrate. The workpiece is polished to the RMS 182 nm by the classical technology and the MRF processing condition is the same as the first substrate. The polishing area is extended to Φ 614 mm and the dwell time is set to zero beyond the tool polishing path scope during the simulation of dwell time. After the first polishing, the surface error reaches RMS 20 nm; During the second polishing, the mirror and error map are both rotated 180° for further eliminating the residual edge error on the trailing scope by previous process, the surface error reaches RMS 6.5 nm and the edge effect is also well controlled to the large extent, as shown as Fig. 11. The evolution of surface error along the X axis is shown in Fig. 12.

Fig. 10
figure 10

Edge controlling experiment on the steep concave sphere; a surface error before polishing; b surface error after polishing 3 μm uniformly; c surface error of removal amount

Full size image
Fig. 11
figure 11

Edge controlling experiment on the concave asphere; a MRF polishing process; b original surface error; c residual error after the first run; d residual error after the second run

Full size image
Fig. 12
figure 12

Surface error evolution along the X axis

Full size image

6 Conclusion

The unpredictable behaviors of polishing pad in the mirror edge are the paramount factors leading to the edge effect. For further reducing the edge error in the MRF process, the high-effective, stable polishing parameters including MR fluid viscosity, immerging depth, polishing wheel speed as well as fluid flowing rate are analyzed in detail and the characteristics of MRF TIF in edge area are also analyzed in detail. The experimental results indicate that the TIF can keep high stability in the transitional area and leading area whenever the polishing wheel overhangs the workpiece edge at about 2 mm; however, in the trailing area, the polishing wheel needs to enter the edge about 2–4 mm aiming to obtain a stable TIF. On the other side, the calibration and compensation of MRF TIF prognosticate that the 4–5 mm DFD can suppress the residual error to a large extent, so the effective edge extension is about 2–3 mm. The EPCA of dwell time is also presented in this paper. The simulation results show that the residual error is obviously suppressed in the turn-up edge surface if the EPCA is taken into account. The sphere substrate experiment results show that the edge effect can be suppressed below 1.5 mm after the surface material is polished to about 3 μm uniformly. Another lightweighting parabolic mirror substrate experiment result indicates that the surface error can reach RMS 6.5 nm from original RMS 182 nm after two iteration processes, while the edge effect is well controlled to a large extent. The simulation results coincide well with the corresponding experimental results, which strongly verify the feasibility of the edge-controlling theory presented in this paper.