1 Introduction

Constitutive models within the framework of classical continuum mechanics, combined with mechanical indexes obtained from laboratory and in-situ tests, are often used to solve geotechnical problems. However, microscopic physical insights are often missing. It has been widely known that microscopic behaviour is the origin of the macroscopic mechanical behaviour of granular materials. The microscopic responses can be studied in aspects such as the arrangement of voids and particles [1], inter-particle sliding and rolling and inter-particle force etc. in granular materials.

Fabric tensor [1–3] is a statistical quantity to collect vector directions such as particle orientation, contact normal and contact force. The fabric tensors play different roles in macro- and microscopic bridging. Based on the relations between macroscopic variables (e.g. plastic strain) and contact normal, some micromechanically based constitutive models [4–6] have been developed. Among these models, Nemat-Nasser [6] developed a kinematic model for granular matters using fabric tensor and fabric rate to describe microstructure and kinematic hardening. Rothenburg et al. [7] have proposed a yielding condition in terms of parameters defining the anisotropy in contact forces, and then Ouadfel and Rothenburg [8] decomposed stress tensor into components reflecting contact forces and microscopic fabrics, namely the stress–force–fabric relationship.

The Discrete Element Method (DEM), which was originally proposed and used in dry sands by Cundall and Strack [9], has been widely accepted as an efficient tool to relate macro- and microscopic mechanical behaviours, including fabric tensors, of idealised granular matters. It is accessible but difficult and expensive to obtain contact orientation and particle orientation using technologies such as X-ray micro-computed tomography \((\upmu \hbox {CT})\) [10] and stereocomparator [11]. It is more difficult to measure microforces using sophisticated techniques such as photoelasticity [11]. That is why the DEM technique has commonly been applied to investigate the fabric tensors and their influence on the macroscopic mechanical behaviour for idealised granular assemblies under different testing conditions [12–19]. The limited laboratory data can be used to justify the law on fabric obtained from DEM simulations.

Particle shape affects the mechanical behaviour of particulate materials greatly [20]. Inherent anisotropy is developed because of preferentially oriented particles, voids and contact orientations during particle deposition processes [21]. The inherent anisotropy is enhanced by non-circle particle shapes. Elliptical particles can be employed to simulate non-circle particles and can reproduce rolling resistance of natural granular matters, and hence have been used in the Discrete element modeling [22–38]. Moreover, elliptical particle assemblies are moderately suitable to investigate the fabrics in granular materials [31].

In the present DEM study, medium-dense elliptical particle assemblies with particle aspect ratios of 1.4 and 1.7 were generated and one-dimensionally compressed to reproduce an appropriate in-situ stress state and simulate inherent anisotropy of sands. Strain-rate controlled constant volume monotonic and cyclic simple shear tests were simulated using a recently developed two-dimensional DEM code NS2D [39, 40]. Fabric tensors describing (1) particle orientation, (2) contact normal and sliding contact normal, and (3) contact force, strong and weak contact forces were defined. Two features of each fabric tensor were examined, i.e. anisotropy and major principal direction and their time derivatives, namely fabric anisotropy rate and fabric direction rate, were studied.

2 DEM simulations

2.1 Contact between elliptical particles

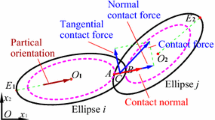
The numerically stable contact detection algorithm proposed by both Ng [32] and Ting [35] was applied in our recently developed in-house DEM code NS2D, which can simulate the interactions between elliptical particles. Figure 1a presents how the contact point C is defined between two overlapping ellipses i and j. First, by shrinking ellipse i, i.e. representing the ellipse using a smaller one which has the same shape and centroid as the original one, a unique common point A between the ellipse j and the shrunk ellipse i can be obtained. In the same way, a unique common point B between the ellipse i and the shrunk ellipse j can be obtained. Contact normal is defined as a unit vector in the direction from point A to point B. The midpoint C of the line segment AB is taken as the contact point. The particle orientation is defined as the major-axis direction of an ellipse. Besides, the contact force direction is the direction of the total contact force between two ellipses.

Fig. 1
figure 1

a Contact between two ellipses and b equivalent particle diameter distribution of the DEM assemblies

Full size image

The contact forces are updated incrementally. To calculate the contact force between two ellipses, a contact model and the relative contact velocity of two contacting ellipses are needed. A simple contact model is used, consisting of an elastic normal contact and an elasto-perfect plastic tangential contact with the maximum tangential contact force being \(\mu F_{\mathrm{n}}\), where \(\mu \) is the friction coefficient and \(F_{\mathrm{n}}\) is the normal contact force. The method to calculate contact velocity is detailed in [33, 38].

2.2 Sample preparation

Each specimen consists of 2032 elliptical particles with a density of 2600 \(\hbox {kg}/\hbox {m}^{3}\). The width of the square specimens is about 44 times of the mean grain size, which is considered to be sufficient for the DEM simulation of a cell test. Figure 1b presents the distribution of equivalent particle diameter, which is defined as the geometric mean of the lengths of the major and minor axes of an ellipse. The equivalent diameter ranges from 6 mm to 9 mm, with a mean diameter of \(d_{50 }= 7.6\) mm and a uniformity coefficient of \(C_{\mathrm{u}}=d_{60}/d_{10} = 1.3\), where, \(d_{\mathrm{x}}\) is the diameter corresponding to x percent finer in a particle size distribution curve.

Two medium-dense specimens were investigated, with particle aspect ratios of 1.4 and 1.7 (defined as the length ratio of major axis over minor axis of an ellipse) and with respect void ratios of 0.20 and 0.19. The so-called dense, medium-dense and loose specimens are distinguished by their mechanical performances in biaxial tests, i.e., strain softening, perfect plasticity and strain hardening in stress–strain relationships. Hence, the so-called medium-dense specimens have different void ratios because of different particle aspect ratios. The preparation procedures of the two specimens are totally the same and the differences lie in different aspect ratios and void ratios.

Fig. 2
figure 2

Particle orientation diagrams after precompression of the DEM assemblies with a \(A_{\mathrm{m}}=1.4\) and b \(A_{\mathrm{m}} = 1.7\)

Full size image

The specimens were prepared by the Multi-layer Under-compaction Method (UCM) [39] which is efficient to generate homogeneous specimens. To generate a specimen, the particles are firstly generated and compacted in layers with an inter-particle frictional coefficient of 1.0. The compacting direction is defined as the vertical direction. Then, the specimen is precompressed to a vertical load of 12.5 kPa (precompression) with frictional coefficient of 0.5 and with side walls fixed to simulate in-situ stress conditions. The normal and tangential stiffnesses of each contact are 1.5\(\times ~10^{9}\) and \(1.0~\times ~10^{9}\) N/m, respectively. A time step of 1.0\(\times ~10^{-4}\) s is applied which is larger than the critical one. Such a time step does not affect the stress–strain behaviour in this simulation because of the “slow” shear strain rate and small particle size discrepancy. Figure 2, the directional distribution of particle orientation, demonstrates that the “in-situ” granular material exhibits inherent anisotropy before consolidation and shearing.

2.3 Procedures of numerical simple shear tests

After precompression, a simple shear test was carried out in two stages, consolidation and shearing stages. In order to study the influence of initial anisotropy, two shear modes were applied as shown in Fig. 3. In the consolidation stage, a specimen was loaded one-dimensionally \((K_{0}\) compression) to a vertical/horizontal stress of 200 kPa or 400 kPa for shear mode I/II. In the subsequent shearing stage, the particle-wall friction coefficient was set to 0.5 (which was zero before). In shear mode I, the top and bottom walls were vertically fixed, and moved horizontally following the side walls, which were rotated with a rotation rate of \(\dot{\theta }\). In shear mode II, the side walls were horizontally fixed, and moved vertically following the top and bottom walls, which were rotated with a rotation rate of \(\dot{\theta }\).

In the monotonic simple shear tests, the rotation rate was kept constant, while in the cyclic tests the rotation rate was changed periodically, as

$$\begin{aligned} \dot{\theta }=\left\{ {{\begin{array}{l} {\dot{\theta }_{0},\qquad \hbox { monotonic }} \\ {\dot{\theta }_{0} \cos (\frac{2\pi t}{T_{0} }), \hbox { cyclic }} \\ \end{array} }} \right. \end{aligned}$$
(1)

where \(\dot{\theta }_0 \) is 0.05 rad/min in the monotonic tests and 0.15 rad/min in the cyclic tests, t is the time elapsed and \(T_{0} = 120\) s is the period in the cyclic tests.

Fig. 3
figure 3

Illustration of two shear modes applied in the DEM simple shear tests

Full size image

2.4 Stress–strain performance

Figure 4 shows the normal and shear stresses on the non-rotating walls (horizontal walls in shear mode I and vertical walls in shear mode II) during the monotonic simple shear test on the specimen with a particle aspect ratio of 1.7. The slight increase in normal stress during the test results from dilation tendency of the specimen. The shear stress increases with the shear strain until it comes to a critical value. There are no apparent differences in the normal and shear stresses between the two shear modes.

3 Fabric description of microstructure

Fabric tensor can be used to describe any directional dependent quantities, which can be particle orientation, contact normal and contact force. A second-order tensor for this purpose can be defined as [1–3]:

$$\begin{aligned} F_{ij}= & {} \frac{1}{N}\sum _{k=1}^N {n_i^k } n_j^k\, =\, \langle n_i n_j\rangle \;\nonumber \\= & {} \frac{1}{N}\left[ {{\begin{array}{ll} {\mathop \sum \limits _{k=1}^N {\cos \alpha _k \cos \alpha _k } }&{} {\mathop \sum \limits _{k=1}^N {\cos \alpha _k \sin \alpha _k } } \\ {\mathop \sum \limits _{k=1}^N {\sin \alpha _k \cos \alpha _k } }&{} {\mathop \sum \limits _{k=1}^N {\sin \alpha _k \sin \alpha _k } } \\ \end{array} }} \right] \;\;\; \end{aligned}$$
(2)

where N is the number of elements that could be contacts or particles, \(n_{i} (i=1, 2)\) are the direction cosines and \(\alpha _{\mathrm{k}}\) are the angles between the direction of an element and x axis.

A magnitude [41] can be used to describe the anisotropy of granular materials, as

$$\begin{aligned} \Delta =\frac{1}{N}\sqrt{\left( \sum _{k=1}^N {\cos 2\alpha _k } \right) ^{2}+\left( \sum _{k=1}^N {\sin 2\alpha _{k}}\right) ^{2}} \end{aligned}$$
(3)

Following the definition of fabric tensor, the eigenvalues are as

$$\begin{aligned} {\begin{array}{l} {F_1 } \\ {F_2 } \\ \end{array} } =\frac{F_{11} +F_{22} }{2}\pm \frac{\sqrt{(F_{11} -F_{22} )^{2}+\hbox {4}F_{12} F_{21} }}{2} \end{aligned}$$
(4)

The deviator fabric \(F_1 -F_2 \) is suggested to quantify the degree of structural anisotropy [42]. The expression is the same as Eq. (3).

The major principal direction of the fabric tensor \(F_{ij}\) can be expressed as

$$\begin{aligned} \Phi _=\frac{1}{2}\arctan \left( {\frac{F_{12} +F_{21} }{F_{11} -F_{22} }} \right) =\frac{1}{2}\arctan \frac{\mathop {\sum }\nolimits _{k=1}^N {\sin 2\alpha _k } }{\mathop {\sum }\nolimits _{k=1}^N {\cos 2\alpha _k } } \end{aligned}$$
(5)

In the coordinate system in Fig. 3, \(\Phi \) equals 0 if the major principal direction is horizontal.

Fig. 4
figure 4

Normal and shear stresses on non-rotated walls during monotonic tests on the medium-dense specimen with \(A_{\mathrm{m}}=1.7\): a normal stress, b shear stress

Full size image
Fig. 5
figure 5

Fabric rates of particle orientation in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

The following aspects of microstructure were investigated: (1) particle orientation \((\Delta _\mathrm{P},\Phi _\mathrm{P} )\) which describes the arrangement of the major-axes of elliptical particles, (2) contact normal \((\Delta _\mathrm{C},\Phi _\mathrm{C} )\) which describes the arrangement of contact directions, and sliding contact normal \((\Delta _\mathrm{S},\Phi _\mathrm{S} )\) which is defined as the contact normal of sliding contact, (3) contact force direction \((\Delta _\mathrm{F} ,\Phi _\mathrm{F} )\) which describes the distribution of total contact force directions, and strong/weak contact force direction \((\Delta _{\mathrm{SF}} ,\Phi _{\mathrm{SF}} )/(\Delta _{\mathrm{WF}} ,\Phi _{\mathrm{WF}} )\) which describes the distribution of total contact force whose magnitude is larger/smaller than the average value.

Fabric rates are characterised by the rates of change in the anisotropy and the major principal direction of a fabric tensor with respect to time, i.e. \(\dot{\Delta }\) (fabric anisotropy rate) and \(\dot{\Phi }\)(fabric direction rate). The time increment is 1 s when calculating the fabric rates in the simulation. Fabric rates of different aspects of microstructure will be investigated. Hereafter, to obtain dimensionless fabric rates, \(\dot{\Delta }\) and \(\dot{\Phi }\) are normalised by \(\dot{\theta }_0 \), refer to Eq. (1), as

$$\begin{aligned} \dot{\Delta }^{\mathrm{N}}=\dot{\Delta }/\dot{\theta }_0 ,\;\;\;\dot{\Phi }^{\mathrm{N}}=\dot{\Phi }/\dot{\theta }_0 \end{aligned}$$
(6)

4 Fabric rates in monotonic simple shear tests

Fabric rates at the beginning of shearing are much larger than that under subsequent shear strains because of the sudden change of the magnitude and orientation of major principal stresses. Therefore, the initial part of the data is disregarded.

Fig. 6
figure 6

Fabric rates of contact normal in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image
Fig. 7
figure 7

Fabric rates of sliding contact normal in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

4.1 Particle orientation

Figure 5 shows the normalised fabric anisotropy and direction rates of particle orientation in the monotonic simple shear tests. In Fig. 5a, b, the fabric anisotropy rates are larger than zero throughout the tests, which suggests that the anisotropy of particle orientation increases with shear strain. The fabric rates increase gradually from zero to about 0.2 in shear mode I for both samples with \(A_{\mathrm{m}}= 1.4\) and 1.7 and then virtually stay constant. In shear mode II, the fabric rate decreases firstly from about 0.3 /0.25 to approximately 0.03/0.05 and then increases to about 0.3 /0.25 for the sample with \(A_{\mathrm{m}}=1.4/1.7\). Hence, shear mode can affect the way fabric anisotropy responds to shear strain as a result of the initial anisotropy. The aspect ratio also exhibits slight quantitative influence on fabric anisotropy development. In Fig. 5c, d, the fabric direction rates are positive, implying that the principal directions of the particle orientations rotate in the same direction with the rotation of the sample. In shear mode I, the fabric direction rate decreases from about 0.45/0.28 to about 0.18 /0.1 for the sample with \(A_{\mathrm{m}} = 1.4/1.7\). In shear mode II, the fabric direction rate decreases from about 0.3/0.2 to about 0.1 /0.0 for the sample with \(A_{\mathrm{m}} = 1.4/1.7\). The fabric direction rate in shear mode I is larger than that in shear mode II for both samples, manifesting the influence of initial structural anisotropy on particle rotation. The particles with \(A_{\mathrm{m}} = 1.4\) are easier to rotate than those with \(A_{\mathrm{m}} = 1.7\) because of less rotation frustration in the former case where the particle shape is closer to a circle than that in the latter case.

Fig. 8
figure 8

Fabric rates of contact force in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image
Fig. 9
figure 9

Fabric rates of strong contact force in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

4.2 Contact normal and sliding contact normal

Figure 6 shows the normalised fabric anisotropy and direction rates of contact normal. In Fig. 6a, b, the fabric anisotropy rates are negative and decrease in absolute value until a shear strain of 4 %, after which the rates fluctuate irregularly around zero. This observation indicates that the contact normal anisotropy virtually remains unchanged after a shear strain of 4 %. The fluctuation range in the sample with \(A_{\mathrm{m}} = 1.4\), between −1.5 and 1.5 in shear mode I and between −3 and 3 in shear mode II, is much smaller than that in the sample with \(A_{\mathrm{m}} = 1.7\), between −5 and 5 in both shear modes. This is because particles with larger aspect ratio cause greater local disturbance when they are displaced. Such disturbance can be overall balanced by subsequent disturbance. Similar observations are made for the fabric direction rates in Fig. 6c, d. There is no noticeable difference in fabric rates caused by shear direction.

Figure 7 shows the normalised fabric anisotropy and direction rates of sliding contact normal. In Fig. 7a, b, the fabric anisotropy rates of the sample with \(A_{\mathrm{m}} = 1.4\) fluctuate irregularly between −10 and 10 in both shear modes while that of the sample with \(A_{\mathrm{m}} = 1.7\) between −20 and 20 after the shear strain exceeds 4 %. In Fig. 7c, d, the fabric direction rates of sliding contact normal fluctuate between −50 and 50 after the shear strain exceeds 4 %. There are some scattered fluctuations much larger than 50 in Fig. 7d, which do not, however, influence the main conclusions. The fluctuation ranges of fabric rates in the sample with \(A_{\mathrm{m}} = 1.4\) are smaller than that with \(A_{\mathrm{m}} = 1.7\). This can be explained by the large disturbance (obviously accompanied with contact sliding) caused by particles with large \(A_{\mathrm{m}}\). The fluctuation in the directional distribution of sliding contact normal in Fig. 7 is more violent than that of all contact normal in Fig. 6. There is no noticeable difference in fabric rates caused by shear direction.

Fig. 10
figure 10

Fabric rates of weak contact force in monotonic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

4.3 Contact force, strong contact force and weak contact force

Figures 8, 9 and 10 show the normalised fabric anisotropy and direction rates of contact force and strong and weak contact forces. In Fig. 8a, b, the fabric anisotropy rates of contact force fluctuate dramatically between −4 and 4 for both samples in both shear modes after the shear strain exceeds 4 %. In Fig. 9a, b, for the strong contact force, the fluctuation of fabric anisotropy rate is between −6 and 6. In Fig. 10a, b, for the weak contact force, the fluctuation of fabric anisotropy rate is between −4 and 4 for the sample with \(A_{\mathrm{m}} = 1.4\) and between −6 and 6 for the sample with \(A_{\mathrm{m}} = 1.7\). Fluctuations of fabric anisotropy rates of contact force and strong and weak contact forces are almost the same. For the weak contact force, fluctuations of fabric anisotropy rates are slightly influenced by the aspect ratio. But for the total contact force and strong contact force, the influence of the aspect ratio is not obvious. Similar observations can be made for the fabric direction rates.

Table 1 Average values of fabric rates in DEM monotonic simple shear tests
Full size table
Fig. 11
figure 11

Fabric rates of particle orientation in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

Table 1 summarises the average values and fluctuation amplitudes of fabric rates in DEM monotonic simple shear tests. Apart from the fabric rates of particle orientation, the average values of fabric rates are very small compared to their fluctuation amplitudes. Both the anisotropy and principal direction of contact normal vary in shearing since the average values are relatively large with respect to their fluctuation amplitudes. Nevertheless, the average values for sliding contact normal are very small with respect to their fluctuation amplitudes regardless of being collected throughout shearing or after the shear strain exceeds 4 %, which indicates the isotropy of energy dissipation by contact sliding. The anisotropies of total contact force and strong and weak contact forces vary slightly as their average values are small while larger variations occur with their principal directions.

Fig. 12
figure 12

Fabric rates of contact normal in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

5 Fabric rates in cyclic simple shear tests

As mentioned in Sect. 4, the fabric rates at the beginning of shearing are much larger than that under subsequent shearing. Hence, the initial part of the data is also disregarded. Recall that the period \(T_{0}\) in cyclic shear tests is 120 s, which is marked in the following figures by vertical dash lines.

5.1 Particle orientation

Figure 11 shows the normalised fabric anisotropy and direction rates of particle orientation in the cyclic simple shear tests. In Fig. 11a, b, the fabric anisotropy rates oscillate between −0.5 and 0.5 in the sample with \(A_{\mathrm{m}}=1.4\), while in the sample with \(A_{\mathrm{m}}=1.7\) between −1.0 and 1.0/between −0.2 and 0.2 in shear mode I/II. Oscillations of the fabric anisotropy rates in shear mode I and II are asynchronous but with approximately the same period (60 s). In Fig. 11c, d, the fabric direction rates oscillate between −0.4 and 0.4 in the sample with \(A_{\mathrm{m}}=1.4\) while in the sample with \(A_{\mathrm{m}}=1.7\) between −0.5 and 0.5. In shear mode I and II, oscillations of fabric direction rates are asynchronous but the periods are the same (120 s). The asynchronism indicates the influence of structural anisotropy on the fabric direction rates of particle orientation.

5.2 Contact normal and sliding contact normal

Figures 12 and 13 show the normalised fabric anisotropy and direction rates of contact normal and sliding contact normal. The fabric anisotropy and direction rates fluctuate irregularly around zero. In Fig. 12a, b, the fluctuation range of the fabric anisotropy rates of contact normal is between −5 and 5 in the sample with \(A_{\mathrm{m}}=1.4\) while in the sample with \(\hbox {A}_{\mathrm{m}}=1.7\) it is extremely larger, between −50 and 50 for shear mode I and between −25 and 25 for shear mode II. In Fig. 13a, b, the fabric anisotropy rates of sliding contact normal in the sample with \(A_{\mathrm{m}}=1.4\) fluctuate between −25 and 25/between −15 and 15 in shear mode I/II while the sample with \(A_{\mathrm{m}}=1.7\) between −50 and 50/between −30 and 30 in shear mode I/II. Similar observations can be made for the fabric direction rates in Figs. 12c, d and 13c, d.

Fig. 13
figure 13

Fabric rates of sliding contact normal in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image
Fig. 14
figure 14

Fabric rates of contact force in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

The fluctuations are random but some scattered fluctuations do not influence the main conclusions. Larger aspect ratio results in a larger fluctuation range as the larger disturbance (obviously accompanied with contact sliding) caused by particles with larger \(A_{\mathrm{m}}\). Larger disturbance with the contact sliding causes a larger fluctuation range for the sliding contact normal than that for the total contact normal. There is no noticeable difference in fabric rates caused by shear modes.

Fig. 15
figure 15

Fabric rates of strong contact force in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image
Fig. 16
figure 16

Fabric rates of weak contact force in cyclic tests: a, b fabric anisotropy rates, c, d fabric direction rates

Full size image

5.3 Contact force, strong contact force and weak contact force

Figures 14, 15 and 16 show the normalised fabric anisotropy and direction rates of contact force and strong and weak contact forces. In Fig. 14a, b, the fabric anisotropy rates of contact force fluctuate between −4 and 4 in the sample with \(A_{\mathrm{m}}=1.4\) while between −5 and 5 in the sample with \(A_{\mathrm{m}}=1.7\). In Fig. 15a, b, the fluctuation range of the fabric anisotropy rates of strong contact force is between −5 and 5 in the sample with \(A_{\mathrm{m}}=1.4\) while in the sample with \(A_{\mathrm{m}}=1.7\) between −5 and 5/between −3 and 3 in shear mode I/II. In Fig. 16a, b, the fabric anisotropy rates of weak contact force in the sample with \(A_{\mathrm{m}}=1.4\) fluctuate between −4 and 4/between −5 and 5 in shear mode I/II while in the sample with \(A_{\mathrm{m}}=1.7\) between −5 and 5. The fluctuate ranges of the fabric direction rates of total, strong and weak contact forces are between −25 and 25 except some scattered fluctuations in Figs. 14c, d, 15c, d and 16c, d.

The fluctuation ranges of the fabric anisotropy rates of contact force and strong and weak contact forces are almost the same and so as the fabric direction rates. There is no noticeable difference in fabric rates caused by particle aspect ratio and shear direction.

Table 2 Positive and negative average values of fabric rates in DEM cyclic simple shear tests
Full size table

Table 2 summarises the positive and negative average values and amplitudes of fabric rates in DEM cyclic simple shear tests. The positive and negative average values are approximately the same as the fabric rates oscillate around zero in the cyclic tests. In relatively regular curves, the average value is about half of the corresponding amplitude, while in the curves with scatted fluctuation, the average value is much larger than half of the corresponding amplitude. This scatter indicates significant change of the fabric anisotropy or principal direction during the cyclic shear tests.

6 Conclusions

Fabric tensor is a kind of statistical quantity to collect vector directions to bridge microscopic arrangement and macroscopic behaviour. In a two-dimensional description, there are two typical features for a fabric tensor, i.e. fabric anisotropy describing the anisotropy degree and fabric direction defined as the major principal direction. Fabric rates are defined as the time derivatives of the two features. This paper presents the fabric anisotropy and direction rates of several fabric tensors, i.e. particle orientation, contact normal, sliding contact normal, contact force and strong and weak contact forces, of elliptical particle assemblies in monotonic and cyclic simple shear tests. Specimens with two particle aspect ratios of 1.4 and 1.7 were tested in two shear modes using the Discrete element method. The conclusions are as follows:

  1. (1)

    Both the fabric anisotropy and direction rates of particle orientation are positive (below 0.5) throughout shearing in the monotonic tests, which suggests that the anisotropy of particle orientation increases with the shear strain and the principal direction of particle orientation rotates with the rotating direction of the specimen. Both the fabric anisotropy and direction rates fluctuate between −0.5 and 0.5 in the cyclic tests. The shear mode can affect the way fabric anisotropy rate responds to shear strain as a result of the initial structural anisotropy. The particle shape (aspect ratio) also exhibits slight quantitative influence on the fabric rates.

  2. (2)

    Fabric rates of contact normal, sliding contact normal, contact force and strong and weak contact forces fluctuate dramatically around zero after the shear strain exceeds 4 % in the monotonic tests and throughout the cyclic tests. The fluctuation amplitudes for sliding contact normal are larger than that for total contact normal ascribed to the large disturbance accompanied with contact sliding. Particle aspect ratio affects the fabric rates of total and sliding contact normals but there is no noticeable difference caused by shear modes. The fluctuation amplitudes of both fabric anisotropy and direction rates of the three contact force fabrics are similar. The influences of particle aspect ratio and the shear mode on the fabric rates of contact force, strong and weak contact forces are not noticeable.

  3. (3)

    Fabric rates of particle orientation are much smaller than that of contact normals and contact forces. Both orientations of particles and contacts redistribute towards a steady state when a specimen is sheared. The particle orientation based fabric tensor is harder to evolve than the contact normal or contact force based one because the reorientation of particles is more difficult than that of contacts. To change the orientations of particles, space is needed to allow the rotation of particles and the relaxation of interlocking [21].

In addition, particle shape (particle aspect ratio) exhibits quantitative influence on some fabric rates, including particle orientation and contact normals. However, more specimens with different aspect ratios need to be examined in detail to further analyse the relation between the aspect ratio and some macroscopic characteristics, such as soil anisotropy, shear strength and non-coaxiality, which is beyond the main purpose of this paper and which will make the paper too long, and thus reduce its readability.