1 Introduction

The vast majority of the gear dynamics models are based on rigid discs connected by a time-varying elastic mesh interface [1,2,3,4,5]. Recently, however, efforts have been made to account for gear body flexibility. Li [6,7,8] built a full FE model of lightweight gears and studied the influence of the corresponding additional deflections on tooth contact conditions. Parker et al. [9] used an elastic ring on constant stiffness foundation for flexible ring-gears and developed a 2D spur gear model combining finite element and analytical models [10]. Still in the context of planetary gears, Abousleiman et al. [11] inserted the results of condensed 3D finite element models of planet-carriers whereas Wu and Parker [12] used the thin ring theory to account for ring gear elasticity. Bettaieb et al. [13] and Liu et al. [14] included a condensed 3D finite element of gear body into spur and helical gear models. In this paper, the semi-analytical formulation of the dynamic factor for mesh forces proposed by Velex and Ajmi [15, 16] is revisited in the context of models integrating gear body flexibility. The formula was initially established for solid gears under the conditions of small relative variations of mesh stiffness, hence mainly for helical gears, and linear behaviour (no contact losses). Within this domain of validity, the results from the dynamic factor formula are critically assessed and confronted with those delivered by the hybrid gear dynamic models proposed in [17, 18], which can capture the static and modal contributions of thin-rimmed/-webbed gears.

2 Model presentation—analytical dynamic ratio formula

2.1 Hybrid dynamic model

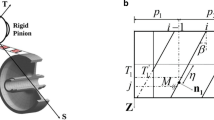
The modular hybrid gear dynamic model (Fig. 1a) includes lumped parameter and finite elements. It is assumed that all the contacts between the teeth occur on the theoretical line of actions in the base plane (Fig. 1b), which are discretised into small segments centred on the potential points of contact Mij, where subscript i refers to the line of contact and j to the segment. A local stiffness kij [19] is attributed to every ij segment and distributed along the contact lines, making it possible to connect the pinion and gear degrees-of-freedom by a time-varying, possibly non-linear, Winkler foundation representative of the mesh interface elasticity [17]. The mechanical environment is simulated by combining lumped parameter and shaft elements along with sub-structures (super-elements), which account for gear body contributions [20] as illustrated in Fig. 1a in the particular case of a thin-rimmed gear. The corresponding state equations are solved by a time-step Newmark’s integration scheme combined with a unilateral contact algorithm verifying that all contact forces on the mating teeth are compressive [3].

Fig. 1
figure 1

a Hybrid gear model and b base plane [18]

Full size image

2.2 Dynamic ratio approximate formula

The gear dynamic factor formula in [16] is based on a classical 3D shaft finite element—lumped parameter dynamic model with rigid body gears [3]. Assuming that the relative mesh stiffness variation is small, a main order approximation of the instant dynamic factor is derived under the form [16]:

$$r\cong 1+\sum _{k}\sqrt{\rho _{k}\frac{k_{\phi k}}{k_{m}}}\mathrm{Z }\left(k\right)$$
(1)

with

ρk and kϕk,:

the percentage of modal strain energy in the mesh interface and the modal stiffness respectively for Φk, kth mode shape obtained with a time-averaged stiffness matrix (over one mesh period in this paper),

km,:

the average (scalar) mesh stiffness

Ζ(k),:

the contribution of the kth mode shape to the dynamic response when considering transmission error-based excitations, i.e.,

$$\mathrm{Z }\left(k\right)=\sum _{n\geq 1}\frac{\overline{A}_{n}^{*}\left[\left(\frac{\varpi _{k}}{n}\right)^{2}-1\right]+2\overline{B}_{n}^{*}\xi _{k}\left(\frac{\varpi _{k}}{n}\right)}{\left[\left(\frac{\varpi _{k}}{n}\right)^{2}-1\right]^{2}+4\xi _{k}^{2}\left(\frac{\varpi _{k}}{n}\right)^{2}}\sin n\vartheta +\frac{\overline{B}_{n}^{*}\left[\left(\frac{\varpi _{k}}{n}\right)^{2}-1\right]-2\overline{A}_{n}^{*}\xi _{k}\left(\frac{\varpi _{k}}{n}\right)}{\left[\left(\frac{\varpi _{k}}{n}\right)^{2}-1\right]^{2}+4\xi _{k}^{2}\left(\frac{\varpi _{k}}{n}\right)^{2}}\cos n\vartheta$$
(2)

where

  • ξk is the damping factor of mode k

  • \(\vartheta =\Omega _{1}t\), is an angular position (Ω1 constant pinion rotation speed)

  • \(\varpi _{k}=\frac{1}{\Omega _{1}}\sqrt{\frac{k_{\phi k}}{m_{\phi k}}}\), kϕk and mϕk modal stiffness and mass, is the kth natural frequency (with time-averaged mesh stiffness)

  • \(\overline{A}_{n}^{*}=\frac{A_{n}^{*}}{\upsilon _{x0}}\) and \(\overline{B}_{n}^{*}=\frac{B_{n}^{*}}{\upsilon _{x0}}\), with \(\upsilon _{{x_{0}}}\)the average static mesh deflection, are the dimensionless coefficients derived from transmission errors as:

$$\Gamma _{k}TE_{S}^{''}=-\sum _{n\geq 1}n^{2}\left[A_{n}^{*}\sin n\vartheta +B_{n}^{*}\cos n\vartheta \right]$$
(3)

\(\Gamma _{k}=\frac{\cos \beta _{b}}{\upsilon _{x0}}\frac{\left(\phi ^{\boldsymbol{T}}\mathbf{M}\overset{\frown }{\mathbf{X}}_{\mathbf{0}}\right)_{/k}}{m_{\phi k}}\), \(\overset{\frown }{\mathbf{X}}_{\mathbf{0}}=\overline{\mathbf{K}}^{\mathbf{-}\mathbf{1}}F_{S}\mathbf{V}\), \(\overline{\mathbf{K}}\) averaged stiffness matrix, FS static mesh force,

\(TE_{S}^{''}\) is the second order derivatives (with respect to ϑ) of the quasi-static transmission error under load. In contrast with [16], the no-load transmission error does not appear in the present study as it has been conducted without any errors or tooth modifications.

3 Elements of validation

3.1 Test case definition

The test case defined in Fig. 2 is an aeronautical power transmission with a solid pinion and a lightweight gear. The pinion torque is 400 Nm and the gear data are in Table 1.

Fig. 2
figure 2

Aeronautical transmission, a solid pinion and b lightweight gear

Full size image
Table 1 Gear data
Full size table

3.2 Solid gear

For validation purposes, the original lightweight gear is replaced in the section by the solid gear shown in Fig. 3.

Fig. 3
figure 3

Solid gear for validation purposes, a solid gear geometry and b 3D FEM model to be used in the hybrid dynamic model

Full size image

The modes with the highest percentages of strain energy stored in the mesh interface are listed in Table 2. These modes are those which contribute mostly to dynamic tooth forces hence to the dynamic factor. Most of them are bending modes for the pinion shaft, as their maximum energy is stored in the beam elements of the pinion. The 4th mode corresponds to a 2 Nodal Diameter (2 N.D.) mode for the gear [22], showing that even solid gears can contribute to dynamic tooth loads via their deformable bodies. It can be noticed, however, that the dominant modes for mesh forces are mainly those which would be obtained by considering rigid discs, thus validating this modelling option for solid pinions and gears.

Table 2 Modal strain energy percentages (above 5% in the mesh interface), only the modes with more than 20% of the total strain energy in the mesh interface are kept for nE1 ISO 6336-1:2006 calculation [21]
Full size table

The dynamic responses in Fig. 4 have been calculated between 0 and 2500 rad/s on the pinion shaft. Two different parameters are represented versus speed, which are the maximum dynamic factor R (maximum dynamic-to-static mesh force ratio at a given speed or the maximum of r defined in (2)) and the RMS of the axial displacement at the node on the gear rim shown in Fig. 3b. The dynamic factor has been calculated by numerical time integration of the hybrid model equations of motion (solid line) and by using the maximum of r derived from the approximate formula (2) (dotted line with cross marks) using the hybrid model modes (hence a deformable solid gear). A third curve has been superimposed (dotted line), which corresponds to the results obtained by assimilating the gear to a rigid disc. The dynamic factor using the ISO standard [21] with the theoretical critical speed nE1 given in [21] (red dotted curve in Fig. 4) and that obtained based on the modes with more than 20% of strain energy in the mesh interface (green dotted curve) have been added.

Fig. 4
figure 4

Approximate formula with 5 harmonics and 5% and more of energy

Full size image

It can be noticed that the three first sets of results are very close. In this example of solid gear, the rigid disc or deformable gear body models give similar results but, as expected, the major critical speeds for tooth loading are slightly lower when gear flexibility is simulated. Interestingly, the approximate analytical dynamic factor calculated by keeping the few modes with more than 5% of strain energy in the mesh interface only (Table 2), agrees very well with the hybrid model results. Slight deviations can be observed with a peak around 1300–1400 rad/s, not reproduced by the analytical formula (2), which corresponds to a critical speed associated with gear body displacements as illustrated in Fig. 4b and the 2 ND mode in Table 2. The very limited couplings between mesh force and gear body modes probably explains the very good agreement between the analytical and numerical results in this example with a solid gear. The critical speed derived from the theoretical ISO curve is not correctly positioned but the ISO dynamic factor formulae using the modes with maximum energy in the tooth mesh are better. For both curves, the amplitudes comparable reasonably well with those obtained by numerical simulations.

4 Analysis of the thin-rimmed/-webbed gear

Similar comparisons have been extended to the thin-rimmed/-webbed gear shown in Fig. 2. The corresponding percentages of modal strain energy in the mesh interfaces are given in Table 3. Because of the web flexibility, the 2 N.D. gear body mode (number 4 in both Tables 2 and 3) has dramatically moved from 6129 to 2134 Hz. The previous bending modes for the pinion shaft with the highest percentages of strain energy in the mesh obtained for a solid gear are replaced by coupled modes affecting more components in the transmission, thus showing that highly flexible thin-rimmed/-webbed gears can influence dynamic tooth loads. These coupled modes still are the most energetic re the mesh interface, whereas gear body mode contributions remain limited.

Table 3 Strain energy distribution for modes with energy greater or equal to 5% in the meshing for the transmission with the thin-rimmed/-webbed gear, only the modes with more than 20% of the total strain energy in the mesh interface are kept for nE1 ISO 6336-1:2006 calculation [21]
Full size table

The response curves in Fig. 5 show results of the same nature as those in Fig. 4 but for the thin-rimmed gear arrangement. In spite of the more complex interactions between the gear body and the mesh interface, the approximate formula (2) can still capture most of the dynamic tooth loads and particularly the two major response peaks. Some secondary peaks are not predicted by (2), which correspond to amplifications of gear body vibrations (see the second graph in Fig. 5) and are dynamically coupled to the mesh. Their amplitudes, however, remain limited. The displacement curve shows far more dynamic activity than in the case of a solid gear, thus highlighting the role of coupled modes. The curves deduced from the ISO standard formulae [21] have been superimposed and it can be observed that they fail to correctly predict the dynamic mesh forces. The agreement is worse than compared with the solid gear example in Fig. 4, as expected based on the conditions of validity of the ISO formulae (for solid gears only).

Fig. 5
figure 5

Comparison between Dynamic Ratio (R) and R.N. radial displacement RMS over a speed range

Full size image

5 Conclusions

A modular hybrid dynamic gear model which includes lumped parameters and 3D finite elements to account for the flexibility of thin-rimmed/-webbed gears has been used to assess the validity of the approximate formula of Velex and Ajmi [15, 16] to calculate mesh force dynamic factors. This formula is based on the hypotheses of the 3D rigid body gear model, and relies on the hypothesis of linear behaviour (no tooth contact losses) and small mesh stiffness time-variations (hence, more adapted to helical gears). The comparisons have been conducted on an aeronautical power transmission, by considering: a) a solid gear simulated as a rigid disc and by using 3D block finite elements and, b) the actual thin-rimmed, thin-webbed gear.

Overall, it seems that the analytical formula (2) can give a reasonable estimate of the dynamic mesh forces versus speed and can identify the major tooth critical speeds even for thin-rimmed applications. As expected, it fails to account for gear body mode contributions as it was developed in the context of pinions and gears assimilated to rigid discs connected by a time-varying elastic Winkler foundation. One major advantage of (2) is clearly the computational time as it only takes a few minutes for a complete response curve as opposed to days for the more involved hybrid model. It is therefore believed that this analytical formula can be useful at the early design stage and could probably be combined with the analytical formulations for transmission errors such as those proposed by in [23] in order to account for more realistic excitations including tooth shape deviations and errors.