Introduction

Lithium-ion batteries has been widely used in new energy vehicles due to their high energy density, long cycle life, and high work efficiency [1, 2]. However, the lithium-ion batteries used in complex conditions will inevitably display some degree of polarization. This increases the terminal voltage of the battery and leads to a virtual potential of the fully charged battery; this then reduces the energy density of the battery. Hu et al. [3] proposed a fractional-order equivalent circuit model and parameterized this using a Hybrid Genetic Algorithm/Particle Swarm Optimization method. The model can predict the voltage response with a root-mean-squared error of less than 10 mV under various driving-cycle-based tests. Perez et al. [4] proposed an innovative approach to devising optimally health-conscious fast-safe charge protocols. This mathematical model of a multi-objective optimal control problem was formulated via a coupled electro-thermal aging battery model. The Legendre-Gauss-Radau pseudo spectral method with adaptive multi-mesh-interval collocation was employed to solve the highly nonlinear six-state optimal control problem. Here, severe polarization leads to accumulation and crystallization of large amounts of Li+ near the negative electrode of the lithium-ion battery. This in turn affects the safety and service life of the battery [5, 6]. Therefore, research on the polarization characteristics of power lithium-ion batteries has become a key point in the optimal design of battery power systems [7–9].

Most early studies on the characteristics of power lithium-ion batteries used experimental methods [10,11,12] and were complicated using many resources. Unfortunately, it still remains difficult to achieve multi-physics control due to the complicated experimental environment.

Research on polarization characteristics based on numerical models has developed rapidly in recent years via advances in electrochemical theory and computer technology. The literature [12,13,14,15] details the influence of the polarization voltage on the terminal via the equivalent circuit model of lithium-ion batteries. Nyman et al. analyzed the principle of the generation of the polarization voltage using electrochemical numerical model. Yang et al. [16] analyzed the polarization characteristics of lithium-ion batteries in different charging modes based on the electrochemical-thermal coupling model. Yao et al. [17] studied the effects of SOC, charge/discharge rate, charge/discharge mode, and ambient temperature on the polarization voltage of lithium-ion batteries via experimental method. Li et al. [18] quantitatively analyzed the ohmic polarization, concentration difference polarization, and activation polarization of LiFePO4 power batteries under different discharge rate based on the electrochemical-thermal coupling model. Kang et al. [19] proposed a practical method to analyze the time dependency of the elementary polarization in the process of current pulse discharging. The influence of the uncompensated ohm resistance, interfacial impedance, and diffusion impedance to the total cathode polarization was then deeply studied and examples of high-power batteries have been reported. Ohzuku et al. [20] discovered that the chemical polarization characteristic of the lithium insertion electrodes participated in the electrode processes for storing and delivering electricity in batteries. However, complete elimination of the ohm voltage drop superimposed with chemical polarization is difficult, mainly because of the porous nature of the electrolyte thin film used to separate electrodes.

This paper used engineering to improve a real lithium-ion battery via a high-fidelity electrochemical-thermal coupling model, which restores the working state of lithium-ion battery under complicated working conditions with high precision mathematical model. The polarization voltage of the power lithium-ion battery under cyclic charging-discharging conditions is studied according to the high-fidelity electrochemical coupling model. The HPPC experimented method is applied to analyze the polarization of internal resistance characteristics of power lithium-ion batteries under different working conditions. The results of the polarization voltage of the numerical model are very consistent with the law of polarization internal resistance obtained by HPPC experiments. This indicates that the model is effective and the analysis results are reliable.

The paper is organized as follows: the “Experimental equipment and the battery” section describes the experimental equipment and the battery to be researched. The “Electrochemical-thermal coupling model” section illustrates the construction of the electrochemical-thermal coupling model. The “Analysis of calculation results” section reports the effects of cyclic charge/discharge, charge-discharge current rate, temperature, and cycle times on the polarization voltage are analyzed based on the mathematical model. The “HPPC experimental analysis” section discusses the relationships between the internal resistance of the battery with the SOC, temperature, and current multiplier from HPPC experiments; these are then compared with the results of previous mathematical models.

Experimental equipment and the battery

The battery charging/discharging equipment is the Bet’s battery test system (BTS15005C) made in Ningbo, China. Figure 1 b shows that up to four independent experiments can be operated simultaneously due to the multiple channels of the system. It can realize different experimental conditions such as constant current, constant voltage, and constant power. The experimental data can be collected in real time with high accuracy. The incubator is a high-temperature test chamber (HL404C, Fig. 1a) manufactured in Chongqing, China. The temperature range can reach − 40 to 150 °C. The equipment’s specific parameters are detailed in Table 1.

Fig. 1
figure 1

Pictures of experimental equipment: a incubator; b Bet’s battery test equipment

Full size image
Fig. 2
figure 2

Picture of LG (PHEV) battery

Full size image
Table 1 Equipment parameters
Full size table
Table 2 Parameters of the LG (PHEV) battery
Full size table

Electrochemical-thermal coupling model

The structure and principle of the electrochemical-thermal coupling model

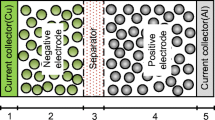
The research object of this paper is a laminated polymer-powered lithium-ion battery. The electrochemical principle model is based on the pseudo-two-dimensional (P2D) model proposed by Newman et al. [21]. Since the cell model is much smaller in the thickness direction (x) and the particle radius direction (r) than in the length direction and the width direction, the transfer of lithium ions in the liquid phase is generally considered to be uniformly transmitted along x. The electrochemical model is established by taking the x-direction as the unit surface. Figure 3 shows that the model is made of five parts, including a positive current collector, a positive electrode, a diaphragm, a negative electrode, and a negative current collector. The gel polymer electrolyte fills the entire interior of the cell as a medium for Li+ transfer between the positive and negative electrodes. A schematic diagram of the electrochemical-thermal coupling model is shown in Fig. 4. The electrochemical model generates heat rate that affects the temperature of the single cell according to the energy equation; the cell temperature change would affect the battery performance parameters according to the Arrhenius equation.

Fig. 3
figure 3

Electrochemical schematic diagram of the power lithium-ion battery model

Full size image
Fig. 4
figure 4

Schematic diagram of the electrochemical–thermal coupling model

Full size image

Equations of the electrochemical–thermal coupling model

The electrochemical model can be described by five state partial differential equations, including the following: solid-phase and liquid-phase electron conservation equations, solid-phase and liquid-phase charge conservation equations, and reaction kinetics equation. These five equations reflect the material distribution of the solid phase in the r direction, the potential distribution of the solid phase in the x-direction, the material distribution and potential distribution of the liquid phase in the x-direction, and the electrochemical reaction rate [22]. Meanwhile, the electrochemical model also considers side reactions during cyclic charge and discharge. The effect of temperature changes of a single-cell lithium-ion battery on the electrochemical model is reflected in the Arrhenius equation, and the effect of the electrochemical model of the cell on the cell temperature is determined via the heat production equation. The heat production model consists of the battery’s energy conservation equation and the heat generation equation of the battery.

Electron conservation equation

The numerical model conforms to the theory of porous electrodes. The solid phase ions are evenly distributed in the electrode. Each point in the x-direction of the electrode has an embedded particle. Therefore, there is an r-direction particle distribution at the corresponding position in the x-direction, and the distribution satisfies Fick’s second law:

$$ \frac{\partial {c}_s\left(x,t,r\right)}{\partial t}-\frac{D_s}{r^2}\left[{r}^2\frac{\partial {c}_s\left(x,t,r\right)}{\partial_r}\right]=0\kern0.5em r\in \left(0,{R}_s\right) $$
(1)

where r ∈ (0, Rs) is the radial coordinate cs(x, t, r) is the lithium-ion concentration distribution function inside the solid phase spherical particles, and Ds is the solid phase diffusion coefficient.

Lithium-ion concentration distribution inside the initial solid phase spherical particles is given as:

$$ {\left.\partial {c}_{\mathrm{s}}\left(x,t,r\right)\right|}_{t=0}=\partial {c}_{\mathrm{s},0} $$
(2)

The boundary conditions are:

$$ {\left.{D}_{\mathrm{s}}\frac{\partial {c}_{\mathrm{s}}\left(x,t,r\right)}{\partial r}\right|}_{r=0}=0 $$
(3)
$$ {\left.{D}_{\mathrm{s}}\frac{\partial {c}_{\mathrm{s}}\left(x,t,r\right)}{\partial r}\right|}_{r={R}_{\mathrm{s}}}=-\frac{j_{\mathrm{f}}\left(x,t\right)}{a_{\mathrm{s}}F} $$
(4)

Here, jf(x, t) is the distribution function of the local current density in the x-direction with time t, representing the electrochemical reaction rate of the particle surface (jf(x, t) ≥ 0 represents the release ion); F is the Faraday constant, and as is the specific surface area of the particle and satisfies the following equation:.

$$ {a}_{\mathrm{s}}=\frac{3{\varepsilon}_{\mathrm{s}}}{R_{\mathrm{s}}} $$
(5)

Here, εs is the solid phase volume fraction

The formula for the conservation of lithium ions in electrolytes is:

$$ \frac{\partial }{\partial t}{\varepsilon}_{\mathrm{e}}{c}_{\mathrm{e}}\left(x,t\right)=\frac{\partial }{\partial x}\left[{D}_{\mathrm{e}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right)\right]+\left(1-{t}_{+}\right)\frac{j_{\mathrm{f}}\left(x,t\right)}{F} $$
(6)

where ce(x, t) is the lithium-ion concentration distribution function in the electrolyte phase, εe is the liquid volume fraction, t+ is the transfer coefficient of Li+, and \( {D}_{\mathrm{e}}^{\mathrm{e}\mathrm{ff}} \) is the effective particle diffusion coefficient of the liquid phase satisfying the Rugman correction. According to the Bruggeman relationship, \( {D}_{\mathrm{e}}^{\mathrm{e}\mathrm{ff}}={D}_{\mathrm{e}}{\varepsilon}_{\mathrm{e}}^{\mathrm{Brugg}}, \) where De is the diffusion coefficient of the electrolyte phase.

The governing equation for the lithium-ion concentration in the positive and negative regions is:

$$ \frac{\partial }{\partial t}{\varepsilon}_{\mathrm{e},\mathrm{j}}{c}_{\mathrm{e}}\left(x,t\right)=\frac{\partial }{\partial x}\left[{D}_{\mathrm{e},\mathrm{j}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right)\right]+\left(1-{t}_{+}\right)\frac{j_{\mathrm{f}}\left(x,t\right)}{F}\kern0.5em j=\mathrm{p},\mathrm{n} $$
(7)

The diaphragm area is

$$ \frac{\partial }{\partial t}{\varepsilon}_{\mathrm{e},\mathrm{film}}{c}_{\mathrm{e}}\left(x,t\right)=\frac{\partial }{\partial x}\left[{D}_{\mathrm{e},\mathrm{film}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right)\right] $$
(8)

where εe, n, εe, film, and εe, p are the volume fractions of the positive electrode, the electrolyte, and the negative electrode, respectively. Terms εe, t+, and \( {D}_{\mathrm{e}}^{\mathrm{e}\mathrm{ff}} \) are in the positive electrode, the electrolyte, and the negative electrode; these are constants having unequal values. The boundary conditions are as follows:

$$ \frac{\partial }{\partial x}{c}_{\mathrm{e}}\left(x,t\right){\left|{}_{x=0}=0,\frac{\partial }{\partial x}{c}_{\mathrm{e}}\left(x,t\right)\right|}_{x=L}=0 $$
(9)
$$ -{D}_{\mathrm{e},\mathrm{n}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right){\left|{}_{x={\updelta}_{\mathrm{n}}^{-}}=-{D}_{\mathrm{e},\mathrm{film}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right)\right|}_{x={\updelta}_{\mathrm{n}}^{+}} $$
(10)
$$ -{D}_{\mathrm{e},\mathrm{film}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right){\left|{}_{x={\delta}_{\mathrm{n}}+{\updelta}_{\mathrm{film}}^{-}}=-{D}_{\mathrm{e},\mathrm{film}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{C}_{\mathrm{e}}\left(x,t\right)\right|}_{x={\delta}_{\mathrm{n}}+{\updelta}_{\mathrm{film}}^{+}} $$
(11)

As shown in Fig. 3, δn, δfilm, and δp represent the thickness of the positive electrode, diaphragm, and negative electrode region, respectively, and L is the total thickness of the battery from the negative electrode to the positive electrode.

The initial concentration of the liquid phase is:

$$ {\left.{C}_e\left(x,t\right)\right|}_{\mathrm{t}=0}={C}_e\left(x,t\right)\kern0.5em x\in \left(0,L\right) $$
(12)

Charge conservation equation

The conservation of charge in the solid phase of the electrode satisfies Ohm’s law:

$$ \frac{\partial }{\partial x}\left[{\sigma}^{\mathrm{eff}}\frac{\partial }{\partial x}{\phi}_s\left(x,t\right)\right]-{j}_{\mathrm{f}}\left(x,t\right)=0\kern0.5em x\in \left(0,L\right) $$
(13)

where ϕs(x, t)and σeff are the solid phase potential distribution function and the effective conductivity, respectively; σeff can be evaluated by the active material reference conductivity, i.e., σeff = σεs.

The conductivity is assumed to be constant (i.e., \( x\in \left(0,{\delta}_{\mathrm{n}}\right)\ {\sigma}^{\mathrm{eff}}={\sigma}_{\mathrm{n}}^{\mathrm{eff}} \),\( x\in \left({\delta}_{\mathrm{n}}+{\delta}_{\mathrm{film}},L\right)\ {\sigma}^{\mathrm{eff}}={\sigma}_{\mathrm{p}}^{\mathrm{eff}} \)) in the negative electrode, the separator, and the positive electrode. The boundary conditions on the current collector are proportional to the applied current:

$$ -{\sigma}^{\mathrm{eff}}\frac{\partial }{\partial x}{\phi}_{\mathrm{s}}\left(x,t\right){\left|{}_{x=0}=-{\sigma}^{\mathrm{eff}}\frac{\partial }{\partial x}{\phi}_{\mathrm{s}}\left(x,t\right)\right|}_{x=L}=\frac{I(t)}{A} $$
(14)

where A is the plate area, and I(t) is the anode discharge current that conforms to the symbol convention. Zero current conditions are required to meet the boundary conditions in the diaphragm.

$$ \frac{\partial }{\partial x}{\phi}_{\mathrm{s}}\left(x,t\right){\left|{}_{x={\delta}_{\mathrm{n}}}=\frac{\partial }{\partial x}{\phi}_{\mathrm{s}}\left(x,t\right)\right|}_{x={\delta}_{\mathrm{n}}+{\delta}_{\mathrm{film}}}=0 $$
(15)

The law of conservation of the charge of the electrolyte phase is as follows:

$$ \frac{\partial }{\partial x}\left[{\kappa}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{\phi}_{\mathrm{c}}\left(x,t\right)\right]+\frac{\partial }{\partial x}\left[{\kappa}_{\mathrm{D}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}\ln {c}_{\mathrm{e}}\left(x,t\right)\right]+{j}_{\mathrm{f}}\left(x,t\right)=0 $$
(16)

where ϕc(x, t) is the electrolyte phase potential, and κeff is the effective ionic conductivity. According to the Bruggeman relationship, \( {\kappa}^{\mathrm{e}\mathrm{ff}}=\kappa {\varepsilon}_{\mathrm{e}}^{\mathrm{Brugg}} \) can be obtained, where κ is the ionic conductivity of the electrolyte and \( {\kappa}_{\mathrm{D}}^{\mathrm{eff}} \) is the effective ion diffusion conductivity of the electrolyte. Thus, \( {\kappa}_{\mathrm{D}}^{\mathrm{eff}}=\frac{2 RT{\kappa}^{\mathrm{eff}}}{F}\left({t}_{+}-1\right) \).

The boundary conditions at the two current collectors are zero flux.

$$ \frac{\partial }{\partial x}{\phi}_e\left(x,t\right){\left|{}_{x=0}=\frac{\partial }{\partial x}{\phi}_e\left(x,t\right)\right|}_{x=L}=0 $$
(17)

The flux continuity can be described as following at the electrode membrane interface:

$$ {\kappa}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{\phi}_{\mathrm{c}}\left(x,t\right)+{\kappa}_{\mathrm{D}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{c}_{\mathrm{e}}\left(x,t\right){\left|{}_{x_{-}}={\kappa}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{\phi}_{\mathrm{c}}\left(x,t\right)+{\kappa}_{\mathrm{D}}^{\mathrm{e}\mathrm{ff}}\frac{\partial }{\partial x}{c}_{\mathrm{e}}\left(x,t\right)\right|}_{x_{+}} $$
(18)

Electrode dynamic

The material distribution of the field variables cs(x, t, r), ce(x, t), ϕs(x, t), and ϕc(x, t) is inflected by the aforementioned differential Eqs. [1], [2], [3], and [4]; the Butler-Volmer electrochemical kinetic equations are solved by coupling four field variables together. The influence of the SEI film growth of the battery on the battery performance parameters must be considered to ensure the high-fidelity of the numerical model in the state of cyclic charge and discharge. Since the SEI film thickness of the battery side reaction occurs mainly in the negative electrode region, the numerical model used here only analyzes the side reaction state of the negative electrode. The internal current density of the battery is given as:

$$ {j}_{\mathrm{f}}\left(x,t\right)={j}_{\mathrm{f},\mathrm{m}}\left(x,t\right)+{j}_{\mathrm{f},\mathrm{s}}\left(x,t\right) $$
(19)

where jf, m(x, t) is the main reaction current density distribution, and the time relationship function satisfies Eq. (6); jf, s(x, t) is the side reaction current density distribution function. Since the film thickness of side reaction of the battery is irreversible, the electrode dynamics equation describing the film thickness of side reaction can be replaced by the Tafel equation in the formula (7):

$$ {j}_{\mathrm{f},\mathrm{s}}\left(x,t\right)={a}_s{i}_o\left(x,t\right)\left[\exp \left(-\frac{\alpha F}{RT}\right){\eta}_s\left(x,t\right)\right] $$
(20)
$$ {j}_{\mathrm{f},\mathrm{s}}\left(x,t\right)={a}_{\mathrm{s}}{i}_0\left(x,t\right)\left[\exp \left(-\frac{\alpha F}{RT}\right){\eta}_{\mathrm{s}}\left(x,t\right)\right] $$
(21)

where as is the battery transfer coefficient, i0(x, t) is the current density of the corresponding one-way absolute reaction rate when the electrode potential is 0, and αa, αc, and α are the electrode reaction transfer coefficient, αa + αc = 1.

The over-potential ηs(x, t) of the side reaction satisfies:

$$ {\eta}_s\left(x,t\right)={\phi}_{\mathrm{s}}\left(x,t\right)-{\phi}_{\mathrm{e}}\left(x,t\right)-{U}_{\mathrm{j}}^{\mathrm{ref}}\left({\theta}_{\mathrm{j}}\left(x,t\right)\right)-\frac{R_{\mathrm{RSE},\mathrm{j}}}{a_{\mathrm{s}}}{j}_{\mathrm{f}}\left(x,t\right)\kern0.5em j=\mathrm{n},\mathrm{p}\;x\in \left(0,L\right) $$
(22)

where the equilibrium potential, \( {U}_{\mathrm{j}}^{\mathrm{ref}} \), is usually taken as 0.4 V for the SEI film thickening side reaction. After obtaining the internal anode SEI film thickening side reaction rate, the corresponding thickening rate of the SEI film is as follows:

$$ \frac{\partial {\delta}_{\mathrm{f}\mathrm{ilm}}\left(x,t\right)}{\partial t}=-\frac{M_{\mathrm{p}}}{a_{\mathrm{s}}{\rho}_{\mathrm{s}}F}{j}_{\mathrm{f},\mathrm{s}}\left(x,t\right) $$
(23)

where δfilm(x, t) is the thickness distribution function of the SEI film. Term Mp is the average molar mass of the reaction product, and ρp is the average density of the product. The film resistance distribution of the SEI film is:

$$ {R}_{\mathrm{film}}\left(x,t\right)={R}_{\mathrm{SEI}}+\frac{\delta_{\mathrm{film}}\left(x,t\right)}{\kappa_{\mathrm{p}}} $$
(24)

Since the SEI film thickening side reaction is irreversible, the corresponding rate of battery capacity decay can be expressed as the loss rate of lithium ions:

$$ \frac{\partial Q}{\partial t}={\int}_0^{\delta_{\mathrm{n}}}{j}_{\mathrm{f},\mathrm{s}}\left(x,t\right) Adx $$
(25)

Here, Q is the total amount of recyclable lithium-ions.

Arrhenius equation

To obtain a high-fidelity electrochemical model, the Arrhenius relationship between the model parameter properties and the reaction temperature T satisfies the following equation:

$$ \psi ={\psi}_{\mathrm{ref}}\exp \left[\frac{E_{\mathrm{act}}^{\uppsi}}{R}\left(\frac{1}{T_{\mathrm{ref}}}-\frac{1}{T}\right)\right] $$
(26)

Term ψ is the temperature-related parameter, Tref is the reference temperature, and ψref is the value when the reference temperature is 25 °C. The temperature sensitivity of each single ψ is controlled by the activation energy \( {E}_{\mathrm{act}}^{\uppsi}\left(J/ mol\right) \).

Energy conservation equation

Assuming that the battery reaction temperature is evenly distributed, the thermal model of this paper is a three-dimensional model considering the temperature distribution in the x, y, and z directions. The positive electrode, the negative electrode, and the diaphragm are different materials. Thus, to ensure the accuracy of the model, the energy conservation equations used to distinguish the temperature between the three vary with time as follows:

$$ \rho {C}_{\mathrm{p}}\frac{\partial T}{\partial t}={\lambda}_{\mathrm{x}}\frac{\partial^2T}{\partial {x}^2}+{\lambda}_{\mathrm{y}}\frac{\partial^2T}{\partial {x}^2}+{\lambda}_{\mathrm{z}}\frac{\partial^2T}{\partial {x}^2}+q-{q}_{\mathrm{conv}} $$
(27)

Here, ρ is the average density of the battery, and Cp is the specific pressure specific heat capacity; T is the reaction temperature; λx,  λy, and λz are the thermal conductivity in the x, y, and z directions, respectively. In addition, q is the heat generation rate of the power lithium-ion battery, qconv is the thermal convection on the surface of the battery (heat dissipation rate).

The battery heat generation rate q can be obtained as follows:

$$ q={q}_{\mathrm{i}}+{q}_{\mathrm{j}}+{q}_{\mathrm{c}}+{q}_{\mathrm{r}} $$
(28)

where qi is the irreversible heat of the reaction. Term qj is the ohm heat, qc is the contact resistance heat, and qr is the reversible entropic heat.

The volumetric reaction heat generated in a finite controlled volume is equal to the reaction current j(x, t) multiplied by the over-potential. Term qi + qj is the Joule heat of the reaction, obtained by multiplying the volume of the one-dimensional region of the battery by the reaction heat and the plate area A.

$$ {q}_{\mathrm{i}}+{q}_{\mathrm{j}}=A{\int}_0^Lj\left({\phi}_{\mathrm{s}}-{\phi}_{\mathrm{e}}-U\right) dx $$
(29)

The reversible entropic heat is:

$$ {q}_{\mathrm{r}}=-\left(T\frac{\partial U}{\partial T}\right)I(t) $$
(30)

The ohm heat is generated by the contact resistance Rf between the current collector and the electrode:

$$ {q}_{\mathrm{e}}=I{(t)}^2\frac{R_{\mathrm{f}}}{A} $$
(31)

Since the current collector is a metal, the Joule heat qe generated can be neglected.

The heat convection heat dissipation rate qconv satisfies:

$$ {q}_{\mathrm{conv}}=\frac{2h}{d}\left(T-{T}_{\mathrm{amb}}\right) $$
(32)

where h is the heat exchange coefficient of the surface of the battery. Term d is the distance between the two thermal planes.

Heat generation equation

For the double electrolyte battery, the total generated heat of the battery can be expressed as below ignoring the influence of the mixed enthalpy change and the phase change process (combined with the electrochemical model):

$$ Q=\sum {a}_{\mathrm{s}\mathrm{j}}{i}_{\mathrm{nj}}\left({\varnothing}_{\mathrm{s}}-{\varnothing}_{\mathrm{e}}-{U}_{\mathrm{j}}\right)+\sum {a}_{\mathrm{s}\mathrm{j}}{i}_{\mathrm{nj}}T\frac{\partial {U}_j}{\partial T}+{\sigma}^{\mathrm{e}\mathrm{ff}}\nabla {\varnothing_{\mathrm{s}}}^2+{k}^{\mathrm{e}\mathrm{ff}}\nabla {\varnothing_{\mathrm{e}}}^2+{k}_{\mathrm{D}}^{\mathrm{e}\mathrm{ff}}\nabla {\varnothing}_{\mathrm{e}}\nabla \ln {c}_{\mathrm{e}} $$
(33)

Here, the summation covers all reactions. The first term on the right represents the deviation of the potential in each control volume from the equilibrium potential (irreversible heat). The second term arises from the entropic effects (reversible heat). Summation of the two parts represents the irreversible and reversible heats associated with each electrochemical reaction. The third term represents the ohm heat arising from the matrix phase, while the last two terms arise from ohm heat in the solution phase. Note that all the terms that are needed in Eq. (14) can be predicted using the same electrochemical model; hence it is possible to simulate the thermal–electrochemical behavior of the cell [23].

Parameters of the model

The research object is a new energy vehicle polymer-powered lithium-ion battery. The cathode material is LixC6, and the anode material is LiyMO2. The electrolyte solution is composed of EC: DMC solvent, 1 M LiPF6 and p (VDF-HFP) has a volume ratio of 1:2. The cathode current collector is made of Cu, and the anode current collector material is Al. The material properties and the microscopic model parameters of the power lithium-ion battery are shown in Table 3 and Table 4, respectively.

Table 3 Material properties of power lithium-ion battery
Full size table
Table 4 Microscopic model parameters of power lithium-ion battery
Full size table

The parameters are obtained from the battery manufacturer, the specific conditions of the materials, and experiments.

Analysis of calculation results

Analysis of polarization voltage characteristics under cyclic charge and discharge

When a battery is in operation, the phenomenon whereby the terminal voltage deviates from the equilibrium potential is called as battery polarization [24]. The capacity and health state of the battery are affected by the polarization voltage. Meanwhile, the internal polarization of lithium-ion batteries can be divided into ohmic polarization, concentration polarization, and electrochemical polarization. The electrochemical polarization voltage is very small, and thus is not considered here. The battery is cyclically charged in the numerical model according to the working conditions shown in Fig. 5. It is charged at a constant temperature (25 °C) with a constant charge rate of 1 C to a cut-off voltage U1. Next, it is charged to a cut-off current I2 at a constant voltage, and later discharged to a cut-off voltage U at a constant current; finally, allowed to stand for 1 h.

Fig. 5
figure 5

Current and voltage curve of numerical model

Full size image

In a charge and discharge process, the lithium-ion battery undergoes constant current charging, constant voltage charging, standing, and constant current discharging, and standing. The curves of polarization voltage and terminal voltage of the battery are shown in Fig. 6 during the entire charge and discharge period. In the initial stage of charge and discharge, the polarization voltage of the battery responds rapidly with the change of the terminal voltage. With a rapidly increasing terminal voltage, the polarization voltage decreases to a stable state, and the growth rate of the terminal voltage then slows down. The polarization voltage continues to decrease during the constant voltage charging stage. The terminal voltage and polarization voltage of the stationary stage remain stable after constant voltage charging. The voltage of the constant current discharge phase decreases steadily, and the polarization voltage tends to stabilize after reaching a certain value instantaneously. In addition, once reached the discharge state after the discharge voltage is cut-off, the terminal voltage rises steadily and eventually stabilize, and the polarization voltage then rapidly drops to a certain value, and tends to stabilize.

Fig. 6
figure 6

Current and voltage curve in the numerical mode

Full size image

Figure 7 shows that the ohmic polarization voltage of the battery does not change significantly during charging and discharging. During the constant voltage charging process, the ohmic polarization voltage of the battery gradually decreases, and the ohmic polarization voltage is 0 at the resting state. The concentration polarization voltage and the total polarization voltage of the battery change has a similar trend, and the ohmic polarization voltage in the discharge stage is greater than the ohmic polarization voltage in the charging stage.

Fig. 7
figure 7

Current and voltage curves from the numerical model

Full size image

During the cyclic of the charge/discharge process, there is hysteresis between the polarization voltage and the terminal voltage—this is mainly caused by the polarization voltage, and the responding of the ohmic polarization to the transient voltage of the battery terminal. In addition, the irregularity of the terminal voltage variation of the battery is caused by the concentration polarization voltage. There is a significant difference in the polarization voltage of the battery during the charge/discharge stages. The polarization voltage of the battery in the charging stage is less than the discharge stage.

Influence of the different charge/discharge rate on the polarization voltage

Figure 8 shows the polarization voltage curves of the lithium-ion battery at a charge/discharge rate of 0.5 C and 1.5 C, respectively (at 25 °C). Upon comparing Fig. 8 and Fig. 7, it is obvious that the polarization voltage of the battery is the largest when the charge/discharge rate of the battery is 1.5 C; the corresponding ohmic polarization and concentration polarization are also the largest, and the polarization voltage of the battery is small but without obvious differences in the static state.

Fig. 8
figure 8

Polarization voltage of charge-discharge. a 0.5 C; b 1.5 C

Full size image

Figures 8 and 7 show that a larger charge/discharge current leads to a larger battery polarization voltage and hence a larger corresponding ohmic polarization and concentration polarization. This also shows that when the battery is under high current charging state, it could have an excessively high polarization voltage. This can cause the lithium-ion battery to reach the charging cut-off voltage prematurely resulting a virtual potential.

The positive and negative ions would migrate in the electrolyte considering the charge/discharge process. Inevitably, there is a certain resistance (ohmic internal resistance) during ion migration. In order to overcome this internal resistance, extra voltage must be added to the applied voltage to overcome the resistance and promote ion migration. This extra voltage is transferred to the environment thermally, i.e., ohmic polarization. As the charge and discharge current increases, ohmic polarization will cause a high temperature in the lithium-ion battery during charge/discharge process. The internal resistance of the battery grows with increasing battery discharge current. Ohm’s low states that the polarization tendency of the battery increases with a larger discharge current and more obvious polarization. This is mainly because of the large discharge current. The time required for the battery voltage to reach the discharge cut-off voltage is reduced when the internal resistance increases; thus, the discharge amount is also decreased. On the contrary, the appearance of internal high temperature phenomenon during charging and discharging exacerbates the migration movement of positive and negative ions in the electrolyte. This increases the internal resistance as the current increases resulting in an increase in the ohmic internal resistance. This ultimately promotes ohmic polarization leading to vicious circle.

Moreover, the change in the concentration polarization voltage (the phenomenon where the electrode potential and the equilibrium electrode potential are not equal) is mainly caused by the fact that the ion conduction rate at the electrode is slow, and the ion concentration in the electrolyte body is different from the ion concentration on the electrode surface. During the charge/discharge process, the internal high temperature of the battery has a greater influence on the ion concentration in the electrolyte than on the surface of the electrode. This increases the concentration polarization voltage due to the internal temperature rise of the battery when the charge/discharge has more current.

Impact of the different temperatures on polarization voltage

The polarization voltage curve of the battery at different temperatures are shown in Fig. 9. It clearly shows the polarization voltage of the 1 C cycle charge/discharge rate of the battery at ambient temperatures of − 10 °C, 25 °C, and 45 °C, respectively. The curve of battery polarization voltage is consistent under different ambient temperatures. The polarization voltage is larger when the ambient temperature is lower; thus, the polarization phenomenon is more obvious, which is consistent with prior work [25]. During the standing phase, the polarization voltage of the battery drops sharply and finally stabilizes. The stability value is larger at higher ambient temperature.

Fig. 9
figure 9

Polarization voltage of power lithium-ion battery at different ambient temperatures. a – 10 °C, 25 °C, and 45 °C; b 25 °C and 45 °C

Full size image

Effect of the different cycle number on the polarization voltage

At a constant temperature of 25 °C, the current of cyclic charge/discharge is I1, and the corresponding polarization voltage curve of the battery is shown in Fig. 10. The polarization voltage of the battery changes with cycle times. The polarization voltage in each charge/discharge phase becomes larger and larger as the number of cycles increases; the value of the fallback polarization voltage increases during the stationary phase. In addition, there is more obvious battery polarization with a greater number of cycles. The battery side reactions during the cycle charge/discharge process are accompanied by an increase of the SEI film resistance and a loss of Li+. Therefore, the ohmic polarization voltage increases with the number of cycles. As the fallback amplitude of polarization voltage increases, the concentration polarization voltage of the battery also increases with the number of cycles.

Fig. 10
figure 10

Polarization voltage curve under different cycle times

Full size image

HPPC experimental analysis

Experimental procedure

The internal resistance test of the battery was done according to the HPPC in the Freedom CAR Battery Test Manual. The HPPC test reports the internal resistance value and the regenerative internal resistance value of different discharge depths by applying a pulse current. The flow chart of HPPC is shown in Fig. 11.

Fig. 11
figure 11

Flow chart of HPPC experiment

Full size image

The experimental data of HPPC experiments are shown in Fig. 12. The measured current and voltage data under current I1 are shown in Fig. 12 a and b, respectively, at normal temperature 25 °C with a step discharge/charge state.

Fig. 12
figure 12

Numerical curve of HPPC experiment. a Discharge; b charge

Full size image

The charge/discharge current of the battery changes stepwise (Fig. 13). During charging, the current steps from 1 to 2, and the current steps from 4 to 5 when discharging. As the current changes stepwise, the voltage of the battery also shows a corresponding step response, and then slowly rises. Moreover, the voltage step response is caused by the ohmic internal resistance, and the slow rise after the step is caused by the polarization internal resistance. The ohmic internal resistance of the battery is a transient response, but the polarization internal resistance is a slow response. After the stable charge and discharge for 10 s, the total internal resistance of the battery can be measured by applying voltammetry, and points 3 and 6 in Fig. 13 are the corresponding time of the battery after 10 s of charge/discharge, respectively. The ohmic internal resistance, polarization internal resistance, and total internal resistance of the battery under charge and discharge conditions are Ro, c, Rp, c, Rt, c, Ro, d, Rp, d,and Rt, d.

$$ {R}_{\mathrm{t},\mathrm{c}}={R}_{\mathrm{o},\mathrm{c}}+{R}_{\mathrm{p},\mathrm{c}}\kern0.5em ;\kern0.5em {R}_{\mathrm{t},\mathrm{d}}={R}_{\mathrm{o},\mathrm{d}}+{R}_{\mathrm{p},\mathrm{d}} $$
(34)
Fig. 13
figure 13

Schematic diagram of HPPC internal resistance test. a Discharge; b charge

Full size image

The voltage change is the effect of its ohm resistance at the moment of charge and discharge, then:

$$ {R}_{\mathrm{o},\mathrm{c}}=\frac{U_2-{U}_1}{I}\kern0.5em ;\kern0.5em {R}_{\mathrm{o},\mathrm{d}}=\frac{U_5-{U}_4}{I} $$
(35)

By voltammetry, we can get:

$$ {R}_{\mathrm{o},\mathrm{c}}=\frac{U_3-{U}_1}{I}\kern0.5em ;\kern0.5em {R}_{\mathrm{o},\mathrm{d}}=\frac{U_6-{U}_4}{I} $$
(36)

Relation between the internal resistance of the battery and the SOC

The measured internal resistance of the tested battery under current I1 pulse discharge at 25 °C is shown in Fig. 14a, and the pulsed charging internal resistance is as shown in Fig. 14b. There is almost no change in the ohm resistance of the battery during the charge/discharge phases. The polarization internal resistance of the battery shows a slight rise during discharge when the SOC value is between 0.3 and 1, there is a slight drop during charging. When the SOC value is 0 to 0.3, the polarization internal resistance has a step change, and the polarization internal resistance is the main factor affecting the change in the total internal resistance. The ohmic internal resistance of the battery is greater than the polarization internal resistance from SOC value of 0.3 to 1. The internal resistance of the battery changes during the discharge process and the internal resistance changes during the charging process are equivalent, but there is always a discharge ohmic internal resistance greater than the charging ohmic internal resistance; this is consistent with the polarization voltage characteristic analysis result in the “Analysis of polarization voltage characteristics under cyclic charge and discharge” section.

Fig. 14
figure 14

Relationship between battery polarization internal resistance and battery charged state. a Discharge at 1 C, 25 °C; b charge at 1 C, 25 °C

Full size image

Relation between the internal resistance of the battery and the temperature

The battery is charged and discharged with current I1 at different ambient temperatures. The ohmic internal resistance and the polarization internal resistance are shown in Fig. 15a and b, respectively. The ohmic internal resistance of the battery changes more obviously at different temperatures. The ohmic internal resistance of the battery increases at lower temperatures. This largely determined the material properties of the battery. In addition, there is also a significant change in the polarization internal resistance of the battery at different temperatures. When the temperature is − 10 °C, the polarization internal resistance of the battery is significantly higher than that of 25 °C and 45 °C, but the difference in polarization internal resistance at 25 °C and 45 °C is quite small. In general, the ohmic internal resistance and polarization internal resistance of the battery increase at lower ambient temperature. This is consistent with the analysis of the relationship between the ohmic polarization voltage and the concentration polarization voltage and temperature in the numerical model in the “Impact of the different temperatures on polarization voltage” section.

Fig. 15
figure 15

Relationship between battery internal resistance and ambient temperature. a 1 C, ohmic internal resistance; b 1 C, polarization internal resistance

Full size image

Relation between the internal resistance of the battery and the current rate

The ohmic internal resistance and polarization internal resistance of the battery are shown in Fig. 16 a and b, respectively, at 25 °C and under different charge/discharge currents. There is a small difference in the ohmic internal resistance under different pulse currents. The smaller the charge/discharge current of the battery, the smaller the ohmic internal resistance of the battery. Versus the ohmic internal resistance, there is a significant difference in the polarization resistance of the power lithium-ion battery. The larger the pulse discharge current, the larger the polarization internal resistance of the battery, which is consistent with the numerical analysis results of ohmic polarization voltage and concentration polarization voltage in the “Influence of the different charge/discharge rate on the polarization voltage” section.

Fig. 16
figure 16

Relationship between battery internal resistance and magnitude of current. a 1 C, 25 °C ohmic internal resistance; b 1 C, 25 °C polarization internal resistance

Full size image

Conclusion

  1. (1)

    The ohmic polarization voltage of the battery responds rapidly with changes in the battery’s charge/discharge state; the response of concentration polarization voltage is slow and irregular. There is a significant difference in the polarization voltage of the battery during the charge/discharge stages. The polarization voltage of the battery during the charging stage is less than that in the discharge stage.

  2. (2)

    A larger charge-discharge rate is seen at a lower ambient temperature and at higher cycle number. A larger ohmic polarization voltage and the concentration polarization voltage of the battery leads to a higher virtual potential and lower battery capacity.

  3. (3)

    A larger charge-discharge rate and lower ambient temperature leads to a greater ohmic polarization internal resistance and concentration polarization internal resistance. The influence of the ambient temperature on the internal resistance characteristics is more significant than the charge/discharge rate.

  4. (4)

    Under different SOC conditions, there is no apparent difference in the ohmic internal resistance of the battery, but the difference in polarization internal resistance is obvious. When the SOC is small, the concentration polarization internal resistance of the battery is larger.

The polarization internal resistance of the battery will be further changed via charge/discharge current, ambient temperature, cycle number, and other factors on the polarization of the battery. For example, the increase of the charge/discharge current, ambient temperature, and number of cycles all contribute to the polarization phenomenon of the battery, which also lead to a high battery internal resistance. Meanwhile, the effect of ambient temperature on battery polarization is also considered. This will inevitably cause the temperature rise of the battery under complicated conditions. The obvious temperature rise is not conducive to the charge/discharge of the battery, and this even affects the life of the battery. To reasonably control the unnecessary temperature rise of the battery under complicated working conditions (such as electric vehicles), it is critical to arrange reasonable heat management outside the battery. Currently, the common thermal management of lithium batteries has various forms such as air-cooled, water-cooled, heat pipe cooling, and thermoelectric cooler. In future work, thermoelectric coolers will be rationally optimized and arranged with lithium batteries to ensure reasonable control of temperature rise in the lithium battery under complicated conditions.