Introduction

Several electroanalytical methods include a pre-concentration step in their potential program. This step usually considers the electrochemical or adsorptive accumulation of electroactive species at the surface of the working electrode [1–10]. Once the electroactive species have been accumulated, the potential is scanned and the current sampled. Square-wave voltammetry (SWV) is one of the most widely employed electrochemical techniques for quantitative analysis. This is because it usually involves fast scans and provides high sensitivity [11–15]. Since the current is sampled at the end of every potential pulse, most of capacitive currents are discarded [11–13]. Besides, the oxidation and reduction pulses of SWV are applied sequentially. As a result, the concentration gradients of reagents and products are enhanced close to the electrode surface and the current is higher than that measured with traditional techniques such as cyclic voltammetry [14, 15].

The net peak current (ΔI p) is considered to be the most important parameter of SWV since it is used not only for analytical, but also for mechanistic purposes [11–23]. In this regard, the dependences of ΔI p and the net peak potential (E p) on the square-wave frequency (f) are essential tools for characterizing the mechanism of a given experimental system [16–23]. Particularly for the case of adsorbed species, the values of ΔI p can be employed to calculate the charge transfer rate constant (k s), even for some rather complicated reactions [10, 16–19, 24–26]. Lovrić et al. worked extensively on the theoretical and experimental responses of SWV and especially on those systems where the electrochemical process involves adsorbed species [12, 16–19]. In the case of traces of metal ions, adsorptive accumulation is commonly achieved by adding a suitable ligand that forms a stable and adsorbable complex with the analyte [1–10, 14–19, 27, 28]. The sensitivity of adsorptive stripping voltammetric methods can be notably increased when they are combined with catalytic reactions [1–10]. This last reaction usually refers to a homogeneous redox reaction in which the reduced form of a metal complex is oxidized back to its initial form, yielding an increase of the reduction current. The sensitivity of a catalytic adsorptive stripping voltammetric method strongly depends on the adsorption constant of the electroactive reagent and the efficiency of the catalytic reaction. The former is controlled by the type of ligand while the latter depends on the kind of reagent chosen for the catalytic step. As a result, it is of particular interest to know the rate constants of the electrochemical step and of the coupled redox reaction.

The theory for a catalytic mechanism of soluble species was developed in 1963 by Smith [29]. However, it was necessary to wait almost 20 years until its first application in SWV [30, 31]. Then, the theoretical model was extended to the cases where redox species are firmly immobilized on the electrode surface [32] and where the catalytic electrode mechanism is coupled to the adsorption equilibria of both redox species [10]. The last case can be considered as an electrode reaction in which the adsorbed forms of the redox couple transfer the electrons while both adsorption equilibria are rapidly compensated from the solution.

In the present work, a theoretical model for the catalytic adsorptive stripping response of SWV is presented. The model considers a quasi-reversible electrode process coupled to a catalytic chemical reaction in which the reagent is adsorbed and the product is released to the solution. The adsorbed reactant is in equilibrium with its soluble part, which is a typical situation found in the adsorptive accumulation of traces of metal ions [1–9].

Mathematical model

The following chemical and electrochemical reactions are analyzed:

$$ {O}_{(sol)}\begin{array}{c}\kern1em {K}_{ad}\kern1em \\ {}\kern1em \rightleftarrows \kern1em \\ {}\kern2em \end{array}{O}_{(ads)}\begin{array}{c}\kern1em {k}_s\kern1em \\ {}\kern1em \rightleftarrows \kern1em \\ {}\kern1em n\kern1em \end{array}{R}_{(sol)} $$
(1)
$$ {R}_{(sol)}+{Y}_{(ex)}\begin{array}{c}\hfill {k}_{\mathrm{cat}}^{'}\hfill \\ {}\hfill \to \hfill \\ {}\hfill\ \hfill \end{array}{O}_{(sol)} $$
(2)

It is assumed that the adsorption of the reactant follows a linear isotherm where the adsorption equilibrium has been achieved and where K ad is the adsorption constant. The electrochemical reaction takes place under conditions of low surface coverage and there are no significant interactions between the adsorbed species. In this regard, the electrode reaction occurs through the adsorbed form of the oxidized species and releases the product in the solution, Eq. (1). The adsorption equilibrium of the oxidized species is reversibly compensated from the solution. Also, the mass transfer has been approximated by the diffusion model of a planar electrode. These simplifications correspond to the adsorptive accumulation of traces of a surface-active electroactive species at a macroelectrode [16–18]. The stripping step corresponds to a cathodic SW scan that takes place in an unstirred solution. The parameter k s is the charge transfer standard rate constant, and \( {k}_{\mathrm{cat}}^{'} \) is the second order forward homogeneous rate constant of the catalytic reaction, Eq. (2). Although the backward rate constant of the catalytic step could be also considered, this assumption would increase the number of variables to study and only irreversible catalytic reactions have been reported [29]. Both equations depend on the 2nd Fick’s law according to the following set of differential equations:

$$ \partial {c}_{\mathrm{r}}/\partial t=D\left({\partial}^2{c}_{\mathrm{r}}/\partial {x}^2\right)\hbox{--} {k}_{\mathrm{cat}}{c}_{\mathrm{r}} $$
(3)
$$ \partial {c}_{\mathrm{o}}/\partial t=D\left({\partial}^2{c}_{\mathrm{o}}/\partial {x}^2\right)+{k}_{\mathrm{cat}}{c}_{\mathrm{r}} $$
(4)

It is assumed a common diffusion coefficient value, D = 4 × 10−6 cm2 s−1, and that the species Y is in excess, so its concentration is virtually constant in the course of the voltammetric experiment. Therefore, k cat is a pseudo-first order catalytic rate constant defined as \( {k}_{\mathrm{cat}}={k}_{\mathrm{cat}}^{'}\ {c}_{\mathrm{y}}^{*} \) . Appendix has a list of symbols and abbreviations used in the manuscript. The following boundary conditions are considered for Eqs. (1 and 2):

$$ t=0,\kern0.5em x\ge 0:\kern0.5em \begin{array}{ccc}\hfill \hfill & \hfill {c}_{\mathrm{r}}+{c}_{\mathrm{o}}={c}_o^{*}\hfill & \hfill \hfill \end{array} $$
(5)
$$ {\varGamma}_o^{ini}={K}_{\mathrm{ad}}\ {c}_o^{*} $$
(6)
$$ {c}_{\mathrm{r}}={c}_r^{*}=0 $$
(7)
$$ \begin{array}{ccc}\hfill t>0,\hfill & \hfill x\to \infty :\hfill & \hfill \begin{array}{ccc}\hfill \hfill & \hfill {c}_{\mathrm{o}}\to {c}_o^{*}\hfill & \hfill \hfill \end{array}\hfill \end{array} $$
(8)
$$ {c}_{\mathrm{r}}\to 0 $$
(9)
$$ \begin{array}{ccc}\hfill x=0:\hfill & \hfill \hfill & \hfill \begin{array}{cc}\hfill D{\left(\partial {c}_{\mathrm{o}}/\partial x\right)}_{x=0}=I/nFA\hbox{--} \partial {\varGamma}_{\mathrm{o}}/\partial t\hfill & \hfill \hfill \end{array}\hfill \end{array} $$
(10)
$$ D{\left(\partial {c}_{\mathrm{r}}/\partial x\right)}_{x=0}=\hbox{--} I/nFA $$
(11)
$$ I(t)/nFA={k}_{\mathrm{s}} \exp \left[\hbox{--} \alpha\ \varphi (t)\right]\ \left\{{\left({c}_{\mathrm{o}}\right)}_{x=0}\hbox{--} {\left({c}_{\mathrm{r}}\right)}_{x=0} \exp \left[\varphi (t)\right]\right\} $$
(12)
$$ {\varGamma}_{\mathrm{o}}={K}_{\mathrm{ad}}{\left({c}_{\mathrm{o}}\right)}_{x=0} $$
(13)
$$ \varphi (t)= nF\left[E(t)\hbox{--} E{{}^{\circ}}^{'}\right]/RT $$
(14)

where E(t) is the square-wave potential function, E°′ is the formal potential for a simple redox reaction, n is the number of exchanged electrons, and A is the electrode surface area. The cathodic current has been defined as positive, Eqs. (10–12). Although Eq. (12) is written for soluble species, it does not control the pathway of the electrode reaction. In this regard, the resolution of Eqs. (3 and 4) with the suggested set of boundary conditions determines the functions for the surface concentrations and the way in which the electrode reaction takes place. Other symbols have their usual meaning. The current is normalized according to:

$$ \varPsi (t)=I(t)\ {\left[nFA{c}_o^{*}{\left(f\pi D\right)}^{1/2}\right]}^{\hbox{--} 1} $$
(15)

where f is the square-wave frequency. The solution of the differential Eqs. 3 and 4 with the relevant boundary conditions is obtained by Laplace transforms. However, before going into the Laplace domain, it is necessary to introduce the following change of variables [29]:

$$ \phi ={c}_{\mathrm{r}}+{c}_{\mathrm{o}} $$
(16)
$$ \theta ={c}_{\mathrm{r}} \exp \left({k}_{\mathrm{cat}}t\right) $$
(17)

Thus, a new set of equations is obtained in terms of variables ϕ and θ [29]:

$$ \partial \phi /\partial t=D\left({\partial}^2\phi /\partial {x}^2\right) $$
(18)
$$ \partial \theta /\partial t=D\left({\partial}^2\theta /\partial {x}^2\right) $$
(19)
$$ D{\left(\partial \phi /\partial x\right)}_{x=0}=\hbox{--} \partial {\varGamma}_{\mathrm{o}}/\partial t $$
(20)
$$ D{\left(\partial \theta /\partial x\right)}_{x=0}=\hbox{--} I \exp \left({k}_{\mathrm{cat}}t\right)/nFA $$
(21)

The expression for the current is obtained by using the numerical integration method suggested by Nicholson and Olmstead [33]:

$$ {\varPsi}_{(m)}=\left\{\lambda \hbox{--} a\xi\;{\varXi}_{\mathrm{a}(m)}\hbox{--} \left[{a}^2\xi +{T}_{(m)}\right]{\varXi}_{\mathrm{b}(m)}\right\}{\left\{{\aleph}_{(m)}+a\xi\;{\varXi}_{\mathrm{a}(1)}+\left[{a}^2\xi +{T}_{(m)}\right]{\varXi}_{\mathrm{b}(1)}\right\}}^{\hbox{--} 1} $$
(22)

where λ = ( f π)-1/2; ξ = (a 2 − k cat)−1; Ξ a(m) = \( {\displaystyle \sum_{j=1}^{m-1}} \) Ψ (j) S (i) k cat –1/2; Ξ b(m) = \( {\displaystyle \sum_{j=1}^{m-1}} \) Ψ (j) Q (i); a = D 1/2(K ad)−1; T (m) = exp.[φ(m)]; ℵ (m) = D 1/2 k s −1 exp.[α φ(m)]; S (i) = erf[(k catδ i)1/2] – erf[(k catδ(i – 1))1/2]; i = m – j + 1; Q (i) = exp.[ξ δ i] erfc[(k catδ i)1/2] – exp.[ξ δ (i – 1)] erfc[(k catδ(i – 1))1/2]; δ = (q f)−1 and a value of q = 50 was used as the number of subintervals considered for the numerical integration steps. In other words, the variable δ represents a differential of time and each wave was divided in 50 subintervals. This number of time subintervals ensures a numerical error lower than 0.5 % and provides calculated voltammograms within a second [34].

Results and discussion

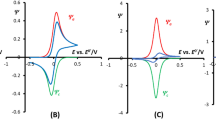
The studies of the electrode kinetics in SWV can be performed by changing f as well as the square-wave amplitude (E sw). The value of f is usually the parameter of choice since it changes the time scale and, thus, the apparent electrode kinetics of the experiment. Figure 1 shows SW voltammograms calculated for systems with different reversibility of the electrochemical reaction when f is varied from 10 to 1000 Hz. The forward (Ψ f) and backward (Ψ b) components of current are indicated in every plot for the sake of clarity. The difference of Ψ f and Ψ b gives the dimensionless net current (ΔΨ). In all cases, the peak of the dimensionless net current (ΔΨ p) increases with f. Since the profiles shown in this figure have been calculated for a rather low value of k cat, they are very similar to those described in the pioneering manuscript of Lovrić et al. [16]. Therefore, the value of ΔΨ p depends linearly on the square root of f for systems with irreversible and reversible electrochemical charge transfer. Nevertheless, the dependence of ΔΨ p on f is not linear and shows a maximum. This maximum is a well-known characteristic that is conditioned by the value of k s and the analyzed timescale [16]. Moreover, the quasi-reversible maximum can be used to estimate the rate of the charge transfer reaction without fitting the experimental data with theoretical curves [18, 35].

Fig. 1
figure 1

Theoretical SW voltammograms for α = 0.5, n = 1, dE = 5 mV, E sw = 50 mV, K ad = 0.3 cm, k cat = 0.01 s−1, k s/cm s−1 = (A) 0.001, (B) 1, (C) 1000, f/Hz = (a) 10, (b) 100, and (c) 1000

Full size image

In the case of irreversible systems, Ψ f and Ψ b have the same sign, Fig. 1A. Besides, the peak potential (E p) changes linearly with log(f ), not shown. For reversible electrochemical reactions, the Ψ f is higher than Ψ b, and the ratio between both currents is constant for all frequencies, Fig. 1C. The shape and size of Ψ f and Ψ b of quasi-reversible electrochemical systems depend on the timescale of the experiment [16].

Theoretical SW voltammograms corresponding to irreversible, quasi-reversible ,and reversible electrochemical reactions are exhibited in Figs. 2A–C, respectively. On the one hand, the diminution of k s shifts E p towards more negative values. On the other hand, SW voltammograms show sigmoid profiles due to the effect of the catalytic reaction. Each of these sigmoid voltammograms is characterized by a respective value of limiting current. The increment of f decreases the magnitude of the dimensionless current because the catalytic reaction has less time to take place. In other words, less amount of product is catalyzed back to the oxidized form of the electroactive species. Since the limiting current of these normalized voltammograms decreases linearly on the square root of f, the dimensional limiting current should be independent of f for systems with high enough values of k cat.

Fig. 2
figure 2

Calculated SW voltammograms for α = 0.5, n = 1, dE = 5 mV, E sw = 50 mV, K ad = 0.3 cm, k cat = 1000 s−1, k s/cm s−1 = (A) 0.001, (B) 1, and (C) 1000, f/Hz = (a) 10, (b) 100, and (c) 1000

Full size image

Figure 3 shows the dependence of ΔΨ p as a function of log (k s) for different values of k cat. Three regions can be observed. It has to be considered that these three regions depend on the timescale of the experiment. All the curves have been calculated at 100 Hz, which is an average value of the available SW frequencies. For k s >100 cm s−1, the system can be considered as electrochemically reversible and the value of ΔΨ p is a constant that depends on k cat. In a similar way, for k s <0.01 cm s−1, the system would present an irreversible charge transfer reaction where the value of ΔΨ p is a constant that also depends on k cat. Finally, for 0.01 cm s−1 < k s < 100 cm s−1, the system would be quasi-reversible, and it might exhibit a maximum depending on the value of k cat. The quasi-reversible maximum is observed for systems with relatively low catalytic contribution, curves (a–c). However, the quasi-reversible maximum disappears for the electrochemical reactions with high values of k cat, curves (d, e).

Fig. 3
figure 3

Dependence of ΔΨ p on the logarithm of k s calculated for α = 0.5, n = 1, dE = 5 mV, E sw = 50 mV, K ad = 0.3 cm, f = 100 Hz, k cat/s−1 = (a) 0.01, (b) 10, (c) 30, (d) 100, and (e) 300

Full size image

The effect of E p on the logarithm of k s is shown in Fig. 4 for different values of k cat. Again, it is possible to distinguish three regions. However, the value of k cat affects the range of k s in which the system behaves as quasi-reversible. For k cat <1 s−1 and for k s >100 cm s−1, the value of E p is constant and the system can be considered as reversible. Also, for k cat <1 s−1 but with k s <0.01 cm s−1, the value of E p changes linearly with log (k s) and has a slope of 0.118 mV dec−1. In both cases, the effect of the catalytic reaction is low. Conversely, the peak potentials depend on both parameters if k cat >1 and k s <100 cm s−1. When k cat >1 and k s >100 cm s−1, the value of ;E p changes linearly with log (k cat) and has a slope of (0.030 ± 0.002) mV dec−1. However, if k cat >1 and k s <0.01 cm s−1, the value of E p changes linearly with log (k cat) and has a slope of (0.087 ± 0.003) mV dec−1. For intermediate values of k s, the system is considered to be quasi-reversible and the value of k cat produces serious changes on E p. Under those conditions, the dependence of E p on log (k s) can change from a constant value to a linear behavior.

Fig. 4
figure 4

Dependence of E p on the logarithm of k s calculated for α = 0.5, n = 1, dE = 5 mV, E sw = 50 mV, K ad = 0.3 cm, f = 100 Hz, k cat/s−1 = (a) 0.01, (b) 10, (e>) 30, (d) 100, and (e) 300

Full size image

Despite the dependencies described above might be of some interest, it is important to take in mind that the kinetic of those systems is controlled by the conditional values of k s, k cat, and K ad. Thus, the apparent kinetic of those parameters changes and complicates the study when f is varied. Moreover, it becomes practically impossible to find the quasi-reversible maximum of ΔΨ p by varying f. In this regard, it is advisable to modify the concentration of the catalyzer or to vary the value of E sw instead of changing the value of f [32, 36, 37].

As it was stated above, in SWV, the electrode kinetics can be studied also by varying E sw. Figure 5 shows SW voltammograms calculated for a system in which the catalytic and the charge transfer reactions are in the quasi-reversible range. Figure 5A shows SW voltammograms of the normalized net current and Fig. 5B exhibits the forward and backward components of current. The voltammograms of ΔΨ show quite symmetric bell-shaped curves for those profiles calculated with the lowest values of E sw. Nevertheless, a slight shoulder appears at potentials more negative than E p if E sw < 75 mV, curves (a, b). For rather high values of E sw, the shoulder separates from the main signal, curves (c, d). The voltammetric peaks can present a second shoulder for scans performed with very high values of E sw and both shoulders appear at potentials more negative than E p, curves (e, f).

Fig. 5
figure 5

Theoretical SW voltammograms for α = 0.5, n = 1, dE = 5 mV, K ad = 0.3 cm, k cat = 10 s−1, k s = 0.1 cm s−1, f = 100 Hz, E sw/mV = (a) 10, (b) 25, (c) 75, (d) 125, (e) 175, (f) 225

Full size image

Although in analytical chemistry it is preferred the analysis of the net current, the mechanistic information of electrochemical processes is more evident in Ψ f and Ψ b. In this regard, the forward peaks are quite bell-shaped curves, which are related to the reduction of the adsorbed species. On the contrary, the reduced product is released in solution and has a complex concentration profile. As a result, the function of Ψ b is also complex. However, the limiting current that is observed at negative potentials is a constant independent of E sw. Although the peak values of Ψ f and Ψ b rise with the increment of E sw, they evidence a kind of limiting value. In this regard, above such a limiting value, only the peak width of ΔΨ increases. This limiting value depends on the values of k s and k cat. However, the contribution of both parameters is not simple and requires further analysis.

Figure 6 shows the dependence of E p and ΔΨ p E sw −1 on E sw. As it was indicated above, we are studying if it is possible to extract kinetic information from those curves. The dependence of E p on E sw exhibits changes on the slope at 25 and at 150 mV. However, the ratio ΔΨ p E sw −1 presents maximum values when E sw is close to 25 and 125 mV. Although these dependences might be related to the values of k s and k cat, it is still unclear the contribution of these parameters to the current. Recently, Mirčeski et al. suggested the use of the maximum value of the ratio ΔΨ p E sw −1 for the estimation of k s [24]. Unfortunately, that relationship cannot be directly applied to the reaction scheme of the present study and further analysis is required.

Fig. 6
figure 6

Dependence of E p and ΔΨ p E sw −1 on E sw calculated for α = 0.5, n = 1, dE = 5 mV, K ad = 0.3 cm, f = 100 Hz, k cat = 10 s−1, k s = 0.1 cm s−1

Full size image

Conclusion

The theoretical response of SWV for quasi-reversible electrode processes coupled to a catalytic chemical reaction and where the reagent is adsorbed and the product is released to the solution has been presented. The variation of the SW frequency affects the apparent kinetics of the chemical and electrochemical steps. Characteristics such as the quasi-reversible maximum and the linear dependence of ΔΨ p on f for the case of reversible and irreversible systems prevail when k cat < < 1 s−1. On the contrary, for the case of k cat > 102 s−1, the system is essentially controlled by the catalytic process. For intermediate values of k cat, it is difficult to specify the effect of k cat and k s from the variation of SW parameters. We are focusing our work on founding one or more simple expressions that help experimentalists to estimate the kinetic parameters of their data.