Introduction

The demand for alternative energy storage is growing every year. One of the most promising solution is the electrochemical supercapacitors (ECSC) based on porous electrodes with high surface area whose the main energy is stored in the electric double layer (EDL). The most common type of the porous electrodes used in ECSC is the fine-dispersed carbon electrodes (FDCEs) with a surface area of several hundreds to 3000 m2/g. These electrodes are often produced from activated carbon (AC) [1]. Now that the supercapacitor industry is developing intensively, this encourages researches and their implementation in new practical applications [2].

In a comparison with conventional electrochemical power sources like accumulators, supercapacitors have many advantages such as much longer operating time, almost infinite cyclability, significantly higher power density of stored energy, relative cheapness, ability to work in a wide range of temperature and time of charging–discharging, ecological compatibility, etc. [1, 2]. A very important advantage of ECSC is the fundamental possibility to obtain energy efficiency (the ratio of the energies of discharging and charging), which is close to 100 %. This can be achieved when EDL capacity dominates in total ECSC capacity, and the domination is realized in the double-layer supercapacitors (DLSCs). In contrast, the energy efficiency of accumulators is substantially limited by polarization of the electrode processes due to relatively low exchange currents and slow intercalation.

High energy efficiency is especially important when the ECSCs are used for smoothing of peak load of electrical networks. This field of ECSC application is intensively developing now.

Mathematical models of ECSC can be divided into three different types. First type corresponds to the porous media microscaling modeling. Models of this type focus on mechanisms of the energy storage in porous carbons (see, for example, [3–5]). The second type of models deal with representation of super-capacitor as equivalent circuits (see, for example, [6–8]). The third type of models are carried out within the framework of the theory of porous electrodes [9–11]; this approach can be named as macrokinetics modeling.

The first and the simplest model of this type was a transmission-line model, which can be carried from the work [12]. Due to its simplicity, this model can be used for obtaining analytical solutions [6, 13, 14]. They have been compared with experiments in [13] and used for analyzing of dependences on electrode thickness and heating process in the ECSC [14]. The macrokinetics model has been expanded to take into account the pore size distribution of porous electrode in the work [15]. The ECSC model which takes into consideration the surface conductivity has been developed in [16]. The surface conductivity becomes important when concentration decreases dramatically due to electroadsorption of ions. The model of the supercapacitor electrode which involves intercalation of hydrogen to carbon has been described in [17]; the calculated and experimental data have been also compared. Recently, the model of hybrid asymmetric electrochemical capacitors has developed with taking into account redox couple electrode and a double-layer electrode in [18].

As known, FDCE and, in particularly, activated carbon (AC) comprise a large amount of surface groups: oxygen-, nitrogen-, sulfur-, and other ones [19–22]. A part of these groups participate in quasi-reversible redox reactions, for instance, transition of quinone–hydroquinone. Thus, these reactions make a contribution to the total capacity of ECSC.

This work is devoted to the development of a macrokinetics model in order to investigate the energy efficiency of the supercapacitor and to find the optimal operating modes depending on the device parameters. The model is based on pseudocapacitance of redox reactions of surface groups. ECSC with aqueous electrolyte is observed as such systems have several advantages over nonaqueous ones. They are not only less expensive and more environment friendly but also more reliable with less self-discharge and less degradation rate [23].

The energy efficiency of the supercapacitor system has been studied in [24]; however, pseudocapacitance was not considered. The efficiency of the supercapacitor has also been studied with taking into account side reaction in [25]; namely, a possibility of water decomposition was taken into consideration.

Model description

Let us consider the model of symmetric ECSC (i.e., with the same two electrodes) taking into consideration the quasi-reversible electrochemical redox reactions of surface groups. Equation of charge transfer in the electrolyte can be written as:

$$ \frac{\partial }{\partial x}\left({k}^{\mathrm{e}\mathrm{ff}}\frac{\partial {\varphi}_{\mathrm{e}}}{\partial x}\right)+\frac{\partial }{\partial x}\left({k}_{\mathrm{D}}^{\mathrm{e}\mathrm{ff}}\frac{\partial \ln {c}_{\mathrm{s}}}{\partial x}\right)+\left({j}^C+{j}^{\mathrm{ad}}\right)=0, $$
(1)

where \( {k}^{\mathrm{eff}}={\varepsilon}^{\alpha_i}k(c) \) is the effective conductivity of electrolyte in pores of the electrode, which can be calculated according to the Archie formula, ε is the porosity, α i is the Archie exponent, k(c) is the linear dependence of electrolyte conductivity on the concentration of free electrolyte, and j C is charging current of EDL that is equaled:

$$ {j}^{\mathrm{C}}=SC\frac{\partial \left({\varphi}_{\mathrm{e}}-{\varphi}_{\mathrm{s}}\right)}{\partial t}, $$
(2)

where SC is equal to SC, where S is the specific hydrophilic surface, C is the specific capacitance of EDL per unit of true hydrophilic surface, and φ s is the potential in solid phase.

In Eq. (3), j ad is the adsorption current, which is determined by Butler–Volmer kinetics taking into consideration the Frumkin adsorption isotherm [26]:

$$ {j}^{\mathrm{ad}}=S{i}_0\left\{{A}_1\frac{c}{c_{10}}\left(1-\theta \right) \exp \left(-\beta g\theta \right) \exp \left(\frac{\beta EF}{RT}\right)-{A}_2\theta \exp \left[\left(1-\beta \right)g\theta \right] \exp \left(-\frac{\left(1-\beta \right)EF}{RT}\right)\right\}. $$
(3)

where i 0 is the exchange current for hydrophilic surface, E = (φ s − φ e − E 0) is the overpotential, c is the electrolyte concentration, θ is the fraction of the covered surface, g the rate coefficient of adsorption energy, and the A 1 and A 2 parameters correspond to the concentration c 10, at which the fraction of surface covered with adsorbed ions is equal to the initial fraction of the covered surface θ 0:

$$ {A}_1={\left(1-{\theta}_0\right)}^{-1} \exp \left(\beta g{\theta}_0\right), $$
(4)
$$ {A}_2={\theta_0}^{-1} \exp \left(-\left(1-\beta \right)g{\theta}_0\right). $$
(5)

The equation of electrolyte diffusion is expressed as:

$$ \frac{\partial c}{\partial x}=\frac{\partial }{\partial x}\left({D}^{\mathrm{eff}}\frac{\partial c}{\partial x}\right)+\frac{\left(1-{t}_{+}\right)\left({j}^{\mathrm{ad}}+{q}_i{j}^{\mathrm{C}}\right)}{F}=0 $$
(6)

where \( {D}^{\mathrm{eff}}={\varepsilon}^{\alpha_i}D \) is the effective diffusion coefficient of ions estimated by Archie formula, q i  = ± 1 depending on the electrode.

The equation of conductivity of solid phase is:

$$ \frac{\partial }{\partial x}\left({\sigma}^{\mathrm{eff}}\frac{\partial {\varphi}_{\mathrm{s}}}{\partial x}\right)-\left({j}^{\mathrm{ad}}+{j}^{\mathrm{C}}\right)=0. $$
(7)

where σ eff is the effective conductivity of solid phase of the electrode.

The equation for surface coverage with functional groups that take part in redox reaction looks like:

$$ \frac{\partial \theta }{\partial t}=\frac{j^{\mathrm{ad}}}{S{Q}_{\theta }F}. $$
(8)

where Q θ is the specific molar capacitance of adsorption on true hydrophilic surface.

Equations (1), (2), (3), (4), (5), (6), (7), and (8) determine the work dynamics of the supercapacitor; they consider adsorption kinetics using the Frumkin isotherm. In order to complete the system definition, let us determine the boundary conditions. The boundary conditions for potential gradient in the electrolyte are conditions of zero. They mean zero electrical currents in the electrolyte on the left and right boundaries of the model:

$$ {\left.\frac{\partial {\varphi}_{\mathrm{e}}}{\partial x}\right|}_{x=0}=0,\kern1em {\left.\frac{\partial {\varphi}_{\mathrm{e}}}{\partial x}\right|}_{x=2{L}_{\mathrm{e}\mathrm{le}}+{L}_{\mathrm{sep}}}=0. $$
(9)

The boundary conditions for electrolyte concentration are the equality to zero of the electrolyte concentration gradient on the same boundaries:

$$ {\left.\frac{\partial c}{\partial x}\right|}_{x=0}=0,\kern1em {\left.\frac{\partial c}{\partial x}\right|}_{x=2{L}_{\mathrm{ele}}+{L}_{\mathrm{sep}}}=0. $$
(10)

Let us assume that the potential is set on the left border:

$$ {\left.{\varphi}_{\mathrm{e}}\right|}_{x=0}=0 $$
(11)

and the current is set on the right side:

$$ {\left.{\sigma}^{\mathrm{eff}}\frac{\partial {\varphi}_e}{\partial x}\right|}_{x=2{L}_{\mathrm{ele}}+{L}_{\mathrm{sep}}}=I(t). $$
(12)

As the starting conditions, we shall assume the equality of potentials to zero:

$$ {\left.{\varphi}_{\mathrm{e}}\right|}_{t=0}={\left.{\varphi}_{\mathrm{s}}\right|}_{t=0}=0, $$
(13)

uniform distribution of the concentration:

$$ {\left.c\right|}_{t=0}={c}_{10} $$
(14)

and also uniform distributions of coverage for both electrodes:

$$ {\left.\theta \right|}_{t=0}={\theta}_0. $$
(15)

The measurable potential is calculated as:

$$ U={\varphi}_{\mathrm{s}}\left|{}_{x=0}-{\varphi}_{\mathrm{s}}\right|{}_{x=2{L}_{\mathrm{ele}}+{L}_{\mathrm{s}\mathrm{ep}}} $$
(16)

Experimental

Fine-dispersed carbon electrode

Composite carbon electrodes based on Norit DLC Supra 30 activated carbon (Norit The Netherlands BV) have been obtained. Powder of activated carbon was mixed with a conductive filler, namely UM-76 carbon black (Omsktehuglerod LTD, RF), followed by homogenization in a SVM-04 vibratory mill. The grinding bodies were made of zirconium oxide. The polymeric binder (4 % mass) based on polytetrafluoroethylene (PTFE) and the solvent (isopropyl alcohol) were added. The composite electrodes were prepared using a method of multistage calendaring down to their thickness of 200 ± 10 μm. Mass of electrode based on Norit AC is equal to 41 mg. Before testing the electrode, samples were dried at 120 °C for 48 h.

Study of porous structure of carbon electrodes

Porous structure of the AC electrodes was performed with a method of standard contact porosimetry (MSCP) [27, 28]. The method allows us not only to investigate porous structure of any material in the widest possible range of pore radii (from 1 to 3 × 105 nm) but also to study its hydrophilic–hydrophobic properties. When the working liquid is octane, the porosity curves for all types of pores are obtained. When water is used instead of octane, only hydrophilic pores can be determined. Figure 1 shows the integral curves of pore volume vs effective radius, r*, where r* = r cos (α) (here r is the true pore radius and α is the wetting angle). The curves were obtained using both octane and water. Since octane almost perfectly wets all the materials, then its α ~ 0 and r* ~ r, and for water r* > r.

Fig. 1
figure 1

Integral pore size distributions for the electrode based on Norit carbon. The curves are plotted as pore volume vs effective pore radius. Working liquids: octane (1) and water (2)

Full size image

As seen from the figure, a radius of pores of this electrode is within a very wide range: r < 1 nm for the smallest pores and r = 100 nm for the largest ones. In other words, the pore radius is over five orders of magnitude. The electrode contains all types of pores: micropores (d < 2 nm), mesopores (d = 2–50 nm), and macropores (d > 50 nm). Total porosity, which has been determined using octane as a working liquid, is 0.74. The porosity due to hydrophilic pores determined by water is 0.53. Thus, the porosity caused by hydrophobic pores is 0.21, and the volume fraction of hydrophobic pores is equal to 0.28. The α − r dependence for the electrode based on Norit carbon containing also 4 % PTFE has been calculated from Fig. 1 according to [28]. Result is plotted in Fig. 2.

Fig. 2
figure 2

Wetting angle for water as a function of pore radius. Materials are the Norit carbon powder (1) and the electrode based on carbon Norit (2)

Full size image

The complicated form of this dependence is determined by the irregular distribution of the surface groups, which hydrophilize the carbon surface and hydrophobizing PTFE particles in pores of different sizes. As follows from Figs. 1 and 2, the largest pores with r > 30 nm are hydrophobic, since the PTFE particles cannot penetrate into smaller pores.

Hydrophobicity of pores is explained by partial hydrophobicity of Norit carbon and by hydrophobic binder like PTFE. Total specific surface area, which has been calculated from Fig. 2 according to [28], is equal to 1580 m2/g; this value is 940 m2/g for hydrophilic pores.

For a comparison, Fig. 3 shows the integral pore distributions for the initial powdered Norit carbon, measured using both octane and water.

Fig. 3
figure 3

Integral pore size distributions for the initial powdered Norit carbon. Working liquids: octane (1) and water (2)

Full size image

Regarding this sample, the total porosity is 1.65 cm3/g; the porosity due to hydrophilic and hydrophobic pores is 1.31 and 0.34 cm3/g, respectively. Thus, the volume fraction of hydrophobic pores is 0.20, which is substantially less in a comparison with the electrode based on Norit carbon with 4 % PTFE. This can be explained by a lack of hydrophobic binder in the initial carbon.

Figure 2 shows the correlation (2) between wetting angle for water and pore radius for the Norit carbon, which has been calculated from Fig. 3 according to [28]. Comparing the two curves, it is possible to note that the carbon is much more hydrophilic than the electrode based on these materials but containing 4 % PTFE. Moreover, these curves coincide in the field of small pores (r < 10 nm), since the PTFE particles cannot penetrate into them.

The total specific surface area of the Norit carbon, which has been calculated from Fig. 3 according to [28], is 1705 m2/g. It is higher than the corresponding value for the electrode containing polymeric binder.

Electrochemical measurements

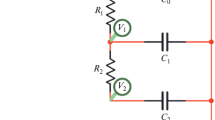
Basic electrochemical measurements were carried out in a sealed Teflon cell, an electrochemical group of which was a matrix system of filter-press type, where electrolyte contained only in the pores of electrodes and separator [29] (see Fig. 1). Nonporous graphite foil was used as a current collector. A 1 M LiClO4 solution prepared from analytical grade reagent in distilled water was used in order to study the symmetric ECSC with electrodes based on AC Norit 4 % PTFE electrolyte. The electrodes in the form of compact discs with a diameter of 2 cm were used. The measurements were performed according to a two-electrode circuit (by voltage) by means of an Elins potentiostat (IPC-Pro3A).

Results of cyclic voltammetry experiment with different scan rates are shown in Fig. 4, where С is the capacitance, which is equal to current divided by voltage scan rates.

Fig. 4
figure 4

Cyclic voltammograms of porous electrodes based on Norit AC at different sweep rates

Full size image

Examples of the model calculations

The solution of the problem that is defined by Eqs. (1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), and (15) was carried out by a method of finite elements. The values of the parameters that were used for the calculations are shown in Tables 1. A special attention was paid to the dependence of energy efficiency on current in the galvanostatic charging–discharging mode since the current is uniquely (inversely) associated with the values of time of charging and discharging. Regarding devices for smoothing peak loads in electrical networks, these times are determined by the specific times of peak loads during the day, week, etc.

Table 1 Parameters of ECSC with electrodes based on Norit AC
Full size table

Measured galvanostatic curves and the corresponding calculated curves are shown in Fig. 5. The experimental curves have been fit with the same current regime as in experiment. These figures show satisfactory accordance between the calculated and experimental discharging and charging curves. This indicates the correctness of the assumed model.

Fig. 5
figure 5

Examples of a comparison of charging–discharging cycles under different currents for the electrode based on Norit AC. Experimental (solid curves) and theoretical (dotted curves) are plotted as charge vs voltage

Full size image

The calculated examples of concentration fields with different currents are shown in Fig. 6.

Fig. 6
figure 6

Concentration fields in space and time under current of charging and discharging of a 1 mA and b 100 mA for ECSC based on Norit AC. Here and further, the dimensionless coordinates are used, where each layer of electrode/separator/electrode has the unit thickness

Full size image

Figure 7 illustrates the distributions of potential difference in the electrolyte and solid phase of the electrode under different currents.

Fig. 7
figure 7

Distribution in space and time of potential difference in electrolyte and solid phase of the electrodes under current of charging and discharging of a 1 mA and b 100 mA for ECSC based on Norit AC

Full size image

The presence of maxima on the η − i plots is very important. This can be explained by a sufficient contribution of the pseudocapacitance of redox reactions of surface groups under small currents. In opposite to the EDL capacitance, the pseudocapacitance is characterized by the polarization resistance as in the case of accumulators. Moreover, the efficiency decreases under high current due to ohmic energy losses in pores, which are filled with electrolyte. In the field of the maximum, the EDL makes the main contribution to the capacitance. As shown in Fig. 8, a very high value of efficiency is reached (~90 %) in this case.

Fig. 8
figure 8

Theoretical and experimental values of efficiency as functions of current for ECSC based on Norit AC

Full size image

For different exchange currents, the efficiency coefficients as functions of current density are plotted in Fig. 9. Both minimum and maximum are observed on the curves. The presence of these extreme points is very important to optimize the ECSC operation mode for smoothing of peak loads of electrical networks.

Fig. 9
figure 9

Efficiency as a function of current density under different exchange currents: a small and b relatively high exchange current (other parameters are given in Table 1)

Full size image

Figure 10 shows the dependencies of the efficiency on charging time for different thicknesses of the electrodes. The curves contain maxima; this is also important to optimize the ECSC operation mode for the above-mentioned purpose.

Fig. 10
figure 10

Efficiency as a function of charging time at different thickness of the electrodes (other parameters are given in Table 1)

Full size image

As an example, the calculated charging–discharging cycling curves are plotted in the coordinates of voltage–time (Fig. 11). The results show a possibility to use the model for the calculation of a change of the characteristics during the cycling process. The fitting parameters are given in Table 1.

Fig. 11
figure 11

Example of cycling at 10 mA; parameters are given in Table 1

Full size image

Results and discussion

Fitting of galvanostatic charging–discharging cycles for ECSC was conducted using the developed model; the fitting parameters are given in Table 1. The EDL capacitance, adsorption parameters, and exchange currents were found. The latter appeared to be rather small, and pseudocapacitance contribution is not so significant in the presented experiments. However, despite the small values of exchange current, they significantly affect the efficiency, which will be shown and discussed below.

The fitting and experimental data are given in Fig. 5, where the cycles are represented in coordinates of charge–voltage; high currents are on the left, and small currents are on the right. The bends of curves are observed at low currents during discharging and charging; the bends are straightened at high currents. ohmic jumps, which correspond to the transition process during current switching, also occur under very high currents.

Examples of electrolyte concentration profiles are shown in Fig. 6, where the thickness of each electrode and the separator is nondimensionalized to the layer thickness, so it is equal to 1. As can be seen, the concentration is distributed uniformly over the entire thickness of the capacitor under cycling with low current. Substantial concentration gradients appear in the electrodes under higher currents; this is due to ohmic losses.

Examples of potential difference profiles in electrolyte and solid phase can be seen in Fig. 7 for small and high currents, where dimensionless coordinates are used.

The dependence of the energy efficiency on the cycling current is shown in Fig. 8. For a comparison, the experimental dependencies of efficiency on current are also given. Both experimental and theoretical curves demonstrate maximum of the efficiency. This is an extremely useful fact for the applications of supercapacitors, especially for smoothing of peak loads in electrical networks.

As mentioned above, the exchange currents required for the fitting of the samples are relatively small. Dependencies of efficiency on cycling current are shown in Fig. 9 for different currents of exchange reactions on the electrodes. The efficiency can reach 95 % at very low exchange currents (Fig. 9a). However, the maximum efficiency decreases rapidly with an initial increase in exchange currents, and then again may be significant at high exchange currents (see Fig. 9b). The dependence of efficiency on current shows two extrema (maximum and minimum) in the case of intermediate exchange currents.

This can be explained as follows. Under high operating currents, the energy losses are determined by the ohmic resistance, which depends quadratically on the current. The efficiency grows during cycling with lower currents, and ohmic losses decrease. Regarding the field of the maximal efficiency, charging of the EDL dominates. However, slow reactions having pseudocapacity (redox reactions of surface groups) play an important role at lower currents; relative losses begin to rise due to increasing of the current fraction, which provides electrochemical reaction. A similar dependence of efficiency with a single extremum (maximum) has been featured by Pillay and Newman [25]. However, when charging occurs under very small currents, which are comparable to those of exchange reaction, the losses begin to decrease. Thus, the system demonstrates two internal extrema of efficiency, namely, a local maximum under high currents and local minimum under small currents.

The influence of the electrode thickness on the efficiency at different times of charging time was also investigated (the other parameters are taken from Table 1). The results are given in Fig. 10. The optimal time has been found for each thickness. In fact, this means that it is necessary to optimize the design of the capacitor in advance for specific practical needs. This is especially important for applications of ECSC for smoothing of peak loads in electrical networks.

Figure 11 shows the calculated curves for the galvanostatic cycling (with time limit). As seen, during cycling, the gradual shift of average voltage to the negative field is observed.

As follows from Table 1, C EDL is equal to 10 μF/сm2 of the true surface of the electrode based on AC Norit. This is in agreement with the data for hydrophilic–hydrophobic carbon materials and for almost hydrophilic carbon materials, respectively [30].

Conclusions

A model of charging–discharging process in the electrochemical supercapacitor has been developed in this paper. The satisfactory agreement between the calculation results of the model and experimental data has been done by fitting parameter of systems. It has been found that the experimental and theoretical efficiency dependences on the charging–discharging current values are significantly nonmonotonic.

The efficiency dependences on constructive parameter have been demonstrated. It has been shown by the model that the efficiency can reach almost 100 % in a system with very low exchange current values.