Introduction

Perovskite materials have a formula of ABX3, where A and B are cations and X is an anion [1, 2], while in the case of antiperovskite, the positions of cations and anions interchange. The crystal structures of both types of materials are similar and can be used in the fields such as semiconductors, fuel cells, batteries, sensors, membrane reactors, and hydrogen production. Antiperovskite materials can extract waste heat and turn it into electricity, making them interesting for any industrial application [3]. Cubic antiperovskite compounds, including carbides and nitrides, have different technological applications due to physical properties such as giant magnetoresistance [4], nearly zero temperature coefficients of resistivity [5], and wide range of band gaps, from super conductor to insulator [6, 7]. The general formula for these compounds is AXB3, where A is group III–V element, X is carbon or nitrogen, and B is s–d metal [8, 9]. These materials crystallize in a cubic structure with space group Pm3m (#221). These properties make these compounds useful for applications such as to read data from hard disk drives, biosensors, microelectromechanical systems (MEMS), and other devices. Moreover, these compounds exhibit excellent mechanical properties [10,11,12] which make their possible utility in automobiles and space technology.

Antiperovskite materials have been studied mostly from many researchers. Experimentally, XNCa3 was synthesized by mixing and powder pressing of Ca3N2. Then the X (X = Ge, Sn, and Pb) element was put into a pellet, and later, the pellet was heated at 1000 °C in flowing dry N2 gases [13]. From the theoretical side, Chern et al. [13] have studied the phase transition of MNCa3 (M = P, As, Sb, Bi, Ge, Sn, Bi) and seen that there are phase transitions from cubic to orthorhombic for PNCa3 and AsNCa3. It is found that SbNCa3 and BiNCa3 cubic antiperovskite compounds are semiconductors by Moakafi et al. [14]. For different volumes, total energy are calculated to obtain the ground state properties, and the calculated total energy-volume data are fitted to Murnaghan’s equation of state (EOS) to obtain lattice parameters, bulk modulus, and its first order pressure derivatives [15]. TiNCa3 and AuNCa3 have been found to be metallic [16, 17]. The bonding properties and electronic structure of BiNCa3 and PbNCa3 using ab initio method have been investigated by Papaconstantopoulos et al. [18]. Later, Vansat et al. [19] have performed the structural properties of AsNCa3, PNCa3, and BiNCa3 using local density approximation (LDA) and are also of the opinion that BiNCa3 is a narrow band gap semiconductor. The structural, electronic, and elastic properties of the cubic antiperovskite XNCa3 (X = Ge, Sn, Pb) have been calculated using density functional theory (DFT) within pseudo-potential plane wave method (PP-PW) by Haddadi et al. [2]. Haddadi et al. [20] have investigated structural and elastic properties of ANCa3 (A = P, As, Sb, and Bi) under pressure. They [2, 20] have calculated bulk modulus and its pressure derivatives of XNCa3 by fitting pressure-volume data to third-order Birch-Murnaghan equation of state (EOS) [21]. The electronic and optical properties of GeNCa3 were studied by Igbal et al. [22]. Also, Iyigor et al. [23] have studied the mechanical, electronic, vibrational and thermodynamical properties by means of generalized gradient approximation approach within the DFT. Here, to obtain lattice constants and bulk modulus, total energies were matched to Murnaghan EOS [15]. Lately, Bilal et al. [24] have studied metallic thermoelectric materials. The authors have investigated the thermoelectric properties of metallic antiperovskites ANCa3 (A = Ge, Sn, Pb), BCFe3 (B = Al, Zn, Ga), and SnCD3 (D = Co and Fe) based nitrogen and carbon using the first principles calculations [24].

Despite these given results, some of the physical properties of PbNCa3 compound are yet scarce in the available literature. Also, there are no calculations exploring the vibrational properties of this perovskite structure and pressure effect. A detailed study of the same properties of PbNCa3 is needed to realize its potential applications in technology. This has motivated us a theoretical analysis of the structural, elastic, electronic, and vibrational properties of PbNCa3 under pressure.

The paper is organized as follows: in the following section, we give computational methods. The important results of our findings are separately presented in section Results and discussion for each property of that system, followed by a conclusion.

Methods

In this work, the first principles calculations have been performed using Cambridge Sequential Total Energy Package (CASTEP) simulation software [25], based on density functional theory [26]. By means of the self-consistent field (SCF) iteration, a density-mixing minimization method, the electronic wave functions are firstly obtained. Then optimized structure has been obtained by using the method of Broyden, Fletcher, Goldfarb, and Shannon (BGFS) [27] under various hydrostatic pressures ranging from 0 to 50 GPa. Perdew-Burke-Ernzerhof (PBE) [28] using Vanderbilt Ultrasoft pseudopotential was enforced for the exchange-correlation terms. Generalized gradient approximation (GGA) was also considered for the electron-electron interaction. The kinetic energy cutoff is taken to be 600 eV for the wave function. The crystal reciprocal-lattice and integration over the Brillouin zone is applied using a 12 × 12 × 12 Monkhorst-Pack [29] k-points sampling procedure for antiperovskite PbNCa3 to geometry optimizations and energy calculations. Pb 5d106s26p2, N 2s22p3, and Ca 3s2 3p64s2 electrons are taken as valence electrons. The maximal Hellmann-Feynman force converge criterion between atoms, the maximum ionic displacement, and the maximum stress are 0.001 eV/Å, 5.0 × 10−5 Å, and 0.002 GPa, respectively.

Results and discussion

Structural properties

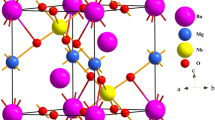
The ternary calcium nitrides PbNCa3 having Pb from the group IV pertain to the nitrides of antiperoveskite-type. The structure of ideal cubic antiperovskite for PbNCa3 materials (#221) includes one formula with the Wyckoff positions of the atoms which are Pb 1a (0, 0, 0), N 1b (0.5, 0.5, 0.5), and Ca 3c (0, 0.5, 0.5) as seen in Fig. 1 . For the calculation of the ground state features of the PbNCa3 compound, the total energy is computed at different volume ranges from 1.5 V0 to 0.5 V0, where V0 is the equilibrium volume of unit cell. The computed total energy-volume data are fitted to the Murnaghan’s EOS [15] and a third-order Birch-Murnaghan EOS [21] for the determination of the ground state features including the bulk modulus B0, its pressure derivatives B0′, equilibrium lattice parameter a0, volume (Vo), and total energy at P = 0 GPa and T = 0 K. The obtained results of the PbNCa3 and similar XNCa3 (X = Ge, Sn, Bi, Sb, P, As) compounds and their comparison with the other theoretical and experimental values can be seen in Table 1. It is shown in the Table 1 that the computed values of the lattice constant (a = 4.942 Å) are in good agreement with the experimental data (a = 4.955 Å) [13] and slightly higher than the theoretical value (4.9197 Å) [2]. In this study, for both EOS, better agreement is obtained with experimental result within 0.26% for PbNCa3 than another theory [2]. This provides the reliability of the present first principles calculations. Comparing lattice parameter for PbNCa3 with those of other similar compounds (XNCa3), the lattice constants of PbNCa3 is the biggest one among the others, which is due to the fact that the radius of the Pb (1.80 Å) is the biggest one among Ge (1.25 Å), Sn (1.45 Å) from group VI, and P (1.0 Å), As (1.15 Å), Sb (1.45 Å), and B (1.60 Å) from group VII. It also can be seen from Table 1 that lattice parameter of PNCa3 [20] is the smallest one due to the smallest atomic radius of P. There are no experimental data about bulk moduli and its pressure derivatives of these compounds in the literature for the comparison. Unlikely, the bulk moduli decrease with the increase in the atomic size of X atoms due to the relationship between bulk modulus and lattice constants which have an inverse proportion. It can be concluded from Tables 1 and 2 that the calculated value of Bulk modulus of elastic constants is close with one obtained from the EOS fitting. The calculated pressure derivatives of the bulk modulus (4.25 and 4.23 for Murnaghan and Birch Murnaghan EOS) for PbNCa3 are well in agreement with theoretical values (4.2) [2]. The smallest one is obtained for GeNCa3 [2], while the biggest one is for SbNCa3 [14].

Fig. 1
figure 1

The unit cell of the PbNCa3

Full size image
Table 1 Computed lattice parameters a0, bulk modulus B0, pressure derivatives of bulk modulus B0′, equilibrium volume V0, total energy Etot (eV), and other results for XNCa3
Full size table
Table 2 Bulk modulus B (GPa), Young Modulus E (GPa), shear modulus G (GPa), Voigt shear modulus (Gv), Reuss shear modulus (GR), G/B ratio, Poisson’s ratio (υ), Zener Anisotropy factor (A), and elastic constants Cij (GPa) of PbNCa3 under zero pressure
Full size table

The normalized volume V/V0 and lattice constants a/a0 versus the pressure for PbNCa3 are given in Fig. 2, where V0 and a0 are features of equilibrium structures at 0 GPa. It is shown in Fig.2 that the a/a0 and V/V0 ratios decrease as the applied pressure increases from 0 to 50 GPa. In order to define pressure dependence values under 0–50 GPa for the structural parameters, the curves in Fig. 2 are fitted to second-order polynomial:

Fig. 2
figure 2

Variations of lattice parameter and cell volume and of PbNCa3 with pressure

Full size image
$$ {\displaystyle \begin{array}{l}\mathrm{a}/\mathrm{ao}=0.99536\hbox{--} 0.00428\ast \mathrm{P}+3.7205\times 10-5\ast \mathrm{P}2\\ {}\mathrm{V}/\mathrm{Vo}=0.98461\hbox{--} 0.01196\ast \mathrm{P}+1.13707\times 10-4\ast \mathrm{P}2\end{array}} $$

Electronic properties

The electronic properties of a material can be obtained by its band structure and density of states (DOS). The computed band structure along the high symmetry directions in the Brillouin zone can be seen in Fig. 3. The Fermi energy is set to zero. For this compound, the bands cross the Fermi level along the particular high symmetry lines of the first Brillouin zone. Energy gap near the Fermi level cannot be observed, and it shows the metallic properties for PbNCa3, although the pressures increased up to 50 GPa.

Fig. 3
figure 3

Band structure and density of states for PbNCa3 at (a) 0 GPa and (b) 50 GPa

Full size image

The total and partial density of states is also given in Fig. 4a. It can be seen that the valence bands localized in two regions. Pb –5d states compose the lowest energy region of the valence band. Moreover, the hybridization of Pb –6 s and N –2p states compose the next bands below the Fermi level. Also, in the conduction band located above the Fermi energy level, Ca 3p-states and Pb-5d-states provide the major contribution.

Fig. 4
figure 4

Calculated (a) partial density of states and (b) total density of states under pressure for PbNCa3

Full size image

The DOS of a system indicates the number of states at each energy level. The electronic behavior has been discussed through the DOS of PbNCa3 in 0, 25, and 50 GPa given in Fig. 4b. It can be seen from Fig. 4b that the shapes of the curve under pressure have no a significant change, showing that the structure of PbNCa3 is stable and no structural phase transformation occurs in the investigated pressures. By the comparison of the DOS in 0, 25, and 50 GPA, it can be seen in Fig. 4b that the TDOS below the Fermi level are pushed to lower energies, while the states above the Fermi level shift to the higher energies. These situations may be related to the smaller distance of atoms under pressure.

Elastic properties

Elastic constants are important parameters of material investigated which can provide a link between the mechanical and dynamical stability and give important information about the nature of the forces and bonding. We have calculated the elastic constants at calculated lattice parameters to study the stability of this compound using the stress-strain method.

In real materials, under high temperature, there are defects due to configuration entropy. The concentrations of the defects increase with increasing temperature. Thus, the experimental elastic constants are smaller than calculated values. The calculations of the elastic constants at zero temperature are useful due to check finite temperature elastic constants. And also because in some case, elastic constants are so small as to make calculations of finite temperature difficult. Finally, zero temperature elastic constants are much more economical than finite temperature elastic constants allowing a rapid exploration of the parameter, and they can be calculated much more accurately.

Besides these practical reasons, zero temperature elastic constants are also interesting due to the fact that these elastic constants show a new physical property of inhomogeneous system. Elastic constants can be defined by the derivative of the stress with respect to strain. When the system is strained, care should be taken to calculate the derivatives at zero force on each atom because there can be local rearrangements of the atoms.

Elastic constants tensor

$$ {C}_{\alpha \beta \sigma \varepsilon}=-\frac{\partial {t}_{\alpha \beta}}{\partial {e}_{\sigma \varepsilon}} $$

At zero temperature

$$ {\left.{C}_{\alpha \beta \sigma \varepsilon}=-\frac{\partial {t}_{\alpha \beta}}{\partial {e}_{\sigma \varepsilon}}\right|}_{F_{i=0}} $$

where the subscript indicates that the derivative must be performed at zero net force on each atom indicating the definition of the equilibrium at zero temperature [31].

Ternary PbNCa3 compound is ideal cubic antiperovskite structure; therefore, C11-, C12-, and C44-independent elastic constants are required to characterize elastic behavior. The second-order elastic constants (Cij) at equilibrium lattice parameter have been computed to study the stability of this compound. The results of obtaining elastic constants are given in Table 2. From Table 2, it can be seen that the calculated elastic constants at P = 0 GPa and T = 0 K are in good agreement with those of Ref. [2] for PbNCa3 and Ref. [2] and [23] for GeNCa3 and SnNCa3. Besides, the dependency of the elastic constants of pressure is a significant characterization of the crystals under varying pressure. The elastic constants as a function of pressure can be seen in Fig. 5. It is easy to observe in Fig. 5 that while C11, C12, and C44 elastic constants show increment with the pressure. The C11 and C12, which are due to the elasticity in length (the longitudinal distortion), rapidly increase with pressure. The C11 and C12 increase by 306.7% and 250.8% when the applied pressure change from 0 to 30 GPa. On the other hand, C44 increases by 63.3% with pressure. Indeed, the C44, which is correlated with the elasticity in shape and gives a measure of stiffness against the shape deformation.

Fig. 5
figure 5

Calculated pressure dependence of the elastic moduli at zero temperature

Full size image

In order to be mechanically stable crystal, the second-order elastic constants must be positive. This definition is known as the Born stability criteria [32]: C11-C12>0, C11>0, C44>0, and C11+2C12>0, and these criteria are satisfied, indicating that this material is mechanical stability in this phase, implying all in the pressure range 0–30 GPa.

An elastic constant calculated correctly is very important in determining the mechanical features of the crystal. For a solid, Young’s modulus (E), shear modulus (G), bulk modulus (B), etc., parameters contain the mechanical properties. The most important elastic parameters of materials such as anisotropy factor A, Young’s modulus (E), shear modulus (G), bulk modulus (B), and Poisson’s ratio are acquired from the calculated elastic constant Cij utilizing the Voigt–Reuss–Hill (VRH) method [33]. For the cubic crystal, the Voigt [34] and Reuss and Angew [35] bounds of B and G are given as

$$ {B}_v={B}_R=B=\frac{C_{11}+2{C}_{12}}{3} $$
(1)
$$ G=\frac{1}{2}\left({G}_v+{G}_R\right) $$
(2)

where GV is Voigt’s shear modulus corresponds to the upper bound of G values (GV = (C11 − C12 + 3C44)/5) and GR is Reuss’s shear modulus corresponds to lower bound of G values (5/GR = 4/(C11 − C12) + 3/C44). The elastic features such as the Young’s modulus (E), Poisson’s ratio (υ), and Zener anisotropy factor (A), which are the most interesting elastic features for utilizations are often analyzed for polycrystalline materials. These values are also calculated in terms of the computed using the following equations [36]:

$$ A=\frac{2{C}_{44}}{C_{11}-{C}_{12}} $$
(3)
$$ V=\frac{1}{2}\frac{B-\frac{2G}{3}}{B+\frac{G}{3}} $$
(4)
$$ E=\frac{9 GB}{G+3B} $$
(5)

The calculated B from obtaining elastic constants, A, υ, E, G, GV, GR, and G/B ratio for PbNCa3, can be seen in Table 2. The pressure dependence of B, G, and E are displayed in Fig.6a. The obtained B and G exhibit linear relationship with the applied hydrostatic pressure. E is defined as the ratio of the tensile stress to the tensile strain and is used to measure the stiffness of the materials. The larger the Young’s modulus E, the stiffer the material is. The Young’s modulus increases with pressure indicating that the stiffness of PbNCa3 compound can be increased by applying external pressure. For GeNCa3 and SnNCa3, the values of B, G, and E for GeNCa3 and SnNCa3 are higher than those of PbNCa3 showing that these compounds are harder than that of PbNCa3.

Fig. 6
figure 6

(a) Bulk modulus B, shear modulus G, Young modulus E, and (b) B/G ratio and Poisson ratio υ of PbNCa3 as a function of pressure at zero temperature

Full size image

It can be seen in Table 2 that both Young’s and shear modulus of PbNCa3 are low, which designates it is a soft material.

The shear modulus (G) indicates the plastic deformation resistance, whereas the bulk modulus (B) indicates the fracture resistance. Pugh [37] formulated a simple relation between bulk and shear moduli (G/B) to estimate ductility. The critical value of the ratio G/B separating the brittle and ductile behavior of materials is around 0.57; i.e., if the G/B > 0.57, the material behaves in a brittle manner; otherwise, it behaves in a ductile manner. Here, the calculated value of the G/B ratio is greater than 0.57, indicating that this compound is brittle in nature as seen in Table 2. The values of G/B decrease in pressure (see Fig.6b). The value of lower limit and upper limit Poisson ratio (υ) are given as 0.25 and 0.5 for central forces in solids, respectively [38]. The values of υ are typically between 0.1 and 0.25 for covalent materials, and interatomic forces are non-central forces [39], while the lower and upper limits of υ are 0.25 and 0.5, respectively, and interatomic forces are central forces [40] for ionic crystals. In our case, υ value is equal to 0.327 at 0 GPa for PbNCa3; i.e., the interatomic forces in the PbNCa3 are central forces and have an ionic contribution in intra-atomic bonding. Now we also presented the pressure dependence of Poisson’s ratio up to 30 GPa. We can see that Poisson’s ratio increases linearly with pressure in Fig. 6b.

For an isotropic crystal, C11−C12 = 2C44, so A = 1, while any value smaller or larger than 1 indicates anisotropy. The A is a measure of the degree of elastic anisotropy in solids. The calculated A value for PbNCa3 is equal to 2.14 at 0 GPa, which deviates in the positive direction from 1. This means that this material is an anisotropic compound and is lower than other theoretical result (2.35) [2].

The antiperovskite materials, including metals, semiconductors, insulators, and superconductors, are applicable in various technologies. In batteries, it is known that solids with superionic conductivity are better than organic liquid electrolytes [40]. Moreover, these materials have varied physical properties: giant magnetoresistance (GMR) [41], almost zero temperature coefficient of resistivity [42], and magnetostriction [43]. Antiperovskites are beneficial, especially in industrial impositions such as GMR. GMR is used in magnetic field sensors, used to read input in devices, also microelectromechanicals and biosensors. Besides, antiperovskites are proper material in all conditions because of its resistivity in zero temperature. Antiperovskites are also favorable in space and automobile technology because of its great mechanical characteristic [10, 44].

Vibrational properties

Phonons are the main stimulation that affects some physical properties, particularly the thermodynamic manner. For the investigation of vibrational features, we have investigated the phonon graph of PbNCa3 compound.

The phonon dispersion relation and phonon density of states have been computed from the force constant method using density functional perturbation theory for PbNCa3. For throughout this calculation, we used the CASTEP code with 2 × 2 × 2 supercell. The phonon dispersion spectrum along the high symmetry directions Χ­R­Μ­Γ­R together with the total and partial phonon density is shown in Fig. 7 at 0 GPa and 50 GPa. In the cubic antiperoveskite-type PbNCa3 primitive cell, there are five atoms. Due to this reason, there should be distribution of 12 optical and 3 acoustic. Moreover, in Fig. 7a, ternary PbNCa3 shows no negative frequency which confirms that it is dynamically stable in this phase at 0 GPa. To see the dynamical stability of PbNCa3 under pressure, phonon frequencies of PbNCa3 are calculated under 50 GPa. Under pressure, no imaginary frequency is found, implying that the Pm3m(221) structure of PbNCa3 under pressure is dynamically stable. Unluckily, there is no available experimental data for PbNCa3 compound based on phonon dispersion curves under pressure The magnitude of frequency increases with increasing pressure. From Fig. 7a, it can be seen that there is a gap in between 2 and 3.5 at 0 GPa, but under 50 GPa pressure, the gap disappears and the minimum point of optical branches at Γ point decreases with pressure, while the maximum point at the R point in optical phonon increases under pressure due to enhancement of interlayer interaction.

Fig. 7
figure 7

Phonon dispersion curves (a) 0 GPa and (b) 50 GPa for PbNCa3

Full size image

Because of the symmetry, the distinct number of phonon modes decreased along the high symmetry directions. The phonon dispersion curves indicate that the acoustic phonon frequencies are mostly due to Pb, since Pb atoms are heavier than N and Ca atoms which result in lower vibration. Mid frequency regions on the optical branches includes a vibration of Ca, while high frequency regions are due to N atoms for both pressures.

To understand the behavior of all phonon modes at Brillouin zone center, we have investigated the pressure dependency of the lattice vibrations at Γ point. According to group theory, the vibrations at Γ point in Pm3m structure of PbNCa3 have the following irreducible representations:

$$ \Gamma\ \left(\mathrm{Pm}3\mathrm{m}\right)=3\ {\mathrm{T}}_{1\mathrm{u}}+{\mathrm{T}}_{2\mathrm{u}}. $$

Three Tıu (triply degenerate) and T2u irreducible representations are infrared (IR) active optical phonon modes. Calculated phonon modes in Thz unit are 3.25 (1.45), 6.99 (7.94), and 8.59 (17.00) Thz for T1u and 4.94 (6.11) for T2u at 0 (50) GPa. The pressure dependence of the phonon frequencies increases generally. Phonon vibration modes occurred by atomic vibrations. To investigate atomic displacement giving the vibration modes, the relevant phonon eigen vectors for T1u and T2u are shown in Fig. 8. The displacement figure associated with polar soft mode was induced by the displacement of Pb in one directions and the displacement of Ca and N ions in the opposite direction for 3.25 Thz at 0 GPa.

Fig. 8
figure 8

Schematic eigen vector displacements of vectors representing the optical zone center Γ phonon modes at 0 GPa (a) and 50 GPa (b) for PbNCa3

Full size image

Conclusions

We have investigated that the computed electronic, mechanical, structural, and dynamic features of PbNCa3 compound have been analyzed using DFT. Lattice parameter and cell volume are analyzed under pressure up to 50 gap, and it is found that it reduces with pressure. The computed elastic constants indicate that this compound exhibits mechanical stability in the cubic phase. PbNCa3 compound has ionic bonding features, and its interatomic forces are central forces. In addition, we have computed the zone center vibrational frequencies of material with density functional perturbation theory approach. All the mode assignments were done and observed no negative phonon frequencies. This fact indicates that compound is dynamically stable in considering phase under pressure. The group theory analysis shows that there is no phase transition due to positive values of phonon mode in the interlayer for under pressure up to 50 GPa. The pressure dependency of the elastic features and their related values (B, G, and E) have been computed. The elastic constants and B, G and E quantities increase linearly from 0 to 30 GPa under pressure.