Investigation of the potential of asymptotic homogenization for elastic composites via a three-dimensional computational study

Abstract

Asymptotic homogenization is employed assuming a sharp length scale separation between the periodic structure (fine scale) and the whole composite (coarse scale). A classical approach yields the linear elastic-type coarse scale model, where the effective elastic coefficients are computed solving fine scale periodic cell problems. We generalize the existing results by considering an arbitrary number of subphases and general periodic cell shapes. We focus on the stress jump conditions arising in the cell problems and explicitly compute the corresponding interface loads. The latter represent a key driving force to obtain nontrivial cell problems solutions whenever discontinuities of the coefficients between the host medium (matrix) and the subphases occur. The numerical simulations illustrate the geometrically induced anisotropy and foster the comparison between asymptotic homogenization and well established Eshelby based techniques. We show that the method can be routinely implemented in three dimensions and should be applied to hierarchical hard tissues whenever the precise shape and arrangement of the subphases cannot be ignored. Our numerical results are benchmarked exploiting the semi-analytical solution which holds for cylindrical aligned fibers.

1 Introduction

The theory of composite materials (see, e.g., [6, 17, 18, 20]) concerns the study of the structural and functional arrangement of two or more different constituents and the analysis of the effective properties of the resulting material. The motivation for these studies resides in a large variety of engineering applications in, for example, metallurgy, polymer technology, fracture mechanics, and biomimetic material design. The primary goal is typically either finding the constituents’ optimal arrangement in terms of desired physical, chemical, or mechanical properties of the composite material (e.g., toughness, stiffness, corrosion resistance, thermal conductivity, etc.) or pursuing a thorough understanding of the properties of a given composite material on the basis of its constituents’ characteristics.

The properties of the composite material depend, in principle, on the local interplay among the individual constituents. These interactions might be extremely complex and usually take place on a spatial scale (the fine scale) which is typically much smaller than the one characterizing the composite material as a whole (the coarse scale).

For practical purposes, it is crucial to highlight the dependence of the effective properties of the composite on (at least some of) the fine scale phenomena. Nevertheless, a complete analysis of everything occurring on such a scale may often be prohibitive from a computational viewpoint, such that, in the last decades, a large literature has been devoted to the development of homogenization techniques. In general, these strategies aim to describe a composite material on the coarse scale, thus reducing computational complexity, and encode fine scale information concerning its constituents’ structure and properties in the effective properties.

The existing literature, when restricting the analysis to linear elastic composite materials, develops according to two main approaches; average field theory and asymptotic homogenization (the two are compared in the review paper [16]).

Average field techniques aim to find the effective elastic properties which relate the fine scale strain and stress averages over a representative volume (RV) which, in a possibly idealized manner, represents the material heterogeneity. For example, the RV can be identified with a finite experimental sample. The application of average theorems and the prescription of uniform loadings on the RV boundary then provide the necessary conditions to deduce the effective material properties (see, e.g., [37]). Clearly, the effective elastic constants should be uniquely determined and independent of the boundary loadings; when this is the case, the chosen RV is called a representative volume element (RVE). The latter condition is fulfilled for a sufficiently large RV. However, the RV should also be reasonably small for the sake of computational efficiency. For example, in [11], the authors investigate the minimum RVE size in the context of cortical bone. The existence of a mesoscale (much greater than the actual finer scale and much smaller than the coarser scale under investigation) characterizing representative volumes is commonly accepted in the average technique literature. For example, in [12], the authors define a representative element volume (REV) requiring the existence of three well separated scales to both minimize fluctuations (which appear when the integration volume size is comparable with the finer scale) and avoid strong heterogeneities (that arise when the volume size is close to the medium coarser scale). This way, a systematic procedure for average continuum equations of multiphase systems is derived. However, although the definition of REV given in [12] resembles that of an RVE (see, e.g., [37] and references therein), the former is specifically designed for balance equations of general thermodynamic properties and is intended to be exploited for integral averages of quantities defined per unit volume only. The integral average of quantities defined per unit area (such as stresses), is performed, instead, over a representative element area. That is in contrast to RVE formulations, where also stresses volume average is performed, as in [11]. Furthermore, in [12], the equivalence between the total amount of coarse and fine scale quantities (including the energy) is stated as a requirement to be fulfilled by the integral operators involved in the averaging process rather than a condition on the representative volume itself (in the context of RVE theory, the representative volume element satisfies the Hill’s condition [13], that is, the equivalence between coarse scale energy and average fine scale energy). Alternatively, the RV can be identified with an idealized infinite medium composed of a number of ellipsoidal shaped homogeneous phases. This approach can then be used to exploit the well-known analytical results due to Eshelby [9], who proved that the state of strain inside an ellipsoidal inclusion within the matrix is constant and depends only upon each individual constituent property and the inclusion aspect ratios (i.e. the ratios between its semi-axes). This fundamental result led to the development of several schemes for the approximation of the effective elastic constants, such as the dilute approximation (where interactions among inclusions are neglected), the Mori–Tanaka method [21] (weak interactions between the matrix and the inclusions are taken into account), and the self-consistent scheme [14] (interactions among phases are taken into account and no clear distinction between matrix and inclusions is made). This way, the effective properties are computed semi-analytically and structurally only depend on the inclusions’ volume fraction and aspect ratios. For example, in [33], the authors investigate the key parameters affecting the mineralized turkey leg tendon elastic properties exploiting the Mori–Tanaka and self-consistent schemes, then comparing the results to experimental data.

The asymptotic homogenization technique (see, e.g., [1–3, 15, 19, 22, 31]) exploits the sharp separation between the fine and the coarse scale to decouple spatial variations and employs multiple scale expansions of the fields. This approach, under the assumption of fine scale periodicity, yields the set of effective governing equations which describe the coarse scale mechanics of the composite material. The geometrical information of the fine scale structure is encoded in the effective model coefficients, which are to be computed solving boundary value problems on the (fine scale) periodic cell. Although fine scale variations within the periodic cell are no further approximated, computational feasibility is achieved as the cell problems are to be solved only once (provided that coarse scale variations of the fine scale structure are neglected) for the whole coarse scale model.

In the current work we start from the asymptotic homogenization problem for a multiphase elastic composite with discontinuous material properties. We show a generalization of the pioneering results that can be found in [3, 22, 31] accounting for an arbitrary number of subphases and general periodic cell shapes. We explicitly highlight the role of the interface loads which drive nontrivial cell problems solutions. Next we perform three-dimensional numerical simulations of the arising cell problems to track the dependence of the effective elastic constants on key parameters characterizing the fine scale geometry. The symmetry of the resulting coarse scale elastic tensor is pointed out and the model outcome is compared to that obtained via Eshelby based techniques. Finally, the cell problems numerical solution is benchmarked exploiting the semi-analytical solution for aligned cylindrical fibers, see [24]. The novel numerical results highlight for the first time the main model features compared to well-known, routinely implemented schemes. The paper is organized as follows:

• In Sect. 2 we introduce the asymptotic homogenization technique and present the derivation of the generalized asymptotic homogenization model for multiphase linear elastic composites.

• In Sect. 3 we describe our numerical approach to compute the effective elasticity tensor.

• In Sect. 4 we present numerical results and compare them with Eshelby based techniques. A benchmark comparison of the numerical results versus the semi-analytical solution which holds for aligned cylindrical fibers, cf. [24], is also provided. The equivalence of the two models for aligned cylindrical fibers is shown in “Appendix”.

• In Sect. 5 we discuss the results and present future perspectives.

Although the topic of this work is of crucial importance in a large variety of applications, systematic three-dimensional numerical simulations of the asymptotic homogenization problem for discontinuous material properties are still missing. The main literature has been focusing mostly either on fine scale oscillations of the elastic coefficients (see, e.g., [26], where the classical results derived in [3] are exploited and also extended to strain gradient linear elasticity and the solution of the periodic cell problems is driven only by volume forces) or on fiber reinforced composites, where structural symmetries lead to a dimensional reduction and simplification in the elastic moduli computation. In [23, 24], the authors apply asymptotic homogenization to determine the effective elastic response of periodic fibre reinforced elastic composites. In the latter context, local structural changes are assumed to occur in the plane perpendicular to the fiber axis only, hence spatial scales decoupling is carried out in two dimensions. As a result, the solution can be found via a semi-analytic approach by means of complex variable methods and multipole expansions. For example, in [25], the authors apply this technique to determine the effective elastic properties of cortical bone, identifying the matrix phase with the bony matrix and the fibers with the Haversian canals and resorption cavities.

Notwithstanding that our model is developed for a generic multiphase elastic composite (hence retaining a wide range of applicability), the chief motivation for this work is the study of hierarchical (biological) hard tissues, such as the human bone (see [36] for a detailed review of the bone hierarchical organization). Possible candidate systems are the mineralized collagen fibril and the extrafibrillar space. In the first example, the mineral inclusions and the collagen network can be considered as the subphases and the matrix, respectively. According to this scenario, asymptotic homogenization can be applied to identify the mechanical properties of the coarser hierarchical level, namely, the mineralized collagen fibril bundle, see, e.g., [33].

2 Multiscale modeling

We consider a bounded domain $\varOmega \subset \mathbb {R}^3$, such that $\varOmega =\mathrm {int}(\bar{\varOmega }_c \cup \bar{\varOmega }_m)$ where $\varOmega _c$ and $\varOmega _m$ are disjoint open sets. Here, $\varOmega _c$ represents the matrix phase and $\varOmega _m$ a number N of disjoint subphases $\varOmega _{\alpha }$, namely:

$$\begin{aligned} \varOmega _m=\displaystyle \bigcup ^N_{\alpha =1}\varOmega _{\alpha }. \end{aligned}$$

(1)

The choice of subscripts c (collagen) and m (mineral) reflects the scenario depicted in the introduction. We assume that both the matrix and the inclusions behave as linear elastic materials and we neglect inertia and body forces in $\varOmega$. At this stage, every field and material property is supposed to be a function of space $\varvec{x} \in \varOmega$ and the stress balance equations read

$$\begin{aligned} \nabla \cdot \sigma _c&=0 \quad \text {in}\,\,\varOmega _c, \end{aligned}$$

(2)

$$\begin{aligned} \nabla \cdot \sigma _{\alpha }&=0 \quad \text {in}\,\, \varOmega _{\alpha };\,\,\alpha =1\ldots N. \end{aligned}$$

(3)

From now on, $\alpha =1\ldots N$ is understood every time the index $\alpha$ appears in a relationship, unless otherwise specified. The constitutive relationships for the stress tensors $\sigma _c$ and $\sigma _{\alpha }$ are given by:

$$\begin{aligned} \sigma _c&=\mathbb {C}^c : \nabla \varvec{u}_c , \end{aligned}$$

(4)

$$\begin{aligned} \sigma _{\alpha }&=\mathbb {C}^{\alpha } : \nabla \varvec{u}_{\alpha }, \end{aligned}$$

(5)

where $\varvec{u}_c (\varvec{x})$ and $\varvec{u}_{\alpha }(\varvec{x})$ denote the restrictions of the elastic displacement $\varvec{u}(\varvec{x})$ to $\varOmega _c$ and $\varOmega _{\alpha }$, namely

$$\begin{aligned} \varvec{u}_c=\varvec{u}|_{\varOmega _c};\quad \varvec{u}_{\alpha }=\varvec{u}|_{\varOmega _{\alpha }}. \end{aligned}$$

(6)

The fourth rank tensors $\mathbb {C}^c (\varvec{x})$, $\mathbb {C}^{\alpha }(\varvec{x})$ (with components $C^c_{ijkl},\,C^{\alpha }_{ijkl}$ for $i,j,k,l=1,2,3$) are the elasticity tensors in $\varOmega _c$ and $\varOmega _{\alpha }$, respectively. The symbol “ : ” denotes the double contraction, perfomed between the last two indices of the elasticity tensors and the gradient of the displacements in relationships (4, 5). The constituents’ elasticity tensors are equipped with major symmetry

$$\begin{aligned} C^c_{ijkl}=C^c_{klij};\,\, C^{\alpha }_{ijkl}=C^{\alpha }_{klij} \end{aligned}$$

(7)

and left and right minor symmetry

$$\begin{aligned} C^c_{ijkl}= & {} C^c_{jikl};\,\, C^{\alpha }_{ijkl}=C^{\alpha }_{jikl}, \end{aligned}$$

(8)

$$\begin{aligned} C^c_{ijkl}= & {} C^c_{ijlk};\,\, C^{\alpha }_{ijkl}=C^{\alpha }_{ijlk}, \end{aligned}$$

(9)

the latter implying

$$\begin{aligned} \mathbb {C}^c : \nabla \varvec{u}_c=\mathbb {C}^c : \xi {(\varvec{u}_c)};\,\, \mathbb {C}^{\alpha } : \nabla \varvec{u}_{\alpha }=\mathbb {C}^{\alpha } : \xi {(\varvec{u}_{\alpha })}, \end{aligned}$$

(10)

where

$$\begin{aligned} \xi \left( \bullet \right) =\frac{\nabla (\bullet )+{\nabla (\bullet )}^{{\mathsf {T}}}}{2}, \end{aligned}$$

(11)

i.e. $\xi {(\varvec{u}_c)}$ and $\xi {(\varvec{u}_{\alpha })}$ are the matrix and subphase elastic strain tensors, respectively. Interface conditions across every interface $\varGamma ^{\alpha }{:}=\partial \varOmega _c \cap \partial \varOmega _{\alpha }$, together with proper conditions on the external boundary $\partial \varOmega$, are needed to close the elastic problem (2, 3). We impose continuity of stresses and further assume that the matrix and the subphases are perfectly bonded, such that also the elastic displacements are continuous across every $\varGamma ^{\alpha }$.

Thus, the complete boundary value problem reads

$$\begin{aligned}&\displaystyle \nabla \cdot \sigma _c=0 \quad \text {in}\,\, \varOmega _c, \end{aligned}$$

(12)

$$\begin{aligned}&\nabla \cdot \sigma _{\alpha }=0 \quad \text {in}\,\, \varOmega _{\alpha },\,\, \end{aligned}$$

(13)

$$\begin{aligned}&\sigma _c \varvec{n}^{\alpha }=\sigma _{\alpha }\varvec{n}^{\alpha } \quad \text {on} \,\, \varGamma ^{\alpha }, \end{aligned}$$

(14)

$$\begin{aligned}&\varvec{u}_c=\varvec{u}_{\alpha } \quad \text {on} \,\, \varGamma ^{\alpha },\end{aligned}$$

(15)

$$\begin{aligned}&\quad +\,\text {boundary} \,\,\text {conditions}\quad \text {on}\,\,\partial \varOmega . \end{aligned}$$

(16)

Here, $\varvec{n}^{\alpha }$ denotes the unit vector in $\varvec{x} \in \varGamma ^{\alpha }$ normal to the interface $\varGamma ^{\alpha }$ pointing into the $\alpha$-subphase and $\sigma _c$, $\sigma _{\alpha }$ are given by the constitutive relationships (4) and (5), respectively. The elasticity tensors $\mathbb {C}^c$ and $\mathbb {C}^{\alpha }$ are assumed as smooth functions of $\varvec{x}$ in $\varOmega _c$ and $\varOmega _{\alpha }$, respectively. In general, however:

$$\begin{aligned} \mathbb {C}^c(\varvec{x}) \ne \mathbb {C}^{\alpha }(\varvec{x})\,\,\text {on}\,\,\varGamma ^{\alpha }. \end{aligned}$$

(17)

Next, we apply the asymptotic homogenization technique and exploit the length scale separation in the system to derive the coarse scale elastic model and the related cell problems. The results that can be found in [22] ensure that a linear elastic problem with discontinuous coefficients of the type (12–16) admits a rigorous two-scale convergence limit. Furthermore, this problem has also been tackled in [31], where the due modifications to standard asymptotic homogenization for elastic composites, which apply for discontinuous coefficients, are suggested and formally appear as a volume contribution. In [3], a more general asymptotic homogenization procedure is carried out to formally derive averaged equations of infinite order of accuracy, which can be exploited, for example, for strain gradient elasticity as in [26]. The cell problems involved in the leading order equations are derived and interface loadings across the composite interfaces appear, although their dependence on the difference in the elastic constants is not clearly pointed out. In this section, we present a revisited and generalized formulation of the problem accounting for an arbitrary number of subphases and general periodic cell shapes. We explicitly derive the volume and interface loadings which drive nontrivial cell problem solutions.

2.1 Asymptotic homogenization

We consider a typical length scale d, which locally characterizes the fine scale structure, and the characteristic size L of the whole domain $\varOmega$. We then assume that the following sharp length scale separation between d and L holds:

$$\begin{aligned} \frac{d}{L}=\epsilon \ll 1. \end{aligned}$$

(18)

We now perform a formal two-scale asymptotic expansion widely exploited in the literature to derive the effective governing equations which represent the mechanical behavior of the composite on the coarse scale L and retain information about variations on the fine scale characterized by the length d. We enforce condition (18) relating d (the fine scale) and L (the coarse scale), defining

$$\begin{aligned} \varvec{y}{:}=\frac{\varvec{x}}{\epsilon }. \end{aligned}$$

(19)

Following the usual approach in multiscale analysis, from now on $\varvec{x}$ and $\varvec{y}$ denote formally independent variables, representing the coarse and fine spatial scales, respectively. We further assume that both the displacements and the elasticity tensors are functions of these independent spatial variables, i.e.

$$\begin{aligned} \varvec{u}_c= & {} \varvec{u}_c(\varvec{x},\varvec{y}),\,\, \varvec{u}_{\alpha }=\varvec{u}_{\alpha }(\varvec{x},\varvec{y}), \end{aligned}$$

(20)

$$\begin{aligned} \mathbb {C}^c= & {} \mathbb {C}^c(\varvec{x},\varvec{y}),\,\, \mathbb {C}^{\alpha }=\mathbb {C}^{\alpha }(\varvec{x},\varvec{y}), \end{aligned}$$

(21)

such that the differential operators transform accordingly:

$$\begin{aligned} \nabla \rightarrow \nabla _{\varvec{x}}+\frac{1}{\epsilon } \nabla _{\varvec{y}}. \end{aligned}$$

(22)

We formally define the following multiple scales expansion of the elastic displacement $\varvec{u}$ in powers of $\epsilon$:

$$\begin{aligned} \varvec{u}^{\epsilon }(\varvec{x},\varvec{y})=\sum _{l=0}^{\infty } \varvec{u}^{(l)}(\varvec{x},\varvec{y})\epsilon ^l. \end{aligned}$$

(23)

We apply the power series representation (23) to the restrictions $\varvec{u}_c$ and $\varvec{u}_{\alpha }$, i.e. we define

$$\begin{aligned} \varvec{u}^{(l)}_c=\varvec{u}^{(l)}|_{\varvec{y}\in \varOmega _c};\quad \varvec{u}^{(l)}_\alpha =\varvec{u}^{(l)}|_{\varvec{y}\in \varOmega _\alpha }\,, \end{aligned}$$

(24)

and substitute the result, accounting for relationship (22), into the system (12–15) and Eqs. (4, 5). The resulting differential system, multiplying each equation by a suitable power of $\epsilon$ and exploiting (10), reads

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{\epsilon }_c)\right) +\epsilon \nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}^{\epsilon }_c)\right) \nonumber \\&\quad +\,\epsilon \nabla _{\varvec{x}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}} (\varvec{u}^{\epsilon }_c)\right) +\epsilon ^2\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}^{\epsilon }_c)\right) =0 \end{aligned}$$

(25)

in the matrix $\varOmega _c$,

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{\epsilon }_{\alpha })\right) +\epsilon \nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{\epsilon }_{\alpha })\right) \nonumber \\&\quad +\,\epsilon \nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}} (\varvec{u}^{\epsilon }_{\alpha })\right) +\epsilon ^2\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{\epsilon }_{\alpha })\right) =0 \end{aligned}$$

(26)

in the subphases $\varOmega _{\alpha }$, as well as

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}_c^{\epsilon })) \varvec{n}^{\alpha }-(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}_{\alpha }^{\epsilon })) \varvec{n}^{\alpha } \nonumber \\&\quad =\epsilon (\mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}_{\alpha }^{\epsilon })) \varvec{n}^{\alpha }-\epsilon (\mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}_c^{\epsilon })) \varvec{n}^{\alpha } \end{aligned}$$

(27)

and

$$\begin{aligned} \varvec{u}^{\epsilon }_c=\varvec{u}^{\epsilon }_{\alpha } \end{aligned}$$

(28)

on the interfaces $\varGamma ^{\alpha }$. We assume $\varvec{y}$-periodicity for every field and material property (denoted collectively by $\psi$), that is, there exists a family of vectors

$$\begin{aligned} \varvec{R}(\eta ,\,\kappa ,\,\upsilon ){:}=\eta \varvec{I}_1+\kappa \varvec{I}_2+\upsilon \varvec{I}_3, \end{aligned}$$

(29)

with fixed $\varvec{I}_1,\,\varvec{I}_2,\,\varvec{I}_3 \in \mathbb {R}^3$ such that

$$\begin{aligned} \psi (\varvec{x},\varvec{y})=\psi (\varvec{x},\varvec{y+R}),\,\, \forall \eta ,\, \kappa ,\, \upsilon \in \mathbb {Z}. \end{aligned}$$

(30)

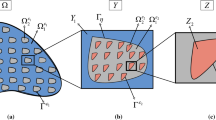
The periodic vector introduced in definition (29) is the three-dimensional generalization of that proposed in [24]. Since we assume that the set of vectors $\left\{ \varvec{I}_1,\,\varvec{I}_2,\,\varvec{I}_3\right\}$ constitutes a basis of $\mathbb {R}^3$, this formulation enables us to consider, in principle, arbitrarily shaped periodic cells in three dimensions, thus not necessarily cuboid (the latter one is obtained for the particular case $\varvec{I}_1 \propto \varvec{e}_1$, $\varvec{I}_2 \propto \varvec{e}_2$, $\varvec{I}_3 \propto \varvec{e}_3$, where $\varvec{e}_1$, $\varvec{e}_2$, $\varvec{e}_3$ denote the standard Cartesian basis vectors). From now on, we identify the domain $\varOmega$ with its corresponding periodic cell and $\varOmega _c$, $\varOmega _{\alpha }$ denote the corresponding matrix and $\alpha$-subphase in the cell, respectively. We also denote by N the number of distinct subphases within the periodic cell. The fine scale length d introduced above Eq. (18) is then identified as the minimum (linear) periodic cell size which can completely represent the fine scale structure, see Fig. 1.

Fig. 1

A two-dimensional cartoon representing the fine and coarse scales. On the right hand side, the coarse scale domain, where the fine scale structure is homogenized, is shown. On the left hand side, a sample periodic unit representing the fine scale is shown and the different subphases are clearly visible

Remark 1

Note that, in principle, the resulting periodic cell could also vary with respect to the coarse scale variable $\varvec{x}$ (see e.g., [5, 15, 27, 28]), nevertheless, we restrict our analysis to the particular case of macroscopic uniformity (i.e. the periodic cell can be uniquely chosen independently of the coarse scale variable) for the sake of simplicity. In general, given a macroscopically uniform domain $\mathcal {D}=\mathcal {D}(\varvec{y})$ we have, for any regular vector field $\varvec{v}=\varvec{v}(\varvec{x},\varvec{y})$

$$\begin{aligned} \nabla _{\varvec{x}}\cdot \int _{\mathcal {D}} \varvec{v}(\varvec{x},\varvec{y})\,\,\text {d}\varvec{y}= \int _{\mathcal {D}}\nabla _{\varvec{x}}\cdot \varvec{v}(\varvec{x},\varvec{y})\,\,\text {d}\varvec{y}. \end{aligned}$$

(31)

$\square$

In the following section, we equate coefficients of $\epsilon ^l$ for $l=0,1,2,\ldots$ in (25–28) to obtain a homogenized model in terms of the leading (zeroth) order elastic displacement field in the coarse scale domain $\varOmega _H$ (see Fig. 1). Since the quantities involved in the definition of this problem can also vary on the local scale $\varvec{y}$, it is useful to define the following cell average operators

$$\begin{aligned}&\displaystyle \left\langle \bullet \right\rangle =\frac{1}{|\varOmega |}\int _{\varOmega } \!\!\bullet \, \text {d}\varvec{y};\quad \displaystyle \left\langle \bullet \right\rangle _c =\frac{1}{|\varOmega |}\int _{\varOmega _c} \!\!\!\bullet \, \text {d}\varvec{y};\nonumber \\&\displaystyle \left\langle \bullet \right\rangle _{\alpha } =\frac{1}{|\varOmega |}\int _{\varOmega _{\alpha }}\!\!\!\!\bullet \, \text {d}\varvec{y}, \end{aligned}$$

(32)

where $|\varOmega |$ represents the periodic cell volume.

2.2 The coarse scale model derivation

Equating coefficients of $\epsilon ^0$ in (25–28) we obtain

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(0)}_c)\right) =0 \,\,\text {in}\,\, \varOmega _c , \end{aligned}$$

(33)

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(0)}_{\alpha })\right) =0 \,\,\text {in}\,\, \varOmega _{\alpha } ,\end{aligned}$$

(34)

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(0)}_c))\varvec{n}^{\alpha }=(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(0)}_{\alpha }))\varvec{n}^{\alpha } \,\,\text {on} \,\, \varGamma ^{\alpha },\end{aligned}$$

(35)

$$\begin{aligned}&\varvec{u}^{(0)}_c=\varvec{u}^{(0)}_{\alpha } \,\, \text {on} \,\, \varGamma ^{\alpha }, \end{aligned}$$

(36)

whereas equating coefficients of $\epsilon ^1$ in (25–28) yields

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(1)}_c)\right) +\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(0)}_c)\right) \nonumber \\&\quad =-\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}^{(0)}_c)\right) \,\, \text {in}~\varOmega _c, \end{aligned}$$

(37)

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{\alpha })\right) +\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(0)}_{\alpha })\right) \nonumber \\&\quad =-\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{(0)}_{\alpha })\right) \,\, \text {in}~\varOmega _{\alpha }, \end{aligned}$$

(38)

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(1)}_c))\varvec{n}^{\alpha }-(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{\alpha }))\varvec{n}^{\alpha } \nonumber \\&\quad =(\mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{(0)}_{\alpha }))\varvec{n}^{\alpha }-(\mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}^{(0)}_c))\varvec{n}^{\alpha } \,\, \text {on}~\varGamma ^{\alpha }, \end{aligned}$$

(39)

$$\begin{aligned}&\varvec{u}^{(1)}_c=\varvec{u}^{(1)}_{\alpha } \,\,\text {on}~\varGamma ^{\alpha }. \end{aligned}$$

(40)

Finally, when equating coefficients of $\epsilon ^2$ in (25–27) we obtain

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{c} : \xi _{\varvec{y}}(\varvec{u}^{(2)}_{c})\right) +\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{c} : \xi _{\varvec{x}}(\varvec{u}^{(1)}_{c})\right) \nonumber \\&\quad =-\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{c} : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{c})\right) -\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{c} : \xi _{\varvec{x}}(\varvec{u}^{(0)}_{c})\right) \,\text {in}\,\varOmega _c, \end{aligned}$$

(41)

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(2)}_{\alpha })\right) +\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{(1)}_{\alpha })\right) \nonumber \\&\quad =-\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{\alpha })\right) -\nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{(0)}_{\alpha })\right) \,\text {in}\,\varOmega _{\alpha }, \end{aligned}$$

(42)

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(2)}_c))\varvec{n}^{\alpha }-(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(2)}_{\alpha }))\varvec{n}^{\alpha } \nonumber \\&\quad =(\mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}^{(1)}_{\alpha }))\varvec{n}^{\alpha }-(\mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}^{(1)}_c))\varvec{n}^{\alpha }\,\, \text {on}~\varGamma ^{\alpha } \end{aligned}$$

(43)

The only periodic solutions of the cell problem (33–36) are $\varvec{y}$-constant functions. Hence, since continuity across the interfaces $\varGamma ^{\alpha }$ holds, the leading order displacement field reads

$$\begin{aligned} \varvec{u}^{(0)}(\varvec{x})=\varvec{u}^{(0)}_c(\varvec{x})=\varvec{u}^{(0)}_{\alpha }(\varvec{x})=:\bar{\varvec{u}}(\varvec{x})\,. \end{aligned}$$

(44)

Employing relationship (44) in Eqs. (37–40), we obtain the following differential problem for the fields $\varvec{u}^{(1)}_c(\varvec{x}, \varvec{y})$, $\varvec{u}^{(1)}_{\alpha }(\varvec{x},\varvec{y})$:

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(1)}_c)\right) =-\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^c : \xi _{\varvec{x}}(\bar{\varvec{u}})\right) \,\,\text {in}\,\,\varOmega _c, \end{aligned}$$

(45)

$$\begin{aligned}&\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{\alpha })\right) =-\nabla _{\varvec{y}} \cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\bar{\varvec{u}})\right) \,\text {in}\,\varOmega _{\alpha }, \end{aligned}$$

(46)

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}^{(1)}_c))\varvec{n}^{\alpha }-(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}^{(1)}_{\alpha }))\varvec{n}^{\alpha }\nonumber \\&\quad =((\mathbb {C}^{\alpha }-\mathbb {C}^c) : \xi _{\varvec{x}}(\bar{\varvec{u}}))\varvec{n}^{\alpha }\,\,\text {on}~\varGamma ^{\alpha }, \end{aligned}$$

(47)

$$\begin{aligned}&\varvec{u}^{(1)}_c=\varvec{u}^{(1)}_{\alpha } \,\,\text {on}~\varGamma ^{\alpha }. \end{aligned}$$

(48)

The problem (45–48) is a linear elastic-type periodic boundary value problem equipped with displacement continuity and stress jump interface conditions on $\varGamma ^{\alpha }$. Exploiting linearity, the solutions $\varvec{u}^{(1)}_c$ and $\varvec{u}^{(1)}_{\alpha }$ are given by the following ansätze

$$\begin{aligned} \varvec{u}_c^{(1)}=\chi ^c : \xi _{\varvec{x}}(\bar{\varvec{u}});\quad \varvec{u}_{\alpha }^{(1)}=\chi ^{\alpha } : \xi _{\varvec{x}}(\bar{\varvec{u}}). \end{aligned}$$

(49)

The third rank tensor $\chi$,

$$\begin{aligned} \chi ={\left\{ \begin{array}{ll}\chi ^c &{} :\,\,\varvec{y} \in \,\, \varOmega _c \\ \chi ^{\alpha } &{} : \,\, \varvec{y} \in \,\, \varOmega _{\alpha }, \end{array}\right. } \end{aligned}$$

(50)

is the solution of the following cell boundary value problems

$$\begin{aligned} \displaystyle&\frac{\partial }{\partial y_j}\left( C_{ijpq}^c \xi _{pqkl}(\chi ^c) \right) =-\frac{\partial C_{ijkl}^c}{\partial y_j}&\text {in}~\varOmega _c, \end{aligned}$$

(51)

$$\begin{aligned}&\frac{\partial }{\partial y_j}\left( C_{ijpq}^{\alpha } \xi _{pqkl}(\chi ^{\alpha }) \right) =-\frac{\partial C_{ijkl}^{\alpha }}{\partial y_j}&\text {in}~\varOmega _{\alpha }, \end{aligned}$$

(52)

$$\begin{aligned}&C_{ijpq}^c \xi _{pqkl}(\chi ^c)n^{\alpha }_j-C_{ijpq}^{\alpha } \xi _{pqkl}(\chi ^{\alpha })n^{\alpha }_j \nonumber \\&\quad =(C^{\alpha }-C^c)_{ijkl} n^{\alpha }_j&\text {on}~\varGamma ^{\alpha }, \end{aligned}$$

(53)

$$\begin{aligned}&\chi ^c_{ikl}=\chi ^{\alpha }_{ikl}&\text {on}~\varGamma ^{\alpha }, \end{aligned}$$

(54)

where we set

$$\begin{aligned} \begin{aligned}&\xi _{pqkl}(\chi ^c)=\frac{1}{2}\left( \frac{\partial \chi _{pkl}^c}{\partial y_q}+\frac{\partial \chi _{qkl}^c}{\partial y_p}\right) , \\&\xi _{pqkl}(\chi ^{\alpha })=\frac{1}{2}\left( \frac{\partial \chi _{pkl}^{\alpha }}{\partial y_q}+\frac{\partial \chi _{qkl}^{\alpha }}{\partial y_p} \right) \end{aligned} \end{aligned}$$

(55)

and sum over repeated indices p, q, j is understood. The problem (51–54) is then closed by periodic conditions on $\partial \varOmega$, whereas a further condition is required to obtain uniqueness, for example, simply fixing the solution in one point or requiring

$$\begin{aligned} \left\langle \chi _{ikl}^c \right\rangle _c=\left\langle \chi _{ikl}^{\alpha } \right\rangle _{\alpha }=0\quad i,k,l=1,2,3\,. \end{aligned}$$

(56)

Remark 2

Note that, from a practical point of view, the cell problem (51–54) stated in terms of third and fourth rank tensors, corresponds, accounting for right minor symmetry of the constituents’ elasticity tensors, to six elastic-type cell problems, one for each fixed $(k,l),\, k\ge l$. Each of these problems is equipped with periodic conditions on the cell boundary and nontrivial solutions are not driven by prescribed tractions or displacements, as for example in [32]. Here, nontrivial solutions are due to local variations of the elastic constants within the composite subphases, which formally appear as volume forces on the right hand side of (51, 52), and due to the interface loadings which appear in the stress jump conditions (53). In the latter case, the contribution is directly related to the difference in the elastic constants between the matrix and each phase, as well as to the geometrical properties of the interface. The interface loadings are nonzero even when the elastic properties of the subphases are constant. Whenever this is the case, these interface loadings are the unique driving force for the cell problems (51–54).$\square$

We now aim to formulate the effective governing equations for the elastic composite material. We apply the integral average operators (32) over $\varOmega _c$ and $\varOmega _{\alpha }$ in Eqs. (41) and (42) for $\alpha =1\ldots N$, respectively. We then sum every resulting contribution and apply the divergence theorem in $\varvec{y}$, such that, rearranging terms, we obtain:

$$\begin{aligned}&\displaystyle \sum ^{N}_{\alpha =1}\frac{1}{|\varOmega |}\left[ \int _{\varGamma ^{\alpha }} (\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{u}_c^{(2)})) \varvec{n}^{\alpha }\,\text {dS} \,\,\right. \nonumber \\&-\left. \int _{\varGamma ^{\alpha }} (\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{u}_{\alpha }^{(2)})) \varvec{n}^{\alpha }\,\text {dS}+\int _{\varGamma ^{\alpha }} (\mathbb {C}^c : \xi _{\varvec{x}}(\varvec{u}_c^{(1)})) \varvec{n}^{\alpha }\,\text {dS}\,\,\right. \nonumber \\&\left. -\int _{\varGamma ^{\alpha }} (\mathbb {C}^{\alpha } : \xi _{\varvec{x}}(\varvec{u}_{\alpha }^{(1)})) \varvec{n}^{\alpha }\,\text {dS}\right] \nonumber \\&+\frac{1}{|\varOmega |} \int _{\varOmega _c} \nabla _{\varvec{x}} \cdot \left( \mathbb {C}^c : (\xi _{\varvec{y}}(\varvec{u}_c^{(1)})+\xi _{\varvec{x}}(\bar{\varvec{u}}))\right) \,\,\text {d}\varvec{y}\,\, \nonumber \\&+\displaystyle \sum ^{N}_{\alpha =1}\frac{1}{|\varOmega |}\int _{\varOmega _{\alpha }} \nabla _{\varvec{x}} \cdot \left( \mathbb {C}^{\alpha } : (\xi _{\varvec{y}}(\varvec{u}_{\alpha }^{(1)})+\xi _{\varvec{x}}(\bar{\varvec{u}}))\right) \,\,\text {d}\varvec{y}=0, \end{aligned}$$

(57)

where the contributions over the cell boundaries $\partial \varOmega$ cancel due to $\varvec{y}$-periodicity. We account for interface conditions (43), such that also each contribution over the interfaces $\varGamma ^{\alpha }$ in (57) reduces to zero. Finally, enforcing macroscopic uniformity (31) and ansätze (49), relationship (57) reduces to the following effective governing equations for every $\varvec{x} \in \varOmega _H$, namely

$$\begin{aligned} \nabla _{\varvec{x}}\cdot \left( \mathbb {\tilde{C}}(\varvec{x}) : \xi _{\varvec{x}}(\bar{\varvec{u}})\right) =0. \end{aligned}$$

(58)

The effective elasticity tensor $\mathbb {\tilde{C}}$ is given by

$$\begin{aligned} \mathbb {\tilde{C}}=\left\langle \mathbb {C}^c+\mathbb {C}^c\mathbb {M}^c\right\rangle _c+\displaystyle \sum _{\alpha =1}^{N}\left\langle \mathbb {C}^{\alpha }+\mathbb {C}^{\alpha }\mathbb {M}^{\alpha } \right\rangle _{\alpha } \end{aligned}$$

(59)

or componentwise by

$$\begin{aligned} \begin{aligned} \tilde{C}_{ijkl} =&\left\langle C_{ijkl}^c+C_{ijpq}^cM_{pqkl}^c\right\rangle _c\\&+ \displaystyle \sum _{\alpha =1}^{N} \left\langle C_{ijkl}^{\alpha }+C_{ijpq}^{\alpha } M_{pqkl}^{\alpha } \right\rangle _{\alpha }. \end{aligned} \end{aligned}$$

(60)

In the above equation, the auxiliary fourth rank tensors $\mathbb {M}^c$ and $\mathbb {M}^{\alpha }$ are defined componentwise as

$$\begin{aligned} \begin{aligned} M_{pqkl}^c&=\xi _{pqkl}(\chi ^c)=\frac{1}{2}\left( \frac{\partial \chi _{pkl}^c}{\partial y_q}+\frac{\partial \chi _{qkl}^c}{\partial y_p}\right) \,,\\ M_{pqkl}^{\alpha }&=\xi _{pqkl}(\chi ^{\alpha })=\frac{1}{2}\left( \frac{\partial \chi _{pkl}^{\alpha }}{\partial y_q}+\frac{\partial \chi _{qkl}^{\alpha }}{\partial y_p} \right) \,. \end{aligned} \end{aligned}$$

(61)

3 Computational setup and procedure

In this section we give specific details about the composite material which we will investigate in Sect. 4 and describe the computational procedure to numerically compute the effective elasticity tensor $\mathbb {\tilde{C}}$, cf. (59).

In general, the numerical computation of $\mathbb {\tilde{C}}(\varvec{x})$ is carried out according to the following scheme:

• (a) Fix the geometry of the periodic cell $\varOmega$ at $\varvec{x}$, including the number N of the embedded subphases.

• (b) Fix the material properties $\mathbb {C}^c(\varvec{x},\varvec{y})$ and $\mathbb {C}^{\alpha }(\varvec{x},\varvec{y})$ for $\varvec{y}\in \varOmega$.

• (c) Solve the elastic-type cell problems (51–54) to determine the tensors $\mathbb {M}^c(\varvec{x})$ and $\mathbb {M}^{\alpha }(\varvec{x})$, cf. (61).

• (d) Compute the effective elasticity tensor $\mathbb {\tilde{C}}(\varvec{x})$, cf. (59).

The coarse scale elastic problem (58) holds for general heterogeneous and anisotropic properties $\mathbb {C}^c(\varvec{x},\varvec{y})$ and $\mathbb {C}^{\alpha }(\varvec{x},\varvec{y})$ of the constituents. However, in order to emphasize the effect of the fine scale geometry on the effective elasticity tensor (both quantitatively and in terms of symmetries), we focus on the simplest possible choice, that is, we assume $\varvec{y}$-constant and $\varvec{x}$-constant isotropic elastic phases. Furthermore, we assume that the elasticity tensor of all subphases is the same. Thus we write

$$\begin{aligned} \begin{aligned} C^c_{ijkl}&=\lambda _c \delta _{ij}\delta _{kl}+\mu _c(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})\,,\\ C^{\alpha }_{ijkl}&=C^m_{ijkl}=\lambda _m \delta _{ij}\delta _{kl}+\mu _m(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})\,, \end{aligned} \end{aligned}$$

(62)

where $(\lambda _c, \mu _c)$ and $(\lambda _m, \mu _m)$ represent the matrix and subphases Lamé constants, respectively, and we consider the following matrix-subphase discontinuity

$$\begin{aligned} \left( \lambda _c,\, \mu _c \right) \ne \left( \lambda _m,\,\mu _m\right) . \end{aligned}$$

(63)

In all computations we use the following parameter set

$$\begin{aligned} \begin{aligned} \lambda _c&= 2.88\,[\text {GPa}]\,,&\mu _c&= 1.92\,[\text {GPa}],\\ \lambda _m&=54.69\,[\text {GPa}]\,,&\mu _m&=42.97\,[\text {GPa}], \end{aligned} \end{aligned}$$

(64)

which is obtained from the Young’s moduli and Poisson’s ratios reported for the collagen and mineral (hydroxyapatite) bone constituents in [33], namely

$$\begin{aligned} \begin{aligned} E_c&= 5\,[\text {GPa}]\,,&\nu _c&=0.3 \,,\\ E_m&=110\,[\text {GPa}]\,,&\nu _m&=0.28\,. \end{aligned} \end{aligned}$$

(65)

The $\varvec{y}$-constant nature of $\mathbb {C}^c$ and $\mathbb {C}^{\alpha }$ simplifies the cell problems (51–54) to

$$\begin{aligned} \displaystyle&\nabla _{\varvec{y}}\cdot \left( \mathbb {C}^c : \xi _{\varvec{y}}(\varvec{\chi }_{kl}^c)\right) =0 \,\,\text {in}\,\, \varOmega _c, \end{aligned}$$

(66)

$$\begin{aligned}&\nabla _{\varvec{y}}\cdot \left( \mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{\chi }_{kl}^{\alpha })\right) =0 \,\,\text {in}\,\, \varOmega _{\alpha }, \end{aligned}$$

(67)

$$\begin{aligned}&(\mathbb {C}^c : \xi _{\varvec{y}}(\varvec{\chi }_{kl}^c))\varvec{n}^{\alpha }-(\mathbb {C}^{\alpha } : \xi _{\varvec{y}}(\varvec{\chi }_{kl}^{\alpha }))\varvec{n}^{\alpha } \nonumber \\&\quad =\varvec{f}^{\alpha }_{kl} \,\text {on} \, \varGamma ^{\alpha }, \end{aligned}$$

(68)

$$\begin{aligned}&\varvec{\chi }^c_{kl}=\varvec{\chi }^{\alpha }_{kl} \,\,\text {on} \,\, \varGamma ^{\alpha }, \end{aligned}$$

(69)

for $k,l=1,2,3$, $k\ge l$, where the auxiliary displacement vectors $\varvec{\chi }_{kl}^c$, $\varvec{\chi }_{kl}^{\alpha }$ are defined as

$$\begin{aligned} \varvec{\chi }_{kl}^c=\left( \chi _{1kl}^c,\,\chi _{2kl}^c,\,\chi _{3kl}^c\right) ;\, \varvec{\chi }_{kl}^{\alpha }=\left( \chi _{1kl}^{\alpha },\,\chi _{2kl}^{\alpha },\,\chi _{3kl}^{\alpha }\right) . \end{aligned}$$

(70)

The forces driving each of the six elastic-type cell problems (66–69) are the interface loads $\varvec{f}^{\alpha }_{kl}$ only, which depend on the jump in the elastic constants between the matrix and each subphase and on the geometry of the subphases as encoded in the normal unit vectors $\varvec{n}^{\alpha }$, see Eq. (53). Enforcing the assumption of isotropic matrix and subphases, i.e. (62), the interface loads $\varvec{f}_{kl}^{\alpha }$ take the specific form

$$\begin{aligned}&\varvec{f}_{11}^{\alpha }=\lambda ^{*}\varvec{n}^{\alpha }+2\mu ^{*}\varvec{e}_1 n_1^{\alpha }, \end{aligned}$$

(71)

$$\begin{aligned}&\varvec{f}_{22}^{\alpha }=\lambda ^{*}\varvec{n}^{\alpha }+2\mu ^{*}\varvec{e}_2 n_2^{\alpha } , \end{aligned}$$

(72)

$$\begin{aligned}&\varvec{f}_{33}^{\alpha }=\lambda ^{*}\varvec{n}^{\alpha }+2\mu ^{*}\varvec{e}_3 n_3^{\alpha }, \end{aligned}$$

(73)

$$\begin{aligned}&\varvec{f}_{23}^{\alpha }=\varvec{f}_{32}^{\alpha }=\mu ^{*}(n^{\alpha }_3 \varvec{e}_2+n^{\alpha }_2 \varvec{e}_3) , \end{aligned}$$

(74)

$$\begin{aligned}&\varvec{f}_{13}^{\alpha }=\varvec{f}_{31}^{\alpha }=\mu ^{*}(n^{\alpha }_3 \varvec{e}_1+n^{\alpha }_1 \varvec{e}_3), \end{aligned}$$

(75)

$$\begin{aligned}&\varvec{f}_{12}^{\alpha }=\varvec{f}_{21}^{\alpha }=\mu ^{*}(n^{\alpha }_2 \varvec{e}_1+n^{\alpha }_1 \varvec{e}_2), \end{aligned}$$

(76)

where

$$\begin{aligned} \lambda ^{*}=\lambda _m-\lambda _c;\quad \mu ^{*}=\mu _m-\mu _c. \end{aligned}$$

(77)

For each boundary load given in (71–76), we compute a corresponding numerical solution of the elastic-type problem (66–69) using the finite element software Comsol Multiphysics employing its Structural Mechanics Module and Matlab LiveLink scripting. This combination of software is also employed to then compute the 36 defining entries of each of the both, left and right, minor symmetric tensors $\mathbb {M}^c$ and $\mathbb {M}^{\alpha }$ using (61) and eventually to obtain $\mathbb {\tilde{C}}$ via (60). We give some detail of this process below.

The finite element mesh of the periodic cell $\varOmega$ is constructed such that, firstly, surface meshes are created for the interfaces $\varGamma ^\alpha$, $\alpha =1,\ldots N$, and then, secondly, those surface meshes are extended into a three-dimensional mesh covering the whole periodic cell. This approach provides for the definition of interface conditions via boundary pairs and allows to combine a particularly fine surface mesh on the interfaces, which then also extends into their vicinity, with a gradually coarser volume mesh as the distance from the interface increases. This is illustrated in Fig. 2. Recall that the stress-jump condition on the interfaces is the primary driver of the solution of the cell problems and thus a sufficiently fine mesh around the interfaces is paramount for an accurate numerical solution. Further below, see Remark 3, we give information on the employed mesh refinement strategy to ensure a sufficiently accurate numerical solution.

Fig. 2

A representative computational mesh for a single spherical inclusion. The mesh on the interface between the matrix and the inclusion is more refined to better capture the boundary loads contribution

The parametrization of the stress balance Eqs. (66, 67) is straightforward in our case: we have zero volume forces and a constant, isotropic elasticity tensor per subdomain $\varOmega _c$ and $\varOmega _\alpha$. The stress jump and auxiliary displacement continuity conditions across the interfaces $\varGamma ^\alpha$, i.e. (68, 69), are enforced via respective conditions on a boundary pair for each subphase. Finally, the periodic boundary conditions on the outer boundary $\partial \varOmega$ are implemented. These settings render the solution of the elastic-type problem unique up to a constant. This constant is not important for our purpose since it vanishes when the partial derivatives of the solution are taken as in (61). However, computationally we require a unique solution of the elastic-type problems in the periodic cell and this is achieved by additionally demanding that the auxiliary displacement is zero in one corner point of $\varOmega$, thus fixing the constant.

The principle of virtual work is employed by Comsol Multiphysics to implement the elastic-type problem described above in weak form. This is done separately for each subdomain, i.e. the matrix and each inclusion phase, where an elastic-type problem holds. The individual weak forms are then coupled through the enforcement of the interface and boundary conditions. The problem for the auxiliary variables $\varvec{\chi }_{kl}^c$, $\varvec{\chi }_{kl}^{\alpha }$ is solved in the geometrical setting provided by the Comsol feature assembly. The subdomains $\varOmega _c$ and $\varOmega _\alpha$ are not merged to form a simple union, as in the latter case continuity of stresses, which does not apply in our case, is automatically implemented. We retain, instead, the boundaries for each subdomain, as this allows for the required flexibility in the prescription of the interface conditions, which is exploited to specify the stress discontinuity conditions (68) across the boundary pairs. We use quadratic Lagrange elements on our finite element mesh for representing the auxiliary displacements. The resulting sparse linear system is solved with a sparse direct solver (Pardiso) after preordering of the unknowns and equations such that fill-in, and thus excessive memory requirements, are reduced. This provides the finite element solutions $\varvec{\chi }_{kl}^c$, $\varvec{\chi }_{kl}^{\alpha }$.

All entries of the third rank tensors $\chi ^c$ and $\chi ^\alpha$ are numerically approximated by piecewise quadratic finite element functions once the six elastic-type problems (66–69) corresponding to the six interface loads $\varvec{f}_{kl}^{\alpha }$, cf. (71–76), have been solved. Their derivatives are linear functions on each element and they can be evaluated conveniently (and without additional error) and so can all entries of the both, left and right, minor symmetric auxiliary fourth rank tensors $\mathbb {M}^c$ and $\mathbb {M}^{\alpha }$ using (61). The entries of the effective elasticity tensor $\mathbb {\tilde{C}}$ are then computed following (60) by calculating the averages without additional errors. The whole process from the finite element approximations for $\chi ^c$ and $\chi ^\alpha$ to the effective elasticity tensor $\mathbb {\tilde{C}}$ is expressed in Comsol Multiphysics using its integral postprocessing capability.

Remark 3

(Refinement of the finite element mesh) Recall that the auxiliary displacements $\varvec{\chi }_{kl}$ are completely driven by the boundary loads $\varvec{f}_{kl}^{\alpha }$ on the interfaces $\varGamma ^\alpha$. Therefore, in order to faithfully capture this information, our mesh in $\varOmega$ is more refined around the boundary pairs representing the interfaces $\varGamma ^{\alpha }$ than in the bulk away from these interfaces. Furthermore, we use a sequence of increasingly refined meshes of $\varOmega$. These meshes are constructed using Comsol Multiphysics’ predefined mesh parameter settings ranging from extremely coarse to extremely fine meshes. In order to ensure an appropriate level of accuracy in the computed effective elasticity tensor, we accept the numerical solution for all $\varvec{\chi }_{kl}$ on a finer mesh A when the componentwise difference between $\tilde{\mathbb {C}}^A$ computed on that mesh and $\tilde{\mathbb {C}}^B$ computed on the next-coarser mesh B satisfies the following mixed absolute-relative criterion:

$$\begin{aligned} \displaystyle \max _{\beta ,\, \gamma =1,\ldots 6} \left| \tilde{C}_{\beta \gamma }^{A}-\tilde{C}_{\beta \gamma }^{B}\right| \big /\left( |\tilde{C}_{\beta \gamma }^{A}|+1\right) \le tol \ll 1. \end{aligned}$$

(78)

The number tol in (78) represents a suitable tolerance value. In Eq. (78) and from now on, the elasticity tensor $\mathbb {\tilde{C}}$ is represented as a $6\times 6$ symmetric matrix $\tilde{\mathsf {C}}$ by adopting the so called Voigt notation, e.g., [7]. $\square$

Finally we state that for every numerical test which we report in the following Sect. 4, the above criterion (78) is satisfied for $tol=10^{-2}$.

4 Numerical results

In this section we make use of the computational framework described in Sect. 3 and explore the variations of the effective elasticity tensor $\mathbb {\tilde{C}}$, cf. Eq. (59), as they arise from geometrical changes of the fine structure of the composite material. We in particular consider the case when there exists a substantial jump between the matrix and the subphases elastic properties, as exemplified by the vastly different Young’s moduli, see Eq. (65). The geometrical settings are chosen to highlight the main features of the asymptotic homogenization technique and to compare the results to those obtained by Eshelby based techniques. In the following subsections we present three numerical test cases, see Table 1, which differ in the number N of subphases and their shape within the periodic cell $\varOmega$, the shape of the periodic cell $\varOmega$ itself, as well as the subphases volume fraction $\phi _m$ defined as:

$$\begin{aligned} \phi _m=\frac{|\varOmega _m|}{|\varOmega |};\quad |\varOmega _m|=\displaystyle \sum ^N_{\alpha =1} |\varOmega _{\alpha }|\,. \end{aligned}$$

(79)

The test case presented in Sect. 4.3 can be reduced to a two-dimensional setting where a semi-analytic solution is available and thus also provides a benchmark for our three-dimensional numerical simulation approach.

Table 1 Overview of the numerical test cases

4.1 Single spherical inclusion in a cubic periodic cell

We consider the case of a single spherical inclusion in a cubic cell and perform a parametric study by varying the inclusion volume fraction $\phi _m$. This way we can highlight the coarse scale elastic response, given by the effective elasticity tensor $\mathbb {\tilde{C}}$, via a reduced number of parameters. In particular, the analysis of a single spherical inclusion represents the simplest possible example that can be compared to Eshelby based methods, such as the Mori–Tanaka and the self-consistent schemes. The overall cell geometry is invariant under permutation of the three orthogonal coordinate axes. However, even this simplest possible fine scale structure is not geometrically isotropic and, as a consequence, we obtain an elasticity tensor with cubic symmetry, i.e.

$$\begin{aligned} \tilde{\mathsf {C}}= \left[ \begin{array}{llllll} \tilde{C}_{11} &{}\quad \tilde{C}_{12} &{}\quad \tilde{C}_{12} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \tilde{C}_{12} &{}\quad \tilde{C}_{11} &{}\quad \tilde{C}_{12} &{}\quad 0 &{}\quad 0\quad &{}\quad 0\\ \tilde{C}_{12} &{}\quad \tilde{C}_{12} &{}\quad \tilde{C}_{11} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} \end{array}\right] , \end{aligned}$$

(80)

see, e.g., [8]. Three independent parameters are therefore needed to completely specify the elastic behavior of the material. In particular, exploiting standard engineering notation (see, e.g., [4]), we can deduce the effective Young’s modulus $E_H$, Poisson’s ratio $\nu _H$, and shear modulus $\mu _H$ via the general definitions

$$\begin{aligned} \begin{aligned} E_H&=\frac{\tilde{C}_{11}(\tilde{C}_{11}+\tilde{C}_{12})-2 \tilde{C}^2_{12}}{\tilde{C}_{11}+\tilde{C}_{12}}\,;\\ \nu _H&=\frac{\tilde{C}_{12}}{\tilde{C}_{11}+\tilde{C}_{12}}\,;\quad \mu _H=\tilde{C}_{44}\,. \end{aligned} \end{aligned}$$

(81)

The material resistance to shear and uniaxial loading is given by the effective coefficients $E_H$ and $\mu _H$, respectively, whereas the Poisson’s ratio $\nu _H$ measures the ratio of transverse to axial strain. The deviation from isotropy of the composite material is quantified by

$$\begin{aligned} \text {DEV}=\tilde{C}_{11}-(\tilde{C}_{12}+2\tilde{C}_{44}) \end{aligned}$$

(82)

and shown in Fig. 3. This effect is driven by the periodic cell geometry and accounts for the arrangement of the inclusions within the fine scale domain.

Fig. 3

The deviation from isotropy is shown as a function of the volume fraction $\phi _m$ for a single spherical inclusion in a cubic cell

Assuming that $\mathbb {\tilde{C}}$ satisfies the classical Voigt [34] and Reuss [30] upper and lower bounds, namely

$$\begin{aligned} {\mathsf {A}}:(\mathbb {C}^R : {\mathsf {A}}) \le {\mathsf {A}}:(\mathbb {\tilde{C}} : {\mathsf {A}}) \le {\mathsf {A}}:(\mathbb {C}^V : {\mathsf {A}}) \end{aligned}$$

(83)

for every second rank tensor ${\mathsf {A}}$ where

$$\begin{aligned} \mathbb {C}^R=\left\langle \mathbb {C}^{-1} \right\rangle ^{-1} \quad \text {and}\quad \mathbb {C}^V=\left\langle \mathbb {C} \right\rangle \,, \end{aligned}$$

(84)

then, defining $E_R$, $\mu _R$, $E_V$, $\mu _V$ as the Reuss and Voigt Young’s and shear moduli, respectively, it follows that

$$\begin{aligned} \mu _R\le \mu _H\le \mu _V\, \quad \text {and}\quad E_R\le E_H\le E_V\,. \end{aligned}$$

(85)

These bounds are proven in [29] by applying the relationships (83) to suitable linear combination of the following second rank tensors

$$\begin{aligned} \begin{aligned}&\varvec{e}_1 \otimes \varvec{e}_1;\quad&\varvec{e}_2 \otimes \varvec{e}_2\,; \\&\varvec{e}_1 \otimes \varvec{e}_2+\varvec{e}_2 \otimes \varvec{e}_1\\ \end{aligned} \end{aligned}$$

(86)

to obtain the bounds (85) accounting for definitions (81). These relationships are satisfied in our numerical tests as shown in Figs. 4 and 5. Quantitatively, we observe a significant deviation of the effective Young and shear moduli from their corresponding upper bound estimates, i.e. $E_H \ll E_V$ and $\mu _H \ll \mu _V$. Above, the bounds (83) have been assumed. However, they should be rigorously proved since classical results, which apply to representative volume elements (see, e.g., [6, 20, 37]), rely on Hill’s condition (see, e.g., [13]), i.e. on the equivalence between the coarse scale energy and the average fine scale energy, which does not apply to asymptotic homogenization. In the latter case, the periodic cell problem properties are to be taken explicitly into account, as done in [19], where the authors exploited variational arguments to obtain the standard Voigt and Reuss bounds for an heterogeneous two-phase material composite without discontinuities of the elastic constants at the interface. It is beyond the scope of this computational study to address delicate theoretical issues such as rigorous proofs of energy bounds and symmetry of the effective elasticity tensors, which we address, instead, in [29].

Fig. 4

The asymptotic homogenization Young’s modulus for a single spherical inclusion compared to Eshelby based methods

Fig. 5

The asymptotic homogenization shear modulus for a single spherical inclusion compared to Eshelby based methods

The major difference between the asymptotic homogenization scheme and Eshelby based methods resides in the lack of isotropy of the former, cf. Fig. 3. Recall that the Mori–Tanaka method is derived assuming an infinitely extended matrix which comprises identically shaped ellipsoidal inclusions at fixed volume fraction and aspect ratios. The self-consistent scheme is derived assuming that such a domain is composed of a number of interacting phases and no clear distinction between the matrix and the inclusions is made, such that volume fraction and aspect ratios are to be specified for each phase. For the sake of simplicity of the following analysis, we set every aspect ratio for the matrix phase to one, i.e. corresponding to spherical “inclusions”.

In both Eshelby models, anisotropy can only arise as a consequence of the inclusion aspect ratios, and spherical inclusions lead to coarse scale isotropy. The elastic response predicted by asymptotic homogenization (which accounts, in principle, for an arbitrary complex geometry of the inclusions) is, instead, also affected by the periodic cell geometry itself, which is supposed to represent the structural organization of the subphases within the matrix. In the particular test case considered in this section, the cubic shape of $\varOmega$ induces the cubic symmetry in $\tilde{\mathbb {C}}$.

The explored techniques differ also quantitatively for this simple example. The asymptotic homogenization and self-consistent methods both predict the stiffer behavior for uniaxial loading, see Fig. 4, as these techniques fully account for interaction among phases, unlike the Mori–Tanaka scheme, where phases are weakly coupled only via uniform strain conditions at infinity which involve the average strain in the matrix. The stiffer response with respect to torsional loading is predicted by the self-consistent scheme, see Fig. 5, as a consequence of the shear interactions between the two spherical phases taken into account (we remind that, according to the self-consistent scheme assumptions [14], each phase is characterized by an idealized ellipsoidal shape and no matrix can be clearly identified). The greater resistance to transverse compression (at fixed uniaxial loading) is given by asymptotic homogenization, see Fig. 6, in qualitative agreement with the RVE study reported in [32] for randomly distributed spheres.

Fig. 6

The asymptotic homogenization Poisson’s ratio for a single spherical inclusion compared to Eshelby based methods

4.2 Two cubic inclusions in a cubic periodic cell

We now consider two parallel aligned cubic inclusion $\varOmega _{1}$ and $\varOmega _{2}$ at fixed (combined) volume fraction $\phi _m$, see Table 1. We define a growth index $p \in \displaystyle \left\{ 0,1,\ldots 20\right\}$ such that

$$\begin{aligned} \phi _{1}=\frac{|\varOmega _{1}|}{|\varOmega |}=\frac{p \phi _m}{20}~\Rightarrow ~\phi _{2}=\frac{|\varOmega _{2}|}{|\varOmega |}=\frac{(20-p)\phi _m}{20}. \end{aligned}$$

(87)

The limit cases $p=0$ and $p=20$ correspond to single cubic inclusions. For reasons of symmetry, we perform a parametric analysis in the range $1 \le p \le 10$. For every growth index p the two inclusions are identically shaped and differ by their size only. The geometric settings corresponding to $p=1$ and $p=10$ are shown in Fig. 7.

Fig. 7

Visualization of the double cubic inclusion geometry for $p=1$ (top) and $p=10$ (bottom)

The resulting structure is invariant under permutation of the axes which span the $\varvec{e}_1$ and $\varvec{e}_3$ directions. As a consequence, we obtain an effective elasticity tensor $\mathbb {\tilde{C}}$ with tetragonal symmetry, i.e.

$$\begin{aligned} \tilde{\mathsf {C}}= \left[ \begin{array}{llllll} \tilde{C}_{11} &{}\quad \tilde{C}_{12} &{}\quad \tilde{C}_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \tilde{C}_{12} &{}\quad \tilde{C}_{22} &{}\quad \tilde{C}_{12} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \tilde{C}_{13} &{}\quad \tilde{C}_{12} &{}\quad \tilde{C}_{11} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{55} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} \end{array}\right] , \end{aligned}$$

(88)

such that six independent elastic constants arise. The anisotropy ratio of the composite is defined as the ratio of $\tilde{C}_{22}$ to $\tilde{C}_{11}$ and is shown for $1\le p \le 10$ in Fig. 8. According to these results, anisotropy can develop in a preferential direction also with two identically shaped inclusions and the growth index p can serve as a control. The reason is that asymptotic homogenization predicts the coarse scale elastic constants on the basis of the whole periodic cell structure and symmetry and in the case considered here the geometric variation along the $\varvec{e}_2$ direction and the cubic symmetry of the cell result in the tetragonal structure given by (88). This anisotropy, in contrast, cannot be captured by Eshelby based techniques as the aspect ratios of the inclusions are the same (same shape) and the structural organization of the subphases has no impact on the results. Thus Eshelby based techniques provide an effective stiffness tensor independent of the growth index p.

Fig. 8

The growth of the anisotropy ratio $\tilde{C}_{22}/\tilde{C}_{11}$ as a function of the growth index p

Remark 4

Note that we did not specify the distance between the two inclusions, although the results are, in principle, also affected by this geometrical feature. However, the dependence of the effective elastic constants on the distance between inclusions proved to be extremely weak (of the order of magnitude of our numerical tolerance, see Eq. (78)). We attribute this weak effect to the strong influence of periodicity on the cell boundaries $\partial \varOmega$. However, whenever the typical distance between inclusions (and/or the inclusions size itself) is extremely smaller than the typical cell size d, it might be nontrivial to computationally fully resolve the whole structure within the periodic cell. In this case, it might be convenient to setup a more refined multiscale formulation that accounts for this additional spatial scale separation. $\square$

4.3 Single cylindrical fiber in a prismatic hexagonal periodic cell

We consider a single cylindrical fiber $\varOmega _{1}$ embedded in a prismatic hexagonal cell as illustrated in Fig. 9. The resulting effective elasticity tensor is transverse isotropic, i.e.

$$\begin{aligned} \tilde{\mathsf {C}}= \left[ \begin{array}{llllll} \tilde{C}_{11} &{}\quad \tilde{C}_{11}-2\tilde{C}_{66} &{}\quad \tilde{C}_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \tilde{C}_{11}-2\tilde{C}_{66} &{}\quad \tilde{C}_{11} &{}\quad \tilde{C}_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \tilde{C}_{13} &{}\quad \tilde{C}_{13} &{}\quad \tilde{C}_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{44} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{C}_{66} \end{array}\right] . \end{aligned}$$

(89)

Remark 5

Note that in the particular case considered in this section we do not obtain a tetragonal symmetric structure, since the two-dimensional cross section, i.e. the hexagon with an embedded circle, represents a plane of isotropy. Anisotropy can thus only develop in the orthogonal direction, such that a transverse isotropic elasticity tensor is obtained. $\square$

Fig. 9

Illustration of the cylindrical inclusion embedded in a prismatic hexagonal cell

In this geometrical setting, the three-dimensional problems in our asymptotic homogenization scheme, which we solve by finite elements in our computational approach, can be reduced equivalently to problems in two dimensions, see “Appendix”. The authors in [23, 24] propose a semi-analytical technique to solve the latter problems and, using the same code as exploited in the study of cortical bone in [25], we can compute the effective stiffness tensor of the composite. Since the underlying problems of the two approaches are equivalent for the study of fibers, but rely on completely different solution techniques, this particular test case can be regarded as a benchmark for the two numerical solution procedures.

In particular, we applied both techniques in a parametric study by varying the volume fraction of the fiber $\phi _m$, see Table 1. The results of both schemes coincide up to numerical errors. We report a maximum componentwise relative error of the order of $\approx 2\,\%$, which is due to both the numerical approximation of the cell problems solutions via finite elements and to the errors encoded in the semi-analytical approximation, which is based on truncated series expansions, see [24]. In Fig. 10 we present a comparison between the two methods for the representative components $\tilde{C}_{11}$ and $\tilde{C}_{33}$.

Fig. 10

The numerical and semi-analytical outcome for the components $\tilde{C}_{11}$ and $\tilde{C}_{33}$ is shown. The results match almost exactly

5 Discussion and concluding remarks

In this work we have exploited the classical asymptotic homogenization technique to provide a generalized theoretical and computational framework which fosters three-dimensional numerical computation of the effective elastic properties of a composite elastic material. The effective model coefficients are to be calculated solving the periodic cell problems (51–54), where the interface loads depend on the discontinuities in the composites’ elastic coefficients. The most important features of our asymptotic homogenization approach for elastic composites are listed below.

• We can account for any kind of geometrical complexity in terms of number and shape of subphases within the periodic cell. We are not forced to assume a specific shape representing the subphases (as the ellipsoidal one characterizing Eshelby based techniques), as shown, for example, in Sects. 4.2 and 4.3, where cubic and cylindrical subphases are taken into account.

• The model encodes a clear distinction between the matrix and the embededded subphases. This is, for example, in contrast to the self-consistent scheme [14], where each phase is represented as an ellipsoidal inclusion.

• We fully account for interactions among phases in the periodic cell and each consituent is neither diluted nor approximated when formulating the cell problems.

• Geometrically induced anisotropy, which develops starting from isotropic constituents, reflects all subphases relative dimensions (such as the aspect ratios for ellipsoidal inclusions) and the whole periodic cell structure, including:

  • (a) The periodic cell geometry. For example, in Sect. 4.1, the cell geometry induces an effective elasticity tensor with cubic symmetry for the particular case of a single spherical inclusion. In Sect. 4.3, the hexagonal prismatic periodic cell, together with the cylindrical fibre, provides for the existence of a plane of isotropy which in turn results in a transverse isotropic effective elasticity tensor.

  • (b) The arrangement of subphases within the cell. For example, in Sect. 4.2, the arising tetragonal symmetry is dictated by the inclusions arrangement (which induces geometrical variation along the $\varvec{e}_2$ direction) and the cubic periodic cell geometry. Note that for the asymptotic homogenization it makes a difference if subphases are identically shaped but of different size, whereas that is not the case for Eshelby based techniques, where only the total volume fraction is relevant.

• Whenever all subphases are aligned fibers, dimensional reduction can be performed, see “Appendix”.

Our numerical results suggest that asymptotic homogenization for a multiphase elastic composite with discontinuos material properties should be implemented whenever there is, on one hand, the need to minimize the computational effort arising from simulating the fully resolved small scale features and, on the other hand, the need to account for the precise subphases shape and structural arrangement. In fact, the main advantage of this approach is to foster computational feasibility without altering the single subphase geometrical properties and preserving the structural ordering within the composite, provided that fine scale periodicity is assumed. Whenever a medium merely consists of inclusions that can be resonably approximated by spheres or ellipsoids and there is no available information concerning their arrangement, Eshelby based techniques can be chosen. These rely on semi-analytical schemes which basically require no computational effort, especially when subphases interactions are not fully taken into account, as in the Mori–Tanaka scheme. The asymptotic homogenization scheme can be nontrivial to implement and requires more computational effort whenever the number of subphases, their geometrical complexity, and their total volume fraction are substantially increasing, as, in this case, the result is to be captured via a highly resolved finite element mesh around the subphase interfaces.

The mathematical model we explored in this work comprises a number of simplifying assumptions, including periodicity of the fine scale structure, macroscopic uniformity, linearized elasticity, and perfectly bonded subphases. We comment on these in turn.

Fine scale periodicity is classically assumed when applying the asymptotic homogenization technique, and the existence of a reference periodic cell is necessary to actually solve the local problems on a reasonably small subset of the whole fine scale domain. However, when asymptotic homogenization is used to formally derive the coarse scale equations only, local boundness of the fine scale solution is sufficient, see for example the derivation of the classical poroelasticity equations carried out in [5].

A slow modulation of the fine scale geometry, that is, admitting coarse scale variations of the fine scale geometry, could be introduced although this, in general, introduces additional apparent volume forces in the coarse scale effective equations, as Eq. (31) would not hold anymore. A non macroscopically uniform setting could greatly affect the computational cost, as the (locally periodic) cell problems would have to be solved for each coarse scale point. We refer to, for example, [27, 28] for a thorough discussion about macroscopic uniformity and geometrical modulation of local structure in the context of porous media flow and poroelasticity, respectively. Whenever this scenario better represents the actual physical system at hand, high performance parallel computing could be exploited to solve the cell problems via independent instances, thus reducing the overall computational cost.

Generalizations to nonlinear constitutive behavior of the constituents are nontrivial when dealing with asymptotic homogenization, especially when a practical outcome is to be obtained as the solution of well-posed cell problems. However, a few examples can be found in the literature in the context of elasto-plasticity, e.g., [10].

We have not considered interface debonding among phases, which in general modifies the mechanical properties of elastic composites. As an illustrating example we refer to [35], where the authors experimentally test the effect of interface debonding for bovine compact bone. A challenging extension to the current model then resides in deducing the qualitative and quantitative properties of the arising effective elasticity tensor with respect to various displacement jump prescriptions dictated by the actual physiology at hand.

Finally, although the methodology derived and explored in this paper has focused on a generic elastic composite, the next natural step is to apply this approach to hierarchical physical systems of practical interest, such as musculoskeletal mineralized tissues. This way, predictions based on realistic geometries will allow model validation (by comparison against experimental data) and provide insights concerning the interplay among the system constituents which could be directly exploited for biomimetic materials development.

Appendix: The asymptotic model for aligned fibers

In order to compare our results to those found in [24], we specialize our model by matching any assumption enforced by the authors of that paper. We identify our domain $\varOmega$ with a periodic composite reinforced by aligned fibers, where each subphase $\varOmega _{\alpha }$ is a fiber which extends up to the domain boundary, whereas $\varOmega _c$ represents the host medium. Once periodicity is exploited, the periodic cell then comprises a number N of aligned fibers which extend from bottom to top of it. They are, without loss of generality, aligned with the $\varvec{e}_3$ axis. See Fig. 9, where the geometrical setting related to the particular case of a single cylindrical fiber in a regular prismatic lattice is depicted.

Material properties $\mathbb {C}^c$ and $\mathbb {C}^{\alpha }$ are assumed constant with respect to both the fine scale $\varvec{y}$ and the coarse scale $\varvec{x}$. According to this scenario, the cell problem (51–54) reads

$$\begin{aligned} \displaystyle&C_{ijpq}^c \frac{\partial ^2 \chi _{pkl}^c}{\partial y_j \partial y_q} =0\,\, \text {in}\,\, \varOmega _c, \end{aligned}$$

(90)

$$\begin{aligned}&C_{ijpq}^{r} \frac{\partial ^2 \chi _{pkl}^{r}}{\partial y_j \partial y_q} =0\,\, \text {in}\,\, \varOmega _{r}, \end{aligned}$$

(91)

$$\begin{aligned}&C_{ijpq}^c \frac{\partial \chi _{pkl}^c}{\partial y_q} n_j^{r}+C_{ijkl}^cn^{r}_j \nonumber \\&\quad =C_{ijpq}^{r} \frac{\partial \chi _{pkl}^{r}}{\partial y_q} n_j^{r}+C_{ijkl}^{r}n^{r}_j \,\, \text {on} \,\, \varGamma ^{r}, \end{aligned}$$

(92)

$$\begin{aligned}&\chi ^c_{ikl}=\chi ^{r}_{ikl} \,\, \text {on} \,\, \varGamma ^{r}, \end{aligned}$$

(93)

$r=1,\ldots N$ and summation over repeated indices $j,p,q=1,2,3$ is understood. In the above problem, we slightly rearranged terms, we replaced the dummy index $\alpha$ with r, cf. [24], and exploited property (10). We then recognize that the unknowns $\chi ^c$, $\chi ^{r}$ do not depend on $y_3$ for reasons of symmetry. In particular, since

$$\begin{aligned} n^r_1=n^r_1(y_1,y_2);\quad n^r_2=n^r_2(y_1,y_2);\quad n_3^r=0, \end{aligned}$$

(94)

and the elasticity tensors $\mathbb {C}^c$ and $\mathbb {C}^r$ are $\varvec{y}$-constant, the solution ansatz

$$\begin{aligned} \chi ^c (y_1,y_2);\quad \chi ^{r}(y_1,y_2) \end{aligned}$$

(95)

satisfies the cell problems (90–93). Hence, the cell problems (90–93) are now to be solved in two dimensions only and they can be rewritten, setting $\mathbb {C}^c=\mathbb {C}^0$, as

$$\begin{aligned}&C_{i\alpha s \beta }^{r} \frac{\partial ^2 \chi _{skl}^{r}}{\partial y_{\alpha } \partial y_{\beta }} =0\,\, \text {in}\,\, D_{r}, \end{aligned}$$

(96)

$$\begin{aligned}&C_{i\alpha s\beta }^0 \frac{\partial \chi _{skl}^0}{\partial y_\beta } n_{\alpha }^{r}+C_{i\alpha k l}^0n^{r}_{\alpha }\nonumber \\&\quad =C_{i\alpha s\beta }^{r} \frac{\partial \chi _{skl}^{ r}}{\partial y_{\beta }} n_{\alpha }^{r}+C_{i\alpha kl}^{r}n^{r}_{\alpha } \,\,\, \text {on} \,\, \partial D^{r}, \end{aligned}$$

(97)

$$\begin{aligned}&\chi ^0_{ikl}=\chi ^{r}_{ikl} \,\,\, \text {on} \,\, \partial D^{r}, \end{aligned}$$

(98)

$r=0,1,\ldots N$, and summation over repeated indices $s=1,2,3$, $\alpha , \beta =1,2$ is understood. Here, the domain $D \subset \mathbb {R}^2$ represents the two-dimensional cross section of the periodic cell $\varOmega$. We set $\varOmega _0=\varOmega _c$ and introduce the following notation for the sake of convenience:

$$\begin{aligned}&\varOmega =D\times (0,1); \quad \varOmega _{r}=D_{r} \times (0,1);\nonumber \\&\bar{D}=\bigcup ^{N}_{r=0} \bar{D}_{r}; \quad \varGamma ^{r}=\partial D_{r}\times (0,1). \end{aligned}$$

(99)

Accounting for notation (99), the componentwise definition of the effective elasticity tensor (60), and continuity (98), we finally have:

$$\begin{aligned}&\tilde{C}_{ijkl}=\sum _{r=0}^N \phi _r C_{ijkl}^r+\sum ^{N}_{r=1} \left( C_{ijs\beta }^{r}-C^{0}_{ijs \beta } \right) \left\langle M^r_{s \beta k l}\right\rangle _r,\nonumber \\&\phi _r=\frac{|\varOmega _r|}{|\varOmega |}=\frac{|D_r|}{|D|}, \end{aligned}$$

(100)

$$\begin{aligned}&\left\langle M^r_{s\beta k l}\right\rangle _r= \left\langle \frac{\partial \chi _{skl}^r}{\partial y_{\beta }} \right\rangle _r=\frac{1}{|D|} \int _{\partial D_r} \chi _{skl}^r n_{\beta }^{r}\,\,\text {dl}. \end{aligned}$$

(101)

The functional form of the effective elasticity tensor (100), as well as the corresponding cell problems (96–98) and auxiliary tensor (101), exactly coincide¹ with those found in [24], which were derived accounting for a periodic fiber reinforced composite and applying asymptotic homogenization to the domain cross section only.