1 Introduction

Low-dimensional spin systems with the antiferromagnetic exchange often demonstrate ground state which cannot be expected from the classical point of view. These ground states either completely fluctuate or have ordered spin components with a strong quantum reduction. The most bright examples are given by Heisenberg quantum chains of spins S=1/2 or S=1. For both these examples, the ground state is in a classic sense disordered, i.e., there is no ordered spin component at a lattice site, but, nevertheless, there are strong correlations and well-defined excitations corresponding to quantized quasiparticles. For \(S=\) 1/2 chain, the spin–spin correlations decay algebraically (ground state is quantum-critical) and quasiparticles, so called spinons, have fractionalized spin S=1/2, resulting in a gapless continuum of transferred energy for neutron or photon scattering, see, [1,2,3,4]. For S=1, the ground state is again disordered, but the correlation length is final. Quasiparticles are S=1 triplets separated from the ground state by a so-called Haldane gap [5]. Recently, many other quantum spin systems were found, both theoretically and experimentally, such as spin ladders, kagome lattices, etc. [6, 7].

Now we study experimentally the spectrum of excitations in a simple but very enlightening model which is intermediate between completely fluctuating system and partially ordered one—a spin \(S=1/2\) chain with an Ising type anisotropy (so-called XXZ chain). This system was extensively studied theoretically because of intriguing entangled states [8,9,10,11]. At the same time, it may be adequately realized in the target compound of our study Cs\(_2\)CoCl\(_4\) which was tested in many aspects experimentally [9, 11,12,13,14]. The spin Hamiltonian of XXZ chain in a magnetic field is

$$\begin{aligned} {{\mathcal {H}}} = \sum _i (J(S_x^i S_x^{i+1} + S_y^i S_y^{i+1} +\varDelta S_z^i S_z^{i+1}) + g_\alpha \mu _B H_\alpha S_\alpha ^i ), \end{aligned}$$
(1)

here \(S_\alpha ^i\) are spin component operators for site i of the chain, \(g_\alpha\) are g-factor tensor components and \(H_\alpha\) are components of the magnetic field. g-factor tensor is proposed to be diagonal.

We will be interested in the case of positive \(\varDelta\) corresponding to the anisotropy of the easy plane type. This system has a remarkable ground state and field-induced phase transitions [8, 9, 11, 14]. In a zero field, there is a quantum-critical gapless spin liquid, in a transverse magnetic field \(H_x\), the ground state is a 1D long-range ordered flopped antiferromagnet with sublattice magnetization strongly reduced by zero-point fluctuations. At a critical value of magnetic field \(H_x=1.6 J/g_x\mu _B\), the ordered state disappears with restoration of a 1D spin-liquid state due to the non-commuting action of magnetic field and anisotropy, which causes the entanglement of states [11]. In this field, the magnetic moment should be of about of 90 percent of saturation. The saturation is expected only asymptotically in higher fields. Naturally, a 3D long-range order should occur at a low-temperature \(T_{N}<<J/k_{B}\) in a real quasi-1D antiferromagnet with the inevitable interchain coupling. Nevertheless, in a temperature range \(T_N<T<<J\), the spin configuration within chains should be close to that of a single XXZ chain at T=0. The adjacent chains should be not correlated because of the temperature exceeding weak interchain exchange. Note that the Nèel temperature of the quasi-1D antiferromagnet with the intrachain exchange \(J_\parallel\) and interchain exchange \(J_\perp\) may be approximately estimated from the expression [15]

$$\begin{aligned} k_B T_N \simeq J_\perp \sqrt{\ln \frac{J_\parallel }{k_B T_N}.} \end{aligned}$$
(2)

In case of a quasi-1D antiferromagnet, i. e. at \(J_\perp \ll J_\parallel\), this expression implies that \(k_B T_N \ll J_\parallel\) and the above temperature interval should be really wide enough.

The remarkable fact is that XXZ 1D system may be in a good approximation realized in crystals of Cs\(_2\)CoCl\(_4\) [9,10,11, 13, 14]. In this system, magnetic ions Co\(^{2+}\) (S=3/2) are placed in bc planes of the orthorhombic lattice within the layers stacked along a-axis. Within each layer, magnetic ions form a sublattice of isosceles triangles. The bonds with exchange integral \(J_{\frac{3}{2}}\)=0.74 K are placed on bases of triangles along the b-axis. The lateral exchange as well as the interplane exchange coupling is estimated to be at least an order of magnitude weaker, see, [9, 13]. Taking in account the frustration of the lateral exchange [16], we can view the exchange network as almost ideal chain structure. A further reduction of the S=3/2 problem to the problem of effective pseudospin s=1/2 is described in [9, 13, 14]. Because of the energy split in 14 K of the crystal field sublevels with \(S_z=\pm 3/2\) and \(S_z= \pm 1/2\), in the low temperature approximation, magnetic ions may be considered as pseudospins \(s=1/2\). The pseudospin representation of the initial \(S=3/2\) Hamiltonian with the exchange parameter \(J_{3/2}\)=0.74 K, single-ion anisotropy D = 7 K, and isotropic g-factor \(g_{3/2}=1.94\) results directly in the Hamiltonian (1), see [14] with parameters \(J=J_{1/2}= 4J_{3/2}\), \(\varDelta\) = 0.12, and anisotropic g-factor with \(g_{x}\) component \(g_{1/2}=3.26\). Naturally, this representation is valid only for \(k_BT\ll D\) and \(g_{1/2}\mu _B H_x \ll D\). Here \(\varDelta\) and \(g_{1/2}\) are calculated using the above values of of \(J_{3/2}\) and D, see [14]. Thus, Cs\(_2\)CoCl\(_4\) is a very promising model system for realization of XXZ chain states.

Fig. 1
figure 1

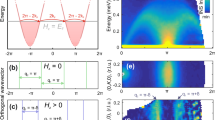
Temperature evolution of 40.99 GHz ESR line in the range 7\(-\)0.1 K. For clarity, the five upper curves are stretched vertically three times. Magnetic field 9.02 kOe, corresponding to g=3.25, is marked by a vertical dashed line. The magnetic fields corresponding to the resonance of \(H_1\)-mode are marked by triangles and corresponding to \(H_2\)-mode by circles and joined by a solid line

Full size image

The previous studies of inelastic neutron scattering [10, 11] explore spectra of excitations in the ordered state below 0.2 K where many features of XXZ chain spectra were detected in a high-energy part of the spectrum. In the present work, we target the crossover of the excitation spectrum from the pseudospin paramagnet to the spin liquid (intrachain correlated but interchain disordered state) and further to the spectrum of the ordered phase. As a result of the multifrequency electron spin resonance (ESR) study in a wide temperature range, we observe a regime of decoupled pseudospins, and then a crossover to spin liquid of the decoupled but intra-correlated chains and finally—a transition to spin-wave-like spectrum of the ordered state.

2 Experiments

In our experiment, the absorption of microwave energy is detected in the sample placed in cylindrical cavity at the maximum of the microwave magnetic field. The microwave power transmitted through the resonator at a fixed frequency vs magnetic field was recorded. A set of the fixed frequencies covers the range between 25 and 125 GHz. The ESR fields correspond to the minima of the transmitted signal. A small amount of DPPH (2,2-diphenyl-1-picrylhydrazyl was placed near the sample which provides g=2.00 marker. Having the records taken at different frequencies, we reconstruct the frequency vs field dependencies of the ESR. The low temperature down to 0.1 K was produced in the homemade microwave spectrometer combined with a portable dilution cryostat insert [17]. Magnetic fields up to 80 kOe were generated by a superconducting solenoid. The resonator of the diameter of 15.5 mm and height of 10 mm has the frequency of the TE\(_{011}\) mode at the frequency f= 27 GHz, TE\(_{012}\) mode at 35 GHz and higher modes in the range 25–125 GHz.

Fig. 2
figure 2

Temperature dependencies of resonance fields, integral intensities and linewidths of 40.99 GHz ESR modes observed in fields \(H_1\) and \(H_2\). \(T_{c1}\) and \(T_{c2}\) are the critical temperatures observed in [13]

Full size image
Fig. 3
figure 3

Frequency-field diagram of \(H_1\) and \(H_2\) ESR modes. Different symbols correspond to different temperatures. Solid lines present the upper and lower maxima of \(S(0,\omega )\) as calculated in [11], see text

Full size image

3 Experimental results

Several examples of the ESR records present the temperature evolution of the 40.99 GHz ESR line in Fig. 1. We see a single rather broad ESR line in the temperature range between 7 and 4 K with a weak temperature dependence of the resonance field \(H_1\) between 7.8 and 8.4 kOe. At the diminishing temperature between 3 and 0.9 K, the field \(H_1\) is stabilized at 8.9 \(\pm 0.1\) kOe. At the cooling in the interval from 2 to 0.4 K, the spectral density is partially transferred to a higher resonance field \(H_2\) which varies in a narrow interval between 12.6 and 12.2 kOe. We note further these modes as \(H_1\) and \(H_2\) modes. Below \(T=\)0.9 K, most spectral weights are already placed near the field \(H_2\) and continue to stay here till about 0.3 K where, at further cooling through the temperature 0.2 K, the resonance field of the main ESR line shifts slightly to lower field and several satellites appear both above and below \(H_2\). These last transformations are observed near the transition to an ordered phase. According to the thermodynamic measurements of [13], in a magnetic field of 12.5 kOe, there are two phase transitions, at a temperature \(T_{c1}\)=0.35 K to a phase with an unknown order parameter and at a temperature of \(T_{c2}=\)0.2 K to a spin-flopped antiferromagnetic phase. Near \(T_{c2}\), the change in the ESR absorption is well-pronounced by an abrupt narrowing of the resonance line and drop of the intensity, as well as by emerging satellites. Near \(T_{c1}\) =0.35 K, intensity starts to drop, but we do not see significant changes between 0.4 and 0.3 K to fix a critical behavior.

The temperature dependencies of resonance fields, integral intensities, and linewidths of modes \(H_1\) and \(H_2\) at the frequency 40.99 GHz are presented in Fig. 2. The values presented here are extracted by a Lorentzian fit of the ESR curves. This figure illustrates the process of diminishing the intensity of the \(H_1\) ESR and increasing of the \(H_2\) intensity upon cooling. Also the temperature range of existence of both kind of ESR signals may be distinctly determined: \(H_1\) ESR certainly exists at 2 K \(<T<\) 4 K, while the high-field mode occurs at 0.3 K \(<T<\) 2 K.

The transition of the resonance field from \(H_1\) to \(H_2\) occurs via a continuous spectral density flow to a new position, without the shift of the resonance field. Experiments on other frequencies of the range show that the fields \(H_1\) and \(H_2\) are frequency-dependent. We plot the values of \(H_1\) and \(H_2\) taken at different frequencies in the range 25–125 GHz in Fig. 3. The upper resonance frequency (observed at \(H_1\)) is linear in magnetic field and crosses the zero field at the linear extrapolation to zero. The g-factor value determined by the linear fit

$$\begin{aligned} f=g\mu _B H/ \hbar \end{aligned}$$
(3)

corresponds to g=3.3\(\pm 0.1\). The lower-frequency resonance, observed at fields \(H_2\) at lower temperatures \(0.35<T<1 K\) is shifted down in frequency approximately for 14 GHz with respect to \(H_1\)-resonance.

4 Discussion

The experimental value of g=3.3\(\pm 0.1\) corresponds well to the specific “pseudospin” value [14]

$$\begin{aligned} g_{1/2}=2 g_{3/2}\left( 1-\frac{3J_{3/2}}{2D}\right) =3.26. \end{aligned}$$
(4)

This g-factor points to the formation of the pseudospin s=1/2 state at the temperatures far below \(2D/k_B\) = 14 K. The crossover to the \(H_2\)-resonance corresponds to the exchange correlations emerging at the temperature of the order of about 1 K, which is below the value of of intrachain exchange \(J_{1/2}\)= 3.0 K. Here we expect the excitation spectra of the XXZ chain in a transverse (noncommuting) field. These excitations were theoretically studied by the DMRG method [10, 11]. It was found that the excitations are analogous to spinons in a Heisenberg S=1/2 antiferromagnetic chain, and the correlation function determining the susceptibility has the \(\omega ,k\)-dependence in a form of continuum, evolving with the magnetic field in a spin wave-like branch. One can compare the continuum of transferred energy for neutrons or photons (with \(\varDelta S\)=1) for Heisenberg chains and XXZ chains, looking at the intensity plots of [18] and [11]. The presentation of the corresponding dynamic structure factor \(S^{\alpha \alpha }(k,\omega )\) in a false color form may be found in the Supplement of [11]. We used the results obtained in [11] for the structure factor averaged on the polarization of the exciting field presented in Fig.S12 of this work. Analogous results of [10] demonstrate that the dynamic structure factor calculated for \(\varDelta\) = 0.25 and \(\varDelta\)= 0.12 practically coincides. Thus, we can use the more detailed \(\varDelta\) = 0.25 results of [11] for the interpretation. These results show that the continuum of \(S^{\alpha \alpha }(k,\omega )\) in a moderate field and in a long-wave limit has two maxima at the lower and the upper boundary energies. The lower maximum is more intense than the upper one. In Fig. 3, we plot the values of lower and upper limits of polarization-averaged structure factor \(S(0,\omega )\) taken from Fig.S12 of [11]. For adopting the theoretical value of magnetic field, given in units of \(J_{1/2}\), we use the value of g=3.3 derived in our experiments. One can see a good correspondence of the frequencies of the resonances observed at 0.4 K \(<T<\) 2 K in the field \(H_2\) to the frequency of the lower maximum at the boundary of the XXZ-S=1/2 chain continuum. From this correspondence, we conclude that at the temperature 0.4 K \(<T<\) 2 K, the spin system of Cs\(_2\)CoCl\(_4\) resembles the intra-correlated XXZ chains, which still do not have interchain correlation. Thus, the DMRG calculation of XXZ chain chain in a transverse field is satisfactory confirmed by ESR experiment in the long wave range, which is typically not tested by neutrons. We also observe the transformation of the ESR line at the phase transition \(T=\) 0.35 K and at the antiferromagnetic transition \(T=\) 0.2 K in accordance with the phase transitions reported in thermodynamic research [13]. This antiferromagnetic resonance will be reported elsewhere.

5 Conclusions

In a chain S=3/2 anisotropic antiferromagnet, we observe the low-temperature ESR response corresponding to uncorrelated pseudospins \(s=\)1/2 with a characteristic g-factor 3.3. At further cooling, we find a crossover from the ESR absorption of uncorrelated pseudospins \(s=\)1/2 to the absorption spectrum of the 1D S=1/2 XXZ-anisotropic antiferromagnet, and, finally at the temperature of the Nèel transition, we find a multimode antiferromagnetic resonance, which will be a subject of a future separate study.