1 Introduction

Quantum computers based on quantum phenomena such as superposition and entanglement [1] are expected to perform tasks which surpass the capabilities of modern classical digital computers [2]. First quantum computers arose quite recently and refer to noisy intermediate-scale quantum (NISQ) technology. Quantum calculations open new possibilities for solving problems in various fields of physics one of which is magnetic resonance including dynamics of many-body systems [3]. Although the accuracy of today’s calculations on quantum computers is insufficient owing to errors of quantum gates, it is still possible to perform quantum calculations for some relatively simple tasks [4,5,6,7,8,9,10]. Taking into account fantastic advantages of quantum computers over their classical counterparts which is expected to be released in future, development of quantum algorithms is a challenging and useful task.

The primary problem to be explored in this paper is simulating the simplest algorithms associated with multiple-quantum (MQ) NMR experiments on a quantum computer to compare the results obtained using contemporary tool with those obtained theoretically. This allows us to get start of implementing quantum computation in algorithms of MQ NMR. To proceed, we investigate the MQ NMR dynamics of a spin dimer [11] on a quantum computer. The chosen initial state of a spin dimer can be either the pure ground state or the thermodynamic equilibrium (mixed) one. We implement a method of generating a mixed quantum state (i.e., a state described by a density matrix rather then wave function) which serves as an input signal for a quantum computer. This step is essential for realization of different quantum protocols because a priori only a pure state can be generated as an input state of a quantum algorithm. To generate a mixed state, we use purification method which can be formulated as follows. For any mixed state \(\rho ^{(A)}\) of a quantum system A, there exists a system B and the pure state \(|\Psi \rangle _{AB}\) of the quantum system \(A\cup B\) such that

$$\begin{aligned} \rho ^{(A)}={\text{ Tr }}_B|\Psi \rangle _{AB} ~_{AB}\langle \Psi |. \end{aligned}$$
(1)

Thus, to generate a mixed state of a 2-qubit system (dimer) we use a 4-qubit system only at input of a protocol. After that, two extra qubits are not used in further calculations. Although the method requires extra quantum resources (2 extra qubits in our case), this seems to be the only way of initiating a mixed state from the pure one.

We demonstrate a profit from quantum computation for magnetic resonance which can be formulated as follows. If the dynamics of a quantum system in MQ NMR experiment is described by the Hamiltonian including only nearest neighbor interactions, then the intensity profile for such system includes only intensities of 0- and \(\pm 2\)-order coherences, \(I_0\), \(I_{\pm 2}\) [12]. Performing quantum computation we measure certain probabilities as outputs which allows us to find the intensity of 0-order coherence \(I_0\). Then, using the conservation law of the sum of intensities of MQ NMR coherences [13] in the evolution process (\(I_0+ I_2 + I_{-2} =const\), \(I_2=I_{-2}\)), we can find \(I_2\).

The article is organized as follows. In Sect.2, the principles of quantum algorithms and the main quantum gates are presented. The introduction to the theory of spin-dimer dynamics in the MQ NMR experiment is given in Sect.3 for different initial states of a dimer. In Sect.4, quantum calculation of the MQ NMR dynamics of a spin dimer with the pure ground and thermodynamic equilibrium initial states is given. We briefly discuss our results in the concluding section 5.

2 Main Quantum Gates and Quantum Algorithms

The states of a qubit can be written as \(|0\rangle\) or \(|1\rangle\) which correspond to spin (\(s=1/2\)), respectively, up and down. Consequently, a two-qubit system considered below has four computational basis states denoted as \(|00\rangle\), \(|01\rangle\), \(|10\rangle\) and \(|11\rangle\). A pair of qubits can also exist in superposition of these four states such that the state vector describing the two qubits is

$$\begin{aligned} |\psi \rangle =\alpha _{00} |00\rangle + \alpha _{01} |01\rangle + \alpha _{10}|10\rangle +\alpha _{11}|11\rangle ,\;\; {|\alpha _{00}|^2 +|\alpha _{01}|^2 +|\alpha _{10}|^2 +|\alpha _{11}|^2=1,} \end{aligned}$$
(2)

where the amplitudes \(\alpha _{00}\), \(\alpha _{01}\), \(\alpha _{10}\) and \(\alpha _{11}\) are the complex numbers.

Different single qubit gates are considered in [1]. We will use below one-qubit rotations and two-qubit controlled NOT (CNOT) operation [1]. For example, the matrix representation of the rotation operator \(R_x(\theta )\) by an angel \(\theta\) about the axis x can be written as

$$\begin{aligned} R_x(\theta ) = \exp \Big (- i\frac{\theta }{2} \sigma _x\Big ) =\left( \begin{array}{cc} \cos \frac{\theta }{2} &{} -i \sin \frac{\theta }{2}\\ {-}i \sin \frac{\theta }{2}&{}\cos \frac{\theta }{2} \end{array} \right) , \end{aligned}$$
(3)

where \(\sigma _x\) is the Pauli operator [1]. The rotation operators \(R_y\) and \(R_z\) are defined analogously:

$$\begin{aligned} R_y(\theta ) = \exp \Big (- i\frac{\theta }{2} \sigma _y\Big ) ,\;\; R_z(\theta ) = \exp \Big (- i\frac{\theta }{2} \sigma _z\Big ), \end{aligned}$$
(4)

where \(\sigma _y\), \(\sigma _z\) are the corresponding Pauli operators. The CNOT is very important in quantum computing. It can be used to entangle and disentangle different quantum states. Moreover, according to the Solovay–Kitaev theorem [1] any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and one-qubit rotations. Thus, one-qubit rotations and CNOT form the basis of an arbitrary quantum algorithm.

The CNOT gate operates on a quantum register consisting of two qubits. It flips the second qubit (the target qubit) if and only if the state of the first qubit (the control qubit) is \(|1\rangle\). The action of the CNOT gate can be represented in the computational basis by the matrix

$$\begin{aligned} CNOT=\left( \begin{array}{llll} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}1&{}0 \end{array} \right) . \end{aligned}$$
(5)

Below these gates are used for investigation of dynamics of spin dimer in the MQ NMR experiment.

3 MQ NMR Dynamics of Spin Dimers [14] with a Pure and Thermodynamic Equilibrium Initial States

MQ NMR dynamics of spin dimers in solids is described by either the Schrödinger equation

$$\begin{aligned} i\frac{d |\psi (t)\rangle }{dt}=H_{12} |\psi (t)\rangle \end{aligned}$$
(6)

in the case of a pure initial state, or the Liouville–von Neumann equation for the density matrix \(\rho (t)\)

$$\begin{aligned} i\frac{d \rho (t)}{dt}=[H_{12},\rho (t)] \end{aligned}$$
(7)

in the case of a mixed initial state. In MQ NMR experiment [11], a spin system (\(s=1/2\)) in a strong external magnetic field with the dipole–dipole interactions is irradiated by the special pulse sequence. As a result, the system is described by the averaged nonsecular two-spin/two-quantum Hamiltonian governing MQ dynamics. This Hamiltonian for the dimer can be written as [13]:

$$\begin{aligned} H_{12}=-\frac{1}{2} D( I_1^+I_2^+ + I_1^-I_2^-), \end{aligned}$$
(8)

where \(I_i^+\) and \(I_i^-\), \(i=1,2\), are raising and lowering angular momentum operators of dimer’s spins and D is the dipolar coupling constant. The Hamiltonian (8) allows us to describe MQ spin dynamics in MQ NMR experiments [11] only under stroboscopic observation.

3.1 Pure Ground State

Let the spin system be in the pure ground state at \(t=0\),

$$\begin{aligned} |\psi (0)\rangle = | 00\rangle . \end{aligned}$$
(9)

Then the solution of Eq. (6) can be written as

$$\begin{aligned} |\psi (t)\rangle = e^{-iH_{12} t} { |00\rangle .} \end{aligned}$$
(10)

Calculation with (8), (9), (10) leads to the simple result:

$$\begin{aligned} |\psi (\tau )\rangle = \cos \frac{\tau }{2} |00\rangle + i\sin \frac{\tau }{2} |11\rangle ,\;\;\tau =D t. \end{aligned}$$
(11)

Presentation (11) is very useful for performing quantum calculation.

Now we find the intensities of MQ NMR coherences associated with state (11). For this purpose, we write the appropriate density matrix

$$\begin{aligned} \rho (\tau )= & {} |\psi (\tau )\rangle \langle \psi (\tau )| \nonumber \\= & {} \cos ^2\frac{\tau }{2} |00\rangle \langle 00| + \sin ^2\frac{\tau }{2} |11\rangle \langle 11| {+}\frac{i}{2} \sin \, \tau |11\rangle \langle 00| {-} \frac{i}{2} \sin \, \tau |00\rangle \langle 11|. \end{aligned}$$
(12)

By virtue of Eq. (12) and taking into account that the signal of the longitudinal magnetization is observed in the MQ NMR experiment [11], we find the intensity \(J_0(\tau )\) of the 0-order MQ NMR coherence [14] using the definition of intensity of n-order coherence:

$$\begin{aligned} J_n={\text{ Tr }}\;\rho ^{(n)}(\tau ) \rho ^{(ht;-n)}(\tau ), \;\;{ n=0,\pm 2}, \end{aligned}$$
(13)

where superscript n means n-order coherence, \(\rho ^{(0)}\), \(\rho ^{(ht;0)}\) are the diagonal parts of the matrices \(\rho\) and \(\rho ^{ht}\), while \(\rho ^{(\pm 2 )}\), \(\rho ^{(ht;\pm 2)}\) are their non-diagonal parts and \(\rho ^{(ht)}\) is [15]

$$\begin{aligned} \rho ^{(ht)} = e^{-i H_{12} \frac{\tau }{D}} I_z e^{-i H_{12} \frac{\tau }{D}}= \left( \begin{array}{cccc} \cos \tau &{}0&{}0&{}-i \sin \tau \\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ i \sin \tau &{}0&{}0&{}-\cos \tau \end{array} \right), \end{aligned}$$
(14)

\(I_z\) is the operator of the projection of the total spin angular momentum on the direction of the external magnetic field (z-axis). The intensity \(J_0(\tau )\) is

$$\begin{aligned} J_0(\tau )={\cos ^2\frac{\tau }{2}} \cos \tau - {\sin ^2\frac{\tau }{2}} \cos \tau = \cos ^2\tau , \end{aligned}$$
(15)

and the intensities \(J_{\pm 2}(\tau )\) of the \(\pm 2\)-order MQ NMR coherences,

$$\begin{aligned} J_{\pm 2}= \frac{\sin ^2\tau }{2}. \end{aligned}$$
(16)

3.2 Thermodynamic Equilibrium Initial State

We consider now a spin dimer in a strong external magnetic field [15]. The thermodynamic equilibrium density matrix \(\rho (0)\) of the system is

$$\begin{aligned} \rho (0)=\frac{e^{\beta I_z}}{Z},\;\;Z={\text{ Tr }} e^{\beta I_z}, \;\beta = \frac{\hbar \omega _0}{kT}, \end{aligned}$$
(17)

where \(\omega _0\) is the Larmor frequency, T is the temperature, \(\hbar\) and k are, respectively, the Plank and Boltzmann constants, \(I_z= I_{1z } + I_{2z}\), \(I_{jz}\) (\(j=1,2\)) is the projection of the angular momentum operator of the spin j on the axis z, and Z is the partition function. Under condition of MQ NMR experiment, the dynamics is governed by Hamiltonian (8); therefore, the dimer density matrix \(\rho (t)\) can be written in the computational basis as follows:

$$\begin{aligned} \rho ({\tau })= \,& {} e^{-{\frac{i H_{12}}{D}\tau }} \rho (0) e^{{\frac{i H_{12}}{D}\tau }} \nonumber \\= & {} \frac{1}{2(1+\cosh \,\beta )} \left( \begin{array}{llll} \cosh \,\beta + \cos \,\tau \sinh \,\beta &{}0&{}0&{} {-} i\sin \,\tau \sinh \,\beta \\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ i\sin \,\tau \sinh \,\beta &{}0&{}0&{}\cosh \,\beta - \cos \,\tau \sinh \,\beta \end{array} \right) . \end{aligned}$$
(18)

The diagonal part of the density matrix (18) is responsible for the intensity \(J_0(\tau )\) of the 0-order coherence matrix, and the off-diagonal elements, \(\rho _{\pm 2}=\,\frac{{\mp } i\sin \,\tau \sinh \,\beta }{{2(1+\cosh \,\beta )}}\), are responsible for the intensities \(J_{\pm 2}(\tau )\) of the \(\pm 2\)-order coherence matrices. These intensities are following:

$$\begin{aligned} J_0= \,& {} \cos ^2 \tau \tan \frac{\beta }{2},\nonumber \\ J_{{\pm 2}}= \,& {} \frac{1}{2}\sin ^2 \tau \tan \frac{\beta }{2}. \end{aligned}$$
(19)

Notice that formulae (15) and (16) for the intensities \(J_0\) and \(J_2\) of the dimer with the pure ground initial state are the low-temperature limits \(\beta \rightarrow \infty\) of formulae (19).

4 Simulation of Spin-Dimer Dynamics on Quantum Computer

To simulate the evolution operators on a quantum processor, they must be represented in terms of one-qubit rotations and CNOTs. We perform this simulation for both initial states considered above. All calculations are performed on the 5-qubit quantum processor of IBM QE.

4.1 Pure Ground Initial State

To simulate the evolution (10) (or (11)) of a pure ground state on a quantum computer, we remark that the evolution operator in (10) can be written in terms of a rotation operator and CNOT as follows:

$$\begin{aligned} e^{-i H_{12} \frac{\tau }{D}} |00\rangle =C_{12} R_{x1}({-}\tau )|00\rangle. \end{aligned}$$
(20)

Therefore, the initial pure state \(|00\rangle\) of a spin dimer allows us to describe the quantum operations determined by Eqs. (10) and (11) in the following concentrated form :

$$\begin{aligned} |\psi (\tau )\rangle =C_{12} R_{x1}({-}\tau )|00\rangle . \end{aligned}$$
(21)

This operation can be simulated on a quantum processor according to the scheme in Fig.1.

Fig. 1
figure 1

The scheme for simulating the dynamics of the pure ground state of a spin-dimer on a quantum processor

Full size image

After the rotation of the first qubit by the angle \(\theta ={-\tau }\) about the axes x (see Eq.(3)) the initial state changes as follows:

$$\begin{aligned} |00\rangle \rightarrow \cos {\frac{\tau }{2}} |00\rangle {+} i \sin {\frac{\tau }{2}} |10\rangle . \end{aligned}$$
(22)

After applying CNOT (5) to state (22) using the first spin as a control qubit, we obtain the following state of the system:

$$\begin{aligned} \cos {\frac{\tau }{2}} |00\rangle {+} i \sin {\frac{\tau }{2}} |10\rangle \rightarrow \cos {\frac{\tau }{2}} |00\rangle {+} i \sin {\frac{\tau }{2}}|11\rangle \equiv |\psi (\tau )\rangle . \end{aligned}$$
(23)

We see from (23) that the probabilities of states \(|00\rangle\) and \(|11\rangle\) are

$$\begin{aligned} a_1(\tau ) =\cos ^2\frac{\tau }{2},\;\; a_2(\tau ) =\sin ^2\frac{\tau }{2}. \end{aligned}$$
(24)

Using Eqs.(15), (16) and (24), we obtain via formulae (13) and (14) the intensities of 0- and \({\pm 2}\)-order coherences in terms of the measured probabilities \(a_i\), \(i=1,2\):

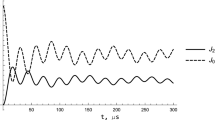
$$\begin{aligned} J_0(\tau ) =(2 a_1(\tau ) -1)^2,\;\;J_{{\pm 2}}(\tau ) = 2 a_1(\tau ) a_2(\tau ). \end{aligned}$$
(25)

In Fig.2, we compare the theoretical intensities of MQ NMR coherences of the 0- and 2-order (see Eqs.(15) and (16)) with the intensities (25) found using results of calculation on the quantum processor. One can see a good agreement between both results.

Fig. 2
figure 2

Pure ground initial state. The evolution of the intensities of the MQ NMR coherences of the 0- and 2-order (\(J_0\) and \(J_2\)). Intensities obtained theoretically using Eqs.(15) and (16) (solid line) slightly differ from the intensities found using results of calculation on the quantum processor (circles), see Eqs.(25)

Full size image

4.2 Thermodynamic Equilibrium Initial State

The dimer’s thermodynamic equilibrium initial state (17) can be considered as a tensor product of 1-qubit states:

$$\begin{aligned} \rho (0)= \,& {} \rho _1(0) \otimes \rho _{2}(0) , \;\; \end{aligned}$$
(26)
$$\begin{aligned} \rho _k(0)=\, & {} \frac{e^{\beta I_{k z}}}{Z_k},\;\;Z_k={\text{ Tr }} e^{\beta I_{kz}},\;\;{k=1,2}. \end{aligned}$$
(27)

We shall emphasize that the state (27) is a mixed state, but we can simulate the evolution only of a pure state on a quantum processor. Therefore, we have to purify the initial state (26) [1] in a way mentioned in the Introduction. It is simple to show that one additional spin is enough to purify the thermodynamic equilibrium state of a single spin. In fact, let \(|\psi _{12}\rangle\) be the 2-qubit state of the form

$$\begin{aligned} |\psi _{12}\rangle =\cos \frac{\theta }{2} |00\rangle + \sin \frac{\theta }{2} |11\rangle . \end{aligned}$$
(28)

Tracing the density matrix \(|\psi _{12}\rangle \langle \psi _{12}|\) over one of qubits yields the following 1-qubit state:

$$\begin{aligned} {\text{ diag }}(\cos ^2\frac{\theta }{2}, \sin ^2\frac{\theta }{2}) \end{aligned}$$
(29)

which coincides with \(\rho _k(0)\) (27), \(k=1,2\), if

$$\begin{aligned} \cos ^2\frac{\theta }{2} = \frac{e^{{\beta /2}}}{2\cosh \,\beta /2}\;\;\Leftrightarrow \;\; \cos \,\theta = \tanh \frac{\beta }{2}. \end{aligned}$$
(30)

Therefore, the purification of 2-qubit state (26) yields the following pure state of the 4-qubit system:

$$\begin{aligned} |\psi (0)\rangle = (\cos \frac{\theta }{2} |00\rangle + \sin \frac{\theta }{2} |11\rangle )\otimes (\cos \frac{\theta }{2} |00\rangle + \sin \frac{\theta }{2} |11\rangle ), \end{aligned}$$
(31)

which can be prepared on a quantum processor as follows:

$$\begin{aligned} |\psi (0)\rangle = C_{12} R_{y1}(\theta ) C_{34} R_{y3}(\theta ) |0000\rangle , \end{aligned}$$
(32)

where \(C_{ij}\), \(j>i\), is the CNOT (5) and \(R_{ky}(\theta )\) (\(k=1,3\)) is the rotation operator by an angle \(\theta\) about the axis y. We consider the thermodynamic equilibrium state of the dimer consisting of the 2nd and 3rd qubits of the 5-qubit register assuming tracing over the 1st and 4th spins (the 5th qubit is not included into the scheme). Therefore, we apply the evolution operator to the 2nd and 3rd spins only:

$$\begin{aligned} |\psi (t)\rangle = e^{-iH_{23} t} |\psi (0)\rangle . \end{aligned}$$
(33)

By virtue of the result of Ref. [16], we can write

$$\begin{aligned} e^{-iH_{23} t} = R_{x2}(\frac{\pi }{2}) R_{x3}(-\frac{\pi }{2}) C_{23} R_{x2}(-\tau /2) R_{z3}(-\tau /2) C_{23} R_{x2}(-\frac{\pi }{2}) R_{x3}(\frac{\pi }{2}). \end{aligned}$$
(34)

Using the scheme in Fig.3, we simulate the initial state (32) and evolution (34) on a quantum computer. As a result, we obtain the following pure state of four qubits

Fig. 3
figure 3

The scheme for simulating the dynamics of the dimer’s thermodynamic equilibrium initial state on a quantum processor

Full size image
$$\begin{aligned} |\psi (\tau )\rangle= & {} \cos \frac{\tau }{2} \cos ^2 \frac{\theta }{2} |0000\rangle + \frac{1}{2} \sin \theta |0011\rangle + i \sin \frac{\tau }{2} \cos ^2 \frac{\theta }{2} |0110\rangle \nonumber \\&+ i \sin \frac{\tau }{2} \sin ^2 \frac{\theta }{2} |1001\rangle + \frac{1}{2} \sin \theta |1100\rangle +\cos \frac{\tau }{2} \sin ^2 \frac{\theta }{2} |1111\rangle . \end{aligned}$$
(35)

Measurements over the 2nd and 3rd spins yield the probabilities \(p_{nm}\) of their states:

$$\begin{aligned} p_{nm}=\sum _{k,l=0,1}|\langle k nm l|\psi (\tau )\rangle |^2,\;\;n,m=0,1, \end{aligned}$$
(36)

where the sum is over the states of the first and fourth spins. By virtue of Eq.(35), Eq.(36) yields:

$$\begin{aligned} p_{00}=\, & {} \frac{1}{8}(3+4\cos \,\tau \cos \,\theta + \cos (2\theta )),\nonumber \\ p_{11}=\, & {} \frac{1}{8}(3-4\cos \,\tau \cos \,\theta + \cos (2\theta )),\nonumber \\ p_{01}=\, & {} p_{10}=\,\frac{\sin ^2\theta }{4}, \end{aligned}$$
(37)

which are the diagonal elements of the 2-qubit reduced density matrix of the 2nd and 3rd spins:

$$\begin{aligned} \rho _{23}= \,& {} Tr_{1,4}|\psi (\tau )\rangle \langle \psi (\tau )|\nonumber \\= \,& {} \left( \begin{array}{llll} p_{00}&{}0&{}0&{}\rho _{14}\\ 0&{}p_{01}&{}0&{}0\\ 0&{}0&{}p_{10}&{}0\\ \rho _{14}^*&{}0&{}0&{}p_{11} \end{array} \right) ,\;\;\rho _{14}=\,-\frac{i}{2}\sin \tau \cos \theta . \end{aligned}$$
(38)

For the intensity \(J_0\) of the 0-order MQ NMR coherence, according to the standard rules [15] and taking into account (30), we obtain

$$\begin{aligned}&J_0(\tau )={ \cos \tau } (p_{00}-p_{11}). \end{aligned}$$
(39)

The conservation low of the sum of MQ NMR coherences [15] allows to calculate the intensities of the \({\pm }2\)-order MQ NMR coherence:

$$\begin{aligned}&J_{\pm 2}(\tau )= \frac{1}{2}\Big ( \tan \frac{\beta }{2}-J_0(\tau )\Big ). \end{aligned}$$
(40)

We compare the intensities (39) and (40) found using the results of calculation on the quantum computer with the theoretical results (19). One can see a good agreement between them in Fig.4.

Fig. 4
figure 4

Thermodynamic equilibrium initial state with \(\beta =2.12\). The evolution of the intensities of the MQ NMR coherences of the 0- and 2-order (\(J_0\) and \(J_2\)). Intensities obtained theoretically using Eqs.(19) (solid line) slightly differ from the intensities found using results of calculation on the quantum processor (circles), see Eqs.(39) and (40)

Full size image

5 Conclusion

According to the existing theory of MQ NMR [13], intensities of MQ NMR coherences of the zero and second orders for the spin dimer are determined by probabilities of states \(|00\rangle\) and \(|11\rangle\) in the course of the spin system evolution. In our paper, these probabilities are calculated on the quantum computer. We use the theoretical relationships connecting these probabilities and intensities of MQ NMR coherences.

The main goal of our articles is to demonstrate the possibilities of present-day quantum computers and to estimate an accuracy of the used quantum gates. For this end we investigate the spin-dimer dynamics on a 5-qubit platform of IBM superconducting quantum computer. Two initial states are considered: the pure ground state and the thermodynamic equilibrium one. Intensities of the 0- and 2-order MQ NMR coherences found on the basis of calculation on the quantum computer are compared with theoretically obtained intensities and a good agreement between them is demonstrated.

We emphasize that, up to our knowledge, we first implement the purification method for creating the mixed state on the quantum computer. In our case, the thermodynamic equilibrium mixed initial state (26,27) of a subsystem A (qubits 2 and 3 in Fig.3) is created using the additional subsystem B (qubits 1 and 4 in Fig.3) and the proper pure initial state (31) of the joined system \(A\cup B\) (qubits 1, 2, 3, 4) by tracing out the above pure state over the subsystem B, Eq.(1).

We believe that quantum computer calculations open large perspectives in solving problems of spin dynamics and magnetic resonance.