On plane wave scattering at the piezothermoelastic half-space with impedance boundary condition

Abstract

Piezothermoelasticity and wave interaction studies hold immense significance in designing functional devices ranging from transducers to sensors for a variety of purposes like energy harvesting and structural health monitoring. These applications catalyze interest in this article which addresses the problem of reflection of plane wave at the boundary of piezothermoelastic half-space. Through this study, the effect of impedance parameter on amplitude and energy ratios of the reflected waves is studied. Four wave modes are indicated upon reflection and a linear system of equations is formed to obtain a closed-form expression for amplitude and energy ratios. These equations are solved by suitable mathematical tools leading to expression for amplitude ratios as a function of incidence angle. For a suitable piezothermoelastic medium, the ratios are plotted against incidence angle and the findings are compared for two well-known theories of thermoelasticity, namely, Lord–Shulman (LS theory) and Green–Lindsay (GL theory). The analytical outcomes suggest approximate values of impedance and incidence angle for preferred energy division between reflected waves. It is recognized that adding impedance increases the amplitude of the quasi-longitudinal (qP) wave and decreases that of the quasi-transverse wave, making it suitable for devices that require a more robust qP wave signal detection.

1 Introduction

Understanding piezothermoelasticity helps in characterizing materials for various applications, such as sensors, actuators, energy harvestors and smart materials. It provides insights into how materials respond to mechanical, thermal, and electrical stimuli, which is crucial for enhancing their performance. Comprehension of piezothermoelastic behavior is essential for designing and optimizing the efficiency of the aforementioned devices. By studying the coupled effects of mechanical stress, temperature variations, and electric fields, it is possible to develop more efficient and reliable devices. The phenomenon of piezoelectricity was discovered by Curie and Curie [1] in 1880 while studying pyroelectricity. Some materials can convert mechanical energy into electrical energy and vice versa. This property is called piezoelectricity. This phenomenon has demonstrated its applicability across various sectors, including nanotechnology, healthcare, acoustics, seismology, and more. Insights on piezoelectricity combined with wave propagation allow us to dive even further into the realm of material sciences providing deeper insight into a solid surface without destroying it. Voltmer and White [2] were the first to relate the phenomenon of piezoelectricity with surface elastic waves. Following this, the propagation or reflection of surface and body waves in piezoelectric medium has been explored substantially. Among others, significant contributions to piezoelectric study with respect to wave propagation have been made by Sharma et al. [3], Chattopadhyay et al. [4], Chatterjee et al. [5], and Chaudhary et al. [6].

Existing literature reflects that variations in incidence angles and other input parameters exercise significant influence, capable of altering the mechanical characteristics of a piezothermoelastic device. Wave scattering is a common occurrence in these devices owing to a wave falling obliquely on a surface. The material properties also significantly impact the nature of the reflected waves. Knott [7] studied the problem of reflection and refraction with an emphasis on seismological applications. Pal and Chattopadhyay [8] studied the reflection of waves at free boundary of an elastic half-space. Singh [9], Pang et al. [10], Sahu et al. [11] further advanced research with their contribution using different material attributes and boundary conditions. Latest trends in this regard include studying the effects of functional grading, various kinds of boundary conditions, initial stress, and interaction of different smart materials with thermoelastic surfaces. Such works have been carried out by Guha et al. [12] and Karmakar and Sahu [13]. By including pre-stress, moving load and other micro-structure details, more realistic models were developed in later decades. Contributions in this regard have been made by Chaudhary et al. [14], Celebi et al. [15].

Thermoelasticity can be defined as the mechanical deformations shown by an elastic body resulting from thermal changes acting on the material. The classical theory of heat conduction was given by Biot [16], where parabolic equations were involved. This theory lacks physical plausibility as it does not consider any time delay in sensing the disruption across the length of a material. Lord and Shulman [17] presented a theory that includes one thermal relaxation parameter. This addition converts the equation to hyperbolic, removing the paradox of infinite speed of heat transfer. Green and Lindsay [18] further generalized the equations by adding one more relaxation coefficient. The equations align with the entropy equation given by Muller [19] and do not contradict Fourier’s law of heat conduction. Deresiewicz [20], Sinha and Sinha [21] investigated wave reflection in thermoelastic solids. Abd-Alla et al. [22] explored the phenomenon of SV wave reflection in a thermoelastic medium. Deschamps and Cheng [23], Vashishth and Sukhija [24] have provided significant results for thermoelastic medium incorporating voids and fluid. Studies using other approaches like numerical simulation, method of Eigen values have also been carried out concerning different theories of thermoelasticity [25].

While studying wave reflection, usually a traction-free boundary is assumed as it models a free surface which is encountered while studying waves traveling through the Earth’s crust also known as the Neumann boundary condition. On the other hand, in electromagnetism, acoustics, or device manufacturing, boundaries with impedance (Robin-type boundary condition) are also common. These replicate the impact of a thin layer of other material over the half-space and mathematically relate stress and displacement across an interface based on the differences in acoustic impedance. Impedance boundary conditions are used to model wave reflections at interfaces between different geological layers with contrasting physical properties, such as density and seismic wave velocity. These conditions relate the stresses and displacements across the interface based on the differences in acoustic impedance. This was first studied by Tiersten in his breakthrough paper [26] where approximate equations were used to study the effect of a thin plating on the surface of an elastic medium. These conditions were then studied by Malischewsky [27] and Bovik [28] and consequently derivative terms of traction were added to the boundary condition. Further research was carried out by Godoy, Durán, Nédélec [29] where an isotropic half-space with impedance was studied. Guha and Singh [30] analysed the effects of impedance boundary in piezomagnetic fiber-reinforced half-space. Biswas and Sahu [31] derived a secular equation of qP wave after reflection from a boundary infused with impedance. Structural Health monitoring is an important aspect of impedance boundary. State of the art reflects on the development of numerical methods to study damage identification in the last decade [32].

The present work aims to study the thermal effects on the scattering of quasi-plane (qP) wave from the surface of a piezothermoelastic medium. Driven by the design of devices such as ultrasonic transducers, the study conceptualizes the material as a piezothermoelastic half-space. The aim is to maximize efficiency and minimize power wastage. Keeping this in mind, the paper studies amplitude and energy flux ratios for different impedance parameter values. Analytical approach is adopted to derive expressions for amplitude ratios from the constitutive equations of the media and a numerical example is considered to closely study the ratio for different values of the impedance parameter, thus emphasizing upon the boundary. Furthermore, the results are compared for two well-known theories of thermoelasticity, namely, Lord-Shulman and Green-Lindsay. Energy conservation is demonstrated through figures for LS and GL theories and division of energy between different reflected waves is also discussed. The outcomes of the present study are applicable for enhancing the efficiency of ultrasonic transducers, essential components of ultrasonic flow meters.Validation of the work has been done by comparing stress-free cases in the existing literature, some of which are given in [33] and [34].

2 Formulation of problem

2.1 Basic constitutive equations of piezothermoelastic medium

The stress acting on a piezothermoelastic medium is related to the electric field and temperature in the following manner

$$\begin{aligned} \sigma _{ij} = c_{ijkl}e_{kl} - \beta _{ij} ( T + \tau _{1} \delta _{2\kappa } \dot{T} ) - \eta _{kij} E_{k} \quad \quad \text {for} \,\, i,j,k,l =1,2,3 \end{aligned}$$

(1)

Electric displacement is given by

$$\begin{aligned} D_i = \eta _{ijk}e_{jk} +\epsilon _{ij}E_{j} +p_{i} (T + \tau _{1} \delta _{2\kappa } \dot{T}) \end{aligned}$$

(2)

The fundamental equations of strain and electric potential are

$$\begin{aligned} e_{kl}= & \frac{1}{2} (u_{k,l} + u_{l,k}) \end{aligned}$$

(3a)

$$\begin{aligned} E_{i}= & -\phi _{,i} \end{aligned}$$

(3b)

and the equations of motion are

• 1. Gauss’ Quasi-static law

  $$\begin{aligned} D_{i,i} = 0 \hspace{0.5cm} \end{aligned}$$

  (4a)

• 2. Conservation of linear momentum

  $$\begin{aligned} \sigma _{ij,j} = \rho \ddot{u_i} \hspace{0.5cm} \end{aligned}$$

  (4b)

• 3. Heat conduction equation

  $$\begin{aligned} K_{ij}T_{,ij} - \rho C_e ( \dot{T} +\tau _0 \ddot{T}) = T_0 \beta _{ij} ( \dot{u}_{i,j} +\tau _0 \delta _{1\kappa } \ddot{u}_i )- T_0 p_k ( \dot{\phi }_ {,k} + \tau \delta _{1 \kappa } \ddot{\phi }_{,k} ) \end{aligned}$$

  (4c)

where $\sigma _{ij}, e_{kl}, T, D_{i}, E_{k}$ and $\phi$ are stress tensor, strain tensor, temperature, electric displacement component, electric field vector, and electric potential function respectively. $K_{11}$ and $K_{33}$ are coefficients of thermal conductivity in a direction normal to the axis of symmetry and along the axis of symmetry respectively. $c_{ij}= c_{ji}$ are elasticity constants. $\eta _{ijk}$ are piezoelectricity constants and $\beta _{11}$ and $\beta _{33}$ are thermal stress moduli. $t_0$ and $t_1$ are thermal relaxation times. $\rho$ is the density and $p_3$ is the pyroelectricity constant and $C_e$ is the specific heat at constant rate.

For a transversely isotropic, thermally conducting piezoelectric material [35], the constitutive equations are given by

$$\begin{aligned} \begin{pmatrix} \sigma _{11} \\ \sigma _{22}\\ \sigma _{33}\\ \sigma _{23}\\ \sigma _{13}\\ \sigma _{12} \end{pmatrix} = \begin{pmatrix} c_{11} & \quad c_{12} & \quad c_{13} & \quad 0 & \quad 0 & \quad 0\\ c_{12} & \quad c_{22} & \quad c_{23} & \quad 0 & \quad 0 & \quad 0\\ c_{13} & \quad c_{23} & \quad c_{33} & \quad 0 & \quad 0 & \quad 0\\ 0 & \quad 0& \quad 0& \quad c_{44} & \quad 0 & \quad 0\\ 0 & \quad 0& \quad 0& \quad 0 & \quad c_{44} & \quad 0\\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad c_{66} \end{pmatrix} \begin{pmatrix} e_{11}\\ e_{22}\\ e_{33}\\ e_{23}\\ e_{13}\\ e_{12} \end{pmatrix} - \begin{pmatrix} 0 & \quad 0& \quad \eta _{31}\\ 0 & \quad 0& \quad \eta _{31}\\ 0 & \quad 0& \quad \eta _{33}\\ 0 & \quad \eta _{15} & \quad 0\\ \eta _{15} & \quad 0 & \quad 0 \\ 0 & \quad 0& \quad 0 \end{pmatrix} \begin{pmatrix} E_1\\ E_2\\ E_3 \end{pmatrix} - \begin{pmatrix} \beta _{11}\\ \beta _{11}\\ \beta _{33}\\ 0\\ 0\\ 0 \end{pmatrix} \begin{pmatrix} T + t_1 \dot{T} \end{pmatrix}\nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned} \begin{pmatrix} D_1\\ D_2\\ D_3 \end{pmatrix} = \begin{pmatrix} 0 & \quad 0& \quad 0& \quad 0 & \quad \eta _{15} & \quad 0 \\ 0 & \quad 0& \quad 0& \quad \eta _{15} & \quad 0 & \quad 0 \\ \eta _{31} & \quad \eta _{31} & \quad \eta _{33} & \quad 0 & \quad 0 & \quad 0 \end{pmatrix} \begin{pmatrix} e_{11}\\ e_{22}\\ e_{33}\\ e_{23}\\ e_{13}\\ e_{12}\\ \end{pmatrix} + \begin{pmatrix} \epsilon _{11} & \quad 0 & \quad 0\\ 0 & \quad \epsilon _{11} & \quad 0\\ 0 & \quad 0 & \quad \epsilon _{33} \end{pmatrix} \begin{pmatrix} E_1\\ E_2\\ E_3 \end{pmatrix} + \begin{pmatrix} p_1\\ p_2\\ p_3 \end{pmatrix} \begin{pmatrix} T+t_1 \dot{T} \end{pmatrix}\nonumber \\ \end{aligned}$$

(6)

where $c_{66} = \frac{c_{11}-c_{12}}{2}$

2.2 Dynamics of the qP wave in piezothermoelastic half-space

Fig. 1

Geometry of the problem

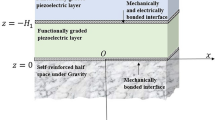
This problem investigates the scattering of an incident qP wave at the boundary of a piezothermoelastic half-space. The boundary condition is embedded with impedance, the significance of which shall be analyzed through the study. QP, qSV, EA and T waves originate as a result of reflection from the surface. Let $x_1$ axis of the Cartesian coordinate system be parallel to the free surface and let $x_3$ axis point vertically downwards. Origin ’O’ is situated at the point of wave interaction with the surface, see Fig. 1. The medium is assumed to be transversely isotropic and symmetric about $x_3$ axis. The displacement components $(u_1, u_2, u_3)$, electric potential $\phi$ and temperature T are functions of $x_1, x_3$ and time t only.

Thus the components of waves are

$$\begin{aligned} u_1 = u_1 (x_1, x_3,t),\hspace{0.1in} u_2 =0,\hspace{0.1in} u_3 =u_3(x_1,x_3,t) \end{aligned}$$

$$\begin{aligned} \phi = \phi (x_1, x_3,t),\hspace{0.1in} T =T(x_1, x_3,t) \end{aligned}$$

Substitution of (1), (3b), (4a), and (4b) in Constitutive Eqs. (5) and (6) yields the following four equations

$$\begin{aligned} & c_{11} u_{1,11} + c_{44}u_{1,33} + ( c_{13}+c_{44} ) u_{3,13} +( \eta _{31}+ \eta _{15} ) \phi _{,13} -\beta _{11} ( T_{,1} + \tau _1 \delta _{2 \kappa } \dot{T}_{,1} ) = \rho \ddot{u}_1, \end{aligned}$$

(7)

$$\begin{aligned} & (c_{44}+c_{13})u_{1,13} +c_{44}u_{3,11}+c_{33}u_{3,33} +\eta _{15} \phi _{,11} +\eta _{33} \phi _{,33} - \beta _{33} (T_{,3} + \tau _1 \delta _{2 \kappa } \dot{T}_{,3}) = \rho \ddot{u}_3, \end{aligned}$$

(8)

$$\begin{aligned} & K_{11}T_{,11}+ K_{33} T_{,33}- \rho C_e (\dot{T} + \tau _0 \ddot{T}) - T_0 (\beta _{11} ( \dot{u}_{1,1} + \tau _0 \delta _{1 \kappa } \ddot{u}_{1,1})\nonumber \\ & \quad + \beta _{33} (\dot{u}_{3,3} + \tau _{0} \delta _{1 \kappa } \ddot{u}_{3,3}))+T_0 p_3 ( \dot{\phi }_{,3}+ \tau _0 \delta _{1\kappa } \ddot{\phi }_{,3})= 0 \end{aligned}$$

(9)

$$\begin{aligned} & \eta _{15}u_{3,11} +( \eta _{15} +\eta _{31}) u_{1,13} + \eta _{33} u_{3,33} - \epsilon _{11} \phi _{,11} -\epsilon _{33} \phi _{,33} + p_3 (T_{,3} + \tau _1 \delta _{2\kappa } \dot{T}_{,3})=0 \end{aligned}$$

(10)

The above equations represent a harmonic wave in terms of u traveling in the $x_1-x_3$ plane, the solution of which can be expressed as

$$\begin{aligned} \{u_1 , u_3, T , \phi \} = \{U, W, V, \Phi \} exp[ ik (x_1 + r x_3 - ct)] \end{aligned}$$

(11)

where c and k are phase velocity and wave numbers of the wave respectively, r is the projection ratio of wave number of $x_3$ on the $x_1$ axis. $U, W, V, \phi$ are the amplitudes of $u_1, u_3, T$ and $\phi$ respectively. To obtain the expressions in r, substitute the form of $u_1, u_3, T, \phi$ from Eq. (11) in (7), (8), (9), and (10). Further simplification yields a system of linear equations in r which is best represented as

$$\begin{aligned} & \begin{pmatrix} Y_{11}& \quad Y_{12} & \quad Y_{13}& \quad Y_{14}\\ Y_{21}& \quad Y_{22} & \quad Y_{23}& \quad Y_{24}\\ Y_{31}& \quad Y_{32} & \quad Y_{33}& \quad Y_{34}\\ Y_{41}& \quad Y_{42} & \quad Y_{43}& \quad Y_{44}\\ \end{pmatrix} \begin{pmatrix} 1\\ A\\ B\\ C \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0\\ 0 \end{pmatrix} \end{aligned}$$

(12)

$$\begin{aligned} & \text {Or, } \textbf{Y} \textbf{P}=0 \end{aligned}$$

(13)

where entries of $P= [ 1, A, B, C]^T$ give amplitude ratios corresponding to reflected waves and elements of $\textbf{Y}$ are mentioned in “Appendix 1”.

For simplicity, $\{ u_1, u_3, T, \phi \}= \{U, W, V, \Phi \} exp[ ik (x_1 + r x_3 - ct)]= \{ 1, A, B, C\} U exp[ik (x_1 + r x_3 - ct)]$ where A, B, C are the amplitude ratios $A= \frac{W}{U}$, $B = \frac{V}{U}$ and $C = \frac{\Phi }{U}$. The above system has a non-zero solution if and only if the determinant of the coefficient matrix vanishes, which is a secular equation in r. For each fixed value of c, an 8th degree equation is obtained in r. The roots in r can be obtained using MATHEMATICA software. These roots, i.e., 4 roots and their conjugates correspond to 4 wave modes. These waves are: qP wave, qSV wave, EA wave and T wave.

Let $r_1$, $r_3$, $r_5$, $r_7$ be the roots corresponding to each of the reflected qP, qSV, EA and T waves. Since most energy is dissipated in the form of qP and qSV waves, the roots that have greater absolute values correspond to bulk waves and roots with smaller absolute values stand for thermal (T) and electroacoustic (EA) waves. Let $r_2$ be the root that corresponds to the incident qP wave.

For each value of $r_n$, $n= 1,2,\ldots ,8$, the amplitude ratios can be calculated using Cramer’s rule.

$$\begin{aligned} A = \frac{\begin{vmatrix} -Y_{11}&\quad Y_{13}&\quad Y_{14}\\ -Y_{21}&\quad Y_{23}&\quad Y_{24}\\ -Y_{31}&\quad Y_{33}&\quad Y_{34} \end{vmatrix}}{\begin{vmatrix} Y_{12}&\quad Y_{13}&\quad Y_{14}\\ Y_{22}&\quad Y_{23}&\quad Y_{24}\\ Y_{32}&\quad Y_{33}&\quad Y_{34} \end{vmatrix} } \end{aligned}$$

(14)

Similarly,

$$\begin{aligned} & B = \frac{\begin{vmatrix} Y_{12}&\quad -Y_{11}&\quad Y_{14}\\ Y_{22}&\quad -Y_{21}&\quad Y_{24}\\ Y_{32}&\quad -Y_{31}&\quad Y_{34} \end{vmatrix}}{\begin{vmatrix} Y_{12}&\quad Y_{13}&\quad Y_{14}\\ Y_{22}&\quad Y_{23}&\quad Y_{24}\\ Y_{32}&\quad Y_{33}&\quad Y_{34} \end{vmatrix} } \end{aligned}$$

(15)

$$\begin{aligned} & C = \frac{\begin{vmatrix} Y_{12}&\quad Y_{13}&\quad -Y_{11}\\ Y_{22}&\quad Y_{23}&\quad -Y_{21}\\ Y_{32}&\quad Y_{33}&\quad -Y_{31} \end{vmatrix}}{\begin{vmatrix} Y_{12}&\quad Y_{13}&\quad Y_{14}\\ Y_{22}&\quad Y_{23}&\quad Y_{24}\\ Y_{32}&\quad Y_{33}&\quad Y_{34} \end{vmatrix} } \end{aligned}$$

(16)

Using above amplitude ratios, the expression for displacement, temperature and electric potential can be written as follows

$$\begin{aligned} \{ u_1, u_3, T, \phi \}= \{1, A_s, B_s, C_s\} U_s exp[ik(x_1 +r_s x_3 -ct] + \sum _{n =1,3,5,7} \{1, A_n, B_n, C_n \} U_n exp[ik(x_1 + r_n x_3 -ct)] \end{aligned}$$

(17)

where s corresponds to the index of incident waves (qP, qSV, EA or T) waves and n corresponds to that of reflected waves. Similarly, the equation of stress tensor, electric displacement, and temperature change can be derived as

$$\begin{aligned} \{ \sigma _{33}, \sigma _{13}, D_3, T_{,3} \} & = ik \{ M_{1s}, M_{2s}, M_{3s}, B_s \} U_{s} exp[ik(x_1 +r_s x_3 -ct)] \nonumber \\ & \quad + \sum _{n= 1,3,5,7} ik \{ M_{1n}, M_{2n}, M_{3n}, B_n\} U_{n} exp[ik (x_1 + r_n x_3 - ct)] \end{aligned}$$

(18)

where values of $M_{1n}, M_{2n}, M_{3n}$ are mentioned in the “Appendix 2”.

2.3 Boundary conditions

• 1. Impedance boundary condition In the study of Seismic waves, surfaces encountered are mostly free of mechanical stress, also known as the Neumann boundary condition. However, in smart devices like piezoelectric sensors, SAW devices and MEMs, boundary conditions are usually a linear combination of functions and their derivatives, also known as Robin’s boundary conditions or Impedance boundary condition. Tiersten [26] was the first to introduce the concept of the impedance boundary condition. It was reinstated by Malischewsky and Bovik [27] in terms of stress and displacement. The impedance boundary condition following Tiersten [26] for two dimensions can be written as

  $$\begin{aligned} \sigma _{i3} +\epsilon _{i}u_{i} \text { for } x_3 =0 \end{aligned}$$

  (19)

  where $\sigma$ has the dimensions of stress, $u_i$ is the displacement and $\epsilon$ has the dimensions of stress per unit length. $\epsilon _i$ depends upon frequency and elastic parameters. In the current discussion, it is assumed that the normal and tangential reactions are proportional to frequency and displacement. Mathematically, it can be written as

  $$\begin{aligned} & \sigma _{13} + \omega Z_{1} u_1 = 0 \end{aligned}$$

  (20)
  $$\begin{aligned} & \sigma _{33} + \omega Z_{3} u_3 = 0 \end{aligned}$$

  (21)

  where $Z_1, Z_3$ are the impedance parameters. For simplicity, we assume $Z_1 = Z_3 = Z$. If Z = 0,

  $$\begin{aligned} \sigma _{13} = \sigma _{33}=0 \end{aligned}$$

  (22)

  which is the traction-free boundary conditions. Similarly, as $Z \rightarrow \infty$, this implies that the displacement component in the direction parallel to the axis vanishes.

• 2. Electric displacement An electrically open boundary at $x_3 =0$ i.e., stationary charge gets accumulated but the resultant electric displacement is null, is considered at the said boundary of the thermally conducting, piezoelectric half-space. Mathematically,

  $$\begin{aligned} D_3 = 0 \end{aligned}$$

  (23)

• 3. Adiabatic The boundary of the half-space is not in contact with a thermally conducting material, i.e., it is insulated and is expressed mathematically as

  $$\begin{aligned} T_{,3} =0 \end{aligned}$$

  (24)

Equations (20) to (24) give required boundary conditions for this problem. Substituting these in Eqs. (17) and (18),

$$\begin{aligned} & \sum _{n=1,2,3,5,7} { ik M_{3n} U_{n} exp[ ik ( x_1+ r_n x_3 -ct )] }= 0 \end{aligned}$$

(25)

$$\begin{aligned} & \sum _{n=1,2,3,5,7} { ikr_n B_n U_n exp[ik (x_1 +r_n x_3 -ct ]} = 0 \end{aligned}$$

(26)

$$\begin{aligned} & \sum _{n= 1,2,3,5,7 } (ik M_{2n} +\omega Z_1 )U_n exp[ik (x_1 +r_n x_3 -ct ] = 0 \end{aligned}$$

(27)

$$\begin{aligned} & \sum _{n= 1,2,3,5,7 } (ik M_{1n} +\omega Z_3 )U_n exp[ik (x_1 +r_n x_3 -ct ] = 0 \end{aligned}$$

(28)

The above four equations give a matrix of the form $G X = H$

$$\begin{aligned} \begin{pmatrix} G_{11} & \quad G_{12 } & \quad G_{13} & \quad G_{14}\\ G_{21} & \quad G_{22 } & \quad G_{23} & \quad G_{24}\\ G_{31} & \quad G_{32 } & \quad G_{33} & \quad G_{34}\\ G_{41} & \quad G_{42 } & \quad G_{43} & \quad G_{44} \end{pmatrix} \begin{pmatrix} U_1\\ U_3\\ U_5\\ U_7\\ \end{pmatrix} = \begin{pmatrix} H_1\\ H_3\\ H_5\\ H_7\\ \end{pmatrix} U_2 \end{aligned}$$

(29)

Dividing the above equation by $U_2$ (amplitude of the incident qP wave), gives amplitude ratios of reflected waves with incident wave. The matrix entries of G are mentioned in “Appendix 3”.

3 Numerical example and graphical representation

From the derived expressions, it is clear that the amplitude ratios of different waves and the energy they carry depend upon the thermal and elastic properties of the half-space as well as incidence angle and frequency of the wave. The objective is to understand the impact of the impedance parameter on the amplitude ratios of reflected waves. Equations of GL and LS theories are utilized to compare the amplitude ratios at different impedance parameters. However, the formulation above is general and an example would provide clarity and enhance our understanding. The composite material considered as half-space is Cadmium Selenide(CdSe). The material constants for CdSe are mentioned in Table 1 [24].

Table 1 Material Constants for Cadmium Selenide

3.1 Reflection angles

Fig. 2

Reflection angles

Figure 2a and b show the variation of angle of reflected waves i.e. qP, qSV, EA and T waves against the incidence angle. For LS theory, the reflection angle of qP wave is the same as incidence qP angle, as depicted by the yellow line, while reflection angle for qSV angle is always less than the incidence angle, reaching a maximum of $29^{\circ }$ at incidence angle $90^{\circ }$. Electroacoustic wave is parallel to the surface, therefore makes $90^{\circ }$ with the normal throughout the range of incidence angle from $0^{\circ }$ to $90^{\circ }$. T wave gets reflected making negligible angle with the normal. Figure 2b shows the reflection angles for GL theory. Here, qP wave gets reflected with the same angle as that of the incidence angle whereas, qSV wave makes a smaller angle compared to the incident wave, reaching a maximum of around $30^{\circ }$. The reflection angles show a monotonic behaviour with respect to the incidence angle. T-wave makes $0^{\circ }$ with the normal. EA wave shows variation for the GL theory (Fig. 2b). The reflection angle begins around $85^{\circ }$ then the curve falls sharply and makes an angle as low as $50^{\circ }$ for incidence angle $10^{\circ }$ then suddenly increases to $90^{\circ }$ around the incidence angle $25^{\circ }$. Till $25^{\circ }$, the curve experiences deflection from its usual behavior, it then keeps steady at $90^{\circ }$ till the end.

3.2 Amplitude ratios (LS theory)

Fig. 3

Variation of amplitude ratios for different values of impedance Parameter Z under LS theory

Figure 3a illustrates the fluctuation in amplitude ratio of reflected qP wave plotted against that of the incident wave. As observed, the impedance parameter has a prominent effect on the same. The ratios corresponding to different values of impedance appear to coincide for an incidence angle less than $20^{\circ }$. They are also, close to 1 and monotonically decreasing. However, for slightly greater angles, i.e. between $20^{\circ }$ to $38^{\circ }$, the amplitude ratio is highest for ${\textrm{Z}} = 0.8$, followed by ${\textrm{Z}} = 0.4$ and then ${\textrm{Z}} = -0.2$ or ${\textrm{Z}} = 0.2$. The lowest ratio is reported for the stress-free boundary condition (${\textrm{Z}} = 0.0$). Furthermore, for the range $40^{\circ }$ to $70^{\circ }$, the highest ratio is observed for the impedance value 0.4, followed by ${\textrm{Z}} = 0.2$ and ${\textrm{Z}} = - 0.2$ and then ${\textrm{Z}} = 0.8$ while the lowest still goes for ${\textrm{Z}} = 0.0$. For angles greater than $70^{\circ }$, the ratios for impedance values ${\textrm{Z}} = 0.2$, − 0.2, and ${\textrm{Z}} = 0.4$ seem to coincide. As the angles come closer to $90^{\circ }$, the ratio approaches 1 irrespective of the impedance value. The minimum ratio attained by the stress-free case is 0.55, by ${\textrm{Z}} = 0.8$ case is 0.78, and even higher for other impedance values. Figure 3b portrays the amplitude ratio of the reflected qSV wave, contrary to that of qP wave, the amplitude ratio for the stress-free boundary condition is the highest. ${\textrm{Z}} = 0.2$ and ${\textrm{Z}} = - 0.2$ do not show a visible difference in the ratios and are greater than that for ${\textrm{Z}} = 0.4$. The qSV ratio for ${\textrm{Z}} = 0.8$ is low around angles $10^{\circ }$ and increases after $10^{\circ }$ while always staying less than that for ${\textrm{Z}} = 0.0$.

As for the EA wave, the amplitude is highest for the stress-free case and lowest for Z = 0.4 for the range of input angle $0^{\circ }$ to $60^{\circ }$ (Fig. 3c). ${\textrm{Z}} = 0.8$ results in a slightly lower amplitude followed by ${\textrm{Z}} = 0.2$. For angles greater than $70^{\circ }$, a similar trend is reported for ${\textrm{Z}} = 0.0$ and ${\textrm{Z}} = 0.8$ and then the ratio is followed by the other impedance values. For this wave as well, curves for impedance values ${\textrm{Z}} = 0.2$ and ${\textrm{Z}} = - 0.2$ seem to coincide. For the range $60^{\circ }$ to $70^{\circ }$, the ratios get closer to 0, the closest being for Z = 0.0. For the T wave, the amplitude ratio is around $10^{-20}$ compared with the incident wave amplitude. For an incidence angle of $0^{\circ }$, The amplitude ratio for T wave is $2 \times 10^{-20}$ and it decreases monotonically till it reaches 0 for $90^{\circ }$. On comparing different impedance values, it is evident that the ratio is lowest for ${\textrm{Z}} = 0.0$, followed by ${\textrm{Z}} = 0.2$ (which coincides with ${\textrm{Z}} = - 0.2$), and then for other considered values. Upon careful observation, we see that the ratio is greatest for Z = 0.8 for the regime $\theta < 55^{\circ }$, after which there is a slight change, and that for ${\textrm{Z}} = 0.4$ reaches a higher value. Around $90^{\circ }$, amplitude ratio for the T wave reaches 0 for any impedance value.

3.3 Amplitude ratios (GL theory)

Fig. 4

Variation of amplitude ratios for different values of impedance parameter Z (GL theory)

Under GL theory of thermoelasticity, there is no visible difference in the amplitudes of the qP wave based on impedance for the region $\theta < 30^{\circ }$ following which the curve sees the greatest dip for the stress-free case. The lowest amplitude ratio is achieved around $65^{\circ }$ irrespective of impedance value. The ratio attains its minimum of 0.65 for ${\textrm{Z}} = 0.0$, followed by ${\textrm{Z}} = 0.8$ case which attains a minimum of around 0.8. For ${\textrm{Z}} = 0.4$, 0.2, and − 0.2, the minimum value stays around 0.9 around $\theta = 50^{\circ }$ which then increases to reach its peak value i.e. 1 near $\theta = 90^{\circ }$. The amplitude ratio for reflected qSV wave is high for small incidence angles, the highest being for impedance $=$ − 0.2 and lowest for ${\textrm{Z}} = 0.8$ (Fig. 4b). Figure is plotted for the range $10 ^{\circ }$ to $90 ^{\circ }$. Initially, the ratio goes very high(6) for impedance ${\textrm{Z}} = - 0.2$ and is at 2.5 for ${\textrm{Z}} = 0.8$, and then decreases to 0. From angles $15^{\circ }$ the ratio witnesses a sharp dip from a high value to almost 0.01 for all impedance values around $20^{\circ }$ and then begins to increase swiftly to reach a maximum of around 1.8, and then decreases monotonically. Thereafter, the highest amplitude ratio is observed for the stress-free boundary condition whereas no significant change in the ratios is seen after reaching $40 ^{\circ }$ and the ratios converge to 0 at $90^{\circ }$.

In case of EA waves, the ratios begin with 0 for all impedance values and rapidly increase to their peak around $\theta = 20^{\circ }$. The peak values attained are 0.7 and 0.36 for Z = 0.8 and Z = 0.4 respectively. From then on, the ratios witness a sharp decrease as they fall to a value around 0.05 near $50 ^{\circ }$ and then steadily decrease to 0 at $\theta = 90^{\circ }$. The Stress-free case demonstrates the lowest ratio till an incidence angle $\theta = 35^{\circ }$ then it increases and depicts the highest ratio for the region $\theta > 45^{\circ }$. There is no significant difference in values for $Z = 0.2$ and $Z = - 0.2$ after $20^{\circ }$ however, the ratio for ${\textrm{Z}} = - 0.2$ remains slightly lower than that for Z = 0.2. The amplitude ratio of the T wave to the incident wave is in the range $10^{-20}$. From the Fig. 4d, the ratios begin from $6.5 \times 10^{-19}$, increase to $7.5 \times 10^{-19}$ near the incidence angle $20^{\circ }$ and then swiftly decrease to 0 for higher angles. Among the different values of impedance parameters, initially, a higher amplitude ratio is observed for the stress-free boundary case, and the lowest ratio is observed for $Z = 0.8$. The result then reverses for angles above $40^{\circ }$ and the ratio is higher for ${\textrm{Z}} = 0.8$ and lowest for ${\textrm{Z}} = 0.0$.

4 Energy partition

Fig. 5

Energy flux sum under LS and GL theory

For bulk waves, the energy flux carried by incident and reflected waves following the works of Scott [36] and Kuang and Yuan [37] is given by

$$\begin{aligned} W = \frac{\omega }{2 \pi } \int _{- \frac{\pi }{\omega }}^{\frac{\pi }{\omega }}P(t)dt \end{aligned}$$

(30)

Following Vashishth et al. [24] energy flux density in considered medium is

$$\begin{aligned} {<}P_R{>} = \frac{1}{2}\omega Re \left( -\sigma _{31}\bar{\dot{u}}_{1} - \sigma _{33}\bar{\dot{u}}_{3} +\phi \bar{\dot{D}}_3 - K_{33}\bar{T}_{,3} \frac{T}{T_0} \right) \end{aligned}$$

(31)

The average energy flux of incident wave is

$$\begin{aligned} {<}P_I{>} = \frac{1}{2}\omega ^2 q_1 \rho c^2 |U_1|^2 \end{aligned}$$

(32)

The average energy flux of reflected waves is

$$\begin{aligned} {<}P_r{>}= \frac{1}{2} {\omega }^2 Re \left( M_{2r}+M_{1r}\bar{A_r} + M_{3r}\bar{C_r} + \frac{ i K_{33}}{T_0 \omega } q_r \bar{B_r}^2 \right) |U_r|^2 , \hspace{0.5cm} r =1,3,5,7. \end{aligned}$$

(33)

$M_{1r}, M_{2r},M_{3r}$ are defined in “Appendix 2”. Energy coefficients can be written as the ratio of energy flux of reflected waves to the incident wave. The energy coefficients are

$$\begin{aligned} E_{qp}= P_1/P_2,\hspace{0.2in} E_{qSV}= P_3/P_2,\hspace{0.2in} E_{EA}=P_5/P_2, \hspace{0.2in} E_{T} = P_7/P_2; \end{aligned}$$

The study is supported by the observation (Fig. 5a, b) that

$$\begin{aligned} E_{qP}+E_{qSV}+E_{EA}+E_{T} \approx 1 \end{aligned}$$

(34)

Figure 5a and b show the energy sum for LS and GL theory respectively. For small angles, the ratio is nearly 1 which is also the case for angles nearing $90^{\circ }$ for both the theories. The half-space is thermally and electrically conducting, the energy is lost owing to the viscoelastic effect. Highest energy loss is observed for impedance = 0, near incidence angle $50^{\circ }$ followed by ${\textrm{Z}} = 0.2$ and − 0.2 whereas least energy is lost for ${\textrm{Z}} = 0.4$. As the incidence angles near $90^{\circ }$, the energy sum becomes 1.

As for Green and Lindsay theory, the energy ratio variates more non-uniformly. For small angles, the sum is close to 1 and even goes above 1 for angles around $15^{\circ }$, these are the angles where the qSV wave ratio experiences a great increase. The energy sum is the highest for ${\textrm{Z}} = - 0.2$, followed by ${\textrm{Z}} = 0.0$ for the region $\theta < 20^{\circ }$. There is a transition angle close to $25^{\circ }$ where the sum becomes 1 and then the value for ${\textrm{Z}} = 0.8$ becomes greater, followed by ${\textrm{Z}} = 0.4$. For the region $\theta > 25^{\circ }$ the stress-free boundary case demonstrates the lowest energy sum.

Fig. 6

Energy ratio between qP and qSV wave

Fig. 7

Energy ratio between qP and qSV wave

Fig. 8

Energy ratio between qP and qSV wave

Fig. 9

LS theory vs GL theory for different impedance values

4.1 Energy ratio division

Figure 6a and b show the division of energy between qP and qSV waves through a range of incidence angles for the impedance value ${\textrm{Z}} = 0.0$. For LS theory, most energy is carried by the qP wave near small angles and angles nearing $90^{\circ }$. In the region $50^{\circ }< \theta < 80^{\circ }$, qSV wave carries more energy and its ratio to the energy of the incident wave reaches as high as 0.6 for the angle $\theta = 70^{\circ }$. Comparing the same with GL theory, it is evident that qP wave carries most energy and it dips lower than qSV ratio only for a small range which is $64^{\circ }< \theta < 70^{\circ }$ where qP and qSV waves carry 0.433 and 0.44 of the total energy respectively. qSV wave carries negligible energy for the region $\theta < 25^{\circ }$ where the energy is mostly contributed by qP wave. After which, qSV wave carries a higher energy, highest ratio being 0.4.

Figure 7a and b show energy ratio partitioned between qP and qSV waves for the impedance value Z = 0.2. In LS theory, qP wave carries more energy than the qSV wave throughout the range of incidence angle, minimizing only around $\theta = 55^{\circ }$ reaching a value 0.66 and qSV reaches value of 0.24. Similarly for GL theory, qP wave carries most energy throughout the range falling its minimum at $\theta = 65^{\circ }$ with a value 0.4. qSV wave begins to carry energy only after $\theta = 25^{\circ }$, reaching a maximum of 0.4 near $\theta = 65^{\circ }$. Figure 8a and b depict the division of energy ratio between the reflected qP and reflected qSV wave for an impedance parameter value ${\textrm{Z}} = 0.4$, being compared for LS and GL theory. QP wave carries almost 4 times the energy carried by the qSV wave. At $\theta = 60^{\circ }$, amplitude is at its minimum, and reflected qP wave still carries 0.75 of the incident qP wave whereas, qSV wave carries only 0.2 of the total energy. Beyond $20^{\circ }$, both theories are observed to exhibit comparable patterns except at certain angles (near $37^{\circ }$).

5 Comparative analysis of LS and GL theory for different impedance values

The Fig. 9a–f depict how the amplitude ratios of qP and qSV vary with changes in the incidence angle. From Fig. 9a, it is evident that in the stress-free scenario, both LS and GL theories exhibit a ratio close to 1 at small angles. However, the ratio for the GL theory shows a subsequent increase and consistently remains higher than that of the LS theory until both ratios converge to 1 near $90^{\circ }$. The Fig. 9b indicates that initially, the ratio for both LS and GL theories starts around 2. Subsequently, there is a notable fluctuation for the GL theory, although it consistently stays higher than that for the LS theory in the region $\theta < 18^{\circ }$. For angles above $18^{\circ }$, the ratio for GL theory is lower and both ratios eventually converge to 0. A similar trend is observed for other impedance values, i.e. for qP wave, the amplitude ratio for GL theory is higher throughout the range. However, with higher impedance, the distinction becomes low and qP wave ratios do not show any discerning difference for impedance value 0.8. For qSV wave, the amplitude ratio for GL theory is higher for the region $\theta < 20^{\circ }$, which then declines and ultimately decreases to 0. It is worth noticing that as impedance levels increase, a corresponding reduction in variation is observed across both theories.

6 Conclusions

Amplitude and energy ratios of reflected waves to those of incident wave are studied. Expressions for amplitude ratios of each of the reflected waves have been derived and it is noted that they depend upon frequency, material constants, and boundary conditions. Well-known piezoelectric medium CdSe is opted to verify our findings. Using Mathematica, amplitude ratios are plotted against the incidence angle of qP wave. The results are studied and compared under two theories of thermoelasticity, namely, LS and GL theory. Here is a summary of the results. Four waves are generated upon reflection from the surface of a piezothermoelastic medium. These four wave modes include two bulk waves qP, and qSV, and two surface waves EA, and T waves. Reflection angles of bulk waves are highly dependent on incidence angles whereas reflection angle of EA and T waves are consistent for a range of incidence angle. A reasonably high impedance makes the surface reflect qP waves with higher amplitude. It is observed that the boundary reflects most efficiently for $Z = 0.4$. An appropriately high impedance leads to reduced energy loss. The amplitudes are seemingly affected by the absolute value of the impedance parameter. The difference in LS and GL theories is affected by impedance values. A high impedance value results in minimal disparity between the ratios associated with the LS and GL theories. It is noteworthy that changes in the phase velocity do not significantly impact our results on amplitude and energy ratio. It is seen that reflected qP wave carries most energy, followed by qSV wave. This division changes with changes in the impedance value. Clearly, an impedance ${\textrm{Z}} = 0.4$ gives a more robust reflected qP wave, making it suitable for p-type devices. Energy of the incident wave is divided into four reflected waves and graphical representation suggests that the energy conservation law holds for both theories.

Appendices

Appendix 1

Matrix entries for Y (LS Theory)

$Y_{11} = c_{11} + c_{44}r^2 - \rho c^2;$

$Y_{12}= (c_{44} + c_{13})r;$

$Y_{13}= \beta _{11} \frac{i}{k};$

$Y_{14} = r (\eta _{15}+ \eta _{31} );$

$Y_{21}= (c_{44}+ c_{13})r;$

$Y_{22}= c_{44}+ c_{33}r^2 -\rho c^2;$

$Y_{23}= r \beta _{33}\frac{i}{k};$

$Y_{24}= \eta _{15}+r^2 \eta _{33};$

$Y_{31}= c \beta _{11} T_0(1- i ck \tau _0);$

$Y_{32}= crT_0 \beta _{33}(1-i ck\tau _0);$

$Y_{33}= K_{11} +r^2 K_{33} -c \rho C_e (\frac{i}{k} +c \tau _0);$

$Y_{34}= rcp_3 T_0(-1 +i c k \tau _0);$

$Y_{41}= r(\eta _{15}+\eta _{31});$

$Y_{42}= \eta _{15}+\eta _{33}r^2;$

$Y_{43}= -r p_3 \frac{i}{k};$

$Y_{44}= - \epsilon _{11} -\epsilon _{33}r^2;$

Matrix entries for Y (GL Theory)

$Y_{11} = c_{11} - \rho c^2 + c_{44}r^2;$

$Y_{12}= (c_{44}+ c_{13})r;$

$Y_{13}= \beta _{11} ( \frac{i}{k} +c \tau _1);$

$Y_{14} = r (\eta _{15}+ \eta _{31} );$

$Y_{21}= (c_{44}+ c_{13})r;$

$Y_{22}= c_{44}+c_{33}r^2 -\rho c^2;$

$Y_{23}= r \beta _{33} ( \frac{i}{k} +c \tau _1);$

$Y_{24}= \eta _{15}+r^2 \eta _{33};$

$Y_{31}= c \beta _{11} T_0;$

$Y_{32}= crT_0 \beta _{33};$

$Y_{33}= K_{11} +r^2 K_{33} -c \rho C_e (\frac{i}{k} +c \tau _0);$

$Y_{34}= -rcp_3 T_0;$

$Y_{41}= r(\eta _{15}+\eta _{31});$

$Y_{42}= \eta _{15}+\eta _{33}r^2;$

$Y_{43}= -rp_3 (\frac{i}{k} + c\tau _1);$

$Y_{44}= - \epsilon _{11} -\epsilon _{33}r^2;$

Appendix 2

$M_{1n}= c_{13}+c_{33}r_{n}A_{n}+\eta _{33} r_{n}C_{n}- \beta _{33}(\frac{1}{ i k} - c \tau _1 \delta _{2 \kappa }) B_n;$

$M_{2n}= \frac{(r_n +A_n)}{2}c_{44}+\eta _{15}C_n;$

$M_{3n}= \eta _{31}+r_2 \eta _{33} A_2 -\epsilon _{33} r_n C_n +p_3 B_n(\frac{1}{i k} - c \tau _1 \delta _{2\kappa });$

Appendix 3

$G_{11}= M_{31};$

$G_{12}= M_{33};$

$G_{13}= M_{35};$

$G_{14}= M_{37};$

$G_{21}= r_1 B_1;$

$G_{22}= r_3 B_3;$

$G_{23}= r_5 B_5;$

$G_{24}= r_7 B_7;$

$G_{31}= i k M_{21} + \omega Z_1;$

$G_{32}= i k M_{23} + \omega Z_1;$

$G_{33}= i k M_{25} + \omega Z_1;$

$G_{34}= i k M_{27} + \omega Z_1;$

$G_{41}= i k M_{11} + \omega Z_3 A_1;$

$G_{42}= i k M_{13} + \omega Z_3 A_3;$

$G_{43}= i k M_{15} + \omega Z_3 A_5;$

$G_{44}= i k M_{17} + \omega Z_3 A_7;$

$H_1= -M_{30};$

$H_2= -r_0 B_0;$

$H_3 = - i k M_{22} + \omega Z_1;$

$H_4= - i k M_{12} + \omega Z_3 A_2.$