1 Introduction

Microbeams have become prevalent in the fields of microscale devices and systems, i.e., sensors [1, 2], actuators [3, 4], resonators [5] and energy harvesters [6, 7] and so on [8]. Beams used in these applications have the thickness on the order of microns and sub-microns, so that microstructure-dependent size effects are often observed [9, 10] and play an important role on the static deformation and vibration behavior for microbeam structures, which have been validated experimentally, i.e., the enhancement of torsional hardening [11], plastic work hardening [12] and bending rigidity [13] caused by the decrease in beam thickness. Also, there are some observations that reflect a softening effect for material in small scale [14]. Microbeam structures based on conventional strain-based continuum solid mechanics theories do not suffice for an accurate and detailed description of corresponding size-dependent mechanical deformation phenomena due to the absence of an internal length, characteristic of the underlying microstructure, from the constitutive equations.

Considering experimental observations, the size-dependent behavior is an inherent property of materials and plays an important role on the mechanical behavior of microstructures when the size of the models is close to the internal material length scale parameter [15,16,17,18]. Thus, it is inevitable to employ the non-classical elasticity continuum theories (i.e., strain gradient elasticity and couple stress theories) to predict the size-dependent mechanical response of micron-scale structures. In the constitutive equation of size-dependent elasticity continuum theories, some higher-order material length scale parameters appear in addition to the two classical Lame constants for isotropic elastic materials. But in fact, the higher-order material length scale parameters cannot be determined by mechanical experimental measurements easily. Subsequently, Yang et al. [19] proposed the modified couple stress theory, in which constitutive equations involve only one additional internal material length scale parameter besides two classical material constants. They argued that the equilibrium of moments of couples should be satisfied for the modeling of materials in small scales in addition to the classical equilibrium equations of forces and moments of forces. The only one additional internal material length scale parameter can be determined by the experiment tests of microbend, microtorsion and micro-/nanoindentation. After this, the modified couple stress theory has been widely applied to develop the size-dependent formulations for beams in statics and dynamics. Park and Gao [20] analyzed the static mechanical properties of a bending Bernoulli–Euler beam based on the modified coupling stress theory and found the size-dependent behavior of the bending rigidity. Ma et al. [21] established a microstructure-dependent model for the Timoshenko microbeam using the modified couple stress theory and concluded the microstructure-dependent effect of the static bending and free vibration. Kong et al. [22] studied the dynamic characteristics of the microbeam based on the modified couple stress theory and obtained the enhancement behavior of the natural frequency. Ye et al. [23] investigated the size dependency of the static bending of a bilayer microbeam, and the size effect on beam stiffness is significant when the beam height is on orders of the equivalent length scale parameter. Furthermore, the size-dependent natural frequencies of fluid-conveying microtubes [24], the size-dependent nonlinear dynamics of a microbeam [25], the size-dependent buckling behavior of microtubules [26], the size-dependent resonant frequencies and sensitivities of AFM microcantilevers [27], the size-dependent couple stress natural frequency analysis for two- and three-dimensional problems [28], the size-dependent parametrization of active vibration control for periodic piezoelectric microplate [29] have been investigated based on the modified couple stress theory. Scarpa et al. [30], Chowdhury et al. [31], Murmu and Adhikari [32], Ranjbartoreh et al. [33] studied the static and dynamic behavior of non-classical mechanical models related to micro-/nanostructure vibration, wave propagation, etc. and used different mathematical methods such as analytical and semi-analytical to determine the changes in relevant physical parameters, i.e., their mechanical behavior. However, their characteristics of specific boundaries and external loads limit their application in the design of micro/nanostructures, so unconventional mechanical models that are size dependence and suitable for different boundaries and are subject to complex external loads will be better applied in practice.

However, the influence of the microrotation (or particle rotation) on the microstructures is one of the most important points in the modeling of materials in small scales. The microrotation for microstructures, different from macrorotation, is not negligible for static and dynamic behaviors of microbeam model. In fact, the microrotation concept is one of the most important definitions to state theories like micropolar, micromorphic, couple stress and modified couple stress. Mindlin [34] introduced the concept of microrotation within the framework of a non-classical continuum theory to describe the size-dependent performance of structures in microscale. Hadjesfandiari and Dargush [35] presented an excellent brief overview of the couple stress concept and discussed the evolution of the concept and application of rotation in the couple stress theory. And Yang et al. [18] proposed the modified couple stress theory to exploit the microrotation in addition to translations for each material particle and found the real microrotation is different from macrorotations even though the definition of the microrotation is the same as the macrorotations in classical continuum mechanics. The mentioned studies employ the modified couple stress theory which tends to add rotations besides translations for each particle to describe the size-dependent behavior of microbeam structures distinctly, but the absence of considerations regarding microstructure (i.e., ignoring the microinertia term) is the main deficiency. The deficiency of the modified couple stress theory is that it does not describe wave dispersion in solids, properly, especially at high frequencies. Experimental observations and computational simulations confirm a distinct attitude than classical consequences for wave propagation in different types of solid structures, especially in the crystalline solids, porous media or any kind of materials with microstructure. In fact, the wave dispersion for micro/nano structures shows obvious nonlinearity (the wave dispersion for macrostructures is a linear relation); such nonlinearity would be induced higher frequencies in reality. Though some theories of continuum gradient elasticity can capture such nonlinear behavior, the modified couple stress theory can be inability to justify the nonlinear dynamic behavior of structures in high-frequency dispersive analyses. However, some studies considered the microinertia to impose microstructure effects on the wave dispersion relation to approach the problem of obvious nonlinearity in micro-/nanostructures. Georgiadis et al. [36] showed that term of microinertia is indeed important at high frequencies and dispersion curves that mostly resemble with the ones obtained by atomic-lattice considerations. Georgiadis and Velgaki [37] employed the microinertia concept (in subparticles) to bring the microstructure effects into the equations and proved that the couple stress elasticity theory with microstructure does predict dispersive Rayleigh waves at high frequencies. Akbarzadeh Khorshidi and Soltani [38] added a microinertia length scale parameter to the equation of motion to compensate the deficiency of the modified couple stress theory in describing the size effect of the longitudinal dynamic analyses. Soltani et al. [39] modeled the highly nonlinear behavior of dispersion curves of aluminum beams on the basis of the microinertia-based couple stress theory and proved the importance of the higher-order microrotations for dynamic behavior of microstructure-dependent beams. Namely, there is no problem in the static analysis of micro/nanostructures, but the mentioned procedure cannot justify the dynamic behavior of structures, especially in high-frequency dispersive analyses, where the conventional couple stress theories (classical continuum) are not acceptable. It is also evident that all materials behave in a particular size (micro or nano), so it is anticipated that these microrotations become important in such scales. Thus, the equations of motion for microstructures can be more accurate when the microinertia effects are considered.

In addition, there is no extra boundary condition introduced, only the simply-supported boundary condition as a case study is applied and analyzed in the above-mentioned studies of beam models based on the modified couple stress theory. However, when a beam is not two simply supported ends, but is supported in some other ways, i.e., clamped supported ends, or clamped–clamped ends, etc., the static and dynamic performances of the beam are no longer in pure sinusoidal modes. Moreover, the static deformations and the natural dynamic modes of such a beam with an undamped core become coupled as soon as core damping is introduced. The calculation of the free and forced vibrations of these beams therefore presents, apparently, a more difficult problem.

The object of this work is the establishing of a microstructure model for the Timoshenko microbeam based on the modified couple stress theory and Hamilton’s principle, and extending the work on the statics and dynamics by considering the microinertia effect coming from realistic microrotation concept. This microbeam model incorporates the material length scale parameter which can capture the size-dependent effect and the microinertia length scale parameter which can describe the higher-order microrotation relation. This paper rigorously derives the governing equations and boundary conditions for the modified couple stress based Timoshenko beam with microinertia. The integral form solution of the differential equation is shown to yield a special class of complex and can be applied to the general forced vibration problem quite simply and straightforward. The evaluation reveals that the effects of size-dependent and microinertia influence the static and dynamic performances of the microbeams as well as the boundary conditions.

2 Formulation

According to the modified coupling stress theory [19, 21], a linear elastic isotropic material in infinitesimal deformation occupying the region Ω (with the volume element dV) has the strain energy generated by the strain deformation and the symmetrical part of rotational deformation

$$U = \frac{1}{2}\int_{\Omega } {({\varvec{\sigma}}:{\varvec{\varepsilon}} + {\varvec{m}}:{\varvec{\chi}})} {\text{d}}V$$
(1)

where σ and ε are conjugated, corresponding to the symmetric part of stress tensor and the strain tensor; m and χ are conjugated, corresponding to the deviatoric part of the couple stress tensor and the symmetric part of the curvature tensor. The strain and the curvature tensors are defined by

$${\varvec{\varepsilon}} = \frac{1}{2}\left[ {\nabla {\varvec{u}} + (\nabla {\varvec{u}})^{{\text{T}}} } \right]$$
(2)
$${\varvec{\chi}} = \frac{1}{2}\left[ {\nabla {\varvec{\theta}} + (\nabla {\varvec{\theta}})^{{\text{T}}} } \right]$$

where u and θ are the components of the infinitesimal displacement vector and the rotation vector. The rotation vector θ is related to the components of the displacement vector field u as

$${{\varvec{\uptheta}}} = \frac{1}{2}{\text{curl}} {\mathbf{u}}$$
(3)

And the constitutive relations can be written as

$${{\varvec{\upsigma}}} = \lambda {\text{tr}} ({{\varvec{\upvarepsilon}}}){\mathbf{I}} + 2\mu {{\varvec{\upvarepsilon}}}$$
(4)
$${\mathbf{m}} = 2l^{2} \mu {{\varvec{\upchi}}}$$

and the material length scale parameter l is physically a property measuring the effect of couple stress [20, 40], which can be determined by some typical experiments [9, 20, 41, 42], i.e., microbend test, microtorsion test and specially micro-/nanoindentation test. And λ and μ are Lamé’s constants, which is given by λ = Eυ/[(1 + υ)(1‒2υ)], μ = E/[2(1 + υ)] (E is Young’s modulus, υ is Poisson’s ratio).

It should also be mentioned that versions of the couple stress theory do not include inertia and microinertia effects since they are of quasi-static character. Of course, the inertia and microinertia effects appear within the dynamic analysis. Thus, the kinetic energy for microstructure-dependent models is composed of two parts: the rigid body kinetic energy (macroscopic kinetic energy) of the beam as a whole and the kinetic energy (microscopic kinetic energy) caused by the internal strain of the beam, which can be defined as [37, 38, 43]

$$T = \frac{1}{2}\rho \int_{\Omega } {\dot{\mathbf{{u}}}^{2} {\text{d}}V} + \frac{1}{2}I_{\nu } \int_{\Omega } {\dot{{\varvec{\psi }}}^{2} {\text{d}}V}$$
(5)

where ρ is the density, Iv denotes the mass moment of inertia per unit volume related to the microrotation of particles and a superimposed dot denotes a derivative with respect to time. The mass moment of inertia can be expressed as Iv = ρ(lv)2, which the microinertia length scale parameter lv can be defined as the unit cell size of the microstructure of the reaction material. And ψ is the microrotation vector and defined as [34]

$$\psi_{ij} = u_{j,i}$$
(6)

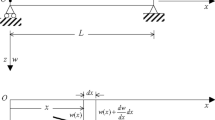
Consider a uniform homogeneous initially straight Timoshenko beam under the kinematic parameters and the loading on the basis of the rectangular Cartesian coordinate system (x, y, z) shown in Fig. 1, where the x-axis is coincident with the centroidal axis of the undeformed beam, the y-axis is the neutral axis and the z-axis is the symmetry axis. In Fig. 1, f(x) and q(x) denote the axial body force and the transverse body forces, respectively; P stands for the transverse body concentrated load; c(x) represents the y-component of the body couples imposed on the sections as couple per unit axial length.

Fig. 1
figure 1

Beam configuration and coordinate system

Full size image

The displacement field in a Timoshenko beam can be assumed as follows [38]

$$u_{1} = u(x,t) - z\phi (x,t),\quad u_{2} = 0,\quad u_{3} = w(x,t)$$
(7)

where u1, u2 and u3 are, respectively, the x-, y- and z-components of the displacement vector u of a point (x, y, z) on a beam cross section. For a point (x, 0, 0) on the centroidal axis, u and w are the x- and z-components of the displacement vector, respectively, and φ is the angle of rotation (about the y-axis) of the cross section with respect to the vertical direction (i.e., the z-axis).

By using Eq. (2), the corresponding strain component can be obtained

$$\varepsilon_{xx} = u_{,x} - z\phi_{,x} ,\quad \varepsilon_{xz} = \frac{1}{2}( - \phi + w_{,x} ),\quad \varepsilon_{yy} = \varepsilon_{zz} = \varepsilon_{xy} = \varepsilon_{yz} = 0$$
(8)

where the lower corner index (,x) indicates the derivation of the variable x. Also, Eqs. (3) and (7) give

$$\theta_{y} = - \frac{1}{2}(\phi + w_{,x} ),\quad \theta_{x} = \theta_{z} = 0$$
(9)

Substitution of Eqs. (9) into (2) yields the following expression for the nonzero components of the symmetric curvature tensor

$$\chi_{xy} = - \frac{1}{4}(\phi_{,x} + w_{,xx} ),\quad \chi_{xx} = \chi_{yy} = \chi_{zz} = \chi_{yz} = \chi_{zx} = 0$$
(10)

In this study, the equilibrium governing equations are derived by the principle of total potential energy. From Eqs. (1) and (8)–(10), the first variation in the total strain energy on the time interval [0, T] can be determined as

$$\begin{aligned} \delta \int_{0}^{T} U {\text{d}}t = & \int_{0}^{T} {\int_{\Omega } {(\sigma _{{ij}} \delta \varepsilon _{{ij}} + m_{{ij}} \delta \chi _{{ij}} )} } {\text{d}}V{\text{d}}t \\ = & \int_{0}^{T} {\int_{\Omega } {(\sigma _{{xx}} \delta \varepsilon _{{xx}} + 2\sigma _{{xz}} \delta \varepsilon _{{xz}} + 2m_{{xy}} \delta \chi _{{xy}} )} } {\text{d}}V{\text{d}}t \\ = & \int_{0}^{T} {\int_{0}^{L} {\left[ { - N_{{,x}} \delta u + \left( {M_{{,x}} - Q + \frac{1}{2}Y_{{,x}} } \right)\delta \phi - \left( {Q_{{,x}} + \frac{1}{2}Y_{{,xx}} } \right)\delta w} \right]} } {\text{d}}x{\text{d}}t \\ & \quad + \int_{0}^{T} {\left[ {N\delta u - \left( {M + \frac{1}{2}Y} \right)\delta \phi } \right.} + \left. {\left( {Q + \frac{1}{2}Y_{{,x}} } \right)\delta w - \frac{1}{2}Y\delta (w_{{,x}} )} \right]{\text{ }}|_{{x = 0}}^{{x = L}} {\text{d}}t \\ \end{aligned}$$
(11)

and its axial force N, resultant moment M, coupling moment Y and transverse force Q are as follows

$$N \equiv \int_{A} {\sigma_{xx} {\text{d}}A,\quad M} \equiv \int_{A} {\sigma_{xx} z{\text{d}}A} ,\quad Y \equiv \int_{A} {m_{xy} {\text{d}}A} ,\quad Q \equiv \int_{A} {\sigma_{xz} {\text{d}}A}$$
(12)

Substituting the displacement field (Eq. (7)) into the kinetic energy Eq. (5), the general form for the dynamic part of the equation of motion in terms of the displacement vector can be expressed as

$$K = \frac{1}{2}\int_{\Omega } {\rho (\dot{u}_{1}^{2} + \dot{u}_{3}^{2} )} {\text{d}}V + \frac{1}{2}\int_{\Omega } {\rho l_{v}^{2} (\dot{u}_{1,x}^{2} + \dot{u}_{1,z}^{2} + \dot{u}_{3,x}^{2} ){\text{d}}V}$$
(13)

Using the variation of Eq. (13), the first variation in the kinetic energy on the time interval [0, T] is

$$\begin{aligned} \delta \int_{0}^{T} K {\text{d}}t &= - \int_{0}^{T} {\int_{0}^{L} {{[}m_{0} (\ddot{u} - l_{v}^{2} \ddot{u}_{,xx} )\delta u + m_{0} (\ddot{w} - l_{v}^{2} \ddot{w}_{,xx} )\delta w + [m_{0} l_{v}^{2} \ddot{\phi } + m_{2} (\ddot{\phi } - l_{v}^{2} \ddot{\phi }_{,xx} )]\delta \phi {\text{]d}}x{\text{d}}t} } \\ &\quad+ \int_{0}^{L} {\{ m_{0} (\dot{u} - l_{v}^{2} \dot{u}_{,xx} )\delta u + m_{0} (\dot{w} - l_{v}^{2} \dot{w}_{,xx} )\delta w + [m_{0} l_{v}^{2} \dot{\phi } + m_{2} (\dot{\phi } - l_{v}^{2} \dot{\phi }_{,xx} )]\delta \phi \} \mathop |\nolimits_{t = 0}^{t = T} {\text{d}}x} \\ &\quad - \int_{0}^{T} {l_{v}^{2} (m_{0} \ddot{u}_{,x} \delta u + m_{0} \ddot{w}_{,x} \delta w + m_{2} \ddot{\phi }_{,x} \delta \phi )} \mathop |\nolimits_{x = 0}^{x = L} {\text{d}}t + l_{v}^{2} (m_{0} \dot{u}_{,x} \delta u + m_{0} \dot{w}_{,x} \delta w + m_{2} \dot{\phi }_{,x} \delta \phi )\mathop |\nolimits_{t = 0}^{t = T} \mathop |\nolimits_{x = 0}^{x = L} \\ \end{aligned}$$
(14)

with

$$m_{0} \equiv \int_{A} \rho {\text{d}}A = \rho A\begin{array}{*{20}c} {} & {} \\ \end{array} m_{2} \equiv \int_{A} \rho z^{2} {\text{d}}A = \rho I_{y}$$
(15)

where Iy is the second moment of cross-sectional area about the y-axis.

The work done by external loads including body forces, body couples and boundary surface tractions is evaluated as

$$\delta \int_{0}^{T} W {\text{d}}t = \int_{0}^{T} {\int_{0}^{L} {{(}f\delta u + q\delta w + c\delta \theta_{y} {\text{)d}}x{\text{d}}t} } + \int_{0}^{T} {(\overline{N}\delta u + \overline{V}\delta w - \overline{M}\delta \phi )|_{x = 0}^{x = L} {\text{d}}t}$$
(16)

where f and q are, respectively, the x- and z-components of the body force per unit length along the x-axis, c is the y-component of the body couple per unit length along the x-axis.

where \(\overline{N}\), \(\overline{V}\) and \(\overline{M}\) are, respectively, the axial resultant force of normal stresses σxx, the transverse resultant force of shear stresses and the resultant moment of normal stresses σxx.

According to Hamilton's principle, the actual motion of the system with prescribed configurations minimizes the difference between its kinetic energy and total potential energy at t = 0 and T, that is,

$$\delta \int_{0}^{T} {[K - (U - W)]dt = 0}$$
(17)

Substituting Eqs. (11), (14) and (16) into Eq. (17) results in

$$ \begin{gathered} \int_{0}^{T} {\int_{0}^{L} {\left\{ \begin{gathered} \left[N_{,x} + f - m_{0} (\ddot{u} - l^{2} \ddot{u}_{,xx} )\right]\delta u + \left[ {Q_{,x} + \frac{1}{2}Y_{,xx} + \frac{1}{2}c_{,x} + q - m_{0} (\ddot{w} - l^{2} \ddot{w}_{,xx} )} \right]\delta w \hfill \\ - \left[ {M_{,x} + \frac{1}{2}Y_{,x} + \frac{1}{2}c - Q + m_{0} l_{v}^{2} \ddot{\phi } + m_{2} (\ddot{\phi } - l_{v}^{2} \ddot{\phi }_{,xx} )} \right]\delta \phi \hfill \\ \end{gathered} \right\}} } {\text{d}}x{\text{d}}t \hfill \\ \qquad\qquad- \int_{0}^{T} {\left\{ {\begin{array}{*{20}l} {\left[(N - \overline{N}) + m_{0} l_{v}^{2} \ddot{u}_{,x} \right]\delta u - \left[ {(M - \overline{M}) + \frac{1}{2}Y - m_{2} l_{v}^{2} \ddot{\phi }_{,x} } \right]\delta \phi } \hfill \\ { + \left( {Q + \frac{1}{2}Y_{,x} + \frac{1}{2}c - \overline{V} + m_{0} l_{v}^{2} \ddot{w}_{,x} } \right)\delta w - \frac{1}{2}Y\delta (w_{,x} )} \hfill \\ \end{array} } \right\}} \mathop |\nolimits_{x = 0}^{x = L} {\text{d}}t \hfill \\ \qquad\qquad+ \int_{0}^{L} {\{ m_{0} (\dot{u} - l_{v}^{2} \dot{u}_{,xx} )\delta u + m_{0} (\dot{w} - l_{v}^{2} \dot{w}_{,xx} )\delta w + \left[m_{0} l_{v}^{2} \dot{\phi } + m_{2} (\dot{\phi } - l_{v}^{2} \dot{\phi }_{,xx} )\right]\delta \phi \} } \mathop |\nolimits_{t = 0}^{t = T} {\text{d}}x \hfill \\ \qquad\qquad + l_{v}^{2} (m_{0} \dot{u}_{,x} \delta u + m_{0} \dot{w}_{,x} \delta w + m_{2} \dot{\phi }_{,x} \delta \phi )\mathop |\nolimits_{t = 0}^{t = T} \mathop |\nolimits_{x = 0}^{x = L} = 0 \hfill \\ \end{gathered} $$
(18)

Note that the integrand of the last term on the left-hand side of Eq. (18) vanishes for the beam whose configurations at t = 0 and T are prescribed. For the arbitrariness of δu, δw and δϕ, the following equilibrium equations can be achieved as

$$\begin{array}{*{20}c} {N_{,x} + f = m_{0} (\ddot{u} - l_{v}^{2} \ddot{u}_{,xx} )} & {} \\ {Q_{,x} + \frac{1}{2}Y_{,xx} + q + \frac{1}{2}c_{,x} = m_{0} (\ddot{w} - l_{v}^{2} \ddot{w}_{,xx} )} & {\forall x \in (0,L)} \\ { - M_{,x} - \frac{1}{2}Y_{,x} + Q - \frac{1}{2}c = m_{0} l_{v}^{2} \ddot{\phi } + m_{2} (\ddot{\phi } - l_{v}^{2} \ddot{\phi }_{,xx} )} & {} \\ \end{array}$$
(19)

and the boundary conditions as follows:

$$\begin{array}{*{20}c} {N = \overline{N}} & {{\text{or}}} & { \, u = \overline{u}} \\ {Q + \frac{1}{2}Y_{,x} + \frac{1}{2}c = \overline{V}} & {{\text{or}}} & {w = \overline{w}} \\ {M + \frac{1}{2}Y = \overline{M}} & {{\text{or}}} & {\phi = \overline{\phi }} \\ {Y = 0} & {{\text{or}}} & {w_{,x} = \overline{w}_{,x} } \\ \end{array} \begin{array}{*{20}l} {\text{ at }} \hfill \\ \end{array} \begin{array}{*{20}l} {x = 0,L} \hfill \\ \end{array}$$
(20)

where the overline represents the prescribed value. From Eqs. (4) and (12) it follows that

$$N = (\lambda + 2\mu )Au_{,x} ,\quad M = - (\lambda + 2\mu )I\phi_{,x}$$
$$Y = - \frac{1}{2}l^{2} \mu A(\phi_{,x} + w_{,xx} ),\quad Q = K_{s} \mu A( - \phi + w_{,x} )$$
(21)

where I ≡ Iy = bh3/12, Ks is the Timoshenko shear coefficient, which is introduced as a correction factor to account for the non-uniformity of the shear strain over the beam cross section, and is taken to be (5 + 5υ)/(6 + 5υ). It is worth noting the couple moment Y, which is the result of the generation of the couple stress component mxy (see Eq. (12)), is involved in the current model in addition to the conventional bending moment M (see Eqs. (20) and (21)). As shown in Eq. (21), Y explicitly depends on the material length scale parameter l, which is related to the underlying microstructure of the beam material.

By using Eqs. (19) and (21), the equilibrium equations of the microbeam in terms of the displacements are obtained as

$$(\lambda + 2\mu )Au_{,xx} + f = m_{0} (\ddot{u} - l_{v}^{2} \ddot{u}_{,xx} )$$
(22)
$$K_{s} \mu A( - \phi_{,x} + w_{,xx} ) - \frac{1}{4}l^{2} \mu A(\phi_{,xxx} + w_{,xxxx} ) + q + \frac{1}{2}c_{,x} = m_{0} (\ddot{w} - l_{v}^{2} \ddot{w}_{,xx} )$$
$$(\lambda + 2\mu )I\phi_{,xx} + \frac{1}{4}l^{2} \mu A(\phi_{,xx} + w_{,xxx} ) + K_{s} \mu A( - \phi + w_{,x} ) - \frac{1}{2}c = m_{0} l_{v}^{2} \ddot{\phi } + m_{2} (\ddot{\phi } - l_{v}^{2} \ddot{\phi }_{,xx} )$$

It can be seen from Eq. (22) that the material scale parameter l has a certain influence on the static behavior (deflection, rotation, etc.) of the beam, while the dynamic feature length parameter lv is related to the time term, which affects the dynamic behavior of the beam together with the material scale parameter l, and their presence helps us describe the size effect of microstructure. With the help of the boundary condition (20), for any x ϵ [0, L], t ϵ (0, T), the equations of motion can be solved to get u(x, t), w(x, t), φ(x, t).

Note that when the scale parameters l and lv are taken to be zero in Eqs. (19–21), and setting υ = 0 and c = 0, the equilibrium equations of classical Timoshenko beam theory are obtained.

$$\begin{array}{*{20}c} {EAu_{,xx} + f = m_{0} \ddot{u}} & {} \\ {K_{s} \mu A( - \phi_{,x} + w_{,xx} ) + q = m_{0} \ddot{w}} & { \, \forall x \in (0,L)} \\ {EI\phi_{,xx} + K_{s} \mu A( - \phi + w_{,x} ) = m_{2} \ddot{\phi }} & {} \\ \end{array}$$
(23)

and the boundary condition (20) are simplified as:

$$\begin{array}{*{20}c} {N = \overline{N}} & {} & {u = \overline{u}} & {} \\ {Q = \overline{V}} & {\text{ or }} & {w = \overline{w}} & {{\text{ at }}x = 0,L} \\ {M = \overline{M}} & {} & {\phi = \overline{\phi }} & {} \\ \end{array}$$
(24)

where the effect of couple moment is not considered; load value reduces to

$$N = EAu_{,x} ,\quad M = - EI\phi_{,x} ,\quad Q = K_{s} \mu A( - \phi + w_{,x} )$$
(25)

Equations (23–25) represent the classical Timoshenko beam model. If no axial deformation is considered (i.e., u(x, t) = 0) which can be further reduced to that formulated in Hutchinson [44] and to that summarized in Wang [45] for static bending if u(x, t) = 0, w(x, t) = w(x), φ(x, t) = φ(x).

Furthermore, if φ(x, t) = w,x, Eqs. (19–21) are converted to those for Euler–Bernoulli beam theory as follows:

$$(\lambda + 2\mu )Au_{,xx} + f = m_{0} (\ddot{u} - l_{v}^{2} \ddot{u}_{,xx} )$$
(26)
$$[(\lambda + 2\mu )I + l^{2} \mu A]w_{,xxxx} - q - c_{,x} = - m_{0} (\ddot{w} - 2l_{v}^{2} \ddot{w}_{,xx} ) + m_{2} (\ddot{w}_{,xx} - l_{v}^{2} \ddot{w}_{,xxxx} )$$

which incorporate the effect of Poisson’s ratio. In addition, for static bending without axial load and without taking into account the Poisson’s effect, u = 0, w = w(x) and υ = 0, Eq. (26) reduce to, with f = 0,

$$(EI + l^{2} \mu A)w_{,xxxx} = q$$
(27)

which is identical to the governing equation derived in Park and Gao [20] for a microstructure-dependent Bernoulli–Euler beam based on the same modified couple stress theory. Clearly, Eq. (27) will be further reduced to the governing equation of the classical Bernoulli–Euler beam theory when l = 0.

3 Static bending and free vibration with arbitrary boundary conditions

3.1 Static bending

The boundary value problem for the static bending of the microbeams is defined by Eq. (19), with u = u(x), w = w(x), φ = φ(x). To simplify the expression of the formula

$$\begin{gathered} \alpha_{1} = (\lambda + 2\mu )A,\quad \alpha_{2} = K_{s} \mu A \hfill \\ \alpha_{3} = \frac{1}{4}l^{2} \mu A,\quad \alpha_{4} = (\lambda + 2\mu )I \hfill \\ \end{gathered}$$
(28)

then the equations of motion derived in Eq. (22) can be simplified to

$$\alpha_{1} u^{\prime\prime} = - f$$
(29)
$$\alpha_{2} ( - \phi{\prime} + w^{{\prime\prime}} ) - \alpha_{3} (\phi^{{\prime\prime\prime}} + w^{{\prime\prime\prime\prime}} ) = - \frac{1}{2}c{\prime} - q$$
$$\alpha_{4} \phi^{{\prime\prime}} + \alpha_{3} (\phi^{{\prime\prime}} + w^{{\prime\prime\prime}} ) + \alpha_{2} ( - \phi + w{\prime} ) = \frac{1}{2}c$$

note that the upper corner (') indicates the ordinary differentiation of the function to the variable x.

To facilitate the solution of the equations of motion (29), we create two new variables:

$$\gamma (x) = - \phi + w^{\prime},\quad \theta (x) = - \phi - w^{\prime}$$
(30)

Using it in Eq. (29)

$$\alpha_{1} u^{\prime\prime} = - f$$
(31)
$$\alpha_{2} \gamma{\prime} + \alpha_{3} \theta^{{\prime\prime\prime}} = - \frac{1}{2}c{\prime} - q$$
$$- \frac{1}{2}\alpha_{4} (\gamma^{{\prime\prime}} + \theta^{{\prime\prime}} ) - \alpha_{3} \theta^{{\prime\prime}} + \alpha_{2} \gamma = \frac{1}{2}c$$

With the first formula in Eq. (31), the axial displacement is easily solved

$$u = - \frac{f}{{2\alpha_{1} }}x^{2} + c_{1} x + c_{2}$$
(32)

With the second formula Eq. (31), θ can be expressed using the variable γ

$$\theta ^{\prime\prime} = - \frac{1}{{\alpha_{3} }}\left( {\alpha_{2} \gamma + \frac{1}{2}c + \int {q{\text{d}}x} + c_{3} } \right)$$
(33)

Substituting Eq. (33) into the third formula in Eq. (31) yields equations that only about variables γ

$$\gamma ^{\prime\prime} - \alpha_{2} \left( {\frac{1}{{\alpha_{3} }} + \frac{4}{{\alpha_{4} }}} \right)\gamma = \frac{1}{{2\alpha_{3} }}c + \left( {\frac{1}{{\alpha_{3} }} + \frac{2}{{\alpha_{4} }}} \right)\left( {c_{3} + \int {q{\text{d}}x} } \right)$$
(34)

namely

$$\gamma ^{\prime\prime} - k^{2} \gamma = A_{1} (x)$$
(35)

where

$$k^{2} = \alpha_{2} \left( {\frac{1}{{\alpha_{3} }} + \frac{4}{{\alpha_{4} }}} \right)$$
(36)
$$A_{1} (x) = \frac{1}{{2\alpha_{3} }}c + \left( {\frac{1}{{\alpha_{3} }} + \frac{2}{{\alpha_{4} }}} \right)\left( {c_{3} + \int {q{\text{d}}x} } \right)$$
(37)

Using Eqs. (36) and (37), the general solution of the variable γ can be obtained:

$$\gamma (x) = c_{4} \cosh (kx) + c_{5} \sinh (kx) + \gamma_{p} (x)$$
(38)

where, the particular solutions γp(x) are

$$\gamma_{p} (x) = \sinh (kx)\int {\frac{{A_{1} (x)\cosh (kx)}}{k}} {\text{d}}x - \cosh (kx)\int {\frac{{A_{1} (x)\sinh (kx)}}{k}} {\text{d}}x$$
(39)

Substituting Eqs. (38) and (39) into Eq. (33) and integrating them twice yield the variable θ

$$\begin{gathered} \theta = - \frac{{4K_{s} }}{{l^{2} k^{2} }}\left[ {c_{4} \cosh (kx) + c_{5} \sinh (kx)} \right] - \frac{{4K_{s} }}{{l^{2} }}\int {\gamma_{p} (x){\text{d}}x^{2} } \\ - \frac{1}{{\alpha_{3} }}\left( {\int {q{\text{d}}x^{3} } + \frac{1}{2}\int {c{\text{d}}x^{2} } + \frac{1}{2}c_{3} x^{2} } \right) + c_{6} x + c_{7} \\ \end{gathered}$$
(40)

where \(\int f(x){{\text{d}}x}^{n}\) represents the nth integral of f(x).

Using the new variables introduced γ, θ and Eq. (29), the required beam deflection and rotation angle can be obtained

$$\phi = - \frac{1}{2}(\gamma + \theta ),\begin{array}{*{20}l} {} \hfill \\ \end{array} w = \frac{1}{2}\int {(\gamma - \theta )} {\text{d}}x + c_{8}$$
(41)

Based on the y-component of the body couple, c is taken to be 0; the applied load, q(x), can also be expanded in a Fourier series as:

$$q(x) = \sum\limits_{n = 1}^{\infty } {Q_{n} } \sin \left( {\frac{n\pi x}{L}} \right)$$
(42)

For given q(x), Qn can be readily determined to be

$$Q_{n} = \frac{2}{L}\int_{0}^{L} q (x)\sin \left( {\frac{n\pi x}{L}} \right){\text{d}}x.$$
(43)

For the current problem, q(x) = Pδ(x‒L/2), where δ is the Dirac delta function. The use of this q(x) in Eq. (43) then gives

$$Q_{n} = \frac{2}{L}P\sin \left( {\frac{n\pi }{2}} \right)$$
(44)

With Eqs. (38‒41), the corresponding boundary conditions can be substituted to complete the solution of w(x), φ(x).

If the microstructural effect (l = 0) caused by the material scale parameter l is ignored, the equations of motion (31) are further simplified to:

$$\alpha_{1} u^{\prime\prime} = - f$$
(45)
$$\alpha_{2} \gamma{\prime} = - q$$
$$- \frac{1}{2}\alpha_{4} (\gamma^{{\prime\prime}} + \theta^{{\prime\prime}} ) + \alpha_{2} \gamma = 0$$

; then, the solution for the axial displacement, deflection and angle of the classical Timoshenko beam can be obtained:

$$u = - \frac{f}{{2\alpha_{1} }}x^{2} + c_{1} x + c_{2}$$
(46)
$$w = \frac{1}{{\alpha_{4} }}\left( {\int {q{\text{d}}x^{4} } - \frac{1}{6}\alpha_{2} c_{3} x^{3} } \right) - \frac{1}{{\alpha_{2} }}\int {q{\text{d}}x^{2} } + \frac{1}{2}c_{4} x^{2} + (c_{3} + c_{5} )x + c_{6}$$
$$\phi = \frac{1}{{\alpha_{4} }}\left( {\int {q{\text{d}}x^{3} } - \frac{1}{2}\alpha_{2} c_{3} x^{2} } \right) + c_{4} x + c_{5}$$

3.2 Free vibration

As can be seen from Eq. (22), the equilibrium equations of one-dimensional microbeams for the free vibration problem are

$$\alpha_{1} u_{,xx} + f = m_{0} (\ddot{u} - l_{v}^{2} \ddot{u}_{,xx} )$$
(47)
$$\alpha_{2} ( - \phi_{,x} + w_{,xx} ) - \alpha_{3} (\phi_{,xxx} + w_{,xxxx} ) + \frac{1}{2}c_{,x} + q = m_{0} (\ddot{w} - l_{v}^{2} \ddot{w}_{,xx} )$$
$$\alpha_{4} \phi_{,xx} + \alpha_{3} (\phi_{,xx} + w_{,xxx} ) + \alpha_{2} ( - \phi + w_{,x} ) - \frac{1}{2}c = m_{0} l_{v}^{2} \ddot{\phi } + m_{2} (\ddot{\phi } - l_{v}^{2} \ddot{\phi }_{,xx} )$$

Let all external forces vanished (i.e., f = 0, q = 0, c = 0, \(\overline{N }=0\), \(\overline{V }=0\), \(\overline{M }=0\)). Because f = 0, for any x ϵ [0, L], there is u = u(x, t) = 0, the first formula in Eq. (47) is satisfied, and for w = w(x, t), φ = φ(x, t) consider the following expression:

$$w = w_{0} w_{s} (x)e^{{i\omega_{n} t}} \begin{array}{*{20}c} {} & {} \\ \end{array} \phi = \phi_{0} \phi_{s} (x)e^{{i\omega_{n} t}}$$
(48)

where w0, φ0 are the unknown coefficients and ws, φs are the static solutions of the microbeam (ws = ws(x), φs = φs(x)).

Substituting Eq. (48) into Eq. (47) leads to the following system of algebraic equations:

$$- (\alpha_{2} \phi_{s}^{{\prime\prime\prime}} + \alpha_{3} \phi_{s}^{{\prime\prime\prime}} )\phi_{0} + 2[\alpha_{2} w_{s}^{{\prime\prime}} - \alpha_{3} w_{s}^{{\prime\prime\prime\prime}} + m_{0} (w_{s} - l_{v}^{2} w_{s}^{{\prime\prime}} )\omega_{n}^{2} ]w_{0} = 0$$
(49)
$$\{ (\alpha_{4} + \alpha_{3} )\phi_{s}^{{\prime\prime}} - \alpha_{2} \phi_{s} + [(m_{0} l_{v}^{2} + m_{2} )\phi_{s} - m_{2} l_{v}^{2} \phi_{s}^{{\prime\prime}} ]\omega_{n}^{2} \} \phi_{0} + 2(\alpha_{3} w_{s}^{{\prime\prime\prime}} + \alpha_{2} w_{s}{\prime} )w_{0} = 0$$

Rewrite Eq. (49) in the form of a matrix expression

$$\begin{gathered} \left[ {\begin{array}{*{20}c} { - \alpha_{2} \phi_{s}{\prime} - \alpha_{3} \phi_{s}^{{\prime\prime\prime}} } \\ {(\alpha_{4} + \alpha_{3} )\phi_{s}^{{\prime\prime}} - \alpha_{2} \phi_{s} + [(m_{0} l_{v}^{2} + m_{2} )\phi_{s} - m_{2} l_{v}^{2} \phi_{s}^{{\prime\prime}} ]\omega_{n}^{2} } \\ \end{array} } \right. \hfill \\ \left. {\begin{array}{*{20}c} {2[\alpha_{2} w_{s}^{{\prime\prime}} - \alpha_{3} w_{s}^{{\prime\prime\prime\prime}} + m_{0} (w - l_{v}^{2} w_{s}^{{\prime\prime}} )\omega_{n}^{2} ]} \\ {2(\alpha_{3} w_{s}^{{\prime\prime\prime}} + \alpha_{2} w_{s}{\prime} )} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\phi_{0} } \\ {w_{0} } \\ \end{array} } \right\} = 0 \hfill \\ \end{gathered}$$
(50)

If the equation has a nonzero solution, then the determinant of the coefficient matrix is required to be 0, that is,

$$S_{2} \omega_{n}^{4} + S_{1} \omega_{n}^{2} + S_{0} = 0$$
(51)

where

$$S_{2} = - 2m_{0} (w - l_{v}^{2} w_{s} ^{\prime\prime})[(m_{0} l_{v}^{2} + m_{2} )\phi_{s} - m_{2} l_{v}^{2} \phi_{s} ^{\prime\prime}]$$
(52)
$$\begin{aligned} S_{1} = & - 2(\alpha_{4} + \alpha_{3} )\phi_{s} ^{\prime\prime}m_{0} (w_{s} - l_{v}^{2} w_{s} ^{\prime\prime}) + 2\alpha_{2} \phi_{s} m_{0} (w_{s} - l_{v}^{2} w_{s} ^{\prime\prime}) \\ & \quad - 2\alpha_{2} w_{s} ^{\prime\prime}[(m_{0} l_{v}^{2} + m_{2} )\phi_{s} - m_{2} l_{v}^{2} \phi_{s} ^{\prime\prime}] + 2\alpha_{3} w_{s} ^{\prime\prime\prime\prime}[(m_{0} l_{v}^{2} + m_{2} )\phi_{s} - m_{2} l_{v}^{2} \phi_{s} ^{\prime\prime}] \\ \end{aligned}$$
$$\begin{aligned} S_{0} = & - 2(\alpha_{2} \phi_{s}{\prime} + \alpha_{3} \phi_{s}^{{\prime\prime\prime}} )(\alpha_{3} w_{s}^{{\prime\prime\prime}} + \alpha_{2} w_{s}^{{\prime\prime}} ) - 2\alpha_{2} (\alpha_{4} + \alpha_{3} )\phi_{s}^{{\prime\prime}} w_{s}^{{\prime\prime}} \\ & \quad + 2\alpha_{3} (\alpha_{4} + \alpha_{3} )\phi_{s}^{{\prime\prime}} w_{s}^{{\prime\prime\prime\prime}} + \alpha_{2} \phi_{s} (\alpha_{2} w_{s}^{{\prime\prime}} - \alpha_{3} w_{s}^{{\prime\prime\prime\prime}} ) \\ \end{aligned}$$

The solution of Eq. (51) can be solved

$$\omega_{n}^{2} = \frac{{ - S_{1} \pm \sqrt {S_{1}^{2} - 4S_{0} S_{2} } }}{{2S_{2} }}$$
(53)

The sign ( ±) in the formula is always selected to take the smallest value.

3.3 Boundary conditions

This section will give the boundary conditions for the case of simply support at both ends (S–S), clamped support at both ends (C–C), and clamped support at left ends and simply support at the right end (C–S). Since axial forces have little effect on static bending problems, axial problems are not considered next.

(i) For S–S, the boundary conditions can be identified as

$$w|_{x = 0} = w|_{x = L} = 0,\quad Y|_{x = 0} = Y|_{x = L} = 0,\quad M|_{x = 0} = M|_{x = L} = 0$$
(54)

In terms of φ and w, Eqs. (47) become after using Eqs. (20)

$$w^{\prime\prime}|_{x = 0} = w^{\prime\prime}|_{x = L} = 0,\quad \phi ^{\prime}|_{x = 0} = \phi |_{x = L} = 0$$
(55)

this ultimately translates to

$$\gamma ^{\prime} - \theta ^{\prime} = 0,\begin{array}{*{20}c} {} \\ \end{array} \gamma ^{\prime} + \theta ^{\prime} = 0,\begin{array}{*{20}c} {} \\ \end{array} \frac{1}{2}\int {(\gamma - \theta )} {\text{d}}x + c_{8} = 0\begin{array}{*{20}c} {} \\ \end{array} {\text{at}}\begin{array}{*{20}c} {} \\ \end{array} x = 0,L$$
(56)

(ii) For C–C, the boundary conditions can be identified as

$$w|_{x = 0} = w|_{x = L} = 0,\quad \phi |_{x = 0} = \phi |_{x = L} = 0,\quad w^{\prime}|_{x = 0} = w^{\prime}|_{x = L} = 0$$
(57)

; this ultimately translates to

$$\frac{1}{2}\int {(\gamma - \theta )} {\text{d}}x + c_{8} = 0,\begin{array}{*{20}c} {} \\ \end{array} - \frac{1}{2}(\gamma + \theta ) = 0,\begin{array}{*{20}c} {} \\ \end{array} \frac{1}{2}(\gamma - \theta ) = 0\begin{array}{*{20}c} {} \\ \end{array} {\text{at}}\begin{array}{*{20}c} {} \\ \end{array} x = 0,L$$
(58)

(iii) For C–S, the boundary conditions can be identified as

$$w|_{x = 0} = w|_{x = L} = 0,\quad \phi |_{x = 0} = 0,\quad w^{\prime}|_{x = 0} = 0,\quad w^{\prime\prime}|_{x = L} = 0,\quad \phi ^{\prime}|_{x = L} = 0$$
(59)

; this ultimately translates to

$$\begin{array}{*{20}l} {\frac{1}{2}\int {(\gamma - \theta )} {\text{d}}x + c_{8} = 0,} \hfill & { - \frac{1}{2}(\gamma + \theta ) = 0,} \hfill & {\frac{1}{2}(\gamma - \theta ) = 0\begin{array}{*{20}c} {} \\ \end{array} {\text{at}}\begin{array}{*{20}c} {} \\ \end{array} x = 0} \hfill \\ {\frac{1}{2}\int {(\gamma - \theta )} {\text{d}}x + c_{8} = 0,} \hfill & {\gamma ^{\prime} - \theta ^{\prime} = 0,} \hfill & {\gamma ^{\prime} + \theta ^{\prime} = 0\begin{array}{*{20}c} {} \\ \end{array} {\text{at}}\begin{array}{*{20}c} {} \\ \end{array} x = L} \hfill \\ \end{array}$$
(60)

4 Numerical results

To illustrate the size-dependent and microinertia effects on statics and dynamics of the microbeam problem, some numerical results have been obtained and presented in this section. For illustration purpose, the beam considered here is taken to be made of epoxy [9, 21] and material properties used in the calculations are taken to be E = 1.44 GPa, υ = 0.38, l = 17.6 μm and the material density ρ = 1.22 × 103 kg/m3. Besides, the material length scale l relates to the characteristic size of the investigated microstructure and the parameter l can be determined by the relation l/h = 0 ~ 1.0 [46, 47]. Thus, the thickness dimension of the beam should meet h ≥ l. The geometric dimensions of the microbeam are selected as L/h = 20, b/h = 2, unless otherwise stated.

In addition, the appropriate microinertia length scale parameter lv is estimated to be equal to the order of micrometers or nanometers to be fit to the experimental results. Here, the estimated value of lv can approximately be set as 0 ≤ lv/l ≤ 1. This size is a reasonable value in accordance with the microstructure of beams.

4.1 Static analysis

To exhibit the efficiency and accuracy of the newly derived solution, some illustrative examples are solved and the results are compared with the existing data available in the literature. In this case, the present static behaviors of the Timoshenko microbeam made of epoxy are compared with those of Ma et al. [21]. Figure 2 compares the deflections and rotations of the beam predicted by the present model, literature and the classical Timoshenko beam model, respectively. It can be clearly seen that the deflection and rotation predicted by the current model are in good agreement with those predicted by Ma et al. [21] and are less than those predicted by the classical model. This shows that the newly derived solutions proposed in this paper are effective and accurate. In addition, Fig. 2 also shows that the differences in the deflection and rotation values predicted by the current model and the classical model are significantly large when the thickness of the beam is small (h = l = 17.6 μm), but they are diminishing when the thickness of the beam becomes larger (h = 2 l = 35.2 μm). It is indicated that the size-dependent effect is significant when the size of the beam is at small scale. This agrees with what was observed experimentally.

Fig. 2
figure 2

Comparison of the static deflections and rotations of the simply supported Timoshenko microbeam models

Full size image

Figure 3 shows the model’s size on the static deflections and rotations for three different boundary conditions. From the curves, it can be seen that as the thickness of the beam increases (h = l, 2 l and 4 l), the static deflections and rotations of the beam decrease significantly, i.e., the static deformations (deflection and rotation) predicted by the modified couple stress theory for the case of h = l are 1.9 and 5.6 times than those for the cases of h = 2 l and h = 4 l, respectively. This phenomenon conforms to that obtained in Fig. 2. It is indicated that size-dependent effect is very important for microstructures, and the smaller the thickness of the beam, the greater the deformations of the beam. Moreover, Fig. 3a–c shows that the deflections and rotations predicted by the modified couple stress theory solution are shown with three various boundary conditions (S–S, C–C and C–S). Figure 3 shows that the curves of deflection and rotation of the microbeam are symmetric with respect to x = L/2 with S–S and C–C, while not symmetric with C–S. It also can be seen that the difference among the three sets of predicted maximum values with three various boundary conditions is diminishing in the order from S–S, C–S to C–C. Obviously, because the two boundary conditions S–S and the C–C are symmetrical constraints at the two ends of the microbeam, the degrees of freedom at both ends are the same, so the corresponding deformations are symmetry. However, for the asymmetrical boundary conditions C-S, the degrees of freedom at two ends of the microbeam are not the same, and the degree of freedom at the right end is more than that at the left end; thus, results in its deformation peak will be closer to the right end. This agrees with what was observed experimentally. These observations indicate that the boundary condition has a very important role on the mechanical behavior of the microbeam.

Fig. 3
figure 3

Variation in static deflection and rotation for different model’s sizes and boundary conditions

Full size image

4.2 Dynamic analysis

The first natural frequency of the simply supported Timoshenko beam predicted by the current model, literature and classical model is delineated in Fig. 4 for various values of h/l. It can be seen from the figure that when the microinertia length scale parameter is set as lv = 0, the first natural frequencies predicted by the newly derived solution are consistent with those predicted by Ma et al. [21], which indicates that the newly derived solution proposed in this paper is accurate and effective. In addition, Fig. 4 shows that the first natural frequency values predicted by the current model and the classical model decrease with the increment of the thickness of the beam, but the differences in the first natural frequency values predicted by the current model and the classical model are receding when the thickness of the beam, h, is large (with h = 4 l = 70.4 um or bigger here). The observation indicates that size-dependent effect is only important for very thin beams (thickness in the micron range) and that they have an increasing impact as beam thickness decreases.

Fig. 4
figure 4

Comparison of the first natural frequency of the simply supported Timoshenko microbeam for different material length scales

Full size image

Figure 5 shows the curves of the variation in the first natural frequency of the beam with the microbeam thickness for cases of three various boundary conditions (S–S, C–C and C–S). Under the same size of the beam, the comparison of the curves in Fig. 5 shows that the condition of C–C affects the first natural frequency of the microbeam most, C-S does less, and S–S does the least. This is because of the fact that the natural frequency is dependent on the boundary condition of the model. That is, fewer constraints mean more degrees of freedom, and more degrees of freedom result in the higher natural frequency.

Fig. 5
figure 5

Variation in the first natural frequencies with three various boundary conditions

Full size image

The microinertia effect can be observed in some of dynamic analyses such as frequency dispersion analysis, especially in the crystalline solids, porous media, or any kind of materials with microstructure. Especially for microscale model, the microinertia effect cannot be negligible. In the following, the dynamic behavior versus various model sizes and boundary conditions predicted by elastic Timoshenko microbeam using the microinertia effect are investigated. Figure 6 shows the variation in the first natural frequency of the Timoshenko beam with the microinertia length scale parameter. Figure 6 shows as the ratio of the microinertia length scale parameter to the material microlength scale parameter increases, the first natural frequency declines. It is indicated that the effect of microinertia weakens the dynamic behavior of the microbeam. Thus, it is necessary to add the microinertia effect to capture the real highly dynamic behavior of microstructure-dependent model.

Fig. 6
figure 6

Variation in the first natural frequency of the Timoshenko beam with the microinertia length scale parameter

Full size image

In order to compare the form of the first natural frequency curves obtained by the present analysis with the form of the natural frequency curves provided by the newly derived solution, we consider several relations between the model’s sizes h/l and the boundary conditions (S–S, C–C and C–S). Here, the parameter Dr is used to evaluate the impact of the microinertia effect on the dynamic behavior of the microbeam, which is defined as

$${\text{Dr}} = \left| {\frac{{\omega_{1} |_{{l_{v} = 0}} - \omega_{1} |_{{l_{v} = l}} }}{{\omega_{1} |_{{l_{v} = 0}} }}} \right| \times 100\%$$

Table 1 compares the values of Dr, respectively, predicted with various model’s sizes and boundary conditions. It is clearly observed that the value of Dr is significant when the ratio of the beam thickness to the material length scale parameter h/l is small; however, it diminishes as the ratio increases. For example, the maximum value of Dr is up to 2.32% when h/l = 1. This indicates that the microinertia effect is only significant when the size of the model is several microns or even smaller. And moreover, the effect of boundary condition on Dr is also quantitatively shown in Table 1. The numerical results displayed for the cases of three various boundary conditions, the values of Dr with C–C are larger than those with S–S and C–S, respectively. It can be inferred from this observation that the boundary condition affects the microinertia effect. As a result, it is indicated that the scale of the microinertia length scale parameters should be the same as the scale of studied structures. In other words, this parameter is a scale-dependent parameter and has a connection with the lattice structure of materials.

Table 1 Natural frequency of the S–S boundary changes with beam thickness
Full size table

5 Conclusion

This study examines the behaviors of size-dependent and microinertia used in statics and dynamics on the basis of the simplified couple stress theory. The present model contains two distinct scale parameters to describe the microstructure-dependent, the material length scale parameter and the microinertia length scale parameter. The governing equations of equilibrium and all boundary conditions for the Timoshenko beam model are developed by a combination of the basic equations and a variational statement. The closed-form analytic solutions are obtained and suitable for various formats of boundaries and mechanical loads. As an example, three boundary value problems have been considered to delineate its size-dependent static and also the free-vibration behavior. The accuracy of the analytic solutions based on the derived equations is verified by comparing with those from the literature. The results indicate that the material length scale parameter is dependent on the dimensions of the structure. For instance, this parameter is calculated for a range of beam thickness so that the larger values in the static deflections and the dynamic natural frequency are predicted for smaller the beam thickness. These results trend agree well with the size-dependent effect at the micron scale observed in experiments. According to the definition used in this study, the microinertia effect can harden dynamic behavior. It is observed that a dynamic structure with continuous increase in the microinertia length scale parameter will experience the decrease in the natural frequency predicted by the current model, especially when the structure is at micro-/nanoscale. In addition, the static and dynamic behaviors can be effectively tuned by the boundary conditions. More constraints (C–C boundary) will decrease the static deformations and increase the dynamic natural frequency, and with that contrast in constraints (S–S boundary) also comes the contrast in behavior. This work fully demonstrates the necessity of the size dependence and microinertia effects when describing the behaviors of microstructures; however, its internal mechanism is difficult to understand, and only by fully mining the size effect in the future can "size" become one of the design parameters of future technology applications.