1 Introduction

Cables are widely used in ultra-high voltage transmission lines [1], large stadiums, cable-supported bridges [2], and taut mooring systems [3]. Most of these structures are supported by multiply cables [4]. However, large-amplitude vibrations [5, 6] or even collisions [7, 8] are likely to be induced under various excitations due to their flexibilities.

The large amplitudes [9, 10] and the phase differences [11] are two key necessary conditions of cable collisions, which reflect the amplitude-frequency characteristics and the phase-frequency characteristics, respectively. Problems associated with the former have attracted much attention and have generally been well illustrated in the past few decades [12, 13]. More and more attention has been paid to the phase-frequency characteristics or phase differences. For example, Zhao [12] investigated the phase-frequency curves of the nonlinear vibration of suspended cable under the temperature effect. Benedettini and Rega’s [14] investigation of suspended cables under lateral load found that the response lags behind the excitation and that the phase difference is related to the excitation frequency. Bossens and Preumont [15] conducted a large-scale active control model test, which indicated that the phase difference between the active and the cable force also carries with the excitation frequency. Kim [16] proved that there was a phase difference between the vertical vibration of the largest cantilever end of the cable-stayed bridge and the vibration of the cable during construction. Baicu [17] conducted experiments on a horizontal suspended cable with lateral excitation applied at one end and found that its phase-frequency curve contains two peaks, a plus one and a minus one. In the research of a base excited pendulum [18], the phase is introduced in order to better predict the behavior of the system leading to detection of the slow invariant manifold and its dynamic characteristic points.

It can be seen that the phase-frequency characteristics of the suspended cable are closely related to the excitation. In summary, many investigations on the response phase of cable structures mainly focused on the phase shift value in the linear solution, that is, the \(\gamma \) in the term of \(a\cos (\Omega t-\gamma )\), where a and \(\Omega \) are the response amplitude and excitation frequency, respectively. It should be emphasized that \(\gamma \) is actually not the phase but the phase offset of the response relative to the excitation, that is, the phase difference between the response signal and the excitation signal. However, in nonlinear systems, the system response contains not only the linear solution but also the higher-order approximate terms (HOAT). Taking the Duffing oscillator as an example, the second-order asymptotic perturbation solution under harmonic excitation with a frequency \(\Omega \) close to its linear natural frequency \(\omega \) is [19]:

$$\begin{aligned} a\cos (\Omega t-\gamma )+a_{3}\cos (3\Omega t-3\gamma )=\hat{a}(t)\cos (\Omega t-\gamma +\Theta (t)), \end{aligned}$$
(1)

where \(\gamma \) is a constant, the amplitude a is a nonlinear function, which needs to be obtained by solving the modulation equations derived from perturbation analysis, \(\hat{a}(t)\) and \(\Theta (t)\) are

$$\begin{aligned}{} & {} \hat{a}(t)\equiv \sqrt{a^{2}+a^{2}_{3}+2aa_{3}\cos (2\Omega t-2\gamma )}, \end{aligned}$$
(2a)
$$\begin{aligned}{} & {} \Theta (t)\equiv \tan ^{-1}\frac{a_{3}\sin (2\Omega t-2\gamma )}{a+a_{3}\cos (2\Omega t-2\gamma )}. \end{aligned}$$
(2b)

It can be seen from Eq. (1) that the response phase and frequency are affected by the HOAT. Boashash [20] also pointed out in his investigation of multicomponent signals that the phase of a signal formed by the superposition of two cosine signals is a nonlinear combination of their phases. The classic experiment of Van der Pol [21, 22] also shows that: periodic variation of the threshold can force the system to oscillate with the frequency of variation, which can both decrease or increase the frequency of oscillation, implying the variation of the phase. Actually, these frequency- or phase-modulated characteristics are usually exist in weakly nonlinear systems subject to harmonic excitations [23,24,25,26]. In these nonlinear systems, extraction of accurate transient dynamic characteristics is especially important for in-operation damage detection, which usually uses sudden changes of vibration amplitudes or frequencies to estimate the areas subjected to unexpected sudden loads. Therefore, a more comprehensive investigation of the phase-frequency characteristics of suspended cables should also consider the influence of HOAT and examine their instantaneous phase or instantaneous phase difference.

This paper aims at making a comparison for the instantaneous phase-frequency characteristics of a suspended cable subjected to the two typical excitation types, namely the in-planar external excitation [27,28,29,30] and parametric excitation [31,32,33,34,35]. The Multiple Scales Method (MSM) is used to solve the system’s response under different parameters, and the instantaneous phases are obtained using the Hilbert transform. The distributions of the amplitudes of the phase differences between responses and excitations are compared in the (\(\lambda ^{2}-\Omega \)) plane. It was found that the instantaneous phase-frequency characteristics of suspended cable are different under the external and parametric excitation. The instantaneous phase differences originated from two aspects: one is the drift term (DT), and the other is the doubling-frequency term (DFT).

2 Mechanical model

2.1 Basic assumption

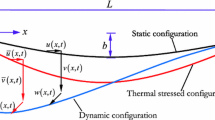
The simplified model of the suspended cable (as shown in Fig. 1) is used as the research object. Assume that the excitation frequencies of external and parametric excitation are identical, and the symbol \(\Omega \) is applied to represent their excitation frequency. Set \(F_{1}\) as the external excitation amplitude in the suspended cable model, and \(u_{b}\), \(v_{b}\), \(U_{b}(t)\), and \(V_{b}(t)\) as horizontal excitation amplitude, vertical excitation amplitude, horizontal displacement, and vertical displacement under the in-plane parametric excitation. l and d denote the cable length and sag, respectively. Considering the direction consistency of suspended cable vibration and parametric excitation, it is only necessary to establish a local vibration coordinate system \(o-xy\), where the origin o is the left anchorage point, x is the suspended cable direction coordinate, and y is the downward coordinate of the vertical suspended cable in the cable plane. The corresponding displacements in each direction are denoted by u and v, respectively. The following assumptions are also adopted:

  1. (1)

    the bending stiffness of the suspended cable is small enough to be neglected;

  2. (2)

    the suspended cable is a tensile only element;

  3. (3)

    the axial dynamic strain of the suspended cable in the vibration process is small enough;

  4. (4)

    the suspended cable is hinged at both ends.

Fig. 1
figure 1

Dynamic model of horizontal suspended cables

Full size image

2.2 Dynamic equations

Based on the Hamilton variational principle, the equation of motion is obtained by considering the geometric nonlinearity of the cable. Under the quasi-static assumption, the u axial acceleration and velocity terms are ignored, that is, the axial vibration is not considered, and then, the displacement u(x, t) is obtained by considering the boundary conditions. The equation is reduced to obtain the nonlinear dynamic equilibrium equation of in-plane external excitation as follows [30]:

$$\begin{aligned} \ddot{v} + c\dot{v} - \frac{{v''}}{{{\pi ^2}}} - \frac{\alpha }{{{\pi ^2}}}\left( {y'' + v''} \right) \int _{0}^1 \left( y'v'+\frac{v'^2}{2}\right) {\textrm{d}}x= F_{1}\cos {\Omega }t, \end{aligned}$$
(3)

where \(F_{1}\) is the external excitation amplitude and  \(\Omega \) is the external excitation frequency. The nondimensional static profile of the cable is \(y(x)=4b x(1-x)\), where the symbol b is the sag-to-span ratio. The following variables are used in the nondimensional process with the omission of the asterisks to simplify the expression of Eq. (3).

$$\begin{aligned} \begin{aligned}&{}x^*=\frac{x}{l},~y^*=\frac{y}{l},~v^*=\frac{v}{l},~\alpha =\frac{EA}{H},\\&{}t^*=\frac{\pi }{l}\sqrt{\frac{H}{m}}t,~U_{b}(t)^*=\frac{U_{b}(t)}{l},~c^*=\frac{l}{\pi }\sqrt{\frac{1}{mH}}c, \end{aligned} \end{aligned}$$
(4)

where a prime represents the derivative with respect to the coordinate x, and a dot represents the derivative with respect to time t; m is the mass per unit length of the cable; c is the damping coefficient;\(H=mgl^{2}/(8d)\) is the cable force; E is the elastic modulus; A is the cross-sectional area.

In the same way, the nonlinear dynamic equation under the in-plane parametric excitation can be obtained as follows [36]:

$$\begin{aligned} \ddot{v}+c\dot{v}-\frac{v''}{\pi ^2}-\frac{\alpha }{\pi ^2}\left( y''+v''\right) \left[ U_{b}(t)+\int _{0}^1 \left( y'v'+\frac{v'^2}{2}\right) {\textrm{d}}x\right] =0, \end{aligned}$$
(5)

where \(U_b(t)\) is the parametric excitation as shown in Fig. 1b.

2.3 Discretization model

2.3.1 External excitation

The vibration model under distributed excitation is shown in Fig. 1a, and the boundary conditions of the suspended cable are as follows:

$$\begin{aligned} v(0,t)=0,v(l,t)=0. \end{aligned}$$
(6)

Under the action of external excitation, the suspended cable vibration displacement is considered to be caused by pure modal vibration, so let:

$$\begin{aligned} v(x,~t)=\sum _{n=1}^N\eta _{n}\left( t\right) \phi _{n}\left( x\right) , \end{aligned}$$
(7)

where the anti-symmetric (n=even) mode shape is given by

$$\begin{aligned} \phi _n(x)=\sqrt{2}\sin (\omega _n\pi x),\quad \omega _n=2,4,6,\ldots \end{aligned}$$
(8)

and the symmetric (\(n={\text {odd}}\)) mode shape is given by

$$\begin{aligned} \phi _n(x)=k_n\left[ \cos (\omega _n\pi x)-1+\tan \Big (\frac{\omega _n\pi }{2}\Big )\sin (\omega _n\pi x)\right] ,\quad \omega _n=1,3,5,\ldots , \end{aligned}$$
(9)

where \(k_n\) and \(\omega _n\) is determined by the normalization condition, which yields

$$\begin{aligned}{} & {} k_n=\sqrt{\frac{2\omega _n\pi \cos ^2\Big (\frac{\omega _n\pi }{2}\Big )}{(2+\cos \omega _n\pi )\omega _n\pi -3\sin \omega _n\pi }}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \tan \Big (\frac{\omega _n\pi }{2}\Big )=\frac{\omega _n\pi }{2}-\frac{1}{16\alpha b^2}\left( \frac{\omega _n\pi }{2}\right) ^3. \end{aligned}$$
(11)

The Galerkin method is used for modal truncation to obtain the discrete model as [37]:

$$\begin{aligned} \begin{aligned} \ddot{\eta _k}+2\mu _{vk}\dot{\eta _k}+\omega _{k}^2\eta _k&= \frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \left( U_kP_{nr}+2U_rP_{nk}\right) \eta _n\eta _r\\&\qquad -\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \sum _{j=1}^N P_{nk}P_{rj}\eta _n\eta _r\eta _j+f_{1k}\left( t\right) , \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} f_{1n}\left( t\right) =f_{1}\left( t\right) \int _{0}^{1}\phi _n{\textrm{d}}x= \left\{ \begin{aligned}&{}-\frac{k_n\omega _n^2\pi ^2}{64\alpha b^{2}}f_{1}\left( t\right){} & {} {}\textrm{for}~n={\textrm{odd}},\\&{}~0{} & {} {}\textrm{for}~n=\textrm{even}. \end{aligned} \right. \end{aligned}$$
(13)

2.3.2 Parametric excitation

The vibration model under parametric excitation is shown in Fig. 1b, and the boundary conditions of the suspended cable are as follows:

$$\begin{aligned} v(0,t)=0,v(l,t)=V_{b}(t). \end{aligned}$$
(14)

Under the parametric excitation, the vibration displacement of the suspended cable is considered to be generated by pure modal vibration and static displacement, so let:

$$\begin{aligned} \begin{aligned} v(x,~t)=\sum _{n=1}^N \eta _{n}\left( t\right) \phi _{n}\left( x\right) +V_b(t)x. \end{aligned} \end{aligned}$$
(15)

The Galerkin method is used for modal truncation to obtain [38]:

$$\begin{aligned} \begin{aligned} \ddot{\eta _k}+2\mu _{vk}\dot{\eta _k}+\omega _{k}^2\eta _k&= \frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \left( U_kP_{nr}+2U_rP_{nk}\right) \eta _n\eta _r\\&\qquad -\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \sum _{j=1}^N P_{nk}P_{rj}\eta _n\eta _r\eta _j\\&\qquad -\frac{\alpha }{2\pi ^2}\sum _{n=1}^N P_{nk}\eta _n\Delta \\&\qquad +\frac{\alpha }{2\pi ^2}U_k\Delta -\ddot{R_v}-2\mu _{vk}\dot{R_v}, \end{aligned} \end{aligned}$$
(16)

where \(k=1,2,3,\ldots ,\mu =2\int _{0}^{1}c\phi _{k}^2{\textrm{d}}x\), and

$$\begin{aligned}&U_n=\int _{0}^{1}\phi _ny''{\textrm{d}}x= \left\{ \begin{aligned}&{}\frac{k_n\omega _n^2\pi ^2}{8\alpha b}{} & {} {}\textrm{for}~n={\textrm{odd}},\\&{}~0{} & {} {}\textrm{for}~n=\textrm{even}; \end{aligned} \right. \end{aligned}$$
(17)
$$\begin{aligned}&P_{rj}=\int _{0}^{1}\phi _r'\phi _j'{\textrm{d}}x= \left\{ \begin{aligned}&{}-\frac{k_rk_j\omega _r^2\omega _j^2\pi ^4}{64\alpha b^2}{} & {} {}\textrm{for}~r,j={\textrm{odd}},~{\textrm{and}}~r\ne j,\\&{}\frac{k_r^2\omega _r\pi \left[ \omega _r\pi -\sin (\omega _r\pi )\right] }{2\cos ^2(\omega _r\pi /2)}{} & {} {}\textrm{for}~r=j={\textrm{odd}},\\&{}\omega _r^2\pi ^2{} & {} {}\textrm{for}~r=j=\textrm{even},\\&{}0{} & {} {}{\mathrm {for~other~cases}}; \end{aligned} \right. \end{aligned}$$
(18)
$$\begin{aligned}&\Delta =2\left[ U_b(t)\right] +\left[ V_b(t)\right] ^2; \end{aligned}$$
(19)
$$\begin{aligned}&R_v=\displaystyle \int _{0}^{1}\left[ V_b(t)x\right] \phi _k{\textrm{d}}x. \end{aligned}$$
(20)

3 Multiple scale analysis

As the dynamical systems have distinct characteristic physical behavior at different lengths or “slow”/ “fast” time scales, following the MSM, a small bookkeeping parameter \(\varepsilon \) is used. To analyze the primary resonance, we need to reorder the damping, the nonlinearity, and the excitation terms so that they can appear at the same time in the perturbation scheme, and an approximate solution is obtained based on the MSM [23]:

$$\begin{aligned} \eta _k(t;~\varepsilon )\simeq \varepsilon \eta _{k1}(T_0,~T_1,~T_2) +\varepsilon ^2\eta _{k2}(T_0,~T_1,~T_2)+\varepsilon ^3\eta _{k3}(T_0,~T_1,~T_2), \end{aligned}$$
(21)

where the multiple time scales are defined by \(T_n=\varepsilon ^n t\). The first and second derivatives with respect to time are

$$\begin{aligned}{} & {} \frac{{\textrm{d}}}{{\textrm{d}}t}=D_0+\varepsilon D_1+\varepsilon ^2D_2+\cdots , \end{aligned}$$
(22a)
$$\begin{aligned}{} & {} \frac{{\textrm{d}}^2}{{\textrm{d}}t^2}=D_0^2+2\varepsilon D_0D_1+\varepsilon ^2(D_1^2+2D_0D_2)+\cdots , \end{aligned}$$
(22b)

where \(D_n\equiv \partial /\partial T_n\).

3.1 External excitation

Setting \(f_{jk}(t)\) to the order of \(O(\varepsilon ^3)\). Besides, the damping terms are also perturbed to the order of \(O(\varepsilon ^2)\), that is \(\mu \rightarrow \varepsilon ^2\mu \). Sorting by the power of \(\varepsilon \), get the in-plane equation [37]:

Order \(\varepsilon \)::
$$\begin{aligned} D_0^2\eta _{k1}+\omega _k^2\eta _{k1}=0, \end{aligned}$$
(23)
Order \(\varepsilon ^2\)::
$$\begin{aligned} \begin{aligned} D_0^2\eta _{k2}+\omega _k^2\eta _{k2}=&{}-2D_0D_1\eta _{k1}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N\left( U_kP_{nr}+2U_rP_{nk}\right) \eta _{n1}\eta _{r1},\\ \end{aligned} \end{aligned}$$
(24)
Order \(\varepsilon ^3\)::
$$\begin{aligned} \begin{aligned} D_0^2\eta _{k3}+\omega _k^2\eta _{k3}=&{}-2D_0D_1\eta _{k2}-2D_0D_2\eta _{k1}-2\mu _vD_0\eta _{k1}-D_1^2\eta _{k1}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \left( U_kP_{nr}+2U_rP_{nk}\right) \left( \eta _{n1}\eta _{r2}+\eta _{n2}\eta _{r1}\right) \\&{}-\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \sum _{j=1}^N P_{nk}P_{rj}\eta _{n1}\eta _{r1}\eta _{j1}-f_{1k}\left( T_{0}\right) . \end{aligned} \end{aligned}$$
(25)

We considering the primary resonance [39], and set

$$\begin{aligned}{} & {} \Omega =\omega +\varepsilon \sigma , \end{aligned}$$
(26a)
$$\begin{aligned}{} & {} \eta _{m1}=A_m(T_1,T_2)e^{i\omega _mT_0}+cc, \end{aligned}$$
(26b)
$$\begin{aligned}{} & {} \eta _{k1}=0\quad \forall \; k \ne m, \end{aligned}$$
(26c)
$$\begin{aligned}{} & {} f_{1k}\left( T_{0}\right) =F_{1}\cos {\Omega T_{0}}\quad \forall \; k, \end{aligned}$$
(26d)

where cc represents the complex conjugate of the preceding terms. Substituting Eq. (26) into Eq. (24) and eliminating the secular terms yields

$$\begin{aligned} \begin{aligned} D_1A_m=0. \end{aligned} \end{aligned}$$
(27)

The solution of \(\eta _{k2}\) is

$$\begin{aligned} \eta _{k2}=E_{1k}(A_m^2e^{2i\omega _mT_0}+cc)+E_{2k}A_m\bar{A}_m\quad \forall \; k. \end{aligned}$$
(28)

Substituting Eqs. (26) and (28) into Eq. (25), and setting \(k=m\) yields

$$\begin{aligned} \begin{aligned} D_0^2\eta _{m3}+\omega _m^2\eta _{m3}=&{}-2D_0D_2\eta _{m1}-2\mu _vD_0\eta _{m1}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{r=1}^N \left( U_mP_{mr}+2U_rP_{mm}\right) \eta _{m1}\eta _{r2}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \left( U_mP_{nm}+2U_mP_{nm}\right) \eta _{m1}\eta _{n2}\\&{}-\frac{\alpha }{2\pi ^2}P_{mm}^2\eta _{m1}^3 -F_{1}\cos {\Omega T_{0}}. \end{aligned} \end{aligned}$$
(29)

Then, substituting Eq. (27), \(\eta _{m1}\) and \(\eta _{k2}\) in Eq. (29), eliminating the secular terms from \(\eta _{m3}\), and introducing the detuning parameter, one obtains

$$\begin{aligned} 2i\omega _m\Big (\frac{{\textrm{d}}A_m}{{\textrm{d}}t}+\mu _{1m}A_m\Big ) +\Gamma _{em}A_m^2\bar{A}_m=\frac{1}{2}F_{1}e^{i\sigma T_{1}}, \end{aligned}$$
(30)

where

$$\begin{aligned} \Gamma _{em}=\frac{3\alpha }{2\pi ^2}P_{mm}^2-\frac{\alpha ^2}{2\pi ^4} \sum _{r=1}^{N}(U_rP_{mm}+2U_mP_{mr})^2\frac{3\omega _r^2-8\omega _m^2}{\omega _r^2(\omega _r^2-4\omega _m^2)}. \end{aligned}$$
(31)

Expressing the complex function \(A_m\) in polar form as

$$\begin{aligned} A_m=\frac{1}{2}a_me^{i\beta _m}. \end{aligned}$$
(32)

Substituting Eq. (32) into Eq. (30) and separating real and imaginary parts yield

$$\begin{aligned}{} & {} \omega _ma_m'+2\omega _m\mu _ma_m- \left( \frac{1}{2}\right) F_{1}\sin (\gamma )=0, \end{aligned}$$
(33a)
$$\begin{aligned}{} & {} \omega _ma_m\gamma '-\omega _ma_m\sigma +\Gamma _{em}a_m^3/8- \left( \frac{1}{2}\right) F_{1}\cos (\gamma )=0, \end{aligned}$$
(33b)

where \(\gamma =\varepsilon \sigma t-\beta _m\). The steady-state solutions can be found by sets \(a_m'=0\) and \(\gamma '=0\), and one obtains

$$\begin{aligned}{} & {} \omega _m\mu _ma_m- \left( \frac{1}{2}\right) F_{1}\sin (\gamma )=0, \end{aligned}$$
(34a)
$$\begin{aligned}{} & {} -\omega _ma_m\sigma +\Gamma _{em}a_m^3/8- \left( \frac{1}{2}\right) F_{1}\cos (\gamma )=0. \end{aligned}$$
(34b)

Following Eq. (34), one obtains the frequency-response equation as:

$$\begin{aligned} \begin{aligned} (\omega _m\mu _v)^2a_m^2+\left( \frac{1}{8}\Gamma _{em}a_m^2-\omega _m\sigma \right) ^2a_m^2 =\frac{1}{4}F_{1}^2, \end{aligned} \end{aligned}$$
(35)

Using Eqs. (26), (28), and (32), the two-term expansion of the solution of Eq. (21) is

$$\begin{aligned} \eta _{m}=\varepsilon a_m\cos (\Omega t-\gamma ) +\frac{1}{2}\varepsilon ^2a_m^2\sum _{r=\textrm{odd}}^{N}\left[ E_{1r}\cos (2\Omega t-2\gamma )+\frac{1}{2}E_{2r}\right] +O(\varepsilon ^3). \end{aligned}$$
(36)

3.2 Parametric excitation

Set \(U_b\) and \(V_b\) to the order of \(O(\varepsilon ^2)\), assuming that the support excitation amplitudes of all directions are in the same order of magnitude. Besides, the damping terms are also perturbed to the order of \(O(\varepsilon ^2)\), that is \(\mu \rightarrow \varepsilon ^2\mu \). Sorting by the power of \(\varepsilon \), the in-plane equation can be obtained [38]:

Order \(\varepsilon \)::
$$\begin{aligned} D_0^2\eta _{k1}+\omega _k^2\eta _{k1}=0, \end{aligned}$$
(37)
Order \(\varepsilon ^2\)::
$$\begin{aligned} \begin{aligned} D_0^2\eta _{k2}+\omega _k^2\eta _{k2}=&{}-2D_0D_1\eta _{k1}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N\left( U_kP_{nr}+2U_rP_{nk}\right) \eta _{n1}\eta _{r1}\\&{}+\frac{\alpha }{\pi ^2}U_kU_b(t)-\ddot{R_v}, \end{aligned} \end{aligned}$$
(38)
Order \(\varepsilon ^3\)::
$$\begin{aligned} \begin{aligned} D_0^2\eta _{k3}+\omega _k^2\eta _{k3}=&{}-2D_0D_1\eta _{k2}-2D_0D_2\eta _{k1}-2\mu _vD_0\eta _{k1}-D_1^2\eta _{k1}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \left( U_kP_{nr}+2U_rP_{nk}\right) \left( \eta _{n1}\eta _{r2}+\eta _{n2}\eta _{r1}\right) \\&{}-\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \sum _{r=1}^N \sum _{j=1}^N P_{nk}P_{rj}\eta _{n1}\eta _{r1}\eta _{j1} -\frac{\alpha }{2\pi ^2}\sum _{n=1}^N P_{nk}\eta _{n1}U_b(t), \end{aligned} \end{aligned}$$
(39)

and set

$$\begin{aligned}{} & {} \Omega =\omega +\varepsilon \sigma \end{aligned}$$
(40a)
$$\begin{aligned}{} & {} \eta _{m1}=A_m(T_1,T_2)e^{i\omega _mT_0}+cc, \end{aligned}$$
(40b)
$$\begin{aligned}{} & {} \eta _{k1}=0\quad \forall \; k \ne m, \end{aligned}$$
(40c)

where cc represents the complex conjugate of the preceding terms. Substituting Eq. (40) in Eq. (38), and eliminating the secular terms yields

$$\begin{aligned} \begin{aligned} -2i\omega _mD_1A_m+f_{2}e^{i(\sigma T_1)}=0, \end{aligned} \end{aligned}$$
(41)

where \(f_{2}\) is the term associated with the parametric excitation

$$\begin{aligned} \begin{aligned} f_{2}=\frac{\alpha }{2\pi ^2}U_ku_b+\frac{\Omega ^2}{2}V, \end{aligned} \end{aligned}$$
(42)

and

$$\begin{aligned} V=v_b\int _{0}^{1}x\phi _n{\textrm{d}}x= \left\{ \begin{aligned}&{}-\frac{k_n\omega _n^2\pi ^2}{128\alpha b^2}v_b{} & {} {}\textrm{for}~n={\textrm{odd}},\\&{}~-\frac{\sqrt{2}}{\omega _n\pi }v_b{} & {} {}\textrm{for}~n=\textrm{even}. \end{aligned} \right. \end{aligned}$$
(43)

The solution of \(\eta _{k2}\) is

$$\begin{aligned} \eta _{k2}=E_{1k}(A_m^2e^{2i\omega _mT_0}+cc)+E_{2k}A_m\bar{A}_m\quad \forall \; k, \end{aligned}$$
(44)

where

$$\begin{aligned}{} & {} E_{1k}=\frac{\alpha }{2\pi ^2}\left( \frac{U_kP_{mm}+2U_mP_{mk}}{\omega _k^2-4\omega _m^2}\right) , \end{aligned}$$
(45a)
$$\begin{aligned}{} & {} E_{2k}=\frac{\alpha }{\pi ^2}\left( \frac{U_kP_{mm}+2U_mP_{mk}}{\omega _k^2}\right) . \end{aligned}$$
(45b)

Substituting Eqs. (40) and (44) into Eq. (39) and setting \(k=m\) yields

$$\begin{aligned} \begin{aligned} D_0^2\eta _{m3}+\omega _m^2\eta _{m3}=&{}-2D_0D_1\eta _{m2}-2D_0D_2\eta _{m1}-2\mu _vD_0\eta _{m1}-D_1^2\eta _{m1}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{r=1}^N \left( U_mP_{mr}+2U_rP_{mm}\right) \eta _{m1}\eta _{r2}\\&{}+\frac{\alpha }{2\pi ^2}\sum _{n=1}^N \left( U_mP_{nm}+2U_mP_{nm}\right) \eta _{m1}\eta _{n2}\\&{}-\frac{\alpha }{2\pi ^2}P_{mm}^2\eta _{m1}^3 -\frac{\alpha }{2\pi ^2}P_{mm}\eta _{m1}u_be^{i\Omega t}. \end{aligned} \end{aligned}$$
(46)

Then, substituting \(\eta _{m1}\) and \(\eta _{k2}\) in Eq. (46), eliminating the secular terms from \(\eta _{m3}\), and introducing the detuning parameter, one obtains

$$\begin{aligned} 2i\omega _m(D_2A_m+\mu _vA_m)+D_1^2A_m+\Gamma _{em}A_m^2\bar{A}_m=0, \end{aligned}$$
(47)

where

$$\begin{aligned} \Gamma _{em}=\frac{3\alpha }{2\pi ^2}P_{mm}^2-\frac{\alpha ^2}{2\pi ^4} \sum _{r=1}^{N}(U_rP_{mm}+2U_mP_{mr})^2\frac{3\omega _r^2-8\omega _m^2}{\omega _r^2(\omega _r^2-4\omega _m^2)}. \end{aligned}$$
(48)

From Eq. (41), one obtains

$$\begin{aligned} D_1^2A_m=\frac{\sigma }{2\omega _m}f_{2}e^{i(\sigma T_1)}. \end{aligned}$$
(49)

Substituting \(D_1^2A_m\) in Eq. (47) yields

$$\begin{aligned} 2i\omega _m(D_2A_m+\mu _vA_m)+\frac{\sigma }{2\omega _m}f_{2}e^{i(\sigma T_1)}+\Gamma _{em}A_m^2\bar{A}_m=0. \end{aligned}$$
(50)

It can be easily verified that Eqs. (41) and (50) are the first two terms in a multiple scales expansion of

$$\begin{aligned} 2i\omega _m\Big (\frac{{\textrm{d}}A_m}{{\textrm{d}}t}+\varepsilon ^2\mu _vA_m\Big ) +\varepsilon \left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) f_{2}e^{i(\varepsilon \sigma t)}+\varepsilon ^2\Gamma _{em}A_m^2\bar{A}_m=0. \end{aligned}$$
(51)

Substituting Eq. (32) in Eq. (51) and separating the real and imaginary parts yields

$$\begin{aligned}{} & {} \omega _ma_m'+\varepsilon ^2\omega _m\mu _va_m+ \varepsilon \left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) f_{2}\sin (\gamma )=0, \end{aligned}$$
(52a)
$$\begin{aligned}{} & {} \omega _ma_m\gamma '-\varepsilon \omega _ma_m\sigma +\varepsilon ^2\Gamma _{em}a_m^3/8+ \varepsilon \left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) f_{2}\cos (\gamma )=0, \end{aligned}$$
(52b)

where \(\gamma =\varepsilon \sigma t-\beta _m\). The steady-state solutions can be found by setting \(a_m'=0\) and \(\gamma '=0\), and one obtains

$$\begin{aligned}{} & {} \varepsilon \omega _m\mu _va_m+ \left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) f_{2}\sin (\gamma )=0, \end{aligned}$$
(53a)
$$\begin{aligned}{} & {} -\omega _ma_m\sigma +\varepsilon \Gamma _{em}a_m^3/8+ \left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) f_{2}\cos (\gamma )=0. \end{aligned}$$
(53b)

Following Eq. (53), one obtains the frequency-response equation as:

$$\begin{aligned} \begin{aligned} (\varepsilon \omega _m\mu _v)^2a_m^2+\left( \frac{1}{8}\varepsilon \Gamma _{em}a_m^2-\omega _m\sigma \right) ^2a_m^2=\left( \frac{\varepsilon \sigma }{2\omega _m}-1\right) ^2f_{2}^2, \end{aligned} \end{aligned}$$
(54)

Using Eqs. (40), (44), and (32), the two-term expansion of the solution of Eq. (21) is

$$\begin{aligned} \begin{aligned} \eta _{m}&{}=\varepsilon a_m\cos (\Omega t-\gamma )\\&{}+\frac{1}{2}\varepsilon ^2a_m^2\sum _{r=\textrm{odd}}^{N}\left[ E_{1r}\cos (2\Omega t-2\gamma )+\frac{1}{2}E_{2r}\right] +O(\varepsilon ^3).\\ \end{aligned} \end{aligned}$$
(55)

4 Analysis of the instantaneous phase

In order to study the phase-frequency characteristics of suspended cable under the presence of DT and DFT, numerical analysis is carried out on the suspended cable under external and parametric excitation, respectively. The cable parameters are shown in Table 1.

Table 1 Cable parameters [40]
Full size table

4.1 Time history curves

The dimensionless external excitation frequency \(\Omega =1.0\) and amplitude \(F_{1}=0.01\) are taken as an example to illustrate the effect of HOAT on the response time history curves. The response under various \(\lambda ^2\) are calculated, and Fig. 2 shows the response time history curves of the suspended cable when \(\lambda ^2\) is 3.91, 3.07, 2.68, respectively.

Fig. 2
figure 2

Time history curves for different \(\lambda ^{2}\)

Full size image

It can be seen from Fig. 2a that there is a downward drift in the time history curves under each \(\lambda ^2\), which is caused by the DT. By comparing the time history curves under each \(\lambda ^2\) in Fig. 2a, it can be observed that when \(\lambda ^2= 3.91\), there are many minimum of the response amplitude. Compared with the peak on curve of \(\lambda ^2= 2.68\) and \(\lambda ^2= 3.91\) in Fig. 2a, that of the \(\lambda ^2= 3.91\) is relatively flat. At the same time, it can be observed from Fig. 2b when \(\lambda ^2= 3.07\), the curve changes more obviously. The whole curve moves down to the negative axis, and the subordinate peaks stand out more apparently. The reason is that the DFT under the \(\lambda ^2\) parameters has a greater impact on the cable vibration responses.

4.2 The instantaneous phase

Obviously, the phase varies as the change of time history curves’ profile, and the phase is different at different times. Thus, the Hilbert transform is used to resolve the instantaneous phases. The in-plane solution \(\eta _{i}(t)\) is transformed to obtain the phase shift \({{\tilde{\eta }}}_{i}(t)\) of 90 degrees, and the transformation is as follows:

$$\begin{aligned} {\tilde{\eta }}_{i}(t)=H{\eta _{i}}=h(t)\times \eta _{i} =\int _{-\infty }^{\infty }\eta _{i}(\tau )h(t-\tau ){\textrm{d}}\tau =\frac{1}{\pi }\int _{-\infty }^{\infty }\frac{\eta _{i}(\tau )}{t-\tau }{\textrm{d}}\tau , \end{aligned}$$
(56)

where \(h(t)=\frac{1}{\pi t}\).

The Hilbert transform means that the response solution \(\eta _{i}(t)\) is passed through a linear system with impulse response \(h(t)=\frac{1}{\pi t}\) to output response \({\tilde{\eta }}_{i}(t)\), which keeps the amplitude of each frequency component unchanged in the frequency domain, but the phase is shifted by 90 degrees. The complex solution \(\eta _{i}\) can be represented by the real solution \(\eta _{i}(t)\) and the transformed solution \({\tilde{\eta }}_{i}(t)\), that is, \(\eta _{i}=\eta _{i}(t)+i{\tilde{\eta }}_{i}(t)\). To facilitate the calculation of the instantaneous phase, a three-dimensional curve as shown in Fig. 3 is plotted here with time as the abscissa, \(\eta _{i}(t)\) as the ordinate, and \({\tilde{\eta }}_{i}(t)\) as the vertical coordinate. The angle between the line connecting any point on the curve to the origin and the positive direction of the abscissa is the instantaneous phase \(\theta \mathrm{{ = }}\arctan ({{\tilde{\eta }}_i}(t)/{\eta _i}(t))\).

Fig. 3
figure 3

Complex solution diagram of Hilbert transform

Full size image

The excitation and response time history curves are transformed into instantaneous phase curves by the Hilbert as shown in Fig. 4. And as shown in Fig. 4a, the instantaneous phase of response varies with the change of \(\lambda ^{2}\). When the influence of the HOAT is small, the instantaneous phase change shows a linear change, while when the influence of the HOAT is large, the change shows a nonlinear one. For excitation without higher-order terms, the instantaneous phase is linearly reduced as shown in Fig. 4b.

Fig. 4
figure 4

Instantaneous phases

Full size image

In order to obtain the instantaneous phase of the response, for the convenience of analysis and comparison, a dimensionless parameter is defined as

$$\begin{aligned} p=\frac{\theta _r-\theta _{e}}{\pi }=\frac{\Delta p}{\pi }, \end{aligned}$$
(57)

where \(\theta _r\) and \(\theta _e\) are the instantaneous phase of response and excitation, and \(\Delta p=\theta _r-\theta _{e}\) is the instantaneous phase difference.

The complex plane diagram and the time history curves of the instantaneous phase difference amplitude are drawn to analyze the changes characteristics of the instantaneous phase difference between the excitation and the response, and the cause of the maximum instantaneous phase difference, as shown in Fig. 5.

Fig. 5
figure 5

Complex plane diagrams and instantaneous phase time history curves

Full size image

The corresponding point rotates around the response curves as time changes, and the instantaneous phase presents periodicity. Figure 5a shows the complex plane diagram and the instantaneous phase difference time history curve when \(\lambda ^2= 3.91\). Caused by existence of the large drift of the response vibration, the response projection curve shifts to the left, which in turn causes emergence of the instantaneous phase difference. When \(\lambda ^2= 3.07\), a small circle appears at the left end of the response projection curve in the complex plane as shown in Fig. 5b, which corresponds to the lower peak of the response time history curve. It can be seen that this is affected by the DFT. The larger the coefficient of the DFT, the more obvious is the small circle. At the same time, the response projection curve is shifted left to the second and third quadrants so that the instantaneous phase of the response and the excitation produces a large phase difference at the right endpoint, and a sudden change point appears on this instantaneous phase difference time history curve. As shown in Fig. 5c, when \(\lambda ^2= 2.68\), the maximum instantaneous phase difference is less than \(0.2\pi \). It can be seen that a large instantaneous phase difference will not be produced under this parameter by the response and excitation.

Instantaneous phase difference is based on the difference of instantaneous phase between response and excitation. Considering the range of difference is between \(-\pi \) and \(\pi \), the time history curve of the instantaneous phase difference is drawn with the dimensionless time as the abscissa and the instantaneous phase difference as the ordinate as shown in Fig. 6.

As can be seen from Fig. 6, the period is the same comparing time history curve of instantaneous phase difference and that of time history curve. The instantaneous phase difference between the response and the excitation is no longer a constant over time, which is affected by the DFT and the DT in the HOAT. The peak value of the instantaneous phase difference fluctuation is only 0.31, and the changing waveform is relatively smooth at \(\lambda ^2= 3.91\). Similarly, its peak value of the instantaneous phase difference is 0.20 when \(\lambda ^2= 2.68\). The peak value is close to 0.96, indicating that the value of instantaneous phase difference is close to \(\pi \) at \(\lambda ^2= 3.91\), and there are obvious sudden changes of the instantaneous phase differences near the peak. Here the instantaneous phase is based on the original equilibrium position. The larger value of the instantaneous phase difference in Fig. 6 appears at the upper wave peak. Due to the influence of the DT, the response is separated from the exciting vibration centerline, which further leads to an increase in the instantaneous phase difference.

Fig. 6
figure 6

Instantaneous phase difference time history curve

Full size image

5 Comparison of the instantaneous phase difference

In order to facilitate further research on the amplitude of p, a new dimensionless parameter is defined as:

$$\begin{aligned} p_{\max }=\frac{\Delta p_{\max }}{\pi }, \end{aligned}$$
(58)

where \(\Delta p_{\max }\) is the amplitude of \(\Delta p\). In the following analysis, the distribution of \(\Delta p_{\max }\) is used to discuss the instantaneous phase-frequency characteristics of suspended cables with different parameters.

5.1 External excitation

The response of the cables under the external excitation is numerically analyzed. The data of corresponding time history curves are obtained by changing \(\lambda ^2\) and excitation frequency \(\Omega \) of the suspended cables, where \(\lambda ^2\) varies from 1.0 to 6.0 with an interval of 1.0 and the excitation frequency \(\Omega \) varies from 0.9 to 1.35 with an interval of 0.01.

Figure 7 is a contour image of the maximum phase difference \(\Delta p_{\max }\) distributed in the (\(\lambda ^{2},\Omega \)) plane under external excitation. Figure 7a is the image with \(\lambda ^2\) in the range of 1.0 to 6.0, and Fig. 7b is a partially enlarged image with \(\lambda ^2\) in the range of 2.81 to 3.37 where the regions undergo intensively calculation during numerical analysis to ensure the accuracy of the image. It can be seen from Fig. 7a that \(p_{\max }\) has a sudden change in the narrow region of \(\lambda ^2\approx 3.0\), and the value is close to 1. The phase difference is close to \(\pi \). However, the value of \(p_{\max }\) is below 0.5 in other region. The enlarged image indicates that the change trend of \(p_{\max }\) on the left and right sides of \(\lambda ^2=3.06\) is a roughly antisymmetric distribution. When \(\lambda ^2<3.06\), \(p_{\max }\) increases with increasing \(\Omega \) under constant \(\lambda ^2\), while when \(\lambda ^2>3.06\), the changing trend is opposite. In addition, it can be seen from the partially enlarged image that the region where \(p_{\max }\) is close to 1 varies with the relation between \(\lambda ^2\) and \(\Omega \), roughly centered on the intersection of the two straight lines \(\Omega =-1.585\lambda ^2+5.975\) (line I-I) and \(\lambda ^2=3.06\) (corresponding to \(\Omega =1.125\)). In other words, the region where \(p_{\max }\) is close to 1 gradually widens along \(\Omega =-1.585\lambda ^2+5.975\).

Fig. 7
figure 7

The \(p_{\max }\) contour maps in (\(\lambda ^{2}-\Omega \)) plane under external excitation. a (\(\lambda ^{2}-\Omega \)) plane of global view; b (\(\lambda ^{2}-\Omega \)) plane of enlarged view

Full size image

For a clearer view, the variation curves of \(p_{\max }\) with \(\lambda ^2\) for \(\Omega =1.3,1.18,1.125,1.07\) and 0.95 are plotted in Fig. 8a. Here, 1.125 is the certain horizontal line of the (\(\lambda ^{2},\Omega \)) plane in Fig. 7b, and the other four values of \(\Omega \) are symmetrically selected around 1.125. As shown in Fig. 8a, \(p_{\max }\) increases suddenly around \(\lambda ^2= 3.06\) under the five excitation frequencies \(\Omega \), and the five lines show basically but not exactly symmetric profiles. As \(\Omega \) increases, the peak value shifts slightly to the negative direction of \(\lambda ^2\), and vice versa. Similarly, to ascertain the distribution along the line I-I and its vertical direction II-II, the variation curves of \(p_{\max }\) along sections I and II are plotted in Fig. 7b, where the horizontal axis is nondimensionalized because the data points of the two sections are different. As shown in Fig. 8b, both curves are symmetric about the center.

Fig. 8
figure 8

Selected \(p_{\max }\) curves under external excitation. a \(\lambda ^{2}-p_{\max }\) curves of specific \(\Omega \); b sectional views on symmetric axes I and II

Full size image

5.2 Parametric excitation

Similarly, the Hilbert transform is performed on the time history curves data under the parametric excitation. The variation of the maximum instantaneous phase difference is obtained with \(\lambda ^2\) and \(\Omega \) as shown in Fig. 9. Compared with that of the external excitation, the value of \(p_{\max }\) under parametric excitation is smaller in all regions on the (\(\lambda ^2,\Omega \)) plane, and its maximum value is only about 0.3. In addition, it only concentrates in a small region near \(\lambda ^2\approx 3.00\) and \(\Omega \approx 1.12\). The region of \(\lambda ^2\) between 2.81 to 3.37 partially enlarge it, and get the enlarged image as shown in Fig. 9b. It can be seen that the region of \(p_{\max }\approx 0.3\) is very small. The changing trend of the contour image of \(p_{\max }\) is also roughly antisymmetric about \(\lambda ^2=3.06\).

Fig. 9
figure 9

The \(p_{\max }\) contour maps in (\(\lambda ^{2}-\Omega \)) plane under parametric excitation. a (\(\lambda ^{2}-\Omega \)) plane of global view; b (\(\lambda ^{2}-\Omega \)) plane of enlarged view

Full size image

Figure 10a shows the variation of \(p_{\max }\) along with the Irvine parameter \(\lambda ^2\) under different dimensionless parametric excitation frequencies \(\Omega \) of 1.14, 1.122, 1.117, 1.112 and 1.094, respectively. It can be seen from Fig. 10a that the \(p_{\max }\) curves of \(\Omega =\)1.122, 1.117 and 1.112 show a sudden increase, and reach the peak value close to 0.36. However, for \(\Omega =\)1.14 and 1.094, the values of \(p_{\max }\) are much smaller. In the same way, the \(p_{\max }\) curves along the lines I and II are shown in Fig. 10b. Similar to the case of external excitation, both Fig. 10a and Fig. 10b show basically but not exactly symmetric profiles.

Fig. 10
figure 10

Selected \(p_{\max }\) curves under parametric excitation. a \(\lambda ^{2}-p_{\max }\) curves of specific \(\Omega \); b sectional views on symmetric axes I and II

Full size image

5.3 Comparative analysis

From the above contour images of \(p_{\max }\), regardless of external excitation or parametric excitation in the parameter plane of \(\lambda ^2-\Omega \), the instantaneous phase difference amplitude of the response and excitation would abruptly change in a small region near \(\lambda ^2\approx 3.00\). Moreover, there is an antisymmetric distribution from the enlarged image. The difference is that \(p_{\max }\) under external excitation is generally greater than that of parametric excitation. The maximum value of the former is about 1.0, and the maximum value of the latter is only 0.3. The former is distributed near a narrow band with \(\lambda ^2\approx 3.00\), while the latter is distributed near a dot field of \(\lambda ^2\approx 3.00\) and \(\Omega \approx 1.12\). In addition, comparing the \(p_{\max }\) contour image in the (\(\lambda ^{2}-\Omega \)) planes and the \(p_{\max }-\lambda ^{2}\) curves under two kinds of excitation, it can be seen that the change of excitation frequency has different effects on the instantaneous phase difference, when the suspended cable is subjected to different types of excitation.

According to the analytical expression, the approximate forms of the external excitation and the parametric excitation are the same in the form (Eqs. 36 and 55). The reason for the difference in the responses and phase differences between the two excitations lies in the different secular terms, which leads to a change in the response amplitudes. This can be seen from Eqs. (27) and (41), where there are additional term \(f_{2}e^{i\sigma T_{1}}\) related to parametric excitation in Eq. (41). At the same time, when Eq. (47) is compared with Eq. (30), there is one difference between the two, for example the term of \(\frac{\sigma }{2\omega _{m}}f_{2}e^{i\sigma T_{1}}\) shown in Eq. (47) and the term of \(\frac{1}{2}F_{1}e^{i\sigma T_{1}}\) shown in Eq. (30). Therefore, the equations after separating the real and imaginary parts are different. Although the obtained frequency response Eqs. (35) and (54) are similar in structure, the terms on the right are different. As a result, the response amplitudes a are different, resulting in different DT and DFT of the HOAT solution, and thus generating different phase-frequency characteristics.

5.4 Discussion

To some extent, this paper would be regarded as a foundation for much other subsequent research work. Thus, potential specific applications to engineering are not concerned in this paper. Nevertheless, the authors would like to address the following:

The problem of instantaneous phase-frequency characteristics is essentially a frequency modulation caused by the nonlinear effect. That is, the response frequency of the system is not exactly equal to the excitation frequency due to the nonlinearity, but there is a frequency modulation effect based on the excitation frequency [19, 20, 22]. Therefore, the response frequency shows a “periodic" fluctuation. So if one wants to know the accurate response frequency at a specific time, it is necessary to examine the instantaneous frequency at that time rather than the average frequency over a period of time, which shows the characteristic of “transient." In order to describe this phenomenon more accurately and in detail, Eq. (55) is further reorganized as follows:

$$\begin{aligned} \begin{aligned} {\eta _m}&{}={a_0} + {\hat{a}}(t)\cos \left[ {\Omega t-\gamma +\Theta (t)}\right] +O\left( {{\varepsilon ^3}}\right) , \end{aligned} \end{aligned}$$
(59)

where

$$\begin{aligned}{} & {} {a_0} {}= \frac{{{\varepsilon ^2}{a_m}}}{4}\sum \limits _{r = \textrm{odd}}^N {{E_{2r}}}, \end{aligned}$$
(60a)
$$\begin{aligned}{} & {} {\hat{a}}(t) {}= \varepsilon {a_m}\sqrt{1 + {{\left( {\frac{\varepsilon }{2}\sum \limits _{r = \textrm{odd}}^N {{E_{1r}}} } \right) }^2} + \varepsilon \sum \limits _{r = \textrm{odd}}^N {{E_{1r}}} \cos \left( {\Omega t - \gamma } \right) }, \end{aligned}$$
(60b)
$$\begin{aligned}{} & {} \Theta (t) {}= \arctan \frac{{\varepsilon \sum _{r = \textrm{odd}}^N {{E_{1r}}\sin \left( {\Omega t - \gamma } \right) } }}{{2 + \varepsilon \sum _{r = \textrm{odd}}^N {{E_{1r}}\cos \left( {\Omega t - \gamma } \right) }}}. \end{aligned}$$
(60c)

From Eq. (59), one could easily figure out that the response frequency of the system is near to but not exactly equal to \(\Omega \) because the time-dependent phase \(\Theta (t)\) would undoubtedly change the instantaneous frequency periodically. Here, \(\Theta (t)\) is just the reflection of the system’s nonlinearity. For the nonlinear system identification of cables under transit excitation, this would be a key challenge in extracting accurate dynamic characteristics from noise-contaminated dynamic responses [19].

The first-order derivative of the instantaneous phase with respect to time is the instantaneous frequency, and there is a deterministic relationship between the instantaneous frequency and the instantaneous cable force. Therefore, the distribution difference of the instantaneous phase-frequency characteristic \(p_{\max }\) of the suspended cable in the (\(\lambda ^{2}-\Omega \)) plane under these two types of excitations may have reference significance for the study of the time-vary or dynamic maximum cable tension [41,42,43,44], which is worthy of further study.

Because the instantaneous phase is the reality phase of each moment, it is also the basis for studying the relative motion between two adjacent cables with identical/similar parameters in cable-stayed bridges and other similar structures. For example, attach cross-ties or diversity dampers between stayed cables to mitigate vibrations [45, 46].

6 Conclusion

The governing equations of external- and parametric-excited suspended cables were discretized by the Galerkin discretization and solved by the MSM. Then, the Hilbert transform was used to analyze the cable’s primary responses. The distributions of instantaneous phase differences in the (\(\lambda ^{2},\Omega \)) plane were drawn to compare the instantaneous phase-frequency characteristics of the external- and parametric-suspended cables. The following conclusions can be drawn:

After considering the terms of the high-order approximation solution, instantaneous phase differences between responses and excitations are no longer time-independent values but periodically time-vary ones. Simultaneously, the response frequency of this nonlinear system is also periodically varying about the excitation frequency.

The instantaneous phase differences originated from the following two aspects: one is the DT which shifting the curves in the complex plane, and then affecting the maximum value of the instantaneous phase difference; the other is the DFT which changing the shapes of curves in the complex plane, and then affecting the variation characteristics of the instantaneous phase.

For a suspended cable under external or parametric excitations, the amplitudes of instantaneous phase differences between responses and excitations would both increase sharply in the local region centered on \(\lambda ^{2}\approx 3.0\) and \(\Omega \approx 1.125\), and both with approximately antisymmetric distributions in the (\(\lambda ^{2},\Omega \)) plane. However, the sharp-change-region of the former is within a narrow band of \(\lambda ^{2}\approx 3.0\), while the latter is concentrated near the central point. In addition, the maximum amplitude of instantaneous phase differences is about 1 under the external excitations and only about 0.3 under parametric excitations.