1 Introduction

Climate zoning is extremely important to subsidize implantation and planning in various sectors, such as industry, agriculture, and transportation and to subsidize other sciences, such as hydrology, architecture, biology, and medicine, in order to discover, explain, and explore the normal performance of atmospheric phenomena (Vianello and Alves 1991) for the sustainable use of a determined region (Mitchell et al. 2004). Regarding agricultural production, climatic impact results in vulnerability of rural populations, not only because of climate variability but also because of its unpredictability, uncertainty, and human adaptability to climate changes (Swart et al. 2003; Rivington et al. 2007). Thus, in consequence of climatic uncertainties, it has become necessary to study different event possibilities as a base for adequate decision making to minimize the risk and negative impacts from adverse climate phenomena (Hansen 2002; Swart et al. 2003; Calder et al. 2008). In relation to hydrological studies, the climatic characterization is an important tool to inform about suitability or vulnerability of local and global water resources and subsidizing adoption of political initiatives about utilization of water in agricultural enterprises, as well as to understand the variability of distribution of water along the land surface and the impact of floods and catastrophic droughts in the natural resources under the influence of global climate change (Salinger 2005).

In climatological studies, normally, the elaboration of the climatological water balance of a location or region is considered one of the best references for climatic characterization. The climatological water balance proposed by Thornthwaite and Mather (1955) allows information to be obtained on local or regional water availability, calculating water entries in the soil plant system according to soil water storage capacity. From climatological water balance, parameters can be extracted to calculate the moisture index proposed by Thornthwaite (1948), which is used as a climatic indicator to define regions regarding their climatic homogeneity. For this, temperature can be used to estimate the potential evapotranspiration (ETp) by the Thornthwaite method (1948) and to represent water loss process in soil plant system. However, it has been demonstrated in some research that temperature is not sufficient as an indication of the energy available for evapotranspiration. Furthermore, in some regions, the winds can play an important role in evapotranspiration, and the effects of cold or warm air advection are not considered by this method. In spite of all these arguments, the Thornthwaite formulation obtained world popularity, in part, because it only requires temperature values for its determination (Vianello and Alves 1991). However, in 1990, the methods recommended by the Food and Agriculture Organization (FAO) (Doorenbos and Pruitt 1977) were revised by a group of specialists in evapotranspiration, concluding that the best results were obtained with the Penman–Monteith method. Thus, it was recommended by FAO, after some parameterizations, such as standard method to estimate the reference evapotranspiration (ETo) (Smith et al. 1990), frequently reported in the literature as Penman–Monteith–FAO method. Thus, the International Commission on Irrigation and Drainage and FAO considered Penman–Monteith method (Allen et al. 1998) as the standard method for ETo estimates based on meteorological data, and it was also used to assess other methods (Smith 1991). In this method, the best ETo estimates are obtained in the function of their physic–mathematic formulation of the evapotranspiration process and by the greatest number of variables considered, increasing the accuracy of the estimates (Allen et al. 1998). However, its practical use has been restricted by the requirement for a greater number of climate elements.

In order to perform a climatic classification, mainly when refined mesh data are unavailable, it becomes necessary to verify the most appropriate interpolator for improving the climatic characterization (Vieira et al. 2002). In this context, Skirvin et al. (2003) used altitude deviations to improve estimates of kriging rainfall and temperature in the St. Peter Microdata, Southeast Arizona, in an area of 10,000 km2. Chappell (1998) also used cokriging technique to improve accuracy and reduce costs for cesium mapping in soil of Nigeria using altitude as covariable. In this case, a Spot satellite image was used to generate altitude data in a spatial resolution of 20 m. Ashraf et al. (1997) also characterized the spatial pattern of climatic variables from 17 stations in the states of Nebraska, Kansas, and Colorado, USA, observing spatial structure of cross semivariograms and cross covariances with a magnitude of approximately 600,000 m. Similarly, Martínez-Cob and Cuenca (1992), comparing kriging and cokriging estimates of evapotranspiration in the regions of Oregon, USA, observed higher accuracy of ordinary cokriging when compared to kriging method. Nevertheless, simple cokriging methodology has not been applied to study the spatial variability of moisture index, annual rainfall, and average annual air temperature based on coordinates of altitude, latitude, and longitude.

In this context, it is fundamental to evaluate climatic conditions of places where daily meteorological data are unavailable for climate characterization. Nevertheless, it is necessary to evaluate the quality of different methods of interpolation, in order to proceed the estimation of climatic data along the space, analyzing its performance, in order to subsidize decision support about which is the best interpolation method to characterize the spatial structure of the analyzed phenomena.

Considering the accurate existence of a systematic collection of climate elements in the climatological stations of the INMET National Network of Meteorological Surface Observations and the correlation of these elements with altitude, latitude, and longitude (Sediyama and Mello 1998), it was aimed at with the present study to verify the use of universal simple cokriging methodology to study the structure, magnitude, and spatial variability of Thornthwaite moisture index, annual rainfall, and average annual air temperature, for the period of 1961 to 1990, in Minas Gerais, using altitude, latitude, and longitude as covariables. Another purpose is to verify the consistence of the applied methodology for possible extrapolation in other areas of Earth surface, being a useful component for agroclimatic zoning and ecological–economical zoning studies, providing knowledge about the homogeneity of several climatic types in the whole state of Minas Gerais.

2 Material and methods

2.1 Data origin and moisture index calculation

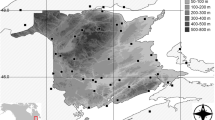
All data used in this study and the end products were georeferenced using Albers Equal Area cartographic projection, similar to that adopted by Carvalho and Louzada (2007). The Thornthwaite annual moisture index and the climate elements, annual rainfall, and average annual air temperature were obtained from primary data of 39 INMET climatological stations located in Minas Gerais state, Brazil, and in nearby states (Fig. 1) presented in the Climatological Normals book, for the average period of 1961 to 1990 (Brasil 1992). The digital elevation model was obtained by the NASA Shuttle Radar Topography Mission (SRTM) 2000, in 90-m spatial resolution (NASA JPL 2008). The resolution of this model was transformed to 1 km using mean zonal operators of spatial analysis in geographical information system.

Fig. 1
figure 1

Political regions of Minas Gerais state (a), location of INMET climatological stations (b), and spatial resolution used to obtain the altitude, longitude, and latitude observations (c)

Full size image

Based on a rude analysis of the observed data of climatic variables distributed around Minas Gerais state and the empiric knowledge about climatic aspects, an accentuated climatic diversity due to the large territorial dimension of the state, characterized by relief with characteristics of mountainous, plains, and plateaus, range of latitude and longitude variation, is noticed, causing an accentuated differentiation in solar radiation, temperature, and rain fall. Vegetation aspects are also quite diversified, considering presence of native species as well as due to the agricultural exploration. On the other hand, the coast east of the state is influenced by the Atlantic Ocean, mainly in the south portion, associated to higher altitudes.

The moisture Index (Iu) was estimated from parameters taken from Thornthwaite and Mather (1955) climatological water balance (CWB), and the reference evapotranspiration estimation was based on Penman–Monteith–FAO methodology (Fig. 2).

Fig. 2
figure 2

Flow chart of the procedure used to obtain Thornthwaite annual humidity index (Iu). Where: Monthly climatological elements—EC is the mean, maximum, and minimum temperature (°C); relative humidity (%); atmospheric pressure (mb); wind (m s−1); sunshine hours (h). P is the monthly rainfall (mm). ETP-PM-FAO is the reference evapotranspiration estimated by the Penman–Monteith–FAO method (mm). BHC is the climate water balance. Def hid is the annual water deficiency (mm). Exc hid is the water surplus. Ia is the aridity index. Ih is the moisture index. Iu is the Thornthwaite annual humidity index

Full size image

Therefore, the Iu was obtained from CWB of which extracts the annual totals of the potential evapotranspiration (ETP), hydric excess (Exc), and hydric deficiency (Def), according to the following equations:

$$ {\hbox{Iu}} = {\hbox{Ih}} - {\hbox{Ia}} $$
(1)

where Ih is the hydric index, Ia is the aridity index. Ih and Ia were calculated, respectively, by:

$$ {\hbox{Ih}} = 100\left( {\frac{\text{Exc}}{{\hbox{ETP}}}} \right) $$
(2)
$$ {\hbox{Ia}} = 100\left( {\frac{\text{Def}}{{\hbox{ETP}}}} \right) $$
(3)

The Iu classification was revised by Mather (1974) and a group of specialists in India in 1980 (ICRISAT 1980), generating a new adaptation for climate classification, defined according to the following climatic types (Table 1).

Table 1 Climatic types proposed by Mather (1974) and ICRISAT (1980), based on the moisture index generated from the parameters of climatological water balance, described in Thornthwaite and Mather (1955)
Full size table

It is worth emphasizing that, in Eq. 1, the parameter Ia (aridity index) was not multiplied by a 0.6 factor because this factor was used when the moisture index was calculated from the parameters of the CWB, originally proposed by Thornthwaite in 1948. Therefore, Eq. 1 is valid for the CWB that was later improved according to Thornthwaite and Mather (1955) and adopted in the present study.

In conceptual terms, the Penman–Monteith–FAO method was considered as a reference evapotranspiration (ETo) estimator, in accordance to Allen et al. (1998). This method is commonly applied in irrigation management after multiplication by an appropriate crop coefficient to be irrigated, denominated crop coefficient, in order to determine the crop evapotranspiration. Nevertheless, in the context of the present study, this method was considered as an estimator of potential evapotranspiration in substitution to the Thornthwaite method, originally proposed by himself in the elaboration of CWB, in 1948. This procedure was adopted because the method of Penman–Monteith–FAO (Allen et al. 1998) is considered, internationally, the most accurate for ETo or ETp estimation in several places, when compared with the Thornthwaite method.

Penman–Monteith–FAO estimates of ETo or ETp were defined by (Allen et al. 1998):

$$ {\hbox{ETo}} = \sum\limits_{i = 1}^n {\left( {\frac{s}{{s + \gamma *}}\left( {{\hbox{Rn}} - G} \right)\frac{1}{\lambda } + \frac{{\gamma 900}}{{\left( {s + \gamma *} \right)\left( {T + 273} \right)}}{U_2}\left( {{\hbox{es}} - {\hbox{ea}}} \right)} \right){\hbox{NDM}}} $$
(4)

where,

ETo is the evapotranspiration, being, in this case, expressed in millimeter per month, due to the NDM parameter (numbers of day in the month) in the end of equation; n is the months of the year; γ is the psychometric coefficient (kPa °C−1); s is the slope of saturation vapor pressure curve (kPa °C−1); γ* is the modified psychometric coefficient (kPa °C−1); Rn is the net radiation on crop surface (MJ m−2 day−1); G is the soil heat flux (Mj m−2 day−1); λ is the latent heat of vaporization (MJ kg−1); T is the mean air temperature (°C); U 2 is the wind speed at 2 m above ground surface (m s−1); es is the saturation water vapor pressure (kPa); and ea is the actual water vapor pressure (kPa). All these parameters were calculated by models presented in full detail by Allen et al. (1998). The necessary primary data for these calculations were extracted from Climatological Normals book, from the average period of 1961 to 1990 (Brasil 1992), which are mean, minimum, and maximum temperatures, atmospheric pressure, wind speed, duration of sunshine, and relative humidity.

After obtaining moisture index, annual rainfall, and average temperature values for each location, the universal simple cokriging geostatistical analysis method (Isaaks and Srivastava 1989; Chilès and Delfiner 1999; Wackernagel 2003) was used to interpolate the climatic data, considering its spatial correlation with altitude, latitude, and longitude, using 1 km spatial resolution, along Minas Gerais state (Fig. 1).

2.2 Geostatistical modeling

Box–Cox transformation was applied to rainfall, altitude, longitude, and latitude data; log transformation was applied to temperature data. In these situations, kriged predictions were back-transformed and returned to the same scale as the original data.

Trend of variables was removed using global polynomial interpolation. First trend type was used for humidity index, rainfall, temperature, and altitude. Second trend was used for longitude and latitude.

The basic model for trend removal used in universal kriging is (Chilès and Delfiner 1999):

$$ Z(x) = m(x) + Y(x) $$
(5)

where Z(x) is the variable under study, m(x) is the trend, and Y(x) is the fluctuation or residual about this trend.

The trend can be represented as a linear combination with unknown coefficients of known basis trend functions \( f_i^l(x),\;l = 0, \ldots, {L_i}, \)which in general may be different for the different random functions:

$$ E{Z_i}(x) = {m_i}(x) = \sum\limits_l {{a_{il}}f_i^l(x)} $$
(6)

2.3 Universal simple cokriging

Moisture index, annual rainfall, average annual air temperature, altitude, latitude, and longitude were considered as regionalized variables represented by random functions \( \left\{ {Z(x):x \in D \subset {R^n}} \right\} \) and finite dimensional distribution of a set of multidimensional distributions \( \left[ {Z\left( {{x_1}} \right),Z\left( {{x_2}} \right), \ldots, Z\left( {{x_k}} \right)} \right] \) for all k values and any configuration of the points x 1 , x 2 ,...x k . Each Z i (x) is sampled over a set S i of N i  > 0 points, \( {S_i} = \left\{ {{x_\alpha } \in \;D:{Z_i}\left( {{x_\alpha }} \right)\;known} \right\} \), where \( {x_\alpha } \) is the notation for generic data points (Chilès and Delfiner 1999). Cross semivariograms and cross covariances were used to characterize the structure and magnitude of spatial dependence of moisture index (N = 39), annual rainfall (N = 39), average annual air temperature (N = 39), as well as its relationship with the covariables altitude (N = 586.589), latitude (N = 586.589), and longitude (N = 586.589). The cross semivariogram is defined by (Chilès and Delfiner 1999):

$$ {\hat{\gamma }_{ij}}(h) = \frac{1}{{2N(h)}}\sum\limits_{x\beta - x\alpha \cong h} {E\quad \left[ {{Z_i}\left( {{x_\beta }} \right) - \quad {Z_i}\left( {{x_\alpha }} \right)} \right]\left[ {{Z_j}\left( {{x_\beta }} \right) - \quad {Z_j}\left( {{x_\alpha }} \right)} \right]}, $$
(7)

where N(h) is the number of pairs \( ({x_\alpha },{x_\beta }) \) separated by the distance h.

It was considered as for random multivariate intrinsic functions, where

$$ \left\{ {\begin{array}{*{20}{c}} {E\left[ {{Z_i}\left( {x + h} \right) - {Z_i}(x)} \right] = 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\hbox{for}}\,i = 1, \ldots, p} \hfill \\{Cov\left[ {{Z_i}\left( {x + h} \right) - {Z_i}(x),{Z_j}\left( {x + h} \right) - {Z_j}(x)} \right] = 2{\gamma_{ij}}(h)\,{\hbox{exists}}\,{\hbox{and}}\,{\hbox{depends}}\,{\hbox{only}}\,{\hbox{on}}\,h.} \hfill \\\end{array} } \right. $$
(8)

Therefore, the spatial dependency between two variables Z i (x) and Z j (x) can be measured by the function of cross covariance (Goovaerts 1997):

$$ {C_{ij}}(h) = E\left\{ {\left[ {{Z_i}(x) - {m_i}} \right]\left[ {{Z_j}\left( {x + h} \right) - {m_j}} \right]} \right\},\;\forall i,j $$
(9)

or by the cross variogram:

$$ {\gamma_{ij}}(h) = \frac{1}{2}E\left\{ {\left[ {{Z_i}(x) - {Z_i}\left( {x + h} \right)} \right]\left[ {{Z_j}(x) - {Z_j}\left( {x + h} \right)} \right]} \right\},\,\;\forall i,j $$
(10)

Note that γ ij (h) = γ ji (h), but C ij (h)cannot be equal to C ji (h). It means that cross covariance is not a symmetric function in relation to h. Thus, the relationship between cross semivariogram and cross covariance, when it exists, is defined by the following equation (Chilès and Delfiner 1999):

$$ {\gamma_{ij}}(h) = {C_{ij}}(0) - \frac{1}{2}\left[ {{C_{ij}}(h) + {C_{ij}}\left( { - h} \right)} \right] $$
(11)

If the cross covariance is written as summation of two terms dependents of h (Soares 2000):

$$ {C_{ij}}(h) = \frac{1}{2}\left[ {{C_{ij}}(h) + {C_{ij}}\left( { - h} \right)} \right] + \frac{1}{2}\left[ {{C_{ij}}(h) - {C_{ij}}\left( { - h} \right)} \right], $$
(12)

it is possible to verify that the cross semivariogram only incorporates the first term of the function because it is a symmetric function in relation to h. In practice, the asymmetric component of cross covariance is usually ignored due to its complexity to be modeled (Soares 2000).

The theoretical cross semivariogram and cross covariance models were estimated by (Chilès and Delfiner 1999):

$$ {\hbox{Spherical}}\,{\hbox{model}}:C(h) = \left\{ {\begin{array}{*{20}{c}} {1 - \frac{3}{2}\frac{h}{a} + \frac{1}{2}\frac{{{h^3}}}{{{a^3}}}} \hfill & {\quad \quad \quad, {\hbox{if}}\,h\, \leqslant \,a} \hfill \\0 \hfill & {\quad \quad \quad, {\hbox{if}}\,h\, \geqslant \,a} \hfill \\\end{array} } \right. $$
(13)

where, C is the covariance, a is the range, and h is the distance. The spherical model exhibits a linear behavior near the origin but flattens out at larger distances and reaches sill at h = a. The scale parameter α of the spherical model coincides with the range (Isaaks and Srivastava 1989; Chilès and Delfiner 1999).

After fitting cross semivariograms and cross covariances, the spatial interpolation of data by simple cokriging method was proceeded . In this case, the means of the observations and the random functions were known. Thus, to eliminate tendentiousness, these means were subtracted and the mean zero was used (Chilès and Delfiner 1999):

$$ {Y_i}(x) = {Z_i}(x) - {m_i}(x). $$
(14)

To estimate Z 0 = Z 1 (x 0) from carrying out the random function Z i (x) in the sampled sets S i , i ∊ I a linear estimator was considered:

$$ Z** = \sum\limits_i {\sum\limits_\alpha {{\lambda_{i\alpha }}} {Z_i}\left( {{x_\alpha }} \right)} = \sum\limits_i {\lambda_i^\prime {Z_i}} . $$
(15)

Assuming that each random function Z i (x) has a trend of its own and that the trend coefficients of the different variables are not related, using the linear estimator, the following equation is required to be zero for all drift coefficient vectors α i and α 1

$$ E\left( {Z** - {Z_0}} \right) = \sum\limits_i {\lambda_i^\prime {F_i}{a_i} - f_{10}^\prime {a_1}} $$
(16)

where \( {F_i} = \left[ {f_i^l\left( {{x_\alpha }} \right)} \right] \) is the matrix of trend functions arranged by columns l and rows \( \alpha \left( {{x_\alpha } \in {S_i}} \right) \) and a i = (a il ) is the column vector of drift coefficients for the random function Z i ; \( {f_{10}} = \left( {f_1^l\left( {{x_0}} \right)} \right) \) is the vector of drift functions values at the point x 0 and a 1=(a 1l ) is the vector of drift coefficients for the random function Z i .

There are two cases to consider, when \( {S_1} = \left\{ \emptyset \right\} \) or \( {S_1} \ne \left\{ \emptyset \right\} \):

$$ \lambda_i^\prime {F_i} = {\delta_{i1}}f_{10}^\prime \quad where\;{\delta_{i1}} = \left\{ {\begin{array}{*{20}{c}} {1\quad if\;\;i = 1} \hfill \\{0\quad if\;i \ne 1} \hfill \\\end{array} } \right. $$
(17)

Under mean zero, the mean square error is equal to the error variance:

$$ E\left( {Z** - Z_0 } \right)^2 = E\left[ {\sum\limits_i {\sum\limits_j {\lambda ^\prime _i Z_i Z_j \lambda ^\prime _j - 2\sum\limits_i {\lambda ^\prime _i Z_i Z_0 + Z_0 Z_0 } } } } \right], $$
(18)
$$ = \sum\limits_i {\sum\limits_j {\lambda_i^\prime } {C_{ij}}{\lambda_j} - 2\sum\limits_i {\lambda_i^\prime } {c_{i0}} + {c_{00}}} . $$
(19)

Canceling the partial derivatives in relation to λ i and minimizing the variance subject to the unbiasedness constraints lead to the system with Lagrange parameters vector \( {\mu_i} = \left( {{\mu_{il}}} \right)\prime, \;l = 0, \ldots, {L_i} \); the universal simple cokriging system was attained:

$$ \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^p {{C_{ij}}} {\lambda_j} + {F_i}{\mu_i} = {c_{i0}}} \hfill & {i = 1,. \ldots, p} \hfill \\{F_i^\prime {\lambda_i} = {f_{10}}{\delta_{il}}} \hfill & {i = 1,. \ldots, p} \hfill \\\end{array} .} \right. $$
(20)

The cokriging variance was estimated by:

$$ {\sigma^2}_{CK} = E{\left( {Z** - {Z_0}} \right)^2} = {c_{00}} - \sum\limits_{i = 1}^p {\lambda_i^\prime {c_{i0}} - \mu_1^\prime {f_{10}}.} $$
(21)

Universal simple cokriging estimates were interpolated to characterize the spatial variability of annual moisture index, annual rainfall, and average annual air temperature in pixels of 1-km spatial resolution, using eight polygon classes for annual moisture index (Mather 1974; ICRISAT 1980) and ten classes, with equal intervals, for annual rainfall and average annual air temperature.

Theoretical spherical and exponential models were compared. The decision about the best theoretical model was based on the cross-validation analysis and error coefficients.

Cross-validation is a powerful validation technique used to check the performance of kriging model. It consists of removing data, at a time, and then trying to predict it. Thus, predicted values can be compared to observed values in order to assess how well the interpolation is working, according to its self-consistency and lack of bias (Isaaks and Srivastava 1989; Cressie 1993; Goovaerts 1997; Chilès and Delfiner 1999; Burrough and McDonnell 1998).

The mean standardized prediction errors:

$$ \frac{{\sum\limits_{i = 1}^n {\left( {Z** - {Z_i}(x)} \right)/\widehat{\sigma }\left( {{x_i}} \right)} }}{n}, $$
(22)

the root-mean square standardized prediction errors were defined by:

$$ \sqrt {{\frac{{\sum\limits_{i = 1}^n {{{\left[ {\left( {Z** - {Z_i}(x)} \right)/\widehat{\sigma }\left( {{x_i}} \right)} \right]}^2}} }}{n}}}, $$
(23)

where, Z** was the cokriging estimation, Z i (x), the observed value, \( \widehat{\sigma }\left( {{x_i}} \right) \), the prediction standard error for x i location.

Considering an ideal cokriging performance, mean standardized prediction errors should be 0 and the root-mean square standardized prediction errors should be 1 (Cressie 1993).

As addition to the cross-validation, maps of the standard errors were associated with the universal simple cokriging interpolated maps.

3 Results and discussion

It was possible to characterize the spatial dependency and to interpolate moisture index, annual rainfall, and average annual air temperature under the influence of covariables altitude, latitude, and longitude. Universal simple cokriging models performed better when compared to the simple cokriging models. Universal simple cokriging technique presented satisfactory performance to map the spatial variability of moisture index, annual rainfall, and average annual air temperature based on kriging error coefficients, considering that mean standardized prediction errors and root-mean square standardized prediction errors presented values near to 0 and 1, respectively, according to ideal conditions of the estimator as related by Cressie (1993) (Table 2).

Table 2 Quality coefficients of simple cokriging and universal simple cokriging estimates used to characterize the humidity index (Iu), rainfall (P), and temperature (T) in Minas Gerais
Full size table

According to Goovaerts (2000), the disadvantage of kriging when compared to cokriging methods is that covariables such as topography cannot be incorporated in the models. With this, the tendency to increase rainfall with increase in altitude due to the orography of mountainous relief, determining air vertical elevation and its condensation by diabatic cooling, is not considered. Probably, similar factors to these were also influential to moisture index and average annual air temperature because Sediyama and Mello (1998) also observed the possibility of using covariables altitude, latitude, and longitude to estimate normal mean, maximum, and minimum monthly and annual temperatures in Minas Gerais. Skirvin et al. (2003) also used altitude deviations to improve estimates of kriging rainfall and temperature in the St. Peter Microdata, Southeast Arizona, in an area of 10,000 km2, but the cokriging technique was not applied.

Spherical cross semivariogram and cross covariance models were fitted to moisture index, annual rainfall, and average annual air temperature, with range values of 284,180.93, 284,715.03 and 281,043.58 m, respectively (Table 3).

Table 3 Theoretical spherical cross semivariogram and cross covariance parameters used to characterize the structure and magnitude of spatial dependency of the humidity index (Iu), rainfall (P), and temperature (T) of Minas Gerais
Full size table

Thus, climatological stations situated at distances greater than the range obtained for the analyzed variables did not correlate in space. Ashraf et al. (1997) characterized the spatial pattern of climatic variables from 17 stations in the states of Nebraska, Kansas, and Colorado, USA and also observed spatial structure of cross semivariograms and cross covariances with a magnitude of approximately 600,000 m, similar to that observed in the present study. Chappell (1998) also used cokriging technique to improve accuracy and reduce costs for cesium mapping in soil of Nigeria using altitude as covariable. In this case, a Spot satellite image was used to generate altitude data in spatial resolution of 20 m.

Analysis of experimental and theoretical graphs of cross semivariogram and cross covariogram models showed the spatial dependency of moisture index, rainfall, and temperature and the cross spatial correlation of these variables with altitude, latitude, and longitude. There was a tendency to cross semivariograms and cross covariances variation with distance increase, up to a value at which the local effects had no more influence, culminating in the stability of the models, separating clearly the structured and random universe, satisfying the stationary assumptions (Figs. 3, 4, and 5).

Fig. 3
figure 3

Experimental (dots) and theoretical (solid line) cross semivariograms (γ) and cross covariances (C) of the humidity index (Iu) with Iu (a), Iu with longitude (lo) (b), Iu with latitude (la) (c), Iu with altitude (al) (d), lo with lo (e), lo with la (f), lo with al (g), la with la (h), la with al (i), and al with al (j) of Minas Gerais

Full size image
Fig. 4
figure 4

Experimental (dots) and theoretical (solid line) cross semivariograms (γ) and cross covariances (C) of annual rainfall (P) with P (a), P with longitude (lo) (b), P with latitude (la) (c), P with altitude (al) (d), lo with lo (e), lo with la (f), lo with al (g), la with la (h), la with al (i), and al with al (j) of Minas Gerais

Full size image
Fig. 5
figure 5

Experimental (dots) and theoretical (solid line) cross semivariograms (γ) and cross covariances (C) of average annual air temperature (T) with T (a), T with longitude (lo) (b), T with latitude (la) (c), T with altitude (al) (d), lo with lo (e), lo with la (f), lo with al (g), la with la (h), la with al (i), and al with al (j) of Minas Gerais

Full size image

Regarding the spatial variability of the analyzed variables, more humid regions with lower average annual air temperature were observed in the maps of moisture index over most of region of Triângulo Mineiro, South Minas, Upper São Francisco, and Zona da Mata of Minas Gerais. In contrast, regions in the North and northeast of Minas Gerais were classified with dryer and warmer climates. As addition, maps of the standard errors were associated with the universal simple cokriging interpolated maps because the generated surfaces reflected the mean or average behavior of the spatial process, and, as an average, it should be recognized that it is generally smoother than the actual process. Thus, it was possible to quantify the uncertainty associated with the humidity index, rainfall, and temperature maps (Fig. 6).

Fig. 6
figure 6

Universal simple cokriging and standard error prediction maps of the humidity index, annual rainfall (mm), and mean annual temperature (°C) of Minas Gerais

Full size image

These results showed considerable climate contrasts in Minas Gerais, probably due to the influence of oceanic, continental, and other air masses together with altitude because, according to Vianello and Alves (1991), there is a greater diversity of factors in this state that influences climate in function of its geographic location in South America continent.

As the impacts of climate on agricultural production result in vulnerability of rural populations, not only because of climate variability but also because of its unpredictability (Hansen 2002), it is expected that universal simple cokriging methodological analysis for climate characterization presented in this study can certainly contribute as a base for adequate decision making to minimize risks and negative impacts of adverse phenomena on ecology and social economy of Minas Gerais. Furthermore, it is recommended to plan land use and occupation observing the predominant climate characteristics of each region because, according to Lioubimtseva et al. (2005), with anthropological interference in the environment there is modification in albedo (surface reflectivity index), affecting water balance and soil nutrients, both on a regional and global scale. On the other hand, with the practice of irrigation, more favorable climate conditions can be induced in some regions, with a new balance between climate and vegetation. However, in some cases, irrigation used excessively or associated to improper land use can accelerate the desertification process of a region.

4 Conclusions

The use of geostatistics and universal simple cokriging technique enabled the characterization of spatial variability of Thornthwaite annual moisture index, annual rainfall, and average annual air temperature, for the average period of 1961 to 1990, in Minas Gerais state, using altitude, latitude, and longitude as covariables.

The spatial correlation observed between annual moisture index, annual rainfall, and average annual air temperature with altitude, latitude, and longitude showed great potential of universal simple cokriging method to map and to improve the detailing and spatial resolution of a database of variables on a macro climate scale from a database of variables on a meso climate scale.