1 Introduction

The Arctic Ocean is continually in motion, driven by the wind blowing over the ice (and over ice floes), affecting the near-surface flow in the water below the ice, which also moves under the action of a near-surface geostrophic current. The motions that we observe are dominated by the Beaufort Gyre, sitting in the Canada Basin, and the Transpolar Drift current (TDc) which flows under the ice and across the North Pole towards the Fram Strait. This flow transports 2000–3000 km3 of ice, per year, from the East Siberian and Laptev Seas out into the North Atlantic. Our interest here is centred on the TDc, the aim being to give a careful mathematical description of this flow using a set of suitable rotating, spherical coordinates, coupled to an appropriate model for the water–ice-wind interaction. The underlying philosophy that we follow is to treat this problem within the realm of mathematical fluid dynamics, starting from a set of general governing equations and invoking only the thin-shell approximation.

The flow that we shall describe and analyse is fairly complex, comprising a number of elements that must be included. Firstly, there is a prevailing wind which blows, with little variation, from Russia towards Greenland (although the direction of the ice flow, and of the TDc, are to the left of this—an important property that we must incorporate and explain). This, via the wind stress at the surface of the ice, and the shear stress between the ice and the water, contributes to the motion of the TDc, by adding an Ekman component to the ocean’s flow velocity. Secondly, there is a near-surface geostrophic flow which is driven by the pressure gradients near the surface, produced primarily by the difference in salinity between the relatively fresh water—mainly river outflow—feeding on to the Russian continental shelf and the saltier water closer to the North Atlantic. Thirdly, there is the issue of how best to model the shear stresses between air and ice, and between ice and water, in such a way that this is reasonably accurate and leads to the possibility of analytical progress. A fourth element that all this feeds into, and interacts with, is the growth/reduction in the thickness of the ice sheet as it moves. It is clear that, although we can start from a generally agreed set of governing equations—the Navier–Stokes equations—the interaction between water–ice-wind requires a significant element of modelling and choice. It is observed that the combined effect of all these contributions is to produce a TDc which moves faster than the deeper parts of the ocean, but slower than the surface ice; it moves at a speed of about 7.5 ms−1 in the neighbourhood of the North Pole, rising to about 20 ms−1 as it flows out through the Fram Strait. Useful background information can be found, for example, in [1, 2], and a general description, setting the scene for these types of calculation, can be found in [3].

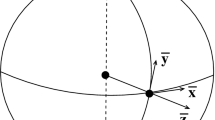
The main thrust of this work is to show that a single simplifying assumption (that the ocean constitutes a thin shell at the surface of the Earth) enables the construction of a complete solution. However, this is possible only when a suitable system of rotating, spherical coordinates is used. The familiar geographical spherical coordinates (see Fig. 1a) are not valid at the two poles, this being a consequence of the ‘hairy ball’ theorem which states that any continuous vector field on the sphere must vanish at some point. (Because of the symmetry of the coordinates here, this becomes two points.) Consequently an alternative coordinate system must be introduced. The idea—a rotation of the geographical coordinates—has been developed in [3], and expanded in detail (with much background information) in [4]; see Fig. 1b. We comment that the singularity at the poles was also removed, but in a slightly different way and specific to a discussion of barotropic modons on a sphere, in [5], and note the correction to the reference number. A similar rotation, coupled to the delta-plane model and used to describe quasi-geostrophic flows, can be found in [6]. The contention here is that the rotation of the North Pole to the Null Island is simpler, more elegant and more transparent. An application of our approach to the TDc has already been given in [7], but limited to the f-plane approximation in conjunction with the local tangent plane. A brief description of the associated solution was presented in [7], the aim there being to lay the foundations for further investigations. Here, we show that the geometrical restriction is altogether unnecessary and, furthermore, we are able to extend and improve the solutions relevant to the TDc and more fully explain many aspects of this motion. Indeed, this same system of coordinate reformulation can be adopted for other flows, allowing validity at and close to the North Pole. For example, the discussion of wind-drift currents in the Arctic Ocean away from the North Pole (see [8, 9]), could be extended to the neighbourhood of the pole. So, in the light of these comments, the plan for this paper is as follows.

Fig. 1
figure 1

a, b: In the left panel, a, we show the familiar spherical coordinates, with angles measured relative to the Equator and in its associated plane; Z is the Null Island. In the right panel, b, we have the new, rotated, coordinate system, with angles measured relative to the Great Circle, and its associated plane, that passes through the two poles

Full size image

In Sect. 2, we present the general governing equations, introduce a suitable non-dimensionalisation and show how the thin-shell parameter, ε, appears. The limiting process, \(\varepsilon \to 0\), is invoked, with all the other parameters held fixed. In Sect. 3 we develop the equations that describe the various elements that contribute to the solution and then, in Sect. 4, we outline the model that we have chosen for the water–ice-wind interaction (which is similar to that used in [7]). Section 5 is devoted to the presentation of the solutions (to leading order) that link the three components of the motion: the TDc, the ice movement and the wind velocity. An example of this solution is presented in graphical form in Sect. 6 and, finally, in Sect. 7, we give a brief summary, with a discussion of the relevance of, and possible future investigations prompted by, this work.

2 Governing equations

We take the Earth to be a sphere (of radius \(\approx 6371 km\)), ignoring the precise shape of the Earth’s geoid. Suitable corrections to the shape can be included, if desired (see [10]), but these are unimportant in the study of the TDc (see [11]). The geographical coordinates are shown in Fig. 1a, where the singularities—that is, where \(\left( {{\mathbf{e}}_{\phi } , {\mathbf{e}}_{\theta } } \right)\) are not well defined—occur at the two poles. This system is rotated, the angles \(\left( {\phi , \theta } \right)\) now being measured around the Great Circle which passes through the poles, and relative to the associated plane through the sphere; see Fig. 1b. The two points on the sphere where the tangent vector field is undefined are now at the Null Island (Z) and the point diametrically opposite (on the Equator). The North Pole is situated at \(\phi = {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}, \theta = 0\). We write \(r^{\prime}\) as the distance (radius) from the centre of the Earth, \(\theta \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\) and \(\phi \in\)[0, 2π); the velocity in this system is \(\left( {u^{\prime}, v^{\prime}, w^{\prime}} \right)\). The governing equations in the new coordinates take an identical form to the familiar set, but they are to be fixed on a rotating Earth where the axis of rotation, relative to these coordinates, is different. The Navier–Stokes equation in this new set of rotating coordinates is

$$\begin{aligned} & \rho ^{\prime}\frac{{{\text{D}} }}{{{\text{D}}t^{\prime}}}\left( {u^{\prime}, v^{\prime}, w^{\prime}} \right) + \frac{\rho ^{\prime}}{{r^{\prime}}}\left( { - u^{\prime}v^{\prime}\tan \theta + u^{\prime}w^{\prime}, u^{{\prime}{2}} \tan \theta + v^{\prime}w^{\prime}, - u^{{\prime}{2}} - v^{{\prime}{2}} } \right) \\ & \quad + 2\Omega ^{\prime}\left( { - v^{\prime}\sin \phi .\cos \theta - w^{\prime}\sin \phi .\sin \theta , u^{\prime}\sin \phi .\cos \theta - w^{\prime}\cos \phi , u^{\prime}\sin \phi .\sin \theta + v^{\prime}\cos \phi } \right) \\ & \quad + r^{\prime}\Omega ^{{\prime}{2}} \left( {\sin \phi .\cos \phi .\cos \theta , \sin^{2} \phi .\sin \theta .\cos \theta , - \sin^{2} \phi .\sin^{2} \theta - \cos^{2} \phi } \right) \\ & \quad = - \nabla ^{\prime}p^{\prime} + \rho ^{\prime}\left( {0, 0, - g^{\prime}\frac{{R^{{\prime}{2}} }}{{r^{{\prime}{2}} }}} \right) + \nabla_{{\mu }^{\prime}}^{2} \left( {u^{\prime}, v^{\prime}, w^{\prime}} \right) \\ & \quad - \frac{1}{{r^{{\prime}{2}} \cos^{2} \theta }}\left( {\mu_{h}^{\prime} u^{\prime}, \mu_{h}^{\prime} v^{\prime}, 2\mu_{v}^{\prime} \left( {w^{\prime}\cos^{2} \theta - v^{\prime}\sin \theta .\cos \theta } \right)} \right) + \frac{{2\mu_{h}^{\prime} }}{{r^{{\prime}{2}} }}\frac{\partial }{\partial \theta }\left( {0, w^{\prime}, - v^{\prime}} \right) \\ & \quad + \frac{{2\mu_{h}^{\prime} }}{{r^{{\prime}{2}} \cos \theta }}\frac{\partial }{\partial \phi }\left( {w^{\prime} - v^{\prime}\tan \theta , u^{\prime}\tan \theta , - u^{\prime}} \right), \\ \end{aligned}$$
(1)

where the prime denotes dimensional (physical) variables; these will be removed when we nondimensionalise. Here, \(t^{\prime}\) is time, \(p^{\prime}\left( {\phi , \theta , r^{\prime}, t^{\prime}} \right)\) is the pressure in the water and \(\rho ^{\prime}\) is the constant density of the water (which is a reasonable assumption for the upper layer of the Arctic Ocean). Also, \(R^{\prime} \approx 6371 km\), the radius of the Earth, \(g^{\prime} \approx 9\cdot 81 ms^{ - 2}\), the mean acceleration of gravity at the surface of the Earth, and \(\Omega ^{\prime} \approx 7\cdot 29 \times 10^{ - 5} rads^{ - 1}\), this being the constant rate of rotation of the Earth about its axis. The coefficients of the vertical and horizontal dynamic eddy viscosities are \(\mu ^{\prime}_{v}\) and \(\mu ^{\prime}_{h}\), respectively, which we have taken to be constants—an acceptable model for flows near the surface of the ocean. The operators used in Eq. (1) are

$$\frac{{{\text{D}} }}{{{\text{D}}t^{\prime}}} \equiv \frac{\partial }{\partial t^{\prime}} + \frac{u^{\prime}}{{r^{\prime}\cos \theta }}\frac{\partial }{\partial \phi } + \frac{v^{\prime}}{{r^{\prime}}}\frac{\partial }{\partial \theta } + w^{\prime}\frac{\partial }{\partial r^{\prime}};\quad \nabla ^{\prime} \equiv \left( {\frac{1}{r^{\prime}\cos \theta }\frac{\partial }{\partial \phi }, \frac{1}{r^{\prime}}\frac{\partial }{\partial \theta }, \frac{\partial }{\partial r^{\prime}}} \right)$$

and

$$\nabla_{{\mu }^{\prime}}^{2} \equiv \mu_{v}^{\prime} \left( {\frac{{\partial^{2} }}{{\partial r^{{\prime}{2}} }} + \frac{2}{r^{\prime}}\frac{\partial }{\partial r^{\prime}}} \right) + \frac{{\mu_{h}^{\prime} }}{{r^{{\prime}{2}} }}\left( {\frac{1}{{\cos^{2} \theta }}\frac{{\partial^{2} }}{{\partial \phi^{2} }} + \frac{{\partial^{2} }}{{\partial \theta^{2} }} - \tan \theta \frac{\partial }{\partial \theta }} \right).$$

The equation of mass conservation, for constant density, is

$$\frac{1}{r^{\prime}\cos \theta }\left( {\frac{\partial u^{\prime}}{{\partial \phi }} + \frac{\partial }{\partial \theta }\left( {v^{\prime}\cos \theta } \right)} \right) + \frac{1}{{r^{{\prime}{2}} }}\frac{\partial }{\partial r^{\prime}}\left( {r^{{\prime}{2}} w^{\prime}} \right) = 0.$$
(2)

The first stage in the simplification of this system is to redefine the pressure as

$$p^{\prime} = \frac{{\rho ^{\prime}g^{\prime}R^{{\prime}{2}} }}{r^{\prime}} + \frac{1}{2}\rho ^{\prime}r^{{\prime}{2}} \Omega ^{{\prime}{2}} \left( {\sin^{2} \phi .\sin^{2} \theta + \cos^{2} \phi } \right) + P^{\prime}\left( {\phi , \theta , r^{\prime}, t^{\prime}} \right),$$

and then we write \(r^{\prime} = R^{\prime} + z^{\prime}\). The non-dimensionalisation that is appropriate for this problem is

$$z^{\prime} = D^{\prime}z, \left( {u^{\prime}, v^{\prime}, w^{\prime}} \right) = U^{\prime}\left( {u, v, \kappa w} \right), P^{\prime} = \rho ^{\prime}U^{{\prime}{2}} P, t^{\prime} = \frac{R^{\prime}}{{U^{\prime}}}t$$

where \(D^{\prime}\) is a suitable depth scale and \(U^{\prime}\) an average speed of the water–ice-wind motion. The constant κ is chosen to be consistent with the type of motion under consideration. We introduce the thin-shell parameter

$$\varepsilon = \frac{D^{\prime}}{{R^{\prime}}},$$

and then consistency requires that \(\kappa = {\text{O}}\left( \varepsilon \right)\); we choose \(\kappa = \varepsilon\). The natural depth scale is the Ekman thickness

$$D^{\prime} = \sqrt {\frac{{\mu_{v}^{\prime} }}{\rho ^{\prime}\Omega ^{\prime}}} ,$$

which is about 20 m, and then we define the parameters

$$\omega = \frac{D^{\prime}\Omega ^{\prime}}{{U^{\prime}}}, R_{eq} = \frac{\rho ^{\prime}U^{\prime}R^{\prime}}{{\mu_{q}^{\prime} }}\quad ({\text{for }}q \equiv h, v),$$

the former being an inverse Rossby number and the latter the two Reynolds numbers, which can be written as

$$R_{ev} = \frac{\omega }{\varepsilon }, R_{eh} = \left( {\frac{{\mu_{v}^{\prime} }}{{\mu_{h}^{\prime} }}} \right)\frac{\omega }{\varepsilon }.$$

We impose the limiting process \(\varepsilon \to 0\), keeping ω and \({\mu ^{\prime}_{v} }/ {\mu ^{\prime}_{h} }\) fixed; Eqs. (1) and (2) become (with an overall error of O(ε) in each equation and writing out the components of the Navier–Stokes equation):

$$\frac{{{\text{D}}u}}{{{\text{D}}t}} - uv\tan \theta - \frac{2\omega }{\varepsilon }\left( {v\cos \theta + \varepsilon w\sin \theta } \right)\sin \phi = - \frac{1}{\cos \theta }\frac{\partial P}{{\partial \phi }} + \frac{\omega }{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + 2\varepsilon \frac{\partial u}{{\partial z}}} \right);$$
(3)
$$\frac{{{\text{D}}v}}{{{\text{D}}t}} + u^{2} \tan \theta + \frac{2\omega }{\varepsilon }\left( {u\sin \phi - \varepsilon w} \right)\cos \theta = - \frac{\partial P}{{\partial \theta }} + \frac{\omega }{\varepsilon }\left( {\frac{{\partial^{2} v}}{{\partial z^{2} }} + 2\varepsilon \frac{\partial v}{{\partial z}}} \right);$$
(4)
$$- \left( {u^{2} + v^{2} } \right) + \frac{2\omega }{\varepsilon }\left( {u\sin \phi .\sin \theta + v\cos \phi } \right) = - \frac{1}{\varepsilon }\frac{\partial P}{{\partial z}} + \omega \frac{{\partial^{2} w}}{{\partial z^{2} }};$$
(5)
$$\frac{\partial u}{{\partial \phi }} + \frac{\partial }{\partial \theta }\left( {v\cos \theta } \right) + \frac{\partial w}{{\partial z}}\cos \theta = 0.$$
(6)

For steady flow—and we will restrict our discussion to this case—we have

$$\frac{{{\text{D}} }}{{{\text{D}}t}} \equiv u\frac{\partial }{\partial \phi } + v\frac{\partial }{\partial \theta } + w\frac{\partial }{\partial z},$$

with the same overall error. It is not possible to produce a mathematically complete justification for the existence of an asymptotic solution (based on \(\varepsilon \to 0\)) because of the complexity of this system, but the solutions that we seek and present, correct at leading order, are sufficiently well-behaved to indicate that no singularities can arise at higher order. Of course, such higher-order terms can be used to obtain (small) corrections to the solutions that we shall describe.

3 The velocity field (at leading order)

The next stage in the analysis is to extract the relevant asymptotic approximations from Eqs. (3)–(6). This involves the introduction of a geostrophic flow (which we assume is given) and the Ekman contribution to the velocity field.

3.1 Geostrophic flow

This flow is defined by a solution of

$$- 2\omega v_{g} \cos \theta .\sin \phi = - \frac{1}{\cos \theta }\frac{{\partial P_{g} }}{\partial \phi };\quad 2\omega u_{g} \cos \theta .\sin \phi = - \frac{{\partial P_{g} }}{\partial \theta },$$
(7)

independent of z; this pair of equations shows that

$$\frac{\partial }{\partial \phi }\left( {u_{g} \cos \theta .\sin \phi } \right) + \frac{\partial }{\partial \theta }\left( {v_{g} \cos^{2} \theta .\sin \phi } \right) = 0.$$

The route that we take here is to choose a stream function, \(\psi \left( {\phi , \theta } \right)\), where

$$u_{g} = \frac{1}{\cos \theta .\sin \phi }\frac{\partial \psi }{{\partial \theta }}, v_{g} = - \frac{1}{{\cos^{2} \theta .\sin \phi }}\frac{\partial \psi }{{\partial \phi }},$$
(8)

making a choice which corresponds to a suitable model for the geostrophic flow from the neighbourhood of the Laptev and East Siberian Seas to the Fram Strait. This solution produces a contribution to the perturbation pressure in the form \(P = {\raise0.7ex\hbox{${P_{g} }$} \!\mathord{\left/ {\vphantom {{P_{g} } \varepsilon }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\varepsilon $}}.\)

3.2 Ekman flow

The Ekman component in the velocity field is the same size (in terms of ε) as the geostrophic flow (although we expect the former to be rather smaller than the latter); we write

$$\left( {u, v} \right) = \left( {u_{g} , v_{g} } \right) + \left( {u_{E} , v_{E} } \right)$$

with

$$P = \frac{1}{\varepsilon }P_{g} + P_{E} ,$$

the geostrophic flow being that defined above. Thus, at leading order as \(\varepsilon \to 0\), we obtain

$$- 2v_{E} \cos \theta .\sin \phi = \frac{{\partial^{2} u_{E} }}{{\partial z^{2} }};$$
(9)
$$2u_{E} \cos \theta .\sin \phi = \frac{{\partial^{2} v_{E} }}{{\partial z^{2} }};$$
(10)
$$\frac{{\partial P_{E} }}{\partial z} = - 2\omega \left( {u_{E} \sin \theta .\sin \phi + v_{E} \cos \phi } \right);$$
(11)
$$\frac{\partial }{\partial \phi }\left( {u_{g} + u_{E} } \right) + \frac{\partial }{\partial \theta }\left[ {\left( {v_{g} + v_{E} } \right)\cos \theta } \right] + \frac{\partial w}{{\partial z}}\cos \theta = 0.$$
(12)

The solution of (9) and (10) that is relevant here is

$$\left. {\begin{array}{*{20}r} \hfill {u_{E} = A\left( {\phi , \theta } \right){\text{e}}^{\lambda z} \cos \left( {\lambda z - \gamma \pi } \right)} \\ \hfill {v_{E} = A\left( {\phi , \theta } \right){\text{e}}^{\lambda z} \sin \left( {\lambda z - \gamma \pi } \right)} \\ \end{array} } \right\}$$
(13)

where \(\lambda = \sqrt {\sin \phi .\cos \theta }\) (= 1 at the North Pole), producing decay in z < 0. The Ekman flow described by (13) is, at the surface, in the direction given by

$$\frac{{v_{E} }}{{u_{E} }} = - \tan \left( {\gamma \pi } \right),$$

with an arbitrary amplitude \(A\left( {\phi , \theta } \right)\). Equation (11) shows that we have an additional contribution to the pressure perturbation, generated by the Ekman flow; furthermore, there is the familiar upwelling/downwelling, \(w\left( {\phi , \theta , z} \right)\), given by the solution of Eq. (12). This w is produced by both the geostrophic and Ekman flows, but we note that the geostrophic contribution is zero at the North Pole (and small in the neighbourhood of it); indeed, this term is absent in the f-plane approximation (see [7]). When it is present, it generates a term in w which is linear in z, but this solution is valid only in the surface layer of the ocean. Such a behaviour must match to the appropriate flow at greater depths (but this is not pursued here).

3.3 The Transpolar Drift current

The TDc is the sum of the geostrophic and Ekman flows and, in particular, we focus on the current at the surface of the ocean (z = 0); we write this as \(\left( {u_{T} , v_{T} } \right)\) and so we have

$$\left( {u_{T} , v_{T} } \right) = \left( {u_{g} \left( {\phi , \theta } \right) + A\left( {\phi , \theta } \right)\cos \left( {\gamma \pi } \right), v_{g} \left( {\phi , \theta } \right) - A\left( {\phi , \theta } \right)\sin \left( {\gamma \pi } \right)} \right).$$

In our approach, we are given the geostrophic flow and then, for the Ekman flow, we compute the stress that is produced by the ice floating on the ocean (which drives the Ekman component). This stress is, in turn, generated by the stress on the upper surface of the ice, produced by the action of the wind. So, although we are essentially working (in mathematical terms) from the bottom upwards, we must bear in mind that the underlying physics has a geostrophic flow below the ice and a wind above, which combine as the drivers of the motion. Because of the algebraic structure of the problem—as will become evident—we may interpret our solution in precisely these terms: geostrophic flow + wind → motion. In other words, there is no question of any non-uniqueness being associated with the reversal of some of these mathematical interpretations.

4 The water–ice-air boundary condition

We start by choosing the fundamental model that describes the stresses on the upper and lower surfaces of the ice. This is based on the description of the turbulent processes that are involved, which are usually represented by a quadratic drag-law for the stress:

$$\tau ^{\prime} = \rho ^{\prime}C{\mathbf{u}}^{\prime}\left| {{\mathbf{u}}^{\prime}} \right|,$$

where C is the (nondimensional) drag coefficient, \(\rho ^{\prime}\) the appropriate density and \({\mathbf{u}}^{\prime}\) the relative horizontal velocity; see [12]. Thus, in particular, the drag of ice over water (which provides a shear at the surface of the ocean) is written as

$$\mu_{v}^{\prime} \frac{{\partial {\mathbf{u}}^{\prime}}}{\partial z^{\prime}} = - \rho ^{\prime}C_{oi} \left| {{\mathbf{u}}^{\prime} - {\mathbf{u}}_{i}^{\prime} } \right|\left( {{\mathbf{u}}^{\prime} - {\mathbf{u}}_{i}^{\prime} } \right),$$
(14)

where \({\mathbf{u}}^{\prime}\) is the horizontal velocity of the ocean and \({\mathbf{u}}^{\prime}_{i}\) the velocity of the ice; \(C_{oi} \approx 5\cdot 5 \times 10^{ - 3}\) is the corresponding drag coefficient, this being a suitable estimate (see [13]). The boundary condition (14) is evaluated at the surface; we shall be more precise about this shortly. However, the effect of the stresses above and below the ice present a more complicated picture.

The difference in stress above (due to the wind) and below (due to the ocean) generates an internal stress that needs to be modelled; for much of the relevant background, see [6, 14,15,16]. The underlying model is that of a viscous plastic material with an internal pressure. It is sufficient to assume that the internal stress is dominated by this internal pressure ([14]), with a varying thickness of ice throughout the flow, from the start off the coast of Russia to the Fram Strait, i.e. there is always total ice cover in our presentation. Further, the internal pressure is taken to be well-represented as proportional to the ice thickness; with these various simplifying assumptions, the stress relation for the ice can be written

$$\rho_{a}^{\prime} C_{ai} \left| {{\mathbf{u}}_{w}^{\prime} - {\mathbf{u}}_{i}^{\prime} } \right|\left( {{\mathbf{u}}_{w}^{\prime} - {\mathbf{u}}_{{\mathbf{i}}}^{\prime} } \right) + \rho ^{\prime}C_{oi} \left| {{\mathbf{u}}^{\prime} - {\mathbf{u}}_{i}^{\prime} } \right|\left( {{\mathbf{u}}^{\prime} - {\mathbf{u}}_{{\mathbf{i}}}^{\prime} } \right) + \nabla_{2}^{\prime} \left( { - \Pi ^{\prime}h^{\prime}} \right) = 0,$$
(15)

where \(\rho ^{\prime}_{a}\) is the density of the air just above the surface of the ice, \(C_{ai} \approx 1\cdot 8 \times 10^{ - 3}\) is the drag coefficient of air-over-ice and \({\mathbf{u}}^{\prime}_{w}\) is the velocity of the wind near the surface. The internal mechanics of the ice are represented by the ice strength, \(\Pi ^{\prime}\) (a constant), and the ice thickness is \(h^{\prime}\left( {\phi , \theta } \right)\)(for steady motion), with

$$\nabla_{2}^{\prime} \equiv \left( {\frac{1}{r^{\prime}\cos \theta }\frac{\partial }{\partial \phi }, \frac{1}{r^{\prime}}\frac{\partial }{\partial \theta }} \right).$$

Finally, we require an equation which describes how the thickness of the ice varies; in this discussion of the TDc, an important element is the reduction in the ice thickness as it approaches the Fram Strait, essentially dropping to zero as the flow enters the North Atlantic. The model that we adopt (see [14]) is to invoke a continuity equation which balances horizontal flux divergence against the formation/loss of ice due to cooling/heating at the surface of the ice. The heat loss is proportional to the temperature change across the ice (that is, the freezing temperature of ice minus the surface temperature of the ice) which here we take to be a constant. Further, we assume that this heat loss is inversely proportional to the thickness of the ice, and so we have

$$\nabla_{2}^{\prime} \cdot \left( {{\mathbf{u}}^{\prime}_{i} h^{\prime}} \right) = \frac{\Gamma ^{\prime}}{{h^{\prime}}},$$
(16)

where \(\Gamma ^{\prime}\) is a positive constant. It is clear from all the above that we have had to use a significant element of modelling here. The aim is to show that, simple though this model is (and we may note in advance that \(h^{\prime} = 0\) is likely to be troublesome), it captures all the salient features of the TDc: its motion and its connection to the surface wind, and the change in ice thickness in the flow across the North Pole towards the Fram Strait. Of course, this is an area of the analysis that can be explored further, with the hope that a more detailed and accurate model can be constructed (and one which, it is hoped, still enables some analytical headway to be made).

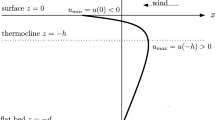
The two conditions that describe the drag on the upper and lower surfaces of the ice, (14) and (15), are to be evaluated at the surface of the ocean, and we must be clear what that means. The ice thickness across the North Pole, and beyond, is no more than about 2 m, which is small when compared with the vertical scale that we have used here (the Ekman thickness: about 20 m). Thus we evaluate both stress conditions (on the top and on the bottom of the ice) on \(z^{\prime} = 0\) (i.e. z = 0 in nondimensional form). We now use the non-dimensionalisation previously introduced to give (in the thin-shell approximation)

$$\frac{{\partial {\mathbf{u}}}}{\partial z} = - c_{oi} \left| {{\mathbf{u}} - {\mathbf{u}}_{i} } \right|\left( {{\mathbf{u}} - {\mathbf{u}}_{i} } \right) = r_{a} c_{ai} \left| {{\mathbf{u}}_{w} - {\mathbf{u}}_{i} } \right|\left( {{\mathbf{u}}_{w} - {\mathbf{u}}_{i} } \right) - \nu \left( {\frac{1}{\cos \theta }\frac{\partial h}{{\partial \phi }}, \frac{\partial h}{{\partial \theta }}} \right)\quad {\text{on}} \,z = \, 0,$$
(17)

with

$$\left( {\frac{1}{\cos \theta }\frac{\partial }{\partial \phi }, \frac{\partial }{\partial \theta }} \right)\cdot \left( {{\mathbf{u}}_{i}^{\prime} h} \right) = \frac{\Gamma }{h},$$
(18)

where

$$c_{oi} = C_{oi} \frac{\rho ^{\prime}U^{\prime}D^{\prime}}{{\mu_{v}^{\prime} }}, c_{ai} = C_{ai} \frac{\rho ^{\prime}U^{\prime}D^{\prime}}{{\mu_{v}^{\prime} }}, r_{a} = \frac{{\rho_{a}^{\prime} }}{\rho ^{\prime}}, \nu = \frac{\Pi ^{\prime}H^{\prime}D^{\prime}}{{\mu_{v}^{\prime} R^{\prime}U^{\prime}}}, \Gamma = \frac{\Gamma ^{\prime}R^{\prime}}{{U^{\prime}H^{{\prime}{2}} }};$$

we have written \(h^{\prime} = H^{\prime}h\) where \(H^{\prime}\) is an average (or maximum) thickness of the ice. It is expected that the contribution to the velocity of the ice from the change in ice thickness (which appears in (17)) is very small; the only situation where this may not be true is if the derivatives of h become large, which we will comment on later.

5 Solutions for the TDc, for the motion of the ice and for the wind flow

The equations that we have developed—(7) and (8) for the geostrophic flow, (9)–(12) with (13) for the Ekman flow, and (17) and (18) for the interaction with the ice and wind—are now examined with the aim of producing relevant solutions. It will be evident, at various stages throughout the analysis, that many choices and further avenues of exploration are possible; we present just one direct route. The development, for the ease of construction, starts with the geostrophic flow, adds the Ekman component and then, via the surface conditions, we find the motion (and variation in thickness) of the ice and finally the wind consistent with the motion of both ice and ocean. Once we have the solution, the interpretation is: given the geostrophic flow and the wind over the ice, this produces a motion (and development) of the ice and the flow of the TDc.

The geostrophic flow is most naturally expressed in terms of a variable that describes a loxodrome path (i.e. a rhumb line) together with either \(\phi\) or θ; we choose \(\phi\). So we introduce

$$\xi = \phi - \frac{\pi }{2} - k\ln \left( {\frac{\cos \theta }{{1 - \sin \theta }}} \right),$$
(19)

where k is a constant, with \(\xi =\) constant being a loxodrome; an example is shown in Fig. 2. (All calculations were performed using Maple.) It is clear that this path deviates little from a straight line in the region of interest, from the seas off Russia to the Fram Strait. A simple choice which captures the character of the geostrophic flow, with an increase in speed towards the Fram Strait, is the stream function (see (8))

$$\psi = - u_{0} \left( {1 + \alpha \Phi } \right)\xi ,$$
(20)

where \(\Phi = \phi - \frac{\pi }{2}\), with \(u_{0} > 0, \alpha > 0\) constants. This produces the velocity components of the geostrophic flow as

$$u_{g} = \frac{{u_{0} k\left( {1 + \alpha \Phi } \right)}}{{\cos^{2} \theta .\sin \left( {\Phi + \frac{\pi }{2}} \right)}}, v_{g} = \frac{{u_{0} \left[ {1 + \alpha \left( {\Phi + \xi } \right)} \right]}}{{\cos^{2} \theta .\sin \left( {\Phi + \frac{\pi }{2}} \right)}},$$
(21)

with \(\xi = \Phi - k\ln \left( {\frac{\cos \theta }{{1 - \sin \theta }}} \right)\). For the purposes of our presentation, we will give the details for the flow (and for the ice movement and evolution, and for the wind) along a path \(\xi =\) constant which follows a mid-line through the TDc from \(\left( {\Phi_{0} , \theta_{0} } \right)\) to \(\left( {\Phi_{1} , \theta_{1} } \right)\). A reasonable choice for these two positions is

$$\left( {\Phi_{0} , \theta_{0} } \right) = - \left( {5^{o} , 5^{o} } \right)\;{\text{and }}\left( {\Phi_{1} , \theta_{1} } \right) = \left( {2^{o} , 12^{o} } \right).$$
(22)
Fig. 2
figure 2

A loxodrome path with the section that follows the mid-line of the TDc in red

Full size image

For information, the orientation of the TDc in the Arctic Ocean is shown in Fig. 3.

Fig. 3
figure 3

Sketch of the general direction of the TDc (in red), starting from neighbourhood of the Laptev and East Siberian Seas (LS & ESS) and entering the Fram Strait (FS). GL = Greenland, CB = Canada Basin, NP = North Pole. The θ coordinate points towards the Null Island (Z) and Φ points West (W)

Full size image

The Transpolar Drift current is the sum of the geostrophic and Ekman flows, and so from (13) and (21) we have the TDc given by

$$u_{T} = u_{g} + u_{E} = \frac{{u_{0} k\left( {1 + \alpha \Phi } \right)}}{{\cos^{2} \theta .\sin \left( {\Phi + \frac{\pi }{2}} \right)}} + A\left( {\phi , \theta } \right)\cos \left( { - \gamma \pi } \right);$$
(23)
$$v_{T} = v_{g} + v_{E} = \frac{{u_{0} \left[ {1 + \alpha \left( {\Phi + \xi } \right)} \right]}}{{\cos^{2} \theta .\sin \left( {\Phi + \frac{\pi }{2}} \right)}} + A\left( {\phi , \theta } \right)\sin \left( { - \gamma \pi } \right).$$
(24)

The Ekman component could have a variable amplitude, \(A\left( {\phi , \theta } \right)\) (and indeed a variable \(\gamma \left( {\phi , \theta } \right)\)), but it is sufficient, for our purposes, to restrict the discussion to the case A = constant, γ = constant. The amplitude (speed) of the Ekman flow is considerably less than that of the geostrophic flow, and we select γ so that the Ekman component at the surface is directed towards Greenland as the TDc passes through the Fram Strait; this is consistent with the observations (see [17]).

The movement of the ice is obtained from (17), with

$$\left. {\frac{{\partial {\mathbf{u}}}}{\partial z}} \right|_{z = 0} = \left. {\frac{{\partial {\mathbf{u}}_{E} }}{\partial z}} \right|_{z = 0} = A\lambda \sqrt 2 \left( {\cos \left( {\frac{\pi }{4} - \gamma \pi } \right), \sin \left( {\frac{\pi }{4} - \gamma \pi } \right)} \right),$$

which gives

$$A\lambda \sqrt 2 \cos \left( {\frac{\pi }{4} - \gamma \pi } \right) = - \gamma_{oi} \left| {{\mathbf{u}} - {\mathbf{u}}_{i} } \right|\left( {u_{g} + u_{E} - u_{i} } \right);$$
$$A\lambda \sqrt 2 \sin \left( {\frac{\pi }{4} - \gamma \pi } \right) = - \gamma_{oi} \left| {{\mathbf{u}} - {\mathbf{u}}_{i} } \right|\left( {v_{g} + v_{E} - v_{i} } \right),$$

where

$$\left| {{\mathbf{u}} - {\mathbf{u}}_{i} } \right| = \sqrt {\left( {u_{g} + u_{E} - u_{i} } \right)^{2} + \left( {v_{g} + v_{E} - v_{i} } \right)^{2} } .$$

Solving these, and requiring that \(u_{i} > u_{g} + u_{E}\), we obtain

$$u_{i} = u_{g} + u_{E} + \delta \sqrt {A\lambda } \cos \left( {\frac{\pi }{4} - \gamma \pi } \right);$$
(25)
$$v_{i} = v_{g} + v_{E} + \delta \sqrt {A\lambda } \sin \left( {\frac{\pi }{4} - \gamma \pi } \right),$$
(26)

where \(\delta = \sqrt {{\raise0.7ex\hbox{${\sqrt 2 }$} \!\mathord{\left/ {\vphantom {{\sqrt 2 } {\gamma_{oi} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\gamma_{oi} }$}}}\).

The evolution of the thickness of the sea ice which, in turn, feeds into the determination of the wind velocity, is a more involved calculation. From (18) we have

$$\frac{1}{\cos \theta }\frac{\partial }{\partial \phi }\left( {u_{i} h} \right) + \frac{\partial }{\partial \theta }\left( {v_{i} h} \right) = \frac{\Gamma }{h}$$
(27)

where \(\left( {u_{i} , v_{i} } \right)\) is given in (25), (26). Thus the equation for \(h\left( {\Phi , \theta } \right)\)—it is now more convenient to work with Φ rather than \(\phi\)—becomes

$$\begin{aligned} & \frac{1}{\cos \theta }\frac{\partial }{\partial \Phi }\left\{ {\left[ {\frac{{k\left( {1 + \alpha \Phi } \right)}}{{\cos^{2} \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)}} + a\cos \left( { - \gamma \pi } \right) + \eta \sqrt \lambda \cos \left( {\frac{\pi }{4} - \gamma \pi } \right)} \right]h} \right\} \\ & \quad + \frac{\partial }{\partial \theta }\left\{ {\left[ {\frac{{1 + 2\alpha \Phi - \alpha k\ln \left( {\frac{\cos \theta }{{1 - \sin \theta }}} \right)}}{{\cos^{2} \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)}} - a\sin \left( { - \gamma \pi } \right) + \eta \sqrt \lambda \sin \left( {\frac{\pi }{4} - \gamma \pi } \right)} \right]h} \right\} = \frac{{{\raise0.7ex\hbox{$\Gamma $} \!\mathord{\left/ {\vphantom {\Gamma {u_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{0} }$}}}}{h}, \\ \end{aligned}$$
(28)

where \(a = {\raise0.7ex\hbox{$A$} \!\mathord{\left/ {\vphantom {A {u_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{0} }$}}, \eta = {\raise0.7ex\hbox{${\delta \sqrt A }$} \!\mathord{\left/ {\vphantom {{\delta \sqrt A } {u_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{0} }$}}\) which, with A = constant, are both constants, and

$$\lambda = \sqrt {\cos \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)} .$$

For the purposes of our presentation, we require the solution of (28) only along the path followed by the TDc from \(\left( {\Phi_{0} , \theta_{0} } \right)\) to \(\left( {\Phi_{1} , \theta_{1} } \right)\); see (22) and Fig. 2. Now, in order to produce a simple description of the variation in ice thickness, and for ease of explanation, we make an adjustment. We take the path to be a straight line, with all the coefficients in (28) fixed (constant)—they vary little along the path—and then we obtain

$$\left[ {MN + k\left( {1 + \alpha \Phi } \right)} \right]\frac{\partial h}{{\partial \Phi }} + \left[ {1 + MQ + \alpha \left( {2\Phi - k\theta } \right)} \right]\frac{\partial h}{{\partial \theta }} = \frac{{{\raise0.7ex\hbox{${M\Gamma }$} \!\mathord{\left/ {\vphantom {{M\Gamma } {u_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{0} }$}}}}{h},$$
(29)

where

$$M = \cos^{2} \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right),$$
$$N = a\cos \left( { - \gamma \pi } \right) + \eta \cos \left( {\frac{\pi }{4} - \gamma \pi } \right)\sqrt {\cos \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)} ,$$
$$Q = a\sin \left( { - \gamma \pi } \right) + \eta \sin \left( {\frac{\pi }{4} - \gamma \pi } \right)\sqrt {\cos \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)} .$$

(The numerical version of this problem, which will provide the results that we quote in the next section, is based on the original equation, (28); however, the numerical differences between the two versions, for flow along the TDc mid-line, are small. Indeed, (29) is a very good basis for extracting, in a simple manner, the important properties of the solution.) The general solution of (29) is

$$h = \sqrt {b\ln \left( {1 + \frac{MN}{k} + \alpha \Phi } \right) + F\left( \zeta \right)} \ge 0,$$
(30)

where F(.) is an arbitrary function of \(\zeta = \left( {1 + \frac{MN}{k} + \alpha \Phi } \right)\left[ {M\left( {\frac{N}{k} - Q} \right) + \alpha \left( {k\theta - \Phi } \right)} \right],\)

with

$$b = \frac{2\Gamma M\cos \theta }{{\alpha ku_{0} }}\,\;(=\rm{constant \;here}).$$

The function F(ζ) makes it possible to prescribe the thickness of the ice along an initial line which, in this context could be, for example, the 85oN line to the north of the Laptev and East Siberian Seas. Here, we opt for a simpler specification of this function: we write

$$F\left( \zeta \right) = B\zeta + C,$$
(31)

where B and C are constants, chosen so that h = 1 at \(\left( {\Phi_{0} , \theta_{0} } \right)\) and h = 0 just beyond \(\left( {\Phi_{1} , \theta_{1} } \right)\) (because we must avoid h = 0 in the solution of (26)); we have chosen the non-dimensionalisation of h to be the maximum thickness of the ice. The result is to produce an ice thickness which decreases from one end to the other on the TDc mid-line path. The initial profile of the ice thickness, along a given line, that corresponds to this solution, can be found from (30) using the chosen F(ζ).

Finally, we determine the wind that blows over the ice and which is consistent with, i.e. generates, the solution that we have constructed. From (17) we find that

$$u_{w} = u_{i} + \frac{1}{{\sqrt {r_{a} \gamma_{ai} } }}\sqrt {\frac{{A\lambda \sqrt 2 \cos \left( {\frac{\pi }{4} - \gamma \pi } \right) + \frac{\nu }{\cos \theta }\frac{\partial h}{{\partial \phi }}}}{{\sqrt {1 + \Lambda^{2} } }}} ;$$
$$v_{w} = v_{i} + \frac{1}{{\sqrt {r_{a} \gamma_{ai} } }}\sqrt {\frac{{A\lambda \sqrt 2 \sin \left( {\frac{\pi }{4} - \gamma \pi } \right) + \nu \frac{\partial h}{{\partial \theta }}}}{{\sqrt {1 + \Lambda^{2} } }}} ,$$

where

$$\Lambda = \frac{{A\lambda \sqrt 2 \sin \left( {\frac{\pi }{4} - \gamma \pi } \right) + \beta \frac{\partial h}{{\partial \theta }}}}{{A\lambda \sqrt 2 \cos \left( {\frac{\pi }{4} - \gamma \pi } \right) + \frac{\beta }{\cos \theta }\frac{\partial h}{{\partial \phi }}}}.$$

However, the rôle of the rate of change of ice thickness is, for most of the movement along the TDc, unimportant—we will comment more on this shortly—and then we simply have

$$\begin{aligned} u_{w} & = u_{i} + \sigma \sqrt {\cos \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)} \cos \left( {\frac{\pi }{4} - \gamma \pi } \right), \\ v_{w} & = v_{i} + \sigma \sqrt {\cos \theta .\sin \left( {\frac{\pi }{2} + \Phi } \right)} \sin \left( {\frac{\pi }{4} - \gamma \pi } \right), \\ \end{aligned}$$
(32)

with \(\left( {u_{i} , v_{i} } \right)\) given in (25), (26) and

$$\sigma = \sqrt {\frac{A\sqrt 2 }{{r_{a} \gamma_{ai} }}} .$$

We note, using the solution based on (31), that the derivatives \(\frac{\partial h}{{\partial \theta }}, \frac{\partial h}{{\partial \Phi }}\) are proportional to \(1/{\sqrt h }\) and so, as \(h \to 0\), these contributions will become important. But we have already excluded h = 0 from our considerations and so, over most over the length of the TDc, the wind is described by (32) (because ν is small); in this investigation, we will ignore the contribution of the wind over the final stages of the motion where h is small. Clearly, this is an area that could be explored in more detail, but the result is likely to produce no more than a minor refinement to the description presented here (although it could raise some intriguing modelling and mathematical issues). We will write more on this issue later.

The three elements that comprise the motion described by the solution—ocean, ice, wind—are represented in the vector diagrams shown in Fig. 4. This summarises the flow structure: the TDc moves to the right of the geostrophic current and is faster; the ice moves to the right of the TDc and is faster; the wind blows to the right of the ice flow and is faster. We note, however, that we should interpret these diagrams as though we are given suitable (that is, consistent with the prevailing directions of each) wind flow and geostrophic current; these then determine the direction of flow of the TDc and of the floating ice.

Fig. 4
figure 4

From left to right: a the geostrophic flow and the Ekman component producing the TDc; b the motion of the ice relative to the TDc; c the wind blowing over the ice, relative to the direction of ice flow

Full size image

6 Example of the solution

So far we have presented a theoretical description of this ocean-ice-wind complex, explaining the background, model and simplifications that we invoked in order to make progress; we now take this approach a little further. It is helpful, we suggest, to offer, in a graphical form, a specific example of some of the results that we have obtained. To do this we must choose suitable parameter values, which we will report in what follows.

The development has been built around the aim to obtain all the relevant details for the flow properties along the loxodrome path that sits more-or-less on the mid-line of the TDc. Thus we shall give an example of the speeds of the TDc, of the ice and of the wind along this path, where the geostrophic flow—the main driver of the TDc—increases about three-fold from \(\left( {\Phi_{0} , \theta_{0} } \right)\) to \(\left( {\Phi_{1} , \theta_{1} } \right)\). First, the loxodrome curve joining these two points is shown in Fig. 5, where we have set (see (22))

$$\left( {\Phi_{0} , \theta_{0} } \right) = - \left( {5^{o} , 5^{o} } \right)\;{\text{and }}\left( {\Phi_{1} , \theta_{1} } \right) = \left( {2^{o} , 12^{o} } \right);$$

these give \(\xi \approx - 0\cdot 051, k \approx 0\cdot 41\) (see (19)). We now compute the speed of the TDc (from (23), (24)), the speed of the ice (from (25), (26) and the speed of the wind (from (32) along this loxodrome path; the results are shown in Fig. 6. The values of the various parameters used here are:

$$\gamma = \frac{\pi }{6}, u_{0} \approx 2\cdot 98, \alpha = 5\cdot 4, \frac{A}{{u_{0} }} = 0\cdot 1, \delta \sqrt A = 0\cdot 1, \sigma = 0\cdot 1.$$
Fig. 5
figure 5

The section of the loxodrome along the mid-line of the TDc

Full size image
Fig. 6
figure 6

The speeds of the three components of the flow: TDc (red), ice (blue), wind (green)

Full size image

Because these data have been used to produce the behaviour along the TDc mid-line, these speed curves should be read in conjunction with the relative directions of the three components, as sketched in Fig. 4. We note that the directions of the TDc, the ice and the wind differ only slightly from being parallel, with our choice of parameter values (which accord with the observations) and so the speeds along the mid-line provide a good guide to these flow properties. Clearly an extended and more detailed examination could be undertaken and suitable details extracted. In our version, we see that we have an increase in speed from TDc to ice to wind, with directions consistent with observations; see [16, 18,19,20,21].

In Fig. 7 we show an example of the decrease in ice thickness along the mid-line of the TDc, using a linear function of the characteristic variable (see (31) with (30)) but based on the original equation for h, (28), with \(\eta = 0\cdot 1\). The boundary conditions that we have imposed are: h = 1 at \(\left( {\Phi_{0} , \theta_{0} } \right)\) and h = 0 at \(\left( {\Phi_{2} , \theta_{2} } \right)\) on the loxodrome, where \(\theta_{2} = 1\cdot 05\theta_{1}\), i.e. we set the ice thickness to be zero outside the domain that we are plotting, and so h = 0 is not attained in our solution. This shows the expected reduction in ice thickness, although we note that this ice-thickness curve has infinite derivatives where h = 0 (which we noted earlier). Thus a model that is to accommodate h = 0 at some finite point must be more sophisticated than we have used here; this needs further investigation.

Fig. 7
figure 7

Ice thickness along the TDc mid-line

Full size image

7 Discussion

The main aim of the work presented here is to show that oceanic flows in the neighbourhood of the North Pole can be analysed on the basis of a correct choice of spherical coordinates, coupled with the thin-shell approximation. In the context of the ocean-ice-wind complex, there are other issues—essentially the choice of boundary conditions—which we will come to shortly.

The spherical coordinates that we use, being a rotation of the familiar geographical coordinates, have been introduced and analysed in earlier work [3, 4]. The nett result is a simple extension of the classical formulation, the changes being due to the different orientation of the Earth’s axis of rotation in the new system. (We comment that there is a complication in deriving the relationship between the geographical and rotated coordinates, but that is irrelevant here.) The underlying governing equations are altogether familiar and, more significantly, they can be reduced to a consistent asymptotic form simply by invoking the thin-shell approximation. This ensures that we retain all the relevant geometrical physical properties for motion in a thin layer on the surface of a rotating sphere. In particular, there is no need to work with the f-plane approximation and an associated tangent plane. We have seen that this set of equations admits both a geostrophic flow and an Ekman flow, these being the essential elements in the description of the Transpolar Drift current. This aspect of the problem is routine, leading to a solution (with considerable freedom) that is easily constructed and interpreted. However, complications arise when we examine the nature of the boundary condition at the surface.

At the surface we have used the conventional rule for modelling the drag associated with turbulent processes: a stress proportional to the square of the relative speed. This, we might reasonably argue, is an uncontested and accepted model. The real difficulties are evident when we connect the stresses on the upper and lower surfaces of the ice, via the internal properties of the ice. This is an area of considerable debate, requiring some significant modelling. On the basis of much of the seminal work on this (see [6, 14,15,16]), we have opted for a simple rule, using only an internal pressure of the ice represented by a constant ice strength. The upshot is to produce an elementary version of the boundary condition that transmits the stress from the wind, through the ice, to the ocean. But this must be coupled to a model for the decrease/increase in ice thickness as the ice moves, required to generate the derivatives of the thickness function needed in the stress condition (as well as provide a description of the change in thickness). A very simple model (see [14]) takes the heat loss to be inversely proportional to the thickness of the ice. As we have seen, this leads—at least for the otherwise acceptable solution that we have presented—to infinite derivatives where the thickness drops to zero. For the analytical details and, perhaps more importantly, the numerical version of these, we avoided this singularity by requiring it to sit outside the domain that we have considered. It is clear that a more precise and carefully-constructed model for the properties of the ice (both internally and the mechanism for thickness change) is required. In this initial investigation, which has shown that the general approach that we have adopted, is both reasonable and viable, we have not explored this further. Nevertheless, this is an important issue that must be investigated (and we plan to do so in some follow-up work). This will involve both a more accurate modelling process and, most likely, the need for a more extensive mathematical analysis.

With all the caveats that we have just outlined, we briefly summarise what we have found. Under the umbrella of the thin-shell approximation, the governing equations that we derive are linear, and so the construction—selection—of suitable solutions is routine (and the quadratic structure of the stress conditions at the surface does not complicate this picture unduly). So we have chosen a suitable geostrophic flow which, when combined with the classical Ekman solution, has produced a TDc. This has led directly to the formulation of the problem for the movement of the ice and of the wind blowing over it, although this latter calculation was somewhat simplified. In particular, the contribution from the rate of change of ice thickness (over distance) was ignored—it is small except near the point where the ice vanishes—and then a simple solution of the ice-thickness equation was chosen. This produced an analytical and numerical solution which accords well with the observations: the directions of flow of each component and speed variation of the flow towards the Fram Strait. The variation in ice thickness is less satisfactorily reproduced in our solution, but that—as previously observed—is due to the model used here.

In summary, we submit that we have presented a good case for the use of suitable rotated, spherical coordinates, in conjunction with the thin-shell approximation, in these types of problem. However, the weakness of these analyses rests on the need to introduce and formulate suitable stress conditions at the surface, together with the physical principles underpinning the change in ice thickness. So, on the one hand, we have a convincing and robust description of the fluid dynamics, and many choices are possible for further investigation: more variability in the geostrophic and Ekman flows, including the effects of topography, for example. On the other hand, although the general formulation of the equations and boundary conditions is, we believe, reliable, the details describing the nature and the rôle of the ice sheet requires more work. There are many avenues ripe for further investigation.