Monotonicity of the period map for the equation $-\varphi ''+\varphi -\varphi ^{k}=0$

Abstract

In this paper, we establish the monotonicity of the period map in terms of the energy levels for certain periodic solutions of the equation $-\varphi ''+\varphi -\varphi ^{k}=0$, where $k>1$ is a real number. We present a new approach to demonstrate this property, utilizing spectral information of the corresponding linearized operator around the periodic solution and tools related to Floquet theory.

1 Introduction

Let $\varphi :\mathbb {R}\rightarrow \mathbb {R}$ be a periodic solution of the equation

$$\begin{aligned} -\varphi ''+ \varphi -\varphi ^k = 0, \end{aligned}$$

(1.1)

where $k>1$ is a real number and $\varphi =\varphi (x)$ is a function depending on $x\in \mathbb {R}$. We easily verify that, the function defined by

$$\begin{aligned} \mathcal {E}(\varphi , \xi ) = \frac{\xi ^2}{2} -\frac{\varphi ^2}{2}+\frac{\varphi ^{k+1}}{k+1}, \end{aligned}$$

(1.2)

is a first integral for the two dimensional system associated to Eq. (1.1), where $\xi =\varphi '$. In other words, this means that the pair $(\varphi ,\xi )$ satisfies $\mathcal {E}(\varphi ,\xi )=B$ for convenient values $B\in \mathbb {R}$. When $k>1$ and $\frac{1-k}{2(k+1)}<B<0$, we obtain periodic orbits that spinning around the center point (1, 0). When $k>1$ is particular an odd number, we also obtain periodic solutions but for all $B>0$. In this case, the periodic solutions change their sign, and all initial conditions associated with the solution are located outside the separatrix curve. (a curve that converges to the saddle point (0, 0) in the associated phase portrait).

The period map $L=L(B)$ of the periodic solution $\varphi$ depends on B and it can be expressed by

$$\begin{aligned} L=\displaystyle 2\int _{b_1}^{b_2}\frac{dh}{\sqrt{-\frac{2h^{k+1}}{k+1}+ h^2+2B}}, \end{aligned}$$

(1.3)

where $b_1=\displaystyle \min \nolimits _{x\in [0,L]}\varphi (x)$ and $b_2=\displaystyle \max \nolimits _{x\in [0,L]}\varphi (x)$. This expression is not very handy to obtain the smoothness of the period function L in terms of B since $b_1$ and $b_2$ are zeroes of the function $G(\varphi )=-\frac{2\varphi ^{k+2}}{k+2}+ \varphi ^2+2B$. However, from standard theory of ODE, the solution $\varphi$ of (1.1) depends smoothly on the initial conditions $\varphi (t_0)=\varphi _0$ and $\varphi '(t_0)=\varphi _1$, $t_0\in \mathbb {R}$ and in particular, $\varphi$ and L also depend smoothly on B in a convenient set of parameters (see [9, Chapter 1, Theorem 3.3]).

With the smoothness of the period map in hands, it is important to know the behaviour of this function in terms of the energy levels B or even in terms of the initial data. In fact, questions related to the behaviour of the period function have attracted a considerable attention in the last decades and the study of the monotonicity of the period map is important for several reasons. For instance, if the period map is monotonic, solutions with large periods correspond to initial conditions that are far away from the critical points. On the other hand, if the period map is not monotonic, then the periodic solutions may exhibit bifurcations points in the associated phase portrait and the uniqueness of solutions may be not valid.

Next, we present some contributors. Loud [10] and Urabe [17] have proved the isochronicity¹ of the period function for specific families of planar vector fields. Using tools of ODE, Schaaf [16] has established a general set of sufficient conditions for the monotonicity of the period function for a class of Hamiltonian systems of the form

$$\begin{aligned} \left\{ \begin{array}{llll}\varphi '=-f(\psi ),\\ \psi '=g(\varphi ).\end{array} \right. \end{aligned}$$

(1.4)

By assuming suitable assumptions on the smooth functions f and g, it is possible to prove that the period function is strictly increasing for periodic solutions turning around the center point (0, 0) (see also Rothe [15] for an extension of the results in [16]).

Cima et al. [5] (see also Coppel and Gavrilov [6]) studied the same system in (1.4) and they characterized the limiting behaviour of the period L at infinity when the origin is a global center. In adddition, they apply this result to prove that there are no nonlinear polynomial isochronous centers in this family, showing the monotonicity of the period in terms of the energy levels B. Rothe [14] and Waldvogel [19] showed that all Lotka–Volterra systems of the form

$$\varphi '=\varphi (a-b\psi ), \quad \psi '=-\psi (c-d\varphi ),$$

for a and b in a suitable set of conditions, have monotonic period functions. Chow and Wang [4] gave some characterization of the first and second derivatives for the period function in terms of B for the equation

$$\varphi ''+g(\varphi )=0,$$

where g satisfies a suitable set of conditions. As an application, they determine the monotonicity of the period function when $g(s)=e^s-1$. Using a different approach, Chicone [2] also obtained part of the results in [4] and gave a general condition for the monotonicity of period functions for a class of planar Hamiltonian systems. In addition, [2] was the inspiration for the study in Yagasaki [18] to prove the monotonicity of the period function for the Eq. (1.1). In this work, the authors also considered $k>1$ a real number and the periodic solutions turning around the center point (1, 0). A revisited proof of [18] has been established by Benguria, Depassier and Loss in [1].

In our approach, we use a different method to establish the monotonicity of the period map for positive solutions as determined in [18] and we realize that when $k>1$ is in particular an odd number, we can use the same method to determine the same behaviour for the periodic solutions of the Eq. (1.1) that change their sign. As far as we know, this last question never been treated in the current literature and our intention is to give a new perspective to solve this kind of problems since our approach can be used in other models.

Without further ado, we will describe our methods. Indeed, let us consider the linearized operator around $\varphi$ given by

$$\begin{aligned} \mathcal {L}(y)=- y''+ y-k\varphi ^{k-1}y, \end{aligned}$$

(1.5)

defined in $L_{per}^2([0,L])$ with domain $H_{per}^2([0,L])$. Deriving Eq. (1.1) with respect to x, we obtain that $\varphi '$ satisfies $\mathcal {L}\varphi '=0$, so that $\varphi '$ is a periodic element which solves the equation

$$\begin{aligned} - y''+ y-k\varphi ^{k-1}y=0. \end{aligned}$$

(1.6)

Since (1.6) is a second order linear equation, there exists another solution $\bar{y}$ for the equation $\mathcal {L}\bar{y}=0$ and $\{\varphi ',\bar{y}\}$ is a fundamental set of solutions for the Eq. (1.6). Using tools of the Floquet theory (see [11]), we see that function $\bar{y}$ can be periodic or not and it is related with $\varphi '$ through the equality (see [11])

$$\begin{aligned} \bar{y}(x+L)=\bar{y}(x)+\theta \varphi '(x), \end{aligned}$$

(1.7)

for all $x\in \mathbb {R}$. Constant $\theta$ is a real parameter and it determines if $\bar{y}$ is periodic or not in the sense that $\bar{y}$ is periodic if and only if $\theta =0$.

Our strategy to prove the monotonicity of L in terms of B is then to show that $\bar{y}$ is always a non-periodic function by proving that the kernel of $\mathcal {L}$ in (3.5) in (1.5) defined in $L_{per}^2([0,L])$ with domain $H_{per}^2([0,L])$ is always simple (see Lemma 3.7 and Lemma 3.5). After that, we need to use the smoothness of the period function with respect to B to prove that $\frac{\partial L}{\partial B}=-\theta$ (see Lemma 3.2). Thus, since $\bar{y}$ is always non-periodic, we can conclude that $\theta \ne 0$, and the monotonicity of the period map is determined. Our main result can be summarized as follows:

Theorem 1.1

Let $L=L(B)$ be the period function associated to the periodic solution $\varphi$ of the Eq. (1.1).

• (i) If $k>1$ is odd and $\varphi$ is a solution that changes its sign, then $\frac{\partial L}{\partial B}<0$.

• (ii) If $k>1$ and $\varphi$ is a positive non-constant periodic solution, then $\frac{\partial L}{\partial B}>0$.

Our paper is organized as follows. In Sect. 2 we present a brief explanation concerning the existence of positive and solutions that change their sign. Section 3 is devoted to prove Theorem 1.1.

Notation. Here, we introduce the basic notation concerning the periodic Sobolev spaces that will be useful in our paper. For a more complete introduction to these spaces we refer the reader to [8]. In fact, by $L^2_{per}([0,L])$, we denote the space of all square integrable functions which are L-periodic. For $m\ge 0$ integer, the Sobolev space $H^m_{per}([0,L])$ is the set of all periodic functions such that

$$ \Vert f\Vert _{H^m_{per}}^2:= ||f||_{L_{per}^2}^2+\sum _{j=1}^m||f^{(j)}||_{L_{per}^2}^2 <\infty , $$

where $f^{(j)}$, $j=1,\ldots ,m$, indicates the j-th derivative of f in the sense of periodic distributions (see [8] for further details). The space $H^m_{per}([0,L])$ is a Hilbert space with natural inner product denoted by $(\cdot , \cdot )_{H_{per}^m}$. When $m=0$, the space $H^m_{per}([0,L])$ is isometrically isomorphic to the space $L^2_{per}([0,L])$. The norm and inner product in $L^2_{per}([0,L])$ will be denoted by $\Vert \cdot \Vert _{L_{per}^2}$ and $(\cdot , \cdot )_{L_{per}^2}$, respectively.

2 Existence of periodic solutions via planar analysis

Our purpose in this section is to present some facts concerning the existence of periodic solutions for the nonlinear ODE given by

$$\begin{aligned} -\varphi ''+ \varphi -\varphi ^k = 0, \end{aligned}$$

(2.1)

where $k>1$ is a real number.

Equation (2.1) is conservative with

$$\begin{aligned} \mathcal {E}(\varphi , \xi ) = \frac{\xi ^2}{2} -\frac{\varphi ^2}{2}+\frac{\varphi ^{k+1}}{k+1}, \end{aligned}$$

(2.2)

as a first integral, where $\xi =\varphi '$, and thus its solutions are contained on the level curves of the energy.

According to the classical ODE theory (see [3, 9, 12] for further details), $\varphi$ is a periodic solution of the Eq. (2.1) if and only if $(\varphi ,\varphi ')$ is a periodic orbit of the planar differential system

$$\begin{aligned} \left\{ \begin{array}{lllll} \varphi '=\xi ,\\ \\ \xi '=\varphi -\varphi ^k. \end{array}\right. \end{aligned}$$

(2.3)

The periodic orbits for the Eq. (2.3) can be determined by considering the energy levels of the function $\mathcal {E}$ defined in (2.2). This means that the pair $(\varphi ,\xi )$ satisfies the equation $\mathcal {E}(\varphi ,\xi )=B$. If $k>1$ and $B\in \left( \frac{1-k}{2(k+1)},0\right)$, we obtain periodic orbits that turn round at the equilibrium points (1, 0) and these orbits are called positive since they are associated with positive periodic solutions of the Eq. (2.1). In our specific case, (2.3) admits at least two critical points, being a saddle point at the origin and a center point at (1, 0). According to the standard ODE theory, the periodic orbits emanate from the center points to the separatrix curve which is represented by a smooth solution $\widetilde{\varphi }:\mathbb {R}\rightarrow \mathbb {R}$ of (2.1) satisfying $\lim _{x\rightarrow \pm \infty }\widetilde{\varphi }^{(n)}(x)=0$ for all $n\in \mathbb {\mathbb {N}}$. In particular, when k is odd, we see that the presence of two symmetric center points $(\pm 1,0)$ allows to conclude that the periodic orbits which turn around these points can be positive and negative². For every orbit with initial condition outside the separatrix, we obtain periodic solutions for the Eq. (2.1) that change their sign³. Indeed, if $B>0$ we also have periodic orbits and the corresponding periodic solutions $\varphi$ with the zero mean property, that is, periodic solutions satisfying $\int _0^L\varphi (x)dx=0$.

Independently of the type of periodic solutions on which we are working, the period $L=L(B)$ of the solution $\varphi$ can be expressed (formally) as follows:

$$\begin{aligned} L=\displaystyle 2\int _{b_1}^{b_2}\frac{dh}{\sqrt{-\frac{2h^{k+1}}{k+1}+ h^2+2B}}, \end{aligned}$$

(2.4)

where $b_1=\displaystyle \min _{x\in [0,L]}\varphi (x)$ and $b_2=\displaystyle \max _{x\in [0,L]}\varphi (x)$.

On the other hand, the energy levels of the first integral $\mathcal {E}$ in (2.2) parametrize the unbounded set of periodic orbits $\{\Gamma _B\}_B$ which emanate from the separatrix curve. Thus, we can conclude that the set of smooth periodic solutions of (2.1) can be expressed by a smooth family $\varphi =\varphi _{B}$ which is parametrized by the value B. Moreover, for the case $B\in \left( \frac{1-k}{2(k+1)},0\right)$, we see that if $B\rightarrow \frac{1-k}{2(k+1)}$ thus $L\rightarrow 2\pi$, where $2\pi$ is the period of the equilibrium solution (1, 0) of the system (2.3) (see [12, Sect. 2]). On the other hand, if $B\rightarrow 0$ we have $L\rightarrow +\infty$ and both convergences suggest that the period map is increasing in the interval $\left( \frac{1-k}{2(k+1)},0\right)$. On the other hand, when $B\in (0,+\infty )$, we see that if $B\rightarrow 0$, we have $L\rightarrow +\infty$, and if $B\rightarrow +\infty$, we obtain $L\rightarrow 0$. In this case, the suggestion is that the period map is decreasing.

3 The monotonicity of the period map—proof of Theorem 1.1

We need to recall some basic facts concerning Floquet’s theory (see [7, 11]). Let Q be a smooth L-periodic function. Consider $\mathcal {P}$ the Hill operator defined in $L_{per}^2([0,L])$, with domain $D(\mathcal {P})=H_{per}^2([0,L])$, given by

$$\begin{aligned} \mathcal {P}=-\partial _x^2+Q(x). \end{aligned}$$

(3.1)

The spectrum of $\mathcal {P}$ is formed by an unbounded sequence of real eigenvalues

$$\begin{aligned} \lambda _0 < \lambda _1 \le \lambda _2 \le \lambda _3 \le \lambda _4\le \cdots \; \le \lambda _{2n-1} \le \lambda _{2n}\; \cdots , \end{aligned}$$

(3.2)

where equality means that $\lambda _{2n-1} = \lambda _{2n}$ is a double eigenvalue. Moreover, according with the Oscillation Theorem (see [11]), the spectrum is characterized by the number of zeros of the eigenfunctions as: if p is an eigenfunction associated to either $\lambda _{2n-1}$ or $\lambda _{2n}$, then p has exactly 2n zeros in the half-open interval [0, L). In particular, the even eigenfunction associated to the first eigenvalue $\lambda _0$ has no zeros in [0, L].

Let p be a nontrivial L-periodic solution of the equation

$$\begin{aligned} \mathcal {P}(p)=-p''+Q(x)p=0. \end{aligned}$$

(3.3)

Consider $\bar{y}$ the other solution of (3.3) linearly independent of p. There exists a constant $\theta$ (depending on $\bar{y}$ and p) such that (see [11, page 5])

$$\begin{aligned} \bar{y}(x+L)=\bar{y}(x)+\theta p(x). \end{aligned}$$

(3.4)

Consequently, $\theta =0$ is a necessary and sufficient condition to all solutions of (3.3) to be L-periodic. This criterion is very useful to establish if the kernel of $\mathcal {P}$ is one-dimensional or not.

Next, let $\varphi =\varphi _{B}$ be any periodic solution of (2.1). Consider $\mathcal {L}=\mathcal {L}_{B}:H_{per}^2([0,L])\subset L_{per}^2([0,L])\rightarrow L_{per}^2([0,L])$ the linearized operator arising from the linearization of (2.1) at $\varphi$, that is,

$$\begin{aligned} \mathcal {L}(y)=- y''+ y-k\varphi ^{k-1}y. \end{aligned}$$

(3.5)

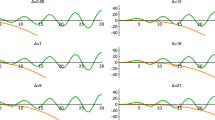
Clearly $\mathcal {P}=\mathcal {L}$, when $Q(x)y(x)= y(x)-k \varphi ^{k-1}(x)y(x)$. By taking the derivative with respect to x is (2.1), we have that $p:=\varphi '$ belongs to the kernel of the operator $\mathcal {L}$. In addition, from our construction, $\varphi '$ has exactly two zeros in the half-open interval [0, L) (see Fig. 1), which implies that zero is the second or the third eigenvalue of $\mathcal {L}$ (see Oscillation’s Theorem in [11])

Fig. 1

Periodic orbits for the Eq. (2.1). Left: positive and periodic orbits for the case $k>1$ that spinning around the center point (1, 0). Right: Positive and negative periodic orbits for the case $k>1$ and odd that spinning around the center points (1, 0) and $(-1,0)$, respectively. Right: periodic orbits that change their sign when the initial conditions are located outside the the separatrix

Next, let $\bar{y}=\bar{y}_{B}$ be the unique even solution of the initial-value problem

$$\begin{aligned} \left\{ \begin{array}{l} -\bar{y}'' +\bar{y}-k\varphi ^{k-1}\bar{y} = 0 ,\\ \bar{y}(0) =-\frac{1}{\varphi ''(0)}, \\ \bar{y}'(0)= 0. \end{array} \right. \end{aligned}$$

(3.6)

Since $\varphi '$ is an L-periodic solution for the equation in (3.6) and the corresponding Wronskian of $\varphi '$ and $\bar{y}$ is 1, there is a constant $\theta =\theta _{\bar{y}}$ such that

$$\begin{aligned} \bar{y}(x+L)=\bar{y}(x)+\theta \varphi '(x). \end{aligned}$$

(3.7)

By taking the derivative in this last expression and evaluating at $x=0$, we obtain

$$\begin{aligned} \theta = \frac{\bar{y}'(L)}{\varphi ''(0)}. \end{aligned}$$

(3.8)

The next result gives that it is possible to decide the exact position of the zero eigenvalue by knowing the precise sign of $\theta$ in (3.4).

Lemma 3.1

• (i) If $\theta >0$, operator $\mathcal {L}$, defined in $L_{per}^2([0,L])$, with domain $H_{per}^2([0,L])$, has exactly two negative eigenvalue which are simple, a simple eigenvalue at zero and the rest of the spectrum is positive and bounded away from zero.

• (ii) If $\theta <0$, the same operator $\mathcal {L}$ has exactly one negative eigenvalue which is simple, a simple eigenvalue at zero and the rest of the spectrum is positive and bounded away from zero.

Proof

See Theorem 3.1 in [13]. $\square$

Now we can give a relation between $\frac{\partial L}{\partial B}$ and $\theta$.

Lemma 3.2

We have that $\frac{\partial L}{\partial B}=-\theta$, where $\theta$ is the constant in (3.8).

Proof

Consider $\bar{y}$ and $\varphi '$ as above. Since $\varphi$ is even and periodic one has $\varphi '(0)=\varphi '(L)=0$. Thus, the smoothness of $\varphi$ in terms of the parameter B enables us to take the derivative of $\varphi '(L)=0$ with respect to B to obtain

$$\begin{aligned} \varphi ''(L)\frac{\partial L}{\partial B}+\frac{\partial \varphi '(L)}{\partial B}=0.\end{aligned}$$

(3.9)

Next, we turn back to Eq. (2.1) and multiply it by $\varphi '$ to deduce, after integration, the quadrature form

$$\begin{aligned} \frac{ \varphi '^2(x)}{2}-\frac{\varphi (x)^2}{2}+\frac{\varphi (x)^{k+1}}{k+1}-B=0,\ \ \ \ \text{ for } \text{ all }\ x\in [0,L]. \end{aligned}$$

(3.10)

Deriving Eq. (3.10) with respect to B and taking $x=0$ in the final result, we obtain from (2.1) that $\frac{\partial \varphi (0)}{\partial B}=\frac{1}{ \varphi ''(0)}$. In addition, since $\varphi$ is even one has that $\frac{\partial \varphi }{\partial B}$ is also even and thus $\frac{\partial \varphi '(0)}{\partial B}=0$. On the other hand, deriving Eq. (2.1) with respect to B, we obtain that $\frac{\partial \varphi }{\partial B}$ satisfies the initial-value problem

$$\begin{aligned} \left\{ \begin{array}{lllll}\displaystyle -\frac{\partial \varphi }{\partial B}''+\frac{\partial \varphi }{\partial B}-k\varphi ^{k-1}\frac{\partial \varphi }{\partial B}=0,\\ \\ \displaystyle \frac{\partial \varphi (0)}{\partial B}=\frac{1}{ \varphi ''(0)},\\ \\ \displaystyle \frac{\partial \varphi '(0)}{\partial B}=0. \end{array}\right. \end{aligned}$$

(3.11)

The existence and uniqueness theorem for ordinary differential equations applied to the problem (3.6) enables us to deduce that $\bar{y}=-\frac{\partial \varphi }{\partial B}$. Therefore, we can combine (3.8) with (3.9) to obtain that $\frac{\partial L}{\partial B}=-\theta$. $\square$

Next lemma is basic for our purposes.

Lemma 3.3

Let $\mathcal {L}$ be the linearized operator defined in (3.5). Thus, $1\in \textrm{range}(\mathcal {L})$.

Proof

First, we see that (2.1) is invariant under translations. This means that if $\varphi$ is a solution of (2.1), thus $\psi _r=\varphi (\cdot -r)$ is also a solution for all $r\in \mathbb {R}$. In particular, if $r=L/4$ we obtain that $\psi :=\psi _{L/4}=\varphi (\cdot -L/4)$ is also a periodic solution for the Eq. (2.1). Therefore, $\varphi '$ is an odd element of $\ker (\mathcal {L})$, so that $\psi '$ results to be even and it is an element of the kernel of $\widetilde{\mathcal {L}}=-\partial _x^2+1-k\psi ^{k-1}$ ($\widetilde{\mathcal {L}}$ is the operator obtained from $\mathcal {L}$ by considering the linearization at $\psi$ instead of $\varphi$). Consider then, $\chi =\bar{y}(\cdot -L/4)$ the corresponding element of the formal equation $\mathcal {L}(\bar{y})=0$ associated to the translation solution $\psi$. Since $\chi$ results to be $L-$periodic and odd, we have

$$\begin{array}{lllll}\displaystyle \int _0^L\chi (x)dx &{}=&{}\displaystyle \frac{1}{2}\int _0^L\chi (x)dx+\frac{1}{2}\int _L^{2L}\chi (x)dx\\ \\ &{}=&{}\displaystyle \frac{1}{2}\int _0^{2L}\chi (x)dx=\displaystyle \frac{1}{2}\int _{-L}^{L}\chi (x)dx=0.\end{array}$$

that is, $\chi$ has the zero mean property.

Let us define the following function:

$$\begin{aligned} h(x)=\left( \int _0^x \chi (s)ds\right) \psi '(x)-\left( \int _0^x\psi '(s)ds\right) \chi (x). \end{aligned}$$

(3.12)

Using the method of variation of parameters, we see that h is a particular solution (not necessarily periodic) of the equation

$$\begin{aligned} -u''+u-k\psi ^{k-1}u=1,\end{aligned}$$

(3.13)

in the sense that $Y=c_1\psi '+c_2\chi +h$ is a general solution associated with the Eq. (3.13), where $c_1$ and $c_2$ are real constants. We need to prove that h is periodic. In fact, it is clear $h(0)=0$ and since $\int _0^L\chi (x)dx=0$, one has from (3.12) and the fact that $\psi '$ is periodic that $h(L)=0$. Deriving (3.12) with respect to x, we obtain after some computations $h'(x)=\left( \int _0^x \chi (s)ds\right) \psi ''(x)-\left( \int _0^x\psi '(s)ds\right) \chi '(x)$, so that $h'(0)=0$. Since $\psi$ is both odd and periodic, it follows that $\psi '$ and $\psi ''$ are also periodic, with $\psi ''$ being an odd function. We have

$$\begin{array}{lll}h'(L)&{}=&{}\displaystyle \left( \int _0^L \chi (s)ds\right) \psi ''(L)-\left( \int _0^L\psi '(s)ds\right) \chi '(L)\\ \\ &{}=&{}\displaystyle \left( \int _0^L \chi (s)ds\right) \psi ''(0)-(\psi (L)-\psi (0))\chi '(L)=0\end{array}$$

so that, h is periodic. Equality (3.13) is then satisfied for the periodic function h, that is,

$$-h''(x)+h(x)-k\psi (x)^{k-1}h(x)=1,$$

for all $x\in \mathbb {R}$. In particular, for $x=t+L/4$ and since $\varphi (t)=\psi (t+L/4)$, we have

$$-h''(t+L/4)+h(t+L/4)-k\varphi (t)^{k-1}h(x+L/4)=1.$$

Defining $\tilde{h}(t)=h(t+L/4)$, we obtain that $\tilde{h}$ is $L-$periodic and it satisfies the equation $-\tilde{h}''(t)+\tilde{h}(t)-k\varphi (t)^{k-1}\tilde{h}(t)=1$, so that $\mathcal {L}(\tilde{h})=1$ as requested in lemma.

$\square$

Lemma 3.4

We have that $\{\varphi ^{k-1},\varphi ^k\}\subset \textrm{range}(\mathcal {L})$.

Proof

By (2.1), we obtain

$$\mathcal {L}(\varphi )=-\varphi ''+\varphi -k\varphi ^k=-\varphi ''+\varphi -k\varphi ^k+\varphi ^k-\varphi ^k=(1-k)\varphi ^k.$$

Thus, $\varphi ^k\in \textrm{range}(\mathcal {L})$.

To prove that $\varphi ^{k-1}\in \textrm{range}(\mathcal {L})$, we need to use the fact that $\mathcal {L}(1)=1-k\varphi ^{k-1}$. By Lemma 3.3 one has $1\in \textrm{range}(\mathcal {L})$, so that $\varphi ^{k-1}\in \textrm{range}(\mathcal {L})$. $\square$

Next lemma establishes item i) of Theorem 1.1. In what follows $n(\mathcal {A})$ and $z(\mathcal {A})$ are respectively the number of negative eigenvalues (counting multiplicities) and the dimension of the kernel of a certain linear operator $\mathcal {A}$.

Lemma 3.5

Let $k>1$ be a positive odd integer. If $\varphi$ is the zero mean periodic solution of (2.1), thus $n(\mathcal {L})=2$ and $z(\mathcal {L})=1$. In particular, we have that $\frac{\partial L}{\partial B}<0$.

Proof

First, we see that $\varphi '$ is an odd eigenfunction of $\mathcal {L}$ associated to the eigenvalue 0 having two zeroes in the interval [0, L). From the Oscillation theorem (see [11]), we obtain that 0 needs to be the second or the third eigenvalue in the sequence of real numbers in (3.2).

On the other hand, since $\varphi$ is even and $\int _0^L\varphi (x) dx=0$, one has $\psi =\varphi (\cdot -L/4)$ is odd and it has the zero mean property. Consider again $\widetilde{\mathcal {L}}=-\partial _x^2+1-k\psi ^{k-1}$ the translated operator obtained from $\mathcal {L}$ by considering the linearization at $\psi$ instead of $\varphi$ and let $\widetilde{\mathcal {L}}_{odd}$ be the restriction of $\widetilde{\mathcal {L}}$ in the odd sector of $L_{per}^2([0,L])$. Notice that such restriction is possible because $\psi ^{k-1}$ is even since $k-1$ is an even number. Since $k+1>2$ is also even, we have $(\widetilde{\mathcal {L}}_{odd}(\psi ),\psi )_{L_{per}^2}=(1-k)\int _{0}^L\psi (x)^{k+1}dx<0$, so that by Courant’s min-max characterization of eigenvalues, we obtain $n(\widetilde{\mathcal {L}}_{odd})\ge 1$. The fact $n(\widetilde{\mathcal {L}})=n(\widetilde{\mathcal {L}}_{odd})+n(\widetilde{\mathcal {L}}_{even})$ and Krein-Rutman’s Theorem enable us to conclude that the first eigenvalue of $\widetilde{\mathcal {L}}$ is simple and it is associated to a positive (negative) eigenfunction which needs to be even. Thus, we obtain since 0 is the second or third eigenvalue of $\widetilde{\mathcal {L}}$ that $n(\widetilde{\mathcal {L}})=n(\mathcal {L})=2$ as requested.

We prove that $z(\mathcal {L})=1$. Indeed, since $n(\widetilde{\mathcal {L}}_{odd})=1$, we see that the corresponding eigenfunction p associated to the first eigenvalue of $\widetilde{\mathcal {L}}_{odd}$ is odd and consequently, $q=p(\cdot -L/4)$ is an even function that changes its sign. Again, by Krein-Rutman’s theorem we have that the first eigenfunction $\lambda _1$ of $\mathcal {L}$ is simple and it is associated to a positive (negative) even periodic function, so that 0 can not be an eigenvalue associated to $\widetilde{\mathcal {L}}_{odd}$. Since $z(\widetilde{\mathcal {L}})=z(\widetilde{\mathcal {L}}_{odd})+z(\widetilde{\mathcal {L}}_{even})$, we obtain from the fact $\psi '$ is even that $z(\widetilde{\mathcal {L}})=z(\widetilde{\mathcal {L}}_{even})=1$. Therefore, using the translation transformation $f=g(\cdot -L/4)$, we obtain $z(\mathcal {L})=z(\mathcal {L}_{odd})=1$ as requested. $\square$

We prove the second part of Theorem 1.1. To do so, it is necessary to prove the following basic result.

Lemma 3.6

Let $L>0$ and $k>1$ be fixed. There exists $\varphi \in H_{per}^1([0,L])$ solution of the following constrained minimization problem

$$\begin{aligned} \nu =\inf \left\{ D(u);\ u\in H_{per}^1([0,L]),\ \int _0^{L} u(x)^{k+1}dx=1\right\} , \end{aligned}$$

(3.14)

where $D: H_{per}^1([0,L])\rightarrow \mathbb {R}$ is the functional defined as

$$\begin{aligned} D(u)=\frac{1}{2}\int _0^{L}u'(x)^2+u(x)^2dx. \end{aligned}$$

(3.15)

In addition, $\varphi$ is smooth and it satisfies Eq. (2.1). Conversely, if $\varphi$ is a positive non-constant solution of (2.1), then $\varphi$ satisfies the minimization problem (3.14).

Proof

Since D is smooth and $D(u)\ge 0$ for all $u\in H_{per}^1([0,L])$, there exists $(u_n)_{n\in \mathbb {N}}$ a minimizing sequence associated to the problem (3.14), that is, there exists $(u_n)_{n\in \mathbb {N}}\subset H_{per}^1([0,L])$ satisfying $\int _0^Lu_n(x)^{k+1}dx=1$ for all $n\in \mathbb {N}$, and

$$\begin{aligned} D(u_n)\rightarrow \nu , \end{aligned}$$

(3.16)

as $n\rightarrow +\infty$. The convergence in (3.16) allows us to conclude that $(u_n)_{n\in \mathbb {N}}$ is a bounded sequence in $H_{per}^1([0,L])$. Since $H_{per}^1([0,L])$ is a Hilbert space, there exists $\varphi \in H_{per}^1([0,L])$ such that

$$\begin{aligned} u_n\rightharpoonup \varphi . \end{aligned}$$

(3.17)

On the other hand, the compact embedding $H_{per}^1([0,L])\hookrightarrow L_{per}^{k+1}([0,L])$ gives us

$$\begin{aligned} u_n\rightarrow \varphi \ \text{ in }\ L_{per}^{k+1}([0,L]). \end{aligned}$$

(3.18)

Consider the function $q:\mathbb {R}\rightarrow \mathbb {R}$ given by $q(s)=s^{k+1}$. The mean value theorem gives us $s^{k+1}-t^{k+1}=(k+1)w^{k}(s-t)$, where w is point in the open interval (t, s). Since $|w|\le |s|+|t|$, we obtain

$$\begin{aligned} |u_n(x)^{k+1}-\varphi (x)^{k+1}|\le 2^{k+1}(k+1)(|u_n(x)|^{k}+|\varphi (x)|^k)|u_n(x)-\varphi (x)|, \end{aligned}$$

(3.19)

for all $x\in [0,L]$. The Hölder inequality and (3.19) allow us to conclude

$$\begin{aligned} \displaystyle \left| \int _0^Lu_n(x)^{k+1}-\varphi (x)^{k+1}dx\right|&\le \displaystyle \int _0^L|u_n(x)^{k+1}-\varphi (x)^{k+1}|dx\nonumber \\&\le C_0\displaystyle ||u_n-\varphi ||_{L_{per}^{k+1}}\left( ||u_n||_{L_{per}^{k+1}}^k+||\varphi ||_{L_{per}^{k+1}}^k\right) , \end{aligned}$$

(3.20)

where $C_0=2^{k+1}(k+1)$. By the convergence in (3.18), we obtain from (3.20) that $\int _0^L\varphi (x)^{k+1}dx=1$ and thus, $\nu \le D(\varphi )$. On the other hand, the weak lower semi-continuity of D and the convergence in (3.17) give us that $D(\varphi )\le \lim \inf _{n\rightarrow +\infty }D(u_n)=\nu$. Thus $D(\varphi )=\nu$ and the infimum is attained at $\varphi$.

An application of the Lagrange multiplier theorem guarantees the existence of $C_1$ such that

$$\begin{aligned} -\varphi ''+\varphi =C_1\varphi ^{k+1}. \end{aligned}$$

(3.21)

The function $\varphi$ is nontrivial because $\int _0^L\varphi (x)^{k+1}dx=1$. Using a standard rescaling argument, we can deduce that the Lagrange multiplier $C_1$ can be chosen as 1, and thus we deduce that $\varphi$ solves Eq. (2.1). In addition, a bootstrap argument applied to the equality in (2.1) also gives that $\varphi$ is smooth. Next, multiplying Eq. (2.1) by $\varphi$ and integrating the result over [0, L], we conclude that $\nu =\frac{1}{2}$.

Conversely, suppose that $\varphi$ is a positive non-constant periodic solution of (2.1). According to the arguments presented in Sect. 2, we can deduce that the period of $\varphi$ satisfies $L>2\pi$. Additionally, since $\varphi >0$ and non-constant, we can assume, without loss of generality, that $\int _0^L \varphi (x)^{k+1}dx=1$. Multiplying the Eq. (2.1) by $\varphi$ and integrating the result over [0, L], we obtain $D(\varphi )=\frac{1}{2}$. Since every solution $\phi$ of the minimization problem (3.14) satisfies $D(\phi )=\nu =\frac{1}{2}$, we obtain that the positive non-constant periodic solution $\varphi$ also satisfies the minimization (3.14) as requested in lemma. $\square$

The proof of the second part of Theorem 1.1 is now presented.

Lemma 3.7

Let $\varphi$ be a positive non-constant periodic solution associated with the Eq. (2.1). We have that $n(\mathcal {L})=z(\mathcal {L})=1$ and in particular $\frac{\partial L}{\partial B}>0$.

Proof

Let $k>1$ be fixed. For $L>2\pi$, we have by Lemma 3.6 that the positive non-constant solution $\varphi$ of the Eq. (2.1) satisfies the minimization problem (3.14).

Next, thanks to the Lemma 3.6, we obtain that $\varphi$ is a minimizer of the functional $G:H_{per}^1([0,L])\rightarrow \mathbb {R}$ given by $G(u)=D(u)-\frac{1}{k+1}\int _0^Lu(x)^{k+1}dx$ subject to the same constraint $\int _0^Lu(x)^{k+1}dx=1$. Since $\mathcal {L}=-\partial _x^2+1-k\varphi ^{k-1}$ is the Hessian operator for G(u) at the point $\varphi$, we obtain that $n(\mathcal {L})\le 1$. On the other hand, solution $\varphi$ is positive and thus

$$(\mathcal {L}(\varphi ),\varphi )_{L_{per}^2}=(1-k)\int _0^L\varphi (x)^{k+1}dx<0.$$

We deduce by Courant’s min-max characterization of eigenvalues that $n(\mathcal {L})\ge 1$ and both results allow to conclude that $n(\mathcal {L})=1$. Let us assume that $z(\mathcal {L})=2$ for some $B_0\in \left( \frac{1-k}{2(k+1)},0\right)$. By Oscillation’s Theorem in [11], it follows that the periodic solution $\bar{y}$ of the Cauchy problem (3.6) has exactly two zeroes in the interval [0, L) and by periodicity, also in the interval $\left[ -L/2,L/2\right)$. Since $\varphi ' \in \ker (\mathcal {L})$ is odd, we see that the periodic function $\bar{y} \in \ker (\mathcal {L})$ is even and it has exactly two symmetric zeroes in the interval $\left[ -L/2,L/2\right)$. Hence, there exists $x_0 \in \left( -L/2,L/2\right)$ such that $\bar{y}(\pm x_0)=0$. Without loss of generality, we can still suppose that

$$\begin{aligned} \bar{y}(x)>0, \; x \in (-x_0, x_0) \quad \text {and} \quad \bar{y}(x)<0, \; x \in \left[ -L/2,-x_0 \right) \cup \left( x_0,L/2\right) .\nonumber \\ \end{aligned}$$

(3.22)

Furthermore, by Lemma 3.4 we have $\varphi ^{k-1},\varphi ^k\in \ker (\mathcal {L})^{\bot }=\textrm{range}(\mathcal {L})$, so that

$$\begin{aligned} (\bar{y},\varphi ^{k-1})_{L^2_{per}}=0 \quad \text {and} \quad (\bar{y},\varphi ^{k})_{L^2_{per}}=0. \end{aligned}$$

(3.23)

Since $\varphi >0$, we obtain that $\varphi (x)^{k-1}(\varphi (x)-\varphi (x_0))$ is positive over $(-x_0,x_0)$ and negative over $\left[ -L/2,x_0 \right) \cup \left( x_0,L/2\right)$ and it has the same behaviour as $\bar{y}$ in (3.22). Thus, $(\varphi ^{k-1}(\varphi -\varphi (x_0)), \bar{y})_{L^2_{per}} \ne 0$ which leads a contradiction with (3.23). Consequently, we have $\ker (\mathcal {L})=[\varphi ']$. $\square$