1 Introduction

Depending on the depth, the geometry of the structures and the human- and/or environmental-induced seismic activities, rock masses in underground mining and geotechnical projects are usually subjected to a complex stress state, which may result in continuous damage and failure at different extents (Yang et al. 2017; Wang et al. 2021). Systematic cyclic loading induced by the rock breakage operation, mechanical excavation, and truck haulage vibrations is a common dynamic disturbance in underground openings that complicate the deformation and failure characteristics of rocks. Rock materials under such loading conditions are more prone to severe failure phenomena such as strain bursting and large-scale collapses (Bagde and Petroš 2005; Munoz and Taheri 2019; Shirani Faradonbeh et al. 2021a; Meng et al. 2021). Therefore, there is a remarkable theoretical significance and engineering value to deeply understand the cyclic loading effect on the damage mechanism and, more importantly, the post-failure behaviour of rocks in terms of safety and long-term stability of the excavations. During the last decades, different researchers have made many attempts to unveil the rock fatigue mechanism under different loading conditions using laboratory experiments (Cerfontaine and Collin 2018). In other words, the damage evolution mechanism in rocks can be characterised more efficiently using cyclic loading tests as it is straightforward to distinguish the elastic and plastic strains during each loading and unloading cycle (Zhou et al. 2019; Tian et al. 2021). According to the holistic classification proposed by Shirani Faradonbeh et al. (2021a), rock fatigue studies can be classified into two main groups of systematic cyclic loading tests and damage-controlled cyclic loading tests. Each of these groups can be performed either under load-controlled or displacement-controlled loading conditions. These loading techniques and their limitations have been discussed in more detail by Shirani Faradonbeh et al. (2021a).

Generally, the rock fatigue studies can be discussed from two viewpoints: the pre-peak and post-peak domain analysis. From the viewpoint of the pre-peak-domain analysis, the literature review shows that cyclic loading depending on loading methods, loading conditions and intrinsic rock properties (e.g. porosity and mineral compositions), can either degrade (Wang et al. 2013; Erarslan et al. 2014; Yang et al. 2015; Taheri et al. 2016a) or improve (Burdine 1963; Singh 1989; Ma et al. 2013; Shirani Faradonbeh et al. 2021b) the peak strength of rocks. For instance, Ma et al. (2013) reported a 171.1% increase in triaxial compressive strength of rock salt subjected to systematic cyclic loading. Similarly, Taheri et al. (2016b) observed an 11% peak strength improvement for the porous Hawkesbury sandstone. They also pointed out that rock strength increases, respectively, with applied stress level and the number of cycles before failure following linear and exponential functions. On the other hand, most of the fatigue cyclic loading studies have reported peak strength and stiffness degradation due to the accumulation of permanent deformations within the rock specimens following a nonlinear S-shaped damage model (e.g. Xiao et al. 2009). Fatigue threshold stress (\(\mathrm{FTS}={q}_{f}/{q}_{m-\mathrm{avg}}\)), the maximum stress level at which rock specimen does not fail during cyclic loading under a constant amplitude, is a significant parameter for long-term stability assessment of underground openings subjected to seismic disturbances. In other words, rock materials never fail (after a few thousand cycles) if the cyclic loading is applied equal or below this threshold. According to Cerfontaine and Collin (2018), different values of FTS can be obtained depending on the tested material. However, FTS is also dependent on other factors, such as loading conditions and confining pressure (Burdine 1963). Therefore, more investigations are needed to unveil the effect of confining pressure on fatigue threshold stress.

From the viewpoint of the post-peak domain, due to difficulties in capturing the complete stress–strain relations of rocks under cyclic loading, especially for brittle rocks which show a class II post-peak behaviour (Wawersik and Fairhurst 1970), very few studies have investigated the influence of the pre-peak cyclic loading on post-failure behaviour. A comprehensive classification of cyclic loading studies and the corresponding load control methods can be found in Shirani Faradonbeh et al. (2021a and b). In most prior studies, the damage-controlled cyclic loading tests (with the incremental loading amplitude) have been used under axial displacement-controlled loading conditions to evaluate the post-peak behaviour (e.g. Yang et al. 2015, 2017; Zhou et al. 2019; Meng et al. 2021). These studies, however, were not sufficient to adequately measure the post-peak response of rocks. This is because, during each loading cycle, the axial load is reversed when a certain amount of displacement is achieved, and after the failure point, since most of the rocks show class II or a combination of class I and class II behaviours, rock failure occurs in an uncontrolled manner. However, Munoz and Taheri (2017) showed that lateral displacement control throughout the test is a promising technique in studying the failure behaviour of rocks subjected to the post-peak cyclic loading. Recently, Shirani Faradonbeh et al. (2021a, b) developed a novel testing methodology based on the lateral strain feedback signal to measure the complete pre-peak and post-peak behaviour of rocks under uniaxial systematic cyclic loading.

Although many studies have been undertaken by different researchers on the evolution of rock fatigue damage and deformability parameters under different loading histories and loading conditions, no significant progress has been made regarding the effect of systematic cyclic loading on the cyclic loading-induced strength hardening, fatigue threshold stress and the post-peak instability of rocks under different confining pressures. This is while in underground rock engineering projects, rock materials are usually subjected to triaxial loading conditions with different levels of confinement accompanied by the systematic cyclic loading induced by different dynamic sources. Therefore, having in-depth knowledge concerning the foregoing parameters plays a critical role in stability assessment and reinforcement design. This study, for the first time, investigates the effect of systematic cyclic loading history on pre-peak and post-peak characteristics of rocks under different confinement levels. Some empirical equations are then proposed to manifest the evolution of peak strength, fatigue threshold stress and rock brittleness parameters. The obtained results are expected to provide a better understanding of the mechanical response of rocks to systematic cyclic loading under various confining pressures.

2 Experimental Profile

2.1 Gosford Sandstone

In this study, Gosford sandstone (Fig. 1a) extracted from the massive Triassic Hawkesbury sandstone of the Sydney Basin, New South Wales, Australia, was chosen as the testing material (Ord et al. 1991; Masoumi et al. 2017). X-ray powder diffraction (XRD) analysis of this medium-grained (0.2–0.3 mm) sandstone revealed that quartz (86%) is the dominant mineral, and illite (7%), kaolinite (6%) and anatase (1%) are other forming mineral composition. Figure 1b displays the SEM analysis result of this sandstone. Sufian and Russell (2013) reported that Gosford sandstone has a total porosity of about 18%, and the density distribution of the pre-existing microcracks within its matrix is homogenous. This type of sandstone is usually known as a uniform or very uniform sandstone (Hoskins 1969; Vaneghi et al. 2018). Cylindrical specimens (Fig. 1a) having 42 mm diameter and 100 mm length were extracted from a single rock block and prepared following the ISRM recommended standards (Fairhurst and Hudson 1999). The specimens were air-dried before conducting the static and cyclic loading tests, and the average dry density of this rock type was approximately about 2.215 g/cm3.

Fig. 1
figure 1

Gosford sandstone used in this study: a prepared specimens and b SEM photograph

Full size image

2.2 Testing Equipment

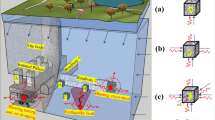
A fully digital closed-loop servo-controlled hydraulic compressive machine, i.e. Instron-1282 with the maximum loading capacity of 1000 kN, was employed to conduct the triaxial monotonic and cyclic loading tests. The testing machine can be programmed and equipped to perform different loading schemes using either the load-controlled or displacement-controlled loading techniques. As shown in Fig. 2a, a Hoek cell with a maximum capacity of 65 MPa was used to apply confining pressure. Also, a pair of LVDTs were installed between the loading platens to measure the axial displacement of the specimens during loading. Strain gauges are commonly used to measure the axial and/or lateral deformations of rocks in triaxial conditions. However, the strain gauges are only effective for local small-strain measurement, and they usually break after the peak stress when the specimen experiences large deformations (Munoz et al. 2016; Bruning et al. 2018). A modified test arrangement is made to overcome this problem; four strain gauges were attached immediately alongside one another around the centre line of the Hoek cell membrane, as displayed in Fig. 2b. Then, the strain gauges were connected to form a Wheatstone bridge (half-bridge circuit). Any deformation in specimen changes the resistance and, therefore, facilitates a unique output voltage (\({V}_{o}\)) as a lateral strain feedback signal. In the Wheatstone bridge shown in Fig. 2b, \({R}_{1}\) and \({R}_{3}\) represent the total resistance values provided by the pairs of strain gauges (each gauge has 120 \(\Omega\) resistance) which are connected in series. To balance the bridge and achieve zero voltage when the specimen is unstrained, two 240 \(\Omega\) precision resistors (i.e. \({R}_{2}\) and \({R}_{4}\)) were used in this circuit. The feedback signal, indeed, is the average of the lateral strain (\({\varepsilon }_{l}\)) values measured by the strain gauges, which is calculated as follows:

$${V}_{o}=\frac{{V}_{ex}}{4}\left(\frac{\Delta {R}_{1}}{{R}_{1}}+\frac{\Delta {R}_{3}}{{R}_{3}}\right)=\frac{{V}_{ex}}{4}.GF.\left({\varepsilon }_{1}+{\varepsilon }_{3}\right),$$
(1)
$$\mathrm{GF}=\frac{\Delta R/R }{\varepsilon },$$
(2)

where \(R\) is the resistance of the undeformed strain gauge, \(\Delta R\) is the change in resistance caused by strain, \(\varepsilon\) is the mechanical strain, \(GF\) is the strain gauge factor and \({V}_{ex}\) is the bridge excitation voltage.

Fig. 2
figure 2

Experimental set-up, a overview of the experiment and b strain gauged membrane

Full size image

Through a high-pressure wire and a feed-through connector fitted to the Hoek cell, the feedback signal is sent to the control unit of the testing machine to adjust the loading rate. By doing so, the membrane gauges are protected from damage during loading, and finally, the complete lateral deformation of rocks can be recorded in both pre-peak and post-peak regimes. Moreover, two miniature AE sensors (type PICO, from the American Physical Acoustics Corp.) were attached to the spherical seats, which have a direct connection to the specimen in the Hoek cell, to record the microcracking process during loading. The pre-amplifier was set to 60 dB of gain (Type 2/4/6) to amplify the acoustic emission (AE) signals during loading. To ensure that mechanical noises induced by the loading system are not recorded during the tests, the AE threshold amplitude was changed from 20 to 60 dB, and it was found that after 40 dB amplitude, no additional noises are recorded. Therefore, this value was set as the AE threshold. The axial load, axial and lateral displacements, and the AE outputs were recorded simultaneously by running the tests.

3 Test Scheme and Conditions

3.1 Uniaxial and Triaxial Monotonic Loading Tests

Before conducting the triaxial monotonic and cyclic loading tests at different confining pressures, the uniaxial compressive strength (\(\mathrm{UCS}\)) of Gosford sandstone should be determined. Shirani Faradonbeh et al. (2021b) performed a series of uniaxial monotonic tests on this rock type under a constant lateral strain rate (\({\mathrm{d}\varepsilon }_{l}/\mathrm{d}t\)) of 2 × 10–6/s. In their study, the axial strain was measured using a pair of external LVDTs, and the lateral strain feedback signal was measured using a direct-contact chain extensometer. Figure 3a shows the normalised stress–strain relations of the performed uniaxial monotonic tests. As it is shown in this figure, the rock specimens are uniform and demonstrate almost similar pre-peak and post-peak stress–strain relations. Therefore, it is assumed that the tested specimens have similar microstructure conditions, and there is no anomaly. Gosford sandstone has an average uniaxial peak strength (\({\mathrm{UCS}}_{\mathrm{avg}}\)) and tangent Young’s modulus (\({E}_{\mathrm{tan}-\mathrm{avg}}\)) values of 48.15 MPa and 13.4 Gpa, respectively.

Fig. 3
figure 3

modified from Shirani Faradonbeh et al. (2021b), b typical time-history of stress and strains for a triaxial monotonic test at 10% confinement level, c representative stress–strain relations for triaxial monotonic tests at different confinement levels and d the variation of peak deviator stress with confinement level

a Normalised stress–strain relations for uniaxial monotonic tests,

Full size image

Based on the determined \({\mathrm{UCS}}_{\mathrm{avg}}\), seven different confinement levels, i.e. \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 10%, 20%, 35%, 50%, 65%, 80% and 100%, were adopted for triaxial monotonic and cyclic compression tests. For each confinement level, three triaxial monotonic tests were carried out. The tests were conducted in a way that the axial load and confining pressure were applied simultaneously to the rock specimen under a constant axial strain rate of \({\mathrm{d}\varepsilon }_{a}/\mathrm{d}t\)= 0.03 mm/min until the desired confining pressure level is achieved. Thereafter, the confining pressure and axial load were kept constant for 5 min to ensure the stress was distributed uniformly (pre-consolidation stage). Then, while the confining pressure was maintained constant, the deviator stress (i.e. \(q={\sigma }_{1}-{\sigma }_{3}\)) was applied under a constant lateral strain rate (\(\mathrm{d}{\varepsilon }_{l}/\mathrm{d}t)\) of 2 × 10–6/s until the complete failure occurs. The lateral strain rate was adjusted during the test based on the feedback signal received from the four strain gauges mounted on the Hoek cell membrane. Figure 3b shows a typical time history of stress and strains during a triaxial compression test at \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=10%. Table 1 presents a summary of results for all conducted triaxial monotonic tests. Figure 3c shows the representative stress–strain relations for the triaxial monotonic tests. According to Table 1 and Fig. 3c, the increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\), affected both the pre-peak and the post-peak characteristics of rocks. Generally, with an increase in confining pressure, the axial strain at the failure point (\({\varepsilon }_{\mathrm{af}}\)) increases. Also, as shown in Fig. 3d, the average peak deviator stress (\({q}_{m-\mathrm{avg}}\)) of Gosford sandstone increased by confining pressure following a quadratic trend. Section 5 discusses the triaxial compression test results in more detail.

Table 1 Summary results of triaxial monotonic loading tests
Full size table

3.2 Triaxial Cyclic Loading Tests

To evaluate the influence of confining pressure and systematic cyclic loading history on the mechanical rock behaviour, including the fatigue threshold stress, post-peak behaviour, and peak strength, a series of systematic cyclic loading tests were performed at different deviator stress levels (\({q}_{un}/{q}_{m-a\mathrm{vg}}\)). For this aim, the testing machine was programmed to perform the cyclic tests automatically and continuously. Figure 4, schematically, shows the testing procedure for a triaxial cyclic loading test with a final monotonic loading. Similar to monotonic loading tests, the axial load and confining pressure were initially applied to the specimen under a constant axial strain rate of 0.03 mm/min until the pre-defined confinement level was reached. Then, the axial load and confining pressure were kept constant for 5 min to pre-consolidate the specimen. Afterwards, the deviator stress was increased under a constant lateral strain rate of 2 × 10–6/s to reach a specific deviator stress level, while \({\sigma }_{3}\) remained constant. The deviator stress was then reversed completely, and systematic cyclic loading was commenced under a higher lateral strain rate of \(\mathrm{d}{\varepsilon }_{l}/\mathrm{d}t\)= 150 × 10–6/s. During the cyclic loading, the axial load did not exceed the prescribed stress level, and confining pressure was always constant. The rock specimens were let to experience a maximum of 1000 loading and unloading cycles. Should the specimen did not fail during 1000 cycles, it was then subjected to a final monotonic loading at a constant rate of \(\mathrm{d}{\varepsilon }_{l}/\mathrm{d}t\)= 2 × 10–6/s until complete failure occurred. By doing so, the post-peak stress–strain behaviour of rocks was obtained in a controlled manner. Table 2 summarises all the loading scenarios and the obtained results for the performed triaxial cyclic loading tests in this study. Figures 5 and 6 show the representative stress–strain results of the specimens that experienced final monotonic loading and failure during cyclic loading, respectively. The stress–strain relations of other cyclic loading tests can be found in “Appendix: Stress-Strain Results of Triaxial Cyclic Loading Tests”. It should be mentioned that the failure morphology of the tested specimens under monotonic and cyclic loading conditions has not been systematically recorded in this study; however, no significant change in failure morphology was observed by changing the confining pressure.

Fig. 4
figure 4

Schematic time-history of deviator stress and lateral strain for triaxial cyclic loading tests

Full size image
Table 2 Summary results of triaxial cyclic loading tests
Full size table
Fig. 5
figure 5

Typical stress–strain results for the tests which did not fail during cyclic loading (test GS-C-13)

Full size image
Fig. 6
figure 6

Typical stress–strain results for the tests which failed during cyclic loading (test GS-C- 19)

Full size image

4 Confining Pressure Effect on Fatigue Threshold Stress

As mentioned earlier, fatigue threshold stress (FTS) is a critical parameter that can be used as an effective compressive strength of the intact rock subjected to static, dynamic and cyclic loads. Depending on the rock type, testing method and loading history, various ranges of values for FTS were reported by different researchers. Table 3 reviews these studies and lists the used materials and testing methods along with the determined FTSs. Table 3 shows that most of the existing studies have been conducted in uniaxial loading conditions. Taheri et al. (2016b) performed the systematic cyclic loading tests on Hawkesbury sandstone under a single confining pressure of \({\sigma }_{3}\)= 4 MPa. In an earlier study, Burdine (1963) performed a series of triaxial dynamic loading tests under three confining pressures (i.e. \({\sigma }_{3}\)= 0.21 MPa, 1.38 MPa and 5.17 MPa) on Berea sandstone. The study showed that with an increase in confining pressure from 0.21 to 5.17 MPa, the fatigue threshold stress increases from 76 to 93% of the monotonic strength.

Table 3 Summary of studies reporting the fatigue threshold stress values
Full size table

In the current study, a more comprehensive range of confining pressure was considered to evaluate the variation of FTS under systematic cyclic loading for Gosford sandstone. As stated in Sect. 3.1, uniform intact rock specimens were tested under uniaxial and triaxial compression loading. Therefore, it is assumed that the tested specimens had similar microstructure conditions, and there was no anomaly. The experimental results discussed in previous sections were relatively consistent, which support this assumption. According to Table 2, for each confinement level, a fatigue threshold stress (\({q}_{f}/{q}_{m-\mathrm{avg}}\)) can be derived. Figure 7 plots the variation of the determined FTS values against the confinement level. As can be seen in this figure, with an increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\) from 10 to 100%, \({q}_{f}/{q}_{m-\mathrm{avg}}\) constantly decreases, which shows the weakening/negative influence of confining pressure on the fatigue life of the rock under cyclic loading. These results indicate that with the increase of depth in underground projects, rock materials may fail at a stress level lower than the determined monotonic strength. The behavioural trend observed for FTS in this study is in contrast to that reported by Burdine (1963). This can be related to the tested material by Burdine (1963) under low confining pressures and dynamic loading conditions. Indeed, due to the high loading rate in dynamic loading conditions, at lower stress levels, the microcracks induced by cycles cannot be accumulated and extended throughout the specimens to create critical damage. In turn, this may result in more elastic behaviour of the specimens, which the improving effect of confining pressure will accompany. Thus, rock failure happens at higher stress levels and higher confinement levels. However, under cyclic loading conditions with a lower loading rate, the microcracks have enough time to be incurred, and rock failure occurs at lower stress levels. In contrast to the dynamic loading conditions, for cyclic loading tests, the confining pressure has an aggravating effect on FTS and results in more accumulation of plastic deformation during cycles (Taheri 2016; Cao et al. 2019; Zhu et al. 2019). The damage evolution under different confining pressures is discussed in detail in Sect. 6.

Fig. 7
figure 7

Variation of fatigue threshold stress with confinement level

Full size image

According to Fig. 7, the FTS can be predicted using the following logarithmic function with high accuracy:

$$\mathrm{FTS}=\frac{{q}_{f}}{{q}_{m-\mathrm{avg}}}=-0.074Ln\left(\frac{{\sigma }_{3}}{{\mathrm{UCS}}_{\mathrm{avg}}}\right)+0.806; {R}^{2}=0.982.$$
(3)

Also, based on the proposed Eq. 3, a binary condition can be defined to classify the failure status of the rock specimens, i.e. occurrence (1) or non-occurrence (0), under a specific stress level and confining pressure as follows:

$$\mathrm{Failure status}=\left\{\begin{array}{ll}1 \quad {q}_{un}/{q}_{m-\mathrm{avg}}>FTS\\ 0 \quad {q}_{un}/{q}_{m-\mathrm{avg}}\le FTS\end{array}\right..$$
(4)

5 Confining Pressure Effect on Post-Peak Instability

As mentioned earlier, the post-peak instability of rocks can be characterised as class I and class II, representing the stable and unstable rock fracturing process under a specific loading history, respectively. Brittleness is an appropriate intact rock property that can be employed to quantify the post-peak instability. Many rock brittleness indices can be found in the literature (Meng et al. 2020). However, as the evolution of strain energy accompanies the process of rock deformation and failure, the energy balance-based indices can better reflect the post-peak instability and the potential of severe failures (Li et al. 2019). Therefore, in this study, the following strain energy-based brittleness indices (\(BI\) s) proposed by Tarasov and Potvin (2013) were used to evaluate the post-peak instability of rocks:

$${\mathrm{BI}}_{1}=\frac{\mathrm{d}{U}_{r}}{\mathrm{d}{U}_{e}}=\frac{M-E}{M}$$
(5)
$${\mathrm{BI}}_{2}=\frac{\mathrm{d}{U}_{a}}{\mathrm{d}{U}_{e}}=\frac{E}{M}$$
(6)
$$\left\{\begin{array}{lll}d{U}_{e}=\frac{{q}_{B}^{2}-{q}_{A}^{2}}{2E} \\ d{U}_{a}=\frac{{q}_{B}^{2}-{q}_{A}^{2}}{2M} \\ {\mathrm{d}U}_{r}=d{U}_{e}-d{U}_{a}\end{array}\right.,$$
(7)

where \({\mathrm{d}U}_{e}\), \({\mathrm{d}U}_{a}\) and \({\mathrm{d}U}_{r}\) are, respectively, the withdrawn elastic energy, the additional/excess energy and the shear rupture energy in the post-peak regime (see Fig. 8). The \({q}_{A}\) and \({q}_{B}\) are the deviator stresses corresponding to points A and B, respectively, and \(E\) and \(M\) are, respectively, the pre-peak and the post-peak modulus.

Fig. 8
figure 8

modified from Tarasov and Potvin (2013)

Change in brittleness degree of BI1 and BI2 with the stress–strain relations and energy evolution,

Full size image

To evaluate the effect of both confining pressure and loading history on rock brittleness, \({\mathrm{BI}}_{1}\) and \({BI}_{2}\) were calculated for all monotonic and cyclic loading tests (the tests that experienced the final monotonic loading). The evolution of the average \(BI\) values was plotted against \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\) in Fig. 9. Shirani Faradonbeh et al. (2021b) performed a series of uniaxial systematic cyclic loading tests on Gosford sandstone at different stress levels and found that below the fatigue threshold stress, the rock brittleness values are similar to those obtained in monotonic loading conditions. In this study, the \(BI\) values were calculated again for all uniaxial monotonic and cyclic loading tests using Eqs. 5 and 6. According to Fig. 9, similar \(BI\) values were obtained for these two types of tests in uniaxial conditions. Also, as can be seen in Fig. 9, with an increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\) from 0 to 65%, the rock brittleness for both monotonic and cyclic loading tests changed similarly from an almost transitional state (i.e. \({BI}_{1}\approx 1\) and \({\mathrm{BI}}_{2}\approx 0\)) to more class II/brittle behaviour. By increasing the confining pressure to a certain amount (i.e. \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=50%), the maximum rock brittleness was achieved, and then, the \(BI\) values showed a decremental trend. A drastic drop in \(\mathrm{BI}\) was observed for \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}>65\%\), specifically for cyclic loading tests, where the rock specimens transferred from the class II region (green area) to the class I region (yellow area). Indeed, there is more opposition against the self-sustaining failure at high confinement levels, and more energy should be added axially by the loading system to yield the specimen completely. Therefore, a transition point at 65% confinement level can be estimated for Gosford sandstone, as the rock specimens transfer from a brittle to ductile failure behaviour. The evolutionary trend observed in Fig. 9 is also consistent with the stress–strain curves of rocks shown in Fig. 3c.

Fig. 9
figure 9

Variation of the average BI values with confining pressure for Gosford sandstone

Full size image

Similar unconventional trends for \(BI\) also have been reported in a few studies (i.e. Tarasov and Potvin 2013 and Ai et al. 2016), for stronger rocks such as quartzite and black shale. According to these studies, the increase in brittleness of rocks with confining pressure can be attributed to the energy-efficient fan-head mode shear failure. Indeed, during Class II failure behaviour, a domino structure of blocks is created by tensile cracks along the future failure plane. Due to the fracture propagation, these blocks are rotated without collapse, behaving as hinges and create a fan-shaped structure in the fracture tip. This, in turn, provides an active force (negative shear resistance) that is beneficial for maintaining the crack propagation and is responsible for the self-sustaining failure behaviour of rocks. Therefore, the increase in confining pressure for these rock types seems to provide a higher amount of active forces and consequently increases rock brittleness. By considering the decremental trend of fatigue threshold stress with confinement level, discussed in the previous section, as well as the incremental trend of rock brittleness with confinement for a specific extent, it can be inferred that with an increase in-depth in rock engineering projects, the propensity of rock structures to violent/brittle failures such as strain bursting at stress levels lower than the determined average peak strength can be aggravated.

The brittleness reduction at high confinement levels can be attributed to the more plastic deformation accumulation induced by the loading and unloading cycles within the specimens, which result in more energy dissipation in the pre-peak regime. This, in turn, provides less amount of elastic strain energy (the source for self-sustaining behaviour) at the failure point, leading to more ductile post-peak behaviour. This behaviour is more evident for cyclic loading tests than monotonic ones due to the more weakening effect of loading and unloading cycles at higher confinement levels. The damage evolution of rocks under different confinement levels is evaluated in more detail in Sect. 6.

6 Confining Pressure Effect on Fatigue Damage Evolution

6.1 Hardening and Weakening Cyclic Loading Tests

Rock specimens usually experience deformation under external forces, and a part of this deformation can be recovered by withdrawing the applied force, representing elastic characteristics. However, owing to intrinsic material properties, e.g., porosity and microcracks, and loading-induced damage, the complete deformation recovery after unloading is not possible. Therefore, a certain amount of irreversible/plastic deformation is retained in the specimens (Taheri and Tatsuoka 2015; Peng et al. 2019). The irreversible strain is accumulated incrementally by applying more cycles, which is accompanied by rock stiffness degradation. Cumulative strain can be utilised to manifest the non-visible damage incurred in the specimen during the systematic cyclic loading tests (Taheri et al. 2016b). According to Table 2, for the specimens that did not fail during 1000 loading and unloading cycles, two types of tests can be distinguished based on peak strength variation: strength weakening tests (i.e., final monotonic loading strength is less than \({\mathrm{UCS}}_{\mathrm{avg}}\)) and strength hardening tests (i.e., final monotonic loading strength is more than \({\mathrm{UCS}}_{\mathrm{avg}}\)). As seen in Table 2, the strength weakening is evident for the tests undertaken under \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\ge\) 80%. To appraise the rock damage evolution in both conditions, the cumulative irreversible axial strain (\({\omega }_{a}^{irr}\)) and tangent Young’s modulus (\({E}_{\mathrm{tan}}\)) were determined for two representative tests. Figure 10 shows the variation of \({\omega }_{a}^{\mathrm{irr}}\) and \({E}_{\mathrm{tan}}\) for specimens GS-C-15 (with 4.38% strength hardening) and GS-C-31 (with − 3.96% strength weakening) at 35% and 100% confinement levels, respectively. The other weakening and hardening cyclic loading tests also showed similar behaviour.

Fig. 10
figure 10

Typical evolution of \({\omega }_{a}^{\mathrm{irr}}\) and Etan for hardening and weakening cyclic loading tests

Full size image

According to Fig. 10, for both specimens, the elastic modulus increased notably for initial cycles, making the specimens stiffer and more difficult to deform. This can be related to the closure of pre-existing defects and yield surface expansion during cyclic loading (Taheri and Tatsuoka 2015; Peng et al. 2019). However, for specimen GS-C-15 (i.e., hardening test), by performing further cycles, the stiffness of the specimen decreased slightly and then remained almost constant until 1000 cycles were completed, which is consistent with the trend observed by Ma et al. (2013) triaxial systematic cyclic loading tests. On the other hand, during the initial cycles for specimen GS-C-15, \({\omega }_{a}^{\mathrm{irr}}\) evolved slightly to a certain amount due to the primary loose hysteretic loops, and then like \({E}_{\mathrm{tan}}\), retained almost constant, which shows that no more damage is cumulated within the specimen. As stated by Shirani Faradonbeh et al. (2021b), this quasi-elastic behaviour can be due to the competition between the mechanisms of grain-size reduction and rock compaction under consecutive loading and unloading cycles. For specimen GS-C-31 (i.e., weakening test), although no failure was recorded during the cycles, a different trend for variations of \({\omega }_{a}^{\mathrm{irr}}\) was observed (see Fig. 10). For the weakening test, \({\omega }_{a}^{\mathrm{irr}}\) increased rapidly, first for several cycles (i.e., initial hysteretic loops), and then by experiencing the dense hysteretic loops, shows a linear increase. At the end of cyclic loading, the increase of \({\omega }_{a}^{\mathrm{irr}}\) becomes more pronounced which may indicate that the specimen could have failed during cyclic loading should the test be continued. These results are consistent with \({E}_{tan}\) variations for the weakening test, shown in Fig. 10. As can be seen in this figure, unlike the hardening test, the damage evolution for weakening test was accompanied by the progressive stiffness degradation of rock during the whole cyclic loading test. Therefore, it can be stated that the strength weakening observed in Table 2 for systematic cyclic loading tests can be relevant to the progressive damage evolution/stiffness degradation of rocks in the pre-peak regime, which is aggravated when confining pressure exceeds the transition point (i.e. \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}>\) 65%). This is while for lower confinement levels, when cyclic stress level is low enough, cyclic loading has no considerable effect on damage evolution; rather, improves peak strength. The above observations are further investigated using AE results.

6.2 Acoustic Emission Results for Hardening and Weakening Tests

Acoustic emission (AE) is a well-known non-destructive technique that can monitor the micro and macrocrack evolution in rocks during loading in real time. Due to the local micro-scale deformations, small fracturing events corresponding to the immediate release of strain energy are created in the form of elastic waves within the specimens. Recording and analysing these elastic waves during the tests can directly measure internal damage (Cox and Meredith 1993; Lockner 1993). Therefore, the AE technique was utilised in this study to better elucidate the cracking procedure during the hardening and weakening cyclic loading tests and further discuss the observed quasi-elastic and hardening/weakening behaviours. In this regard, the evolution of AE hits, representing the number of generated cracks, and its cumulation throughout the representative hardening and weakening tests GS-C-15 and GS-C-31 were, respectively, depicted in Fig. 11a, b. To better unveil the damage mechanism under different confining pressures, the AE results of specimen GS-C-29 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=80%) which showed the greatest peak strength decrease (i.e. − 13.18% strength weakening) are also displayed in Fig. 11c. As shown in Fig. 11, the evolution of AE hits for the specimens can be investigated throughout three main loading phases: initial monotonic loading (phase A), systematic cyclic loading (phase B) and final monotonic loading (phase C). For all three specimens, during the seating of loading platens on the specimens and the closure of pre-existing defects, few AE hits were recorded in stage A and cumulative AE hits increased slightly. For specimen GS-C-15 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=35% and \({q}_{un}/{q}_{m-\mathrm{avg}}\)= 80%), as shown in Fig. 11a, the cumulative AE hits then remained almost constant (i.e. quasi-elastic behaviour) during loading and unloading cycles. The zoomed-in figure also shows only small amounts of low-amplitude AE hits during phase B. The cumulated AE hits at the end of stage B is almost 1.77% of the total damage experienced by the specimen during the test. This shows that no considerable cyclic loading-induced damage is generated should the specimens be loaded below the fatigue threshold stress and at confinement levels lower than the transition point. This behaviour also is consistent with the variation of \({\omega }_{a}^{\mathrm{irr}}\) discussed in the previous section. The majority of rock damage for specimen GS-C-15 occurred in phase C, where the final monotonic loading was applied to the specimen. In this phase, due to opening the compacted microcracks, the generation of new ones and their coalescence close to and after peak strength point, the cohesive strength of rock is gradually substituted by the frictional resistance, which was accompanied by a higher amount of AE hits.

Fig. 11
figure 11

Representative AE results for cyclic loading tests: a hardening test (GS-C-15), b weakening test (GS-C-31) and c weakening test (GS-C-29). A: Initial loading phase, B: Systematic cyclic loading phase and C: Final monotonic loading phase

Full size image

Unlike specimen GS-C-15 which showed a quasi-elastic behaviour during the systematic cyclic loading, a different AE evolution behaviour was observed for specimen GS-C-31 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=100% and \({q}_{un}/{q}_{m-\mathrm{avg}}\)=80%) in phase B. According to Fig. 11b, after a slight increase in AE hits during the initial monotonic loading, the microcracking increased with a higher rate by increasing loading and unloading cycles in phase B, which is manifested by a higher number of AE hits. The cumulated AE hits at the end of phase B is almost 27.09% of the total damage incurred in the specimen throughout the test, which is relatively higher than that observed for specimen GS-C-15. As discussed earlier, this microcracking induced by cyclic loading results in stiffness degradation (see Fig. 10) and more ductile behaviour in the pre-peak regime. The generated damage was not enough to fail the specimen; however, it resulted in strength weakening of -3.96% during the final monotonic loading. For specimen GS-C-29 which experienced a -13.18% decrease in peak strength at 80% confinement level, as seen in Fig. 11c, by applying systematic cyclic loading, the AE hits began to grow first with a lower rate until about 500 cycles were completed. Then, by performing further cycles, the rate of AE hits cumulation increased dramatically, representing the continuous generation of macrocracks within the specimen. According to Fig. 11c, about 93.90% of the total rock damage happened at the end of phase B, which is far greater than those observed for specimens GS-C-15 and GS-C-31. Based on the above observations for AE outputs, it can be stated that for confinement levels beyond the transition point (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 65%), although cyclic loading below the fatigue threshold stress does not lead to fatigue failure during 1000 loading cycles, it creates significant damage, which results in a considerable strength weakening during final monotonic loading.

6.3 Damage Cyclic Loading Tests

In this section, the effect of confining pressure is evaluated on the Gosford sandstone specimens which failed during loading and unloading cycles, i.e., damage cyclic loading tests. Figure 12a displays the variation of \({\omega }_{a}^{\mathrm{irr}}\) for damage cyclic loading tests under different confinement levels. To prevent Fig. 12a be crowded, only one damage test was considered for each confinement level. Generally, the irreversible strain increased quickly at the beginning of the tests. Then, a relatively uniform accumulation in strain followed by a rapid strain increase as the rock specimens head toward failure. As is clear from Fig. 12a, the damage accumulation rate increased by an increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\) from 10 to 100%. This damage evolution, however, is more significant for the tests undertaken under high confining pressures (i.e. over the transition point) where the irreversible/plastic deformations largely incurred in the pre-peak regime. The total accumulated plastic deformation values for specimen GS-C-30 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 80%) and GS-C-33 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 100%) are, respectively, 77.25 × 10–4 and 381.92 × 10–4, which are considerably higher than the values obtained for those undertaken under lower confining pressures. The large pre-peak deformation also is evident from the stress–strain relations shown in the Appendix for these specimens. Also, for lower confinement levels, the specimens follow a three-phase damage evolution law (Xiao et al. 2009) (i.e. transient phase, steady phase and acceleration phase), while it is switched into a two-phase process (i.e. the transient and acceleration phases) for high confinement levels, especially at \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)=100%. Thus, it can be deduced that confining pressure increases the damage evolution rate in rocks, and this is more evident for confinement levels higher than the transition point.

Fig. 12
figure 12

Variation of a ωairr and b, c Etan for damage cyclic loading tests under different confinement levels

Full size image

Figure 12b plots the variation of tangent Young’s modulus (\({E}_{\mathrm{tan}}\)) for damage cyclic loading tests at different \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\). According to this figure, for all damage cyclic loading tests, \({E}_{\mathrm{tan}}\) initially increased in the second loading cycle due to closure of existing microcracks, reduction in rock porosity and expansion of yield surface (Taheri and Tatsuoka 2015). Then, a continuous degradation in \({E}_{\mathrm{tan}}\) at different extents can be observed due to accumulation of the cyclic loading-induced damage. This damage seems to increase with an increase in confining pressure. Figure 12c illustrates the variation of the stiffness reduction from the second loading cycle (i.e., the maximum value of \({\mathrm{E}}_{\mathrm{tan}}\)) until the failure point (i.e., the minimum value of \({E}_{tan}\)) with respect to the applied confinement level. As seen in this figure, generally, the increase in confinement level resulted in stiffness reduction following an exponential manner. According to Fig. 12c, by an increase in confinement level until 80%, the amount of stiffness degradation increases progressively from 2.33 (17.57%) to 3.86 GPa (21.59%), after which a sharp increase in the amount of stiffness reduction, i.e., 5.38GPa (31.67%), can be observed for 100% confinement level. This dramatic degradation in \({E}_{\mathrm{tan}}\) in high confining pressures might be due to the excessive damage (irreversible deformation) cumulated in rock in the pre-peak regime, resulting in more ductile failure behaviour.

6.4 Acoustic Emission Results for Damage Tests

To have an insight regarding the AE evolution of rocks that failed during loading and unloading cycles, the typical results of AE hits for specimen GS-C-33 (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 100% and \({q}_{un}/{q}_{m-\mathrm{avg}}\)= 82.5%) is shown in Fig. 13. As shown in this figure, only two phases of A and B can be distinguished for cyclic damage tests. After an initial increase in AE hits due to closure of pre-existing defects and loading system adjustments, the specimen experienced dense hysteretic loops, and AE hits were accumulated at a constant rate. However, as the applied stress level for this specimen is higher than the estimated fatigue threshold stress for 100% confinement level (i.e., \({q}_{f}/{q}_{m-\mathrm{avg}}\)=80%), the rock specimen entered the second loose hysteric loops' region, and large irreversible deformations were incurred in the specimen, which was accompanied by the cumulation of AE hits with a higher rate (phase B). Finally, by coalesce of the generated micro- and macrocracks within the specimen and experiencing a large amount of axial strain at the failure point/plastic behaviour, i.e., \({\varepsilon }_{\mathrm{af}}\)= 580.75 × 10–4, the specimen failed in the cycle, demonstrating a class I behaviour. The observed damage evolution for specimen GS-C-33 is also consistent with its measured stress–strain relation shown in the Appendix.

Fig. 13
figure 13

Typical AE results for damage cyclic loading tests (σ3/UCSavg = 100% and qun/qm − avg = 82.5%). A: Initial monotonic loading phase and B: Systematic cyclic loading phase

Full size image

6.5 Applied Stress Level Effect on Damage Evolution

As stated earlier, systematic cyclic loading was applied to the specimens at different stress levels (\({q}_{un}/{q}_{m-\mathrm{avg}}\)). To evaluate the effect of the applied stress level on damage evolution of rocks under different confining pressures, the axial strain at the failure point (\({\varepsilon }_{\mathrm{af}}\)) was determined for all monotonic and cyclic loading tests. The results are listed in Tables 1 and 2. For uniaxial monotonic and cyclic loading conditions, \({\varepsilon }_{\mathrm{af}}\) values were adapted from Shirani Faradonbeh et al. (2021b). Figure 14 represents the variation of \({\varepsilon }_{\mathrm{af}}\) for monotonic, hardening, weakening and damage cyclic loading tests with \({q}_{un}/{q}_{m-\mathrm{avg}}\). It can be seen from Fig. 14 that under a specific confinement level (i.e., 35%), cyclic loading at various stress levels has no significant influence on \({\varepsilon }_{\mathrm{af}}\) and their values are almost similar to those obtained for monotonic loading tests. However, for higher confinements, larger values of \({\varepsilon }_{\mathrm{af}}\) is observed at the stress levels equal to or greater than the fatigue threshold stresses due to the accumulation of irreversible strain in the sample during the pre-peak regime before the failure. The above behaviour is more evident in Fig. 15, where the variation of average axial strain at failure point (\({\varepsilon }_{af-\mathrm{avg}}\)) for different stress levels was depicted against \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\). As seen in this figure, for monotonic loading tests, \({\varepsilon }_{\mathrm{af}-\mathrm{avg}}\) evolved linearly with the increase of \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\); this is while, for hardening/weakening and damage cyclic loading tests, this evolution occurred exponentially. According to Fig. 15, for \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\le\) 35%, the monotonic and cyclic loading tests have almost similar \({\varepsilon }_{\mathrm{af}-\mathrm{avg}}\) values, which means that loading and unloading cycles below and beyond the fatigue threshold stress have no striking influence on pre-peak behaviour, and damage evolution under cyclic loading is similar to monotonic loading conditions. However, for higher confinement levels,\({\varepsilon }_{af-\mathrm{avg}}\) increased first gradually until \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 65% representing more accumulation of plastic deformations within the specimens in the pre-peak regime compared with the monotonic loading conditions. The evolutionary trend of \({\varepsilon }_{\mathrm{af}-\mathrm{avg}}\), then, was aggravated for confinement levels of 80 and 100%, where a sharp increase in \({\varepsilon }_{\mathrm{af}-\mathrm{avg}}\) was observed for weakening and damage cyclic loading tests.

Fig. 14
figure 14figure 14

Variation of axial strain at failure point for monotonic and cyclic loading tests under different confinement levels: a 0%, b 10%, c 20%, d 35%, e 50%, f 65%, g 80% and h 100%

Full size image
Fig. 15
figure 15

Average axial strain at failure for monotonic and cyclic loading tests

Full size image

7 Confining Pressure Effect on Strength Hardening/Weakening

7.1 Peak Strength Variation

As seen in Table 2, depending on the stress level that cyclic loading is applied as well as the confinement level, rock specimens have experienced different values of increase/decrease in peak strength during final monotonic loadings. As discussed in Sects. 6.1 and 6.1.1, when the stress level during cyclic loading is low enough (i.e. lower than the estimated FTS), cyclic loading at lower confinement levels did not create macro-damage in the specimens, and a quasi-elastic behaviour dominated the rock damage evolution. This, in turn, resulted in a hardening behaviour under loading and unloading cycles, and consequently, strength improvement, which is observed during final monotonic loading. The rock compaction due to cyclic loading in the hardening region is evident in Fig. 5 for the representative test GS-C-13 (with 4.06% hardening), where the specimen did not experience large axial, lateral and volumetric irreversible strains, and the rock volume was entirely in the compaction stage during cyclic loading. This is while for rocks that failed during cycles (see Fig. 6), relatively higher strain values were recorded, and rocks were mainly in the dilation-dominated stage. The strength hardening induced by cyclic loading also has been reported by other researchers for different rock types under various loading conditions, such as Gosford sandstone (up to 7.82% increase) under uniaxial systematic cyclic loading (Shirani Faradonbeh et al. 2021b), Tuffeau limestone under uniaxial multi-level systematic cyclic loading (up to 28.55% increase) (Shirani Faradonbeh et al. 2021a), hard graywacke sandstone under uniaxial systematic cyclic loading (up to 29% increase) (Singh 1989), Hawkesbury sandstone under triaxial systematic cyclic loading (up to 11% increase) (Taheri et al. 2016b) and rock salt under triaxial systematic cyclic loading (up to 171% increase) (Ma et al. 2013).

Figure 16a represents the variation of peak strength at each confinement level (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{ave}}\)) for the cyclic tests conducted at different stress levels (\({q}_{un}/{q}_{m-\mathrm{avg}}\)). The results of hardening tests under uniaxial conditions (\({\sigma }_{3}\)=0) were extracted from Shirani Faradonbeh et al. (2021b). According to Table 2 and Fig. 16a, it can be observed that at each confinement level, the peak strength varies within a range based on the applied stress level; however, no significant trend can be determined between the applied stress level and peak strength values with confining pressure. This can be partially related to the discrepancy among the tested specimens, which is inevitable in experimental rock mechanics. However, as discussed in Sect. 3.1, the Gosford sandstone specimens have shown similar pre-peak and post-peak stress–strain curves during monotonic loading, indicating that the tested specimens are uniform and almost identical. According to Fig. 16a, the peak strength parameter varies between two distinct zones, i.e. hardening zone and damage zone. Also, the maximum increase and decrease in peak strength values of Gosford sandstone specimens are 7.82% and −13.18%, respectively. Generally, with an increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\), the amount of strength hardening induced by cyclic loading decreased and when \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)> 65% (i.e. transition point), rock specimens demonstrate strength weakening behaviour (see Fig. 16a). To better reflect the mechanism behind the rock moving from hardening into weakening, a parameter is proposed as below:

Fig. 16
figure 16

Variation of a peak strength during final monotonic loading at different stress levels, b differential irreversible strain and c maximum peak strength with confinement level

Full size image
$$\Delta {\varepsilon }_{a}^{\mathrm{irr}}={{(\varepsilon }_{a}^{\mathrm{irr}})}_{f}-{{(\varepsilon }_{a}^{\mathrm{irr}})}_{i},$$
(8)

where \(\Delta {\varepsilon }_{a}^{irr}\) is the differential irreversible axial strain (measured between valley points), and \({{(\varepsilon }_{a}^{\mathrm{irr}})}_{f}\) and \({{(\varepsilon }_{a}^{\mathrm{irr}})}_{i}\) are, respectively, the irreversible axial strains measured for final and initial loading cycles.

Figure 16b demonstrates the variation of \(\Delta {\varepsilon }_{a}^{\mathrm{irr}}\) for cyclic loading tests at different stress levels with \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\). As can be seen in this figure, the range of variation for \(\Delta {\varepsilon }_{a}^{\mathrm{irr}}\) increased continuously with an increase in confining pressure, and this is more significant for \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)> 65%, where a high amount of irreversible deformation was experienced by the specimens. The incremental trend of \(\Delta {\varepsilon }_{a}^{\mathrm{irr}}\) with confinement results in more plastic behaviour and, therefore, pre-peak damage even when cycles do not result in a failure. This, finally, resulted in a decremental trend of the maximum peak strength variation at each confinement level under cyclic loading, as shown in Fig. 16c.

7.2 An Empirical Model for Strength Prediction

As discussed above, the study on strength variation of rocks under the coupled influence of cyclic loading and confining pressure is rare and limited to some specific confining pressures. Therefore, no empirical model can be found in the literature to predict strength variation after loading cycles. Due to the high-complex and nonlinear nature of the problem, the common linear regression analysis technique cannot determine the latent relationship between the peak strength after cyclic loading and its corresponding parameters, such as confining pressure and applied stress level. The classification and regression tree (CART) algorithm was employed in this study to predict the amount of strength hardening/weakening in Gosford sandstone after cyclic loading history. The CART algorithm, developed by Breiman et al. (1984), is a computational-statistical algorithm that can predict the target variable in the form of a decision tree. The tree structure of the CART model contains three main components (see Fig. 17): (1) The root node, which is the best predictor/independent variable. (2) The internal node in which predictors are tested, and each branch represents an outcome of the test. (3) The leaf node, which implies the output of the model. Depending on the output parameter, the developed tree model is a classification tree (for qualitative parameters) or regression tree (for quantitative parameters).

Fig. 17
figure 17

Regression tree developed for the prediction of strength hardening/weakening percentage

Full size image

The CART tree is created by the binary splitting of the datasets from the root node into two sub-nodes (child nodes) using all predictor variables. The best predictor usually is chosen based on impurity or diversity measures (e.g., Gini, twoing and least squared deviation). The aim is to create subsets of the data which are as homogeneous as possible concerning the output variable. For each split, each input parameter (predictor) is evaluated to find the best groupings of categories (for nominal and ordinal predictors) or cut point (for continuous predictors) according to the improving score or reduction in impurity. Thereafter, the predictors are compared, and the predictor with the greatest improvement is selected for the split. This process is repeated until one of the stopping criteria is met (Salimi et al. 2016; Liang et al. 2016; Khandelwal et al. 2017). As peak strength (output parameter) is a quantitative parameter, the constructed tree is a regression tree. Regression tree building centres on three major components: (1) a set of questions, such as \({X}_{i}\le a?\), where \({X}_{i}\) is an input parameter, and \(a\) is a constant. (2) goodness of split criteria for selecting the best split on an input parameter and (3) the creation of summary statistics for terminal nodes. As stated above, the least squared deviation impurity measure (LSD), \(R(t)\), which is simply the within variance for the node \(t\), and is usually used for splitting rules and goodness of fit criteria. \(R(t)\) can be calculated as follows:

$$R\left(t\right)=\frac{1}{{N}_{W}\left(t\right)}\sum_{i\in t}{\omega }_{i}{f}_{i}{({y}_{i}-\overline{y }\left(t\right))}^{2},$$
(9)
$$\overline{y }\left(t\right)=\frac{1}{{N}_{W}\left(t\right)}\sum_{i\in t}{\omega }_{i}{f}_{i}{y}_{i},$$
(10)
$${N}_{W}\left(t\right)=\sum_{i\in t}{\omega }_{i}{f}_{i},$$
(11)

where \({N}_{W}\left(t\right)\) is the weighted number of records in node \(t\), \({\omega }_{i}\) is the value of the weighting field for the record \(i\) (if any), \({f}_{i}\) is the value of the frequency field (if any), \({y}_{i}\) is the value of the target field, and \(\overline{y }\left(t\right)\) is the mean of the dependent variable (target field) at node \(t\). The.

LSD criterion function for split s at node \(t\) is defined as:

$$Q\left(s,t\right)=R\left(t\right)-R\left({t}_{L}\right)-R\left({t}_{R}\right),$$
(12)

where \(R({t}_{R})\) is the sum of squares of the right child node, and \(R({t}_{L})\) is the sum of squares of the left child node. The split s is chosen to maximise the value of \(Q\left(s,t\right)\). Stopping rules control how the algorithm decides when to stop splitting nodes in the tree. Tree growth proceeds until every leaf node in the tree triggers at least one stopping rule. Any of the following conditions will prevent a node from being split: (a) All records in the node have the same value for all predictor fields used by the model. (b) The number of records in the node is less than the minimum parent node size (user-defined). (c) If the number of records in any of the child nodes resulting from the node’s best split is less than the minimum child node size (user-defined). (d) The best split for the node yields less impurity than the minimum change in impurity (user-defined). Also, maximum tree depth values can be defined for the algorithm to control the complexity of the final model. In regression trees, each terminal node’s predicted category is the weighted mean of the target values for records in the node \((\overline{y }\left(t\right))\) (Breiman et al. 1984).

In this study, the applied stress level (\({q}_{un}/{q}_{m-\mathrm{avg}}\)) and confinement level (\({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)) were defined as input variables to predict the percentage of strength hardening/weakening as output variable. Based on the results presented in Table 2 and the conducted cyclic loading tests in uniaxial conditions by Shirani Faradonbeh et al. (2021b), a database containing 28 tests that experienced a monotonic loading after a cyclic loading history was compiled. The test GS-C-29, which showed − 13.18% strength weakening, was identified as an outlier (in terms of statistics) and excluded from the modelling procedure. The CART algorithm has several parameters, including the maximum tree depth, the minimum size of parent and child nodes, and the number of intervals for the output parameter, which should be adjusted during the modelling. As there is no standard method to determine the optimum values of these parameters, a trial-and-error procedure was employed in this study. To do so, the values of the parameters were changed for different runs, and the setting which provided a trade-off between the accuracy and complexity was selected for the final model. Table 4 represents the settings of the best CART model. The modelling procedure was carried out in the MatLab environment. Figure 17 represents the obtained regression tree for the best model. As shown in this figure, the developed regression tree provides a practical tool to estimate the percentage variation of the peak strength straightforwardly. Figure 18 compares the measured values of the peak strength variation with those predicted by the developed CART model. As seen in this figure, the CART model can predict the peak strength variation of Gosford sandstone with high accuracy (\({R}^{2}\)= 0.9) and relatively low mean absolute error, \(\mathrm{MAE}= 0.69\) (\(\mathrm{MAE}=1/n\sum_{i=1}^{n}\left|{x}_{\mathrm{measured}}-{x}_{\mathrm{predicted}}\right|\), where \({x}_{\mathrm{measured}}\), \({x}_{\mathrm{predicted}}\) and \(n\) are the measured peak strength, predicted peak strength and data number, respectively).

Table 4 The settings for the CART model
Full size table
Fig. 18
figure 18

The comparison of the measured and predicted values of peak strength variation

Full size image

8 Conclusions

Triaxial monotonic and cyclic loading tests were undertaken in this study on Gosford sandstone at different confinement levels to scrutinise the effect of both systematic cyclic loading history and confining pressure on the evolution of rock fatigue characteristics. For this aim, a modified triaxial testing procedure was employed to control the axial load during the tests using a constant lateral strain feedback signal. Based on the experimental results, the following conclusions were drawn:

  1. 1.

    The confining pressure displayed a significant effect on fatigue threshold stress (FTS). It was found that with an increase in \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\) from 10 to 100%, FTS decreases from 97 to 80%. This indicates that rocks in great depth experience failure due to cyclic loading at stress levels much lower than the determined monotonic strength.

  2. 2.

    According to the obtained stress–strain relations, the post-peak behaviour of rocks followed an unconventional trend with the increase in confining pressure so that for lower \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\), rock specimens showed a self-sustaining (brittle) failure behaviour, while for higher \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\), the ductile behaviour was dominant. The post-peak instability of rocks was quantified using strain energy-based brittleness indices (\(BIs\)), and a transition point at \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 65% was identified, where the rocks transited from the brittle failure behaviour to ductile one. The results also showed that cyclic loading at confinement levels lower than the transition point has no notable effect on rock brittleness, while for \({\sigma }_{3}/{\mathrm{UCS}}_{\mathrm{avg}}\)= 80% and 100%, the weakening effect of systematic cyclic loading history on rock brittleness was more significant.

  3. 3.

    Fatigue damage evaluation of rocks using different parameters (i.e. \({E}_{\mathrm{tan}}\), \({\omega }_{a}^{\mathrm{irr}}\) and AE hits) showed that for hardening cyclic loading tests, no macro-damage is observed within the specimens, and the stiffness of the rocks remained almost constant during a large number of cycles, representing a quasi-elastic behaviour. However, for weakening cyclic loading tests, although no failure was observed during cycles, \({E}_{\mathrm{tan}}\) and \({\omega }_{a}^{\mathrm{irr}}\) increased and decreased, respectively, with cycle loading. Compared to the hardening cyclic loading tests, the AE activities (micro-cracking) were more evident for specimens with higher strength degradation. On the other hand, for damage cyclic loading tests, it was found that damage is accumulated with a higher rate and extent with an increase in confining pressure.

  4. 4.

    Looking at the variation of axial strain at the failure point (\({\varepsilon }_{\mathrm{af}}\)) for monotonic, hardening/weakening and damage cyclic loading tests, it was found that under confinement levels below the transition point, the applied stress level has no notable effect on the cumulation of irreversible deformations in the pre-peak regime and the values of \({\varepsilon }_{\mathrm{af}}\) are similar to those in monotonic loading conditions. However, for higher confinements, cyclic loading resulted in larger irreversible strain values before the failure point.

  5. 5.

    After a cyclic loading history, the peak deviator stress of Gosford sandstone varied between −13.18 and 7.82%. According to the evolution of damage parameters, the observed quasi-elastic behaviour during cyclic loading and the variation of plastic axial, lateral and volumetric strains for hardening cyclic loading tests, the strength hardening can be related to the rock compaction induced by cyclic loading. It was observed that the increase in confining pressure decreases the amount of strength hardening due to the accumulation of irreversible strains in the rock specimens. An empirical regression tree-based model was proposed to estimate peak strength variation of Gosford sandstone based on the applied stress level and confining pressure. The results showed the high accuracy of the model.