1 Introduction

The earthquake-prone areas in Southwest China are characterised by a rugged topography, with steep high mountains, deep valleys and complicated geological structures (Huang 2009; Li et al. 2017). Due to the unique topography and geological conditions, earthquake-triggered landslides have been major geological hazards in Southwest China (Liu et al. 2014; Song et al. 2018a). On 12 May 2008, the Wenchuan earthquake occurred in Sichuan Province, Southwest China and directly triggered massive landslides (Guo et al. 2014; Huang and Li 2014). Numerous landslides are characterised by local damage, and local boulder collapse is the main geological disaster that occurs in jointed rock masses (Yin et al. 2009; Huang et al. 2012). Some landslides show that local damage first occurs, and a large-scale slide body subsequently forms with the continued earthquake. For example, in the initial stage of the Niulangou landslide, nearly 2.6 million m3 of rock mass slid from an altitude of 1800 m and further caused the slide failure of a local rock mass at 1350 m; eventually, the accumulation of the local failure of rock masses caused a large-scale landslide (Kong et al. 2009). The local failure of the rock mass is closely related to the occurrence of the landslide. Due to the uncertain and random arrangement of structural surfaces in rock masses, the dynamic stability of the slopes becomes very complicated (Aydan 2016; Xu and Yan 2014; Xu et al. 2014; Song et al. 2018b, c).

Numerical methods are very useful for solving complex slope failure problems that cannot be solved using traditional approaches (Jiang et al. 2015; Leshchinsky et al. 2015; Che et al. 2016). Notable efforts have been expended to analyse the failure mechanisms of jointed rock slopes using numerical methods (Jiang et al. 2015; Lian et al. 2018; Liu et al. 2018; Zhao et al. 2018). Lian et al. (2018) investigated the toppling failure of a jointed rock slope using the distinct lattice spring model (DLSM) (Lian et al. 2018). Zheng et al. (2018) proposed a new universal distinct element code trigon approach to simulate the flexural toppling failure of an anti-inclined rock slope. Regassa et al. (2018) proposed an equivalent discontinuous modelling method (EDMM) for jointed rock masses to simulate the rock movements and failures triggered by mining. Xue et al. (2018) explored the failure mechanisms of a rock slope with dip weak layers and the effects of pre-reinforced piles on the slope stability using the finite-element method (FEM). Huang et al. (2018) investigated the effect of obliquely incident earthquake excitation on the seismic stability of rock slopes using FEM. In addition, many researchers have studied the dynamic responses of various rock slopes using shaking-table tests (Liu et al. 2014; Che et al. 2016; Song et al. 2018b; Li et al. 2018), such as a slope with a weak intercalation (Liu et al. 2014), bedding and toppling rock slopes (Fan et al. 2016), and a slope with multi-slip planes (Li et al. 2018). Because the model size, ground motion input parameters and waveform can be controlled, shaking-table tests are particularly effective to simulate the dynamic responses of slopes with complex geological structures (Fan et al. 2017; Li et al. 2018). Given this analysis, numerical methods and experimental methods provide important insight into the stability of complex slopes under the coupled effects of multiple parameters (Liu et al. 2014; Che et al. 2016; Song et al. 2018a, b). Therefore, in combination they can fully examine the dynamic characteristics of slopes.

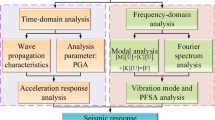
The seismic failure of a rock slope is usually a cumulative failure process; local damage is an obvious early-stage deformation characteristic that affects the occurrence of a landslide. Rock masses usually contain many weak structural surfaces such as beddings, joints and faults (Jiang et al. 2015; Song et al. 2018c). The reflection and refraction of seismic waves occur in slopes because of the effects of discontinuities that change the slope dynamic response characteristics in some frequency components (Fan et al. 2017). Therefore, for slopes with complex geological structures, it is difficult to accurately reveal the dynamic characteristics using the acceleration response in the time domain, e.g., the relationship between the local deformation response and the slope failure. However, a dynamic frequency domain analysis can clarify which frequency components of waves are sensitive to the dynamic characteristics of slopes for use in analysing the effect of the frequency components on the overall and local deformations of slopes. Therefore, a better understanding of the dynamic characteristics of jointed rock slopes in the frequency domain is required.

Modal analysis is an important method for structural dynamic analysis, and the basic type of dynamic frequency domain analysis is called natural frequency analysis (Reale et al. 2016; Zhou et al. 2016). FEM is the most common method in modal analysis, and it is known as computational modal analysis. Compared with DEM, FEM is limited to the analysis of jointed rock masses. The failure process of jointed slopes can be realistically simulated using DEM, which enables the analysis of complex processes, such as sliding, translation, rotation and rock mass fracture between blocks (Jiang et al. 2015; Toe et al. 2018). Small deformation problems are often analysed as linear elastic problems using FEM, which cannot directly simulate the dynamic failure of landslides. However, the dynamic failure problem is not involved in the modal analysis, and the modal structure is an inherent vibration characteristic of the structure in the elastic domain. Therefore, FEM has been the preferred method for modal analysis. Additionally, numerical modal analysis results require test verification, and the tests can further investigate the dynamic failure process of the slope. Thus, the natural frequency characteristics and their effects on the dynamic characteristics of a slope with discontinuous joints should be investigated using modal analysis and tests. In particular, special attention should be paid to the local dynamic response and cumulative damage effect of the slope.

This work uses an actual engineering project as an example and presents numerical and experimental studies on the dynamic characteristics of a rock slope with discontinuous joints. This research includes two aspects: a numerical modal analysis and dynamic characteristic analysis using shaking-table tests. The modal analysis of a slope can reveal the natural frequencies and vibration modes, and predict the dynamic response of the slope. Shaking-table tests can further investigate the effects of natural frequencies on the dynamic characteristics of the slope and the slope dynamic failure evolution process. The modal analyses and tests can fully clarify the cumulative effect of the local damage on the slope failure, and the local failure mechanism of the slopes is thoroughly discussed.

2 Case Study

The study area is nestled in the transition zone between the southeastern edge of the Qinghai–Tibet Plateau and Yunnan–Kweichow Plateau in Yunnan Province, Southwest China. The area is characterised by strong neotectonic movements, and several faults pass through the region. The Jinsha River Bridge is expected to be built in the study area (Fig. 1). The Lijiang slope with an average natural gradient of approximately 40° is located on the right bank of the Jinsha River, and many toppling structural surfaces have developed in the slope in addition to three structural bedding planes (Fig. 2). The distances between adjacent toppling surfaces and successive bedding surfaces are approximately 70 m and 35 m, respectively. The angles of these bedding and toppling surfaces are 15° and 75°. The topographies of the slope and a geological section are shown in Fig. 2. The parameters of the rock and structural surfaces of the slope required to construct the model were obtained according to a series of triaxial tests, uniaxial compression tests, and direct shear tests in the laboratory. The material parameters of the slope are shown in Table 1.

Fig. 1
figure 1

Location of the study area

Full size image
Fig. 2
figure 2

a Topography of Lijiang slope; b geological section of Lijiang slope

Full size image
Table 1 Physico-mechanical parameters of the material parameters of Lijiang slope
Full size table

The anchorage and pier of the Jinsha River Bridge are located on the Lijiang slope (Fig. 2b), and the stability of the slope directly impacts the stability of the bridge. Earthquakes usually occur in the area and, therefore, special attention should be paid to the seismic stability of the Lijiang slope. In addition, because the geological structure of the slope is complex, its seismic damage is often manifested as local damage characteristics, and the local cumulative damage will contribute to a large-scale landslide. In particular, local failure is often closely related to the high-frequency components of seismic waves. The seismic response of the slope based on the acceleration response in the time domain mostly reflects the overall dynamic deformation response characteristics of the slope but cannot be used to determine the local deformation characteristics. The seismic cumulative damage effect of the rock slopes has not received sufficient attention. Therefore, it is necessary to further study the mechanism of local failure and potential damage location based on analyses of the seismic response of the slope with complex geological structures in the frequency domain, which will be of great significance to the seismic reinforcement design of slopes and bridges.

3 Three-Dimensional Finite-Element Model of the Slope and Its Modal Analysis

3.1 Modelling and Parameters

The linear perturbation analysis step in the implicit solution function of ABAQUS is used for the modal analysis. The Lanczos solver and the single-precision algorithm are selected for the numerical calculation. The Lanczos method combines the vector iteration method with the Rayleigh–Ritz method. The principle of the modal analysis is as follows. Based on the theory of elastic mechanics, the dynamic control equation for an undamped system is [M]{Ü} + [K]{U} = 0 (Lee and Lee 2012; Reale et al. 2016), and the corresponding characteristic equation is ([K]-ω2i[M]){U} = 0. Then, the natural frequency (fi) is fi= ωi/2π, where [M] and [K] are the mass matrix and stiffness matrix of the model, respectively. {Ü} and {U} are the acceleration vector and displacement vector of the model, respectively. ωi is the i-th natural circular frequency (i = 1, 2, 3, …, n). It is important to emphasise that {U} is a relative and instantaneous displacement, unlike that in static analysis, and represents the degree of deformation at different positions. {U} represents the change in the displacement of each point with time, but the displacement ratio of the different points is fixed when the system vibrates at a certain natural frequency (fi). Each natural vibration mode represents the free vibration of a single-degree-of-freedom system. The lower order vibration modes play a decisive role in determining the dynamic characteristics of the model, so only a few modes are considered in the modal analysis.

The elastic model is considered in the modal analysis. It is important to optimise the boundary conditions of the finite-element models and their materials, structures, and sizes of subdivision. The modal analysis was performed using the model and considering the discontinuities between rock masses and structural surfaces. In the modal analysis, the effect of the different physical properties of the structural surface and rock mass on the model was considered. The tie connection method was used to set the connection mode between the structural surfaces and the rock mass, the connection mode of which is not surface contact, without setting the viscous damping. In this study, the structural surfaces are simulated as a soft material compared with the rock masses. The infinite element boundary method was used to simulate the actual infinite foundation, which is used at both sides and the base of the model. A three-dimensional finite-element model was established using the Hypermesh commercial software, as shown in Fig. 3. The model was modelled according to the Lijiang slope (Fig. 2). The model size is 829,000 × 390,000 × 361,000 mm and its gradient is approximately 40°. The structural planes were set at a depth of 1 m and a gradient of 15° (bedding) or 165° (toppling) in the slope. C3D8 elements were used to simulate the structural surfaces and rock. Meshes of quadrilaterals and squares with a side length of 5 m were used to explore some qualitative features of the behaviour in the model. Next, 320,138 C3D8 elements and 328,964 grid modes were generated in the model, and 8462 elements were generated in the infinity border. The physical mechanical parameters of the model are shown in Table 1.

Fig. 3
figure 3

Mesh model in the calculations (unit: mm): a FEM model; b profile of the model

Full size image

3.2 Results of the Modal Analysis

The dynamic deformation characteristics of the slope can be identified from the modal analysis. The first three natural vibration modes and natural frequencies of the slope are obtained using the modal analysis, as shown in Fig. 4. Figure 4 shows that the natural vibration mode mainly includes the shear, torsional, and flexural deformations. U slowly increases below the bedding structural surface but rapidly increases above it; in particular, a sudden increase can be found above the topmost structural surface. This phenomenon indicates that the deformation degree of the surface slope above the topmost structural surface is the largest. According to the vibration modes, the bedding structural surface has an amplification effect on the slope deformation, and the surface slope is the main deformation area. Figure 4 also shows that the first three natural frequencies of the slope are 12–15 Hz, 24–26 Hz, and 26–29 Hz. The first vibration mode represents the main dynamic deformation characteristics of the slope. The overall and torsional shear deformations of the surface slope can be found in the first mode (Fig. 4a), which indicates that the earthquakes mainly trigger the shear deformation of the surface slope, and the top slope initiates the deformation. U increases with the elevation and reaches a maximum at the slope crest (Fig. 4a), which suggests that the elevation has an amplification effect on the slope deformation. The analysis of the first vibration mode suggests that the natural frequencies of 12–15 Hz mainly induce the overall shear deformation of the surface slope along the topmost structural surface. Additionally, Fig. 4b shows that the flexural and torsional deformations can be identified in the second vibration mode. The U of the surface slope below the platform is much larger, which suggests that the natural frequencies of 22–24 Hz mainly induce the local deformation of the surface slope. Moreover, Fig. 4c shows that the top slope has the largest U according to an analysis of the third vibration mode, which indicates that the natural frequencies of 26–29 Hz mainly induce the local flexural and torsional deformations of the top slope. Therefore, the frequency components affect the slope deformation characteristics. The high-frequency components (> 22 Hz) mainly induce the local deformation of the surface slope, which is mainly concentrated in the slope crest and platform area. The low-frequency components (12–15 Hz) mainly induce the overall deformation of the surface slope, where the overall shear deformation of the surface slope occurs along the topmost structural plane.

Fig. 4
figure 4

Modal analysis of the model. a First mode; b second mode; c third mode

Full size image

The dynamic deformation mechanism of the slope can also be deduced from the modal analysis. The dynamic deformation difference between blocks that is induced by the low-frequency components (12–15 Hz) is very small, whereas the deformation difference between blocks induced by the high-frequency components (> 22 Hz) is considerably larger in the surface slope. This phenomenon indicates that high-frequency components have a great impact on the slope dynamic deformation characteristics and mainly induce an uneven deformation between blocks in the surface slope, which gradually results in the formation of independent blocks. When earthquakes continue to occur, the local deformation of the slope accumulates to a certain value, and the low-frequency components induce the overall shear deformation of the surface slope, which will lead to the sliding failure of the surface slope.

4 Shaking-Table Tests for a Scale Model of a Rock Slope Containing Discontinuous Joints

4.1 Materials and Methods

The shaking-table test was performed in the Key Laboratory of Loess Earthquake Engineering, Gansu Earthquake Administration of China. The bi-directional electric servo shaking table is 4 m × 6 m. Regular and irregular waves can be used as the input motions, and the effective frequency range is 0.1–70 Hz. A maximum horizontal acceleration of 1.7 g and a maximum vertical acceleration of 1.2 g can be obtained.

To simulate the semi-infinite foundation of the model, the effect of the boundary should be minimized when the experimental tank is designed. A rigid sealed experimental tank comprising organic glass and carbon steel plates was developed for the tests, and its inner dimensions are 2.8 m × 1.4 m × 1.4 m (Fig. 5a). The Lijiang slope is the prototype of this model (Fig. 2). The materials and test parameters of the model were obtained based on the Buckingham π theorem of similarity. The acceleration a, mass density ρ and dimension L were selected as the fundamental parameters, with similarity ratios of Ca= 1, Cρ= 1, and CL= 400, respectively. The similarity ratios of the physical parameters in the tests are listed in Table 2. From the similarity calculation, the parameters of the rock mass simulation materials were as follows: Poisson ratio μ = 0.30; cohesion c = 0.048 MPa; shear modulus G = 25 MPa; friction angle φ = 49°; and density ρ = 28.5 (kN/m3). The simulation materials were mainly formed from barite, steel slag, sand, plaster, and water at ratios of 5:4:1.3:2.1 according to a series of triaxial tests.

Fig. 5
figure 5

Experimental tank and scaled model. a Experimental tank; b prefabricated blocks; c grey paperboard; d model slope

Full size image
Table 2 Similarity ratios of the model
Full size table

Different casting times of the material may cause problems in the model, such as maintenance difficulties and uneven pouring, which will affect the accuracy of the test results. To avoid these problems, the model was constructed with prefabricated blocks (Fig. 5b), which were piled up in four layers. Accordingly, some vertical gaps are present between adjacent blocks, which may adversely affect the test, e.g., the mixture of many high-frequency components in the collected waveform. To eliminate these effects, for the masonry of prefabricated blocks, dislocation masonry is used in the model, and the same material as the blocks was used to fill the gaps. In addition, to accurately simulate the slope sliding failure behaviour, the friction angle of the structural planes should be accurately simulated. Grey paperboard was used to simulate the structural planes because its friction angle is closest to that of the structural planes according to direct reduction tests. The grey paperboard and prefabricated blocks were tightly bonded in the model (Fig. 5c), and the model is as shown Fig. 5d. The size of the model was 186 cm × 140 cm × 89 cm (Length × Width × Height) (Fig. 6). To minimise the adverse effects of the boundary conditions, a buffer layer was set at the bottom of the model (Fig. 6), whose material is identical to the rock mass. The buffer layer is set to enable the model boundary-free deformation and simulate the infinite boundary conditions in the model.

Fig. 6
figure 6

Cross-sectional illustration of the test model apparatus with discontinuous joints, which shows the layout of the monitoring points and accelerometers

Full size image

Twenty three-direction capacitive acceleration sensors (DH301) were used to record the acceleration–time curve. The frequency ranges of the acceleration sensor are 0–1500 Hz horizontally and 0–800 Hz vertically, and its sensitivity is approximately 66 mV/m s−2, with a measuring range (peak) of ± 20 m/s2. The measurement points of the acceleration sensors are shown in Fig. 6, all of which were embedded into the centre of the model to reduce the side boundary effect. Artificial synthetic (AS) waves were used as the input motion, which were synthesised by the local earthquake prediction department. Their time histories and Fourier spectra are shown in Fig. 7, with dominant frequencies of 2.5–4.5 Hz. The loading sequences of the tests are listed in Table 3. The acceleration data from the test should be preprocessed primarily by filter and baseline calibrations. MATLAB was used to compile the Chebyshev II bandpass filter, filter the wave, and obtain the effective waveform frequency, which was mainly in the range of 3–50 Hz.

Fig. 7
figure 7

Input artificial synthetic waves: a time history; b Fourier spectrum

Full size image
Table 3 Test loading sequence
Full size table

4.2 Dynamic Characteristics of the Slope Based on the Natural Frequency Analysis

4.2.1 Natural Frequency Analysis of the Slope

To clarify the natural frequency of the slope, taking the input horizontal AS wave (0.074 g) as an example, the time history and Fourier spectra of the typical monitoring points are shown in Fig. 8. As a natural filter, the slope magnifies the frequency components of the waves that are similar to its self-vibration frequency, which shows the resonance effect in the frequency components (Fan et al. 2017). Four predominant frequencies (f1, f2, f3, and f4) can be identified in Fig. 8: f1 (3–6 Hz), f2 (14–16 Hz), f3 (22–24 Hz), and f4 (27–29 Hz). Changes in the elevation, and topographic and geological conditions will result in changes in the slope amplification effect (Liu et al. 2014; Fan et al. 2016). Figure 8 shows that the PFSAs of f2, f3, and f4 rapidly increase with the elevation, which suggests that they are sensitive to the slope amplification effect. However, the PFSA of f1 has no evident changes because it is close to the predominant frequency of the AS wave, which indicates that it is mainly caused by the input wave. Combined with the modal analysis (Fig. 4), f2, f3, and f4 have a close relationship with the modal characteristics of the slope, which suggests that they are the natural frequencies of the slope. In particular, f2 has the largest PFSA, which indicates that it plays a leading role in the slope failure. It should be noted that the PGA (peak ground acceleration) obtained by the acceleration time histories of the measuring points represents the maximum seismic inertia force of the slope and the maximum seismic amplification effect at a certain moment. The Fourier spectrum is obtained by applying the fast Fourier transform (FFT) to the acceleration time histories of the measuring points, which represents the amplitude distribution of the wave on the frequency axis. The PFSA is the spectrum peak amplitude of the predominant frequency band, which represents the maximum amplification effect in the frequency band. Therefore, f2, f3, and f4 have an obvious amplification effect on the slope, and their PFSAs were used to determine the dynamic characteristics of the slope in the frequency domain.

Fig. 8
figure 8

Time history and Fourier spectra of the measuring points when the input AS wave (0.074 g) is in the x-direction

Full size image

4.2.2 Effect of the Natural Frequencies on the Dynamic Characteristics of the Slope

To determine the effects of the natural frequencies on the dynamic characteristics of the slope, taking input waves of 0.074 and 0.297 g as an example, the PFSA distribution of f2, f3, and f4 is shown in Fig. 9. The PFSA refers to the peak Fourier spectrum amplitude of different natural frequencies and represents the strongest dynamic response of the measuring points at the natural frequency. First, the PFSAs of all monitoring points are extracted; then, the PFSA distribution is drawn using the Inverse Distance to a Power method with Surfer software. The colour code and contour line in Fig. 9 represent the distribution of the PFSA values. Figure 9 shows that the PFSA of the surface slope is much larger, which indicates that the surface slope is the main amplification area. The PFSA is much smaller below the bedding structural plane than that above it, which suggests that the bedding structural plane affects the slope dynamic characteristics. The PFSA distribution analysis shows that the slope dynamic characteristics have obvious topographic and geological effects. In addition, Fig. 9a shows that the PFSA of the surface slope is much larger, which indicates that f2 is the main cause of the overall deformation of the surface slope. Figure 9b shows that the PFSA of the surface slope below the platform is much larger, which indicates that f3 is responsible for the main amplification effect in the area. Figure 9c shows that the top slope has the largest PFSA, which suggests that f4 has an amplification effect on the top slope. In combination with the results of the modal analysis (Fig. 4), it is shown that the frequency components affect the slope dynamic characteristics, and their relationship is shown in Fig. 10. The low-frequency components (f2) mainly trigger the overall deformation of the surface slope, while the high-frequency components (> 22 Hz) mainly trigger the local deformation of the surface slope.

Fig. 9
figure 9

Distribution of PFSA when the input is in the x-direction: a 14–16 Hz; b 22–24 Hz; c 27–29 Hz (Unit: g)

Full size image
Fig. 10
figure 10

Relationship between the deformation area of the slope and the frequency (unit: mm)

Full size image

To further investigate the topographic and geological effects of the slope, the PFSA of the measuring points with the elevation is shown in Figs. 11, 12, 13. Figures 11, 12, 13a show that the PFSA has a positive correlation with the elevation inside the slope and reaches a maximum at the slope crest, which suggests that the elevation has a slope amplification effect. The PFSA also increases with the elevation near the slope surface (Figs. 11b and 13b), but in Fig. 12b, the PFSA increases below the platform and decreases above it. This phenomenon suggests that different natural frequencies have different effects on the slope dynamic characteristics. In addition, Figs. 11, 12, 13a show that the PFSA increases linearly below the bedding structural plane, overall, but increases rapidly above it. Figures 11, 12, 13b show that A6 and A7 have smaller PFSAs, but they rapidly increase above the topmost structural plane. This phenomenon suggests that the bedding structural plane has an amplification effect on the slope dynamic characteristics because the reflection and refraction of a wave through structural planes result in wave superposition in certain frequency components, and the great differences in physical properties between the structural planes and rock masses cause the redistribution of energy (Kumar and Kaur 2014), which magnifies the dynamic characteristics of the slope.

Fig. 11
figure 11

PFSA (f2) of the slope with the elevation when the input is in the x-direction: a inside the slope; b on the slope surface

Full size image
Fig. 12
figure 12

PFSA (f3) of the slope with the elevation when the input is in the x-direction: a inside the slope; b on the slope surface

Full size image
Fig. 13
figure 13

PFSA (f4) of the slope with the elevation when the input is in the x-direction: a inside the slope; b on the slope surface

Full size image

4.3 Dynamic Failure Evolution Process of the Slope

Small earthquakes will not cause landslides but only some local damage; in particular, with the accumulation of local deformation, sliding failure may eventually occur. In the tests, after each seismic force is loaded, a degree of deformation occurs in the slope. Based on the previous deformation, the seismic force is continuously loaded, and the slope dynamic deformation characteristics are further studied based on the previous accumulated deformation. The purpose of the successive loading from 0.074 to 0.446 g is to investigate the dynamic failure evolution process and the cumulative damage effect of the landslide.

To evaluate the dynamic failure evolution process of the slope, taking four points (A10, 16, 18, and 20) as examples, the PFSA with the seismic intensity is analysed in Fig. 14. Figure 14a shows that the PFSA of f2 linearly increases from 0.074 to 0.297 g, but an obvious nonlinear increase can be found from 0.297 to 0.446 g. The PFSA of f3 linearly increases from 0.074 to 0.297 g (Fig. 14b), but a rapid decrease in the increasing rate can be found at 0.297–0.446 g. Figure 14c shows that the PFSA of f4 linearly increases when the seismic intensity is < 0.297 g, but a sudden decrease is identified when it is > 0.297 g. According to the PFSA analysis, the linear increase of the PFSA with the seismic intensity suggests that the slope is stable, although local damage occurs in the surface slope, when the seismic intensity is < 0.297 g; the nonlinear change of the PFSA when it is > 0.297 g suggests that the surface slope has begun to enter the plastic failure stage.

Fig. 14
figure 14

PFSA in the surface slope with the seismic intensity when the input is in the x-direction: af2; bf3; cf4

Full size image

In the damage stage, fractures occur in the surface slope, which destroy the overall lithology of the slope. These cracks lead to an increase in the porosity in the structural surfaces and decreases in the wave velocity and elastic wave energy, which further result in changes to the dynamic response of the slope. Therefore, when the surface slope has begun to suffer dynamic damage, the seismic energy propagation in the rock mass undergoes a great change and causes a dramatic fluctuation or abrupt change in the slope amplification effect. Therefore, the dynamic failure evolution process of the slope can be identified, including the local damage stage (< 0.297 g) and overall failure stage (> 0.297 g). In the failure stage, the increasing rate of the PFSA of f2 decreases to an extent, which indicates that the failure stage can be more clearly determined by analysing the PFSA of f2 from the overall deformation perspective. Moreover, compared with the PFSA of f2 and f3, the increasing trend of the PFSA of f4 abruptly changes, which indicates that the failure stage can be identified using the PFSA of f4 from the local deformation perspective due to the dynamic deformation of the top slope, which is mainly induced by f4, where the top slope is the most damaged and unstable area.

4.4 Dynamic Damage Characteristics of the Slope

The dynamic damage phenomenon of the slope is shown in Fig. 15. A few cracks occurred at the slope surface (Fig. 15a), which suggests that local damage mainly occurs when the seismic intensity is ≤ 0.297 g. The local damage deepens, extends, and coalesces to form the large-scale damage of the surface slope with an increase in the seismic intensity. Finally, the surface slope will experience block sliding along the topmost bedding structural plane when the seismic intensity reaches 0.446 g (Fig. 15b). In addition, Fig. 15b shows that the top slope and surface slope below the platform are seriously damaged, which were mainly induced by f3 and f4, respectively, and indicate that the high-frequency components have a strong impact on the dynamic deformation of the slope before the landslide. Figures 10 and 15b show that the topmost bedding structural plane is the slip surface, which indicates that low-frequency components (f2) mainly induced the overall sliding failure of the surface slope. Combined with the numerical and test results, the failure of the landslide is a progressive destruction process, i.e., a cumulative failure process. The local damage induced by the high-frequency components plays a major role in the cumulative deformation process of the landslide, and the low-frequency components mainly determine the failure mode. The dynamic failure mechanism of the landslide is as follows. The local damage of the slope, which is induced by the high-frequency components, occurs first. Then, the local damage of the surface slope progressively develops with increasing seismic intensity and promotes the damage of the slope. When the local damage accumulates to a certain amount, the low-frequency components further trigger the overall sliding failure of the surface slope.

Fig. 15
figure 15

Damage phenomenon of the slope when the input AS wave is under different seismic intensities. a 0.297 g; b 0.446 g

Full size image

4.5 Comparison of the Numerical Modal Analysis and Test Results

By combining the modal analysis and tests, we determine the natural frequencies of the slope. In combination with the modal analysis, the tests show that the dynamic characteristics of some frequency components are obviously amplified because of the resonance effect of the frequency components near the natural frequency of the slope. If these frequency components are directly taken as the natural frequency without considering the modal analysis, a large error analysis will be generated in the tests. For example, the PFSA of f1 is large; without the modal analysis, it is difficult to determine that f1 is not the natural frequency but rather is caused by the input AS wave. In addition, the modal analysis can predict the dynamic response of the slope and reveal the slope instantaneous deformation characteristics under vibration conditions of different natural frequencies, which is difficult to reveal using the tests. The tests can verify the modal analysis results, investigate the failure evolution process of the slope, and further reveal the effect of the natural frequencies on the dynamic failure of the slope. Therefore, the modal analysis provides qualitative guidance and a means of comparison with the tests and is an important complement to the test analysis. The combination of the modal analysis and tests can thus clarify the relationship between the dynamic characteristics and the natural frequencies. In particular, the local deformation is an important factor in the process of a slope’s cumulative failure.

5 Conclusions

A numerical modal analysis and a series of shaking-table tests were performed to study the dynamic response of a slate slope with discontinuous joints. Some conclusions are as follows.

  1. 1.

    According to the modal analysis, the modes of the slope include the shear, torsional, and flexural modes. The first three natural frequencies are 12–15 Hz, 24–26 Hz, and 26–29 Hz. The frequencies of 12–15 Hz primarily induce the shear deformation of the surface slope along the topmost bedding structural plane, and the frequencies of 24–26 Hz and 26–29 Hz mainly induce the local deformation of the slope. The elevation and bedding structural plane have an amplification effect on the slope deformation, and the surface slope is the main deformation area.

  2. 2.

    According to the tests, the natural frequencies (f2, f3, and f4) affect the dynamic characteristics of the slopes. By analysing the PFSA of the natural frequencies, the amplification effect generally increases with the elevation. The bedding structural surface has an amplification impact on the dynamic characteristics of the slope. The dynamic failure evolution process of the slope can be more clearly identified based on the analysis of the PFSA of f2 and f4, which mainly includes the local damage stage (< 0.297 g) and overall failure stage (> 0.297 g).

  3. 3.

    By combining the modal analysis with the tests, we determine the natural frequencies of the slope. The high-frequency components are the key triggering factors of the local damage of the slope, and the low-frequency components mainly control the occurrence of the landslide. f3 and f4 mainly induce the deformation of the surface slope below the platform and the top slope, respectively, and f2 mainly induces the overall deformation of the surface slope. The local deformation is also an important factor in the cumulative failure process and affects the occurrence of the landslide. The dynamic failure mechanism of the landslide is as follows: the local damage of the slope, which is induced by the high-frequency components, occurs first; during the cumulative failure process, the local damage deepens, extends, and coalesces to form large-scale damage of the surface slope with the increasing seismic intensity. When the local damage accumulates to a certain extent, the surface slope will experience block sliding along the slip surface.

However, the numerical modal analysis cannot truly reveal the dynamic failure process of the slope. In the tests, due to the loss of time and frequency information in the time and frequency domains, respectively, the dynamic characteristics of the slope cannot be fully reflected. Therefore, in future studies, the quantitative analysis of the slope dynamic stability will receive more attention, e.g., using the DEM to simulate the slope dynamic failure. Moreover, based on the energy-based method in the time–frequency domain, the seismic damage process of the slope is quantitatively analysed using the Hilbert–Huang transform and marginal spectrum theory.