Improvement to the Convergence-Confinement Method: Inclusion of Support Installation Proximity and Stiffness

Abstract

The convergence-confinement method (CCM) is a method that has been introduced in tunnel construction that considers the ground response to the advancing tunnel face and the interaction with installed support. One limitation of the CCM is due to the numerically or empirically driven nature of the longitudinal displacement profile and the incomplete consideration of the longitudinal arching effect that occurs during tunnelling operations as part of the face effect. In this paper, the authors address the issue associated with when the CCM is used within squeezing ground conditions at depth. Based on numerical analysis, the authors have proposed a methodology and solution to improving the CCM in order to allow for more accurate results for squeezing ground conditions for three different excavation cases involving various excavation-support increments and distances from the face to the supported front. The tunnelling methods of consideration include: tunnel boring machine, mechanical (conventional), and drill and blast.

1 Introduction

The convergence-confinement method (CCM) (AFTES 1983) is a method which is intended to consider the ground response to tunnel face excavation and the effect of installed support. The method includes a three-step analysis, considering (1) the ground reaction curve (GRC), which relates internal pressure to displacement (convergence) of the tunnel walls; (2) the support reaction curve (SRC) which relates deformation (confinement) of the support pressure to the convergence; and (3) the longitudinal displacement profile (LDP) which relates tunnel wall displacement to the position of the tunnel face. The purpose of the LDP is to determine uniquely the location at which the support is installed (i.e. the initiation of the SRC with respect to the GRC). This is currently established through the association between support installation location along the tunnel and the associated level of displacement (on the GRC) for the equivalent unsupported tunnel at that location. This point of support installation is a key practical outcome of the method. For instance, if a stiff support is added too soon, subsequent tunnel displacement results in excess support stresses in the temporary support elements. If the support is added too late, excess displacement of the unsupported tunnel results in a local dissipation of confinement and allows for detrimental loosening of the rock mass and ultimately ground failure before the support is installed.

The GRC and SRC are analytical solutions defined by their respective analytical formulations and an assumption of plane-strain conditions. The GRC and SRC are two independent solutions that do not influence one another when support is installed within the cavity of the excavation (e.g. steel sets, shotcrete). In the simplest case, the LDP is based on an unsupported case (i.e. with no support). Cantieni and Anagnostou (2009), Bernaud and Rousset (1996) and Vlachopoulos and Diederichs (2009, 2014) and others elaborate on the inaccuracies and practical problems associated with this approach. The objective of the paper is to improve the applicability of the CCM, taking into consideration near face support. The proposed methodology explores the following concepts: accuracy of the current state of practice of employing the SRC based on the unsupported LDPs; the influence of support on the tunnel face displacement and LDPs; accuracy of the current state of supported LDPs; and the influence of the overloading effect of the support. These concepts and the developed methodology and its solution will be addressed within the following sections of this paper.

2 Development of Convergence-Confinement Method

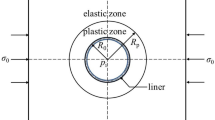
The elastic response captured in the CCM is based on the initial hole-in-a-plate solution by Kirsch (1898). The first inclusion of a plastic zone within the analysis is attributed to Fenner (1938) with a number of formulations proposed since including Panet and Guenot (1982), Duncan Fama (1993), Carranza-Torres and Fairhurst (2000), for example. These plastic zone formulations are based on the assumption that the ground remains as a continuum during yield (no loosening). Considerations of ground loosening were added by Pacher (1964). There are many assumptions that are required for the analytical consideration of the loosening zone. The important practical aspect is that support should be installed soon enough to prevent loosening of the rock mass but late enough to prevent overloading through plastic yield. Figure 1 illustrates the ground loosening section of the ground reaction curve and illustrates the importance of timing and location of support during installation.

Fig. 1

The ground reaction curve (GRC) and support reaction curve (SRC) relationship (modified after Fenner and Pacher, quoted by Rabcewicz 1973). σ_r = radial stress, and P_imin = minimum internal pressure before detrimental loosening

In the above diagram, the early support installed at the face has a significantly higher load at equilibrium than the delayed support and may therefore overload. Delayed installation results in equilibrium before support overload. The support must be installed early enough, however, to provide the conceptual P_imin required to prevent disintegration of the otherwise plastic continuum assumed for the analysis.

Guenot et al. (1985) coupled real-time deformation monitoring with an analytical function for wall displacements as a function of time and advancing face. This analytical function was further expanded by Barlow (1986) to incorporate sequential excavation, installation of support, and displacements occurring ahead of the tunnel face. These analyses, however, are based on a curve-fitting technique to measured data in order to determine the initial (before in front of the tunnel face) and final displacements.

The convergence-confinement formulations are radial in nature. The deformations assumed or calculated must be correlated to a datum (known or assumed radial displacement at the face) or to a longitudinal displacement profile so that the inputs and results of the analysis can be related to the location in the advancing tunnel (relative to the face) and thereby, to rational support timing within the construction sequence. This is not a simple closed-form correlation. A number of published range of values for normalized displacement ($U_{\text{o}}^{*}$) of the tunnel face are listed in Table 1. These equations/values represent the tunnel face displacement alone.

Table 1 List of referenced publications of tunnel face displacement for unsupported analysis

The formal longitudinal displacement profile was introduced by Panet (1995) (denoted in this discussion as LDP₁₉₉₅) to define the optimal placement/timing of support installation, without the need for rigorous numerical analysis. Panet’s work permits tunnel designers to quickly conceptualize both the ideal location for installation of support with respect to the tunnel face and the support response. However, this approach is less valid for cases where large plasticity zones are anticipated (i.e. in weaker rock masses). One solution by Vlachopoulos and Diederichs (2009) resolves this issue through the development of an improved longitudinal displacement profile (denoted in this discussion as LDP₂₀₀₉) which takes into account the effect of the plastic zone developed. Vlachopoulos and Diederichs (2009) assumed perfectly plastic conditions with no dilation (non-associated flow rule) (Hoek et al. 1992). The inputs for the LDP₂₀₀₉ require the solution from the GRC (maximum displacement, u_max, and maximum plastic radius, R_pmax). The piecewise function has split at the location of the tunnel face, defined by another function (1). These Eqs. (1–4) were developed based on a best-fit curve within two- and three-dimensional (3D) numerical analysis, an example of which is shown in Fig. 2 (diamonds), based on the results of Vlachopoulos and Diederichs (2009).

Fig. 2

Correlation between $u_{0}^{*} = u_{0} /u_{{\mathrm{max}} }$ at $X^{*}$ = X/R_t (=0 at the face) and the maximum plastic radius, $R^{*}$ = R_pmax/R_t. The dotted line the curve-fit solution based on the results of Vlachopoulos and Diederichs (2009), Eq. (2). Additional data points for elastic analysis ($R^{*}$ = 1) are based on values published in the literature

In this solution, the displacement at the tunnel face is

$$u_{0}^{*} = \frac{1}{3}{\text{e}}^{{ - 0.15R^{*} }}$$

(2)

If $X^{*}$ < 0 (i.e. condition in the rock mass ahead of the face)

$$u^{*} = \frac{u}{{u_{{\mathrm{max}} } }} = u_{0}^{*} {\text{e}}^{X*}$$

(3)

If $X^{*}$ > 0 (i.e. condition in the open tunnel)

$$u^{*} = 1 - \left( {1 - u_{0}^{*} } \right)e^{{\frac{{ - 3X^{*} }}{{2R^{*} }}}}$$

(4)

$X^{*}$ is the normalized distance from the face (X/R_t), $R^{*}$ is the normalized plastic radius ratio (R_pmax/R_t), R_t is the tunnel radius, u_o is the displacement at the face cross section (unsupported), u_max is the maximum displacement of the tunnel cross section (unsupported)

$$u_{\text{o}}^{*} = \, u_{\text{o}} /u_{{\mathrm{max}} }$$

It must be noted that Fig. 2 also includes additional published findings (squares) based on the normalized displacement at the tunnel face utilizing elastic analysis, The ground material wa ≈ 1, from Table 1. The additional elastic solutions were included to illustrate the sensitivity of this measurement. Factors such as Poisson’s ratio have proven to be critical to the normalized face displacement (Guilloux et al. 1996; Unlu and Gercek 2003). However, the influence of Poisson’s ratio is negligible when comparing depth of plasticity, as done in Vlachopoulos and Diederichs (2009). Additional factors which have an influence on the normalized face displacement, such as mesh size of a numerical model, will be discussed in subsequent sections. Note that the LDP₂₀₀₉ does not include the effect of the installed support. Vlachopoulos and Diederichs (2014) indicate that employment of the LDP₂₀₀₉ for locating the installation point for the support system (in weak ground conditions) will produce error if the location is within 3 tunnel radii from the face.

Vlachopoulos and Diederichs (2014) proposed Eq. (5) for supported LDP (denoted in this discussion as LDP₂₀₁₄) that is a function of the maximum supported displacement and location of the support being installed.

$$\frac{u}{{u_{{\mathrm{max}} } }} = \frac{1}{{1 + {\text{e}}^{{0.6\left( {1 - 0.1\frac{{L_{\text{u}} }}{{R_{\text{t}} }}} \right)\left( {\frac{{L_{\text{u}} }}{{R_{\text{t}} }} - 5\frac{X}{{R_{\text{t}} }} - 1} \right)}} }}$$

(5)

where L_u unsupported span length, R_t radius of the tunnel, and X distance from face.

As the maximum supported displacement depends on the location at which the support is installed, the solution is an iterative approach. The LDP₂₀₁₄ gives a better approximation of the overall profile for a supported case when compared to the LDP₂₀₀₉. When the support is installed close to the tunnel face (within 2 radii), the LDP₂₀₁₄ is not accurate (Vlachopoulos and Diederichs 2014). Furthermore, the LDP₂₀₁₄ does not take into consideration the effect of support stiffness. In terms of location of support installation, the accuracy of the LDP remains a weakness of the CCM (Alejano 2010). Therefore, one must take into consideration the contribution of the support within the CCM as this is currently lacking within the overall method and state of practice involving this rationale.

3 Inclusion of Support Effect within the LDP

In an attempt to address the underestimation of the CCM when support is installed, Bernaud and Rousset (1996) employed an implicit method to solve for displacements at the tunnel face. This method, however, results in an average value of displacement based on the stiffness and distance from the face values examined. This singular solution provided by an average response may be accurate for select cases, but as $R^{*}$ increases, the requirement for the inclusion of the effects of the support stiffness and support installation distance increases as illustrated in “Effect of support on the LDP curvature” section. An additional limitation of Bernaud and Rousset (1996) solution is that their numerical model has a coarse mesh, which is assumed to be caused by computational restrictions at the time of publication. Furthermore, the solution provided by Bernaud and Rousset (1996) only provides the maximum displacement for materials with a Poisson’s ratio of 0.5, which is the theoretical limit for these parameters and is too high for any rock type as shown in Gercek (2007).

Nguyen-Minh and Guo (1996) conducted a parametric analysis to study the relationship between normalized final face displacement ($u_{\text{fo}}^{*} = u_{\text{o}} /u_{\text{osup}}$), due to support, based on the normalized final tunnel displacement ratio ($u_{\text{f}}^{*} = u_{{\mathrm{max}} } /u_{{\mathrm{max}} \sup }$). The ground material was simulated as an elastoplastic material with a stability number ranging from 1.9 to 2.9. 3D conditions were simulated by using a simplified axisymmetric model. The results from this analysis are shown in Fig. 3a). Nguyen-Minh and Guo (1996) was based on the numerical modelling work of Guo (1995) which consisted of a coarse mesh, which is assumed to be caused by computational restrictions at the time of publication. Additionally, the numerical model was only 30 R_t long, too small according to the findings of this paper (discussed in “Boundary conditions: unsupported” section).

Fig. 3

The general relationship between the normalized final face displacement and normalized final tunnel displacement ratio based on an axisymmetric finite element method (FEM) analysis of Nguyen-Minh and Guo (1996). The proposed solution of Oke et al. (2013), based on a fully 3D numerical model (FLAC3D), is presented for comparison (Eq. 6)

An investigation was conducted Oke et al. (2013) in order to study the effects of the influence of the support interaction on the LDP, and specifically, in the tunnel face displacement. The previous investigation utilized full three-dimensional analysis (FLAC3D, Itasca Consulting Group Inc. 2009). The results of the preliminary investigation proposed a modification of the calculation of the displacement at the tunnel face. This modification allowed for an easy adjustment of the LDP₂₀₀₉, as illustrated in Eq. (6), and was developed as a function of the plastic radius (Eq. 7) or the final tunnel displacement (Eq. 8 and Fig. 3b). Simplifications used within the preliminary investigation, as discovered from the analysis conducted for this paper, over-generalized the solution but still acted as a sound foundation for comparison purposes, as done in the following sections.

$$u_{0\sup }^{*} = \frac{{u_{0} }}{{u_{{\mathrm{max}} } u_{\text{fo}}^{*} }} = \frac{1}{{3u_{\text{fo}}^{*} }}{\text{e}}^{{ - 0.15R^{*} }}$$

(6)

$$u_{\text{fo}}^{*} = \log \left( {\left( {4.3882R_{\text{f}}^{*} - 3.3882} \right)^{0.85} } \right) + 1$$

(7)

$$u_{\text{fo}}^{*} = \log \left( {u_{\text{f}}^{*0.85} } \right) + 1$$

(8)

3.1 Overloading of Support

Cantieni and Anagnostou (2009) found that the displacement effect of the stress path on squeezing behaviour will always be larger than the one obtained by the GRC. Cantieni and Anagnostou (2009) credit this to the inability of the plane-strain model to reverse the radial stress that follows the installation of the lining. This reversal of the radial stress is caused by the initial overloading of the support system brought about by the longitudinal arching effect. This longitudinal arching effect has been found to be more pronounced when the support is installed closer to the tunnel face (Ramoni and Anagnostou 2010, 2011) which is generally the case for squeezing ground conditions. Evidence of more pronounced longitudinal arching is captured by the increase normal stresses acting on the installed support. Below is an illustration of the results presented by Cantieni and Anagnostou (2009) (Fig. 4).

Fig. 4

The ground reaction curve (GRC) and numerical results of a rock mass to strength ratio of 7.96. Results and figure modified from Cantieni and Anagnostou (2009), where L_u = unsupported span. L_e = excavation step length, R_t = Radius of tunnel, k = support stiffness, and i denotes excavation sequencing

3.2 Summary of Limitations of CCM

For clarification, the following points are the concerns and issues that currently limit or weaken the application of the CCM for squeezing ground conditions:

• 1. The conventional (classical) inclusion of the LDP in the CCM is based on an unsupported approach,

• 2. There are limited solutions for LDP in supported conditions that consider the stiffness of support and the unsupported span. Those solutions that do exist have their limitations, and,

• 3. The CCM does not take into consideration the effect of the overloading of the support systems caused by longitudinal arching.

These concerns and issues are addressed by the authors in the following sections.

4 Inclusion of Support: Modification to Convergence-Confinement Method

In order to address concerns of the accuracy of the supported LDP within 2 radii of the tunnel face, as well as overloading of the support system, the authors have developed an approach that modifies the LDP and includes the additional stress caused by the overloading. This approach utilizes the following 4 steps (Fig. 5):

Fig. 5

Illustration of the methodology for the modification to the CCM

• 1. Employ the SRC based on the unsupported LDP (grey line),

• 2. Employ the SRC based on the supported LDP (double line),

• 3. Determine the point of initial support equilibrium (iterative solution, repeat step 2), and,

• 4. Adjust for the overloading of the support (dashed double line).

The modification to CCM was the result of numerous 2D axisymmetric numerical analyses. The modification was developed for squeezing ground conditions, as these remain the most susceptible to the influence of support as well as the most relevant application of the CCM.

4.1 Numerical Model

The numerical model employed for this analysis was an axisymmetric analysis (Phase 2, Rocscience 2013) as it was capable of simulating and capturing the three-dimensional effects of a tunnel analysis in isotropic conditions. Assumptions made for axisymmetric analysis are similar to those made for the CCM. The definition of squeezing ground conditions used within this paper was first observed by Sakurai (1983) who asserted that squeezing failure occurs when strain in the tunnel side walls exceeds 1%. The rock mass materials A1, B1, C1, D1, and E1 utilized in this investigation were adopted from Vlachopoulos and Diederichs (2009) and are presented in Table 2 with their corresponding strain (normalized tunnel displacement) according to the Carranza-Torres (2004) solution. Conveniently, these ground materials had P_o/σ_cm ratios from 0.1 to 0.25, which according to Hoek (2001) will experience a ground material response of minor to extremely severe squeezing conditions. The boundary conditions consisted of fixed normal directions (rollers) along the tunnel axis and the boundary perpendicular to the tunnel axis. The corners and the boundary opposite to the tunnel axis were constrained in both directions. The influence of the boundary conditions, in terms of distance away from the zone of interest, was invested in the subsequent sections.

Table 2 Numerical analysis parameters for the parametric analysis used in this study model

The support used within this analysis was adopted from Cantieni and Anagnostou (2009). Cantieni and Anagnostou state that typical support stiffnesses range from 0.1 to 1 GPa/m. Therefore, an extreme range of support stiffness values from 0.01 to 100 GPa/m was employed in order to capture the full/extreme range of support systems. Support stiffnesses used within the numerical analysis conducted in this paper were based on the formulation presented in Carranza-Torres and Fairhurst (2000). Shotcrete elastic properties were held constant, and the thickness was only varied to effect the support stiffness. Additional supports were investigated, as listed in Table 2, in order to compare the three-dimensional analysis (FLAC3D) of the preliminary investigation to the axisymmetric analysis conducted within this paper. The preliminary investigation was simplified to test only a certain support stiffness being installed 1 m (0.4 R_t) away from the excavation face, with an excavation step of 1 m (0.4 R_t).

Three variants of numerical models were developed for assessment based on three common-practice excavation techniques. These techniques are illustrated in Fig. 6. The first Excavation, Case (1), was designed to simulate a tunnel boring machine (TBM), in which the unsupported span, L_u, stays constant (0.4–2 R_t) throughout the whole analysis, and the support length and excavation step length remain the same (0.4 R_t). In addition, Excavation Case (1) was generated to mimic the analysis of Cantieni and Anagnostou (2009) as well as Oke et al. (2013) for comparison purposes. The greatest L_u investigated is 2 R_t because, as previously stated, LDP₂₀₁₄ is accurate when L_u ≥ 2 R_t. This maximum L_u rationale was applied to the remaining two excavation cases. The following is a summary of the parameters used for the parametric analysis used for Excavation Case 1.

Fig. 6

Illustration of excavation, support, and unsupported span sequencing used within the numerical axisymmetric parametric analysis. These sequences relate to typical excavation methods as shown. Note R_t = Radius of tunnel; TBM tunnel boring machine

• 1. Normalized support installation distance (L_u/R_t): 0.4, 0.8, 1.2, 1.6, and 2.0.,

• 2. Ground Material: A1, B1, C1, and D1 from Table 2, and,

• 3. Support stiffness (GPa/m): 0.01, 0.1, 1, 10, and 100.

In addition, to allow for comparison to Oke et al. (2013), support class S1 was also tested with the addition of material class E1. Similar runs were conducted for the remaining two excavation cases with the addition of a normalized support installation distance 0.1 (Excavation Cases 2 and 3) and 0.2 (Excavation Case 2 only). These smaller excavation step sizes were not conducted for Excavation Case 1 because it is impractical to install support that close to the tunnel face due to head of the TBM. The second Excavation Case 2 was designed to simulate mechanical (conventional) excavation (i.e. roadheader), in which support was installed to the tunnel face once the excavation, in 0.1 R_t increments, reached the specified L_u. The last and third Excavation Case 3 was designed to simulate a drill-and-blast excavation where excavation step length would be identical to the supported installation length (installed to the tunnel face) and unsupported span. Investigation of three different excavation cases is warranted as each excavation and support process results in distinct stress and displacement distribution near the tunnel face.

4.1.1 Boundary Conditions: Unsupported

In order to study the impact of the boundary conditions on the numerical model, an initial investigation was carried out. Figure 7 provides an illustration of the assessment of the boundary conditions for the B1 material. Analysis found that the B1 material required the model length to be 25 D_t (or 12.5 D_t distance to centre of model) to be within 5% of the expected numerical solution for the tunnel wall displacement (denoted by black squares in Fig. 7). This result is in agreement with the recommendation of Vlachopoulos and Diederichs (2014) that state that fixed boundaries require a minimum of 3 plastic radii away from the plastic zone. The model length, however, did not capture an accurate response of the displacement of the tunnel wall at the face (denoted with black diamonds). To successfully capture an accurate response of the tunnel face, the model length was increased to 76 D_t. A similar analysis was conducted for the width of the axisymmetric analysis. A width of 48 D_t was found to be within 1% of an analysis with a width of 96 D_t for the B1 material. Therefore, the numerical length (76 D_t) and width (96 D_t) for the other material properties employed the same boundary conditions for B1. A 5% error was found for the unsupported analysis of the A1 material. However, as is illustrated in Fig. 7, the effect of boundary conditions remains less severe for the supported analysis (grey lines).

Fig. 7

Effect of fixed displacement boundary conditions distance (model length) on absolute per cent difference of maximum displacement. Wall denotes maximum radial displacement. Face denotes radial displacement at the face (i.e. X = 0)

4.1.2 Boundary Conditions Supported

The support used for the boundary verification is listed within Table 2, S1. A comparison of the Phase 2 results and the trends that were developed in preliminary investigation (Oke et al. 2013, Eq. 9) for the relationship ratios (supported/unsupported) between the normalized final displacement ratio ($u_{\text{f}}^{*}$) and normalized reduction of final plastic radius ratio ($R_{\text{f}}^{*}$) can be found within Fig. 8. The result of the length of the model and the differences in mesh size distinguish the analyses. The length of the preliminary investigation (FLAC3D) was 12 D_t which the authors expect to yield a potential 10% error for the tunnel face for the B1 material, as shown in Fig. 7. Additionally, the mesh size for both analyses dictates the accuracy of the plastic radius measurement (i.e. if the mesh size is 0.25 m, the plastic radius measurement can only be as accurate to 0.25 m).

Fig. 8

Comparison of the final displacement of the tunnel versus maximum plastic ratio for analysis conducted within this paper employed support with a factor of safety of 1.1 based on the LDP₂₀₀₉, and the dash black line represents the curve-fit from the investigation conducted for this paper

4.1.3 Element Type: Considerations

An assessment of Phase 2 standardized element types was conducted in order to verify the accuracy of the results. The magnitude of the final displacement was compared to those calculated using of the analytical solution of Carranza-Torres (2004). As anticipated, the higher-order elements (8-noded quadrilaterals) were most accurate when compared to the analytical solution (within 3%), with the exception of A1 material (12%), an anticipated outcome as the solution was complete closure. Additionally, the evaluation of the mesh type and size provided an illustration of the effects of the excavation step size, 0.1 R_t compared to 0.4 R_t (or more precisely how the plastic strain rate dependency on the stress path affects the results). Vlachopoulos and Diederichs (2009) state that a maximum excavation step of 0.4 R_t is required to capture a continuous excavation sequence for practical purposes. However, this was found to be inaccurate when increased precision of the higher-order elements (Rugarli 2010), combined with a smaller excavation step of 0.1 R_t, was investigated. The effect of excavation step size has a significant effect on the tunnel face displacement, as illustrated in the following section.

It is important to note that the remainder of this paper utilizes values normalized to unsupported final displacements and unsupported plastic radius based on an analytical solution. The authors acknowledge that the analytical and staged numerical model results have differences due to stress–strain dependencies acting at the excavation face which is not captured in the analytical solutions; however, the proposed solution methodology requires the employment of an analytical solution as the foundation of the method; therefore, all numerical model results are referenced to these analytical results.

4.1.4 Initial Results of Boundary and Mesh Conditions

The Phase 2 axisymmetric results (for which the employed support was S1, from Table 2) can be represented as a power function, as shown in Fig. 8 and Eq. (10). The linear trend established by the preliminary investigation (Oke et al. 2013) was proven to be a reasonable representation of $u_{\text{f}}^{*}$ when the $R_{\text{f}}^{*}$ was below 3. A power function was found to be more accurate than the previous linear function (Eq. 9), for the capture of the analytical trend when compared with the results of the B1 material defined by the GRC of Carranza-Torres (2004).

The agreement between the analytical and numerical response provides confidence in mesh and boundary conditions. These results, however, are unique to the selected support and ground material utilized. A unique solution (Eq. 10, from Oke et al. 2013) was found for the relationship between the final supported displacement and the plastic radius (solely), but has been determined inaccurate for carrying support stiffness and support installation distance.

$$u_{\text{f}}^{*} = 4.4R_{\text{f}}^{*} - 3.4$$

(9)

$$u_{\text{f}}^{*} = R_{\text{f}}^{*2.2}$$

(10)

An additional validation was carried out for the response of the wall displacement of the tunnel face (Fig. 9). The analysis conducted for this paper was compared with the results of Vlachopoulos and Diederichs (2009), Eq. (2). As previously mentioned, the accuracy of Vlachopoulos and Diederichs (2009) numerical analysis is dependent on the mesh size and excavation step. The graded mesh used for the axisymmetric analysis by Vlachopoulos and Diederichs (2009), as well as the uniform mesh used for the analysis presented in this paper, is included in Fig. 9. The uniform mesh utilized for this analysis was selected to ensure uniform measurement of the plastic radius, as well as an even distribution of stresses and deformations. Over the generally applicable range of $R^{*}$, there is a 5% difference between the results of this analysis, Eq. (11) and Vlachopoulos and Diederichs (2009) results.

Fig. 9

Correlation between $u_{0}^{*} = u_{0} /u_{{\mathrm{max}} }$ at $X^{*}$ = X/R_t = 0 (at the face) and the maximum plastic radius, $R^{*}$ = R_pmax/R_t for different excavation step sizes and mesh types. Inset figure is a comparison of the different meshes used for the analysis. R² = 0.99

As the model employed a smaller step size of 0.1 R_t and higher-quality mesh (8-noded quadrilaterals), an accurate representation of the tunnel face closure can be assumed from the results. For the remainder of the paper, Eq. (11) will represent the calculation required to find the initial point of installation of the support based on an unsupported analysis (i.e. Eq. 11 supersedes 2).

$$u_{\text{o}}^{*} = 0.38{\text{e}}^{{ - 0.12R^{*} }}$$

(11)

4.2 Effect of Support on the Tunnel Face Displacement

The first modified component of the LDP to be evaluated is the tunnel face displacement. As previously described, the face displacement is primarily dependent on installation distance (unsupported span) from the tunnel face, and secondarily on the ground material, for the TBM excavation analysis (Excavation Case 1). The results from the parametric analysis of the maximum plastic radius ratio were not accurate enough to capture strong trends due to the mesh size, which supported previous findings with the unsupported analysis. Therefore, reduction of the tunnel face was established solely on the tunnel normalized final displacement ratio, $u_{\text{fo}}^{*}$. The effect of plasticity on the tunnel has already been captured in Eq. (11), while additional effects of plasticity have been deemed insignificant to the $u_{\text{fo}}^{*}$. The results indicated that each excavation case had a similar yet unique solution for the reduction of the tunnel face. Examples of select results are included within Fig. 10 to illustrate some of the differences.

Fig. 10

Results for face displacement based on P_o/σ_cm ratios from 4.0 to 10.1 and support installation at 0.4 R_t (left) and 2.0 R_t (right) from the tunnel face. The dotted line in the left side images represents the solution of Nguyen-Minh and Guo (1996), NM & G’96. Solid lines denote regression analysis. Dash lines denote adjusted curve-fit solutions

The left side of Fig. 10 compares general curvature of the results for Excavation Case 1 and Case 2 for support installed at 0.4 R_t from the tunnel face. Excavation Case 1 results were best captured by the exponential function (Eq. 12a), while Excavation Case 2 results were best captured by the power function (Eq. 12b). Case 3 resulted in a similar result to Excavation Case 2 with a power function. The different functions used to express the reduction of curvature are explained through differences of location of the support installation. Excavation Cases 2 and 3 always installed the support to the tunnel face, while Excavation Case 1 does not. The tunnel face displacement for Excavation Case 1 was additionally found to be a function of unsupported span length and ground conditions. The tunnel face displacement for Excavation Case 2 yielded similar results; however, the authors were not able to express the differences of the material as a function. To remediate this, the authors choose to ignore the A1 results due to the extremity of the ground conditions (100% closure) and instead employed the best-fit solution for all of B1 to D1 results to get an accurate solution of the most realistic ground materials. The results for Excavation Case 2 were still determined to be a function of the unsupported span length, as is illustrated in Fig. 10 (top right and bottom left). Excavation Case 3 yielded similar results as Excavation Case 2, as shown in the bottom right of Fig. 10. Similarly the A1 material was ignored for Excavation Case 3.

The right side of Fig. 10 compares general curvature of the results for Excavation Case 2 and Case 3 for support installed at 2.0 R_t from the tunnel face. The smaller step size in Case 2 (top right of Fig. 10) allows for increased tunnel face displacement then when simulated unsupported (i.e. $u_{\text{fo}}^{*}<{1}$ < 1) for when the support was stiff. This is rationalized by the small step size, and longitudinal arch causes a more extreme stress rotation resulting in further yielding and displacement at the excavation step. It is important to note that poorest correlation of the results occurs when support was installed at 2.0 R_t. It is also important to note that the left side of Fig. 10 included the results of Nguyen-Minh and Guo (1996) which clearly overestimated the normalized tunnel face displacement for the select range of materials used within this investigation.

$$u_{\text{fo}}^{*} = A_{{{\text{f}}1}} \cdot {\text{e}}^{{B_{\text{f1}} \cdot u_{\text{f}}^{*} }}$$

(12a)

$$u_{\text{fo}}^{*} = A_{{{\text{f}}i}} \cdot u_{\text{f}}^{{*B_{\text{fi}} \cdot }}$$

(12b)

4.2.1 Excavation Case 1: TBM

A previously mentioned, evaluation of the remaining unsupported span lengths for Excavation Case 1 offered evidence that curve-fit variables A_f1 and B_f1 were dependent on the material property and unsupported span, as shown in Fig. 11. The results of best fits from variables A_f1 and B_f1 correlated with the normalized rock mass strength ratio ($\sigma_{\text{cm}}^{*} = P_{\text{o}} /\sigma_{\text{cm}}$) as shown in Fig. 12, These correlations had a minimum r² value of 0.991 (except for A1 material, which had a poor correlation), both of which are shown in Eqs. (13a) to (18).

$$A_{\text{f1}} = A_{\text{f1a}} \cdot \frac{{L_{\text{u}} }}{{R_{\text{t}} }}^{{A_{\text{f1b}} }}$$

(13a)

$$B_{\text{f1}} = B_{\text{f1a}} \cdot \frac{{L_{\text{u}} }}{{R_{\text{t}} }}^{{B_{\text{f1b}} }}$$

(14a)

$$A_{\text{f1a}} = - 0.0063\left( {\sigma_{\text{cm}}^{*} } \right)^{2} + 0.0551\sigma_{\text{cm}}^{*} + 1.0919$$

(15)

$$A_{\text{f1b}} = 0.0034\left( {\sigma_{\text{cm}}^{*} } \right)^{2} - 0.021\sigma_{\text{cm}}^{*} - 0.1351$$

(16)

$$B_{\text{f1a}} = - 0.0015\left( {\sigma_{\text{cm}}^{*} } \right)^{2} + 0.01\sigma_{\text{cm}}^{*} + 0.0713$$

(17)

$$B_{\text{f1b}} = - 0.037\left( {\sigma_{\text{cm}}^{*} } \right)^{2} + 0.3609\sigma_{\text{cm}}^{*} - 0.3649$$

(18)

Fig. 11

Excavation Case 1—results from curve-fitting variables “A_f1” and “B_f1” for P_o/σ_cm ranges of 4–10.1

Fig. 12

Excavation Case 1—results from curve-fitting variables “A_f1a”, “A_f1b”, “B_f1a”, and “B_f1b” for P_o/σ_cm ranges of 4–10.1

4.2.2 Excavation Case 2: Mechanical

As previously mentioned, evaluation of the remaining unsupported span lengths for Excavation Case 2 offered evidence that the curve-fit variables A_f2 and B_f2 were only clearly dependent on the unsupported span, as shown in Fig. 13. Furthermore, the A_f2 variable, as shown in the left side of Fig. 13, did not have a strong correlation to the unsupported span, requiring an adjustment to the B_f2 variable (right side of Fig. 13). Therefore, the B_f2 variable was adjusted to correspond with the new A_f2 value, based on the curve fit. The results of best fits for A_f2 and B_f2 are shown in Eqs. (13b) to (14b), respectively.

$$A_{\text{f2}} = 0.019\frac{{L_{\text{u}} }}{{R_{\text{t}} }} + 0.88$$

(13b)

$$B_{{{\text{f}}2}} = 0.347 \cdot {\text{e}}^{{ - 0.528\frac{{L_{\text{u}} }}{{R_{\text{t}} }}}}$$

(14b)

Fig. 13

Excavation Case 2—results from curve-fitting variables “A_f2” and “B_f2” for P_o/σ_cm ranges of 4–7.7

4.2.3 Excavation Case 3: Drill and Blast

Excavation Case 3 yielded similar results to Excavation Case 2, which was to be expected, as the cases differed only in excavation step size. Therefore, the curve-fit variables A_f3 and B_f3 were configured through the same methodology (for Eq. 12b); however, the A_f3 variable was found to be a constant value, rather than a linear trend. Therefore, A_f3 was taken as an average value (Eq. 13c), and B_f3 was adjusted based on constant A_f3 (Eq. 14c). To improve the accuracy of the curve-fitting, the results of Excavation Case 3 when the unsupported span was 0.1 R_t were ignored because Excavation Case 2 had already accurately had captured the results (same data point). Therefore, for a drill-and-blast operation (Excavation Case 3) with a blast length less than of 0.4 R_t, Excavation Case 2 results should be employed for capturing the reduction of the tunnel face.

$$A_{\text{f3}} = 1.17$$

(13c)

$$B_{\text{f3}} = - 0.151\frac{{L_{\text{u}} }}{{R_{\text{t}} }} + 0.3$$

(14c)

4.3 Effect of Support on the LDP Curvature

The incorporation of Eq. (12) into Eq. (6) through an iterative approach created a more accurate prediction of the tunnel face displacement when support is installed. The inclusion of Eq. (12) alone was not enough to capture a supported LDP. The inclusion of the second component of the LDP was necessary in order to ensure more accurate representation of the correct support installation. The second component increased the accuracy of the curvature of the LDP. The general curvature for the excavation portion of an unsupported tunnel (Eq. 4) was defined by the value of 3/2. The value was replaced with a variable M_c to adjust the curvature based on: a. normalized support stiffness ratio (relative stiffness), $k^{{\prime }}$  = k/E_rm, b. the normalized rock mass strength ratio, $\sigma_{\text{cm}}^{*} = P_{\text{o}} /\sigma_{\text{cm}}$ and c. normalized unsupported span (L_u/R_t). The procedure of the curve-fitting process followed the same order (i.e. a–c). Furthermore, the normalization required alteration from the maximum unsupported displacement, u_max, to the maximum supported displacement, u_maxsup. These two adjustments developed an accurate representation of the supported LDP when the unsupported span, L_u, was between 0.4 R_t and 2 R_t. These adjustments are illustrated by Eqs. (19)–(21), which include the modifications from Eqs. (1–3). It is important to note that the numerical model LDPs were developed through the normalization of displacement to respective position which allowed for the collection of the identical number of data points for Excavation Case 3. Additionally, this simplification minimized the resulting oscillating displacement that occurred between support installations, as illustrated in Bernaud and Rousset (1996), which only effected the data points within the support installation segments.

To explain the process of modifying the curvature of the supported LDP, Excavation Case 1 will be used as an example in the following sections.

If $X^{*}$ < 0 (i.e. condition in the rock mass ahead of the face)

$$u_{\sup }^{*} = \frac{u}{{u_{{\mathrm{max}} \sup } }} = u_{0\sup }^{*} {\text{e}}^{X*}$$

(19)

If $X^{*}$ > 0 (i.e. condition in the open tunnel)

$$u_{\sup }^{*} = 1 - \left( {1 - u_{0\sup }^{*} } \right){\text{e}}^{{ - \frac{{M_{\text{c}} X^{*} }}{{R^{*} }}}}$$

(20)

where

$$u_{o\sup }^{*} = 0.38\frac{{u_{\text{f}}^{*} }}{{u_{\text{fo}}^{*} }} \cdot {\text{e}}^{{ - 0.12 \cdot R^{*} }}$$

(21)

4.3.1 Excavation Case 1: TBM

The first step (a) of modifying the curvature of the LDP involved the capture of the effects of the different support stiffness to the respected ground material. In order to provide an illustration of this step, two figures will be presented. Figure 14 illustrates the numerical results (squares) from a change in the support stiffness and the respected curve fitted solution (solid line) for support installed 2.0 R_t from the tunnel face. The four plots within Fig. 14, and subsequent similar figures, present the solution for material A1 (top left), B1 (top right), C1 (bottom left), and D1 (bottom right). The dotted line within Fig. 14 represents the numerical results of Vlachopoulos and Diederichs (2014), Eq. (15). As expected, the LDP₂₀₁₄ is able to relatively capture the numerical results when the support is installed 2.0 R_t from the tunnel face and is notably less accurate as the support decreased in stiffness. Therefore, a further restriction to the LDP₂₀₁₄ could be based on the support stiffness employed (>1GPa/m).

Fig. 14

Excavation Case 1—numerical and curve-fit results for the LDP when support is installed 2.0 R_t from the tunnel face for ground materials A1–D1. The dotted curve, LDP₂₀₁₄, is the empirical solution of Vlachopoulos and Diederichs (2014), Eq. (15). X < 0 is into the face and X > 0 is behind the advancing face (excavated space)

Second, Fig. 15 is similar to Fig. 14 but for the support installation 0.4 R_t from the tunnel face. Figure 15 illustrates that support stiffness has a larger effect on general curvature when support is installed closer to the tunnel face. Notably, however, the impact of the displacement of the tunnel face is the primary factor, but a secondary influence is the unsupported span. The trend of the unsupported span length for the B1 material has been illustrated within Fig. 16. Figure 16 additionally shows that a power function was able to capture the variable M_c for the different support stiffnesses used and different unsupported span lengths. Notably, the results indicate that increasing the unsupported span approaches 3/2 (the curve-fitting value of LDP₂₀₀₉) which agrees with the findings of Vlachopoulos and Diederichs (2014) that the LDP₂₀₀₉ is accurate if L_u > 3.0 R_t.

Fig. 15

Excavation Case 1—numerical and curve-fit results for the LDP when support is installed 0.4 R_t from the tunnel face for ground materials A1–D1. X < 0 is into the face and X > 0 is behind the advancing face (excavated space)

Fig. 16

Excavation Case 1—curvature variable M_c for different support installation distances (unsupported span lengths) with respect to the normalized support stiffness values for B1 ground material

A power function (Eq. 22) with sub-variables A_L and B_L was able to capture the results for the remaining materials investigated. Figure 17 captures the correlation of the sub-variables with the normalized rock mass strength ratio, $\sigma_{\text{cm}}^{*}$ (b), which remains influenced by the unsupported span. This correlation has been expressed in Eqs. (23) and (24), with the following Eqs. (25)–(27) to correlate it with the unsupported span (c) as illustrated in Fig. 18. B_L Eqs. (24), as shown in Fig. 17, were adjusted to have the same y-intercept of 0.159, which resulted in a poor correlation when the unsupported span is 2.0 R_t, as it results in a constant value. Figures 19 and 20 show the results for Excavation Case 2 and Case 3. Analysis determined that the different excavation types did not influence the curvature. Furthermore, the results indicate that the influence of the tunnel face displacement was enough to differentiate between the different cases, as illustrated in the following sections.

$$M_{\text{c}} = A_{\text{L}} \cdot k^{{{\prime }B_{\text{L}} }}$$

(22)

$$A_{\text{L}} = A_{\text{La}} \cdot \sigma_{\text{cm}}^{*} + A_{\text{Lb}}$$

(23)

$$B_{\text{L}} = B_{\text{La}} \cdot \sigma_{\text{cm}}^{*} + 0.159$$

(24)

$$A_{\text{La}} = - 0.772\left( {\frac{{L_{\text{u}} }}{{R_{\text{t}} }}} \right)^{2} - 0.24\frac{{L_{\text{u}} }}{{R_{\text{t}} }} + 4$$

(25)

$$A_{\text{Lb}} = 2.125\left( {\frac{{L_{\text{u}} }}{{R_{\text{t}} }}} \right)^{2} + 0.47\frac{{L_{\text{u}} }}{{R_{\text{t}} }} - 2.973$$

(26)

$$B_{\text{La}} = - 0.004\left( {\frac{{L_{\text{u}} }}{{R_{\text{t}} }}} \right)^{2} + 0.0001\frac{{L_{\text{u}} }}{{R_{\text{t}} }} + 0.016$$

(27)

Fig. 17

Excavation Case 1—curvature variable M_c sub-variables A_L (left) and B_L (right) as a function of normalized rock mass strength ratio, $\sigma_{\text{cm}}^{*} = P_{\text{o}} /\sigma_{\text{cm}}$ for different support installation distances (unsupported span lengths)

Fig. 18

Resulting sub-variables A_La and A_Lb (left axis—dotted lines) and B_La (right axis—dashed line) as a function of the unsupported span

Fig. 19

Excavation Case 2—numerical and curve-fit results for the LDP when support is installed 2.0 R_t from the tunnel face for ground materials A1–D1. The dotted curve, LDP₂₀₁₄, is the empirical solution of Vlachopoulos and Diederichs (2014), Eq. (15). X < 0 is into the face, and X > 0 is behind the advancing face (excavated space)

Fig. 20

Excavation Case 3—numerical and curve-fit results for the LDP when support is installed 2.0 R_t from the tunnel face for ground materials A1–D1. The dotted curve, LDP₂₀₁₄, is the empirical solution of Vlachopoulos and Diederichs (2014), Eq. (15). X < 0 is into the face, and X > 0 is behind the advancing face (excavated space)

4.3.2 Excavation Case 2: Mechanical

Figure 19 captures the numerical and curve-fit results for Excavation Case 2 for the LDP when support is installed 2.0 R_t from the tunnel face for ground materials A1–D1. The empirical solution of Vlachopoulos and Diederichs (2014) was also plotted to illustrate that it is not applicable when the support is installed within 2 R_t to the tunnel face.

4.3.3 Excavation Case 3: Drill and Blast

Figure 20 presents similar results as Fig. 19, but with respect to Excavation Case 3. A noteworthy difference occurs between 0 and 2.0 R_t; the distance between the next support installation (for Excavation Case 2) or drill and blasting length (for Excavation Case 3) is the curvature. As is to be expected for the continuous excavation, Fig. 19 presents a smooth transition, while Fig. 20 presents an abrupt change (blast) closest to the tunnel face (0–0.4 R_t). This is a clear indication of the different stress paths caused by the different excavation cases, which is further captured in the following section.

4.4 The Overloading Effect of the Support Based on Support Stiffness and Unsupported Span

The amount of overloading of support has been captured for the range of support stiffness and ground materials. Overloading was captured through assessing the stress of the completely excavated model at the excavation boundary (tangential/radial stress) and comparing the value to the ground reaction curve. Once again, Excavation Case 1 will be used as an example of the process conducted for this section. Additionally, this enables clear comparison with the result of Cantieni and Anagnostou (2009), shown in Figure 4 (for L_u/R_t = 0.4 and 2).

4.4.1 Excavation Case 1: TBM

Figure 21 presents an example of the Excavation Case 1 influence on B1 material for overloading for the employed different support stiffnesses and different support installation distance. For each scenario, the amount of overload was captured and plotted against the normalized support stiffness, $k^{{\prime }}$. An example of one such plot is illustrated in Fig. 22. Figure 22 consists of the numerical results (squares) for the B1 material, which clearly confirms that overloading is primarily influenced by the support stiffness and is secondarily influenced by the unsupported span length. Equation (28a) represents the overloading as a function of the unsupported span and support stiffness, as illustrated by the smooth lines of Fig. 22. Equation (28a) variables A_oi, B_oi, C_oi, and D_oi were established through a best-fit exercise (minimum r² = 0.9847) and were found to be correlated with the normalized rock mass strength ratio, $\sigma_{\text{cm}}^{*} = P_{\text{o}} /\sigma_{\text{cm}}$. The results of this best fit are illustrated in Fig. 23 and stated as Eqs. (29a) to (32a).

Fig. 21

Excavation Case 1—the ground reaction curve (GRC) and numerical results of a rock mass to strength ratio of 7.7 (B1 material), where L_u = unsupported span. L_e = excavation step length, R_t = Radius of tunnel, k = support stiffness and i denotes excavation sequencing

Fig. 22

Excavation Case 1—B1 material stress overloading for different support stiffness and unsupported span lengths. Solid lines represent the results from Eq. (28a). Normalized support stiffness, $k^{{\prime }}$ = k/E_rm

Fig. 23

Excavation Case 1—results of the curve-fit analysis for parameters A_oi, B_oi, C_oi, and D_oi. The parameter A_oi, denoted with diamond and dash line, uses the right axis only

The numerator for Eq. (28a) was set up as a negative second-degree polynomial function because there was a point that the unsupported span length would yield the maximum amount of overloading stress on the support system for a given material. This maximum amount of overloading was significant for the stiff support (10–100 GPa/m) and for the weakest material (A1 and B1). Within the typical range of support stiffness (0.1–1 GPa/m), the general trend is that there is less overloading of the support system as it is installed further away from the tunnel face. This is an important concept to consider when comparing the results to the other excavation cases and for general tunnel design.

$$P^{\prime } = \frac{{\left( {A_{{{\text{o}}i}} \cdot S^{\prime 2} + B_{{{\text{o}}i}} \cdot S^{\prime } + C_{{{\text{o}}i}} } \right)}}{{\left( {1 + {\text{e}}^{{ - \log \left( {\frac{{k^{\prime 2} }}{{D_{{{\text{o}}i}} }}} \right)}} } \right)}}$$

(28a)

$$A_{{{\text{o}}1}} = - 0.062 \ln \sigma_{\text{cm}}^{*} + 0.099$$

(29a)

$$B_{{{\text{o}}1}} = 0.266 \ln \sigma_{\text{cm}}^{*} - 0.518$$

(30a)

$$C_{{{\text{o}}1}} = - 0.254 \ln \sigma_{\text{cm}}^{*} + 0.8469$$

(31a)

$$D_{{{\text{o}}1}} = 7.9752{\text{e}}^{{ - 0.43\sigma_{\text{cm}}^{*} }}$$

(32a)

4.4.2 Excavation Case 2: Mechanical

The numerator was set up for Eq. (28b) as a log–normal–function because the effect of the spacing for Excavation Case 2 was found that increasing the unsupported span resulted in increasing overloading on the support, the opposite effect that was found in Excavation Case 1. This indicates that for mechanical excavation a smaller unsupported span length is optimum for controlling overloading of the support from the longitudinal arching effect. The resulting curve-fit variables for Excavation Case 2 are expressed in Eqs. (29b) to (32b).

$$P^{{\prime }} = \frac{{\left( {A_{{{\text{o}}i}} \ln S^{{\prime }} + B_{{{\text{o}}i}} } \right)}}{{\left( {1 + {\text{e}}^{{ - \log \left( {\frac{{k^{{{\prime }2}} }}{{D_{{{\text{o}}i}} }}} \right)}} } \right)}}$$

(28b)

$$A_{{{\text{o}}2}} = 0.774{\text{e}}^{{ - 0.364\sigma_{\text{cm}}^{*} }}$$

(29b)

$$B_{{{\text{o}}2}} = 4.0514 \sigma_{\text{cm}}^{* - 1.259}$$

(30b)

$$D_{{{\text{o}}2}} = 20.342{\text{e}}^{{ - 0.59\sigma_{\text{cm}}^{*} }}$$

(32b)

4.4.3 Excavation Case 3: Drill and Blast

Excavation Case 3 had similar results to Excavation Case 2, resulting in the numerator being a log–normal function, to take into consideration the effect of spacing. The resulting curve-fit variables for Excavation Case 3, to be used within Eq. (28b), are expressed in Eqs. (29c) to (32c). Notably comparing Case 2 and Case 3, Case 3 results in significantly greater overloading when it came to stiffer support systems in weaker ground conditions with the max difference of 16.3%.

$$A_{\text{o3}} = - 0.033\sigma_{\text{cm}}^{*} + 0.38$$

(29c)

$$B_{\text{o3}} = - 0.049\sigma_{\text{cm}}^{*} + 0.79$$

(30c)

$$D_{{{\text{o}}3}} = 30.683{\text{e}}^{{ - 0.79\sigma_{\text{cm}}^{*} }}$$

(32c)

5 Results

The Excavation Case 1 scenario with support S1 illustrates the modification effect on the CCM. An additional example will be provided to illustrate the required factor of safety of the unsupported LDP analysis to meet a factor of safety of one for this new analysis, which is reinforced by a numerical model. The first example results for this analysis are presented in Fig. 24. Figure 24 illustrates the 4 steps of the modification of the CCM. The solid grey denotes step 1, the solid black double line denotes steps 2 and 3, and the small dashed double black line denotes step 4. The horizontal dashed grey line denotes the support capacity for the S1 support. The black dashed line in Fig. 24 denotes the support reaction curve based on the numerical analysis. With respect to this specific S1 support numerical analysis solution, analysis accuracy of the tunnel face displacement is within 0.6%. The support employed would have undoubtedly failed, despite the original existence of a factor of safety of 1.1 (using LDP₂₀₀₉). The final result of this modified analysis is within 2.8% of the normalized pressure on the support, and of the normalized tunnel displacement.

Fig. 24

Excavation Case 1—B1 Material results of support S1 based on the proposed modified solution to the CCM. The horizontal line indicates the support capacity of the S1 support

Analysis employing the LDP₂₀₀₉ determined that a factor of safety of 4.5 was required (1400 mm of concrete thickness) for the B1 material in order to get a factor of safety of 1 with the new analysis. These results, along with Phase 2 axisymmetric results, are presented in Fig. 25. Such thickness of concrete is impractical and agrees with the literature that a more ductile support system is more practical for squeezing ground conditions. Figure 25 additionally displays the results if the solution of Vlachopoulos and Diederichs (2014), Eq. (5), was employed. The application of LDP₂₀₁₄ is outside the applicable range, as outlined in Vlachopoulos and Diederichs (2014), but it stands for comparison as it is the only viable supported LDP solution to date. The LDP₂₀₁₄ clearly underestimates the pressure imposed on the support system as well as overestimates the amount of displacement of the excavation.

Fig. 25

Excavation Case 1—B1 Material results of support, 1400 mm of shotcrete, based on the proposed modified solution to the CCM. The horizontal line indicates the support capacity of the 1400-mm shotcrete employed

6 Discussion

After conducting the parametric analysis required for this paper, the authors have found the following limitations within the current literature:

• 1. The results of Nguyen-Minh and Guo (1996) have been determined inaccurate for material response investigation within the paper, as illustrated in Fig. 10. The findings of Nguyen-Minh and Guo (1996) may be more applicable for ground materials which behave more elastically when supported. However, as the material properties used in the Nguyen-Minh and Guo (1996) investigation were not clearly stated, it is difficult to isolate the potential reasons for the difference in the finding;

• 2. The results within the paper prove that confinement (radial support) within the excavation is capable of reducing the influence ahead of the tunnel excavation, with respect to squeezing ground conditions, and is a function of the location of installation and its stiffness. This is contradictory to Lunardi (2000), who found that axisymmetric analysis was not able to control extrusion and pre-convergence by varying the rigidity of tunnel lining and/or the distance from the face;

• 3. The solution provided by Bernaud and Rousset (1996) only provides the maximum displacement for materials with a Poisson’s ratio of 0.5, a value that is too high for almost all rock types, as shown in Gercek (2007); and,

• 4. The results within this paper found that a constant unsupported span (Excavation Case 1) of 2.0 R_t yielded comparable results to LDP₂₀₁₄; however, when the unsupported span of 2.0 R_t was not constant (Excavation Case 2 and 3), the LDP₂₀₁₄ was not accurate. Furthermore, the LDP₂₀₁₄ may be further restricted to support stiffness greater than 1 GPa/m.

This analysis and results are specific to the many different combinations of scenarios investigated. Additional factors which must be taken into consideration are as follows:

• 1. Constants of the analysis

  • a. Constitutive model: perfectly plastic with dilation of zero,

  • b. Numerical model excavation sequencing, and

  • c. Support segment length and sequencing;

• 2. When the support was installed within the model, it was either constant (Excavation Case 1) or up to the tunnel face (Excavation Cases 2 and 3). The analysis does not take into consideration the effect of support not installed up to that face for Excavation Case 2 or 3, due to the number of additional permutations required for analysis. Therefore, if support is not installed to the face for an Excavation Case 2 or 3, it is proposed that an approximate solution would be employed a form of weighted average between comparable Case 2 or 3 results with a Case 1 result;

• 3. The support segment length for Excavation Case 1 was constant throughout the entire analysis at 0.4 R_t. This value of segment length was used because Vlachopoulos and Diederichs (2009) state that a numerical excavation size of 0.4 R_t is required to get a continuous profile. Therefore, the influence of support segments sizes other than 0.4 R_t needs to still be captured, and judgement on the influence of the results needs to be taking into consideration. Furthermore, the excavation step size for Excavation Case 1 was 0.4 R_t as it was deemed physically impossible to have supported installed closer than that within a TBM excavation;

• 4. The analysis did not take into consideration the influence of radial support installed within the rock mass as this would result in a two-material response in the GRC, as presented by Oreste (1996). This two-material response would also affect the longitudinal arching that causes additional load on the support system. The influence of the two-material response must be taken into consideration if radial support is used with the proposed solution;

• 5. The numerical analysis for the TBM excavation (Case 1) does not include the effects of the TBM components, such as face pressure (or cutter head), jacking force, grippers. Inclusion of the TBM components has been found to reduce the modelled plastic radius depth by 29% for a select case (Zhao et al. 2012);

• 6. The research conducted for this paper has been based solely on numerical analysis, and it requires validation through laboratory or field investigations. However, as a majority of this improvement relies on a comparison of supported to unsupported analysis it would be practically impossible to validate in the field;

  • (a) This methodology has been verified to a signal case study (in situ and 3D numerical results) for Excavation Case 2 (Oke et al. 2016)

• 7. The formulations were determined based on regression of the data obtained numerically, selected regressions had poor correlation. Such results indicate limitations in the methodology. However, each stage of the methodology was developed separately and independently of the previous stage. This was executed to allow for improvements to individual steps without influence on prior or preceding steps; and

• 8. The curvature profile of the modified LDP, presented within this paper, is not accurate within the unexcavated ground conditions. This inaccuracy was deemed insignificant due to the fact that the result has no influence on the CCM solution. However, the solution is still more accurate than other current approached (i.e. LDP₂₀₁₄) and will still give a reasonable stress profile ahead of the tunnel face in case the solution was used for approximating stress conditions of pre-support systems (i.e. forepole and/or spile elements) as shown in Oke et al. (2016). Future work will consist of improving the curvature profile within the unexcavated ground portion.

• 9. A limitation of this proposed method is that it is not capable of analysing situations of extreme ground conditions where analytical solutions predict 100% closure of an unsupported excavation.

• 10. It is important to remember that CCM assumes radial uniform loading under circular liner, which is very favourable in structural point of view. Anisotropic loading and non-circular shape lead to bending moments and are much more severe to the structure, and must be taken into considerations.

7 Conclusion

This research has made many contributions to improving the convergence-confinement method, namely by:

• 1. Highlighting the sensitivity (to numerical and parametric variations) of numerically capturing the tunnel face displacement for both unsupported and supported cases, with a discussion of the practical implications of selecting an inaccurate LDP.;

• 2. Developing a more accurate LDP for the supported case when support is installed within 2Rt (one tunnel diameter or span) from the tunnel face;

• 3. Illustrating and providing technical guidance for the analysis of the influence of support, excavation type, and installation location on the tunnel face displacement; and,

• 4. Quantifying the influence of support, excavation type, and installation location on the longitudinal arching effect that applies additional load to the support system.

Ultimately, this research has developed a method to remove the limitation of the CCM when support is installed in squeezing ground conditions that respond perfectly plastically. Therefore, the results of this research provide an approximation for support response for verification exercise in the field and for validation on 3D numerical analysis.