1 Introduction

Underground rock masses are subjected to various types of dynamic disturbances (Zhao et al. 1999; Zhou and Zhao 2011), i.e. earthquakes, blasting, rock collapses (Zhang and Zhao 2014) which spread out from the disturbance sources in forms of stress waves with different frequency characteristics and can be treated as plane waves in far field (Li and Ma 2009). Rock mass is a discontinuous medium due to the existence of abundant rock joints (Jaeger 1971). The stress waves will inevitably interact with the joints during propagation, which normally leads to the waveform alternation, amplitude attenuation and wave velocity decrease (Goodman 1976; King et al. 1986). Based on the theoretical analyses and model tests of wave propagation in the jointed media, Li et al. (2003) proposed a dynamic damage model of the jointed medium. Hao et al. (2002) proposed an anisotropic model with the capability of describing the behaviour of dynamic response of the micro-joints and its interaction with wave propagation. Using this model, the non-isotropic damage zone and stress wave propagation in a rock mass under blasting loads were successfully simulated. Deng et al. (2015) applied a UDEC-AUTODYN method to model a large-scale explosive detonation in a closed space and the following wave propagation in jointed rock masses. By combining the UDEC modelling which is focused on shock wave propagation in jointed rock masses surrounding the explosion chamber, the estimated the peak particle velocity was closer to the test data compared to the purely AUTODYN modelling results. Yang et al. (2015) presented a 3D numerical simulation of the rock damage evolution of a deep-buried tunnel excavation and pointed out that an ultimate blast damage model should be capable of dynamically modelling the entire blasting process, including the high pressure-producing processes and the stress wave propagation in rock mass. On the other hand, Stephansson et al. (1979) presented a theory of wave propagation in shallow jointed rocks to determine the depth of the joint. It is, therefore, significant to study the interactions between stress waves and rock joints, not only for the dynamic damage modelling of rock mass and the stability analysis of the underground structures but also for the detection of joints and the inverse investigation of wave sources.

Extensive theoretical analyses have been performed on wave propagation across rock joints with full consideration of different deformational behaviours. The full solutions of reflection and transmission coefficients for harmonic waves across a single dry fracture in an identical rock material have been obtained by Pyrak-Nolte et al. (1990) and Schoenberg (1980). Zhao et al. (2006) conducted an analysis on P-wave transmission across fractures with nonlinear deformational behaviour. Cai and Zhao (2000) investigated the effects of multiple parallel fractures on wave propagation. In these studies, the displacement discontinuity model (DDM) was adopted, i.e. the joints were described as stress continuous, while displacement as discontinuous boundaries (Myer 2000). The DDM is appropriate to non-welded joints with small apertures relative to the wavelength. For joints filled with a certain amount of saturated sand, clay or gouge which are also frequently encountered in nature, the viscoelasticity should be taken into account (Jaeger et al. 2007; Richer 1977). From the physical point of view, Suárez-Rivera (1992) employed the displacement and velocity discontinuous boundary conditions to describe the action of a fluid-filled fracture. The combined effects of the solid asperities and the liquid film were superposed based on two different assumptions from the Maxwell and Kelvin models, respectively, i.e. both of them bore a common stress or underwent a common displacement. The specific stiffness and viscosity were searched by best fit approximation from the experimental results, and the Maxwell model was found to be more appropriate for reproducing the experimental behaviour of the clay interfaces under incident shear waves (Suárez-Rivera 1992). Afterwards, Zhu et al. (2011) proposed a displacement and stress discontinuity model (DSDM) to simulate the filled joints and obtained solutions for wave propagation across a single joint and a set of joints. The results have been verified by experiments for the normal incident cases (Wu et al. 2013a, b), and suitable parameters for both the Maxwell and Kelvin models were found to agree well with the experimental results for a rock joint filled with wet sand (Zhu et al. 2011). The stress discontinuity was found to have little effect when the normalized initial mass parameter is small (Zhu et al. 2011; Wu et al. 2013a), which means the DDM is still applicable to the common cases in nature. In addition, Perino et al. (2012) studied the influence of both elastic and viscoelastic joints on wave propagation by the scattering matrix method (SMM). The viscoelastic joints were described by Kelvin-Voigt, Maxwell and Burgers models. Since the derivations in these studies were conducted in frequency domain for harmonic waves, additional mathematical methods, such as the Fourier and inverse Fourier transforms, are needed for an incident wave with arbitrary waveform.

For an obliquely incident case, Li and Ma (2009) proposed an approach to calculate the transmitted and reflected waves based on the conservation of momentum of the tiny elements at the wave fronts. The derivation was conducted in time domain, and it has been extended for different incident waveforms and nonlinear rock joints without other mathematical methods (Li 2013). However, the viscoelastic behaviour of the joint has not been taken into account in the previous studies.

In this paper, the approach proposed by Li and Ma (2009) is extended for P- and S-waves propagation across a viscoelastic rock joint based on the DDM. Since there is no consensus yet about whether the Maxwell model or the Kelvin model is more applicable, the viscoelastic deformational behaviour of the rock joint is described by the Maxwell model and the Kelvin model. The proposed solutions are verified by comparing with the previous studies for sinusoidal incident P- and S-waves. Comparison between the theoretical results and the experimental data for the joint filled with viscoelastic materials is conducted to verify the applicability of each model. Parametric studies are then conducted for incident P- and S-waves with arbitrary waveform, followed by the discussions on the alternation of the waveforms and the joint thickness. Two recursive mathematical methods including the virtual wave source method (VWSM) and the time-domain recursive method (TDRM) are adopted to extend the solutions for multiple parallel joints.

2 Theoretical Solution

2.1 Problem Description

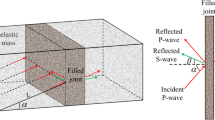
In the far field from the wave source, the seismic wave propagating in a rock mass can be assumed to be a plane wave including two types of waves, i.e. P- and S-waves (Li and Ma 2009). In a general case, when a P- or S-wave obliquely impinges on a discontinuous interface in the rock mass with the incident angle less than a critical value, both reflection and transmission take place and four separate waves from the interface are generated, i.e. reflected P- and S-waves and transmitted P- and S-waves (Jaeger 1971).

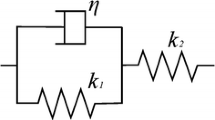
In this study, the rocks beside one joint are assumed to be identical and considered to be an ideally elastic intact medium. From the Snell’s law, the critical angles of incident P- and S-waves are θ c  = 90° and \( \varphi_{c} = \arcsin \left( {{{c_{s} } \mathord{\left/ {\vphantom {{c_{s} } {c_{p} }}} \right. \kern-0pt} {c_{p} }}} \right) \), respectively, where c p and c s are the P- and S-wave propagation velocities in the rock medium. Compared to the wavelength, the thickness of the discontinuity is very small and usually regarded to be zero. To consider a general case for the filled joints, the initial mass of the filling materials is taken into account. Therefore, the stresses on the two sides of a filled joint are regarded to be discontinuous. Meanwhile, the viscoelastic deformational behaviour of the joint, which is commonly embodied by the filled fractures (Suárez-Rivera 1992; Zhu et al. 2011), is described by the Maxwell and Kelvin models and the corresponding joints are termed as the Maxwell joint and the Kelvin joint, respectively.

The incident, reflected and transmitted waves on a single rock joint for an incident plane wave are shown in Fig. 1a, in which P I represents the incident P-wave, P R and S R stand for the reflected P- and S-waves, and P T and S T for the transmitted P- and S-waves, the symbols ‘‘–’’ and ‘‘+’’ indicate the left and right sides of the joint, respectively. The propagation direction of the incident P-wave is considered to be in the XZ plane and the joint plane in the XY plane. Similarly, in Fig. 1b, S I is the incident S-wave, and the others are the same as those defined in Fig. 1a. According to the Snell’s law, the reflection and transmission emergence angles must be equal to the incidence angles for both P- and S-waves. The joint is represented by the Maxwell model in Fig. 1, where h is the thickness of the joint.

Fig. 1
figure 1

Scheme of incident, reflected and transmitted waves on a single rock joint. a Incident P-wave. b Incident S-wave

Full size image

2.2 Compatibility Conditions at the Joint Interface

To conduct mechanical analysis along a joint impinged by an incident seismic P-wave, several tiny stressed triangular elements are extracted from the thin beams of the incident P-wave and the four transmitted and reflected P- and S-waves, respectively, as shown in Fig. 2a–e. Taking Fig. 2a as an example, the tiny element abc for the incident P-wave beam is composed by the left interface of the joint ab, the wave front bc and the side of the wave beam ac. The other elements are composed by the counterparts of the corresponding wave beams. These tiny elements are assumed to be force equilibrium units.

Fig. 2
figure 2

Stresses on the wavefront and rock joint surfaces for incident plane P-wave. a Incident P-wave, b reflected P-wave, c reflected S-wave, d transmitted P-wave, and e transmitted S-wave

Full size image

For the symmetry and infinity of the plane wave beams, the present 2D problem can be considered as a plane strain problem. Therefore, when the normal stress of the incident P-wave on its wave front is \( \sigma_{{P_{\text{I}} }} \), the stress on the side ac can be expressed as \( \gamma / (1 - \gamma )\sigma_{{P_{\text{I}} }} \), where γ is the Poisson’s ratio of the intact rock. The stress state for the tiny element abc without consideration of the body force can be described in Fig. 2a, where σ 1 and τ 1 are the stresses on the left interface of the joint in the normal and tangent directions, respectively. Along the two directions, these stresses on the element abc should comply with the following equilibrium conditions:

$$ \sigma_{1} = \frac{\gamma }{1 - \gamma }\sigma_{{P_{\text{I}} }} \sin^{2} \theta + \sigma_{{P_{\text{I}} }} \cos^{2} \theta $$
(1)
$$ \tau_{1} = \sigma_{{P_{\text{I}} }} \sin \theta \cos \theta - \frac{\gamma }{1 - \gamma }\sigma_{{P_{\text{I}} }} \sin \theta \cos \theta . $$
(2)

These equations can be simplified from Snell’s law, i.e. \( \frac{\sin \varphi }{\sin \theta } = \frac{{c_{s} }}{{c_{p} }} = \sqrt {\frac{1 - 2\gamma }{{2\left( {1 - \gamma } \right)}}} \), to be

$$ \sigma_{1} = \sigma_{{P_{\text{I}} }} \cos 2\varphi $$
(3)
$$ \tau_{1} = \sigma_{{P_{\text{I}} }} \sin 2\varphi \tan \varphi \cot \theta . $$
(4)

According to the conservation of momentum on the wave fronts, there are \( \sigma_{{P_{\text{I}} }} = z_{p} v_{{P_{\text{I}} }} \sigma_{{P_{\text{R}} }} = z_{p} v_{{P_{\text{R}} }} \), \( \sigma_{{P_{\text{T}} }} = z_{p} v_{{P_{\text{T}} }} \), \( \tau_{{S_{\text{R}} }} = z_{s} v_{{S_{\text{R}} }} \), \( \tau_{{S_{\text{T}} }} = - z_{s} v_{{S_{\text{T}} }} \), where \( v_{{P_{\text{I}} }} \), \( v_{{P_{\text{R}} }} \) and \( v_{{P_{\text{T}} }} \) are the particle velocities of the incident, reflected and transmitted P-waves, respectively; \( v_{{S_{\text{R}} }} \) and \( v_{{S_{\text{T}} }} \) are the particle velocities of the reflected and transmitted S-waves, respectively; z p  = ρc p and z s  = ρc s are the rock impedance for P-wave and S-wave, respectively, where ρ is the density of the intact rock; c p and c s are the velocities of P- and S-waves in the intact rock. To simplify the problem, the compressive stress is defined to be positive in the present study. Hence, similarly as the derivation for Eqs. 3–4, the relations between the normal and tangential stresses of the tiny elements can be expressed by the particle velocities as

$$ \left( {\begin{array}{*{20}l} {\sigma_{1} } \hfill \\ {\sigma_{2} } \hfill \\ {\sigma_{3} } \hfill \\ {\sigma_{4} } \hfill \\ {\sigma_{5} } \hfill \\ \end{array} } \right) = {\text{diag}}\left( {\begin{array}{*{20}c} {a_{1} } & \ldots & {a_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {v_{{P_{\text{I}} }} } \hfill \\ {v_{{P_{\text{R}} }} } \hfill \\ {v_{{S_{\text{R}} }} } \hfill \\ {v_{{P_{\text{T}} }} } \hfill \\ {v_{{S_{\text{T}} }} } \hfill \\ \end{array} } \right) $$
(5)

and

$$ \left( {\begin{array}{*{20}l} {\tau_{1} } \hfill \\ {\tau_{2} } \hfill \\ {\tau_{3} } \hfill \\ {\tau_{4} } \hfill \\ {\tau_{5} } \hfill \\ \end{array} } \right) = {\text{diag}}\left( {\begin{array}{*{20}c} {b_{1} } & \ldots & {b_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {v_{{P_{\text{I}} }} } \hfill \\ {v_{{P_{\text{R}} }} } \hfill \\ {v_{{S_{\text{R}} }} } \hfill \\ {v_{{P_{\text{T}} }} } \hfill \\ {v_{{S_{\text{T}} }} } \hfill \\ \end{array} } \right) $$
(6)

where a 1 = a 2 = a 4 = z p  cos 2φ, a 3 = −a 5 = −z s  sin 2φ, b 1 = −b 2 = b 4 = z p  sin 2φ tan φ cot θ and b 3 = b 5 = −z s  cos 2φ.

The resultant stresses on the two sides of the joint can be obtained from the stress states of the tiny elements, which can be expressed in a matrix form as

$$ \left( {\begin{array}{*{20}c} {\sigma^{ - } } & {\sigma^{ + } } \\ {\tau^{ - } } & {\tau^{ + } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma_{1} + \sigma_{2} + \sigma_{3} } & {\sigma_{4} + \sigma_{5} } \\ {\tau_{1} + \tau_{2} + \tau_{3} } & {\tau_{4} + \tau_{5} } \\ \end{array} } \right) . $$
(7)

where σ − and τ − represent the normal and tangential stresses on the left interface of the joint, respectively; σ + and τ + represent the normal and tangential stresses on the right interface of the joint, respectively.

According to the orientation transformation, the velocities on the two interfaces of the joint can be written as

$$ \left( {\begin{array}{*{20}c} {v_{n}^{ - } } \\ {v_{n}^{ + } } \\ {v_{\tau }^{ - } } \\ {v_{\tau }^{ + } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta } & { - \cos \theta } & {\sin \varphi } & 0 & 0 \\ 0 & 0 & 0 & {\cos \theta } & {\sin \varphi } \\ {\sin \theta } & {\sin \theta } & {\cos \varphi } & 0 & 0 \\ 0 & 0 & 0 & {\sin \theta } & { - \cos \varphi } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{P_{\text{I}} }} } \\ {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right) $$
(8)

where \( v_{n}^{ - } \) and \( v_{\tau }^{ - } \) represent the normal and tangential velocities on the left interface of the joint, respectively; \( v_{n}^{ + } \) and \( v_{\tau }^{ + } \) represent the normal and tangential velocities on the right interface of the joint, respectively. Therefore, the stresses and particle velocities along the joint are related to the particle velocities of the waves by Eqs. 7 and 8, respectively, which can be regarded as the equilibrium and geometric compatibility conditions along the joint.

For incident plane S-wave with an incident angle φ, similar compatibility conditions can be derived, but a 1 = z s  sin 2φ and b 1 = −z s  cos 2φ. The velocities along the joint and the waves are written as

$$ \left( {\begin{array}{*{20}c} {v_{n}^{ - } } \\ {v_{n}^{ + } } \\ {v_{\tau }^{ - } } \\ {v_{\tau }^{ + } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sin \varphi } & { - \cos \theta } & {\sin \varphi } & 0 & 0 \\ 0 & 0 & 0 & {\cos \theta } & {\sin \varphi } \\ { - \cos \varphi } & {\sin \theta } & {\cos \varphi } & 0 & 0 \\ 0 & 0 & 0 & {\sin \theta } & { - \cos \varphi } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{S_{\text{I}} }} } \\ {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right) $$
(9)

The above compatibility conditions are related to the stresses and velocities on each side of the joint and have general applicability, while the boundary conditions across the two interfaces of the joint are relevant to the specific joint deformational behaviours which are described by Maxwell model and Kelvin model, respectively.

2.3 Maxwell Model

The boundary condition at the joint mainly refers to the relation in the stresses and displacements between the two interfaces. In the DDM, the displacements between the interfaces are commonly regarded to be discontinuous resulting from the imperfect contact for the non-welded joint or the impendence mismatch for the filled joint, while the stresses are regarded to be continuous for a joint with small thickness compared to the wavelength.

2.3.1 Stress Conditions

By combining Eqs. 7 and 8, the continuous stress conditions between the two interfaces for an incident P or S-wave can be expressed by the particle velocities of waves as

$$ \left( {\begin{array}{*{20}c} {\sigma^{ - } - \sigma^{ + } } \\ {\tau^{ - } - \tau^{ + } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {a_{1} } & {a_{2} } & {a_{3} } & { - a_{4} } & { - a_{5} } \\ {b_{1} } & {b_{2} } & {b_{3} } & { - b_{4} } & { - b_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{P_{\text{I}} }} } \\ {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right) $$
(10)

and simplified to

$$ \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right) = A_{\text{R}}^{ - 1} A_{\text{I}} v_{\text{PI}} + A_{\text{R}}^{ - 1} A_{\text{T}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right) $$
(11)

where

$$ A_{\text{I}} = - \left( {\begin{array}{*{20}c} {a_{1} } \\ {b_{1} } \\ \end{array} } \right) , $$
(12)
$$ A_{\text{R}} = \left( {\begin{array}{*{20}c} {a_{2} } & {a_{3} } \\ {b_{2} } & {b_{3} } \\ \end{array} } \right),\quad {\text{and}} $$
(13)
$$ A_{\text{T}} = \left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right) . $$
(14)

2.3.2 Displacement Discontinuity

The displacement is recognized as discontinuous between the two interfaces for an imperfectly bonded joint (Schoenberg 1980). For a filled joint, the discontinuity in the displacement between the two interfaces is resulted from the deformation of the filling materials. Therefore, the relations between the stresses and displacement discontinuities at the interfaces of the joint, which are commonly used to represent the joint deformational behaviours and regarded as the boundary conditions at the interfaces of the joint, can be deduced from the constitutive model of the filling materials. In this study, the Maxwell model and the Kelvin model are adopted to describe the viscoelastic deformational behaviour of the filling materials.

The Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series and expressed by the governing equation in the form of:

$$ \dot{\varepsilon } = \frac{\sigma }{\mu } + \frac{{\dot{\sigma }}}{E} $$
(15)

where E is the elastic modulus and μ is the coefficient of viscosity of the material; σ and ɛ are the stress and strain, respectively; and the dot notation represents their rates of change with respect to time t.

When Eq. 15 is differentiated with respect to time, there is

$$ v_{n(i)}^{ - } - v_{n(i)}^{ + } = \frac{{\sigma_{i} }}{{\eta_{n} }} + \frac{1}{{k_{n} }}\frac{{\sigma_{i + 1} - \sigma_{i} }}{{\Delta t}} $$
(16)
$$ v_{s(i)}^{ - } - v_{s(i)}^{ + } = \frac{{\tau_{i} }}{{\eta_{s} }} + \frac{1}{{k_{s} }}\frac{{\tau_{i + 1} - \tau_{i} }}{{\Delta t}} $$
(17)

where η and k are defined as the specific viscosity coefficient and stiffness, respectively, and k = E/h, η = μ/h; the subscripts n and s represent the parameters in the normal and tangential directions, respectively; Δt is the time interval which is assumed to be small enough to ensure the accuracy of the calculation.

From Eqs. 7, 8, 16 and 17, for incident P-waves there is

$$ \begin{aligned} & \left( {\begin{array}{*{20}c} {\eta_{n} k_{n} \Delta t} & 0 \\ 0 & {\eta_{s} k_{s} \Delta t} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \theta } & { - \cos \theta } & {\sin \varphi } & { - \cos \theta } & { - \sin \varphi } \\ {\sin \theta } & {\sin \theta } & {\cos \varphi } & { - \sin \theta } & {\cos \varphi } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{P_{\text{I}} }} } \\ {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i} \\ & \quad = \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i} + \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} \\ \end{aligned} $$
(18)

It can be simplified as

$$ \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} = B_{\text{T}}^{\prime - 1} B_{\text{I}} v_{{P_{\text{I}} (i)}} + B_{\text{T}}^{\prime - 1} B_{\text{R}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i} + B_{\text{T}}^{\prime - 1} B_{\text{T}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i} $$
(19)

where

$$ B_{\text{I}} = \left( {\begin{array}{*{20}c} {\eta_{n} k_{n}\Delta t} & 0 \\ 0 & {\eta_{s} k_{s}\Delta t} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \theta } \\ {\sin \theta } \\ \end{array} } \right), $$
(20)
$$ B_{\text{R}} = \left( {\begin{array}{*{20}c} {\eta_{n} k_{n}\Delta t} & 0 \\ 0 & {\eta_{s} k_{s}\Delta t} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & {\sin \varphi } \\ {\sin \theta } & {\cos \varphi } \\ \end{array} } \right), $$
(21)
$$ B_{\text{T}} = \left( {\begin{array}{*{20}c} {\eta_{n} k_{n}\Delta t} & 0 \\ 0 & {\eta_{s} k_{s}\Delta t} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & { - \sin \varphi } \\ { - \sin \theta } & {\cos \varphi } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right),\quad {\text{and}} $$
(22)
$$ B_{\text{T}}^{\prime } = \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right) . $$
(23)

Similarly, from Eqs. 7, 9, 16 and 17, an expression similar to Eq. 19 can be obtained for S-wave incidence, but

$$ B_{\text{I}} = \left( {\begin{array}{*{20}c} {\eta_{n} k_{n}\Delta t} & 0 \\ 0 & {\eta_{s} k_{s}\Delta t} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\sin \varphi } \\ { - \cos \varphi } \\ \end{array} } \right) . $$
(24)

So far, Eqs. 11 to 14 and 19 to 24 present the solutions in a recursive form for a joint with the Maxwell viscoelastic deformational behaviour, from which the particle velocities of the transmitted and reflected waves can be determined through an iterative computation process when the incident wave \( v_{{P_{\text{I}} \left( i \right)}} \) or \( v_{{S_{\text{I}} \left( i \right)}} \) and the initial conditions \( v_{{P_{\text{T}} \left( 0 \right)}} \) and \( v_{{S_{\text{T}} \left( 0 \right)}} \) are known. In each calculation step, the vectors of \( \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i} \) are first obtained from Eqs. 11 to 14, and then by substituting them into Eq. 19, the vectors of \( \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} \) can be determined which are applied into Eq. 11 for the next time step, and so on.

2.4 Kelvin Model

The stress conditions of the Kelvin joint are the same as those of the Maxwell model, while the displacement discontinuity is described differently. The Kelvin model is composed of a spring and a damper in parallel. The governing equation is:

$$ \sigma = E\varepsilon + \mu \dot{\varepsilon }. $$
(25)

When Eq. 25 is differentiated with respect to time, there is

$$ v_{n(i)}^{ - } - v_{n(i)}^{ + } = \frac{1}{{k_{n}\Delta t}}\left\{ {\left( {\sigma_{i + 1} - \sigma_{i} } \right) - \eta_{n} \left[ {\left( {v_{n(i + 1)}^{ - } - v_{n(i)}^{ - } } \right) - \left( {v_{n(i + 1)}^{ + } - v_{n(i)}^{ + } } \right)} \right]} \right\} $$
(26)
$$ v_{s(i)}^{ - } - v_{s(i)}^{ + } = \frac{1}{{k_{s}\Delta t}}\left\{ {\left( {\sigma_{i + 1} - \sigma_{i} } \right) - \eta_{s} \left[ {\left( {v_{s(i + 1)}^{ - } - v_{s(i)}^{ - } } \right) - \left( {v_{s(i + 1)}^{ + } - v_{s(i)}^{ + } } \right)} \right]} \right\} $$
(27)

Combined with Eqs. 7–8, for an incident P-wave there is

$$ B_{\text{T}}^{\prime } \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} = B_{\text{I}} v_{{P_{\text{I}} (i)}} + B_{\text{R}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i} + B_{\text{T}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i} + B_{\text{I}}^{\prime } v_{{P_{\text{I}} (i + 1)}} + B_{\text{R}}^{\prime } \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i + 1} $$
(28)

where

$$ B_{\text{I}} = \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \theta } \\ {\sin \theta } \\ \end{array} } \right) , $$
(29)
$$ B_{\text{I}}^{\prime } = \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \theta } \\ {\sin \theta } \\ \end{array} } \right) , $$
(30)
$$ B_{\text{R}} = \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & {\sin \varphi } \\ {\sin \theta } & {\cos \varphi } \\ \end{array} } \right) , $$
(31)
$$ B_{\text{R}}^{\prime } = \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & {\sin \varphi } \\ {\sin \theta } & {\cos \varphi } \\ \end{array} } \right) , $$
(32)
$$ B_{\text{T}} = \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & { - \sin \varphi } \\ { - \sin \theta } & {\cos \varphi } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right),\quad {\text{and}} $$
(33)
$$ B_{\text{T}}^{\prime } = \left( {\begin{array}{*{20}c} {a_{4} } & {a_{5} } \\ {b_{4} } & {b_{5} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \cos \theta } & { - \sin \varphi } \\ { - \sin \theta } & {\cos \varphi } \\ \end{array} } \right) . $$
(34)

Similarly, from Eqs. 7, 9, 26 and 27, an expression similar to Eq. 28 can be obtained for S-wave incidence, but

$$ B_{\text{I}} = \left( {\begin{array}{*{20}c} {k_{n}\Delta t - \eta_{n} } & 0 \\ 0 & {k_{s}\Delta t - \eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\sin \varphi } \\ { - \cos \varphi } \\ \end{array} } \right),\quad {\text{and}} $$
(35)
$$ B_{\text{I}}^{\prime } = \left( {\begin{array}{*{20}c} {\eta_{n} } & 0 \\ 0 & {\eta_{s} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\sin \varphi } \\ { - \cos \varphi } \\ \end{array} } \right) . $$
(36)

Therefore, the solutions for a joint with the Kelvin viscoelastic deformational behaviour are composed of Eqs. 11 to 14 and 28 to 36. To implement the iterative calculation as that for the Maxwell model, the unknown item \( \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i + 1} \) for each calculation step in Eq. 28 is substituted by the expression of \( v_{{P_{\text{I}} \left( {i + 1} \right)}} \) and \( \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} \) based on Eq. 11. A counterpart equation for the Kelvin model as Eq. 19 can be obtained as:

$$ \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i + 1} = C_{\text{T}}^{\prime - 1} B_{\text{I}} v_{{P_{\text{I}} (i)}} + C_{\text{T}}^{\prime - 1} B_{\text{R}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{R}} }} } \\ {v_{{S_{\text{R}} }} } \\ \end{array} } \right)_{i} + C_{\text{T}}^{\prime - 1} B_{\text{T}} \left( {\begin{array}{*{20}c} {v_{{P_{\text{T}} }} } \\ {v_{{S_{\text{T}} }} } \\ \end{array} } \right)_{i} + C_{\text{T}}^{\prime - 1} C_{\text{T}}^{\prime } v_{{P_{\text{I}} (i + 1)}} $$
(37)

where

$$ C_{\text{T}}^{\prime } = B_{\text{T}}^{\prime } - B_{\text{R}} A_{\text{R}}^{ - 1} A_{\text{T}} ,\quad {\text{and}} $$
(38)
$$ C_{\text{I}}^{\prime } = B_{\text{I}}^{\prime } + B_{\text{R}} A_{\text{R}}^{ - 1} A_{\text{I}} . $$
(39)

To quantify the effects of a single rock joint on the incident waves, the transmission and reflection coefficients are indicated as T kc , R kc (k = p for P-wave and k = s for S-wave), respectively, and are defined as

$$ T_{kc} = \frac{{\hbox{max} \left| {v_{{K_{\text{T}} }} } \right|}}{{\hbox{max} \left| {v_{{K_{\text{I}} }} } \right|}},\quad R_{kc} = \frac{{\hbox{max} \left| {v_{{K_{\text{R}} }} } \right|}}{{\hbox{max} \left| {v_{{K_{\text{I}} }} } \right|}},\quad \left( {k = p,s} \right) $$
(40)

3 Verification

For a single rock joint with elastic deformational behaviour, the transmission and reflection coefficients of an incident P- or S-wave with simply harmonic waveform obliquely impinging on a rock joint were calculated by Pyrak-Nolte et al. (1990), Cook (1992) and Gu et al. (1996), while Li and Ma (2009) obtained solutions for a P- or S-wave incidence with arbitrary waveform. For the seismic response of a viscoelastic rock joint under harmonic incident waves, Suárez-Rivera (1992) investigated normal incidences based on the theory of the displacement and velocity discontinuity boundary conditions which is equivalent to the viscoelastic DDM applied in the current study. Under the consideration of the initial mass of the filled joints, Zhu et al. (2011) provided theoretical data for oblique incidences. In order to verify the solutions proposed in this study and determine the applicable scope, the solutions will be compared with the previous results obtained in frequency domain. A sinusoidal incident wave with 30 cycles is adopted represent the harmonic incident waves in the following calculation. Comparison between the predicted transmitted waves and the experimental data is also conducted to inspect the applicability of each model.

3.1 Normally Incident Wave

When an incident P- or S-wave normally impinges on the joint, i.e. θ = 0 or φ = 0, the relations among the velocities of each wave can be derived from Eq. 11 without involving any parameter of the joint. There are

$$ v_{{P_{\text{I}} \left( i \right)}} + v_{{P_{\text{R}} \left( i \right)}} = v_{{P_{\text{T}} \left( i \right)}} ,\quad v_{{S_{\text{R}} \left( i \right)}} = v_{{S_{\text{T}} \left( i \right)}} = 0 $$
(41)

for an incident P-wave, and

$$ v_{{S_{\text{I}} \left( i \right)}} + v_{{S_{\text{R}} \left( i \right)}} = v_{{S_{\text{T}} \left( i \right)}} ,\quad v_{{P_{\text{R}} \left( i \right)}} = v_{{P_{\text{T}} \left( i \right)}} = 0 $$
(42)

for an incident S-wave. On the other hand, the other recursive relations can be obtained from Eqs. 19 and 28 for the Maxwell model and the Kelvin model, respectively. The relations for the Maxwell model are expressed as

$$ v_{{P_{\text{T}} (i + 1)}} = \frac{{2k_{n}\Delta t}}{{z_{p} }}\left( {v_{{P_{\text{I}} (i)}} - v_{{P_{\text{T}} (i)}} } \right) + v_{{P_{\text{T}} (i)}} - \frac{{k_{n}\Delta t}}{{\eta_{n} }}v_{{P_{\text{T}} (i)}} $$
(43)

for an incident P-wave, and

$$ v_{{P_{\text{T}} (i + 1)}} = \frac{{2k_{s}\Delta t}}{{z_{s} }}\left( {v_{{S_{\text{I}} (i)}} - v_{{S_{\text{T}} (i)}} } \right) + v_{{S_{\text{T}} (i)}} - \frac{{k_{s}\Delta t}}{{\eta_{s} }}v_{{S_{\text{T}} (i)}} $$
(44)

for an incident S-wave. It can be found that the mechanical parameters of both the joint and the rock materials are involved. For a sinusoidal incident wave with infinite cycles, i.e. a harmonic incident wave, with the angle frequency ω, the normalized normal and tangential joint stiffnesses are defined as K n  = k n /(z p ω) and K s  = k s /(z s ω), respectively; while J n  = η n /z p and J s  = η s /z s are the normalized normal and tangential joint viscosity, respectively. It is also found that when the viscosity terms are eliminated, these expressions are identical to those obtained by Li and Ma (2009) for a single elastic joint. In addition, to ensure the convergence of the recursive relations, the interval time Δt should be tiny enough under a relatively small specific viscosity coefficient.

Similarly, from Eq. 28, the relations for the Kelvin model are derived as

$$ v_{{P_{\text{T}} (i + 1)}} = \frac{1}{{1 + {{2\eta_{n} } \mathord{\left/ {\vphantom {{2\eta_{n} } {z_{p} }}} \right. \kern-0pt} {z_{p} }}}}\left[ {\frac{{2k_{n}\Delta t}}{{z_{p} }}\left( {v_{{P_{\text{I}} (i)}} - v_{{P_{\text{T}} (i)}} } \right) + v_{{P_{\text{T}} (i)}} } \right] + \frac{1}{{1 + {{z_{p} } \mathord{\left/ {\vphantom {{z_{p} } {2\eta_{n} }}} \right. \kern-0pt} {2\eta_{n} }}}}\left[ {v_{{P_{\text{I}} (i + 1)}} - v_{{P_{\text{I}} (i)}} + v_{{P_{\text{T}} (i)}} } \right] $$
(45)

for an incident P-wave, and

$$ v_{{S_{\text{T}} (i + 1)}} = \frac{1}{{1 + {{2\eta_{s} } \mathord{\left/ {\vphantom {{2\eta_{s} } {z_{s} }}} \right. \kern-0pt} {z_{s} }}}}\left[ {\frac{{2k_{s}\Delta t}}{{z_{s} }}\left( {v_{{S_{\text{I}} (i)}} - v_{{S_{\text{T}} (i)}} } \right) + v_{{S_{\text{T}} (i)}} } \right] + \frac{1}{{1 + {{z_{s} } \mathord{\left/ {\vphantom {{z_{s} } {2\eta_{s} }}} \right. \kern-0pt} {2\eta_{s} }}}}\left[ {v_{{S_{\text{I}} (i + 1)}} - v_{{S_{\text{I}} (i)}} + v_{{S_{\text{T}} (i)}} } \right] $$
(46)

for an incident S-wave. When η n  → 0 and η s  → 0, the second terms in Eqs. (45) and (46) can be ignored and the first terms also approach the expressions obtained by Li and Ma (2009) for a single elastic joint.

Taking the viscosity terms into account, the reflection and transmission coefficients with respect to normalized frequency under different viscosity parameters for normal cyclic sinusoidal P-wave across the Maxwell joint and the Kelvin joint are shown in Figs. 3 and 4, respectively, in which 1/K n  = z p ω/k n is defined as the normalized frequency. Meanwhile, Suárez-Rivera (1992) derived the solutions for normally incident harmonic SH-wave assuming the displacement and velocity discontinuity boundary conditions at the joint based on the Maxwell and Kelvin models, respectively. Since the solutions for P-wave, SV-wave and SH-wave under normally incident cases are symmetrical, the results presented by Suárez-Rivera (1992) are, in fact, equivalent to those for normally incident P-wave. Good consistency is found between the proposed solutions and the results obtained by Suárez-Rivera (1992).

Fig. 3
figure 3

Reflection and transmission coefficients with respect to normalized frequency under different viscosity parameters for normally incident P-wave across a Maxwell joint. a Reflection coefficients. b Transmission coefficients

Full size image
Fig. 4
figure 4

Reflection and transmission coefficients with respect to normalized frequency under different viscosity parameters for normally incident P-wave across a Kelvin joint. a Reflection coefficients. b Transmission coefficients

Full size image

3.2 Obliquely Incident Wave

The reflection and transmission coefficients of a harmonic P- or S-wave across a filled joint with the Maxwell or Kelvin deformational behaviour were presented by Zhu et al. (2011), in which the initial mass of the filled joint was taken into account and embodied by a non-dimensional parameter termed as the impedance ratio of the filled joint, \( d = \frac{{z_{\text{e}} }}{{z_{s} }} = \frac{{\omega m_{n} }}{{z_{s} }} = \frac{{\omega \rho_{0} h}}{{z_{s} }} \), where z e is the effective acoustic impedance of the filled medium, ρ 0 is the density of the filled medium, m n is the mass of the filled medium of a unit area of the joint plane, h is the joint thickness. The parameter d was found to have little effect on wave propagation for both the Maxwell and Kelvin joints when it is relatively small. Since the parameters used for calculation fell into the range with nearly no affects by the initial mass, it is reasonable to verify the proposed solutions by comparing with those obtained Zhu et al. (2011). The reflection and transmission coefficients of cyclic sinusoidal P- and S-waves under different incident angles for the Maxwell model and the Kelvin model are calculated as shown in Figs. 5 and 6, respectively. Taking the different definition forms for the non-dimensional parameters into account, the parameters adopted by Zhu et al. (2011) are transformed and used in the current calculation, that is, c p  = 6131 m/s, c s  = 3830 m/s, ρ = 2650 kg/m−3, φ c  = sin −1(c p /c s ) = 38.66°, K n  = c p /c s , K s  = 1, J n  = c p /c s and J s  = 1. The discrepancy between the present results and the data from Zhu et al. (2011) is very small. The same variation trend with the incident angle is displayed. Therefore, the proposed solutions for wave propagation across a single rock joint with viscoelastic deformational behaviour are proved to be valid and applicable to an arbitrary incident angle. Parametric studies are conducted in the following section to investigate the effect of the incident wave and the rock joint behaviour on wave propagation.

Fig. 5
figure 5

Reflection and transmission coefficients across a Maxwell joint under different incident angles. a Incident P-wave. b Incident S-wave

Full size image
Fig. 6
figure 6

Reflection and transmission coefficients across a Kelvin joint under different incident angles. a Incident P-wave. b Incident S-wave

Full size image

It is also noted that although the current results obtained directly in time domain and the previous results obtained in frequency domain are very close, there is still some discrepancy between them. It mainly comes from the approximate consideration for the infinite harmonic waves and can be eliminated under enough computational cost. On the other hand, the precision of the current time-domain solutions for an arbitrary wave will not be affected by the errors brought by the Fourier and inverse Fourier transforms, while they are inevitable for the solutions in frequency domain.

3.3 Comparison with Experimental Data

An experimental study was performed to study wave propagation across a filled rock joint using an SHRB apparatus (see Fig. 7) described in detail by Wu et al. (2014). The bar system is comprised of a pair of 1500-mm-long norite bars, and a 200-mm-long norite bar is used as the striker which is launch by a compressed spring with a stiffness coefficient of 9.52 N/mm. Both bars have the same square cross-section that is 40 mm on each side. The density and the P-wave velocity of the norite are 2650 kg/m3 and 6000 m/s, respectively. A layer of kaolin clay with the thickness of 4 mm was filled into a pre-set gap between the incident bar and the transmitted bar to simulate an artificial filled fracture. The particle density, the bulk density and the porosity of the kaolin clay are 2630, 1631 kg/m3 and 38%, respectively. Two strain gauge groups, 200 mm and 400 mm away from the fracture interfaces, are mounted on the incident and transmitted bars, respectively. The incident and transmitted waves are separated from the strain gauge signals based on a wave separation method (Zhao and Gary 1997).

Fig. 7
figure 7

Comparison between experimental data from SHRB test and the predicted results from Maxwell model and Kelvin model

Full size image

On the other hand, the parameters of Maxwell joint and Kelvin joint were determined from an inverse analysis based on an algorithm that minimizes the least-squares differences between the measured transmitted wave and the predicted transmitted wave. The comparison between them is shown in Fig. 7, and the determined parameters are as follows: k n  = 18.2 GPa m−1, η n  = 4.8 MPa s m−1 for the Maxwell model; and k n  = 9.4 GPa m−1, η n  = 1.2 MPa s m−1 for the Kelvin model.

It can be found from Fig. 7 that the predicted results from both the Kelvin and the Maxwell models are in good agreement with the experimental data to certain extent. However, relatively speaking, the curve from the Maxwell model is obviously more closely fits the experimental data. Therefore, the Maxwell model is more suitable for describing the seismic response of joints filled with clay under P-wave incidence. Suárez-Rivera (1992) drew a same conclusion for S-wave incidence. Since the relative applicability between the two models may be not absolute for different filled materials or different circumstances, further studies are still conducted on both the Kelvin and the Maxwell models in the next sections.

4 Parametric Studies and Discussions

4.1 Effects of Normalized Joint Stiffness and Viscosity

For both the Maxwell and Kelvin models, the behaviour of rock joint is described by two parameters, i.e. the specific stiffness k and the viscosity η which are used to simulate the presence of roughness or sand-like filling materials and the presence of liquid or clay coating at the interface, respectively. To ensure adequate coverage of the variation patterns of the reflection and transmission coefficients versus the normalized joint stiffness, they are plotted as a function of the reciprocal of the normalized joint stiffness, i.e. ωz p /k n , which can be regarded as the normalized frequency. The normalized viscosity J is also taken into account, and its reciprocal varies from 0.02 to 10. The results for the Maxwell joint are shown in Fig. 3. It is found that the curves of the reflected coefficient rise with the increase in the normalized frequency, i.e. the decrease in the normalized stiffness, while the curves of transmitted coefficient display opposite changing tendency. As 1/J increases, i.e. the normalized viscosity decreases, the transmission coefficient becomes smaller; on the contrary, the reflection coefficient becomes larger at relatively small values of the normalized frequency.

The curves under different normalized viscosities in Fig. 3a, b show different dependence on the normalized frequency (e.g. the reciprocal of the normalized joint stiffness). This frequency dependence is most prominent for smaller values of the viscosity parameter 1/J as seen in the curves for 1/J = 0.02, and decreases as the viscosity parameter 1/J increases. As seen in the curves for 1/J = 10, the reflection coefficient is almost independent of frequency and varies only with changes in the normalized viscosity. The reason for the changing patterns among curves is that the response of the Maxwell joint is dominated by the most compliant elements. Therefore, there is a transition from a system purely dominated by the elastic component to a system purely dominated by the viscous component, as the viscosity parameter 1/J increases (Suárez-Rivera 1992).

Figure 4a, b, respectively, shows the reflection and transmission coefficients for the Kelvin joint as a function of normalized frequency for the viscosity parameter 1/J varying from 0.02 to 10. Comparison shows that the increase or decline tendency of the coefficients of the Kelvin joint is similar to the response of the Maxwell joint, that is, the attenuation effects of the joint become more pronounced as the increase in the normalized frequency or the viscosity parameter 1/J. However, the frequency dependence is opposite to that of the Maxwell joint, i.e. it becomes stronger as the viscosity parameter 1/J increases. That means the least compliant elements dominate the response of the Kelvin joint.

The parameters of the filled joint were commonly determined from the best fit between the calculated and experimental transmission and reflected coefficients in frequency domain (Pyrak-Nolte 1988; Pyrak-Nolte et al. 1990; Suárez-Rivera 1992; Zhu et al. 2011). From Suárez-Rivera’s studies (Suárez-Rivera 1992), the Maxwell model was found to be more appropriate to reproducing the experimental behaviour of the clay interfaces under shear incident waves. The above experimental results also demonstrate that the Maxwell model is more appropriate to describe the joint filled with clay under P-wave incidence. However, Zhu et al. (2011) obtained suitable parameters for both the Maxwell and Kelvin models to agree well with the experimental results of the joints filled by sand with a water content of 5% under P-wave incidence. It is noted that there is a huge difference in the specific viscosities obtained from the two models. In addition, Wu et al. (2013a, b) conducted wave propagation experiments on rock fractures filled with dry sand and the analysis was based on the Kelvin model in which the viscosity was set to zero. It means the relative applicability between the two models is not absolute for different filled materials or different circumstances. Leaving aside the specific filling materials, the parameter characteristics of the two theoretical model and their applicable conditions can be analysed according to the curve patterns in Figs. 3 and 4. From the comparison between these two figures, it is found that under a certain transmission coefficient the inverted joint viscosity from the Maxwell model is larger than that from the Kelvin model. This can be proven by the parameters from Zhu et al. (2011). For the limiting cases, if the filled materials are regarded as the mixture of solid particles and liquid, the viscosity in the Maxwell model approaches infinity when the filling material is dry and approaches its minimum value when the filling material is completely liquid. It is opposite in the Kelvin model, i.e. the viscosity approaches zero with the absence of liquid (Wu et al. 2013a, b), and approaches the maximum value with the absence of solid particles. Furthermore, it can be seen that the curves of the transmission coefficient shown in Fig. 3b are more dispersed for the Maxwell model under relatively larger values, which means that a tiny change in the joint parameters will result in more obvious variation in the transmission coefficient. In other words, the resolution for the inversion of the parameters is higher. On the contrary, the concentrative degree of the curves for the Kelvin model in Fig. 4b reduces with the decrease in the transmission coefficient. Hence, it can be inferred that the Maxwell model is more appropriate for the cases with less attenuation, while for the cases with more obvious attenuation the Kelvin model is more effective.

4.2 Effect of Incident Angle

As mentioned in Sect. 3.2, Figs. 5 and 6 show the transmission and reflection coefficients as a function of the incident angle under the sinusoidal incident P- or S-wave for a Maxwell joint and a Kelvin joint, respectively. The variation patterns between them are similar though the magnitudes are different under the same parameters. It is found that for both incident P- and S-waves, after experiencing a gentle variation, the transmission coefficients T pc and T sc change dramatically as the incident angle approaches the critical angle, i.e. θ c  = 90° and φ c  = 38.66°. The difference is that they approach zero under incident P-wave but approach unit under incident S-wave. As for the reflected waves with the same wave type as the incident wave, the curves have similar changing trends, that is, both R pc caused by the incident P-wave and R sc caused by the incident S-wave first decrease to a minimum value close to zero and then increase with the increase in the incident angle. It is noted that their minimal points appear at the incident angle of around 60° and 25°, respectively, and the exact values of the incident angle are different for the Maxwell joint and the Kelvin joint. The reflection coefficients for the incident waves of different wave type, i.e. R sc caused by the incident P-wave and R pc caused by the incident S-wave, have different changing trends. For an incident P-wave, R sc increases first and then decreases with increasing incident angle. Hence, there is a peak point in the curve which is at around 40° for both the Maxwell joint and the Kelvin joint. Dissimilarly, R pc caused by the incident S-wave increases from zero to unit until the incident angle increases to the critical angle around which the increase becomes sharp.

4.3 Effects of the Duration of Incident Waves

In Figs. 8 and 9, the transmission and reflection coefficients under half-cycle sinusoidal P-wave incidence with the incident angle of 30° are shown to be a function of the duration of incident waves t d for the Maxwell and Kelvin joints, respectively. In this section, the duration of incident waves t d is equal to half of the duration of the incident waves shown in Sects. 4.1 and 4.2. The parameters of rock materials, including c p , c s and ρ, are the same as those used in Figs. 5 and 6. The specific joint stiffnesses are fixed to be k n  = k s  = 3.5 GPa m−1, and the normalized viscosities J n  = J s  = J vary among 0.5, 1.0 and 5.0. It is found that for both models the increase in the duration of incident waves leads to the decrease in the reflection coefficients R pc and R ps and the increase in the transmission coefficient T pc . T sc is much smaller than the other waves and increases first and then decreases. However, the duration dependences of these coefficients are different between the corresponding curves of the two models. For the Maxwell model, the effect of the duration is more pronounced at relatively small duration for the curves with larger normalized viscosity, while the effect of the normalized viscosity is more obvious at relatively large duration. Conversely, the curves under the Kelvin model with larger normalized viscosity, as seen in the curves for J = 5.0, are almost unchanged with varying duration.

Fig. 8
figure 8

Reflection and transmission coefficients versus duration of the half-cycle sinusoidal incident waves for a Maxwell joint. a Reflection coefficients. b Transmission coefficients

Full size image
Fig. 9
figure 9

Reflection and transmission coefficients versus duration of the half-cycle sinusoidal incident waves for a Kelvin joint. a Reflection coefficients. b Transmission coefficients

Full size image

4.4 Discussions on the Transmission and Reflection Waveforms

Besides the amplitude attenuation on the incident wave, the effect of the joint also brings about the alteration of the waveforms. In Figs. 10 and 11, the transmitted and reflected waves under different specific joint stiffnesses and viscosities are plotted for the Maxwell and Kelvin models, respectively. The incident wave is a half-cycle sinusoidal wave with the incident angle of 30° and the duration of 0.005 s. The parameters of rock materials are the same as the earlier section. In Figs. 10a and 11a, the specific joint stiffnesses k n  = k s  = k keep constant as 10.2 GPa m−1, and three values 8.1, 16.2 and 40.6 MPa s m−1 are adopted for the specific joint viscosities η n  = η s  = η. In Figs. 10b and 11b, η is fixed to be 16.2 MPa s m−1, and k varies among 5.1, 10.2 and 25.5 GPa m−1. In all these figures, the inflexion points are observed close to the tails of the curves of the reflected waves, while the curves of the transmitted waves are relatively smooth. Meanwhile, from the peak points of the transmitted wave P T and the reflected waves R P and R S, it is found that the increases in the specific joint stiffness and viscosity both weaken the attenuation effect on the magnitude of the transmitted wave P T, which is accompanied by the decreases in the magnitudes of the reflected waves. Furthermore, all the peak points of the reflected and transmitted waves shift in time relative to that of the incident wave. However, the shift extent is dependent on the specific joint stiffness and viscosity, and the shift direction is different between the transmitted wave P T and the other waves, that is, the peak point of P T is delayed relative to that of the incident P-wave. The other waves reach their peak values earlier than the incident wave. For the Maxwell model, the shift extents of the peak points of P T, P R and S R increase with the increase in the specific joint viscosity and the decrease in the specific joint stiffness. Conversely, for the Kelvin model, their shifts are more obvious as the specific joint viscosity decreases and the specific joint stiffness increases. In addition, the transmitted wave S T is much smaller than the other waves and its changing trend has a feature of segmentation with the variations of the joint parameters which can also be seen in Sect. 4.3.

Fig. 10
figure 10

Transmitted and reflected waves for a half-cycle sinusoidal incident P-wave across a Maxwell joint under different parameters. a Under different specific joint viscosities. b Under different specific joint stiffnesses

Full size image
Fig. 11
figure 11

Transmitted and reflected waves for a half-cycle sinusoidal incident P-wave across a Kelvin joint under different parameters. a Under different specific joint viscosities. b Under different specific joint stiffnesses

Full size image

4.5 Discussions on the Effect of Normalized Joint Thickness

In essence, the present analysis is based on the DDM in which the joint thickness is regarded as zero. This leads to the ignorance of the magnitude discrepancy and the time delay of the stresses at the two sides of the filled joint.

For the discontinuity in the magnitude of the stresses at the joint interfaces, Zhu et al. (2011) attributed it to the non-ignorable initial mass of the filled joint and quantified it by a non-dimensional parameter termed as the impedance ratio of the filled joint, \( d = \frac{{z_{\text{e}} }}{{z_{s} }} = \frac{{\omega m_{n} }}{{z_{s} }} = \frac{{\omega \rho_{\text{f}} h}}{{z_{s} }} \), where z e is the effective acoustic impedance of the filling medium and ρ f is the density of the filling medium. The parameters can be transformed into a new form as \( H = d = 2\pi \frac{{\rho_{\text{f}} }}{\rho }\frac{h}{\lambda } \), where λ is the wavelength of the incident S-wave. Since it is controlled by the ratio of the joint thickness to the wavelength besides the density ratio of the filled materials and rock medium, this parameter is redefined as the normalized joint thickness H. From the conclusion of Zhu et al. (2011), the effects of the normalized joint thickness on the reflection and transmission coefficients for normally incident harmonic P-wave across a Maxwell joint are shown in Fig. 12. It is found that R pc and T pc change little with the increase in H when H is less than one. Since the density ratio is commonly small, the effect of the initial mass on the wave propagation is not obvious when the joint thickness is less than the value in the same order of magnitude as the wavelength. The experiments conducted by Wu et al. (2013a) realistically demonstrated the reliability of the DDM when the joint thickness is relatively small. The good consistency between the results from the DDM and DSDM in Figs. 5 and 6 provides further evidence for the extension of this conclusion to obliquely incident waves.

Fig. 12
figure 12

(after Zhu et al. 2011, Fig. 5c, p. 1324)

Reflection and transmission coefficients for normally incident P-wave across a Maxwell joint versus the normalized thickness of the filled joint

Full size image

On the other hand, Li et al. (2014) proposed the thin-layer interface model (TLIM) to take the joint thickness into account and ascribed its effects to the time delay between the stresses at the two interfaces of the joint. The analytical results from the TLIM and the zero-thickness interface model were found to be identical under a given incident direction if the ratio of the filled joint thickness to the incident wavelength is small. This conclusion provides further evidence for the applicability of DDM to the cases when the joint thickness has a lower order of magnitude than the wavelength which are most usually encountered in nature. If the joint thickness is comparable to the order of magnitude of the wavelength, new models should be developed to investigate the effect of the joint thickness considering not only the initial mass but also the wave propagation time across the joint.

4.6 Applicability to a Set of Parallel Joints

Rock fractures in nature are usually in parallel form as joint sets. In order to analyse wave propagation across jointed rock masses with the consideration of multiple wave reflections between joints, several mathematical methods have been proposed, i.e. the method of characteristics (MC) (Cai and Zhao 2000), the scattering matrix method (SMM) (Perino et al. 2012), the virtual wave source method (VWSM) (Zhu and Zhao 2013) and the time-domain recursive method (TDRM) (Li et al. 2012). The obtained solutions can be extended conveniently to a set of parallel joints under the assistance of VWSM or TDRM which is appropriate for the derivation in time domain.

Specifically, the virtual wave source (VWS) exists at the joint position and produces four new waves at most (P-wave and S-wave at each side of the joint) when an incident wave propagates across the joint. These waves can be directly obtained from Eqs. 11 to 14 and 19 to 24 for Maxwell joint; or Eqs. 11 to 14 and 28 to 36 for Kelvin joint. Therefore, the transmitted wave across a joint set is the result of wave superposition of different transmitted waves created by VWS.

$$ v_{{P_{\text{T}} }} = \sum\limits_{j = 1}^{\infty } {v_{{P_{\text{T}} j}} } $$
(47)
$$ v_{{S_{\text{T}} }} = \sum\limits_{j = 1}^{\infty } {v_{{S_{\text{T}} j}} } $$
(48)

where \( v_{{P_{\text{T}} }} \) and \( v_{{S_{\text{T}} }} \) are the superposed transmitted P-wave and S-wave, respectively. \( v_{{P_{\text{T}} j}} \) and \( v_{{S_{\text{T}} j}} \) are the transmitted P-wave and S-wave arriving at different times.

To adopt the time-domain recursive method (TDRM), each joint is supposed to be impinged by eight waves, i.e. both right and left running P-waves and S-waves at each side. Correspondently, the mechanical analysis on each joint can be achieved by the superposition of the analysis in this study on incident P-wave and S-wave at each side. Combining with the boundary conditions described by Eqs. 10, 16 and 17 for Maxwell joints; or Eqs. 10, 26 and 27 for Kelvin joints, the right and left running waves at each time can be determined recursively starting from a certain initial condition. Thus, the transmitted wave can be finally obtained.

Take one case (η n  = η s  = 8.1 MPa s m−1, k n  = k s  = 10.2 GPa m−1) in Fig. 11 as a calculated example, the transmission coefficients across N (N = 2, 4, 6) Kelvin joints under different non-dimensional joint spacing from VWSM and TDRM are shown in Fig. 13, where the non-dimensional joint spacing ς is defined as the ratio of the joint spacing to the wavelength of the incident wave. It can be seen that the results obtained by VWSM and TDRM agree well with each other which means both of them can be used to extend the current solutions to a set of parallel joints with viscoelastic deformational behaviour. In fact, the essential concepts of these two methods are similar, i.e. calculating the passing waves across each joint iteratively. But since the superposition of the waves arriving at different times is addressed automatically in every step through TDRM, its computational efficiency is much higher. It is also noted that the transmission coefficients across different number of joints have the same variation trend, i.e. they first increase to the maximum value with increasing joint spacing and then decrease to a constant. It means the first transmitted wave will no longer be affected by the waves arriving later under enough large joint spacing.

Fig. 13
figure 13

Transmission coefficients for incident P-wave across Kelvin joint sets under different non-dimensional joint spacings obtained from VWSM and TDRM

Full size image

4.7 Advantages and Implications

The obtained time-domain solutions for the joint with viscoelastic deformational behaviour have the advantage over the other existing analytical solutions. The absence of Fourier transforms brings higher computational efficiency and wider applicability on parametric studies for an incidence with an arbitrary waveform. Through the solutions in time domain, the effects of various waves or loading parameters on wave propagation across joints can be studied straightforwardly. And, the effects reflected on the waveforms of the resultant waves can also be observed directly.

Furthermore, since the real-time mechanical states on the two sides of the joint are clear in the derivation process of the theoretical solutions in time domain, in both laboratory experiments and engineering practices, the individual wave emerged from the joint can be identified and the joint response referring to the stress and the closure can also be obtained without additional sensors except simple three-directional strain gauges. Meanwhile, the slip or tensile damage on the joint which may be induced under relatively more intense disturbances can also be anticipated conveniently according to the displacement or stress failure criteria. These failure criteria, in turn, can be easily introduced in the solutions attributed to the good expandability of the derivation process, which has been demonstrated by the consideration for multiple joints.

In geotechnical engineering, rock joints filled by viscoelastic materials are commonly encountered and dynamic disturbances such as blasting excavations, rock burst, roof collapse and earthquakes take place frequently. The general purpose of the studies on the joint seismic response can be settled in the inverse analysis for the joint properties and the wave source. Based on the obtained propagation characteristics, the properties of the joint including the stiffness, the viscoelastic parameters, especially the orientation, can be inversely determined when the wave source is known. On the other hand, when the joint properties are acquired by geological survey, the wave source can be determined from the wave signals monitored at accessible locations.

5 Conclusions

To study the effects of filled joints with viscoelastic behaviour on wave propagation, the interaction between plane P- and S-waves with arbitrary impinging angles and a rock joint are analysed in this paper. The time-domain solutions for wave propagation across a joint with viscoelastic deformational behaviour are obtained through the incorporation of the Maxwell and Kelvin models into the DDM. It can be applied to an arbitrary incident wave without additional mathematical method.

Comparisons between the theoretical results and the experimental data obtained from a modified split Hopkinson pressure bar test and are conducted. It is found that the Maxwell model is more appropriate to describe the joint filled by clay under P-wave incidence. Leaving aside the specific filling materials, the parameter characteristics of the two theoretical model and their applicable conditions are analysed. It is inferred that the Maxwell model is more appropriate for the cases with less attenuation, while for the cases with more obvious attenuation the Kelvin model is more effective.

The parametric studies show that the wave transmission and reflection are affected by the normalized joint stiffness, the normalized viscosity, the incident angles and the duration of the incident wave. In addition, the dependences on the specific joint stiffness and viscosity of the transmission and reflection coefficients are different between the Maxwell and Kelvin joints.

Attributed to the time-domain form of the solutions, the alternations of the waveforms of the reflected and transmitted waves are illustrated directly. The extent of time shift of their peak points is found to be different with varying joint parameters.

Furthermore, the solutions are extended for multiple parallel joints by combining with the recursive mathematical methods including the VWS and TDRM. Besides the higher computational efficiency and wider applicability compared with the previous solutions, it provides more direct guidance for the mechanical analysis in both laboratory experiments and engineering practice.