1 Introduction

Rock fragmentation is frequently observed during rock fall events. However, few analytical tools exist to simulate it (Lin et al. 1996), and few, if any, rock fall analysis codes include modeling of fragmentation. For example, in conjunction with the research that produced the results in this paper (Crosta et al. 2006) implemented an energy approach to fragmentation detection within their three-dimensional rockfall analysis code HY-STONE. Impact rock fragmentation is still the most complicated and poorly understood aspect in rock fall analysis. Very few contributions have been made so far. Most of the work related to rock fragmentation considers the evaluation of the dynamic strength of rock materials and tries to understand the effects of the loading rate on the rock fragmentation phenomenon via energy considerations (Chau 2003; Fornaro et al. 1990; Giacomini et al. 2009; Zhang et al. 2000). However, the impact fragmentation process in rock fall analysis cannot be well predicted via energy considerations alone because the process is not only controlled by the energy, but also related to other factors such as impact velocity, incidence angle, pre-existing fractures, and ground stiffness.

In this paper, a discrete element model (DEM) code developed by the first author (Wang 2009; Wang and Tonon 2009, 2010) is used to simulate impact-induced rock fragmentation in rock fall analysis. The physical process of rock fall impact fragmentation is complex because it consists of impact-induced stress waves that propagate, generate thermal energy, and create plastic zones, etc. In order to model this type of process using the DEM code, it is necessary to simplify the problem, such as treating the ground as a half-space elastic homogenous medium. One of the challenges in modeling rock fall impact, in which a block of rock impacts on the ground, is to choose an appropriate model to represent the interaction between the rock block and the ground including the stiffness and damping of the ground.

The paper first briefly introduces an impact model and impact fragmentation model using a discrete element code developed by the authors. Mechanisms of rock fragmentation upon impact are then investigated by considering the effect of impact velocity, ground condition and fracture properties upon impact, and energy loss during impact.

2 DEM Code

The authors (Wang 2009; Wang and Tonon 2009, 2010) developed a 3D DEM code, in which a rock block is modeled as an assembly of spherical particles. The DEM can be generally viewed (Cundall and Hart 1992) as a method that allows for finite displacements and rotations of discrete bodies, and updates contacts automatically as the calculation progresses. When modeling the behavior of intact rock, the particles used in the model are bonded to each other with a specific strength and do not represent the actual material particle size. In the authors’ code, the initial model is set up by using the packing assembly (which is randomly distributed) and considering the initial state as “zero stress” state. This is achieved by introducing an “equilibrium distance”, D eq, at each contact, which is equal to the distance between the centers of the two contacting spheres at the end of the packing (releases the lock-in stress). An interaction range is introduced into the model to simulate materials other than simple granular materials, in particular those which involve a matrix (Hentz et al. 2004). A coefficient of interaction range of 1.1 is used in this work, which means that two particles are in contact if their center-to-center distance is <1.1 times of the summation of their radii.

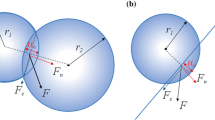
As shown in Fig. 1, there are two cases in which particles are in contact and an “equilibrium distance” is created. In the first case, two particles overlap and “equilibrium distance” is less than the sum of their radii. In the second case, two particles are not physically in contact, but are still considered to be in contact by introducing an interaction range, in which the “equilibrium distance” is larger than the sum of their radii. In the first case, by setting the “equilibrium distance” equal to the center-to-center distance reached after packing and by setting contact stresses to zero (“equilibrium”), the lock-in stress generated from packing is released. In the second case, the “equilibrium distance” between particles is determined as the sum of the two radii multiplied by a coefficient of interaction range.

Fig. 1
figure 1

Concept of equilibrium distance

Full size image

In the DEM, the model parameters (micro-parameters), including deformability and strength, cannot be directly derived from measurable material properties (macro-properties). Deformability parameters include particle Young’s modulus, E c, and the ratio of normal stiffness, K n, to shear stiffness, K s at the contact point. Micro strength parameters include the contact tensile strength T, cohesion c, and friction angle φ, for shear components. It requires extensive calibration work to identify these micro parameters to reproduce specified material behavior. The authors (Wang and Tonon 2009, 2010) developed optimization-based algorithms to identify the micro-parameters that govern the deformability and strength at the contact between any two particles that make up the simulated rock block. The DEM code and the identification algorithm were thoroughly verified and validated in both static and dynamic loading regimes (Wang 2009).

The PFC, particle-bonded model (Potyondy and Cundall 2004), is commonly used in modeling intact rock behavior. The authors’ code is similar to the PFC except that: (1) the concept of equilibrium distance and the coefficient of interaction range is introduced in the authors’ code; (2) the contact shear strength in authors’ model has both cohesion and frictional components, while the contact shear strength component in the PFC particle-bonded model is stress-independent (no frictional part); (3) unlike the PFC particle-bonded model, no additional “cement bond” is used in authors’ code; instead, a coefficient of interaction range, cohesion, and tensile strength at contact are introduced to simulate the cement behavior. Without additional artifacts, the PFC particle-bonded model cannot correctly model pressure-dependent rock behavior [(Potyondy and Cundall 2004), pp 1,342, Fig. 6-1]. This is probably caused by the fact that either the contact shear strength component is stress-independent in the PFC particle-bonded model, or that the PFC lacks a robust model calibration procedure to identify the model micro parameters.

3 Model of the Interaction between Rock Blocks and the Ground

In using the DEM to model the rock impacting against the ground, the ground is simplified as a half-space, elastic, homogeneous, and isotropic media, while the behavior of the rock block is simulated by the DEM. The interaction between the impacting rock block and the ground is essentially a force–displacement relationship, which will be applied to the DEM model as boundary conditions. In other words, the impacting forces due to the penetration of rock blocks into the ground are to be determined and applied as a boundary force in the DEM modeling.

In DEM modeling, impact interactions are treated as point loads acting on both impacting boundary particles and the ground. These point loads applied to the half-space medium can induce surface motions, which will, in turn, influence other impacting boundary particles’ interactions.

Lamb (1903–1904) first investigated the surface motion created by a point source at the surface of an linearly elastic isotropic and homogeneous half-space medium. Under the conditions considered by Lamb, an excitation spreads out from the transient point source as a symmetrical annular wave. As shown in Fig. 2, a particle at the surface first experiences a motion in the form of oscillation at the arrival of P-wave, followed by a relatively quiet period leading up to another oscillation at the arrival of S-wave. These motions are referred by Lamb as the minor tremor and are followed by a much larger oscillation, the major tremor, at the arrival of the R-wave. The results presented by Lamb are in the frequency domain, not in the time domain, and are very difficult to be implemented into our DEM model because the DEM calculation scheme uses explicit time integration. Some analytical solutions for surface motions caused by harmonic or Heaviside impact sources were also presented in the wave number-time domain (Park and Kausel 2004; Richart et al. 1970). Due to the difficulty of determining the surface motion caused by irregular time-dependent excitation, it is impossible to introduce these results into the DEM modeling to account for the impact behavior. For simplicity, the coupling effects of the interactions due to the surface motions generated by other impacting particles are to be neglected.

Fig. 2
figure 2

Surface motion due to a transient point source [after (Richart et al. 1970)]

Full size image

In DEM modeling, the rock block is simulated as an assembly of spherical particles. When an impact occurs, part of the boundary particles (spheres) interact with the ground and the generated interface forces may make the block bounce off the ground. The larger the penetration of those boundary particles into the ground is, the larger the generated “push-back” forces are. The relationship between the “push-back” forces and the penetrations can be depicted by a series of springs and dashpots in both normal and tangential directions attached to the impacting boundary particles as shown in Fig. 3. The stiffness of the springs and the damping coefficients can be estimated from the theory of vibrations for foundations on elastic media as determined below. In this approximation, the spherical boundary particles, which penetrate into the ground, are treated as tiny foundations whose equivalent disk radii are the same as their contact radii as shown in Fig. 3.

Fig. 3
figure 3

Sketch of impact model with springs and dashpots attached to each impacting particle in both normal and shear directions to simulate dynamic interaction between the rock block and the ground. The radius of the simplified disk foundation is equal to the corresponding impacting particle’s radius

Full size image

In the theory of vibrations for foundations on elastic media, the vertical and tangential oscillations of a rigid circular disk foundation can be described in terms of mass-spring-dashpot analog (Richart et al. 1970). For disk foundations resting on an elastic half-space, the spring constants are determined from the static response of the rigid disk to vertical or horizontal loads, and are given as, respectively (Richart et al. 1970)

$$ \begin{aligned} k_{\text{n}} & = {\frac{{4Gr_{0} }}{1 - \nu }}\quad \left( {\text{normal}} \right) \\ k_{\text{s}} & = {\frac{32(1 - \nu )}{7 - 8\nu }}Gr_{0} \quad \left( {\text{tangential}} \right) \\ \end{aligned} , $$
(1)

where k n and k s are normal and shear stiffness of the springs used in the disk foundation, respectively, G, ν are the shear modulus and Poisson’s ratio of the ground, respectively, and r 0 is the radius of the disk foundation. Dashpots are used to provide damping that accounts for the energy loss due to the elastic stress waves propagating away into the ground (geometric damping or radiation damping). The dashpot constants are given as (Richart et al. 1970)

$$ \begin{aligned} c_{\text{n}} & = {\frac{{3.4r_{0}^{2} }}{1 - \nu }}\sqrt {\rho G} \quad \left( {\text{normal}} \right) \\ c_{\text{s}} & = {\frac{18.4(1 - \nu )}{7 - 8\nu }}r_{0}^{2} \sqrt {\rho G} \quad \left( {\text{tangential}} \right) \\ \end{aligned} , $$
(2)

in which c n and c s are damping constants for normal and tangential oscillations respectively, and ρ is the density of the ground material.

When particles penetrate into the ground, contacts develop and there is interaction between the rock block and the ground. The equations of translational motion of particles in normal and tangential directions to the impact plane are then written as

$$ \begin{gathered} m\ddot{z} + {\frac{{3.4r_{0}^{2} }}{1 - \nu }}\sqrt {\rho G} \dot{z} + {\frac{{4Gr_{0} }}{1 - \nu }}z = Q_{z} (t)\quad \left( {\text{normal}} \right) \hfill \\ m\ddot{x} + {\frac{18.4(1 - \nu )}{7 - 8\nu }}r_{0}^{2} \sqrt {\rho G} \dot{x} + {\frac{32(1 - \nu )}{7 - 8\nu }}Gr_{0} x = Q_{x} (t),\quad \left( {\text{tangential}} \right) \hfill \\ \end{gathered} $$
(3)

where Q z (t) and Q x (t) are forces exerted by other neighboring particles in normal (z) and tangential (x) directions, respectively.

4 Investigation on Mechanism of Impact Fragmentation

The mechanism of impact fragmentation is complicated. Among the numerous factors governing the process of impact fragmentation, the following ones have been investigated in this research: magnitude of impact velocity, incidence angle, ground conditions, material properties of the rock block itself, and fracture persistence, opening, cementation, and orientation.

A spherical rock block was generated to simulate rock fall impact and investigate the mechanism of impact fragmentation. The block has a radius of 0.1 m and consists of 600 randomly distributed spherical particles with average radius of 0.011 m according to a Gaussian distribution, in which the ratio of smallest radius over the largest radius is chosen as 1.6 in this paper. The identified model micro parameters for an intact granite are shown in Table 1 (Wang 2009), in which the micro deformability parameters are \( E_{\text{c}} = 27.2{\text{ GPa and }}{\frac{{K_{\text{s}} }}{{K_{\text{n}} }}} = 0.098 \) and the calibrated micro strength parameters are c = 385 MPa, φ = 60° and T = 110.2 MPa. The normal stiffness is determined by K n = E c D eq. These micro parameters were calibrated based on quasi-static experimental results and artificially high damping was used to quickly dissipate kinetic energy and reach equilibrium state. However, when modeling impact, material damping was neglected and no damping was introduced; this approach was validated by the authors by carrying out dynamic compression tests at progressively higher strain rates in the range between 10−5 and 100 s−1. The damping may have an effect on the fragmentation process. This effect is not investigated in the paper. These micro parameters are different from the parameters for macro material properties determined from standard experimental tests. For example, the calibrated micro strength parameters may seem to be much higher than the material’s macro strength parameters. In DEM modeling, failure either in tension or shear is initiated from highly stressed contact bonds and propagates subsequently. Hence, calibrated micro strength parameters could be much higher than macro strength parameters.

Table 1 Model micro parameters used in the simulations
Full size table

4.1 Effect of Impact Velocity

The magnitude of impact velocity and the incidence angle with reference to the ground are directly related to the dynamic interaction between rock blocks and the ground, and hence play important roles in the process of impact fragmentation. Here, incidence angle is defined as the acute angle between the ground and the incident trajectory. For example, for a normal impact, incidence angle is equal to 90°. Generally, for a fixed incidence angle a larger magnitude of impact velocity tends to generate higher impact stresses, which increases the chance for impact fragmentation. On the other hand, for a fixed magnitude of impact velocity, a smaller incidence angle reduces the chance for impact fragmentation while producing greater angular momentum in rock blocks.

This section investigates the effects of the magnitude of impact velocity and the incidence angle on impact fragmentation of homogeneous rock blocks (without initial fractures). The ground has a Young’s modulus of 20 GPa and a Poisson’s ratio of 0.3, which are representative of a relatively “hard” rock mass.

4.1.1 Magnitude of Impact Velocity

In this case, normal incidences are considered in which a rock block perpendicularly impacts the ground. The magnitude of impact velocity varies as 40, 50, and 60 m/s, which are reasonable values in practical rock fall analyses. One of the most important quantities to be monitored during impact fragmentation is the highest impact stress generated during impact. As shown in Table 2 and Fig. 4, at about 50 m/s of impact velocity, fragmentation starts to occur with 43 fragments. When the impact velocity increases to 60 m/s, the number of fragments increases to 334.

Table 2 Number of fragments for different impact velocities under normal incidence
Full size table
Fig. 4
figure 4

Fragmentation (after separation) for different impact velocities; snapshots taken after the block bounces off the ground

Full size image

Note that the fragmentation processes “localize” at the impact zone and all of the fragments generated during impact are very small because they consist of less than three spherical particles. In other words, for a homogeneous rock block, impact fragmentation occurs locally without generating some relatively large fragments as typically observed in the field for large rock blocks, which may contain some pre-existing fractures. The importance of pre-existing fractures is addressed shortly in Sect. 4.3.

Figure 5 clearly depicts the impact process by plotting the time-histories of the system kinetic energy (defined as the sum of the kinetic energies for all particles) and of the impact normal stress. During the approach period, the system kinetic energy decreases while the block penetrates into the ground and reaches almost zero when the block attains its largest penetration, at which point almost all of the system kinetic energy is transformed into strain energy. The impact normal stress increases with penetration, and it reaches its largest value at about the largest penetration. During the restitution period, the stored strain energy is again gradually transformed into system kinetic energy while the impact normal stress decreases until it reaches zero when the block bounces off the ground.

Fig. 5
figure 5

Histories of impact stress and system kinetic energy for different impact velocities

Full size image

Figure 5 shows that the monitored highest impact normal stress increases from about 2,000 to 2,250 MPa when the magnitude of impact velocity increases from 40 to 60 m/s. However, the highest impact normal stress does not increase much when impact velocity increases from 50 to 60 m/s. For a given type of rock block, there is an impact normal stress threshold that controls the fragmentation, which can only occur above this threshold value. When fragmentation occurs, impact normal stress is limited by the generation of fragments. This explains why the largest impact normal stresses at impact velocities of 50 and 60 m/s are very similar.

The monitored impact normal stress was determined by the normal forces divided by the contact areas when impact particles penetrate into the ground. This stress is the dynamic contact stress applied to individual particle and it is much higher than the material strength. This monitored impact contact stress can reflect the “push-back” effect applied to the block.

4.1.2 Incidence Angle

For a constant magnitude of impact velocity, a change of incidence angle can also affect impact fragmentation because the normal component of impact velocity to the ground governs the highest impact stress, which is the main driver for impact fragmentation. The normal component increases with incidence angle, so a larger incidence angle has a greater potential to generate fragmentation. The tangential component of impact velocity, however, plays a role in changing angular momentum.

In this case, the magnitude of impact velocity is kept constant as 60 m/s, while the incidence varies as 30°, 60°, and 90°. As shown in Table 3, for incidence angle of 30°, no fragmentation occurs, while the number of fragments increases to 175 and 334 for an incidence angle of 60° and 90°, respectively.

Table 3 Fragmentation for different incidence angles with the impact velocity of 50 m/s
Full size table

Figure 6 shows that the monitored highest impact normal stress increases from about 1,800 MPa for incidence angle of 30° to 2,250 MPa for incidence angle of 60°, when fragmentation occurs. When the incidence angle further increases from 60° to 90°, the highest impact normal stress does not increase much because, when the normal stress reaches the fragmentation stress threshold that triggers fragmentation, contact failure occurs. For the normal incidence (90° incidence angle) case, the system kinetic energy reaches almost zero when the block attains its largest penetration, at which point almost all of the system kinetic energy is transformed into strain energy. By contrast, the system kinetic energy changes negligibly when the incidence angle is equal to 30°. For a small incidence angle, most of the system energy is transmitted by the tangential component of the velocity rather than the vertical penetration.

Fig. 6
figure 6

Fragmentation (after separation) and histories of impact stress and system kinetic energy for different incidence angles

Full size image

4.2 Effect of Ground Condition

Not only the impact velocity and angle of incidence, but also ground conditions can affect impact fragmentation. A softer ground tends to extend the duration of an impact and produces lower impact stresses, so rigid ground is more likely to cause impact fragmentation compared to soft ground. As seen in Eqs. 1 and 2, the impact model used to simulate the dynamic interaction between rock block and the ground, the shear modulus and Poisson’s ratio of the ground jointly determine the values of stiffness and geometric damping in both normal and tangential directions. Based on Eqs. 1 and 2, the shear modulus of the ground is proportional to the normal and tangential stiffness, and it is proportional to the square of the geometric damping in both normal and tangential directions. The Poisson’s ratio of the ground also has an effect on the values of stiffness and damping. Considering that the Poisson’s ratio of the ground does not vary much (with typical values ranging from 0.15 to 0.35), the effect of the Poisson’s ratio of the ground is not studied here (Poisson’s ratio is fixed as 0.3); ground conditions are only characterized by the Young’s modulus of the ground, E, by the relationship \( G = {\frac{E}{2(1 + \nu )}}. \)

In this case, normal incidences are considered and the magnitude of impact velocity is kept constant as 60 m/s. The Young’s modulus of the ground varies as 1, 10 and 20 GPa: these values cover rock masses from soft-weathered to sound and are higher than typical values for soils (10–400 MPa). As shown in Table 4, for the Young’s modulus of the ground of 1 GPa, no fragmentation occurs. Fragmentation occurs and generates 36 fragments when the Young’s modulus of the ground is equal to 10 GPa. When the ground becomes much stiffer with the Young’s modulus of the ground of 20 GPa, the number of fragments increases to 334.

Table 4 Fragmentation for different ground conditions under normal incidence
Full size table

Figure 7 shows that the impact normal stress increases with the Young’s modulus of the ground. The highest impact stress increases from about 400 to 1,900 MPa when the Young’s modulus of the ground increases from 1 to 10 GPa. Impact fragmentation generates 36 fragments for the ground with a Young’s modulus equal to 10 GPa, and 334 fragments for the ground with a Young’s modulus equal to 20 GPa, while the highest impact normal stress increases from about 1,900 to 2,250 MPa. It has been mentioned previously that the highest impact normal stress is not much greater than the impact fragmentation stress threshold because the impact normal stress is limited by the impact fragmentation process. But for different ground conditions, the impact fragmentation stress threshold may be different.

Fig. 7
figure 7

Fragmentation (after separation from impact surface) and histories of impact normal stress and system energy for different ground conditions under normal incidence

Full size image

Impact duration also plays a role in controlling the impact fragmentation stress threshold needed to generate impact fragmentation. Based on the authors’ research (Wang 2009), the uniaxial compressive strength increases with increasing strain rate. A softer ground tends to extend the impact duration and induces a relatively lower strain rate in the rock blocks, so the stress threshold of impact fragmentation for a soft ground is lower than that for a rigid ground provided that the dynamic strength of rock blocks is strain-rate dependent. On the other hand, impact stresses are nearly proportional to the ground Young’s modulus before fragmentation occurs. For a fixed impact profile, a soft ground tends to produce lower impact stresses. Based on the simulated results shown in Fig. 7, a soft ground tends to reduce the potential for impact fragmentation. This indicates that the effect of the ground Young’s modulus on impact stress overshadows the strength increase with increasing strain rate. Otherwise, a soft ground would generate more fragments than a rigid ground does because the strength of the rock block is lower under softer ground condition when the strain-rate is lower.

4.3 Effect of Fracture Properties of Rock Block

Real rock blocks involved in rock falls are seldom homogeneous. Typically, rock blocks contain fractures. These fractures can play a very important role in impact-induced rock fragmentation. The effects of fracture persistence, aperture, and orientation on impact-induced rock fragmentation were investigated and are presented hereafter.

In the following cases, normal incidences with a magnitude of impact velocity of 30 m/s and Young’s modulus of the ground of 20 GPa are considered. Fractures were treated as “rough” planar with circular shape (Fig. 9). The simulated results of fractured blocks can be compared to the homogeneous case shown in Fig. 8, where no fragmentation occurred.

Fig. 8
figure 8

Impact of a homogeneous rock block on the ground; snapshot taken after the block bounces off the ground

Full size image

4.3.1 Persistence

In this case, two fractures perpendicular to each other form an “X” centered at the center of the block, whose arms bisect the X and Z axes (Fig. 9). Fracture persistence is defined as the ratio of the radius of a “circular” fracture plane over the block’s radius. In the case of a fracture passing through the sphere center, the largest radius is the radius of the spherical block. Fractures were treated as broken contacts along which shear strength was purely frictional with friction angle of 20° (cohesion and tensile strength were set to zero). The contacts close to the proposed fracture planes were broken to represent fractures. As shown in Fig. 9, simulated fracture planes are not planar.

Fig. 9
figure 9

Sketch of “X” and “+” shaped fractures in a spherical block used to numerically investigate the effect of fracture patterns on fragmentation. Fracture persistence is defined as the ratio of the radius of a “circular” fracture plane over the block’s radius

Full size image

The simulated results show that fracture persistence has a very important role in governing the degree and the pattern of impact fragmentation. As shown in Fig. 10, when the fracture persistence is equal to 80%, 46 fragments are generated, but these fragments cannot be observed from outside the block because they are made up of individual particles along the fractures, de-bonded and separated from the rock block due to the impact. When fracture persistence increases to 90%, the number of fragments increases to 55, and part of the perimeter of the block, which is not cut through by the original fractures, starts to break (Fig. 10b) due to the fracture propagation from the fracture tips. Only when the fractures are fully persistent, is there a clear pattern of four big fragments with the bottom one being more fragmented. The number of fragments for fully persistent case is 196.

Fig. 10
figure 10

Impact fragmentation (after separation) for different values of fracture persistence; snapshots are taken after the block bounces off the ground. Fractures are disk- shaped, and the two fracture planes form an “X” shape as shown in Fig. 9

Full size image

4.3.2 Fracture Aperture

In this case, in addition to using broken contact bonds to describe preexisting fractures in the DEM model, open preexisting fractures were modeled by introducing an equilibrium distance, D eq, of a broken contact, which is smaller than the actual center-to-center distance (see Fig. 11). On the other hand, for a closed preexisting fracture, the equilibrium distance, D eq, is initially defined as equal to the actual center-to-center distance. For an open preexisting fracture, when two contacting spheres move close together across the fracture, no contact compression force will be generated before the center-to-center distance reaches the equilibrium distance, D eq. On the other hand, for a closed preexisting fracture, contact compression force will build up immediately when the two contacting spheres move close together across the fracture.

Fig. 11
figure 11

Modeling open and close fractures using broken contact bond and equilibrium distance

Full size image

The fracture aperture was taken as 1% of the actual center-to-center distance. Fractures formed an “X” with 80% fracture persistence. Comparing against the results of 80% fracture persistence (shown in Fig. 10b) with 46 fragments. Figure 12 shows that now 306 fragments are generated including two larger ones. It has been found that impact fragmentation is very sensitive to fracture aperture. This can be attributed to cracks caused by tensile stress waves: when a compressive stress wave produced by the impact encounters a free surface (open fracture), it turns into a tensile stress wave. Usually, rock materials are much weaker in tension than compression. That is why a larger number of fragments were found in the case of open fractures.

Fig. 12
figure 12

Impact fragmentation (after separation) for opened fractures with 80% persistence; snapshot taken after the block bounces off the ground

Full size image

4.3.3 Fracture Orientation upon Impact

In this case, compared against “X” shaped fractures, two fractures in a “+” shape centered at the block center were modeled. Fractures are in the XY- and YZ-planes (Fig. 9), respectively. Figure 13 shows that “+” shaped fractures are more critical to creating fragmentation than “X” shaped fractures. For fracture persistence of 90%, only 55 fragments are generated by the “X” shaped fractures compared to 224 fragments for “+” shaped fractures. As shown in Fig. 13b, 317 fragments are generated, and the two bottom parts individually separated by the fractures are completely crushed. By contrast, there are 196 fragments created after impact with three larger fragments for the case of fully persistent “X” shaped fractures.

Fig. 13
figure 13

Impact fragmentation (after separation) for different persistence values and “+” shaped fractures; snapshots taken after the block bounces off the ground

Full size image

4.4 Energy Loss during Impact and Dynamic Interaction with the Ground

Energy loss is one of the most important quantities in impact modeling. In rock fall impact, considerable kinetic energy is consumed to generate rock fragments, stress waves propagating into the ground, craters into the ground, etc. Usually, the rebound velocity of the rock is significantly less than its impact velocity (An 2006; An and Tannant 2007). In modeling rock impact against the ground with fragmentation, system energy can be tracked to understand the energy transformation during impact. Because the ground is idealized as an elastic material, the energy loss due to crater generation is not included.

The total system energy (E T), includes kinetic energy (E K), strain energy (E S) and energy loss due to friction (E F), geometric damping (E D), and tensile cracking (E C). According to conservation of energy, the total system energy E T is equal to the summation of E K + E S + E F + E D + E C at any time. Gravity is neglected in impact simulations because the gravity force applied to the block is much smaller than the force due to impact stress.

Kinetic energy consists of translational and angular energy of particles, which can be determined as

$$ E_{\text{K}} = \sum\limits_{{N_{\text{p}} }} {\sum\limits_{i = 1}^{3} {\left( {\frac{1}{2}MV_{i}^{2} } \right)} } $$
(4)

where N p is the number of particles, generalized M includes mass and principal moment of inertial of particles, and generalized V i includes translational and angular velocity of particles.

Strain energy is the energy stored in normal and tangential springs at all contacts. It can be expressed as

$$ E_{\text{S}} = \frac{1}{2}\sum\limits_{i = 1}^{{N_{\text{c}} }} {\left( {{\frac{{|F_{i}^{\text{n}} |^{2} }}{{K_{i}^{\text{n}} }}} + {\frac{{|F_{i}^{\text{s}} |^{2} }}{{K_{i}^{\text{s}} }}}} \right)} $$
(5)

where N c is the number of contacts, F n i and F s i are the normal and shear forces, respectively, and K n i and K s i are normal and shear stiffness, respectively.

Energy losses due to friction, geometric damping and tensile cracking are accumulated during impact, and are not recoverable. Friction energy loss occurs after contact shear failure between any two spherical particles. It can be expressed as (An 2006)

$$ E_{\text{F}} \leftarrow E_{\text{F}} - \sum\limits_{i = 1}^{{N_{\text{c}} }} {\left( {F_{i}^{\text{s}} \left( {\Updelta U_{i}^{\text{s}} - (\Updelta U_{i}^{\text{s}} )^{\text{elastic}} } \right)} \right)} $$
(6)

in which ΔU s i is the incremental shear displacement, and ΔU s i  − (ΔU s i )elastic stands for the increment of slip displacement.

Geometric damping energy loss is caused by the dashpots associated with the impact model of ground interaction, which is related to stress waves propagating out via the ground (scattering). This accumulated damping energy loss is written as

$$ E_{\text{D}} \leftarrow E_{\text{D}} + \sum\limits_{{N_{{{\text{p}}\_{\text{imp}}}} }} {\left( {c_{\text{n}} {\text{v}}_{\text{n}} \Updelta u_{\text{n}} + c_{\text{s}} {\text{v}}_{\text{s}} \Updelta u_{\text{s}} } \right)} $$
(7)

where N p_imp is the number of particles in direct contact with the ground during impact, c n and c s are the damping coefficients in Eq. 2, v n and v s are the particle velocity in normal and tangential directions, respectively, and Δu n and Δu s are the incremental displacement in normal and tangential directions, respectively.

Tensile cracking energy loss is the energy release of the stored strain energy in normal springs between any two spherical particles when contact tensile failure occurs. This accumulated tensile crack energy loss is calculated by

$$ E_{\text{C}} \leftarrow E_{\text{C}} + \frac{1}{2}\sum\limits_{{N_{{{\text{c\_crack}}}} }} {\left( {{\frac{{\left( {T \times A_{i}^{\text{C}} } \right)^{2} }}{{K_{i}^{\text{n}} }}}} \right)} $$
(8)

where N c_crack is the number of contacts in tensile failure, T is the tensile contact strength, and A C i is the contact area, which is defined as the area of a disk with a radius equal to the average of the two contacting sphere radii.

All of these forms of energy can be tracked during impact to see how the energy is transformed and how the energy transformation is related to the failure process. As an example, Fig. 14 shows the energy transformation for a normal impact against a relative stiff ground (the Young’s modulus of the ground is equal to 20 GPa) with an impact velocity of 60 m/s generating 334 fragments. The analysis of an extensive number of energy transformations during impact reveals that

Fig. 14
figure 14

System energy transformation and energy loss due to failure and geometric damping during impact

Full size image
  1. 1.

    Energy transformation occurs mainly during impact including approach and restitution stages. Approach stage is defined as the period from the beginning of impact to the maximum penetration. Restitution stage is the period between the maximum penetration and the time of loss of contact.

  2. 2.

    After the block bounces off the ground, negligible energy transformation occurs, stored strain energy is released, and kinetic energy remains relatively constant.

  3. 3.

    The system energy loss includes the energy loss due to shear (friction) and tensile failures and geometric damping. From the monitored energy transformation, failure accompanied by energy loss in shear and tensile failures mainly occurs during the period of impact, which means that no further or very few failures occur after the block bounces off the ground.

  4. 4.

    Friction energy loss accounts for most of the energy loss, while tensile cracking energy loss is not significant. For a softer ground condition (Young’s modulus smaller than 1 GPa), the energy dissipated in geometric damping may increase and exceed the frictional energy loss as the impact duration tends to become longer.

  5. 5.

    Total energy, which is the summation of all types of energy, remains constant during the whole simulation, which means energy conservation.

5 Conclusions

In order to simulate impact-induced rock fragmentation in rock fall analysis, the DEM code developed by the first author has been used with a simplified impact model inspired by the theory of foundations subjected to dynamic loading.

Based on the impact simulations presented in the paper, impact fragmentation occurs locally at the impact zone without generating large fragments for a homogeneous rock block. Closed pre-existing fractures in the impacting rock block generate large fragments only when the fractures are fully persistent; open fractures generate large fragments even at 80% persistence. Fracture orientation at the moment of impact determines the number and shape of large fragments generated.

Fragmentation occurs when the impact normal stress (normal force divided by the particle contact area) reaches a threshold value and the fragmentation process limits the impact normal stresses at this threshold value, which depends on the stiffness of the impacted ground. A softer ground tends to extend the impact duration and induces a relatively lower strain rate in the rock blocks, so the stress threshold of impact fragmentation for a soft ground is lower than that for a rigid ground. On the other hand, impact stresses are nearly proportional to the ground Young’s modulus before fragmentation occurs. For a fixed impact profile (impact angle and velocity), a soft ground tends to produce lower impact stresses. The effect of the ground Young’s modulus on impact stress is much larger than that of strain-rate-dependent strength, and a soft ground tends to reduce the potential for impact fragmentation.

If the incidence angle is equal to 90°, the system kinetic energy is almost zero when the block attains its largest penetration, at which point almost all of the system kinetic energy is transformed into strain energy. When the incidence angle is equal to 30° or less, the system kinetic energy changes negligibly and most of the system energy is transmitted by the tangential component of the velocity rather than the vertical penetration.

Energy transformation and failure occur only during impact including approach and restitution stages. After the block bounces off the ground, negligible energy transformation occurs, stored strain energy is released, kinetic energy remains relatively constant, and no further failure occurs. Friction energy loss accounts for most of the energy loss, while tensile cracking energy loss is not significant. For a softer ground condition (Young’s modulus smaller than 1 GPa), the energy dissipated in geometric damping may increase and exceed the frictional energy loss as the impact duration tends to become longer.

Some authors (Crosta et al. 2006; Giacomini et al. 2009) determine whether a block will fracture or not purely based on the comparison between the impact energy (kinetic energy at impact), and a threshold fragmentation energy, which oftentimes is obtained from the uniaxial compressive strength of the intact rock (Yashima et al. 1987). The complexity of the impact process and the many factors that control fragmentation discussed above (including incidence angle, pre-existing fractures, and ground stiffness) imply that these additional factors must be taken into account.

In the work described, the cratering of the ground during impact is not considered. However, it can greatly influence rock fragmentation and system energy loss during impact. In rock fall analysis, this system energy loss associated with cratering is typically accounted for by introducing coefficients of restitution (Crosta and Agliardi 2003; Giani et al. 2004). However, the dynamic interaction between the rock block and the ground and its effect on rock fragmentation cannot be explicitly modeled by this approach. Further investigations of ground cratering effect on rock fragmentation upon impact are highly recommended. The material damping may also have an effect on the fragmentation process. This effect is not investigated in the paper.