1 Introduction

With the rapid development of micro/nano science and technology, the micro-operation technology has been widely applied in fields of micro-electro-mechanical systems, medical engineering, precision and ultra-precision machining (Codourey et al. 1997; Russell 1993; Clark et al. 2015). In order to adapt to the micro/nano-scale operational objectives, micro/nano-transmission system is greatly demanded of high-precision, high response speed, and large stroke (Sun et al. 2013; Xu et al. 2006). Since the piezoelectric actuators (PZA) have the advantages of high-response, stable output, and non-clearance, the transmission system driven by PZA is becoming the key research field in micro/nano transmission technology (Wang et al. 2015; Yun 2008). Ma et al. developed a bridge-type mechanism based on flexure hinges, applying the elastic beam theory to analyze the influence on the displacement amplification and the natural frequency from parameters (Ma et al. 2006). Shan et al. proposed a circular-hinge-based compliant mechanism with large stroke, high transmission precision and transmission error less than 60 nm, which was analyzed by pseudo-rigid-body method (Shan et al. 2012). A PZA-driven transmission mechanism was designed by Kim et al. of which the size and displacement amplification ratio are respectively 30 mm × 30 mm × 15 mm and 30 (Kim et al. 2004). Li et al. presented a new flexure-based parallel mechanism, the decoupling is achieved in the direction of X/Y, and the transverse displacement amplification ratio can be computed as 0.46 % (Li and Xu 2008). Kim et al. put forward a microscopy scanner based on flexure hinges, of which the scanning is 100 μm × 100 μm × 100 μm (Kim et al. 2005). For the realization of high frequency control of system, a 3-Degree of Freedom (DOF) transmission mechanism was designed by Jia et al. ( 2011). In order to improve the positioning accuracy of 6-DOF transmission system, the geometrical errors were studied by Lin, of which transmission error is decreased to 10–15 % (Lin et al. 2015). Furthermore, numbers of other studies about the micro/nano-transmission system were studied all over the world.

After investigating many micro-operation systems, the motions with large stroke at the micro-scale are crucial in present and future positioning technologies, micro manipulation and optical alignment. However, the operating stroke and positioning precision of these existing systems can not satisfy the requirement in particular situations. Therefore, the objective of this paper is to present a compliant mechanism capable of translational and rotational motions with micro-scale resolution, which can achieve the larger stroke. The mechanism has potential uses in atomic force microscopy and micro/nano-scale Mask Aligner, such as the optical alignment mechanism shown as Fig. 1. The \(\Delta \theta\) and \(\Delta \delta\) can be achieved by micro/nano-transmission platform.

Fig. 1
figure 1

Potential use in optical alignment

Full size image

According to the working principle of flexure hinges (Howell 2013), a 5-DOF micro/nano-transmission platform (MNTP) with compact structure, unidirectional multi-driven mode, and large stroke is designed. The stiffness matrices, stress and strain of flexure hinge are derived by using finite element method. The posture state equations were established after the analysis of mechanics model of MNTP, and the natural frequency and sensitivity are analyzed. Finally, output simulation curves of MNPP are obtained by using MATLAB software, and the computational analysis results are verified by experiments.

2 Structure design of MNTP

According to the theory of compliant mechanism, the force and energy can be transferred by the deformation of flexure hinges, and flexure hinge can be equivalent to the elastic beam. In order to analyze the hinge deformation mechanism, the finite element method was utilized in this paper. Based on the theory of structure design, the bridge-type amplification mechanism (BTAM) was proposed, which amplifies the input displacement provided by PZA, and BTAM has a better displacement amplification ratio than other types. In order to obtain the maximum displacement amplification ratio of BTAM, the optimal structure parameters of BTAM were obtained by using the optimization design. Finally, the mechanism with large stroke is designed as shown in Fig. 2, in which the structure sketches of BTAM I and BTAM II were expressed by the dashed line. The structure dimension is 266 mm × 266 mm × 82 mm. A completely symmetric distribution with MNTP is presented, which can effectively eliminate the displacement coupling error. The MNTP is driven by 16 PZAs. By means of controlling different PZAs, the 5-DOF of moving in the directions of X, Y, Z, and rotation around the axes of X, Y can be achieved. The large stroke of MNTP is achieved by adopting the unidirectional multi-driven mode. In Fig. 2, the opposite structure forms are presented in BTAM I and BTAM II, which are respectively the concave type and convex type. Therefore, as the BTAM is driven by PZA, the opposite output displacements are obtained in BTAM Iand BTAM II. According to the symmetric form, the BTAM 3 is convex type, while BTAM 4 is concave type. As moving in X/Y-direction, two driven modes are designed, which are respectively the single-driven mode and double-driven mode. In single-driven mode, there is only one PZA in position 1, and in double-driven mode, there are two PZAs in positions 1 and 3. When the BTAM 1 is driven by PZA to move the working table, other BTAMs have a hindrance function on the moving of table, which can reduce the output displacement. When BTAM 1 and BTAM 3 are driven simultaneously, the hindrance function can be decreased largely and the output displacement in the X-direction is further enlarged, which is defined as the displacement compensation from single-driven to double-driven mode. In Z-direction, the table is driven by four BTAM, and the positive and negative movement can be achieved. Similarly, by using the mode of diagonal-double input in Z-direction, there is angle output to the table when rotate around the axes of X, Y. Thus, according to the working principle above, the large strokes are achieved in all motions.

Fig. 2
figure 2

Geometrical model of MNTP

Full size image

3 Mechanics analysis of BTAM

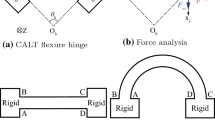
A completely symmetrical structure of BTAM is presented, and each rigid component is connected by flexure hinge without clearance and friction. The mechanics model including geometrical parameters and external loads of flexure hinge is shown as Fig. 3, where a denotes the width, b denotes the length, t denotes the thickness. The Cartesian coordinate frame is utilized in the neutral layer, where the origin is located at node 1, and the X- and Y-axis are respectively along the transverse axis and longitudinal axis of flexure hinge. This coordinate system is defined as local coordinate system. According to the deformation principle, the displacements and external loads of node i in the local coordinate are written as:

Fig. 3
figure 3

Mechanics model of flexible hinge element

Full size image
$$\left\{ {\begin{array}{*{20}c} {\left[ {\delta_{i} } \right] = \left[ {\begin{array}{*{20}c} {y_{i} } & {z_{i} } & {\theta_{xi} } \\ \end{array} } \right]^{T} } \\ {\left[ {F_{i} } \right] = \left[ {\begin{array}{*{20}c} {F_{y}^{i} } & {F_{z}^{i} } & {M_{x}^{i} } \\ \end{array} } \right]^{T} } \\ \end{array} } \right.,$$
(1)

where \(y_{i}\) and \(z_{i}\) are respectively the displacement of node i in y- and z-direction, \(\theta_{{x_{i} }}\) is the rotation angle around x-axis, \(F_{y}^{i}\) and \(F_{z}^{i}\) are respectively the external force of node i in y- and z-direction, and \(M_{x}^{i}\) is the bending moment around x-axis.

3.1 Stiffness of flexure hinge

During the process of elastic deformation, there are two deformation states of bending and tension in flexure hinge. In order to derive the stiffness of flexure hinge, the stiffness matrices of bending and tension are respectively calculated as follows.

Assuming the displacement vectors of one point after the bending deformation in flexure hinge element are \(\bar{u},\bar{v}\). In terms of the bending deformation, the deflection, and the angle around x-axis are mainly considered. The node displacement equation of flexure hinge element is determined by:

$$\left[ {\begin{array}{*{20}c} {\bar{u}_{i} } & {\bar{v}_{i} } \\ \end{array} } \right] = \left\{ N \right\} \bullet \left\{ {\delta^{e} } \right\}$$
(2)

Thus by means of the elastic mechanics, the mechanics model of flexure hinge element is defined as:

$$\left[ {\begin{array}{*{20}c} {F_{zi} } & {M_{xi} } \\ \end{array} } \right]^{T} = K_{b}^{e} \bullet \delta^{e} ,$$
(3)

where \(\left\{ N \right\}\) and \(\left\{ {\delta^{e} } \right\}\) are respectively the shape function and node displacement, \(F_{zi}\) is the external force of hinge element node i in z-direction, \(M_{xi}\) is the bending moment of hinge element node i around x-axis, \(K_{b}^{e}\) is the bending stiffness matrix of flexure hinge element.

According to the Euler–Bernoulli beam theory, the flexure hinge is equivalent to elastic beam. By means of the principle of virtual work, the following equations can be defined:

$$\left\{ {\delta^{e*} } \right\}^{T} \left\{ {F^{e} } \right\} = \int\limits_{V} {\left\{ {\varepsilon^{*} } \right\}^{T} \left\{ \sigma \right\}} d_{V}$$
(4)
$$\left\{ {\begin{array}{*{20}c} {\left\{ {\varepsilon_{b}^{*} } \right\} = z\left[ {B_{b} } \right]\left\{ {\delta^{e*} } \right\}} \\ {\left\{ {\sigma_{b} } \right\} = \frac{12z}{{t^{3} }}\left[ {D_{b} } \right]\left[ {B_{b} } \right]\left\{ {\delta^{e} } \right\}} \\ \end{array} } \right..$$
(5)

Based on Eqs. (4) and (5), the bending stiffness matrix of flexure hinge element is derived as:

$$\left\{ {K_{b}^{e} } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{b} } \right]^{T} \left[ {D_{b} } \right]\left[ {B_{b} } \right]d_{x} d_{y} } } ,$$
(6)

where \(\left\{ {\delta^{e*} } \right\}\) and \(\left\{ {\delta^{e} } \right\}\) are respectively the vectors of node virtual displacement and node displacement. \(F^{e}\) is the external force of bending deformation,\(\varepsilon\) and \(\sigma\) are respectively the strain and stress, \(\varepsilon_{b}\) is the bending strain, z is the coordinate value of hinge element in z-direction, t is the thickness of hinge. \(\left[ {D_{b} } \right]\) and \(\left[ {B_{b} } \right]\) are respectively the elastic matrix and strain matrix of flexure hinge element bending deformation.

During the analysis of tension stiffness matrix of flexure hinge element, only the longitudinal displacement of element is considered. The mechanics model, matrices of stress and strain are respectively described by:

$$\left\{ {F_{y} } \right\} = \left\{ {K_{y}^{e} } \right\}\left\{ {\delta_{y}^{e} } \right\}$$
(7)
$$\left\{ {\begin{array}{*{20}c} {\left\{ {\varepsilon_{y}^{*} } \right\} = \left[ {B_{y} } \right]\left\{ {\delta^{e*} } \right\}} \\ {\left\{ {\sigma_{y} } \right\} = \left[ {D_{y} } \right]\left\{ {\varepsilon_{y} } \right\}} \\ \end{array} } \right..$$
(8)

According to the calculation of bending stiffness matrix, the tension stiffness matrix of flexure hinge element is derived similarly as follows:

$$\left\{ {K_{y}^{e} } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {t\left[ {B_{y} } \right]^{T} \left[ {D_{y} } \right]\left[ {B_{y} } \right]d_{y} d_{x} } } ,$$
(9)

where \(F_{y}\) is the external force of tension deformation, \(K_{y}^{e}\) is the tension stiffness matrix of hinge element in y-direction, \(\varepsilon_{y}\) is the tension strain. \(\left[ {D_{y} } \right]\) and \(\left[ {B_{y} } \right]\) are respectively the elastic matrix and strain matrix of flexure hinge element tension deformation.

In summary, according to the principle of matrix-assembly, two stiffness matrices are expanded. Finally, the stiffness matrix of flexure hinge element is written as follows:

$$\left[ {K^{e} } \right] = \left[ {K_{b}^{e} } \right] + \left[ {K_{y}^{e} } \right].$$
(10)

Based on the geometrical parameters of flexure hinge element in Fig. 3, the evolution of Eq. (10) is determined by:

$$\left[ {K^{e} } \right] = \left[ {\begin{array}{*{20}c} {K_{11}^{y} } & 0 & 0 \\ 0 & {K_{22}^{b} } & {K_{23}^{b} } \\ 0 & {K_{32}^{b} } & {K_{33}^{b} } \\ \end{array} } \right],$$
(11)

where:

$$K_{11}^{y} = \frac{Eta}{{3b(1 - \mu^{2} )}} + \frac{Ebt}{{6a\left( {1 + \mu } \right)}}.$$
$$K_{22}^{b} = \frac{{Et^{3} a}}{{9b(1 - \mu^{2} )}} + \frac{{Et^{3} b}}{{45a\left( {1 + \mu } \right)}}.$$
$$K_{22}^{b} = \frac{{Et^{3} a}}{{9b(1 - \mu^{2} )}} + \frac{{Et^{3} b}}{{45a\left( {1 + \mu } \right)}}.$$
$$K_{22}^{b} = \frac{{Et^{3} a}}{{9b(1 - \mu^{2} )}} + \frac{{Et^{3} b}}{45a(1 + \mu )}.$$

\(\mu\) is the Poisson’s ratio.

The stiffness matrix calculated above is obtained in local coordinate system. By means of the principle of coordinate transformation, the stiffness matrix of flexure hinge in global coordinate system is written as:

$$\left[ {K_{g}^{e} } \right] = \left[ T \right]^{T} \left[ {K^{e} } \right]\left[ T \right].$$
(12)

Each rigid component of BTAM is connected by flexure hinge. Therefore, in terms of the geometrical model of BTAM, as shown in Fig. 4, the global stiffness matrix of BTAM is derived as follows:

Fig. 4
figure 4

Horizontal branched chain of MNTP

Full size image
$$\left[ K \right] = \sum\limits_{i = 1}^{4} {\left[ {T_{i} } \right]^{T} \left[ {K_{g}^{e} } \right]\left[ {T_{i} } \right]}$$
(13)
$$\left\{ {\begin{array}{*{20}c} {T_{i} = \left[ {\begin{array}{*{20}c} {R_{i}^{j} } & {R_{i}^{j} S\left( {r_{i}^{j} } \right)} \\ 0 & {R_{i}^{j} } \\ \end{array} } \right]} \\ {S\left( {r_{i}^{j} } \right) = \left[ {\begin{array}{*{20}c} 0 & { - r_{z} } & {r_{y} } \\ {r_{z} } & 0 & { - r_{x} } \\ { - r_{y} } & {r_{x} } & 0 \\ \end{array} } \right]} \\ \end{array} } \right.,$$
(14)

where \(T_{i}\) is the coordinate transformation matrix from the local coordinate to global coordinate system. \(R_{i}^{j}\) is the rotation matrix from i-coordinate to j-coordinate. \(S(r_{i}^{j} )\) is the anti-symmetric operator of vector \(\overrightarrow {{O_{i} O_{j} }}\).

3.2 Stress and strain

In the process of deformation, the stress and strain are developed in flexure hinge. The work performance can be greatly influenced when the actual value of stress is greater than allowable stress. Therefore, studying the stress and strain is significant. In the analysis of mechanics, the external loads of flexure hinge element are necessarily converted to equivalent load. Flexure hinge is mainly subjected to the concentrated force and bending moment, which are respectively the \(F_{y}\) along y-direction and \(M_{x}\) around x-axis. It is assumed that there is a concentrated load matrix \(\left[ P \right]\) in flexure hinge element. By utilizing the principle of virtual work, the virtual work \(W^{ *}\) of load \(\left[ P \right]\) is determined by:

$$\left[ {W^{*} } \right] = \left\{ {d^{*} } \right\}^{T} \left\{ P \right\} = \left\{ {\delta^{{*^{e} }} } \right\}^{T} \left\{ {R^{e} } \right\}$$
(15)
$$\left\{ F \right\} = \sum\limits_{i = 1}^{4} {T_{i}^{T} } P_{i} T_{i}$$
(16)
$$\left[ {R^{e} } \right] = \left[ {K^{e} } \right]\left\{ {\delta^{e} } \right\},$$
(17)

where: \(d^{ *}\) is the virtual displacement, \(\left\{ {R^{e} } \right\}\) is the equivalent load of flexure hinge element.

According to Eqs. (15), (16), and (17), the \(\left\{ {\delta^{e} } \right\}\) of element node displacement is obtained. By means of Eqs. (5) and (8), the stresses, strains of element bending and element tension are respectively derived. Therefore, the stresses, strains of flexure hinge in one point are respectively expressed as:

$$\left\{ {\begin{array}{*{20}c} {\left\{ \varepsilon \right\} = \left\{ {\varepsilon_{y} } \right\} + \left\{ {\varepsilon_{b} } \right\}} \\ {\left\{ \sigma \right\} = \left\{ {\sigma_{y} } \right\} + \left\{ {\sigma_{b} } \right\}} \\ \end{array} } \right..$$
(18)

Through the comparative analysis of stress state of each point, the maximum value of stress in the hinge is obtained as \(\sigma_{\hbox{max} }\). The results are verified by means of the First strength theory, \(\sigma_{\hbox{max} } \le \left[ \sigma \right]\), the reliability of flexure hinge in external loads can be evaluated, and the structure parameters can be optimized based on the results above.

4 Dynamic analysis of MNTP

In order to analyze the posture state of MNTP accurately, the mechanics model is established as Fig. 5. According to the displacement amplification theory of BTAM, BTAM is simplified as the spring with mass. The stiffness and mass of spring are respectively equivalent to stiffness K, mass M of BTAM. In Fig. 5a, during the working process of MNTP along X/Y-direction, there are two driven-modes which are respectively single-driven mode and double-driven mode. As the working principle shown in Sect. 2, the spring 1 takes effect in single-driven mode, and the rest springs (such as 2, 3, and 4) have a big hindrance function in the moving of x-direction, and the influence of other components is ignored since it is little. However, the spring 1 and 3 take effect in double-driven mode. In particular, spring 3 has a positive driving force in the moving of x-direction, which greatly weakens the hindrance functions taken by other BTAMs in single-driven mode. Then the displacement compensation is achieved. For analyzing the movement in Z-direction and rotational motion around X/Y-axes, the mechanics model of MNTP in X–Z is shown as Fig. 5b. By controlling the different BTAMs, the movement in Z-direction and rotation around X/Y-axes can be achieved.

Fig. 5
figure 5

Mechanics model of MNTP. a Mechanics model of MNTP in X-Y. b Mechanics model of MNTP in X-Z

Full size image

4.1 The establishment of posture state equation

According to the geometrical model and working principle of MNTP, the mass of flexure hinge is ignored, and using the Energy Method, the total kinetic energy is written as follows:

$$T = \sum\limits_{i = 1}^{6} {\frac{1}{2}\dot{u}_{i}^{T} M_{i} \dot{u}_{i} } = \sum\limits_{i = 1} {\frac{1}{2}} \dot{u}_{i}^{T} \left[ {\begin{array}{*{20}c} {m_{i} } & {} & {} \\ {} & \ddots & {} \\ {} & {} & {J_{i} } \\ \end{array} } \right]\dot{u}_{i} ,$$
(19)

where i, \(M_{i}\), \(J_{i}\), \(u_{i}\), are respectively the number, mass, moment of inertia, and displacement vector of rigid component.

The total potential energy of BTAM is mainly the elastic potential energy of flexure hinge, therefore, total potential energy of BTAM is determined by:

$$V = \sum\limits_{j = 1}^{4} {V_{j} } = \sum\limits_{j = 1}^{4} {\frac{1}{2}} v_{j}^{T} K_{j} v_{j} ,$$
(20)

where \(v_{j}\) and \(K_{j}\) are respectively the displacement vector and stiffness matrix of flexure hinge.

The Lagrange equation of elastic system is shown as follows:

$$\frac{d}{dt}\left( {\frac{{\partial \left( {T - V} \right)}}{{\partial \dot{q}_{i} }}} \right) - \frac{{\partial \left( {T - V} \right)}}{{\partial \dot{q}_{i} }} = 0\,\,(i = 1, \, 2),$$
(21)

where \(q_{i}\), T, V are the generalized coordinate, kinetic energy, potential energy of BTAM.

Taking the Eqs. (19), (20), and (21) into account, the equivalent mass \(M_{x}^{e}\) and equivalent stiffness \(K_{x}^{e}\) of BTAM in x-direction are respectively derived as:

$$\left\{ {\begin{array}{*{20}c} {M_{x}^{e} = 2m_{1} + \frac{29}{6}m_{2} + 4m_{3} } \\ {K_{x}^{e} = \frac{{2Et^{3} b}}{{9a(1 - \mu^{2} )L_{8}^{2} }} + \frac{{2Et^{3} a}}{{45b\left( {1 + \mu } \right)L_{8}^{2} }}} \\ \end{array} } \right.,$$
(22)

where \(m_{1}\), \(m_{2}\), \(m_{3}\) are respectively the mass of component in BTAM.

According to the structure form of MNTP, the mass and stiffness were assembled by using the principle of assembly. Finally, the equivalent mass and equivalent stiffness are respectively derived as follows:

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} M_{x} = M_{y} = 4M_{x}^{e} + M_{s} \hfill \\ M_{z} = 4\left( {M_{x}^{e} + M_{p} } \right) + M_{s} \hfill \\ \end{aligned} \\ {K_{x} = K_{y} = \sum\limits_{i = 1}^{4} {K_{ix}^{e} ,K_{z} = 4K_{x}^{e} } } \\ \end{array} } \right.,$$
(23)

where \(M_{x} ,M_{y} ,M_{z} ,\) \(K_{x} ,K_{y} ,K_{z}\), are respectively the equivalent mass and equivalent stiffness of X/Y/Z-direction. \(M_{s}\) and \(M_{p}\) are respectively the mass of working-table and parallel-guiding mechanism.

Besides, The Moment of Inertia \(J_{x}\), \(J_{y}\) of working-table around X/Y-axes and rotational stiffness \(K_{\alpha }^{x}\), \(K_{\alpha }^{y}\) are respectively determined by:

$$\left\{ {\begin{array}{*{20}c} {J_{x} = J_{y} = \frac{1}{4}M_{s}^{e} (R_{1}^{2} + R_{2}^{2} )} \\ {K_{\alpha }^{x} = K_{\alpha }^{y} = \frac{1}{2}K_{x}^{e} R_{1}^{2} } \\ \end{array} } \right..$$
(24)

Therefore, by building the generalized coordinate system of MNTP, the 5-DOF posture state equation of MNTP is written as the Eq. (25).

$$\left[ M \right]\textit{\"{x}} + \left[ C \right]\dot{x} + \left[ K \right]x = \left[ f \right],$$
(25)

where \(\left[ M \right]\) and \(\left[ K \right]\) are respectively the mass matrix and stiffness matrix of mechanism, C is the damping factor of raw material and f is the external loads.

According to the Eq. (25), the posture states of MNTP are obtained, the displacement curves are simulated by the MATLAB software. After the comparative analysis, the displacement compensation is obtained from single-driven to double-driven mode in X/Y-direction. It is denoted as \(\Delta x = x_{2} - x_{1}\). Besides, the computational output results in Z-direction and rotational motion around X/Y-axes are acquired.

4.2 Natural frequency

The dynamic characteristics and anti-interference ability of elastic system are often evaluated by natural frequency. In the dynamic response of elastic system, based on experience, the damping has little influence on elastic system. Thus, the natural frequency of MNTP is derived based on non-damping free vibration:

$$M\textit{\"{q}} + Kq = 0.$$
(26)

The characteristic equations are written as:

$$\left\{ {\begin{array}{*{20}c} {(K - \omega^{2} M)q = 0} \\ {\det \left( {K - \lambda M} \right) = \left| {\begin{array}{*{20}c} {k_{11} - \lambda m_{11} } & \cdots & {k_{1n} - \lambda m_{1n} } \\ \vdots & \ddots & \vdots \\ {k_{n1} - \lambda m_{n1} } & \cdots & {k_{nn} - \lambda m_{nn} } \\ \end{array} } \right|} \\ \end{array} } \right..$$
(27)

Thus, natural frequency of the i-th order is determined by:

$$f_{i} = \frac{{\lambda_{i} }}{2\pi } = \frac{1}{2\pi }\sqrt {\frac{{K_{x}^{i} }}{{M_{x}^{i} }}} .$$
(28)

In order to prevent the resonance phenomenon in the working of MNTP, the natural frequency sensitivities of each parameters are studied, which can optimize the structure of MNTP. The key parameters of MNTP are: length \(L_{2}\), width \(L_{4}\), thickness t, length of rigid component \(L_{8}\), and so on. The differential equation of Eq. (27) is obtained as:

$$\frac{\partial K}{\partial u}q + K\frac{\partial q}{\partial u} - \frac{{\partial \omega^{2} }}{\partial u}Mq - \omega^{2} \frac{\partial M}{\partial u}q - \omega^{2} M\frac{\partial q}{\partial u} = 0,$$
(29)

where: u is the variable of parameter.

$$\frac{\partial \omega }{\partial u} = \frac{1}{2}\omega^{ - 1} q^{T} \frac{\partial K}{\partial u}q - \omega q^{T} \frac{\partial M}{\partial u}q.$$
(30)

The change law of natural frequency to design parameters can be obtained from Eq. (30). If the calculation result is positive, there is a positive correlation between the increase in low-order natural frequency and the increase of design parameter. Contrarily, there is a negative correlation. By means of the analyses above, the natural mode of vibration and natural frequency of MNTP can be optimized.

5 Simulation and experiment

In order to verify the correctness of the theory established above, the MNTP is simulated and calculated with ANSYS 14.5 and MATLAB. Then, the experimental system is set up. Based on the result of finite element, the errors of theoretical and experimental value are respectively calculated.

5.1 Modal analysis

In order to indicate the potential bandwidth of MNTP, a modal analysis is performed by finite element software. The frequency values of the first-sixth order mode are shown as Table 1. The modal vibration shapes of first–third order modes are respectively the motions along the X/Y/Z-direction. The modal vibration shape of fourth order mode is the rotational motion around the axis of Z, and the vibration shapes of fifth-sixth order modes are respectively the rotational motions around the axes of X/Y. In Table 1, the natural frequency of MNTP is 85 Hz. By means of these modal analyses, the dynamic performance of MNTP can be predicted and the undesirable damage of system can be avoided.The results are verified by means of the First

Table 1 Six natural modes of MNTP
Full size table

5.2 Simulation and solution

The mechanism behaviors of MNTP are simulated by means of the finite element software. The fixed hole is selected as fixed support. And under different driving forces F, the mesh plots and output displacement states in each direction are shown in Fig. 6, which are respectively the mesh plots of MNTP, output displacement of X/Y-direction in single-driven mode, output displacement of X/Y-direction in double-driven mode, the output displacement of Z-direction and rotational deformation around X/Y-axes. Moreover, the visual motion behaviors of mechanism are demonstrated by finite element software.

Fig. 6
figure 6

Motion simulation diagram of MNTP. a Mesh plots of MNTP. b Output displacement of X/Y-direction in single-driven mode. c Output displacement of X/Y-direction in double-driven mode. d Output displacement of Z-direction. e Rotational deformation around X/Y-axes

Full size image

In order to obtain the computational simulation curves precisely, the Runge–Kutta method of Matlab mathematical tool box is utilized, which is a commonly used method of solving ordinary differential equations. During the simulation, the damping factor of material (Magnesium alloy) is 1.0, and the transient analyses with step input are respectively conducted. According to the relations between output force and output displacement of PZA under variable loads, by using Eq. (25), the output results in different driven forces are obtained, such as, F = 15.3 N (4 μm), 30.6 N (8 μm), 45.8 N (12 μm), 61.1 N (16 μm). The computational results are shown as Fig. 7, including output displacement of single-driven and double-driven mode in X/Y-direction under the same force, the movement displacement in Z-direction, and the rotational angle around the X/Y-axes. Particularly, the theoretical displacement compensation values from single-driven mode to double-driven mode in X/Y-direction are acquired. As a result, the theoretical values in all motions are obtained.

Fig. 7
figure 7

Displacement simulation curves of MNTP under different inputs. a Displacement simulation curves in X/Y-direction under F = 15.3 N, 30.6 N. b Displacement simulation curves in X/Y-direction under F = 45.8 N, 61.1 N. c Displacement simulation curves in Z-direction under F = 30.6 N, 61.1 N. d Angle simulation curves around X/Y-axes under F = 30.6 N, 61.1 N

Full size image

The simulation curves with a step input are shown as Fig. 7. According to the posture response curves, the displacement response of MNTP has the second-order underdamping characteristic, which has the large initial-oscillation. With the increase of driven forces, the amplitude and adjustment time are greatly increased. In Fig. 7, under the same driven forces, a further output displacement is obtained from single-driven to double-driven mode in X/Y-direction. Such as the output displacement under F = 45.8 N, it is 101.0 μm in single driven mode, while 188.64 μm in double-driven mode, thus, the displacement compensation is 87.64 μm. In Z-direction, the output displacements under F = 30.6 N, 61.1 N are respectively 132.69, 265.43 μm. Besides, under the same driven forces, the rotational angles around X/Y-axes are respectively \(10.01 \times 10^{{{ - }4}}\) rad, \(22.45 \times 10^{ - 4}\) rad.

5.3 Experiments

In order to verify the posture state characteristic of MNTP, the experiment principle diagram is shown in Fig. 8. The experimental system consists of computer, XE-500/501 of PZA controller, PZA, MNTP, and capacitance sensor. The type of PZA is PSt-40VS15, of which maximum load and stroke are respectively 4000 N, 40 μm, and the displacement resolution is 0.8 nm.

Fig. 8
figure 8

Experiment principle diagram

Full size image

The measurement range of capacitance sensor is 5 mm, and displacement resolution is ±100 nm. By using the elastic deformation of flexure hinge, the force and energy can be passed. Therefore, there is a high requirement on the elastic characteristic of material. AZ31b of magnesium alloy is chosen as the raw material. The parameters of material are shown as Table 2.

Table 2 Parameters of AZ31b
Full size table

Because the high precision of dimension in MNTP is required, and the structure of MNTP is monolithic and gapless, there is a big challenge in the construction of mechanism. However, the monolithic structure can be achieved by the Wire cut Electrical Discharge Machining (WEDM) technology. Before the construction, the reasonable positioning way and machining sequence must be considered. During the machining, a few schemes of positioning, clamping, rough machining and finish machining are set up. Then, the desirable mechanism is obtained.

Geometrical parameters of MNTP are showned in Table 3. Measurement experiment of MNTP is set up and shown in Fig. 9, where the MNTP is driven by PZAs, and displacement of working table can be measured by capacitance displacement sensor. Finally, the results of theory, finite element, and experiment are comparatively analyzed, the results are shown in Fig. 10.

Table 3 Geometrical parameters of MNTP
Full size table
Fig. 9
figure 9

Test of MNPP

Full size image
Fig. 10
figure 10

Results of theory, finite element, and experiment. a Output displacement of single-driven mode in X/Y-direction. b Output displacement of double-driven mode in X/Y-direction. c Output displacement in Z-direction. d Output angle around X/Y-axes. e Relative errors of single-driven mode in X/Y-direction. f Relative errors of double-driven mode in X/Y-direction. g Relative errors in Z-direction. h Relative errors around X/Y-axes

Full size image

During the experiment, the maximum PZA stroke is 40 μm, therefore, the ideal maximum input displacement in each end of BTAM is 20 μm. The input displacement range of BTAM is 1–20 μm. According to the Fig. 10, in the experiment, as the input displacement is in the nominal stroke of PZA, the relationship between output displacement and input displacement is approximately linear. In X/Y-direction, the displacement amplification ratio of single-driven mode is approximately 7.5–8.5, while the displacement amplification ratio of double-driven mode is approximately 13.5–15.5. When input displacement is beyond the maximum stroke of BTAM, which is 20 μm, the PZA is overloaded, therefore, the out displacement curves tend to the maximum value, and it cannot be increased. Meanwhile, under the input displacement of 1–20 μm, the theoretical, experimental, and finite element output results of all motions are respectively given in Fig. 10a–d. As is shown, when the input displacement of BTAM is 10 μm in X/Y-direction,the output displacements of theory, finite element and experiment in single-driven mode are respectively 84.4, 75.4, 59.8 μm, however, the output displacements of theory, finite element and experiment in double-driven mode are respectively 156.3, 135.9, 110.5 μm. As a result, the displacement compensations are respectively 71.9, 60.5, 50.7 μm, and the increasing rate of output displacement is approximately 80 %. In addition, when the input displacement of BTAM is 10 μm, the output displacements of theory, finite element and experiment in Z-direction are respectively 165.48, 140.26, 107.75 μm. And under the same input of BTAM, the output angles around X/Y-axes of theory, finite element and experiment are respectively \(12.41 \times 10^{ - 4}\) rad, \(10.40 \times 10^{ - 4}\) rad, \(7.25 \times 10^{ - 4}\) rad. From the results above, the mechanism behaviors of all motions are acquired.

Because of the high accuracy of finite element software, the finite element values are considered as the basis of MNTP performance analysis. As shown in Fig. 10e, f in single-driven mode, the range of error between theoretical values and finite element values is 11.34–12.36 %, and the range of error between experimental values and finite element values is −20.23 to −26.78 %. In double-driven mode, the error between theoretical values and finite element values is 14.91–15.86 %, and the error between experimental values and finite element values is −18.55 to −27.76 %. About the movement in Z-direction, the relative error between theoretical values and finite element values is 17.73–18.56 % and the relative error between experimental values and finite element values is −20.68 to −29.02 %. In the rotational motions around X/Y-axes, the relative error between theoretical values and finite element values is 19.88–20.49 % and the relative error between experimental values and finite element values is −30.29 to −38.01 %. Therefore, the Table 4 can be obtained based on the analyses above. Because of the small relative error, the computational predictions about the mechanism behavior are verified to be reasonable.

Table 4 Analysis results of MNPP
Full size table

According to the results above, the experimental values are smaller than the finite element values, and the change trends are basically same. Because of the nonlinear characteristics of the PZAs, the high temperature during the wire cut electrical discharge machining processing, by which the bending stiffness of the flexure hinge is influenced, and the measurement errors, the errors between the experimental values and finite element values can’t be ignored and the experimental values are fluctuant greatly. The finite element values are close to the theoretical values, and the relative error between them is small, which verifies the correctness of the theoretical model. It can be obtained that the working stroke of the micro/nano transmission platform is greatly improved in all motions, which is very practical.

6 Conclusions

  1. (1)

    A multi-driven, five degrees of freedom micro/nano transmission platform is designed, the deformation mechanics model of BTAM is established based on elastic mechanics, the stiffness matrix of BTAM are derived, the analysis formulas of stress and strain of flexible hinge are also derived to forecast the reliable during the working.

  2. (2)

    The mechanics model of MNTP is set up. The posture state equations of MNTP are established using Lagrange equation to predict the mechanism behavior. In order to forecast the dynamic performance and avoid the undesirable damage, a potential frequency bandwidth is analyzed. Based on the posture state equations of MNTP, the output response curves of translational and rotational motions are acquired using the Matlab simulation to obtain the computational predictions.

  3. (3)

    The mechanism with monolithic structure is machined by the wire cut electrical discharge machining technology. In order to verify the computational analyses and demonstrate the behavior of motion, the simulation by finite element software and experiments are conducted. The theoretical values, finite element values and experimental values are comparatively analyzed from the experiments, especially the output results of X/Y-direction in single-driven and double-driven mode. The change trends are basically same and the relative errors are small, by which the theory is verified. Therefore, the large stroke of translational and rotational motion can be achieved. Particularly, the larger working stroke of movement along X/Y-axes in double-driven mode is acquired. Finally, according to this study, a reference basis of large stroke micro platform is provided, and this paper makes a contribution to the development of micro-operation systems.

7 Acknowledgements

This study was funded by the National Natural Science Foundation of China (51275537), the Independent Research Fund of State Key Laboratory of Mechanical Transmission (No. SKLMT-ZZKT-2012 MS 05), the Open Foundation of Shang Hai Key Laboratory of Spacecraft Mechanism (SM2014D201).