1 Introduction

Micro-electro-mechanical systems (MEMS) technology is advancing rapidly due to its outstanding performance. Small-size and low-cost MEMS switches have been widely applied in commercial and military fields, such as telecommunication, radar, RF and defense systems, etc. (Li et al. 2012; Kim et al. 2012). In particular, MEMS acceleration switches can respond rapidly in specific applications without power consumption. For instance, Wang et al. (2013) developed a low-G horizontally-sensitive inertial micro-switch which switches on when an acceleration threshold is met. Fu et al. (2013) presented a novel MEMS inertial switch used for power management, which can be integrated with detection and control systems without power consumption. Deng et al. (2013) reported an inertial micro-switch based on nonlinear-spring shock stopper which can reduce contact bouncing. Ma (2013) and Kim et al. (2013) also designed several inertial switches which are capable to adjust the acceleration threshold.

Electrical contact performance is one of three key parameters of the MEMS acceleration switch (The other two are response time and contact reliability respectively) (Zhou et al. 2013). Contact resistance plays a key role in electrical performance and depends on sample material, contact pressure, temperature, structure design, surface cleanliness, roughness and flatness (Zhou et al. 2013). Greenwood, et al. (1966) put forward a classic theory of elastic contact, which introduced an item named ‘elastic contact hardness’, a composite quantity depending on the material properties and surface topography. Li et al. (2012) presented an electrical contact resistance model and pointed out that the contact resistance is a function of contact load. Jensen et al. (2005) explored contact heating in the RF MEMS switch and demonstrated that it can reduce the contact resistance significantly. In addition, mechanical cycling would increase the contact resistance because of the insulating film on surface. Broue et al. (2010) proposed a new method to investigate the micro-scale contact mechanism and indicated that the material is a key issue of contact resistance. Jackson et al. (2012) presented the multiple scales of roughness is significant when analyzing the contact resistance. Liu et al. (2011) reported a novel contact model by introducing a micro-spring structure and shown that Pt–Au contact is better than Au–Au contact.

Although many researchers have studied electrical contact performances (Zhou et al. 2013; Greenwood and Williamson 1966; Jensen et al. 2005; Broue et al. 2010; Jackson et al. 2012; Liu et al. 2011; Greenwood and Tripp 1970a; Whitehouse and Archard 1970; Almqvist et al. 2007), MEMS devices fabricated by UV-LIGA technology receive little attention. In this paper, we expand the contact resistance model to evaluate the contact model with a focus on electrical contact performance of a UV-LIGA acceleration switch.

2 Micro-contact theory

2.1 Contact of single asperity

Although contact mechanism has been studied for several decades, new challenges exist on the micro-scale. The micro-scale contact is physically different from macro-scale contact due to the relative size of asperities in two cases (Broue et al. 2010). The surface topography is significant in micro scale, and the real contact area is much smaller than the nominal surface. Therefore, the single asperity contact model must be investigated firstly. After this, the total contact resistance can be derived by analyzing the asperity distribution and applied load on the contact surface. Figure 1 shows a contact between an asperity and a rigid flat.

Fig. 1
figure 1

Contact between an asperity and a rigid flat

Full size image

As shown in Fig. 1, r is the summit radius of asperity, ω is the deformation under the contact pressure load P and a is the radius of contact area which is supposed in a circular shape.

For the purpose of simplification, the rough contact between two electrodes of the MEMS acceleration switch can be replaced by a smooth rigid flat in contact with equivalent rough surface. In addition, the multiple asperities can be replaced with simple geometrical shapes (Kogut and Etsion 2002, 2003).

The contact resistance is mainly related to the parameters of conductivity K, the total real contact area A, the load P and electron mean free path λ which is used to classify the contact resistance model by analyzing the relationship between it and the radius of real contact area.

The electron mean free path λ is the average distance traveled by an electron between successive impacts which determine its direction, energy and other particle movement. It is a significant parameter of contact resistance. In 1901, Thomson proposed λ by using an assumption that the probability of an electron scatted into any solid angle dw is dw/2π when it collides with the surface of the film (Fuchs 1938). Figure 2 shows the electron mean free path λ in a thin film.

Fig. 2
figure 2

Electron mean free path λ in a thin film

Full size image

As shown in Fig. 2, the electron free path λ changes with the angle θ between the direction of motion and z-axis and is given by (Fuchs 1938).

$$ \lambda = \left\{ {\begin{array}{ll} {(t - z_{0} ){/}\cos \theta } & {(0 \le \theta \le \theta_{1} )} \\ {\lambda_{0} } & {(\theta_{1} \le \theta \le \theta_{0} )} \\ { - z_{0} {/}\cos \theta } & {(\theta_{0} \le \theta \le \pi )} \\ \end{array} } \right. $$
(1)

where cos θ 1 = (t − z 0)/λ 0, cos θ 0 = − z 0/λ 0, t is the thickness of the film, and λ 0 is the free path of an electron in the bulk metal. The electron mean free path \( \overline{\lambda } \) is

$$ \overline{\lambda } = \frac{1}{2t}\int_{0}^{t} {dz} \int_{0}^{\pi } {\lambda \sin \theta \;d\theta } = \frac{t}{2}\left[ {\log \frac{{\lambda_{0} }}{t} + \frac{3}{2}} \right] $$
(2)

When t → ∞, \( \overline{\lambda } \) is the mean free path of the bulk metal.

In 1891, Maxwell (1891) proposed a classic theory on contact resistance. He assumed the contact area was circular with radius a m and proposed the contact could be taken as an ohmic contact when λ ≪ a. The complex scattering mechanism plays a leading role in this case and the contact resistance is

$$ R_{m} = \frac{1}{{2\;a_{m} \;K}} $$
(3)

In 1934, Knudsen (1934) reanalyzed Maxwell’s theory and proposed the Maxwell voltage which can be considered as a discontinuous function for the minimum resolution of λ, but could be replaced by a statistical distribution function when λ ≫ a. Ohm’s Law is not applicable in this case and the contact resistance model is

$$ R_{k} = \frac{4\lambda }{{3\pi \;K\;a_{k}^{2} }} $$
(4)

where a k is the circular radius of contact area. Little (1959) and Sharvin (1965) also contributed to the contact resistance theory.

In 1966, Wexler (1966) put forward a correction factor which should be introduced to Ohm’s Law prediction when the mean free path λ and the contact radius a are in the same order. Electricity and heat are transported by electron to phonons which are dominated by elastic scattering in this case. The contact resistance can be derived by a more precise interpolation function and its model is (Sharvin 1965)

$$ R_{w} = \gamma \left( {\frac{\lambda }{a}} \right)\frac{1}{{2a_{m} \;K}} + \frac{4\lambda }{{3\pi \;K\,a_{k}^{2} }} = \gamma \left( {\frac{\lambda }{a}} \right)R_{m} + R_{k} $$
(5)

where γ (λ/a) is the interpolation function which determines the ratio between the two resistance regimes (\( R_{w} (\frac{\lambda }{a} \to 0) = R_{m} \) and \( R_{w} \;(\tfrac{\lambda }{a} \to \infty ) = R_{k} \)) (Wexler 1966). To simplify the interpolation function, Nikolić and Allen (1999) numerically calculated it with an accuracy of 1 % based on Wexler’s study. The corresponding first-order Padeˊ fit is

$$ \gamma_{fit} \left( {\frac{\lambda }{a}} \right) = \frac{{1 + 0.83\;({\lambda\mathord{\left/{\vphantom {\lambda a}} \right. \kern-0pt} a})}}{{1 + 1.33\;({\lambda\mathord{\left/{\vphantom {\lambda a}} \right. \kern-0pt} a})}} $$
(6)

2.2 Contact of nominally flat surfaces

For nominally flat rough surfaces, it is difficult to use Hertzian theory to calculate the real contact area (Greenwood and Williamson 1966). As mentioned before, the contact between two electrodes of the MEMS acceleration switch can be regarded as a nominally flat surface contact with a rigid flat. The contact mechanism must be analyzed to calculate the contact resistance which is related to the contact area. Some assumptions included in our model to simplify analysis, are: heights of asperities will vary randomly, all the summit radiuses are same, these asperities are in individually distribution so that they never interfere with each other, asperity summits are spherical, and these asperities deform without the bulk deformation (Li et al. 2012). Figure 3 shows the schematic of the contact model.

Fig. 3
figure 3

Contact of a rough surface

Full size image

As shown in Fig. 3, r is the summit radius, h is the mean of asperity height, l is the distance between the rigid flat and reference plane, and z is the individual height of an asperity. The asperity will contact with the rigid flat when the height z > l. The existing contact theory of distribution of asperity height mainly includes two distributions: exponential distribution and Gaussian distribution. Because of the lower accuracy of exponential distribution, Gaussian distribution is often chosen for calculation

$$ \phi (z) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left( { - \frac{{z^{2} }}{{2\sigma^{2} }}} \right) $$
(7)

where σ is the standard deviation of asperity summit height. Thus, the probability of the contact between asperities and the rigid flat is (Greenwood and Williamson 1966)

$$ p\;(z > l) = \int_{l}^{\infty } {\phi (z)\;} dz $$
(8)

The expected number of contact asperities n is

$$ n = Np = N\int_{l}^{\infty } {\phi (z)} \;dz $$
(9)

where N is the total number of asperities. Hertzian equations describe the contact behavior of an individual asperity, where w = z − l is the distance between the top of each individual asperity and the rigid flat. Thus, the expected total contact area (Greenwood and Tripp 1970a) is

$$ A = \pi \;Nr\int_{l}^{\infty } {(z - l)} \;\phi (z)\;dz $$
(10)

The expected total load P also can be obtained from Hertzian equations (Greenwood and Tripp 1970) as

$$ P = \frac{4}{3}NE^{\prime } r^{\frac{1}{2}} \int_{l}^{\infty } {(z - l)}^{\frac{3}{2}} \phi (z)\;dz $$
(11)

where \( E^{'} = \frac{{E_{1} \;E_{2} }}{{E_{1} (1 - v_{2}^{2} )\; + \;E_{2} (1 - v_{1}^{2} )}} \) is the called ‘plane-stress modulus’ of the contact material, E 1 and E 2 are elastic modulus of two contact surfaces, v 1 and v 2 are their Poisson’s ratio respectively. From Eqs. (10) and (11), the area of contact can be predicted from the load according to the conventional hardness for plastic contact. As mentioned previously, the asperities are distributed and all resistances are in parallel (see Fig. 4).

Fig. 4
figure 4

Parallel resistance model

Full size image

As shown in Fig. 4, each asperity can be seen as a resistance and the current flow through the parallel asperities. Thus, the total resistance is

$$ R_{total} = \frac{1}{{\sum\nolimits_{i = 1}^{n} {G_{i} } }} $$
(12a)

where G i (i = 1, 2, 3…, n) is the conductance of each pair of two asperities. Assuming the asperity heights fit the Gaussian distribution, the total contact resistance is

$$ R_{total} = \frac{1}{{N\int_{l}^{\infty } {G\;\varphi (z)\;dz} }} $$
(12b)

For Maxwell’s contact model, the expected total contact resistance R mt can be expressed as following according to \( a_{{}} = \sqrt {rw} \) and w = z − l

$$ R_{mt} = \frac{1}{{G_{mt} }} = \frac{1}{{2NKr^{\frac{1}{2}} \int_{l}^{\infty } {(z - l)}^{\frac{1}{2}} \;\varphi (z)\;dz}} $$
(13a)

For Knudsen’s contact model, the expected total contact resistance R kt is

$$ R_{kt} = \frac{4\lambda }{{3\pi NKr\int_{l}^{\infty } {(z - l)\;\varphi (z)\;dz} }} = \frac{4\lambda }{3KA} $$
(13b)

For Wexler G’s contact model, the expected total contact resistance R wt is

$$ R_{wt} = \frac{{\int_{l}^{\infty } {[(z - l)^{\frac{1}{2}} \;\varphi (z) + 0.83\lambda ]\;dz} }}{{\int_{l}^{\infty } {[(z - l)^{\frac{1}{2}} \;\varphi (z) + 1.33\lambda ]\;dz} }}R_{mt} + R_{kt} $$
(13c)

From Eqs. (13a, 13b, 13c), it is known that the contact resistance is related to the expected total contact area A, expected total load P, the electron mean free path λ, the conductivity K, the number of asperity N and the asperity summit radius r.

3 Experiments

3.1 Fabrication

Nickel has been chosen to build the dual-threshold, multi-layer acceleration switch by by UV-LIGA technology due to its advantages such as superior toughness. Figure 5 summarized the process, which starts with cleaning and preprocessing a steel substrate (Fig. 51). Spin coater (KW-4A) is used to spin coat SU-8 2075 for a thickness of 20μmon the substrate (Fig. 52). Then, the steel substrate with SU-8 layer is put into an electric blast drying oven (WG-20) for prebaking. The prebaking temperature increases gradually to improve the adhesion (65 °C for 30 min, 75 °C for 30 min, and 85 °C for 30 min). Patterning (UV lithography at 500 mJ/cm2 for 2 min and SU-8 developer for 3–4 min) and electroforming (as listed in Table 1) follows to achieve the first metal layer (20 μm) (Fig. 53). Similar to the first layer with the exception of the photoresist (SU-8 2015), the second metal layer about 20μmis electroformed on the first layer (Fig. 54). A 200 nm Cu seed layer is sputtered by a sputtering system (JS3X-808) for the suspended structures in the following layer. Then the structures in the third layer (80 μm) are fabricated by using the similar process as the first layer (Fig. 55). By repeating several same steps, the next several layers can be built orderly [Fig. 5(6–8)]. To reduce the internal stress, the device has been put into a vacuum coating equipment (ZZS400, 380 °C for 2 h) for annealing. Finally, the device is treated with boiled inorganic acid to dissolve SU-8. The dual-threshold acceleration switch can be obtained eventually (Fig. 59) at the end of the process. The fabricating processes have been successfully done in the Micro-system Lab at Dalian University of Technology. The SEM picture of the multilayer nickel acceleration switch is shown in Fig. 6.

Fig. 5
figure 5

Fabrication steps for the MEMS switch

Full size image
Table 1 Electroforming solution and process conditions
Full size table
Fig. 6
figure 6

SEM picture of the MEMS acceleration switch

Full size image

The electroforming solution for preparing samples and process conditions are shown in Table 1.

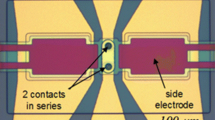
As shown in Fig. 6, the MEMS acceleration switch consists of two parts: dynamic module and electrify module. When a suitable acceleration is applied on this switch, the dynamic module will move towards in the sensitive direction to trigger the electrify module for energizing the circuit. The electrify module consists of two arc-shaped electrodes to increase contact area, but they could be viewed as two flats due to their curvatures are much larger than the summit radiuses of the asperities.

3.2 Experimental set-up

3.2.1 Main parameters measurements

As indicated previously, the contact resistance is determined by the expected total contact area A, expected total load P, the electron mean free path λ, the conductivity K, and the asperity summit radius r. On the other hand, the corresponding topographic parameters are obtained via true color confocal microscope (Carl Zeiss: Axio CSM 700).

3.2.2 Contact resistance measurements

Three requirements should be fulfilled before the measurements start (Nikolić and Allen 1999; Yunus et al. 2009) as follows:

  1. 1.

    The bulk resistance of the sample should be measured precisely.

  2. 2.

    The contact surface should be cleaned to evaluate the contact resistance accurately.

  3. 3.

    The experimental apparatus should be maintained at room temperature of ~25°C to prevent the thermal drift from affecting the results.

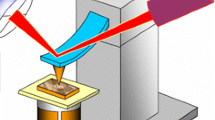
To determine the relationship between the contact resistance and load, an experimental set-up includes a microscope, a micro-control servo system, a computer and a voltmeter has been set up. The schematic layout and test set-up are shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram and test set-up of Rc measurement

Full size image

As shown in Fig. 7, the contact resistance R c was measured by external circuit and the movement of the electrode can be controlled by the micro-control servo system. An insulating layer was set between two electrodes to reduce the interference from the tip. A high precision voltmeter was used to measure the voltage across the sample. The Tip 2 is fixed and Tip 1 moves uniformly to control the deformation between two electrodes.

The contact between two rough surfaces could be elastic, elastic–plastic, and full plastic. The relationship between the load and deformation varies in different regimes (Geisse 2009). For the elastic regime, the contact load, P el , for w ≤ w c , is given by (Geisse 2009; Jackson and Green 2005)

$$ P_{el} = \left( \frac{4}{3} \right)E^{'} \left( r \right)^{\frac{1}{2}} w^{\frac{3}{2}} = P_{c} \left( {\frac{w}{{w_{c} }}} \right)^{\frac{3}{2}} $$
(14)

where w c and P c are critical deformation and critical load separately. For the elastic–plastic regime \( 1 \le \frac{w}{{w_{c} }} \le 6\;{\text{and}}\;6 \le \frac{w}{{w_{c} }} \le 110 \), the empirical expressions are (Greenwood and Tripp 1970)

$$ P_{el - pl} = P_{c} \;1.03\left( {\frac{w}{{w_{c} }}} \right)^{1.425} \left( {1 \le \frac{w}{{w_{c} }} \le 6} \right) $$
(15a)
$$ P_{el - pl} = P_{c} \;1.40\left( {\frac{w}{{w_{c} }}} \right)^{1.263} 6 \le \frac{w}{{w_{c} }} \le 110 $$
(15b)

For the fully plastic regime, the plastic contact load, P pl , is given by (Greenwood and Tripp 1970)

$$ P_{pl} = P_{c} \;4.6\left( {\frac{w}{{w_{c} }}} \right)^{{}} \left( {\frac{w}{{w_{c} }} > 110} \right) $$
(16)

By submitting Eqs. (14), (15a, 15b) and (16) into Eqs. (11) and (13a), three groups of different resistance values can be derived in three regimes. The relationships between load and resistance are shown in Fig. 10. Simultaneously, the load was held for 20 s to determine the average peak resistance. The test should be repeated for several times to understand the cyclic changes of the contact resistance.

4 Results

4.1 Topographic and material properties

The contact performance between two solids is mainly related to three material properties (elastic modulus, Poisson’s ratio and hardness) and three topographic properties (number of asperity, asperity summit radius and standard deviation of their height distribution). Figure 8 shows the confocal microscope image of the electroforming nickel surface.

Fig. 8
figure 8

Confocal microscope image of electroforming nickel surface

Full size image

From Fig. 8, the asperity density, asperity summit radius and standard deviation of asperity height can be calculated. The asperities in a certain area (1452.793 μm2) have been counted and analyzed. Figure 9 shows the distribution of asperity height.

Fig. 9
figure 9

Distribution of asperity height

Full size image

As shown in Fig. 9, the asperity height can be fitted by the Gaussian distribution, with the standard deviation of σ = 0.00604 μm. The total number of asperity within this area is N 1 ≈ 910. Therefore within the contact area between two arc-shaped electrodes, the total number of asperity is N ≈ 26,703. In addition, the asperity summit radius is found to be r = 0.2 μm. The distance between two reference planes is approximately l = 0.01–0.021 μm (Greenwood and Tripp 1970). The mechanical properties are taken to be elastic modulus E = 181.5 GPa (Li et al. 2010) and Poisson’s ratio v = 0.312 (Son et al. 2005). The electron mean free path is λ = 0.455 nm (Majjad et al. 1999) and conductivity is K = 1.43 × 107 S/m (Tanuma et al. 2011). Due to λ is much smaller than a in our device, so its contact resistance can be evaluated by Eq. (13a). Thus, the theoretical relationship between contact resistance and load can be derived from Eqs. (11) and (13a). There is no explicit relationship between the two equations, and the resistance-load characteristics will be derived in Fig. 10 in next section.

Fig. 10
figure 10

Comparison between theoretical value (three different regimes) and experimental results

Full size image

4.2 Contact resistance-load characteristics

The bulk resistance is about 1.1 Ω before measuring the contact resistance. Thus, the contact resistance is the difference between the total resistance and bulk resistance. Figure 10 shows a comparison between the theoretical predictions and the experimental results of contact resistance-load characteristics.

Figure 10 presents the relationships between contact resistance R and load P which come from the theoretical predictions (in three regimes: elastic, elastic–plastic and plastic) and experimental results. The contact resistance decrease as load increases in four cases due to the corresponding increase of the real contact area and the improvement of transfer of electrons. For elastic regime, the contact resistance value is the largest when applying a small load, but it decreases rapidly as increasing the load and it would be the smallest in three regimes. Therefore, a smallest contact resistance would be obtained using a purely elastic contact model. For elastic–plastic regime, the corresponding contact resistance is a little larger than that in the elastic regime and the discrepancy between them is not significant. For plastic regime, the contact resistance value is the largest among three regimes except when the load is small. In addition, the decreasing rate is smaller than that in other two regimes. As shown in Fig. 10, when applying a small load, the corresponding deformation of the asperity is relatively smaller, thus, the elastic contact model should be introduced to improve the accuracy. Similarly, the plastic contact model should be used with increasing load. As we shown, the theoretical prediction of contact resistance-load characteristics correlates well with the experimental results. The possible reasons for this discrepancy between them could be as follows:

  1. 1.

    Contamination such as an insulating film (Macklen 1986) on the surface increases the contact resistance;

  2. 2.

    The radiuses of all asperity summits are not ideally identical as assumed in the theoretical model;

  3. 3.

    The reference plane is not ideally flat as assumed in the theoretical model;

  4. 4.

    The errors may come from test systems, external environmental conditions and other material parameters, etc.

5 Conclusion

The contact performance of the rough MEMS acceleration switch fabricated by UV-LIGA technology has been analyzed by using an expanded micro-contact resistance model. Three different contact resistance models depending on the relationship of contact radius and electron mean free path have been analyzed. The material properties (elastic modulus E, hardness H and Poisson’s ratio v) as well as surface topographic parameters (asperity summit radius r, standard deviation of height distribution σ and the surface density of asperity) have been studied to evaluate the contact resistance-load characteristics. The theoretical prediction of contact resistance-load characteristics correlates well with the experimental results, although there exists experimental discrepancy due to the contaminations, errors from assumptions, surface oxidation and external environmental conditions.